1. Introduction
Currently, the industry is suffering a profound revolution. Different technological tools are being used intensively in factories [
1]: augmented reality, virtual twins, data mining, additive manufacturing, among others. This fact is known as industry 4.0.
Additive manufacturing (AM) was initially used to manufacture prototypes in the product development stage. Today, it is also used to manufacture: customized objects (rapid prototyping), tools for other processes (rapid tooling), small batches of fully functional parts (rapid manufacturing) [
2].
There are different technologies of AM. However, fused deposition modeling (FDM) is the most extended technology [
3,
4,
5]. The low cost of the equipment and the diversity of filaments in the market contribute to this. Although there are many materials available, polylactic acid (PLA) is still one of the most widely used in FDM [
6,
7]. There are several reasons for this [
8]: it is biodegradable, easily printed, does not give off any vapors during printing and there are PLA formulas with mechanical properties similar to acrylonitrile butadiene styrene (ABS) [
9].
For some applications, 3D printed parts must achieve minimum mechanical properties [
8,
10,
11,
12,
13]. In other cases, apart from a high tensile strength value, the parts need to have a proper aesthetic quality [
14,
15,
16]. Some authors have evaluated which factors allow achieving the best rankings in all hedonic, tactile and visual assessments of FDM 3D printed parts [
17]; in the tactile and visual evaluations, the authors conclude that the pieces with the highest scores are those with the lowest values of surface roughness. On the other hand, the surface finish is crucial when printed parts are in contact with human skin, as is the case with frame glasses [
18].
One of the motivations for this work is to determine which printing factors are the most influential in the surface finish on PLA parts printed using FDM. In the literature, you can find previous works in which the influence of different printing parameters on the surface roughness of 3D printed parts has been studied (
Table 1). However, there are printing parameters that have not yet been analyzed, such as print acceleration or flow. This is one of the main contributions of this work.
Traditionally, the experimental study of the quality of manufactured parts has been carried out with statistical tools, such as the Taguchi method and analysis of variance (ANOVA) [
19]. However, the large amount of data currently generated by industry 4.0 sensors and the need to use algorithms capable of modeling non-linear problems has made it necessary to use data mining (also known as machine learning, ML) techniques [
20,
21,
22]. The second motivation for the work is to use data mining (DM) techniques to predict the surface finish of 3D printed parts using FDM.
Razvi et al. [
23] have reviewed the existing literature on the use of DM in additive manufacturing; the papers reviewed have been grouped around four different topics: design, process optimization, monitoring and control, inspection and testing. Amand et al. [
24] have used DM techniques to predict possible defects during the configuration step in FDM 3D printing. Wu et al. [
25] have used the random forest algorithm to generate a model to predict the surface roughness of a 3D printed part from data collected by different sensors placed in the FDM printer. Sohnius et al. [
26] have employed DM techniques to predict the quality of printed parts using FDM from data obtained via the machine vision method. Mahapatra and Sood [
27] proposed the use of artificial neural networks (ANN) to determine the relationship between five input FDM parameters such as layer thickness, orientation, raster angle, raster width, and air gap with surface roughness in the top, bottom, and side surface of the acrylic nitrile butadiene styrene (ABS) built part. Boschetto et al. [
28] proposed a feed-forward neural network to fit experimental data and to determine surface roughness parameter models reliable over the entire part surface. Vahabli and Rahmati [
29] have established a robust model using empirical data based on optimized ANN to estimate the surface roughness distribution in fused deposition modeling ABS parts; this work includes four medical case studies.
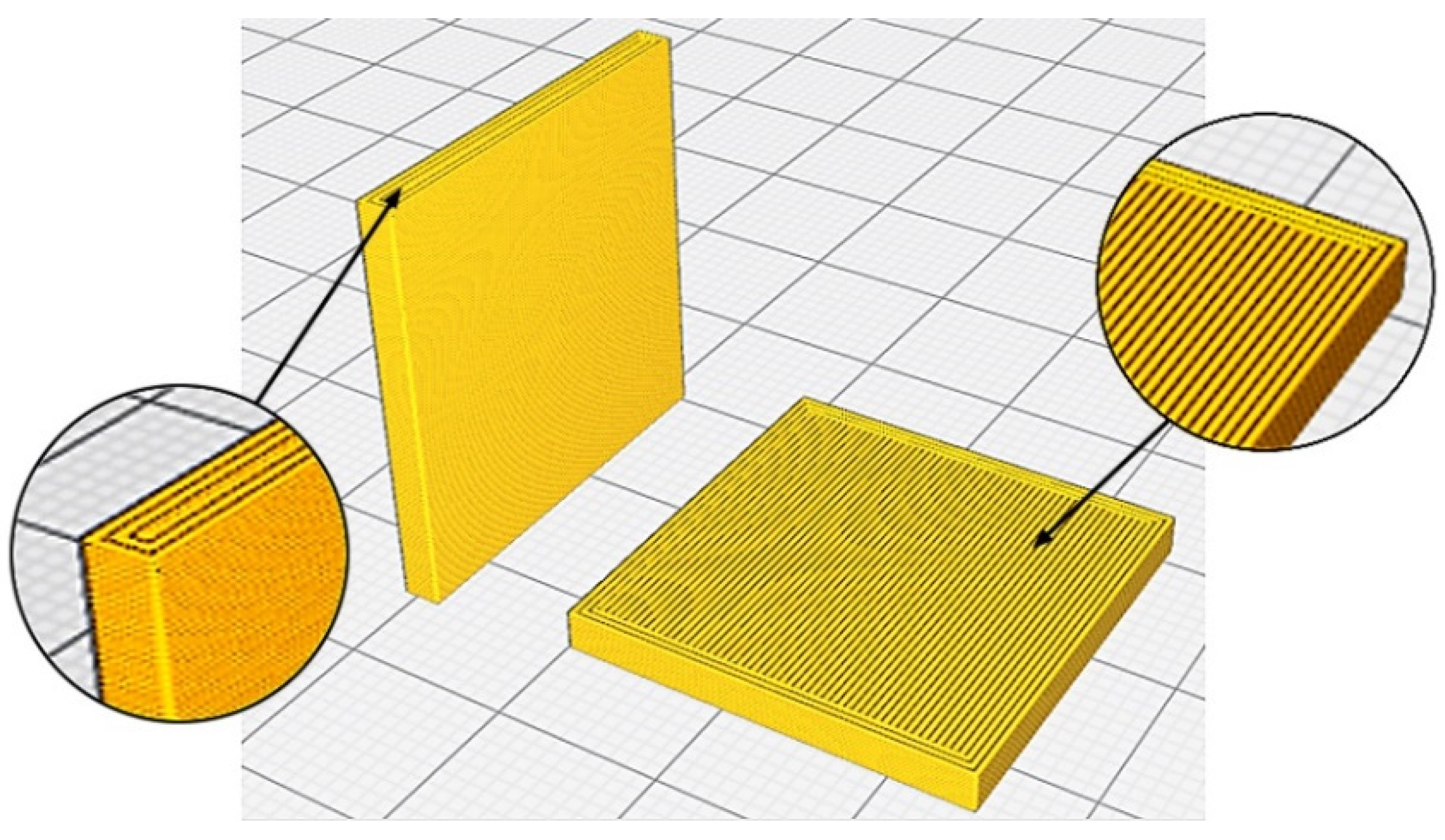
The aim of this work is to generate and validate models via data mining techniques that allow predicting the surface finish of PLA printed parts according to the selected values for the following printing parameters: layer height, extrusion temperature, print speed, print acceleration and flow. For this purpose, 27 horizontal and 27 vertical specimens have been manufactured, according to a fractional experiment design. The surface roughness of these specimens was measured. The results were used to generate and test different models via data mining algorithms (Bayes Net, naïve-Bayes, multilayer perceptron, simple logistics, sequential minimal optimization, IBk, Kstar, J48, logistic model tree and random forest). In addition, using the J48 algorithm, decision trees were generated to determine which printing parameters significantly influence the surface roughness of the parts.
As a practical application of the work, the manufacture of a frame glasses is proposed. There are standard frames on the market, which are adapted to the characteristics of an average person. However, there are people with such a facial morphology that they cannot find glasses in the optical shops. By means of 3D printing, it is possible to manufacture customized frames [
30], in biodegradable materials such as PLA [
18]. One of the most important specifications of a frame glasses is the surface finish, for aesthetic reasons and to reduce friction with the skin of the user.
4. Discussion
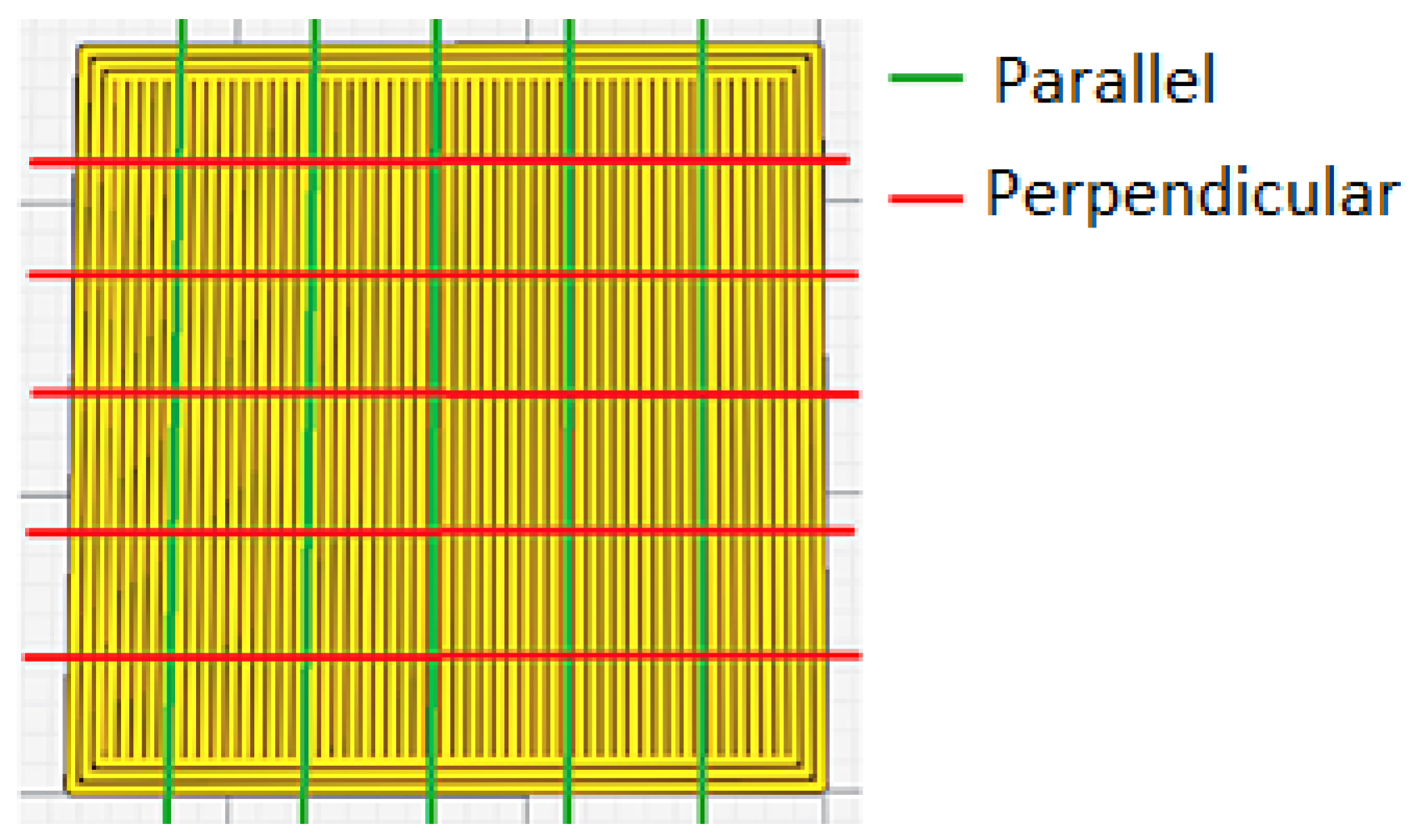
In the present work, data mining techniques have been used to generate models that allow predicting the surface roughness of parts printed in PLA using 3D FDM printing. The classifier algorithms used to generate the models have been: Bayes net, naïve-Bayes, multilayer perceptron (ANN), simple logistic, SMO (SVM), IBk (KNN), KStar, J48 (C4.5), LMT y random forest. The models have been tested by means of a cross-validation (10-folds). The percentage of correctly classified instances and the kappa statistic were used to compare these models with each other. The input variables of the study have been: print orientation, layer height (LH), extrusion temperature (T), print speed (PS), print acceleration (PA) and flow (F). The output variables have been the surface roughness measured in the direction parallel to the extrusion path (Ra,0) and in the direction perpendicular to the extrusion path (Ra,90). A total of 54 specimens have been printed for this purpose: 27 specimens were printed with horizontal orientation (XY) and the other 27 with vertical orientation (XZ).
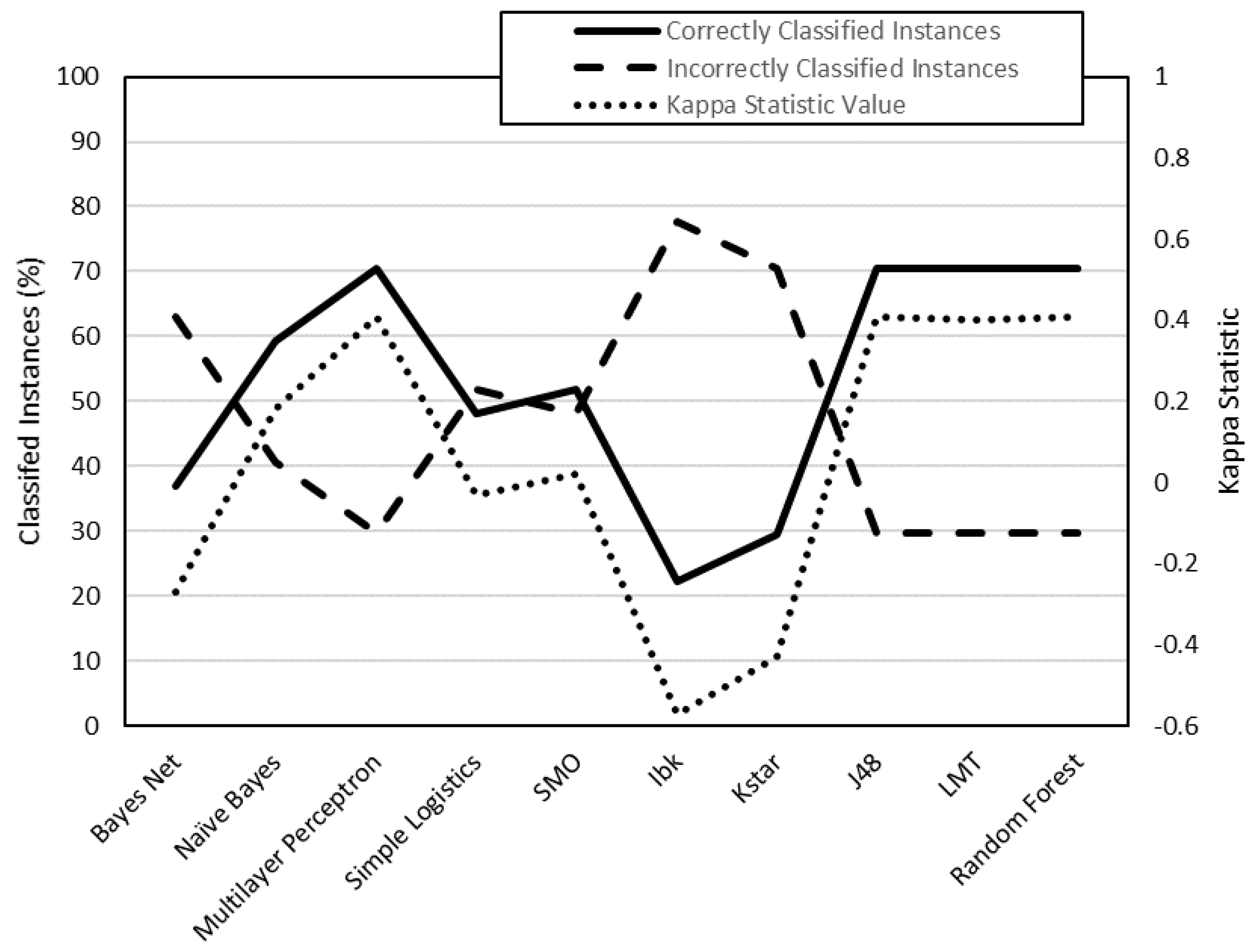
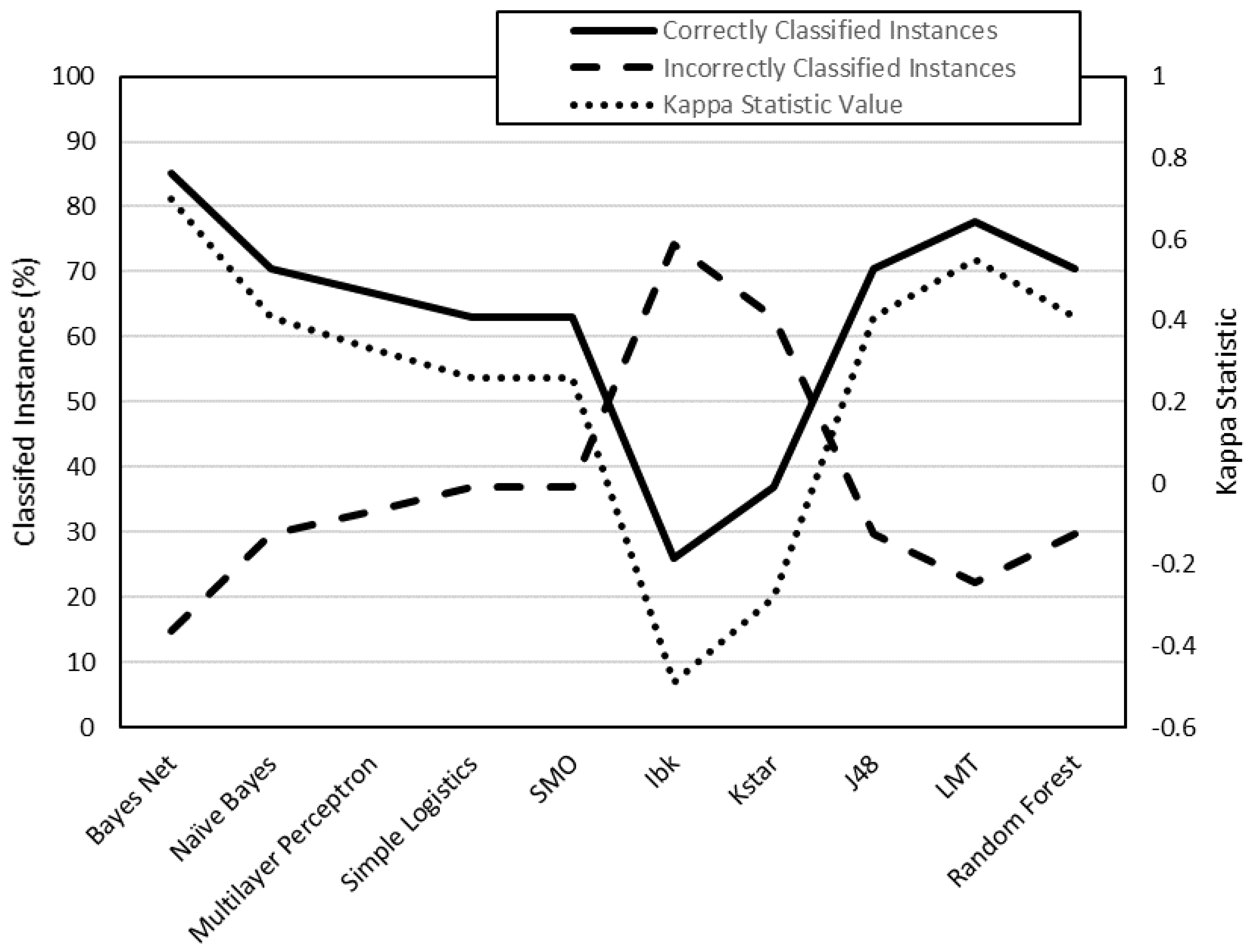
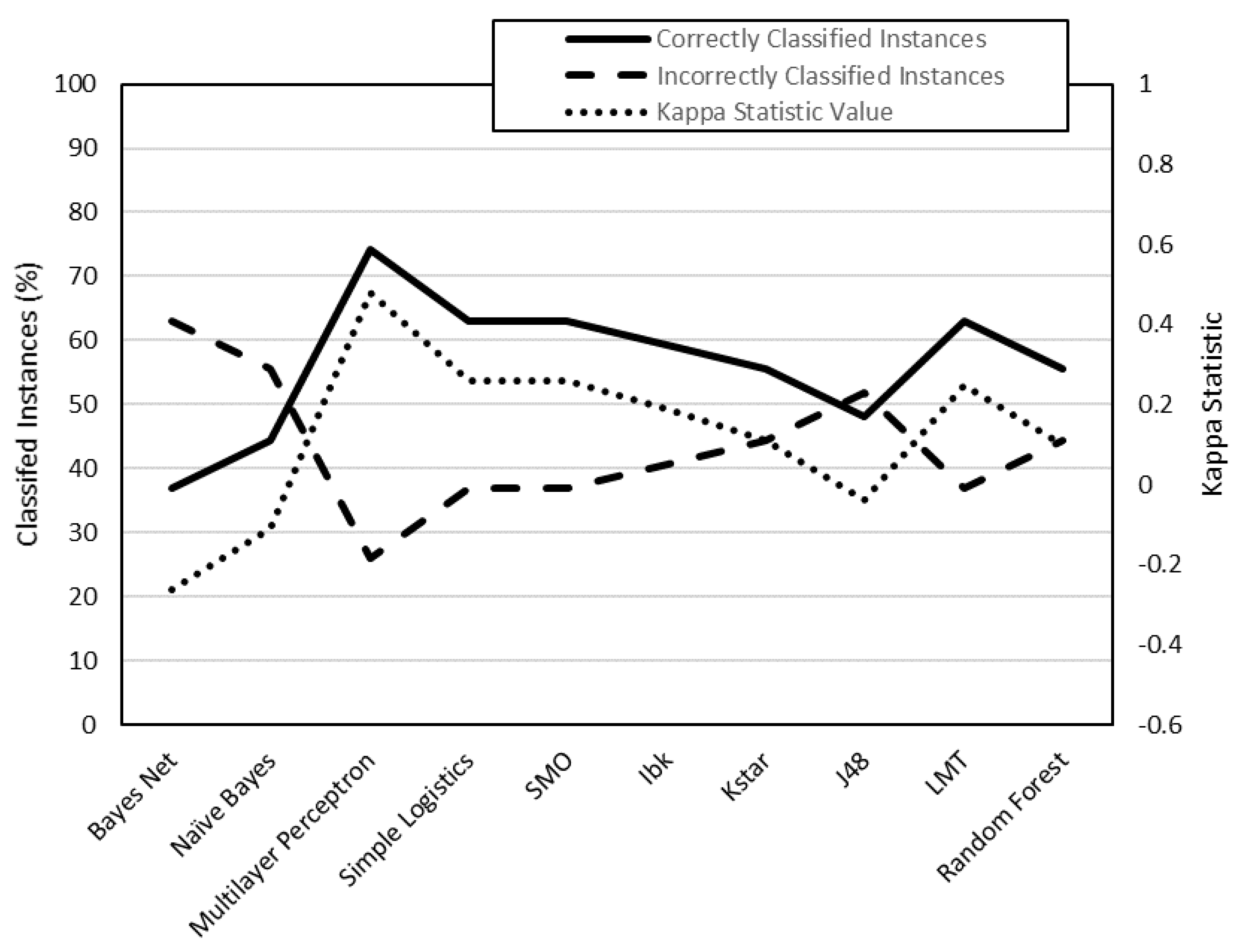
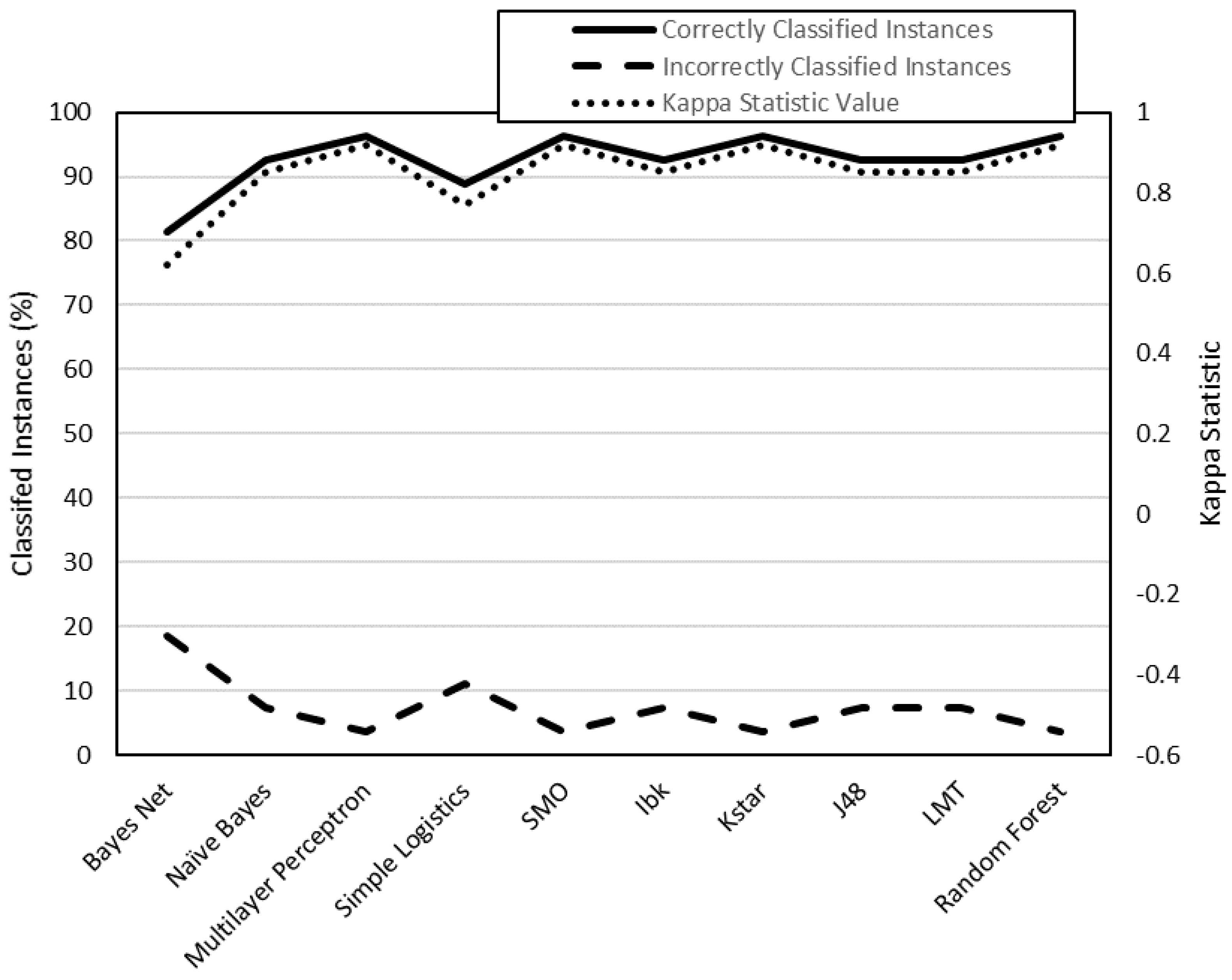
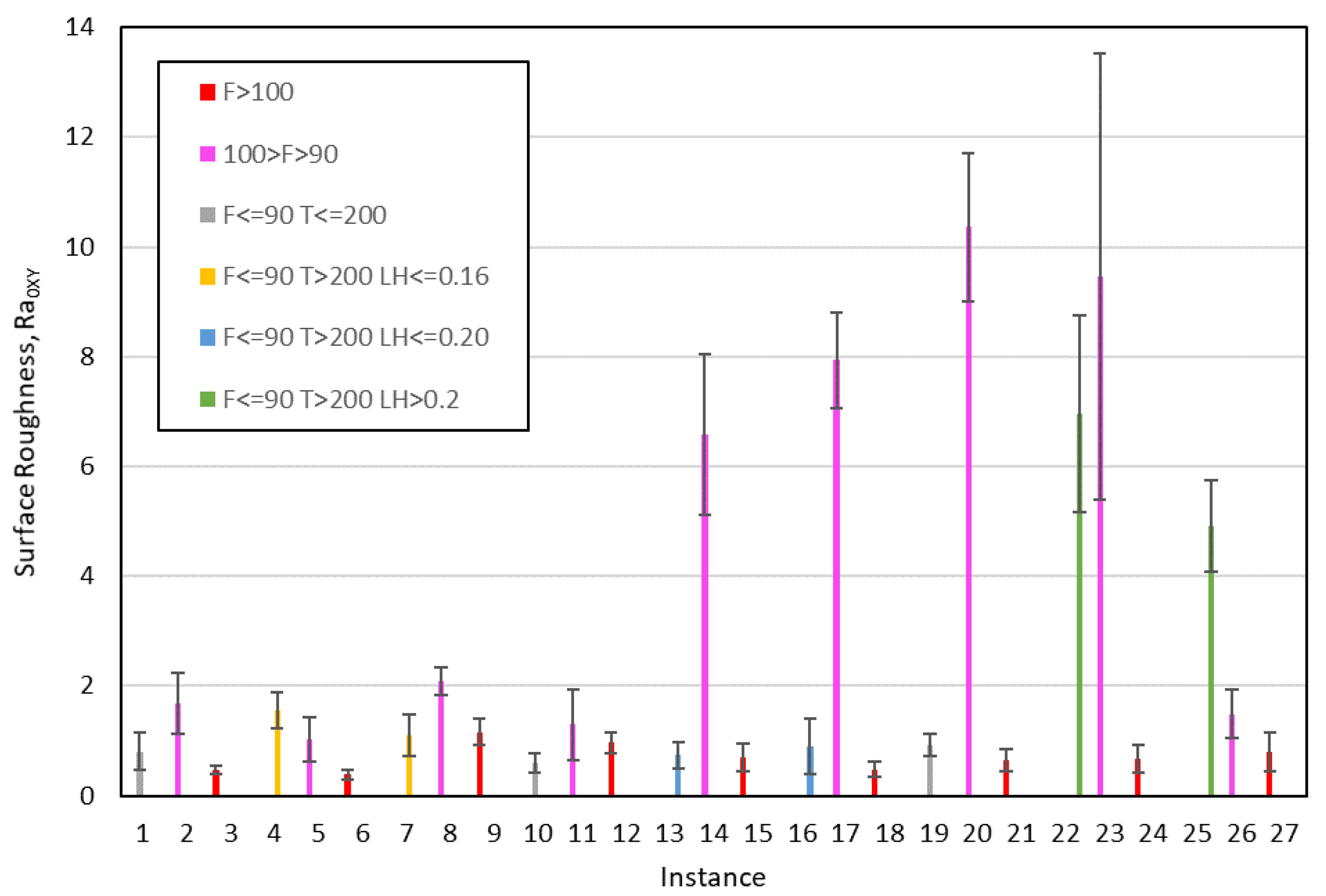
From the results shown in
Figure 3,
Figure 4,
Figure 5 and
Figure 6, it can be stated that one of the models that best classify the instances according to their surface roughness (both for horizontal and vertical specimens) is the one generated by the multilayer perceptron (artificial neural network, ANN) algorithm. In the literature there are works that also use different types of ANN to predict the surface roughness of printed parts using FDM: Boschetto et al. [
28] propose the use of a feed-forward neural network to predict surface roughness on surfaces that form different angles to the vertical, obtaining errors of less than 5%; Vahabli and Rahmati [
29] propose a similar model, using another type of ANN, capable of predicting surface roughness as a function of build angle. However, both works do not take into account the influence of printing parameters on the surface roughness obtained.
Another algorithm that has generated in the present work models with positive results has been the LMT. This fact is consistent with other works of literature: Landwehr et al. [
46] concluded that LMT produces more accurate classifiers than J48 (C4.5), CART, logistic regression, models tree, functional trees, naïve Bayes trees and LOTUS. The problem with this algorithm, like ANN, is that it does not generate a model that can be visualized or easily understood.
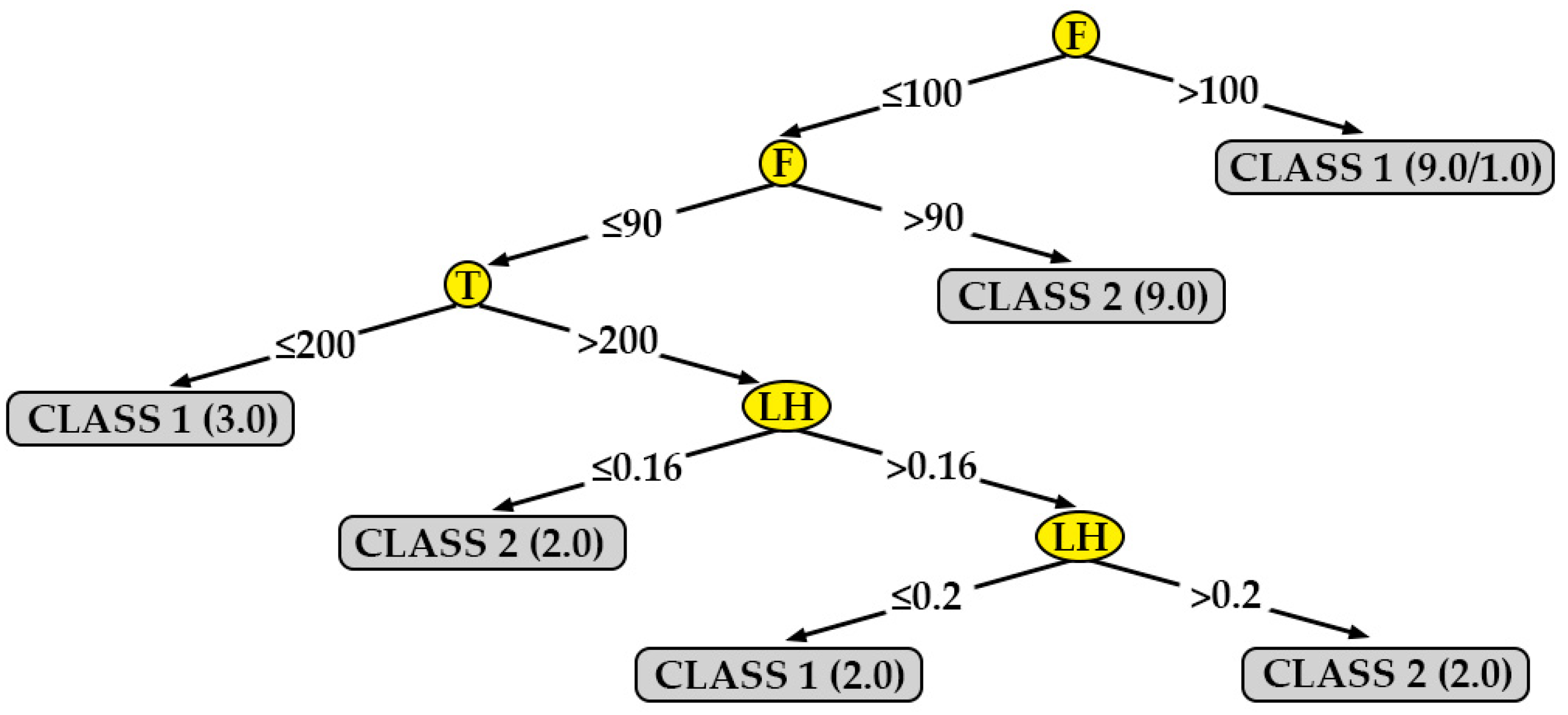
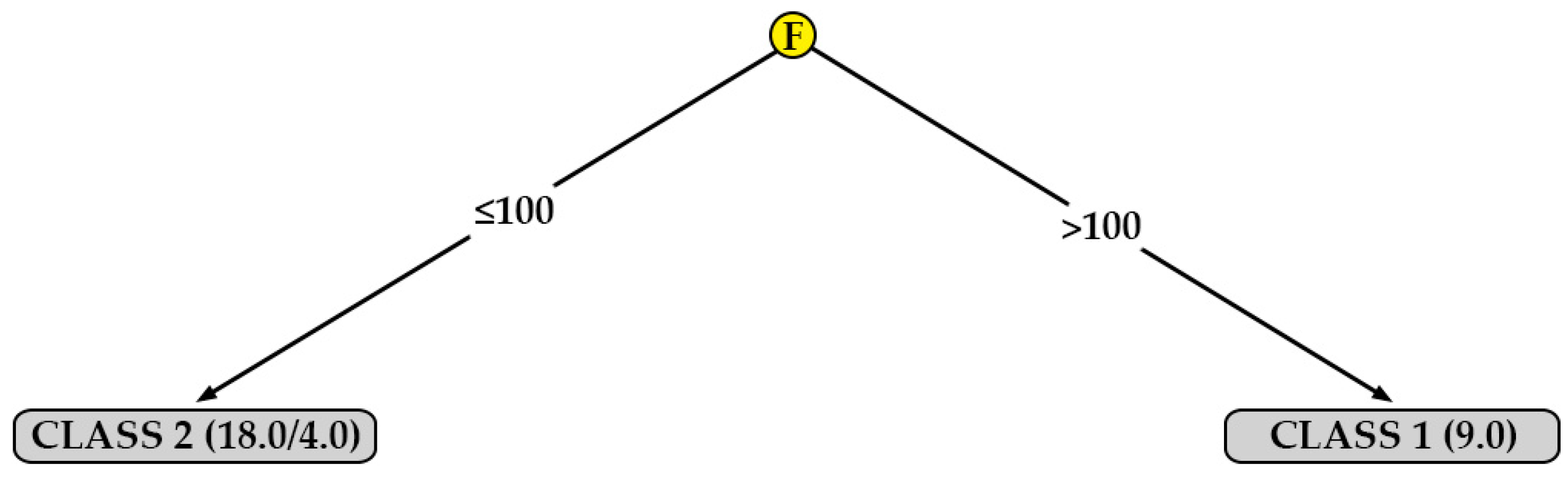
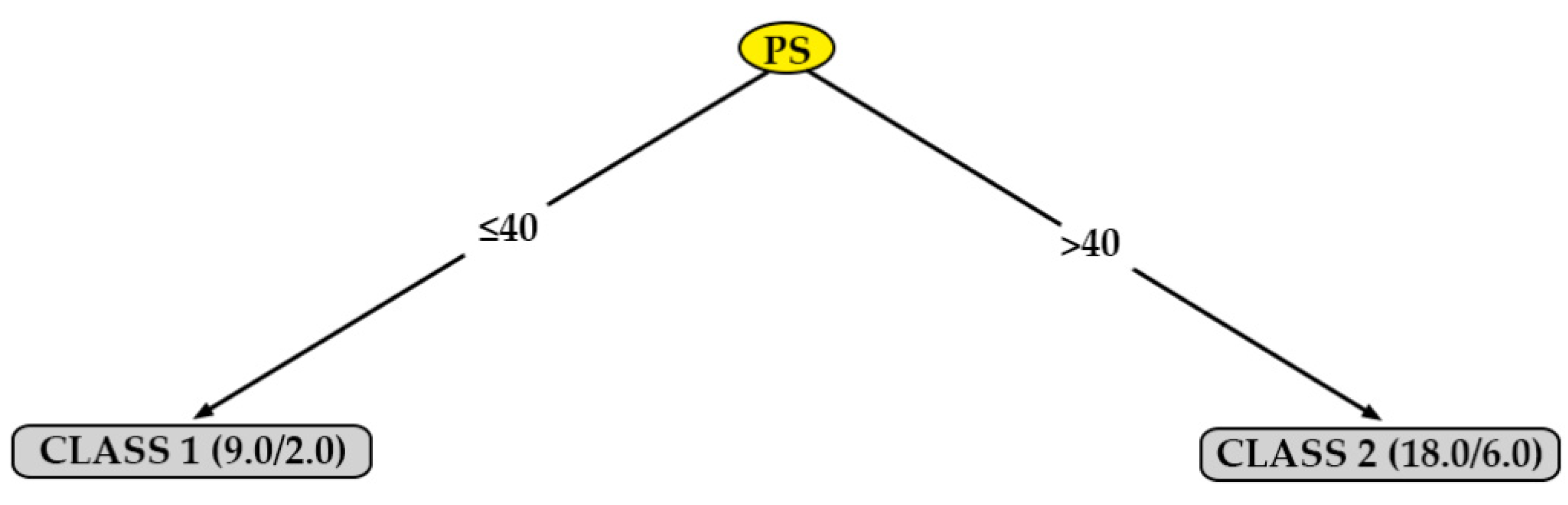
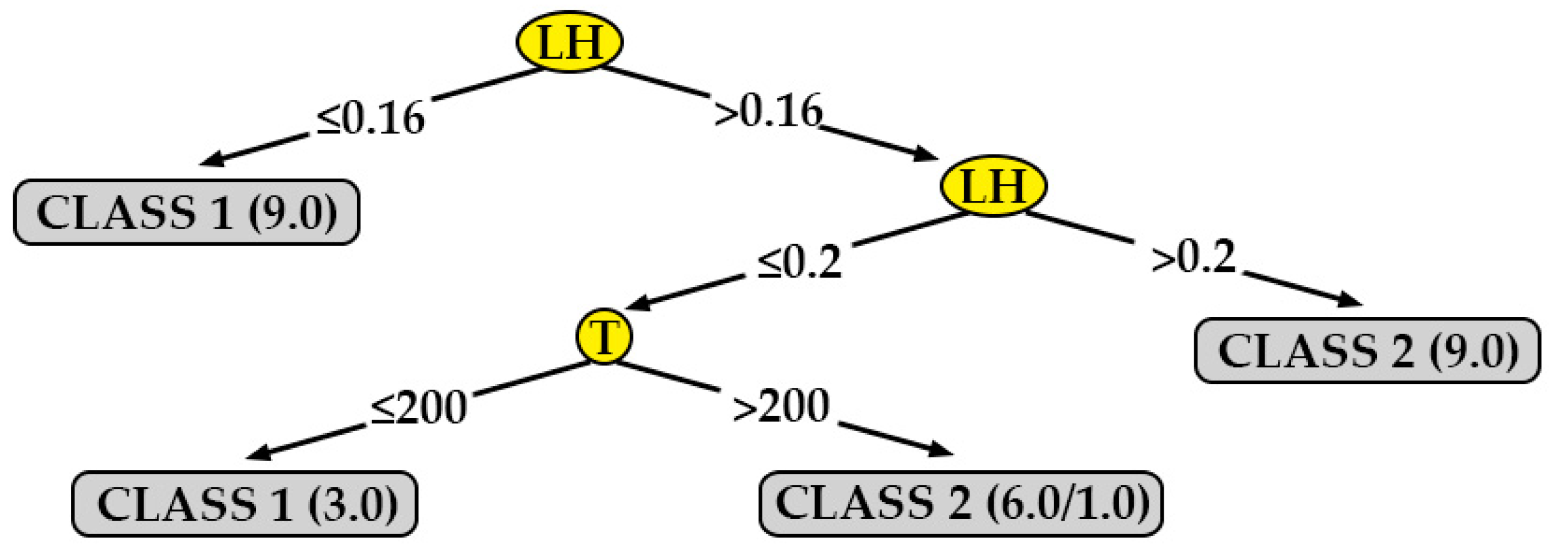
One algorithm that generates a model that can be represented graphically is J48.
Figure 7,
Figure 8,
Figure 9 and
Figure 10 show the decision trees generated by this algorithm for the different measured surface roughness. From the models obtained,
Table 10 has been drawn up. This table summarises the printing variables that must be taken into account in order to obtain a lower surface roughness (class 1). From these decision trees, a basic configuration can be established to obtain a good surface finish simultaneously on XY and XZ orientation, for perpendicular and parallel direction to extrusion path: F equal to 110 % and LH equal to 0.16 mm.
In addition to the above, the following statements can be made:
The decision tree models can be easily interpreted by any 3D printer operator (they are not black-box models) [
47]. For this reason, they are used for modeling other manufacturing processes in literature [
48]. This is important in the current industry that is very concerned with visual management.
Two parameters that had not been previously studied in the literature on PLA specimens were included in this work: print acceleration and flow. While print acceleration seems not to have an influence in any of the cases studied, the flow is revealed as an important parameter in the surface roughness obtained in XY orientation. This result is consistent with those obtained by the authors in similar tests performed on PETG [
47].
In R
a,90,XZ, the most influential parameters are layer height. These results coincide with those obtained by other authors: García-Plaza et al. [
31] state that the layer height parameter is the most influential in upright and on-edge positions (similar to the XZ orientation in the present paper).
Three of the four models generated have achieved a ’moderate’ or ’almost perfect’ rating, according to their kappa statistic values. This fact supports the validity of the results obtained in the present work, as shown in
Figure 11 and
Figure 12. The model generated for R
a0,XZ did not pass the evaluation.
The results obtained in the present work have been used to print a frame glasses in PLA via FDM. A-frame glasses is the perfect example of a customized part/assembly. There are previous works in the literature focused on this topic [
18], although they have not studied the printing parameters that allow to achieve a better surface finish.
5. Conclusions
In the present work, data mining algorithms have been used to generate from experimental tests models capable of predicting the surface roughness of horizontal and vertical parts printed in PLA using FDM. MLP and LMT are the algorithms that obtain the best results in cross validation tests.
The J48 algorithm obtains almost perfect results in one of the models and moderate results in two others. However, unlike MLP and LMT, this algorithm generates decision trees in which it is possible to see which print parameters influence surface roughness.
Of the five parameters studied, two have proved to be the most important for obtaining a better surface finish in XY and XZ specimens: flow and layer height. A flow equal to 110% and a layer height equal to 0.16 mm provides the lowest values of surface roughness (Ra) in PLA printed specimens in XY and XZ orientation. Using these values, a frame of glasses has been printed, as a practical and direct application of this work.