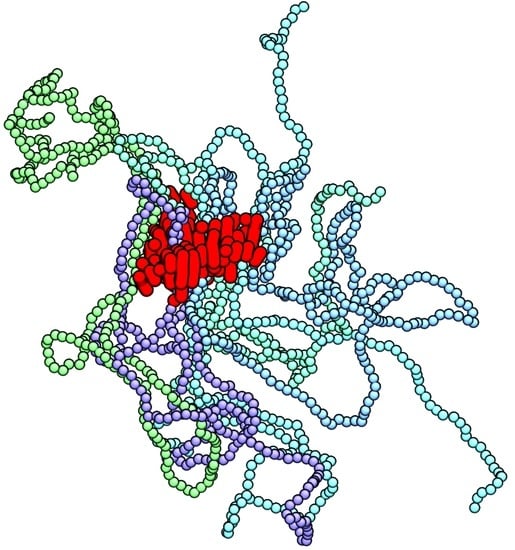
Monodisperse Polymer Melts Crystallize via Structurally Polydisperse Nanoscale Clusters: Insights from Polyethylene
Abstract
1. Introduction
2. Methods
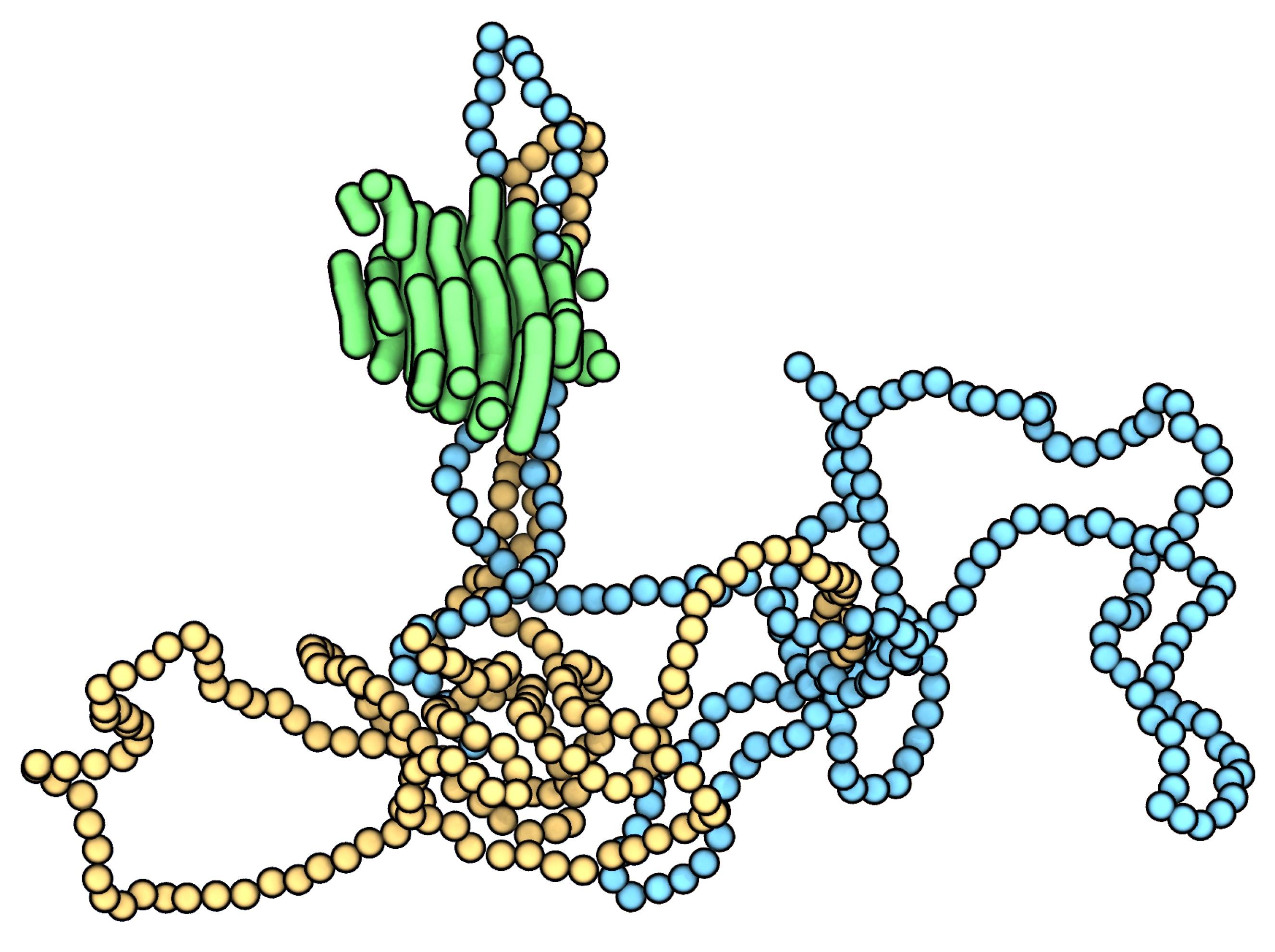
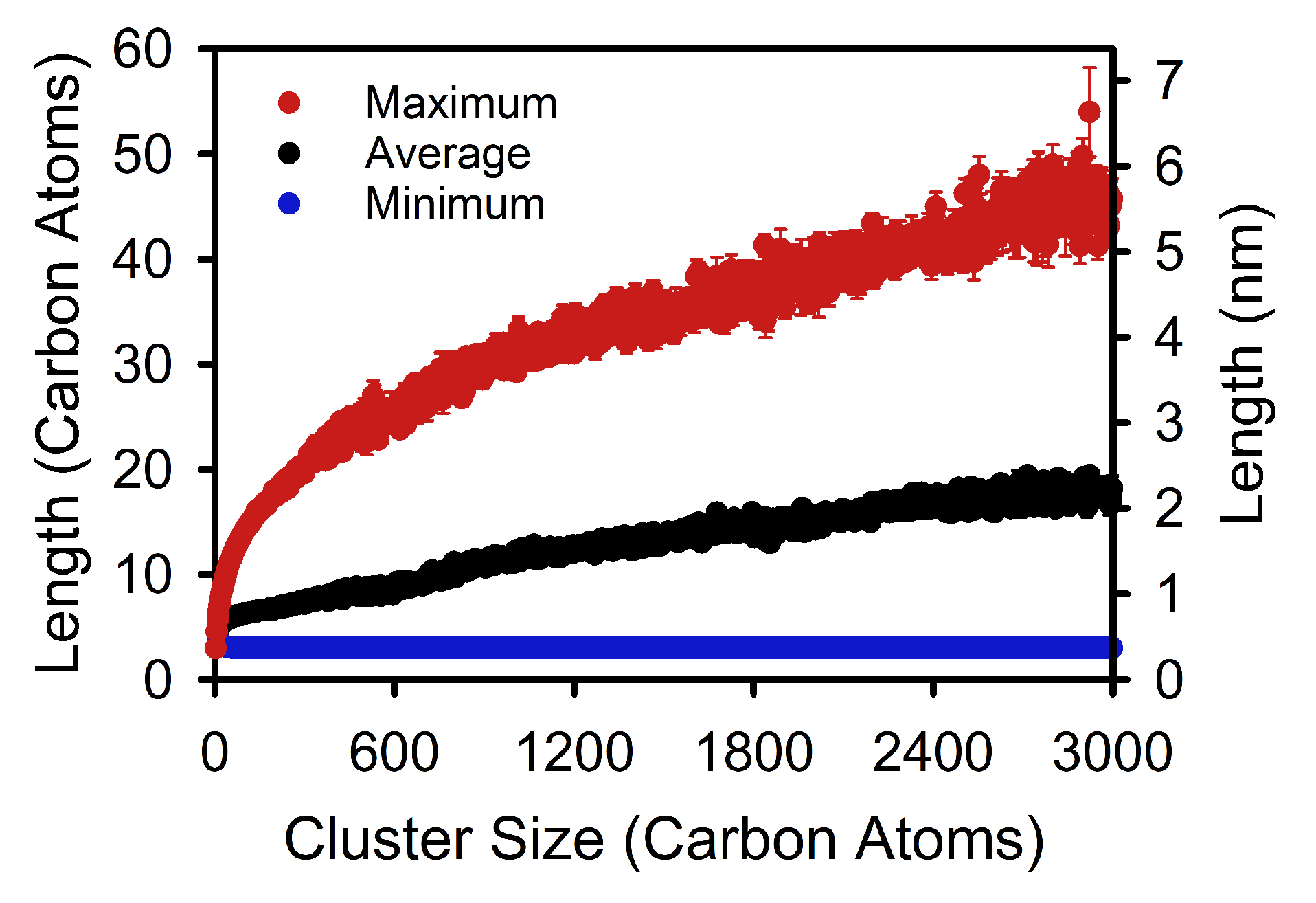
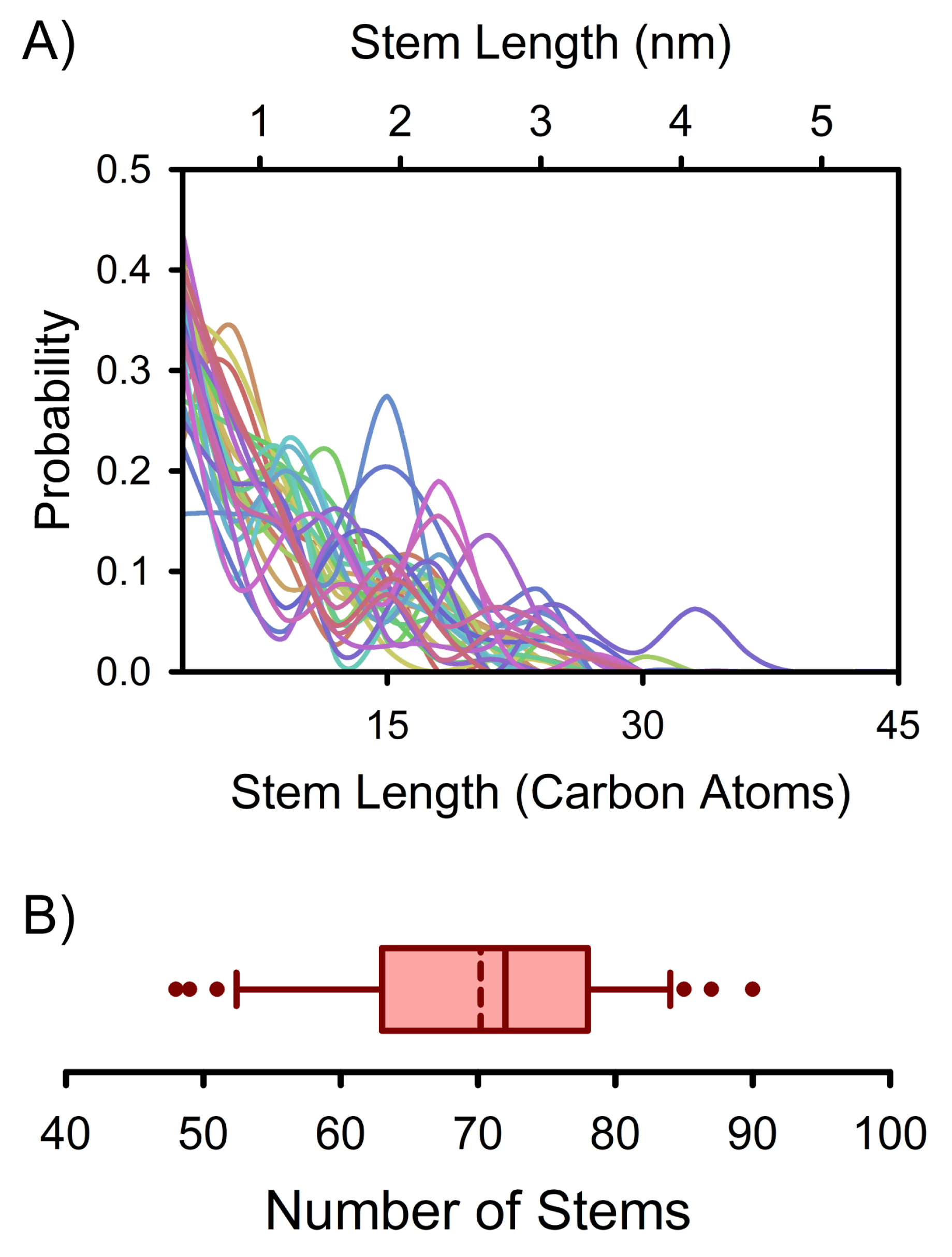
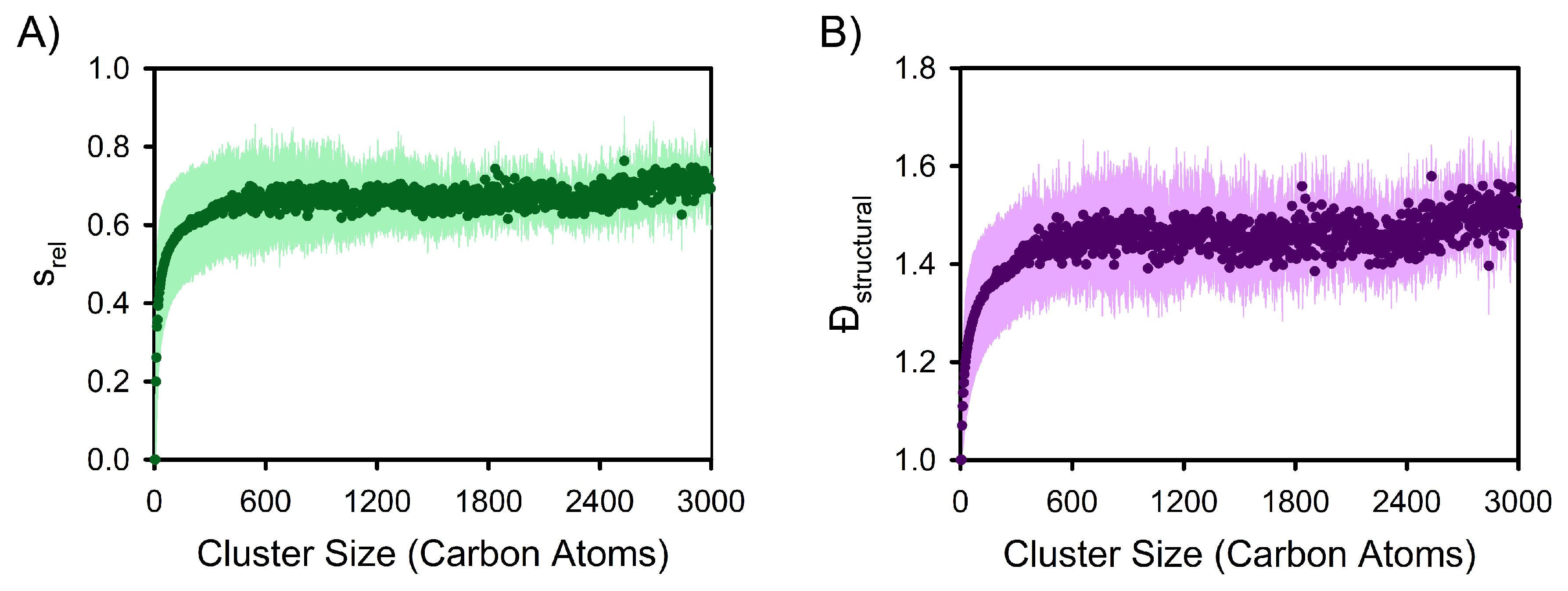
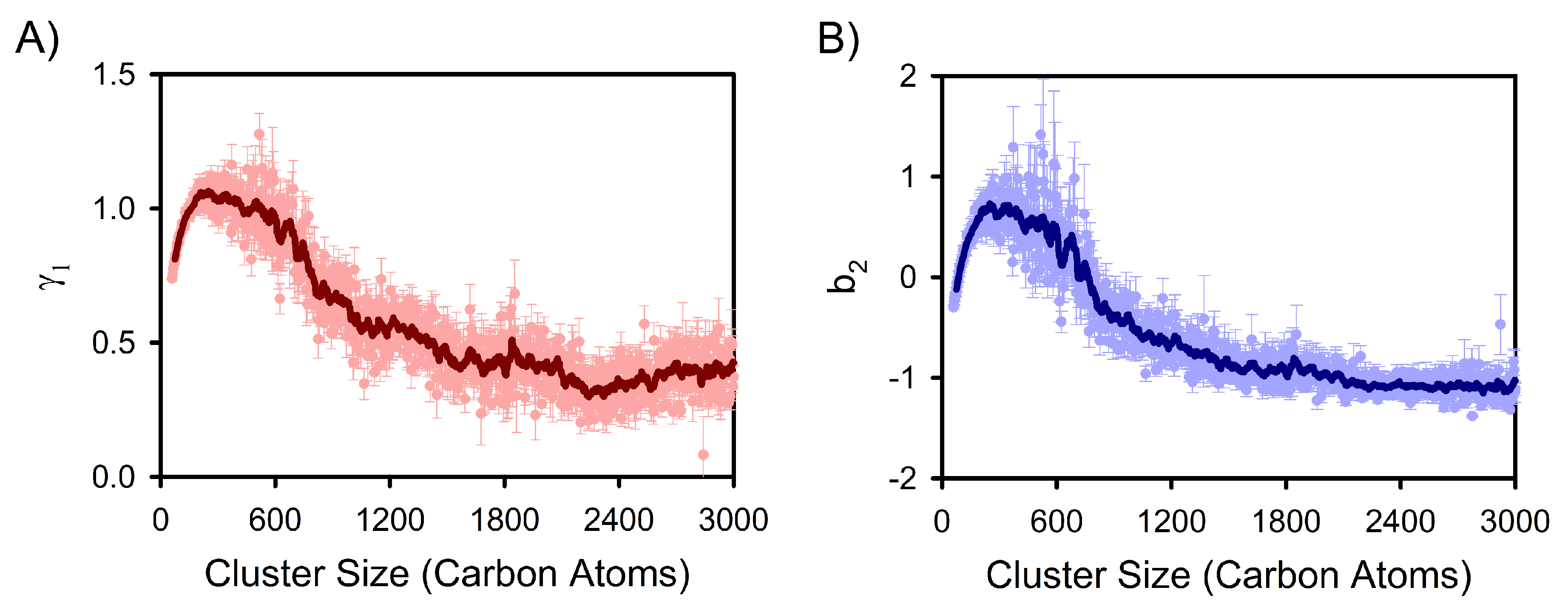
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shen, S.; Henry, A.; Tong, J.; Zheng, R.; Chen, G. Polyethylene nanofibres with very high thermal conductivities. Nat. Nanotechnol. 2010, 5, 251–255. [Google Scholar] [CrossRef] [PubMed]
- Cui, K.; Ma, Z.; Tian, N.; Su, F.; Liu, D.; Li, L. Multiscale and Multistep Ordering of Flow-Induced Nucleation of Polymers. Chem. Rev. 2018, 118, 1840–1886. [Google Scholar] [CrossRef] [PubMed]
- Schick, C.; Androsch, R.; Schmelzer, J.W.P. Homogeneous crystal nucleation in polymers. J. Phys. Condens. Matter 2017, 29, 453002. [Google Scholar] [CrossRef] [PubMed]
- Yue, K.; Liu, G.; Feng, X.; Li, L.; Lotz, B.; Cheng, S.Z.D. A few rediscovered and challenging topics in polymer crystals and crystallization. Polym. Cryst. 2018, 1, e10053. [Google Scholar] [CrossRef]
- Lauritzen, J.I.; Hoffman, J.D. Formation of Polymer Crystals with Folded Chains from Dilute Solution. J. Res. Natl. Bur. Stand., Sect. A 1960, 64A, 73–102. [Google Scholar] [CrossRef]
- Lauritzen, J.I., Jr.; Hoffman, J.D. Extension of theory of growth of chain-folded polymer crystals to large undercoolings. J. Appl. Phys. 1973, 44, 4340–4352. [Google Scholar] [CrossRef]
- Price, F.P. Markoff Chain Model for Growth of Polymer Single Crystals. J. Chem. Phys. 1961, 35, 1884–1892. [Google Scholar] [CrossRef]
- Frank, F.C.; Tosi, M. On the theory of polymer crystallization. Proc. R. Soc. Lond. Ser. A 1961, 263, 323–339. [Google Scholar]
- Lauritzen, J.I.; Passaglia, E. Kinetics of Crystallization in Multicomponent Systems: II Chain-Folded Polymer Crystals. J. Res. Natl. Bur. Stand. Sect. A 1967, 71A, 261–275. [Google Scholar] [CrossRef]
- Point, J.J. A New Theoretical Approach of the Secondary Nucleation at High Supercooling. Macromolecules 1979, 12, 770–775. [Google Scholar] [CrossRef]
- Point, J.J. Reconsideration of kinetic theories of polymer crystal growth with chain folding. Faraday Discuss. Chem. Soc. 1979, 68, 167–176. [Google Scholar] [CrossRef]
- Sadler, D.M.; Gilmer, G.H. Rate-Theory Model of Polymer Crystallization. Phys. Rev. Lett. 1986, 56, 2708–2711. [Google Scholar] [CrossRef] [PubMed]
- Sadler, D.M. New explanation for chain folding in polymers. Nature 1987, 326, 174–177. [Google Scholar] [CrossRef]
- Yi, P.; Locker, C.R.; Rutledge, G.C. Molecular Dynamics Simulation of Homogeneous Crystal Nucleation in Polyethylene. Macromolecules 2013, 46, 4723–4733. [Google Scholar] [CrossRef]
- Morthomas, J.; Fusco, C.; Zhai, Z.; Lame, O.; Perez, M. Crystallization of finite-extensible nonlinear elastic Lennard-Jones coarse-grained polymers. Phys. Rev. E 2017, 96, 052502. [Google Scholar] [CrossRef]
- Verho, T.; Paajanen, A.; Vaari, J.; Laukkanen, A. Crystal Growth in Polyethylene by Molecular Dynamics: The Crystal Edge and Lamellar Thickness. Macromolecules 2018, 51, 4865–4873. [Google Scholar] [CrossRef]
- Paajanen, A.; Vaari, J.; Verho, T. Crystallization of cross-linked polyethylene by molecular dynamics simulation. Polymer 2019, 171, 80–86. [Google Scholar] [CrossRef]
- Yamamoto, T. Molecular dynamics of polymer crystallization revisited: Crystallization from the melt and the glass in longer polyethylene. J. Chem. Phys. 2013, 139, 054903. [Google Scholar] [CrossRef]
- Luo, C.; Sommer, J.U. Growth Pathway and Precursor States in Single Lamellar Crystallization: MD Simulations. Macromolecules 2011, 44, 1523–1529. [Google Scholar] [CrossRef]
- Luo, C.; Kröger, M.; Sommer, J.U. Entanglements and Crystallization of Concentrated Polymer Solutions: Molecular Dynamics Simulations. Macromolecules 2016, 49, 9017–9025. [Google Scholar] [CrossRef]
- Moyassari, A.; Gkourmpis, T.; Hedenqvist, M.S.; Gedde, U.W. Molecular dynamics simulation of linear polyethylene blends: Effect of molar mass bimodality on topological characteristics and mechanical behavior. Polymer 2019, 161, 139–150. [Google Scholar] [CrossRef]
- Moyassari, A.; Gkourmpis, T.; Hedenqvist, M.S.; Gedde, U.W. Molecular Dynamics Simulations of Short-Chain Branched Bimodal Polyethylene: Topological Characteristics and Mechanical Behavior. Macromolecules 2019, 52, 807–818. [Google Scholar] [CrossRef]
- Zhai, Z.; Fusco, C.; Morthomas, J.; Perez, M.; Lame, O. Disentangling and Lamellar Thickening of Linear Polymers during Crystallization: Simulation of Bimodal and Unimodal Molecular Weight Distribution Systems. ACS Nano 2019, 13, 11310–11319. [Google Scholar] [CrossRef]
- Doye, J.P.K.; Frenkel, D. Kinetic Monte Carlo simulations of the growth of polymer crystals. J. Chem. Phys. 1999, 110, 2692–2702. [Google Scholar] [CrossRef]
- Doye, J.P.K.; Frenkel, D. The mechanism of thickness selection in the Sadler-Gilmer model of polymer crystallization. J. Chem. Phys. 1999, 110, 7073–7086. [Google Scholar] [CrossRef][Green Version]
- Meyer, H.; Múller-Plathe, F. Formation of Chain-Folded Structures in Supercooled Polymer Melts Examined by MD Simulations. Macromolecules 2002, 35, 1241–1252. [Google Scholar] [CrossRef]
- Muthukumar, M.; Welch, P. Modeling polymer crystallization from solutions. Polymer 2000, 41, 8833–8837. [Google Scholar] [CrossRef]
- Anwar, M.; Schilling, T. Crystallization of polyethylene: A molecular dynamics simulation study of the nucleation and growth mechanisms. Polymer 2015, 76, 307–312. [Google Scholar] [CrossRef]
- Sommer, J.U.; Luo, C. Molecular dynamics simulations of semicrystalline polymers: Crystallization, melting, and reorganization. J. Polym. Sci. Part B Polym. Phys. 2010, 48, 2222–2232. [Google Scholar] [CrossRef]
- Luo, C.; Kröger, M.; Sommer, J.U. Molecular dynamics simulations of polymer crystallization under confinement: Entanglement effect. Polymer 2017, 109, 71–84. [Google Scholar] [CrossRef]
- Welch, P.M. Examining the role of fluctuations in the early stages of homogenous polymer crystallization with simulation and statistical learning. J. Chem. Phys. 2017, 146, 044901. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Yang, J.; Xu, T.; Tian, F.; Xie, C.; Li, L. Local structure order assisted two-step crystal nucleation in polyethylene. Phys. Rev. Mater. 2017, 1, 073401. [Google Scholar] [CrossRef]
- Tang, X.; Yang, J.; Tian, F.; Xu, T.; Xie, C.; Chen, W.; Li, L. Flow-induced density fluctuation assisted nucleation in polyethylene. J. Chem. Phys. 2018, 149, 224901. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, T. Molecular Dynamics Simulation of Stretch-Induced Crystallization in Polyethylene: Emergence of Fiber Structure and Molecular Network. Macromolecules 2019, 52, 1695–1706. [Google Scholar] [CrossRef]
- Zhai, Z.; Morthomas, J.; Fusco, C.; Perez, M.; Lame, O. Crystallization and Molecular Topology of Linear Semicrystalline Polymers: Simulation of Uni- and Bimodal Molecular Weight Distribution Systems. Macromolecules 2019, 52, 4196–4208. [Google Scholar] [CrossRef]
- Zhang, W.; Larson, R.G. A metastable nematic precursor accelerates polyethylene oligomer crystallization as determined by atomistic simulations and self-consistent field theory. J. Chem. Phys. 2019, 150, 244903. [Google Scholar] [CrossRef] [PubMed]
- Hagita, K.; Fujiwara, S.; Iwaoka, N. An accelerated united-atom molecular dynamics simulation on the fast crystallization of ring polyethylene melts. J. Chem. Phys. 2019, 150, 074901. [Google Scholar] [CrossRef]
- Hall, K.W.; Sirk, T.W.; Percec, S.; Klein, M.L.; Shinoda, W. Divining the shape of nascent polymer crystal nuclei. J. Chem. Phys. 2019, 151, 144901. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Shinoda, W.; DeVane, R.; Klein, M.L. Multi-property fitting and parameterization of a coarse grained model for aqueous surfactants. Mol. Simul. 2007, 33, 27–36. [Google Scholar] [CrossRef]
- Hall, K.W.; Sirk, T.W.; Klein, M.L.; Shinoda, W. A coarse-grain model for entangled polyethylene melts and polyethylene crystallization. J. Chem. Phys. 2019, 150, 244901. [Google Scholar] [CrossRef] [PubMed]
- Hall, K.W.; Percec, S.; Klein, M.L. Polymer nucleation under high-driving force, long-chain conditions: Heat release and the separation of time scales. J. Chem. Phys. 2019, 150, 114901. [Google Scholar] [CrossRef]
- Shinoda, W.; Shiga, M.; Mikami, M. Rapid estimation of elastic constants by molecular dynamics simulation under constant stress. Phys. Rev. B 2004, 69, 134103. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Martyna, G.J.; Klein, M.L.; Tuckerman, M. Nosé-Hoover chains: The canonical ensemble via continuous dynamics. J. Chem. Phys. 1992, 97, 2635–2643. [Google Scholar] [CrossRef]
- Liu, C.; Muthukumar, M. Langevin dynamics simulations of early-stage polymer nucleation and crystallization. J. Chem. Phys. 1998, 109, 2536–2542. [Google Scholar] [CrossRef]
- Yamamoto, T. Molecular dynamics simulation of polymer ordering. II. Crystallization from the melt. J. Chem. Phys. 2001, 115, 8675–8680. [Google Scholar] [CrossRef]
- Ko, M.J.; Waheed, N.; Lavine, M.S.; Rutledge, G.C. Characterization of polyethylene crystallization from an oriented melt by molecular dynamics simulation. J. Chem. Phys. 2004, 121, 2823–2832. [Google Scholar] [CrossRef]
- Yamamoto, T. Molecular dynamics simulations of polymer crystallization in highly supercooled melt: Primary nucleation and cold crystallization. J. Chem. Phys. 2010, 133, 034904. [Google Scholar] [CrossRef]
- Bourque, A.J.; Locker, C.R.; Rutledge, G.C. Heterogeneous Nucleation of an n-Alkane on Tetrahedrally Coordinated Crystals. J. Phys. Chem. B 2017, 121, 904–911. [Google Scholar] [CrossRef] [PubMed]
- Rudin, A. Elements of Polymer Science & Engineering: An Introductory Text and Reference for Engineers and Chemists, 2nd ed.; Academic Press: San Diego, CA, USA, 1999; pp. 53–55. [Google Scholar]
- Rane, S.S.; Choi, P. Polydispersity Index: How Accurately Does It Measure the Breadth of the Molecular Weight Distribution? Chem. Mater. 2005, 17, 926. [Google Scholar] [CrossRef]
- Harrisson, S. The downside of dispersity: Why the standard deviation is a better measure of dispersion in precision polymerization. Polym. Chem. 2018, 9, 1366–1370. [Google Scholar] [CrossRef]
- Yadav, V.; Hashmi, N.; Ding, W.; Li, T.H.; Mahanthappa, M.K.; Conrad, J.C.; Robertson, M.L. Dispersity control in atom transfer radical polymerizations through addition of phenylhydrazine. Polym. Chem. 2018, 9, 4332–4342. [Google Scholar] [CrossRef]
- Lligadas, G.; Grama, S.; Percec, V. Recent Developments in the Synthesis of Biomacromolecules and their Conjugates by Single Electron Transfer-Living Radical Polymerization. Biomacromolecules 2017, 18, 1039–1063. [Google Scholar] [CrossRef] [PubMed]
- Lligadas, G.; Grama, S.; Percec, V. Single-Electron Transfer Living Radical Polymerization Platform to Practice, Develop, and Invent. Biomacromolecules 2017, 18, 2981–3008. [Google Scholar] [CrossRef]
- Ungar, G.; Zeng, X.B. Learning Polymer Crystallization with the Aid of Linear, Branched and Cyclic Model Compounds. Chem. Rev. 2001, 101, 4157–4188. [Google Scholar] [CrossRef]
- Luo, C.; Sommer, J.U. Frozen Topology: Entanglements Control Nucleation and Crystallization in Polymers. Phys. Rev. Lett. 2014, 112, 195702. [Google Scholar] [CrossRef]
- Fujiwara, S.; Sato, T. Structure formation of a single polymer chain. I. Growth of trans domains. J. Chem. Phys. 2001, 114, 6455–6463. [Google Scholar] [CrossRef][Green Version]
- Chandran, S.; Baschnagel, J.; Cangialosi, D.; Fukao, K.; Glynos, E.; Janssen, L.M.C.; Müller, M.; Muthukumar, M.; Steiner, U.; Xu, J.; et al. Processing Pathways Decide Polymer Properties at the Molecular Level. Macromolecules 2019, 52, 7146–7156. [Google Scholar] [CrossRef]
| Simulation Software | LAMMPS [39] |
| Coarse-Grain Model | SDK model [40] (CM and CT beads) |
| Simulation Ensemble | NPT (isobaric-isothermal) |
| Temperature | 285 K |
| Thermostat Details | Nosé–Hoover [44,45] chain thermostats [46] (4-member chains, coupling constants: 1 ps unscaled time) |
| Pressure | 1 atm |
| Barostat Details | Anisotropic chain barostats [43] (4-member chains, coupling constants: 10 ps unscaled time) |
| Boundary Conditions | Periodic |
| Lennard-Jones Cutoff | 1.5 nm |
| Simulation Length | 200,000,000 time steps |
| Time Step Length | 5 fs unscaled time (20.35 fs scaled time) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hall, K.W.; Sirk, T.W.; Percec, S.; Klein, M.L.; Shinoda, W. Monodisperse Polymer Melts Crystallize via Structurally Polydisperse Nanoscale Clusters: Insights from Polyethylene. Polymers 2020, 12, 447. https://doi.org/10.3390/polym12020447
Hall KW, Sirk TW, Percec S, Klein ML, Shinoda W. Monodisperse Polymer Melts Crystallize via Structurally Polydisperse Nanoscale Clusters: Insights from Polyethylene. Polymers. 2020; 12(2):447. https://doi.org/10.3390/polym12020447
Chicago/Turabian StyleHall, Kyle Wm., Timothy W. Sirk, Simona Percec, Michael L. Klein, and Wataru Shinoda. 2020. "Monodisperse Polymer Melts Crystallize via Structurally Polydisperse Nanoscale Clusters: Insights from Polyethylene" Polymers 12, no. 2: 447. https://doi.org/10.3390/polym12020447
APA StyleHall, K. W., Sirk, T. W., Percec, S., Klein, M. L., & Shinoda, W. (2020). Monodisperse Polymer Melts Crystallize via Structurally Polydisperse Nanoscale Clusters: Insights from Polyethylene. Polymers, 12(2), 447. https://doi.org/10.3390/polym12020447