Continuous Two-Domain Equations of State for the Description of the Pressure-Specific Volume-Temperature Behavior of Polymers
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. pvT Measurement
2.3. Differential Scanning Calorimetry (DSC)
2.4. Modeling
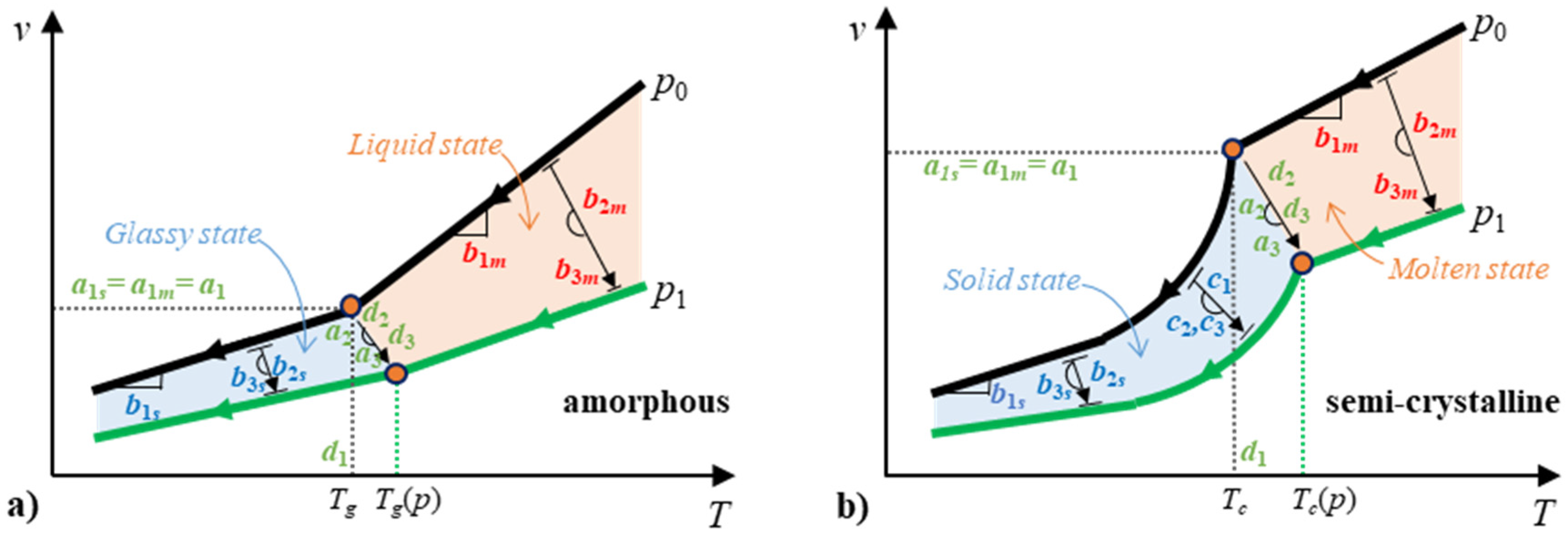
2.4.1. Continuous Two-Domain EoS
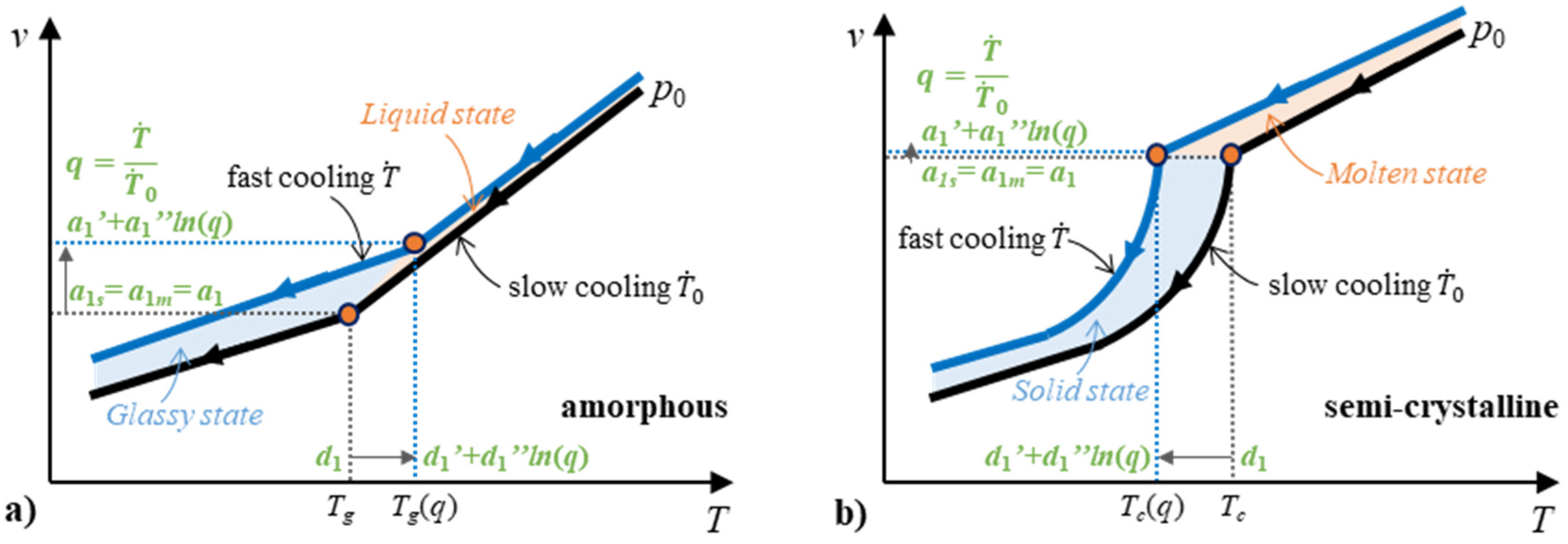
2.4.2. Two-Domain EoS Considering Cooling Rate
3. Results and Discussion
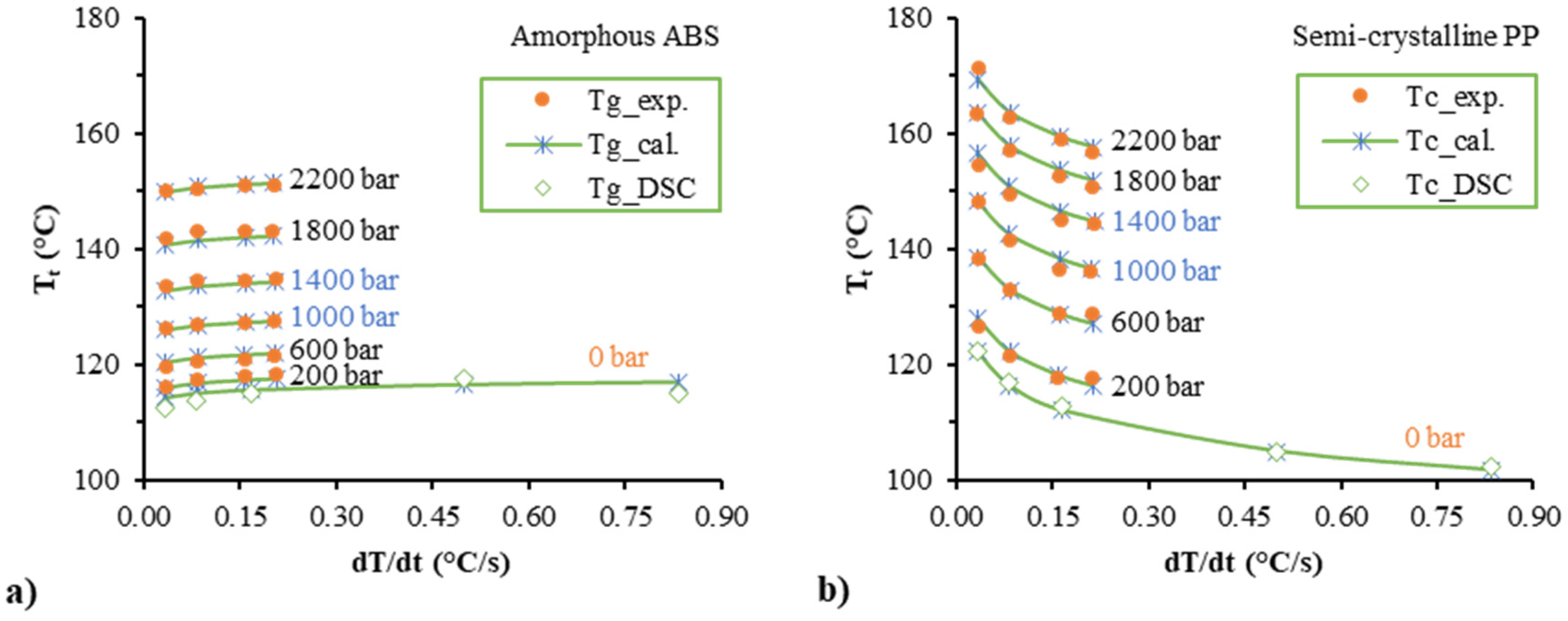
3.1. Influence of the Ccooling Rate
3.2. Transition Temperature and the Corresponding Specific Volume
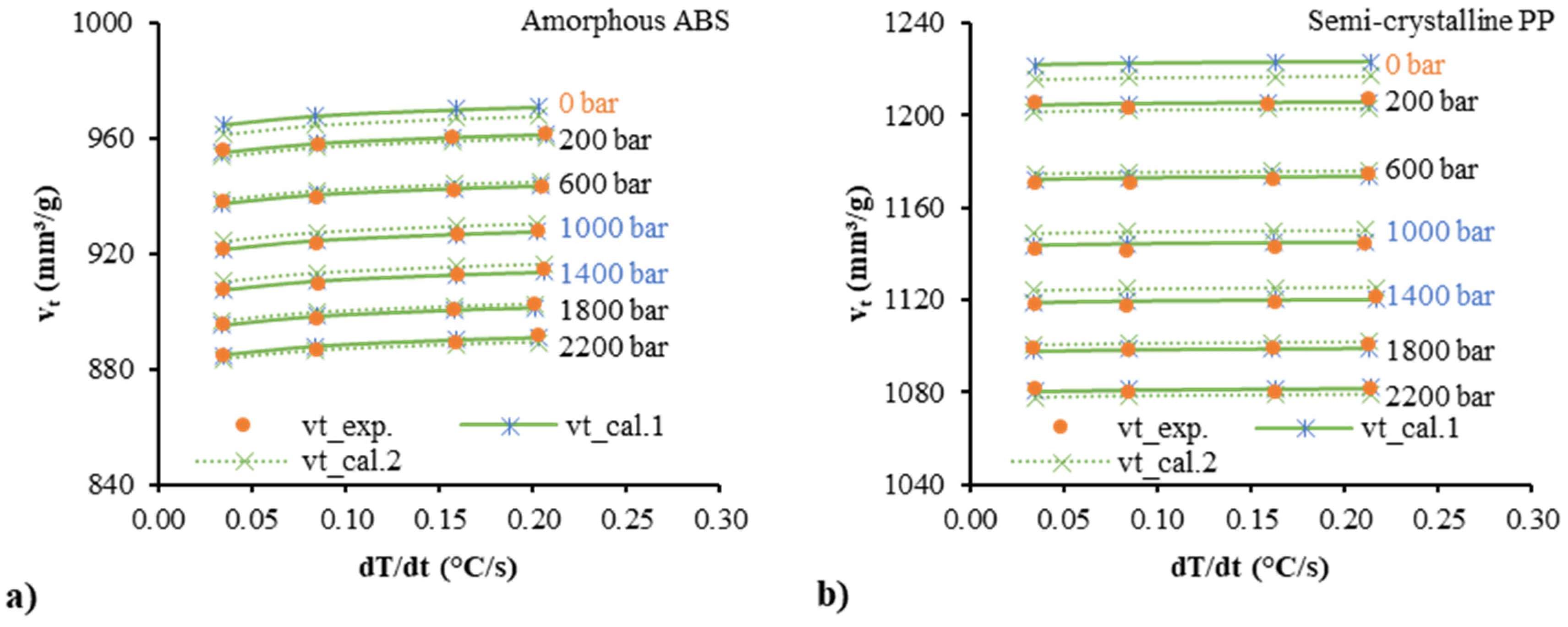
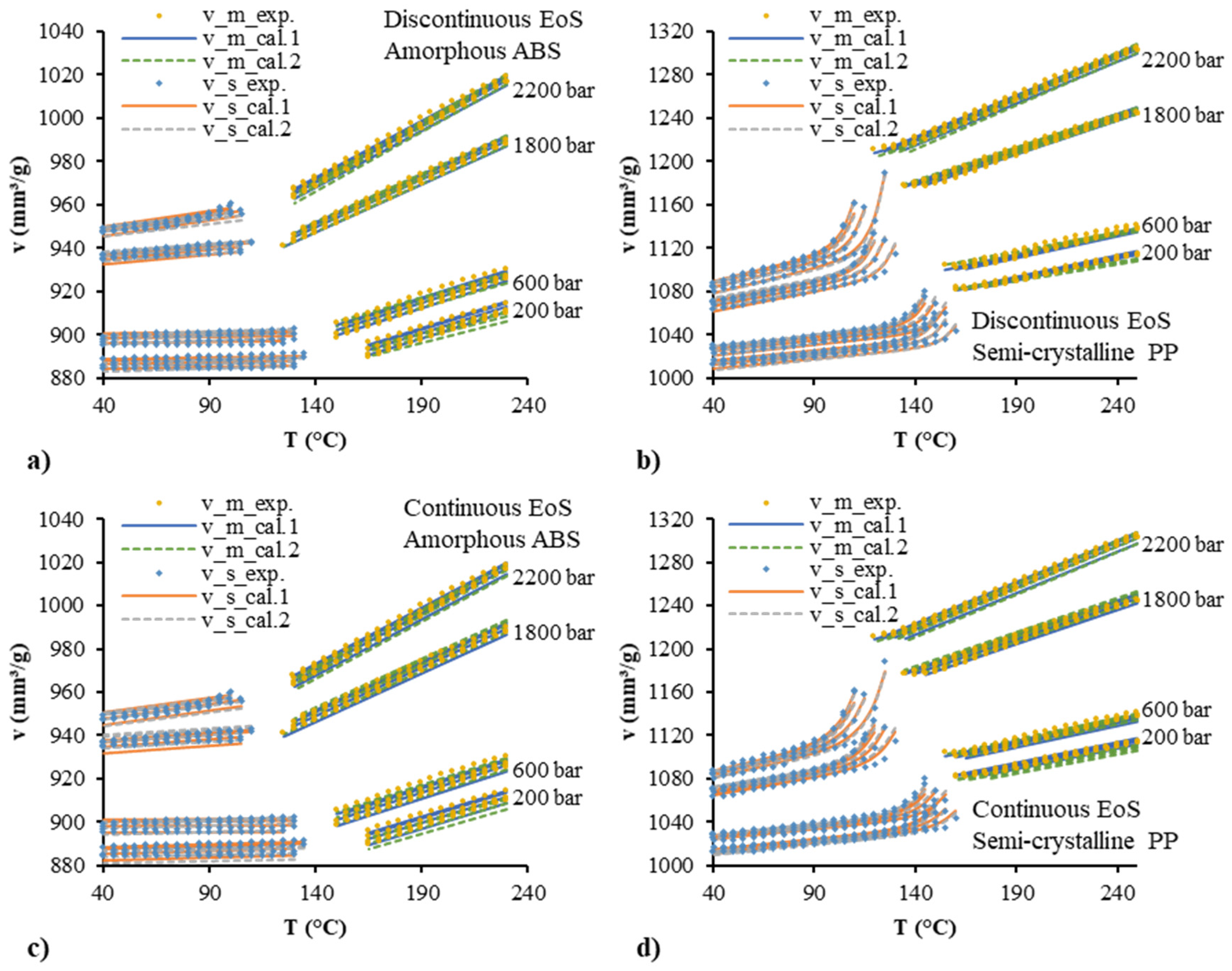
3.3. Comparison between the Experimental Data and the Fitted Data
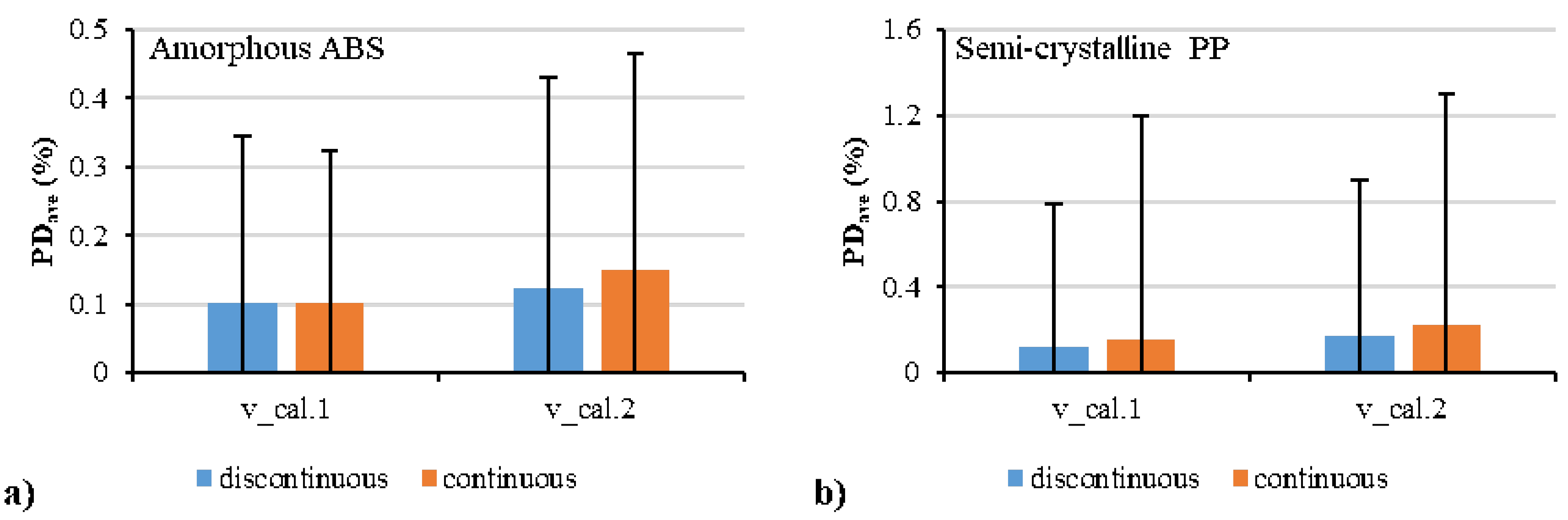
3.4. Validation of the Models
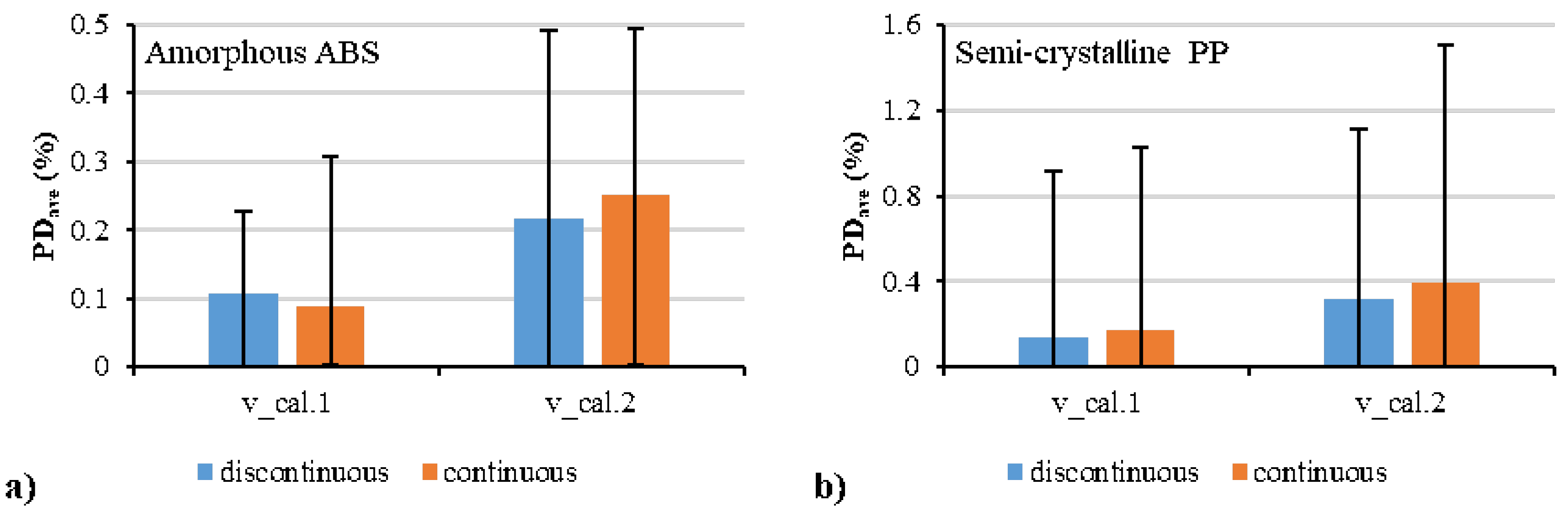
3.5. Prediction with the Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sun, X.; Su, X.; Tibbenham, P.; Mao, J.; Tao, J. The application of modified PVT data on the warpage prediction. J. Polym. Res. 2016, 23, 86. [Google Scholar] [CrossRef]
- Huang, C.T.; Hsu, Y.H.; Chen, B.S. Investigation on the internal mechanism of the deviation between numerical simulation and experiments in injection molding product development. Polym. Test. 2019, 75, 327–336. [Google Scholar] [CrossRef]
- Heidari, B.S.; Davachi, S.M.; Moghaddam, A.H.; Seyfi, J.; Hejazi, I.; Sahraeian, R.; Rashedi, H. Optimization simulated injection molding process for ultrahigh molecular weight polyethylene nanocomposite hip liner using response surface methodology and simulation of mechanical behavior. J. Mech. Behav. Biomed. Mater. 2018, 81, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. PVT properties of polymers for injection molding. In Some Critical Issues for Injection Molding; Wang, J., Ed.; InTech: Rijeka, Croatia, 2012; pp. 3–30. [Google Scholar]
- Nian, S.C.; Wu, C.Y.; Huang, M.S. Warpage control of thin-walled injection molding using local mold temperatures. Int. Commun. Heat Mass 2015, 61, 102–110. [Google Scholar] [CrossRef]
- Wang, J.; Mao, Q. A novel process control methodology based on the PVT behavior of polymer for injection molding. Adv. Polym. Tech. 2013, 32, E474–E485. [Google Scholar] [CrossRef]
- Hopmann, C.; Reßmann, A.; Heinisch, J. Influence on product quality by pvT-optimised processing in injection compression molding. Int. Polym. Process. 2016, 31, 156–165. [Google Scholar] [CrossRef]
- Hopmann, C.; Reßmann, A.; Reiter, M.; Stemmler, S.; Abel, D. A self optimising injection moulding process with model based control system parameterization. Int. J. Comput. Integr. Manuf. 2016, 29, 1190–1199. [Google Scholar] [CrossRef]
- Hopmann, C.; Nikoleizig, P. Inverse thermal mold design for injection molds. Int. J. Mater. Form. 2018, 11, 113–124. [Google Scholar] [CrossRef]
- Hopmann, C.; Schöngart, M.; Nikoleizig, P. Minimisation of warpage for injection moulded parts with reversed thermal mould design. AIP Conf. Proc. 2016, 1779, 020016. [Google Scholar]
- Wang, P.; Fan, Z.; Kazmer, D.O.; Gao, R.X. Orthogonal analysis of multisensor data fusion for improved quality control. J. Manuf. Sci. Eng. 2017, 139, 101008. [Google Scholar] [CrossRef]
- Flory, P.J.; Orwoll, R.A.; Vrij, A. Statistical thermodynamics of chain molecule liquids. I. An equation of state for normal paraffin hydrocarbons. J. Am. Chem. Soc. 1964, 86, 3507–3514. [Google Scholar] [CrossRef]
- Dee, G.T.; Walsh, D.J. Equation of state for polymer liquids. Macromolecules 1988, 21, 811–815. [Google Scholar] [CrossRef]
- Prigogine, I.; Trappeniers, N.; Mathot, V. Statistical thermodynamics of r-MERS and r-MER solutions. Discuss. Faraday Soc. 1953, 15, 93–107. [Google Scholar] [CrossRef]
- Simha, R.; Somcynsky, T. On the statistical thermodynamics of spherical and chain molecule fluids. Macromolecules 1969, 2, 342–350. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. Statistical thermodynamics of polymer solutions. Macromolecules 1978, 11, 1145–1156. [Google Scholar] [CrossRef]
- Tao, F.M.; Mason, E.A. Statistical-mechanical equation of state for nonpolar fluids: Prediction of phase boundaries. J. Chem. Phys. 1994, 100, 9075–9084. [Google Scholar] [CrossRef]
- Hosseini, S.M. ISM equation of state and PVTx profile of polymer solutions. Phys. Chem. Liq. 2019, 57, 565–577. [Google Scholar] [CrossRef]
- Hoseini, S.M. An analytical equation of state for molten polymers. J. Phys. Chem. Electrochem. 2014, 2, 57–65. [Google Scholar]
- Yousefi, F.; Karimi, H. P–V–T properties of polymer melts based on equation of state and neural network. Eur. Polym. J. 2012, 48, 1135–1143. [Google Scholar] [CrossRef]
- Rodgers, P.A. Pressure-volume-temperature relationships for polymeric liquids: A review of equations of state and their characteristic parameters for 56 polymers. J. Appl. Polym. Sci. 1993, 48, 1061–1080. [Google Scholar] [CrossRef]
- Júnior, E.J.P.; Soares, R.P.; Cardozo, N.S.M. Analysis of equations of state for polymers. Polímeros 2015, 25, 277–288. [Google Scholar] [CrossRef]
- Hartmann, B.; Haque, M.A. Equation of state for polymer liquids. J. Appl. Polym. Sci. 1985, 30, 1553–1563. [Google Scholar] [CrossRef]
- Hartmann, B.; Haque, M.A. Equation of state for polymer solids. J. Appl. Phys. 1985, 58, 2831–2836. [Google Scholar] [CrossRef]
- Curro, J.G. Polymeric equations of state. J. Macromol. Sci. Part C Polym. Rev. 1974, 11, 321–366. [Google Scholar] [CrossRef]
- Spencer, R.S.; Gilmore, G.D. Equation of state for high polymers. J. Appl. Phys. 1950, 21, 523–526. [Google Scholar] [CrossRef]
- Schmidt, T.W.; Menges, G. Calculation of the packing phase in injection molding with a two-layer segment model. In Proceedings of the 44th Annual Technical Conference (ANTEC) of the Society of Plastics Engineer (SPE), Boston, MA, USA, 28 April–1 May 1986. [Google Scholar]
- Schmidt, T.W. Zur Abschätzung der Schwindung. Ph.D. Thesis, RWTH Aachen, Aachen, Germany, 1986. [Google Scholar]
- Dymond, J.H.; Malhotra, R. The Tait equation: 100 years on. Int. J. Thermophys. 1988, 9, 941–951. [Google Scholar] [CrossRef]
- Wang, J.; Xie, P.; Yang, W.; Ding, Y. Online pressure–volume–temperature measurements of polypropylene using a testing mold to simulate the injection-molding process. J. Appl. Polym. Sci. 2010, 118, 200–208. [Google Scholar] [CrossRef]
- Yi, Y.X.; Zoller, P. An experimental and theoretical study of the PVT equation of state of butadiene and isoprene elastomers to 200 °C and 200 MPa. J. Polym. Sci. Polym. Phys. 1993, 31, 779–788. [Google Scholar] [CrossRef]
- Song, M.; Qin, Q.; Zhu, J.; Yu, G.; Wu, S.; Jiao, M. Pressure-volume-temperature properties and thermophysical analyses of AO-60/NBR composites. Polym. Eng. Sci. 2019, 59, 949–955. [Google Scholar] [CrossRef]
- He, X. Comparison of Tait, Schmidt and Renner Approaches Based on Experiments. Master’s Thesis, Zhejiang University, Hangzhou, China, 2017. [Google Scholar]
- Wang, J.; Hopmann, C.; Schmitz, M.; Hohlweck, T.; Wipperfürth, J. Modeling of pvT behavior of semi-crystalline polymer based on the two-domain Tait equation of state for injection molding. Mater. Des. 2019, 183, 108149. [Google Scholar] [CrossRef]
- Bushko, W.C.; Stokes, V.K. Estimates for material shrinkage in molded parts caused by time-varying cavity pressures. Polym. Eng. Sci. 2019, 59, 1648–1656. [Google Scholar] [CrossRef]
- Zuidema, H.; Peters, G.W.M.; Meijer, H.E.H. Influence of cooling rate on pVT-data of semicrystalline polymers. J. Appl. Polym. Sci. 2001, 82, 1170–1186. [Google Scholar] [CrossRef]
- van Drongelen, M.; van Erp, T.B.; Peters, G.W.M. Quantification of non-isothermal, multi-phase crystallization of isotactic polypropylene: The influence of cooling rate and pressure. Polymer 2012, 53, 4758–4769. [Google Scholar] [CrossRef]
- Xie, P.; Yang, H.; Cai, T.; Li, Z.; Li, Y.; Yang, W. Study on the pressure-volume-temperature properties of polypropylene at various cooling and shear rates. Polymer 2018, 42, 167–174. [Google Scholar]
- Wang, J.; Hopmann, C.; Schmitz, M.; Hohlweck, T. Influence of measurement processes on pressure-specific volume temperature relationships of semi-crystalline polymer: Polypropylene. Polym. Test. 2019, 78, 105992. [Google Scholar] [CrossRef]
- Wang, J.; Hopmann, C.; Schmitz, M.; Hohlweck, T. Process dependence of pressure-specific volume-temperature measurement for amorphous polymer: Acrylonitrile-butadiene-styrene. Polym. Test. 2020, 81, 106232. [Google Scholar] [CrossRef]
- Suárez, S.A.; Naranjo, A.; López, I.D.; Ortiz, J.C. Analytical review of some relevant methods and devices for the determination of the specific volume on thermoplastic polymers under processing conditions. Polym. Test. 2015, 48, 215–231. [Google Scholar] [CrossRef]
- Chang, R.Y.; Chen, C.H.; Su, K.S. Modifying the Tait equation with cooling-rate effects to predict the pressure-volume-temperature behaviors of amorphous polymers: Modeling and experiments. Polym. Eng. Sci. 1996, 36, 1789–1795. [Google Scholar] [CrossRef]
- Kowalska, B. Thermodynamic equations of state of polymers and conversion processing. Int. Polym. Sci. Technol. 2002, 29, 76–84. [Google Scholar] [CrossRef]
- Mekhilef, N. Viscoelastic and pressure–volume–temperature properties of poly (vinylidene fluoride) and poly (vinylidene fluoride)–hexafluoropropylene copolymers. J. Appl. Polym. Sci. 2001, 80, 230–241. [Google Scholar] [CrossRef]
- Pignon, B.; Tardif, X.; Lefevre, N.; Sobotka, V.; Boyard, N.; Delaunay, D. A new PvT device for high performance thermoplastics: Heat transfer analysis and crystallization kinetics identification. Polym. Test. 2015, 45, 152–160. [Google Scholar] [CrossRef]
- Pionteck, J. Determination of pressure dependence of polymer phase transitions by pVT analysis. Polymers 2018, 10, 578. [Google Scholar] [CrossRef]





| Polymer | Parameter | Estimate | Std. Error | R2 (%) |
|---|---|---|---|---|
| ABS | d1’ (°C) | 111.217 | 1.536 | 99.7 |
| d1’’ (°C) | 0.865 | 0.306 | ||
| d2 (°C/bar) | 0.008 | 0.002 | ||
| d3 (°C/bar2) | 3.74 × 10−6 | 6.58 × 10−7 | ||
| PP | d1’ (°C) | 144.71 | 2.053 | 99.7 |
| d1’’ (°C) | −6.401 | 0.406 | ||
| d2 (°C/bar) | 0.03 | 0.002 | ||
| d3 (°C/bar2) | 3.852 × 10−6 | 8.94 × 10−7 |
| Polymer | Model | Equation | Parameter | Estimate | Std. Error | R2 (%) |
|---|---|---|---|---|---|---|
| ABS | cal.1 | (33) | a1’ (mm3/g) | 952.781 | 1.601 | 99.9 |
| Polynomial | (31) | a1’’ (mm3/g) | 3.414 | 0.319 | ||
| a2 (mm3/(g·bar)) | 0.049 | 0.002 | ||||
| a3 (mm3/(g·bar2)) | 5.789 × 10−6 | 6.86 × 10−7 | ||||
| cal.2 | (2) | a1’ (mm3·bar/g) | 23,649,719 | 374,659 | 99.7 | |
| Schmidt | (31) | a1’’ (mm3·bar/g) | 88,851 | 17,092 | ||
| a2 (bar) | 24,925.451 | 403.474 | ||||
| PP | cal.1 | (33) | a1’ (mm3/g) | 1219.121 | 2.534 | 99.9 |
| Polynomial | (31) | a1’’ (mm3/g) | 0.704 | 0.502 | ||
| a2 (mm3/(g·bar)) | 0.089 | 0.003 | ||||
| a3 (mm3/(g·bar2)) | 1.1483 × 10−5 | 1.103 × 10−6 | ||||
| cal.2 | (2) | a1’ (mm3·bar/g) | 20,850,700 | 339,448 | 99.7 | |
| Schmidt | (31) | a1’’ (mm3·bar/g) | 13,276 | 20,676 | ||
| a2 (bar) | 17,190.134 | 285.183 |
| Polymer | Model | Equation | Parameter | Estimate | Std. Error | R2 (%) |
|---|---|---|---|---|---|---|
| ABS | cal.1 | (32) | b1m (mm3/(g·°C)) | 0.559 | 0.003 | 99.91 |
| (15) | b2m (mm3/(g·°C·bar)) | 2.11521 × 10−4 | 8.131 × 10−6 | |||
| b3m (mm3/(g·°C·bar2)) | 4.2 × 10−8 | 3 × 10−9 | ||||
| (32) | b1s (mm3/(g·°C)) | 0.175 | 0.004 | 99.81 | ||
| (20) | b2s (mm3/(g·°C·bar)) | 2.1499 × 10−4 | 9.644 × 10−6 | |||
| b3s (mm3/(g·°C·bar2)) | 6.7 × 10−8 | 4 × 10−9 | ||||
| cal.2 | (32) | b1m (mm3/(g·°C)) | 1216.716 | 29.363 | 99.79 | |
| (14) | b2m (bar) | 2113.472 | 61.924 | |||
| (32) | b1s (mm3/(g·°C)) | 44.271 | 3.652 | 99.72 | ||
| (19) | b2s (bar) | 154.237 | 33.575 | |||
| PP | cal.1 | (32) | b1m (mm3/(g·°C)) | 0.846 | 0.005 | 99.90 |
| (15) | b2m (mm3/(g·°C·bar)) | 4.14538 × 10−4 | 1.3043 × 10−5 | |||
| b3m (mm3/(g·°C·bar2)) | 9.2 × 10−8 | 6 × 10−9 | ||||
| (32) | b1s (mm3/(g·°C)) | 0.496 | 0.023 | 99.43 | ||
| (20) | b2s (mm3/(g·°C·bar)) | 3.31605 × 10−4 | 2.6266 × 10−5 | |||
| (37) | b3s (mm3/(g·°C·bar2)) | 8.8 × 10−8 | 8 × 10−9 | |||
| c1 (mm3/g) | 90.531 | 1.336 | ||||
| c2 (1/°C) | 0.109 | 0.003 | ||||
| c3 (1/bar) | 3.1409 × 10−4 | 8.201 × 10−6 | ||||
| cal.2 | (32) | b1m (mm3/(g·°C)) | 1280.478 | 29.722 | 99.79 | |
| (14) | b2m (bar) | 1432.768 | 41.907 | |||
| (32) | b1s (mm3/(g·°C)) | 713.539 | 73.594 | 99.19 | ||
| (19) | b2s (bar) | 1718.018 | 278.007 | |||
| (37) | c1 (mm3/g) | 94.12 | 1.654 | |||
| c2 (1/°C) | 0.104 | 0.003 | ||||
| c3 (1/bar) | 3.4312 × 10−4 | 9.75 × 10−6 |
| Polymer | Model | Equation | Parameter | Estimate | Std. Error | R2 (%) |
|---|---|---|---|---|---|---|
| ABS | cal.1 | (11) | a1m’ (mm3/g) | 954.108 | 0.598 | 99.91 |
| (13) | a1m’’ (mm3/g) | 2.945 | 0.093 | |||
| (15) | a2m (mm3/(g·bar)) | 0.046 | 0.001 | |||
| (31) | a3m (mm3/(g·bar2)) | 4.668 × 10−6 | 4.49 × 10−7 | |||
| b1m (mm3/(g·°C)) | 0.571 | 0.006 | ||||
| b2m (mm3/(g·°C·bar)) | 2.49678 × 10−4 | 1.7266 × 10−5 | ||||
| b3m (mm3/(g·°C·bar2)) | 5.9 × 10−8 | 7 × 10−9 | ||||
| (16) | a1s (mm3/g) | 956.846 | 0.603 | 99.81 | ||
| (18) | a2s (mm3/(g·bar)) | 2.535 | 0.088 | |||
| (20) | a3s (mm3/(g·bar2)) | 4.6 × 10−8 | 1 × 10−9 | |||
| (31) | b1s (mm3/(g·°C)) | 4.344 | 0.448 | |||
| b2s (mm3/(g·°C·bar)) | 1.79 × 10−7 | 9 × 10−9 | ||||
| b3s (mm3/(g·°C·bar2)) | 1.75542 × 10−4 | 1.89 × 10−5 | ||||
| cal.2 | (11) | a1m’ (mm3·bar/g) | 25,081,194 | 30,453 | 99.79 | |
| (12) | a1m’’ (mm3·bar/g) | 80,827 | 60,364 | |||
| (14) | a2m (bar) | 26,415.869 | 3.761 | |||
| (31) | b1m (mm3·bar /(g·°C)) | 906.314 | 170.66 | |||
| b2m (bar) | 1452.427 | 156.634 | ||||
| (16) | a1s’ (mm3·bar/g) | 24,400,643 | 111,151 | 99.72 | ||
| (17) | a1s’’ (mm3·bar/g) | 66,735 | 3007 | |||
| (19) | a2s (bar) | 25,614.391 | 121.87 | |||
| (31) | b1s (mm3·bar /(g·°C)) | 75.047 | 8.844 | |||
| b2s (bar) | 446.842 | 81.5 | ||||
| PP | cal.1 | (11) | a1m’ (mm3/g) | 1225.188 | 0.87 | 99.9 |
| (13) | a1m’’ (mm3/g) | -0.789 | 0.143 | |||
| (15) | a2m (mm3/(g·bar)) | 0.086 | 0.001 | |||
| (31) | a3m (mm3/(g·bar2)) | 1.0111 × 10−5 | 6.19 × 10−7 | |||
| b1m (mm3/(g·°C)) | 0.857 | 0.008 | ||||
| b2m (mm3/(g·°C·bar)) | 4.5284 × 10−4 | 2.25 × 10−5 | ||||
| b3m (mm3 /(g·°C·bar2)) | 1.11 × 10−7 | 1 × 10−8 | ||||
| (16) | a1s’ (mm3/g) | 1119.039 | 1.293 | 99.43 | ||
| (18) | a1s’’ (mm3/g) | 3.082 | 0.15 | |||
| (20) | a2s (mm3/(g·bar)) | 0.058 | 0.002 | |||
| (21) | a3s (mm3/(g·bar2)) | 6.272 × 10−6 | 7.13 × 10−7 | |||
| (31) | b1s (mm3/(g·°C)) | 0.508 | 0.018 | |||
| b2s (mm3/(g·°C·bar)) | 2.78594 × 10−4 | 3.005 × 10−5 | ||||
| b3s (mm3/(g·°C·bar2)) | 6 × 10−8 | 1.1 × 10−8 | ||||
| c1 (mm3/g) | 115.55 | 3.59 | ||||
| c2 (1/°C) | 0.144 | 0.005 | ||||
| c3 (1/bar) | 2.46612 × 10−4 | 2.7623 × 10−5 | ||||
| cal.2 | (11) | a1m’ (mm3·bar/g) | 21,997,152 | 27,796 | 99.79 | |
| (12) | a1m’’ (mm3·bar/g) | −13,713 | 36,456 | |||
| (14) | a2m (bar) | 18,064.71 | 90.388 | |||
| (31) | b1m (mm3·bar /(g·°C)) | 1001.603 | 105.288 | |||
| b2m (bar) | 1032.106 | 4.03 | ||||
| (16) | a1s’ (mm3·bar/g) | 28,469,060 | 340,822 | 99.19 | ||
| (17) | a1s’’ (mm3·bar/g) | 83,976 | 4960 | |||
| (19) | a2s (bar) | 25,644.56 | 327.387 | |||
| (21) | b1s (mm3·bar/(g·°C)) | 799.37 | 58.416 | |||
| (31) | b2s (bar) | 1883.346 | 212.861 | |||
| c1 (mm3/g) | 120.666 | 4.016 | ||||
| c2 (1/°C) | 0.13 | 0.005 | ||||
| c3 (1/bar) | 3.81297 × 10−4 | 3.1849 × 10−5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Hopmann, C.; Röbig, M.; Hohlweck, T.; Kahve, C.; Alms, J. Continuous Two-Domain Equations of State for the Description of the Pressure-Specific Volume-Temperature Behavior of Polymers. Polymers 2020, 12, 409. https://doi.org/10.3390/polym12020409
Wang J, Hopmann C, Röbig M, Hohlweck T, Kahve C, Alms J. Continuous Two-Domain Equations of State for the Description of the Pressure-Specific Volume-Temperature Behavior of Polymers. Polymers. 2020; 12(2):409. https://doi.org/10.3390/polym12020409
Chicago/Turabian StyleWang, Jian, Christian Hopmann, Malte Röbig, Tobias Hohlweck, Cemi Kahve, and Jonathan Alms. 2020. "Continuous Two-Domain Equations of State for the Description of the Pressure-Specific Volume-Temperature Behavior of Polymers" Polymers 12, no. 2: 409. https://doi.org/10.3390/polym12020409
APA StyleWang, J., Hopmann, C., Röbig, M., Hohlweck, T., Kahve, C., & Alms, J. (2020). Continuous Two-Domain Equations of State for the Description of the Pressure-Specific Volume-Temperature Behavior of Polymers. Polymers, 12(2), 409. https://doi.org/10.3390/polym12020409








