Thermophoresis: The Case of Streptavidin and Biotin
Abstract
1. Introduction
2. Experimental Section
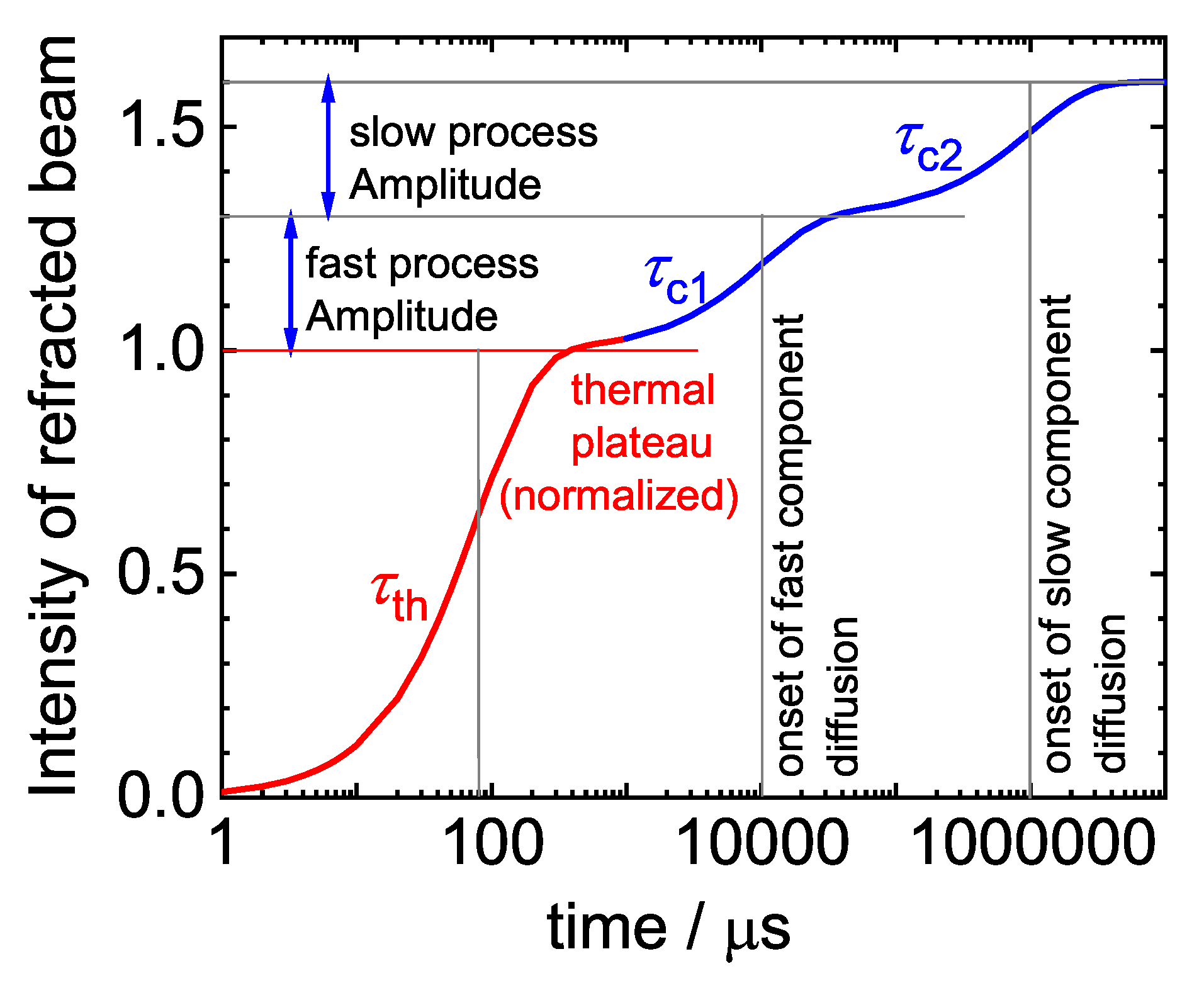
2.1. Thermal Diffusion Forced Rayleigh Scattering
2.2. Sample Preparation
2.3. Contrast Factor Measurement
2.4. Evaluation
3. Results
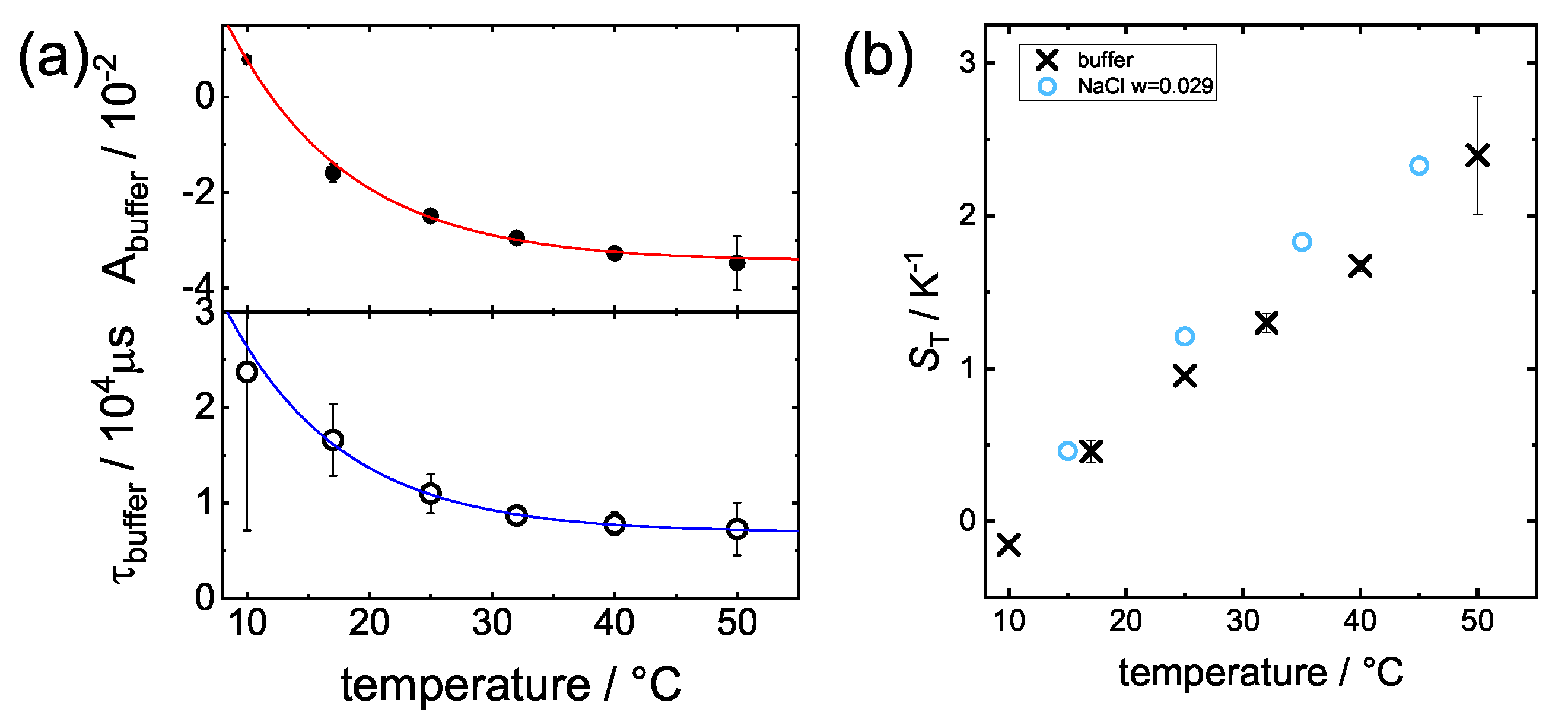
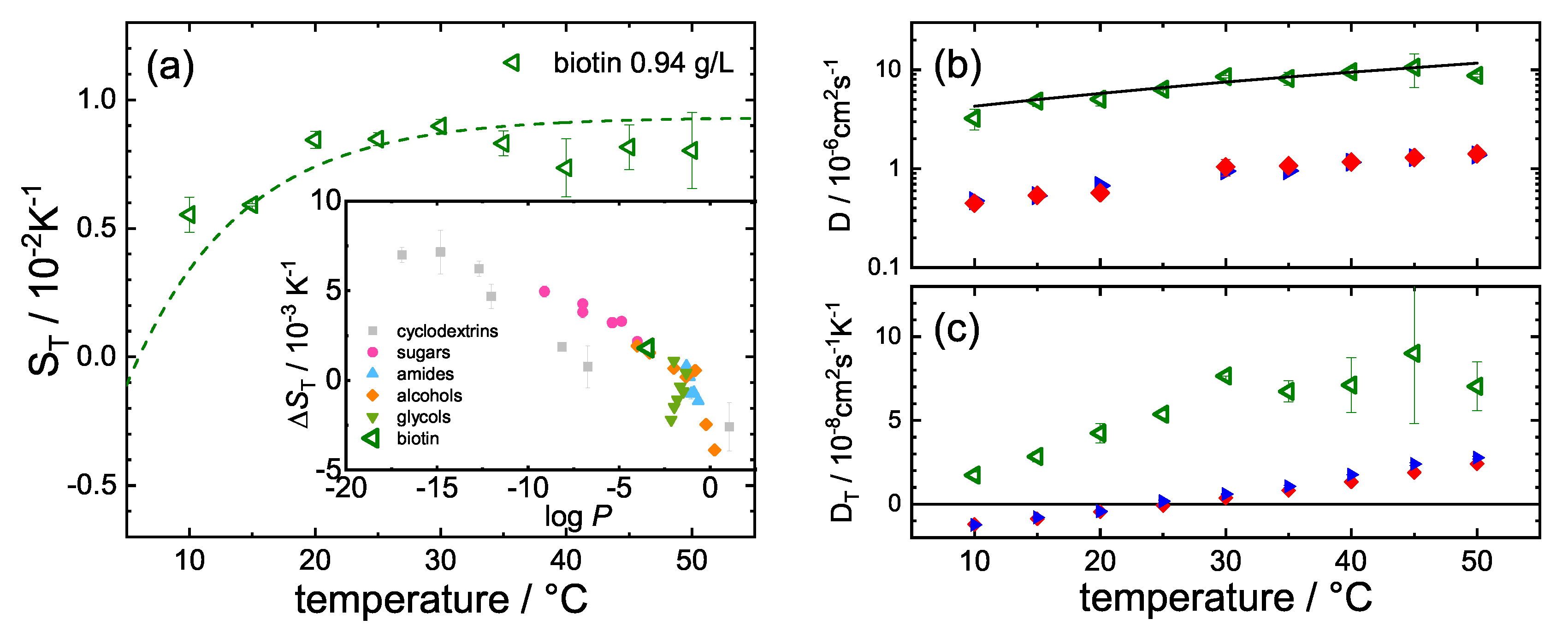
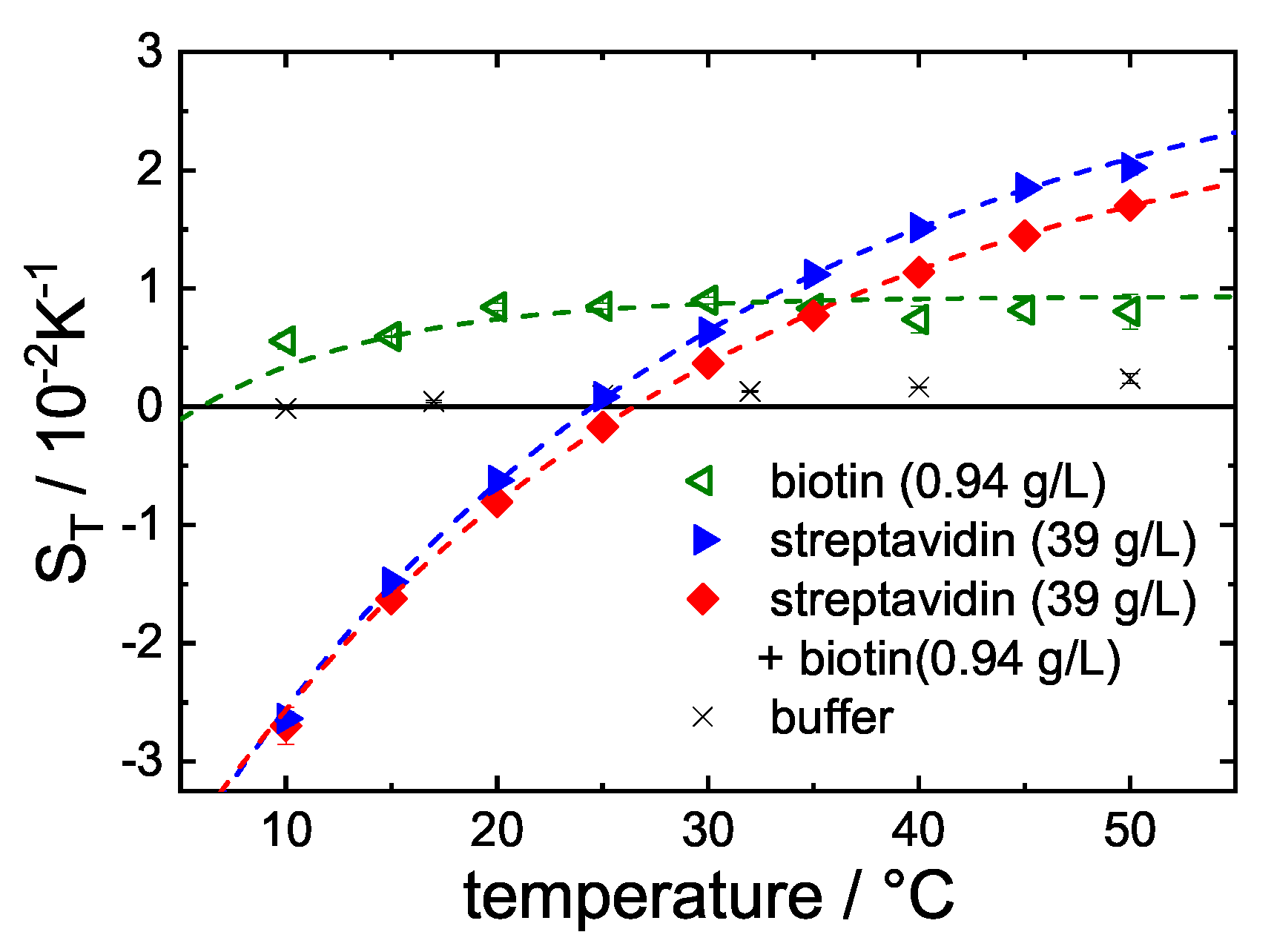
3.1. Change upon Ligand Binding
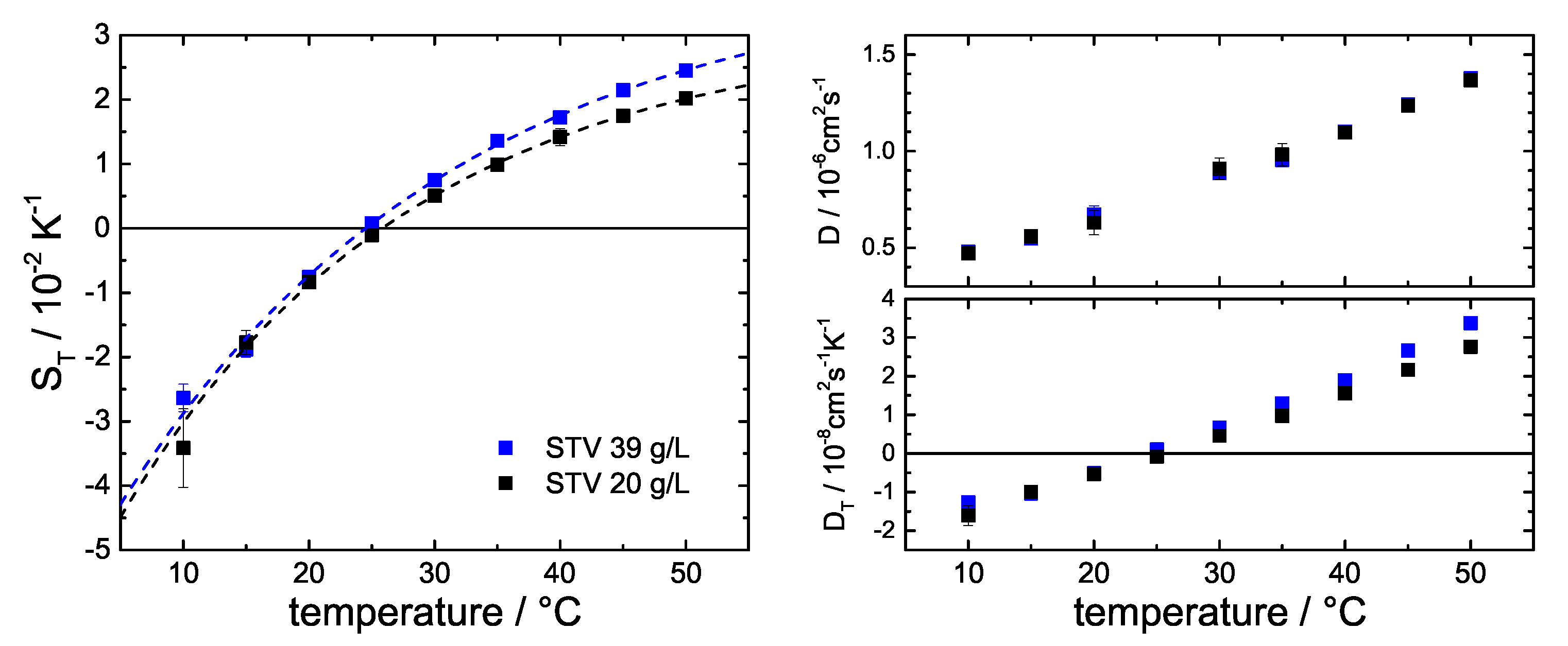
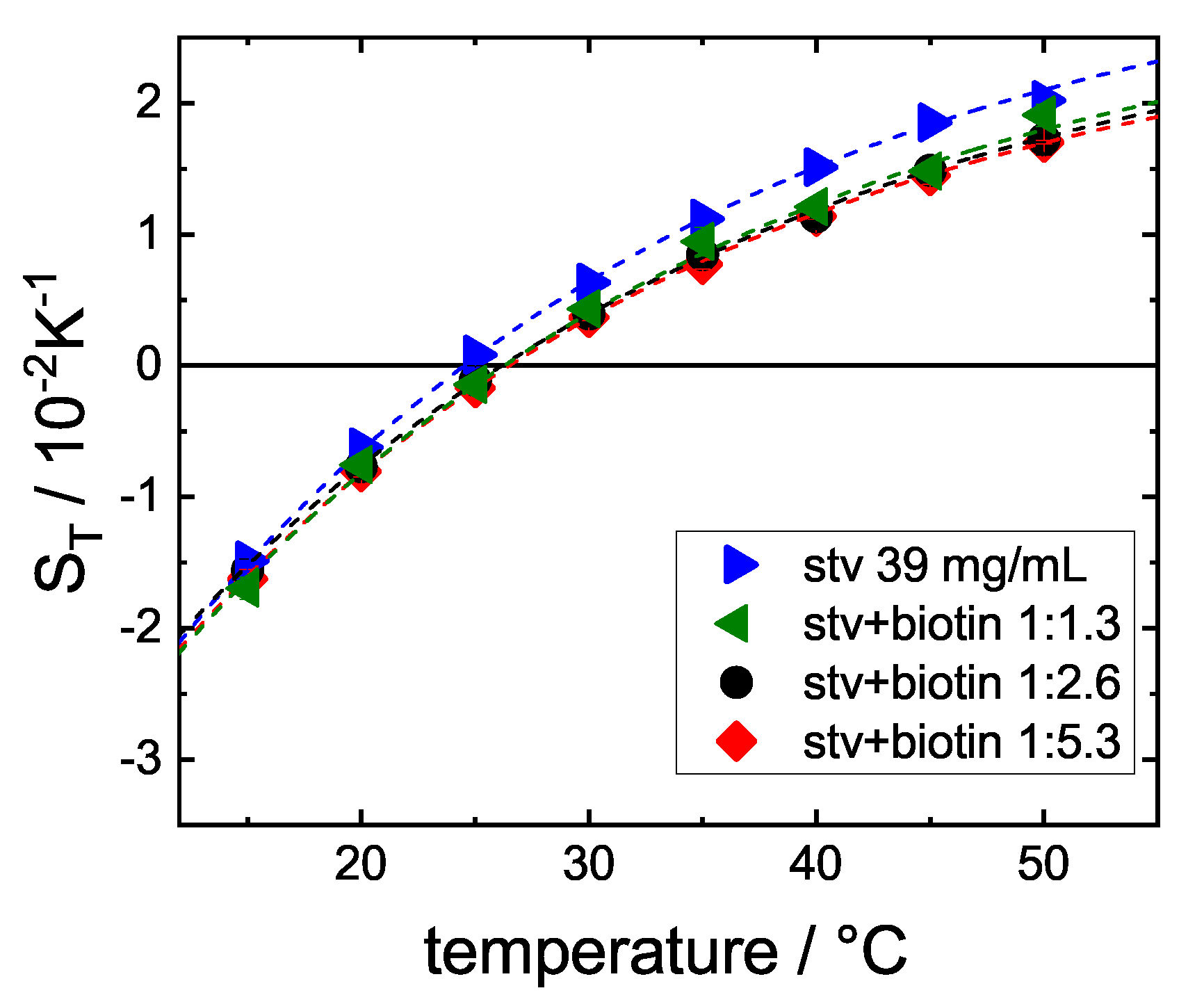
3.2. Influence of Stoichiometry
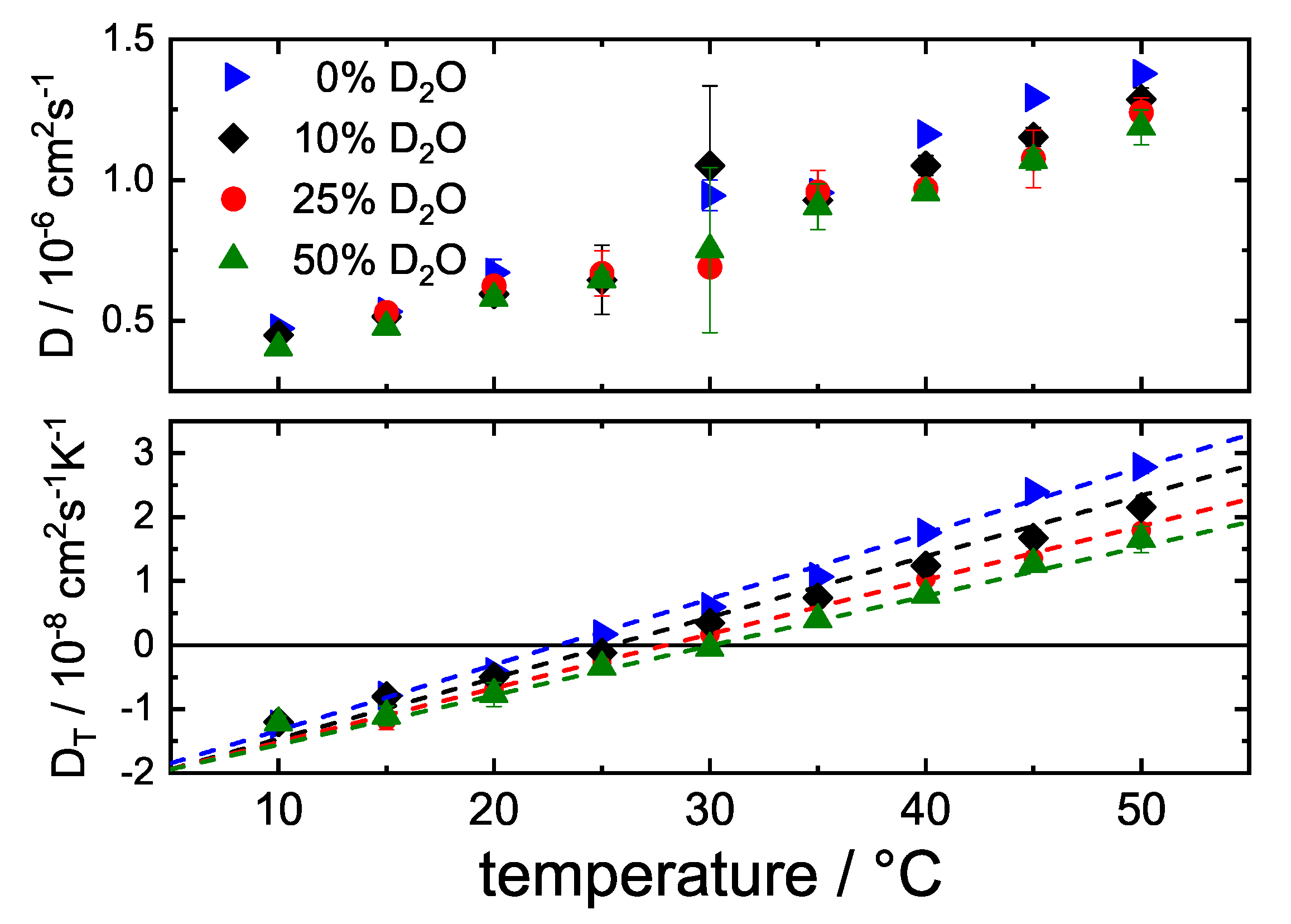
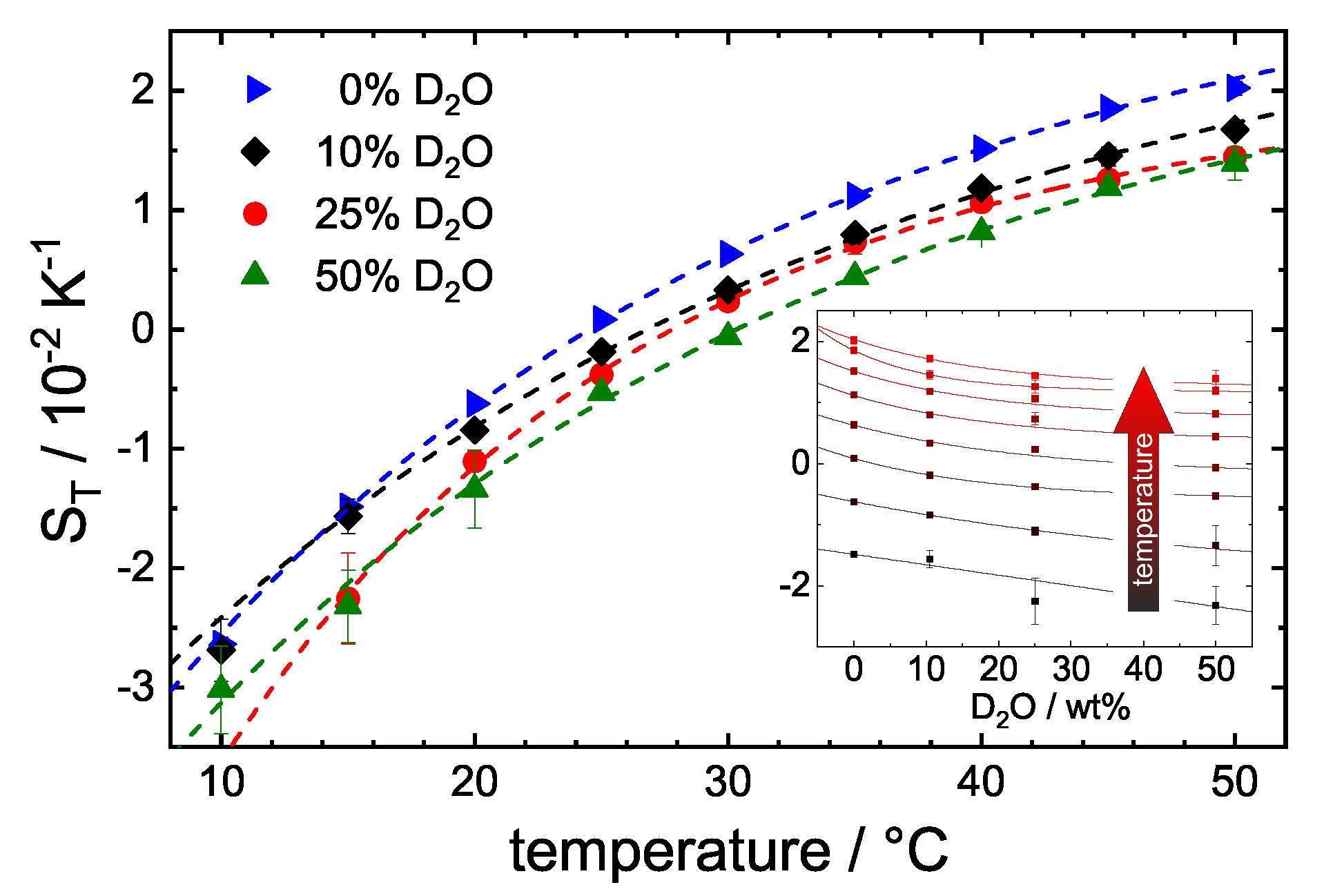
3.3. Influence of DO
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| TDFRS | Thermal Diffusion Forced Rayleigh Scattering |
| QENS | Quasi-Elastic Neutron Scattering |
| STV | Streptavidin |
| B | Biotin |
Appendix A. Evaluation
| Sample | ||||||
|---|---|---|---|---|---|---|
| s | s | s | ||||
| buffer | −0.03521 | 6129 | ||||
| 0.044 | 10570 | |||||
| −0.01206 | 6129 | −0.03256 | 10,570 | |||
| −0.01429 | 6129 | −0.03048 | 10,890 | |||
| −0.00675 | 3034 | −0.03917 | 10,200 | |||
| STV | −0.6232 | 127,600 | ||||
| −0.03087 | 6129 | −0.6228 | 127,600 | |||
| −0.03724 | 6129 | −0.62 | 128,900 | |||
| −0.03382 | 11910 | −0.6146 | 129,700 | |||
| STV + B | −0.03737 | 3153 | −0.5879 | 122,000 | ||
| −0.02486 | 6129 | −0.5737 | 122,100 | |||
| −0.01411 | 10,570 | −0.5636 | 122,100 |
Appendix A.1. Influence of Stoichiometry
| STV:Biotin | Biotin mg/mL | Concentration mol/mL |
|---|---|---|
| 1:1.3 | 0.24 | 9.8 |
| 1:2.6 | 0.48 | 19.6 |
| 1:5.3 | 0.94 | 38.5 |
Appendix A.2. Influence of D2O
Appendix A.3. Comparison of Two Concentrations
References
- Niether, D.; Wiegand, S. Thermophoresis of biological and biocompatible compounds in aqueous solution. J. Phys. Condens. Matter 2019, 31, 503003. [Google Scholar] [CrossRef]
- Baaske, P.; Weinert, F.M.; Duhr, S.; Lemke, K.H.; Russell, M.J.; Braun, D. Extreme accumulation of nucleotides in simulated hydrothermal pore systems. Proc. Natl. Acad. Sci. USA 2007, 104, 9346–9351. [Google Scholar] [CrossRef] [PubMed]
- Niether, D.; Afanasenkau, D.; Dhont, J.K.G.; Wiegand, S. Accumulation of formamide in hydrothermal pores to form prebiotic nucleobases. Proc. Natl. Acad. Sci. USA 2016, 113, 4272–4277. [Google Scholar] [CrossRef] [PubMed]
- Jerabek-Willemsen, M.; Wienken, C.J.; Braun, D.; Baaske, P.; Duhr, S. Molecular Interaction Studies Using Microscale Thermophoresis. Assay Drug Dev. Technol. 2011, 9, 342–353. [Google Scholar] [CrossRef] [PubMed]
- Würger, A. Thermal non-equilibrium transport in colloids. Rep. Prog. Phys. 2010, 73, 126601. [Google Scholar] [CrossRef]
- Köhler, W.; Morozov, K.I. The Soret Effect in Liquid Mixtures—A Review. J. Non-Equil. Thermody. 2016, 41, 151–197. [Google Scholar] [CrossRef]
- Maeda, K.; Shinyashiki, N.; Yagihara, S.; Wiegand, S.; Kita, R. Ludwig-Soret effect of aqueous solutions of ethylene glycol oligomers, crown ethers, and glycerol: Temperature, molecular weight, and hydrogen bond effect. J. Chem. Phys. 2015, 143, 124504. [Google Scholar] [CrossRef] [PubMed]
- Eguchi, K.; Niether, D.; Wiegand, S.; Kita, R. Thermophoresis of cyclic oligosaccharides in polar solvents. Eur. Phys. J. E 2016, 39, 86. [Google Scholar] [CrossRef]
- Niether, D.; Kriegs, H.; Dhont, J.K.G.; Wiegand, S. Peptide model systems: Correlation between thermophilicity and hydrophilicity. J. Chem. Phys. 2018, 149, 044506. [Google Scholar] [CrossRef]
- Seidel, S.A.I.; Dijkman, P.M.; Lea, W.A.; van den Bogaart, G.; Jerabek-Willemsen, M.; Lazic, A.; Joseph, J.S.; Srinivasan, P.; Baaske, P.; Simeonov, A.; et al. Microscale thermophoresis quantifies biomolecular interactions under previously challenging conditions. Methods 2013, 59, 301–315. [Google Scholar] [CrossRef]
- Wienken, C.J.; Baaske, P.; Duhr, S.; Braun, D. Thermophoretic melting curves quantify the conformation and stability of RNA and DNA. Nucleic Acids Res. 2011, 39, e52. [Google Scholar] [CrossRef] [PubMed]
- Niether, D.; Di Lecce, S.; Bresme, F.; Wiegand, S. Unravelling the hydrophobicity of urea in water using thermodiffusion: Implications for protein denaturation. Phys. Chem. Chem. Phys. 2018, 20, 1012–1020. [Google Scholar] [CrossRef] [PubMed]
- Iacopini, S.; Rusconi, R.; Piazza, R. The “macromolecular tourist”: Universal temperature dependence of thermal diffusion in aqueous colloidal suspensions. Eur. Phys. J. E 2006, 19, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Schimpf, M.E.; Giddings, J.C. Characterization of Thermal-Diffusion in Polymer-Solutions by Thermal Field-Flow Fractionation - Dependence on Polymer and Solvent Parameters. J Polym. Sci. Pol. Phys. 1989, 27, 1317–1332. [Google Scholar] [CrossRef]
- Piazza, R.; Iacopini, S.; Triulzia, B. Thermophoresis as a probe of particle-solvent interactions: The case of protein solutions. Phys. Chem. Chem. Phys. 2004, 6, 1616–1622. [Google Scholar] [CrossRef]
- Naumann, P.; Becker, N.; Datta, S.; Sottmann, T.; Wiegand, S. Soret Coefficient in Nonionic Microemulsions: Concentration and Structure Dependence. J. Phys. Chem. B 2013, 117, 5614–5622. [Google Scholar] [CrossRef]
- Debuschewitz, C.; Köhler, W. Molecular origin of thermal diffusion in benzene plus cyclohexane mixtures. Phys. Rev. Lett. 2001, 87, 055901. [Google Scholar] [CrossRef]
- Wittko, G.; Köhler, W. Universal isotope effect in thermal diffusion of mixtures containing cyclohexane and cyclohexane-d(12). J. Chem. Phys. 2005, 123, 014506. [Google Scholar] [CrossRef]
- Wittko, G.; Köhler, W. On the temperature dependence of thermal diffusion of liquid mixtures. Europhys. Lett. 2007, 78, 46007. [Google Scholar] [CrossRef]
- Polyakov, P.; Wiegand, S. Systematic study of the thermal diffusion in associated mixtures. J. Chem. Phys. 2008, 128, 034505. [Google Scholar] [CrossRef]
- Platten, J.K.; Bou-Ali, M.M.; Costeseque, P.; Dutrieux, J.F.; Köhler, W.; Leppla, C.; Wiegand, S.; Wittko, G. Benchmark values for the Soret, thermal diffusion and diffusion coefficients of three binary organic liquid mixtures. Philos. Mag. 2003, 83, 1965–1971. [Google Scholar] [CrossRef]
- Kita, R.; Wiegand, S.; Luettmer-Strathmann, J. Sign change of the Soret coefficient of poly(ethylene oxide) in water/ethanol mixtures observed by thermal diffusion forced Rayleigh scattering. J. Chem. Phys. 2004, 121, 3874–3885. [Google Scholar] [CrossRef] [PubMed]
- Alonso de Mezquia, D.; Wang, Z.; Lapeira, E.; Klein, M.; Wiegand, S.; Mounir Bou-Ali, M. Thermodiffusion, molecular diffusion and Soret coefficient of binary and ternary mixtures of n-hexane, n-dodecane and toluene. Eur. Phys. J. E 2014, 37, 106. [Google Scholar] [CrossRef]
- Seidel, S.A.I.; Wienken, C.J.; Geissler, S.; Jerabek-Willemsen, M.; Duhr, S.; Reiter, A.; Trauner, D.; Braun, D.; Baaske, P. Label-Free Microscale Thermophoresis Discriminates Sites and Affinity of Protein-Ligand Binding. Angew. Chem. Int. Edit. 2012, 51, 10656–10659. [Google Scholar] [CrossRef] [PubMed]
- Muller, C.B.; Weiss, K.; Loman, A.; Enderlein, J.; Richtering, W. Remote temperature measurements in femto-liter volumes using dual-focus-Fluorescence Correlation Spectroscopy. Lab Chip 2009, 9, 1248–1253. [Google Scholar] [CrossRef] [PubMed]
- Duhr, S.; Arduini, S.; Braun, D. Thermophoresis of DNA determined by microfluidic fluorescence. Eur. Phys. J. E 2004, 15, 277–286. [Google Scholar] [CrossRef]
- Green, N.M. [5] Avidin and streptavidin. In Avidin-Biotin Technology; Wilchek, M., Bayer, E.A., Eds.; Methods in Enzymology; Academic Press: Cambridge, MA, USA, 1990; Volume 184, pp. 51–67. [Google Scholar]
- Sano, T.; Cantor, C.R. Cooperative biotin binding by streptavidin. Electrophoretic behavior and subunit association of streptavidin in the presence of 6 M urea. J. Biol. Chem. 1990, 265, 3369–3373. [Google Scholar]
- Chilkoti, A.; Stayton, P.S. Molecular Origins of the Slow Streptavidin-Biotin Dissociation Kinetics. J. Am. Chem. Soc. 1995, 117, 10622–10628. [Google Scholar] [CrossRef]
- Sarter, M.; Niether, D.; Koenig, B.W.; Lohstroh, W.; Zamponi, M.; Jalarvo, N.H.; Wiegand, S.; Fitter, J.; Stadler, A.M. Strong Adverse Contribution of Conformational Dynamics to Streptavidin-Biotin Binding. J. Phys. Chem. B 2020, 124, 324–335. [Google Scholar] [CrossRef]
- Stadler, A.M.; Koza, M.M.; Fitter, J. Determination of Conformational Entropy of Fully and Partially Folded Conformations of Holo- and Apomyoglobin. J. Phys. Chem. B 2015, 119, 72–82. [Google Scholar] [CrossRef]
- Houston, J.E.; Brandl, G.; Drochner, M.; Kemmerling, G.; Engels, R.; Papagiannopoulos, A.; Sarter, M.; Stadler, A.; Radulescu, A. The high-intensity option of the SANS diffractometer KWS-2 at JCNS—Characterization and performance of the new multi-megahertz detection system. J. Appl. Crystallogr. 2018, 51, 323–336. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, S.; Köhler, W. Measurement of Transport Coefficients by an Optical Grating Technique. In Thermal Nonequilibrium Phenomena in Fluid Mixtures; Springer: Basel, Switzerland, 2002; Volume 584, pp. 189–210. [Google Scholar]
- Blanco, P.; Kriegs, H.; Lettinga, M.P.; Holmqvist, P.; Wiegand, S. Thermal Diffusion of a Stiff Rod-Like Mutant Y21M fd-Virus. Biomacromolecules 2011, 12, 1602–1609. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, S.; Ning, H.; Kriegs, H. Thermal diffusion forced Rayleigh scattering setup optimized for aqueous mixtures. J. Phys. Chem. B 2007, 111, 14169–14174. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Afanasenkau, D.; Dong, M.; Huang, D.; Wiegand, S. Molar mass and temperature dependence of the thermodiffusion of polyethylene oxide in water/ethanol mixtures. J. Chem. Phys. 2014, 141, 064904-1–064904-7. [Google Scholar] [CrossRef]
- Ning, H.; Dhont, J.K.G.; Wiegand, S. Thermal-diffusive behavior of a dilute solution of charged colloids. Langmuir 2008, 24, 2426–2432. [Google Scholar] [CrossRef] [PubMed]
- Camerini-Otero, R.D.; Franklin, R.M.; Day, L.A. Molecular weights, dispersion of refractive index increments, and dimensions from transmittance spectrophotometry. Bacteriophages R17, T7, and PM2, and tobacco mosaic virus. Biochemistry 1974, 13, 3763–3773. [Google Scholar] [CrossRef]
- Sechenyh, V.V.; Legros, J.C.; Shevtsova, V. Experimental and predicted refractive index properties in ternary mixtures of associated liquids. J. Chem. Thermodyn. 2011, 43, 1700–1707. [Google Scholar] [CrossRef]
- Becker, A.; Köhler, W.; Müller, B. A Scanning Michelson Interferometer For the Measurement of the Concentration and Temperature Derivative of the Refractive- Index of Liquids. Ber. Bunsen-Ges. Phys. Chem. Chem. Phys. 1995, 99, 600–608. [Google Scholar] [CrossRef]
- Calculator Plugins Were Used for Structure Property Prediction and Calculation, Marvin 19.22.0. ChemAxon. 2019. Available online: http://www.chemaxon.com (accessed on 2 February 2020).
- Lide, D.; Bruno, T.J.; Rumble, J.R. CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data, 100th ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Klumb, L.A.; Chu, V.; Stayton, P.S. Energetic roles of hydrogen bonds at the ureido oxygen binding pocket in the streptavidin-biotin complex. Biochemistry 1998, 37, 7657–7663. [Google Scholar] [CrossRef]
- Hyre, D.E.; Le Trong, I.; Merritt, E.A.; Eccleston, J.F.; Green, N.M.; Stenkamp, R.E.; Stayton, P.S. Cooperative hydrogen bond interactions in the streptavidin-biotin system. Protein Sci. 2006, 15, 459–467. [Google Scholar] [CrossRef]
- Niether, D.; Kawaguchi, T.; Hovancova, J.; Eguchi, K.; Dhont, J.K.G.; Kita, R.; Wiegand, S. Role of Hydrogen Bonding of Cyclodextrin-Drug Complexes Probed by Thermodiffusion. Langmuir 2017, 33, 8483–8492. [Google Scholar] [CrossRef] [PubMed]
- Liese, S.; Gensler, M.; Krysiak, S.; Schwarzl, R.; Achazi, A.; Paulus, B.; Hugel, T.; Rabe, J.P.; Netz, R.R. Hydration Effects Turn a Highly Stretched Polymer from an Entropic into an Energetic Spring. ACS Nano 2017, 11, 702–712. [Google Scholar] [CrossRef] [PubMed]
- Némethy, G.; Scheraga, H.A. Structure of Water and Hydrophobic Bonding in Proteins. IV. The Thermodynamic Properties of Liquid Deuterium Oxide. J. Chem. Phys. 1964, 41, 680–689. [Google Scholar] [CrossRef]
- Cummings, D.L.; Wood, J.L. The strength of the deuterium bond. J. Mol. Struct. 1974, 23, 103–112. [Google Scholar] [CrossRef]
- Jasnin, M.; Tehei, M.; Moulin, M.; Haertlein, M.; Zaccai, G. Solvent isotope effect on macromolecular dynamics in E-coli. Eur. Biophys. J. Biophys. Lett. 2008, 37, 613–617. [Google Scholar] [CrossRef][Green Version]
- Cioni, P.; Strambini, G.B. Effect of Heavy Water on Protein Flexibility. Biophys. J. 2002, 82, 3246–3253. [Google Scholar] [CrossRef]
- Kamholz, A.E.; Schilling, E.A.; Yager, P. Optical measurement of transverse molecular diffusion in a microchannel. Biophys. J. 2001, 80, 1967–1972. [Google Scholar] [CrossRef]
- Steckel, F.; Szapiro, S. Physical properties of heavy oxygen water. Part 1.—Density and thermal expansion. Trans. Faraday Soc. 1963, 59, 331–343. [Google Scholar] [CrossRef]
- Kestin, J.; Imaishi, N.; Nott, S.H.; Nieuwoudt, J.C.; Sengers, J.V. Viscosity of light and heavy water and their mixtures. Phys. A-Stat. Mech. Its Appl. 1985, 134, 38–58. [Google Scholar] [CrossRef]
- Blanco, P.; Bou-Ali, M.M.; Platten, J.K.; Urteaga, P.; Madariaga, J.A.; Santamaria, C. Determination of thermal diffusion coefficient in equimolar n-alkane mixtures: Empirical correlations. J. Chem. Phys. 2008, 129, 174504. [Google Scholar] [CrossRef]
- Blanco, P.; Kriegs, H.; Arlt, B.; Wiegand, S. Thermal Diffusion of Oligosaccharide Solutions: The Role of Chain Length and Structure. J. Phys. Chem. B 2010, 114, 10740–10747. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zhang, Y.; Cremer, P.S. Interactions between macromolecules and ions: The Hofmeister series. Curr. Opin. Chem. Biol. 2006, 10, 658–663. [Google Scholar] [CrossRef] [PubMed]
- Königer, A.; Wunderlich, H.; Köhler, W. Measurement of diffusion and thermal diffusion in ternary fluid mixtures using a two-color optical beam deflection technique. J. Chem. Phys. 2010, 132, 174506. [Google Scholar] [CrossRef] [PubMed]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niether, D.; Sarter, M.; Koenig, B.W.; Fitter, J.; Stadler, A.M.; Wiegand, S. Thermophoresis: The Case of Streptavidin and Biotin. Polymers 2020, 12, 376. https://doi.org/10.3390/polym12020376
Niether D, Sarter M, Koenig BW, Fitter J, Stadler AM, Wiegand S. Thermophoresis: The Case of Streptavidin and Biotin. Polymers. 2020; 12(2):376. https://doi.org/10.3390/polym12020376
Chicago/Turabian StyleNiether, Doreen, Mona Sarter, Bernd W. Koenig, Jörg Fitter, Andreas M. Stadler, and Simone Wiegand. 2020. "Thermophoresis: The Case of Streptavidin and Biotin" Polymers 12, no. 2: 376. https://doi.org/10.3390/polym12020376
APA StyleNiether, D., Sarter, M., Koenig, B. W., Fitter, J., Stadler, A. M., & Wiegand, S. (2020). Thermophoresis: The Case of Streptavidin and Biotin. Polymers, 12(2), 376. https://doi.org/10.3390/polym12020376