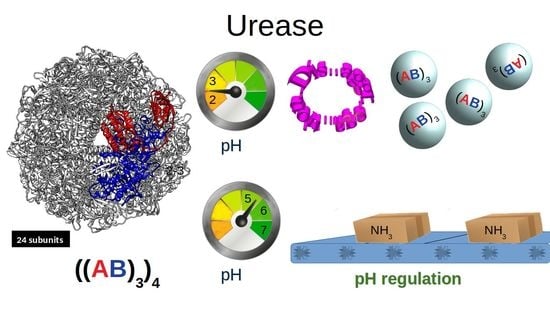
Effect of pH on the Supramolecular Structure of Helicobacter pylori Urease by Molecular Dynamics Simulations
Abstract
1. Introduction
2. Computational Details
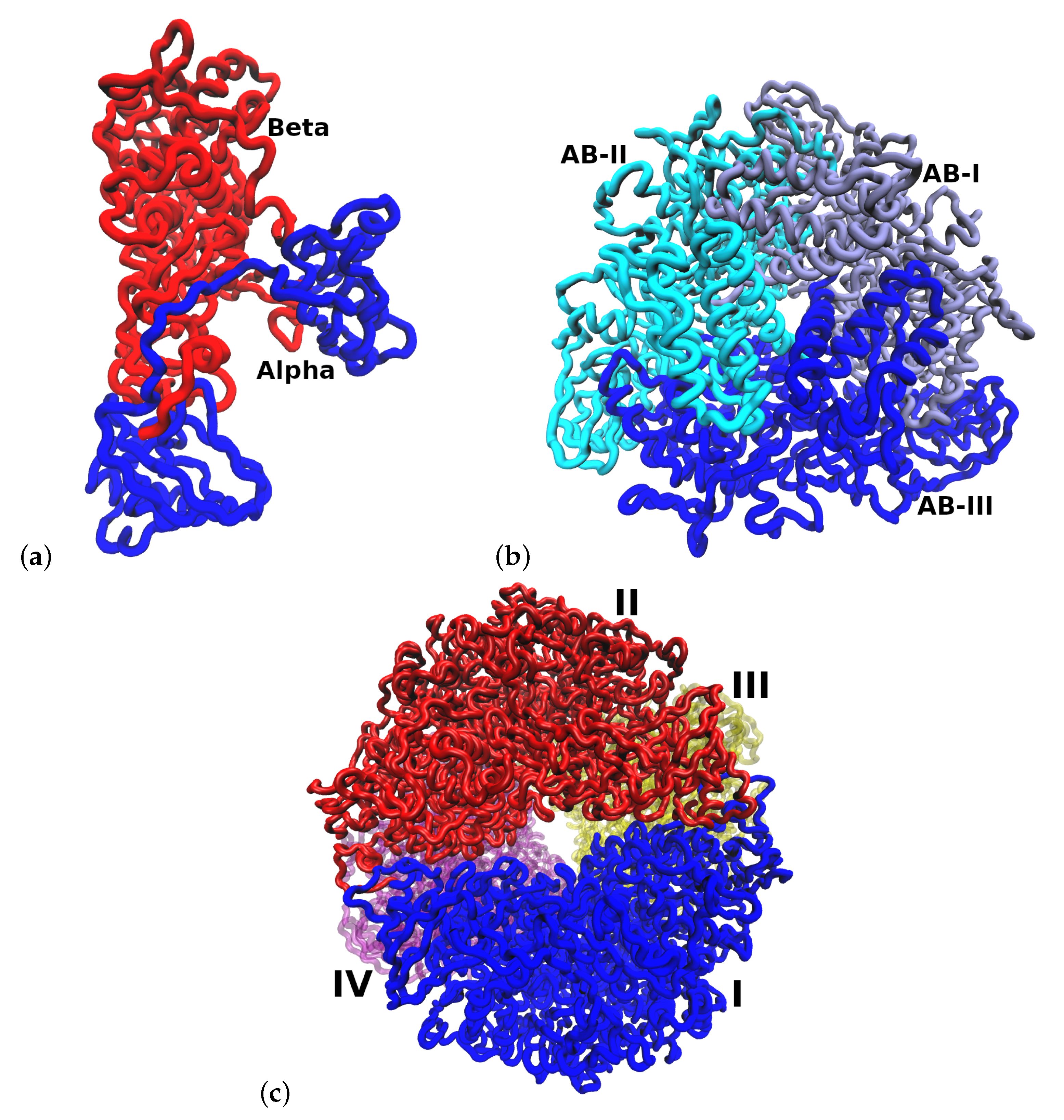
2.1. Multimeric Protein Preparation
2.2. Protonation States of Urease at Different pHs
2.3. Molecular Dynamic Simulations
3. Results and Discussion
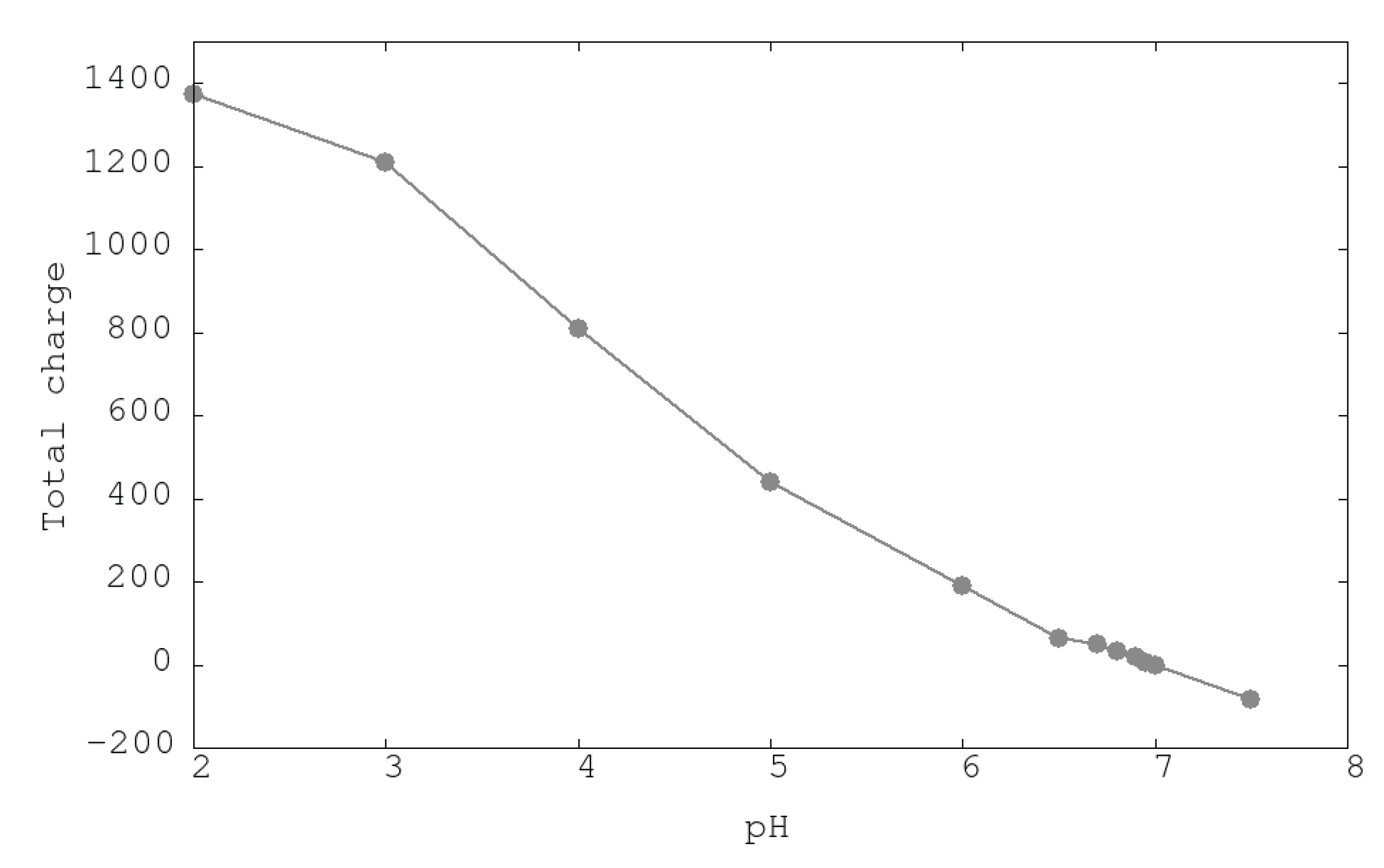
3.1. Urease Charge as a Function of pH
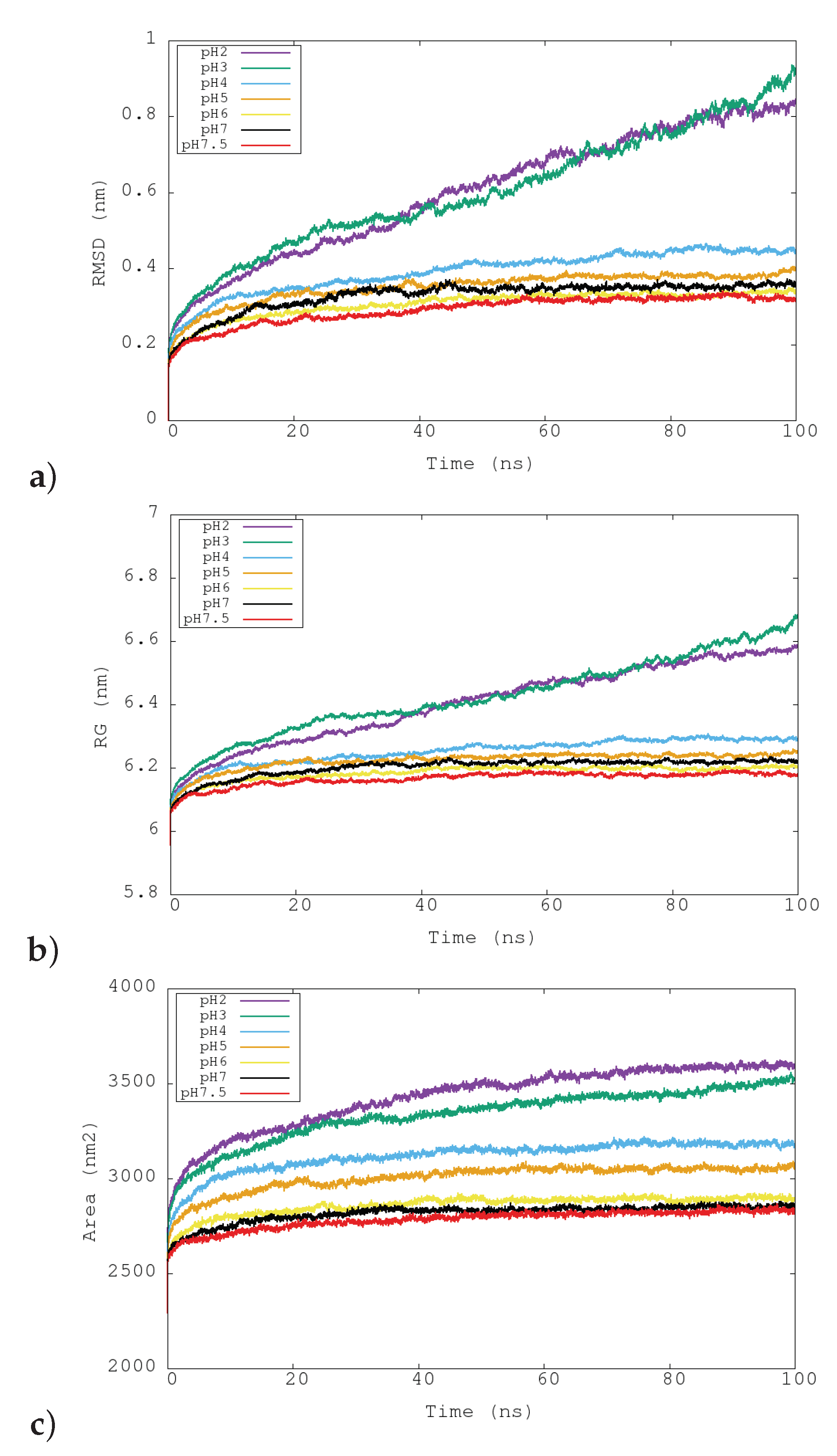
3.2. Structural Changes at Different pHs: RMSD, RG and SASA
3.3. Analysis of Stability at Different pHs: HB and SB
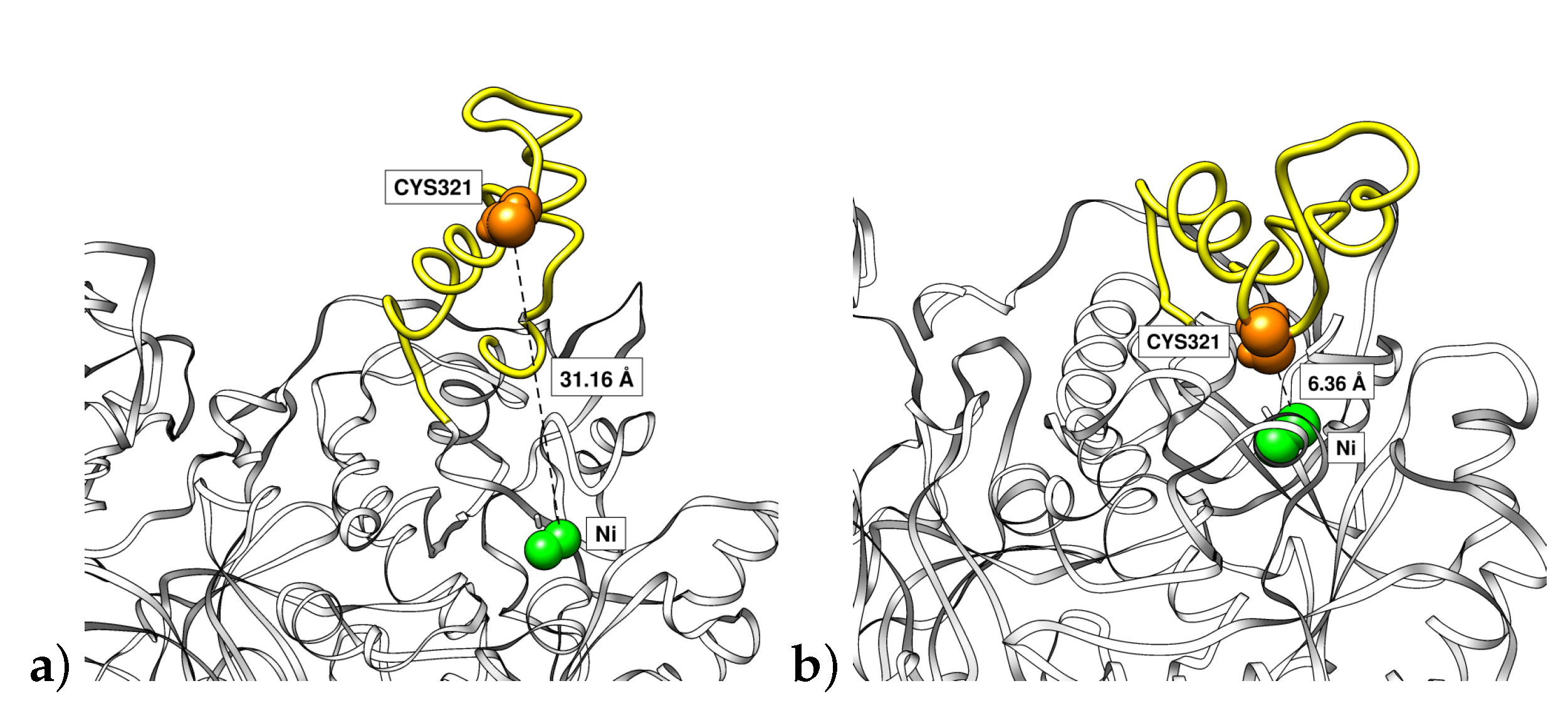
3.4. Mobile Flap at Different pHs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HB | hydrogen bond |
| HP | Helicobacter pylori |
| MD | molecular dynamics |
| QM | quantum mechanical |
| SASA | solvent-accessible surface area (SASA) |
| SB | salt bridge |
| SGCMC | semi-grand canonical Monte Carlo |
| RG | radius of gyration |
| RMSD | root-mean-square deviation |
References
- Ansari, S.; Yamaoka, Y. Survival of Helicobacter pylori in gastric acidic territory. Helicobacter 2017, 22, 1–13. [Google Scholar] [CrossRef]
- Ha, N.C.; Oh, S.T.; Sung, J.Y.; Cha, K.A.; Lee, M.H.; Oh, B.H. Supramolecular assembly and acid resistance of Helicobacter pylori urease. Nat. Struct. Biol. 2001, 8, 505–509. [Google Scholar] [CrossRef]
- Schreiber, S.; Bücker, R.; Groll, C.; Azevedo-Vethacke, M.; Garten, D.; Scheid, P.; Friedrich, S.; Gatermann, S.; Josenhans, C.; Suerbaum, S. Rapid loss of motility of Helicobacter pylori in the gastric lumen in vivo. Infect. Immun. 2005, 73, 1584–1589. [Google Scholar] [CrossRef] [PubMed]
- Ottemann, K.M.; Lowenthal, A.C. Helicobacter pylori uses motility for initial colonization and to attain robust infection. Infect. Immun. 2002, 70, 1984–1990. [Google Scholar] [CrossRef] [PubMed]
- Kao, C.Y.; Sheu, B.S.; Wu, J.J. Helicobacter pylori infection: An overview of bacterial virulence factors and pathogenesis. Biomed. J. 2016, 39, 14–23. [Google Scholar] [CrossRef] [PubMed]
- Arora, R.; Issar, U.; Kakkar, R. In Silico study of the active site of Helicobacter pylori urease and its inhibition by hydroxamic acids. J. Mol. Graph. Model. 2018, 83, 64–73. [Google Scholar] [CrossRef]
- Estiu, G.; Merz, K.M. Catalyzed decomposition of urea. Molecular dynamics simulations of the binding of urea to urease. Biochemistry 2006, 45, 4429–4443. [Google Scholar] [CrossRef][Green Version]
- Roberts, B.P.; Miller, B.R.; Roitberg, A.E.; Merz, K.M. Wide-open flaps are key to urease activity. J. Am. Chem. Soc. 2012, 134, 9934–9937. [Google Scholar] [CrossRef]
- Minkara, M.S.; Ucisik, M.N.; Weaver, M.N.; Merz, K.M., Jr. Molecular dynamics study of Helicobacter pylori urease. J. Chem. Theory Comput. 2014, 10, 1852–1862. [Google Scholar] [CrossRef]
- Xu, Y.P.P.; Qin, J.; Sun, S.M.M.; Liu, T.T.T.; Zhang, X.L.L.; Qian, S.S.S.; Zhu, H.L.L. Synthesis, crystal structures, molecular docking and urease inhibitory activity of nickel(II) complexes with 3-pyridinyl-4-amino-5-mercapto-1,2,4-triazole. Inorganica Chim. Acta 2014, 423, 469–476. [Google Scholar] [CrossRef]
- Macomber, L.; Minkara, M.S.; Hausinger, R.P.; Merz, K.M., Jr. Reduction of urease activity by interaction with the flap covering the active site. J. Chem. Inf. Model. 2015, 55, 354–361. [Google Scholar] [CrossRef] [PubMed]
- Sumner, J.B. The isolation and crystallization of the enzyme urease preliminary paper. J. Biol. Chem. 1926, 69, 435–441. [Google Scholar]
- Anderson, D.E.; Becktel, W.J.; Dahlquist, F.W. pH-induced denaturation of proteins: A single salt bridge contributes 3-5 kcal/mol to the free energy of folding of T4 lysozyme. Biochemistry 1990, 29, 2403–2408. [Google Scholar] [CrossRef] [PubMed]
- Bashford, D.; Karplus, M. pKa’s of ionizable groups in proteins: Atomic detail from a continuum electrostatic model. Biochemistry 1990, 29, 10219–10225. [Google Scholar] [CrossRef]
- Scott, D.R.; Weeks, D.; Hong, C.; Postius, S.; Melchers, K.; Sachs, G. The role of internal urease in acid resistance of Helicobacter pylori. Gastroenterology 1998, 114, 58–70. [Google Scholar] [CrossRef]
- Madurga, S.; Garcés, J.L.; Companys, E.; Rey-Castro, C.; Salvador, J.; Galceran, J.; Vilaseca, E.; Puy, J.; Mas, F. Ion binding to polyelectrolytes: Monte Carlo simulations versus classical mean field theories. Theor. Chem. Accounts 2009, 123, 127–135. [Google Scholar] [CrossRef]
- Madurga, S.; Rey-Castro, C.; Pastor, I.; Vilaseca, E.; David, C.; Garcés, J.L.; Puy, J.; Mas, F. A semi-grand canonical Monte Carlo simulation model for ion binding to ionizable surfaces: Proton binding of carboxylated latex particles as a case study. J. Chem. Phys. 2011, 135, 184103. [Google Scholar] [CrossRef]
- Blanco, P.M.; Madurga, S.; Mas, F.; Garcés, J.L. Coupling of charge regulation and conformational equilibria in linearweak polyelectrolytes: Treatment of long-range interactions via effective short-ranged and pH-dependent interaction parameters. Polymers 2018, 10, 811. [Google Scholar] [CrossRef]
- Blanco, P.M.; Madurga, S.; Narambuena, C.F.; Mas, F.; Garcés, J.L. Role of Charge Regulation and Fluctuations in the Conformational and Mechanical Properties of Weak Flexible Polyelectrolytes. Polymers 2019, 11, 1962. [Google Scholar] [CrossRef]
- Olsson, M.H.; Søndergaard, C.R.; Rostkowski, M.; Jensen, J.H. PROPKA3: Consistent treatment of internal and surface residues in empirical p K a predictions. J. Chem. Theory Comput. 2011, 7, 525–537. [Google Scholar] [CrossRef]
- López, A.; Vilaseca, M.; Madurga, S.; Varese, M.; Tarragó, T.; Giralt, E. Analyzing slowly exchanging protein conformations by ion mobility mass spectrometry: Study of the dynamic equilibrium of prolyl oligopeptidase. J. Mass Spectrom. 2016, 51, 504–511. [Google Scholar] [CrossRef] [PubMed]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindah, E. Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Horn, H.W.; Swope, W.C.; Pitera, J.W.; Madura, J.D.; Dick, T.J.; Hura, G.L.; Head-Gordon, T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665–9678. [Google Scholar] [CrossRef] [PubMed]
- West, A.P.; Millar, M.R.; Tompkins, D.S. Effect of physical environment on survival of Helicobacter pylori. J. Clin. Pathol. 1992, 45, 228–231. [Google Scholar] [CrossRef][Green Version]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- Dunn, B.E.; Campbell, G.P.; Perez-Perez, G.; Blaser, M. Purification and characterization of urease from Helicobacter pylori. J. Biol. Chem. 1990, 265, 9464–9469. [Google Scholar] [PubMed]
- Turbett, G.R.; Høj, P.; Horne, R.; Mee, B.J. Purification and characterization of the urease enzymes of Helicobacter species from humans and animals. Infect. Immun. 1992, 60, 5259–5266. [Google Scholar] [CrossRef] [PubMed]
- Pinkse, M.W.H.; Maier, C.S.; Kim, J.i.; Oh, B.h.; Heck, A.J.R. Macromolecular assembly of Helicobacter pylori urease investigated by mass spectrometry. J. Mass Spectrom. 2003, 38, 315–320. [Google Scholar] [CrossRef] [PubMed]
- Scott, D.R.; Marcus, E.A.; Weeks, D.L.; Sachs, G. Mechanisms of acid resistance due to the urease system of Helicobacter pylori. Gastroenterology 2002, 123, 187–195. [Google Scholar] [CrossRef] [PubMed]
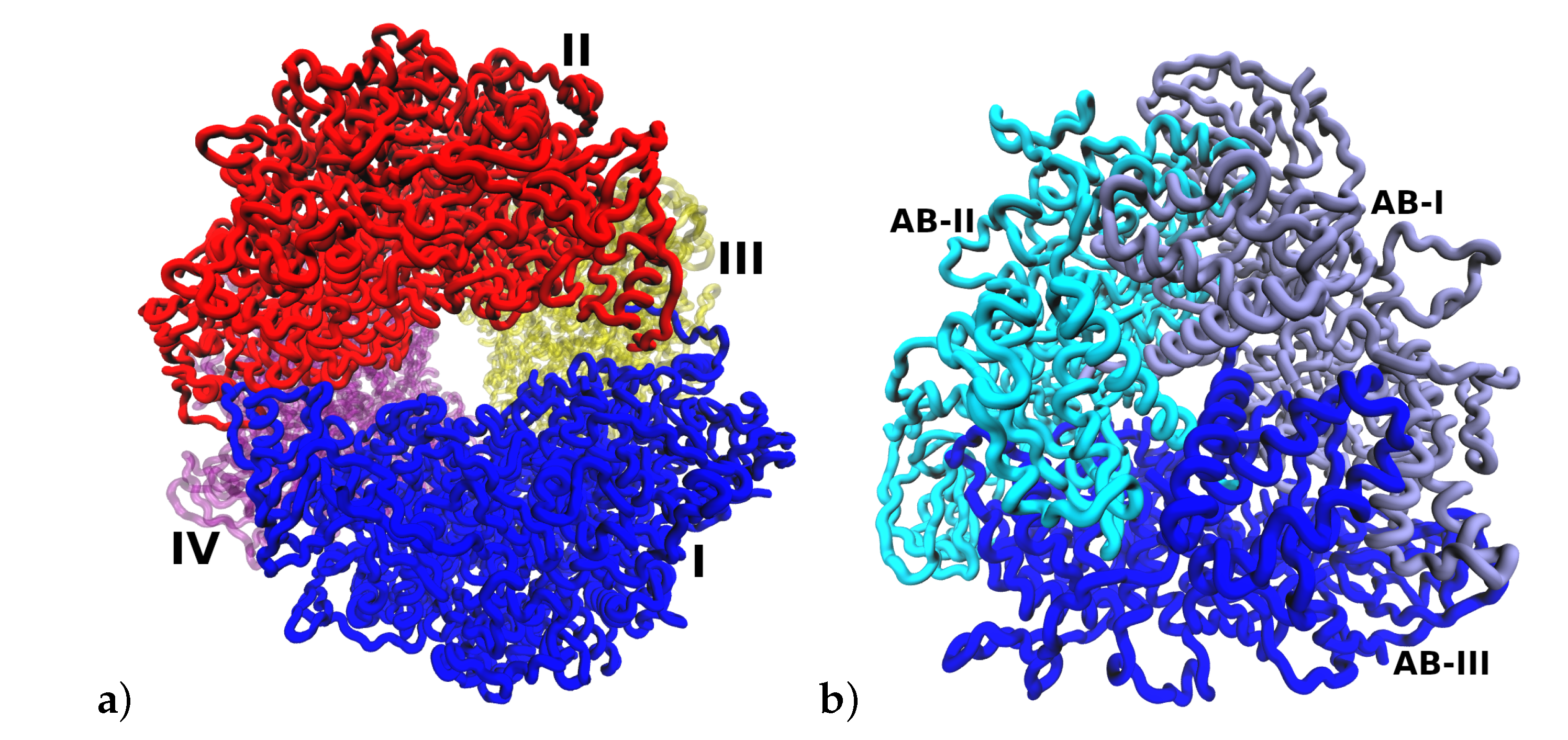
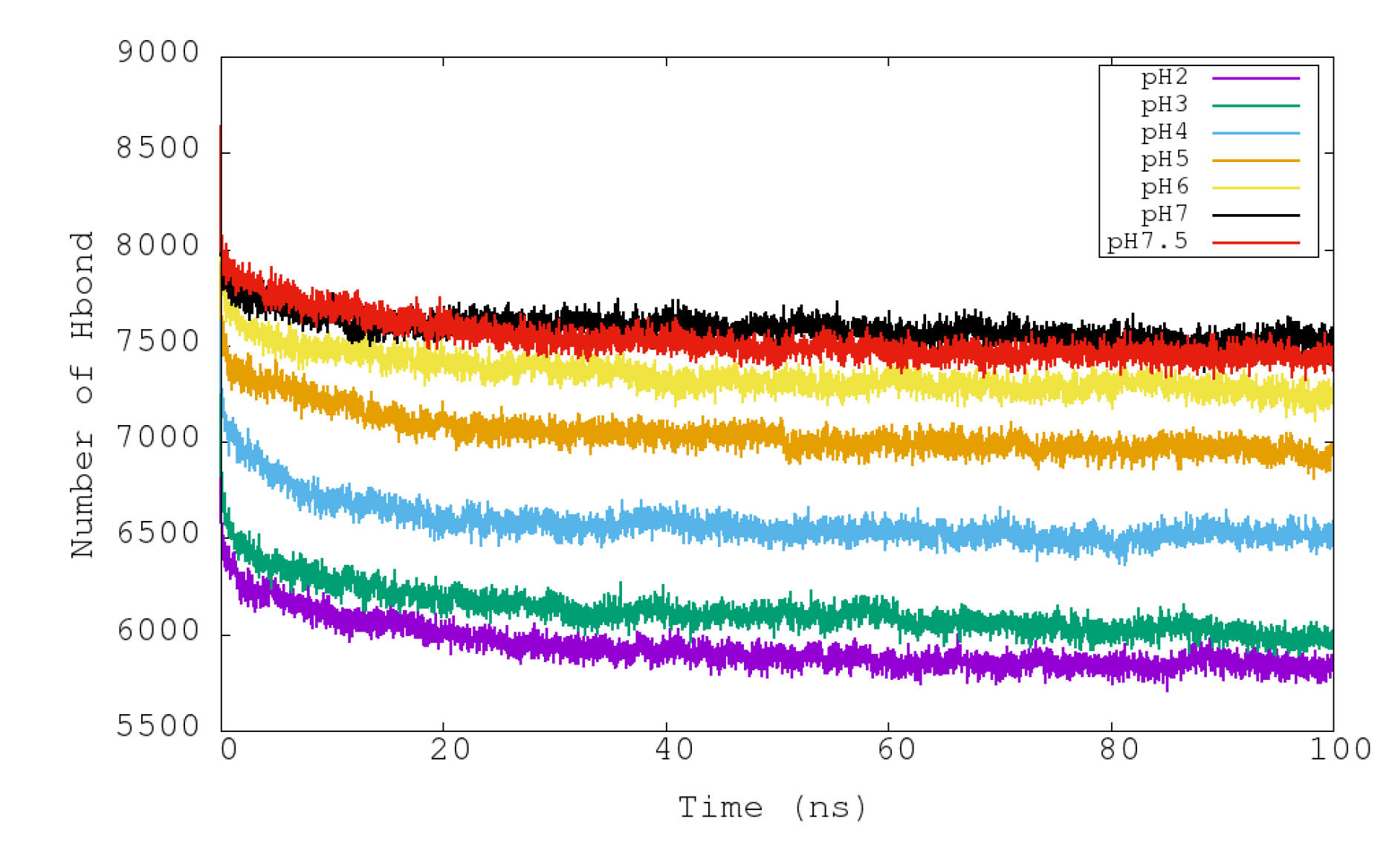

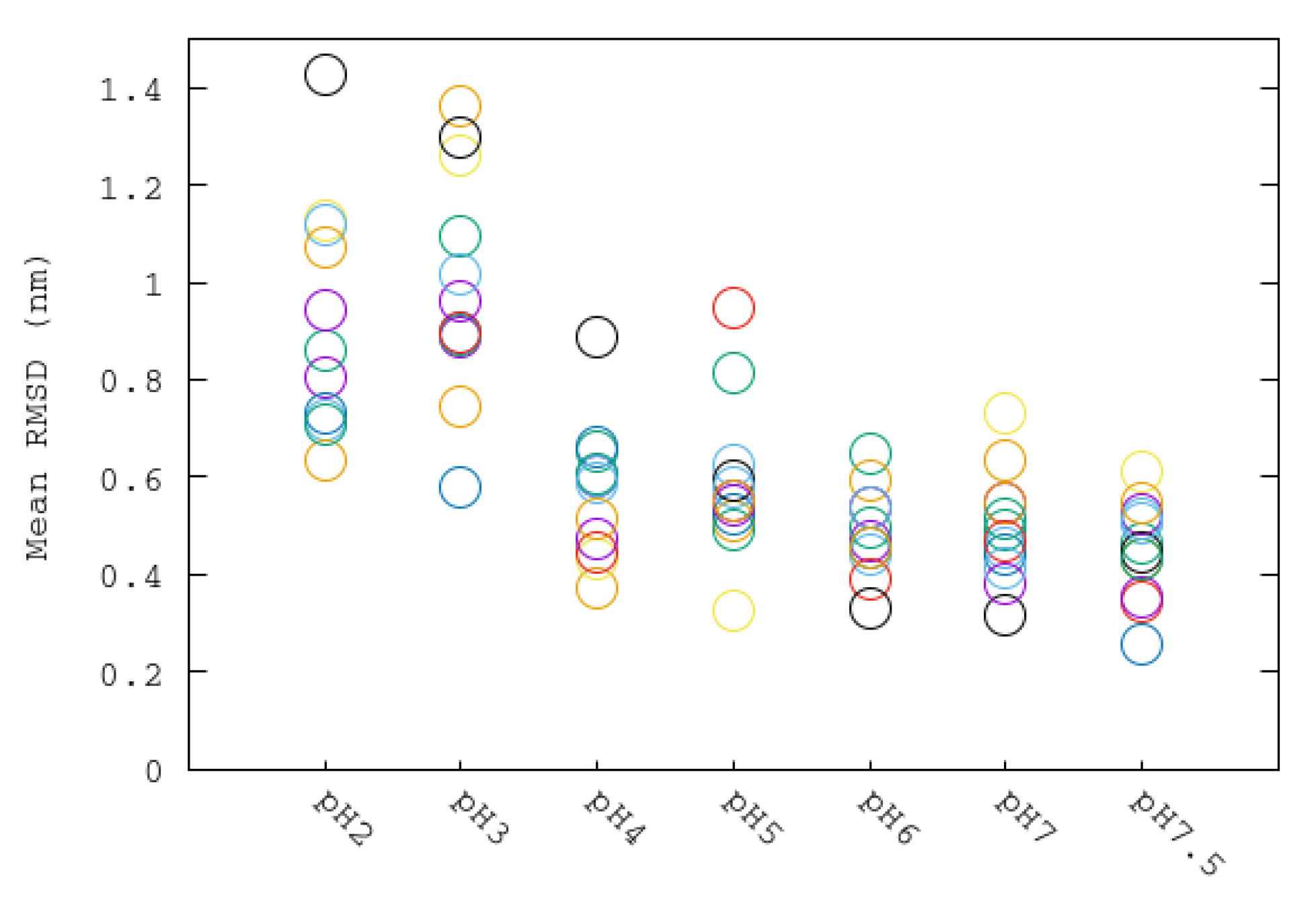
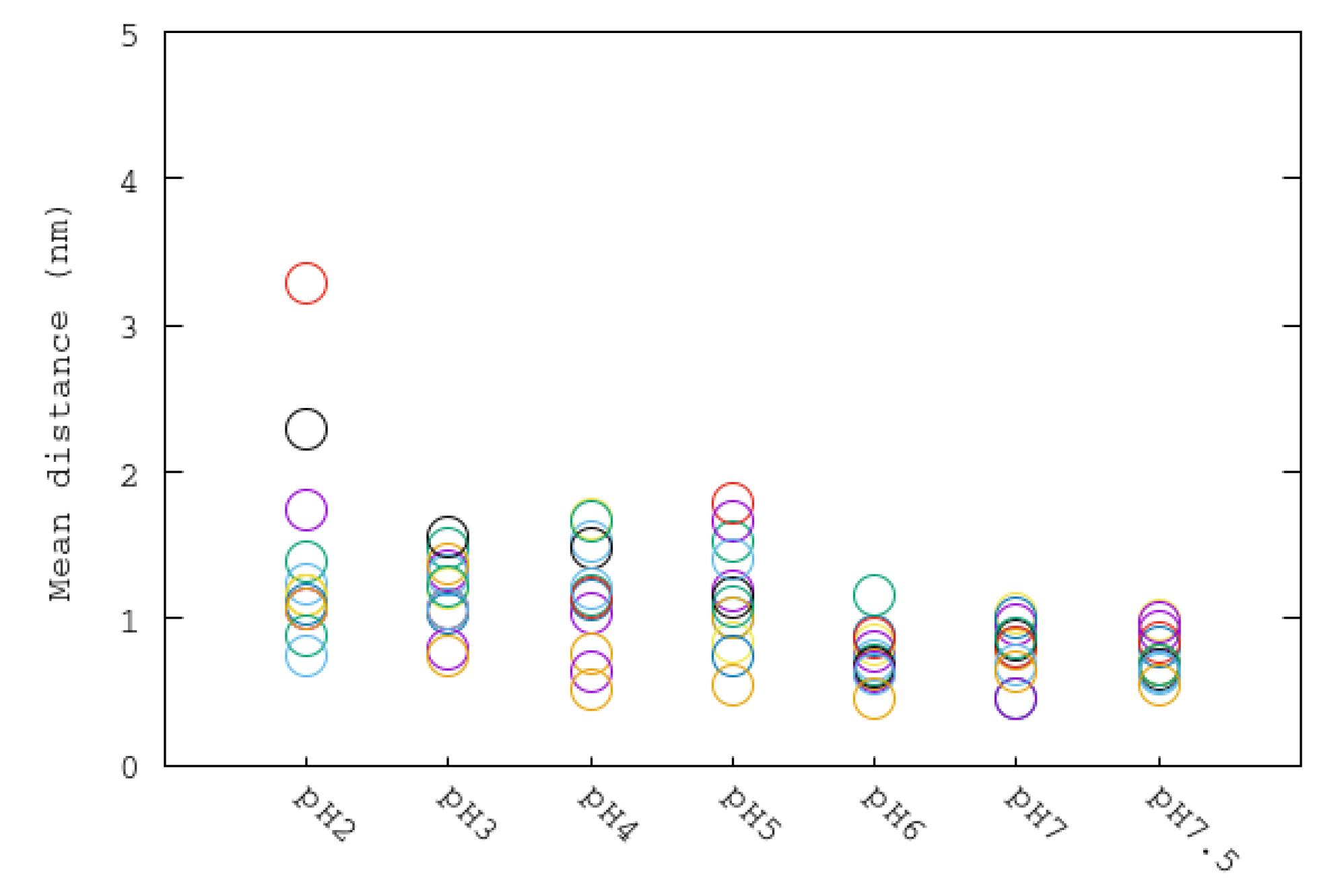
| System | ASP | GLU | ARG | LYS | HIS | Urease |
|---|---|---|---|---|---|---|
| pH2 | −7 | −33 | 360 | 792 | 237 | 1373 |
| pH3 | −73 | −99 | 360 | 792 | 204 | 1208 |
| pH4 | −246 | −281 | 360 | 791 | 162 | 810 |
| pH5 | −415 | −464 | 360 | 789 | 144 | 438 |
| pH6 | −505 | −566 | 360 | 778 | 98 | 189 |
| pH7 | −554 | −627 | 360 | 757 | 37 | −3 |
| PH7.5 | −575 | −653 | 359 | 744 | 18 | −83 |
| AA | Number | p |
|---|---|---|
| ASP | 624 | 4.7 ± 1.6 |
| GLU | 696 | 4.6 ± 1.6 |
| ARG | 360 | 12.3 ± 1.5 |
| LYS | 792 | 10.0 ± 1.2 |
| HIS | 324 | 4 ± 3 |
| pH | RMSD (nm) | RG (nm) | int-RG | ext-RG | SASA (nm) e | HB | SB | Exp. Activity |
|---|---|---|---|---|---|---|---|---|
| 2 | 0.81 ± 0.02 | 6.56 ± 0.01 | 2.69 ± 0.02 | 8.34 ± 0.02 | 3589 ± 13 | 5853 ± 40 | 96 | 0 |
| 3 | 0.83 ± 0.05 | 6.60 ± 0.03 | 2.79 ± 0.04 | 8.40 ± 0.04 | 3482 ± 28 | 6044 ± 56 | 131 | 0 |
| 4 | 0.45 ± 0.01 | 6.29 ± 0.01 | 2.46 ± 0.01 | 8.10 ± 0.01 | 3182 ± 11 | 6518 ± 41 | 183 | 0 |
| 5 | 0.38 ± 0.01 | 6.24 ± 0.01 | 2.41 ± 0.01 | 8.07 ± 0.01 | 3052 ± 11 | 6973 ± 42 | 179 | 0.38 |
| 6 | 0.33 ± 0.01 | 6.20 ± 0.01 | 2.40 ± 0.01 | 8.02 ± 0.01 | 2893 ± 11 | 7287 ± 44 | 182 | 1.75 |
| 7 | 0.35 ± 0.01 | 6.22 ± 0.01 | 2.42 ± 0.01 | 8.03 ± 0.01 | 2852 ± 9 | 7549 ± 47 | 169 | 4.50 |
| 7.5 | 0.32 ± 0.01 | 6.18 ± 0.01 | 2.35 ± 0.01 | 8.01 ± 0.01 | 2828 ± 11 | 7460 ± 41 | 179 | 5.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barazorda-Ccahuana, H.L.; Gómez, B.; Mas, F.; Madurga, S. Effect of pH on the Supramolecular Structure of Helicobacter pylori Urease by Molecular Dynamics Simulations. Polymers 2020, 12, 2713. https://doi.org/10.3390/polym12112713
Barazorda-Ccahuana HL, Gómez B, Mas F, Madurga S. Effect of pH on the Supramolecular Structure of Helicobacter pylori Urease by Molecular Dynamics Simulations. Polymers. 2020; 12(11):2713. https://doi.org/10.3390/polym12112713
Chicago/Turabian StyleBarazorda-Ccahuana, Haruna L., Badhin Gómez, Francesc Mas, and Sergio Madurga. 2020. "Effect of pH on the Supramolecular Structure of Helicobacter pylori Urease by Molecular Dynamics Simulations" Polymers 12, no. 11: 2713. https://doi.org/10.3390/polym12112713
APA StyleBarazorda-Ccahuana, H. L., Gómez, B., Mas, F., & Madurga, S. (2020). Effect of pH on the Supramolecular Structure of Helicobacter pylori Urease by Molecular Dynamics Simulations. Polymers, 12(11), 2713. https://doi.org/10.3390/polym12112713