Degradation of Mechanical Properties of Pine Wood Under Symmetric Axial Cyclic Loading Parallel to Grain
Abstract
1. Introduction
2. Materials and Methods
2.1. Preliminary Tests
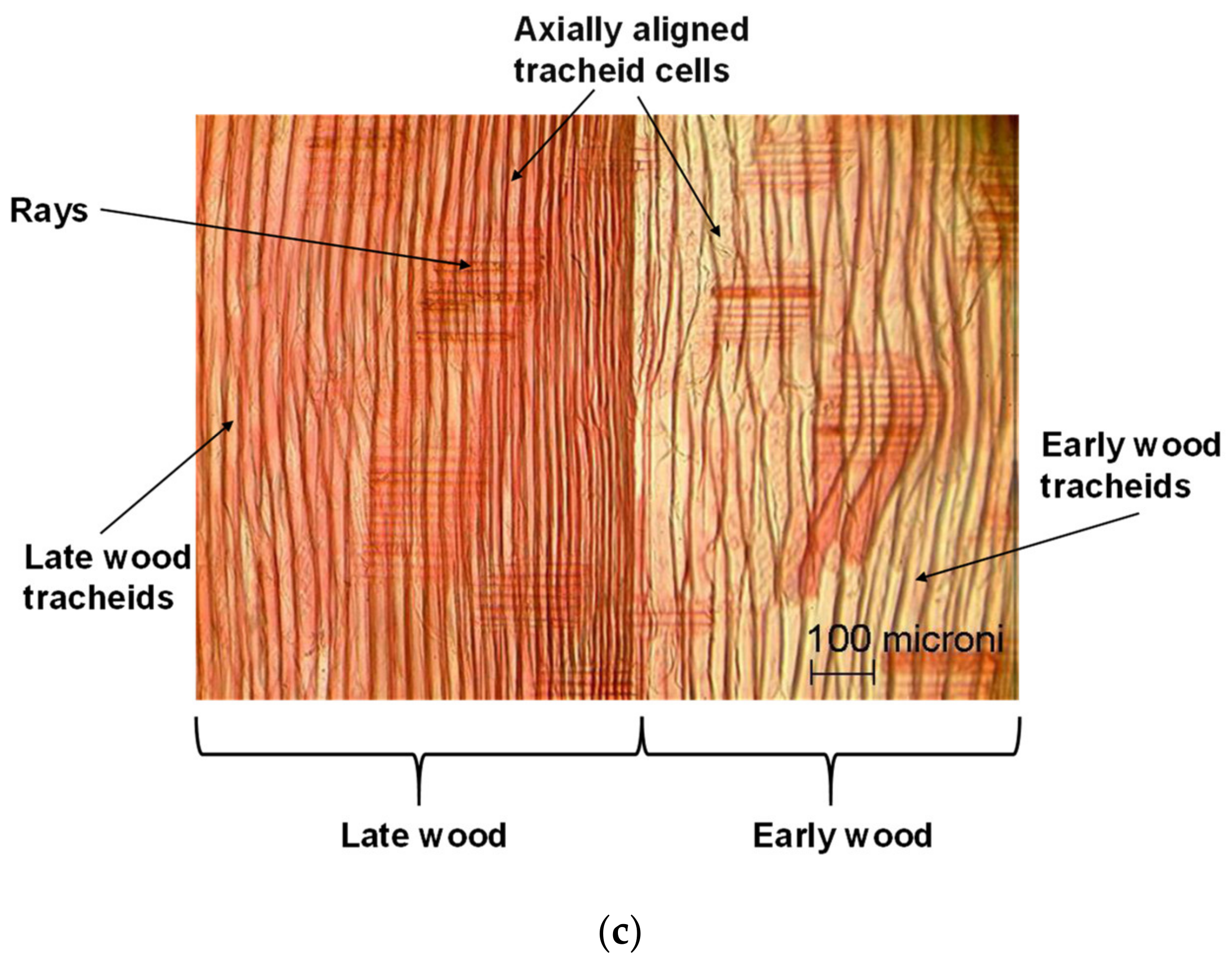
2.2. Materials
2.3. Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gong, M.; Smith, I. Short-term mechanical behaviour of softwood in high-stress-level compression parallel to grain. In Proceedings of the Fourth International Conference on the Development of Wood Science, Wood Technology and Forestry, Missenden Abbey, UK, 14–16 July 1999; pp. 25–34. [Google Scholar]
- Ion, F.; Taranu, N.; Secu, A.; Entuc, I.S.; Scutaru, M.C.; Ungureanu, D. Evaluation of the wood strength class using the experimental approach. Bull. Polytech. Inst. IasiConstr. Archit. Sect. 2017, 63, 121–132. [Google Scholar]
- Silvestru Grigore, C.V.; Dinulică, F.; Spârchez, G.; Hălălișan, A.F.; Dincă, L.C.; Enescu, R.E.; Crișan, V.E. Radial Growth Behavior of Pines on Romanian Degraded Lands. Forests 2018, 9, 213. [Google Scholar] [CrossRef]
- Christoforo, A.L.; Panzera, T.H.; Lahr, F.A.R. Estimation of tensile strength parallel to grain of wood species. Eng. Agric. 2019, 39, 533–536. [Google Scholar] [CrossRef]
- Dai, D.; Fan, M. Wood fibres as reinforcements in natural fibre composites: Structure, properties, processing and applications. In Natural Fibre Reinforcements. Materials, Processes and Applications; Woodhead Publishing: Sawston, UK, 2014; pp. 3–65. [Google Scholar] [CrossRef]
- Feio, A.; Machado, J.; Lourenco, P. Parellel to the grain behavior and NDT correlations for chestnut wood (Castanea sativa Mill). In Proceedings of the International Conference “Conservation of Historic Wooden Structures”, Florence, Italy, 22–27 February 2005. [Google Scholar]
- Fakoor, M.; Sabour, M.H.; Khansari, N.M. A new approach for investigation of damage zone properties in orthotropic materials. Eng. Solid Mech. 2014, 2, 283–292. [Google Scholar] [CrossRef]
- Gaff, M.; Gašparìk, M. Effect of cyclic loading on modulus of elasticity of Aspen wood. Bioresources 2015, 10, 290–298. [Google Scholar] [CrossRef][Green Version]
- Konstantinov, A.Y.; Lomunov, A.K.; Iuzhina, T.N.; Gray, G.T., III. Investigation of wood anisotropy under dynamic loading. Strength Ductility Probl. 2018, 80, 555–565. [Google Scholar] [CrossRef][Green Version]
- Pečnik, J.G.; Kutnar, A.; Militz, H.; Schwarzkopf, M.; Schwager, H. Fatigue behavior of beech and pine wood modified with low molecular weight phenol-formaldehyde resin. Holzforschung 2020. published online. [Google Scholar] [CrossRef]
- Sharapov, E.; Mahnert, K.C.; Militz, H. Residual strength of thermally modified Scots pine after fatigue testing in flexure. Eur. J. Wood Wood Prod. 2016, 74, 875–884. [Google Scholar] [CrossRef]
- Pinho, S.T.; Iannucci, L.; Robinson, P. Physically based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking. Part II: FE implementation. Compos. Part A 2006, 37, 766–777. [Google Scholar] [CrossRef]
- Yildirim, M.N.; Uysal, B.; Ozcifci, A.; Ertas, A.H. Determination of fatigue and static strength of scots pine and beech wood. Wood Res. 2015, 60, 679–686. [Google Scholar]
- Hassani, M.M.; Wittel, F.K.; Hering, S.; Herrmann, H.J. Rheological Model for Wood. Comp. Method Appl. M 2014, 283, 1032–1060. [Google Scholar] [CrossRef]
- Andrianopoulos, N.; Manolopoulos, V. Can Coulomb criterion be generalized in case of ductile materials? An application to Bridgman experiments. Int. J. Mech. Sci. 2012, 54, 241–248. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Șova, D.; Savin, A.; Iliaș, N.; Gorbacheva, G. Physical and Mechanical Properties of Ammonia- Treated Black Locust Wood. Polymers 2020, 12, 377. [Google Scholar] [CrossRef] [PubMed]
- Stanciu, M.D.; Teodorescu, D.H.; Tămaș, F.; Terciu, O.M. Mechanical and Rheological Behaviour of Composites Reinforced with Natural Fibres. Polymers 2020, 12, 1402. [Google Scholar] [CrossRef] [PubMed]
- EN 384. Structural Timber. In Determination of Characteristic Values of Mechanical Properties and Density; CEN European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- ASTM D143-14 Standard Test Method for Small Clear Specimen of Timber; American Society for Testing Material Standard: West Conshohocken, PA, USA, 2014.
- EN 408. Timber Structures-Structural Timber and Glued Laminated Timber -Determination of Some Physical and Mechanical Properties; British Standards Institution: London, UK, 2003. [Google Scholar]
- Varenik, K.A.; Varenik, A.S.; Sanzharovskij, R.C. Boltzmann principle of superposition in the theory of wood creep for deformations in time. In IOP Conf. Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 441, p. 012057. [Google Scholar] [CrossRef]
- Metri, V.; Briels, W.J. Brownian dynamics investigation of the Boltzmann superposition principle for orthogonal superposition rheology. J. Chem. Phys. 2019, 150, 014903. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, D.; Fonseca, E.; Pinto, C.; Borges, P. Tensile strength of pine and ash woods–experimental and numerical study. In Proceedings of the 6th International Conference on Mechanics and Materials in Design, Ponta Delgada, Azores, 26–30 July 2015. [Google Scholar]
- Kloiber, M.; Drdácky´, M.; Machado, J.S.; Piazza, M.; Yamaguchi, N. Prediction of mechanical properties by means of semi-destructive methods: A review. Constr. Build. Mater. 2015, 101, 1215–1234. [Google Scholar] [CrossRef]
- Strömbro, J.; Gudmunson, P. Mechano-sorptive creep under compressive loading–A micromechanical model. Int. J. Solids Struct. 2008, 45, 2420–2450. [Google Scholar] [CrossRef]
- Gutkin, R.; Pinho, S.T. Combining damage and friction to model compressive damage growth in fibre-reinforced composites. J. Compos. Mater. 2014, 49, 2483–2495. [Google Scholar] [CrossRef]
- Sirumbal-Zapata, L.; Málaga-Chuquitaype, C.; Elghazouli, A. A three-dimensional plasticity-damage constitutive model for timber under cyclic loads. Comput. Struct. 2018, 195, 47–63. [Google Scholar] [CrossRef]
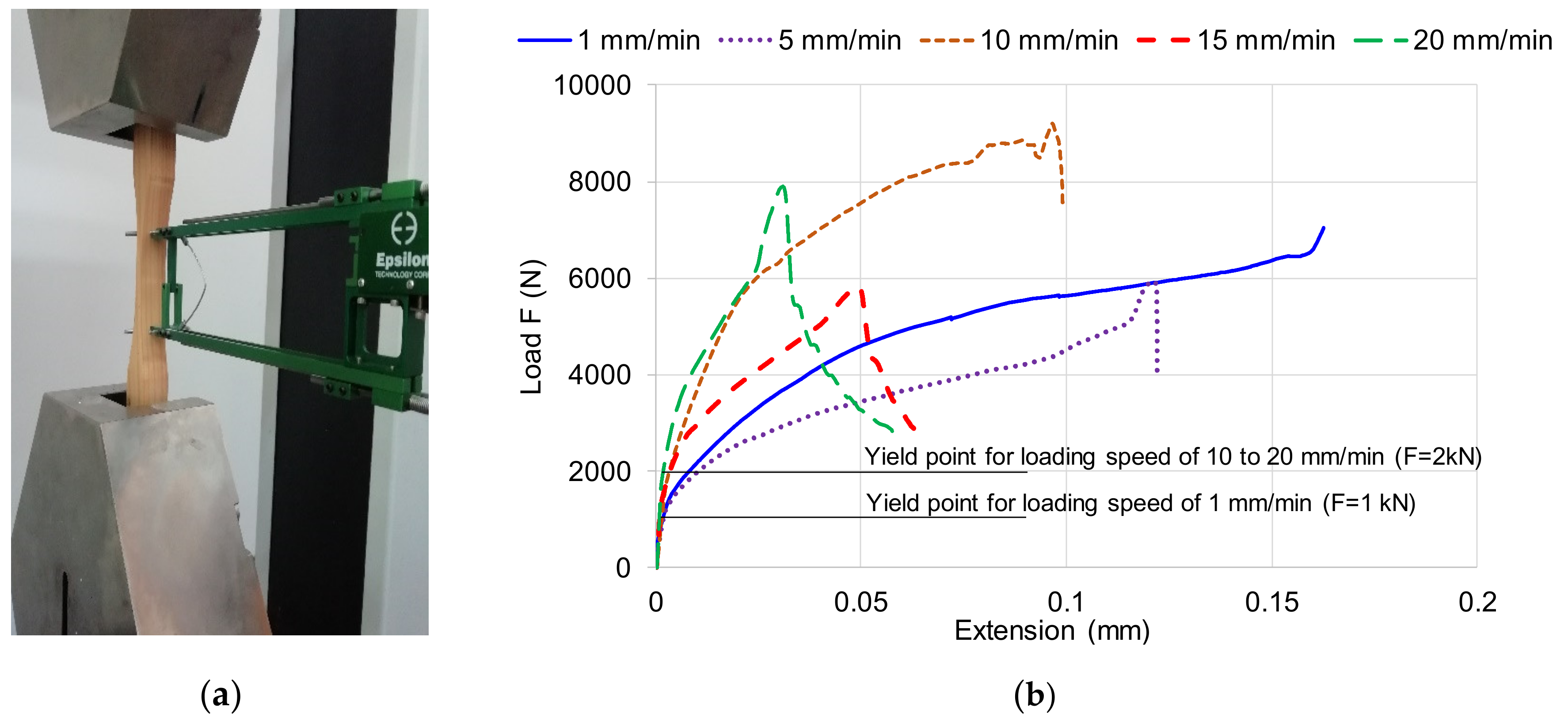
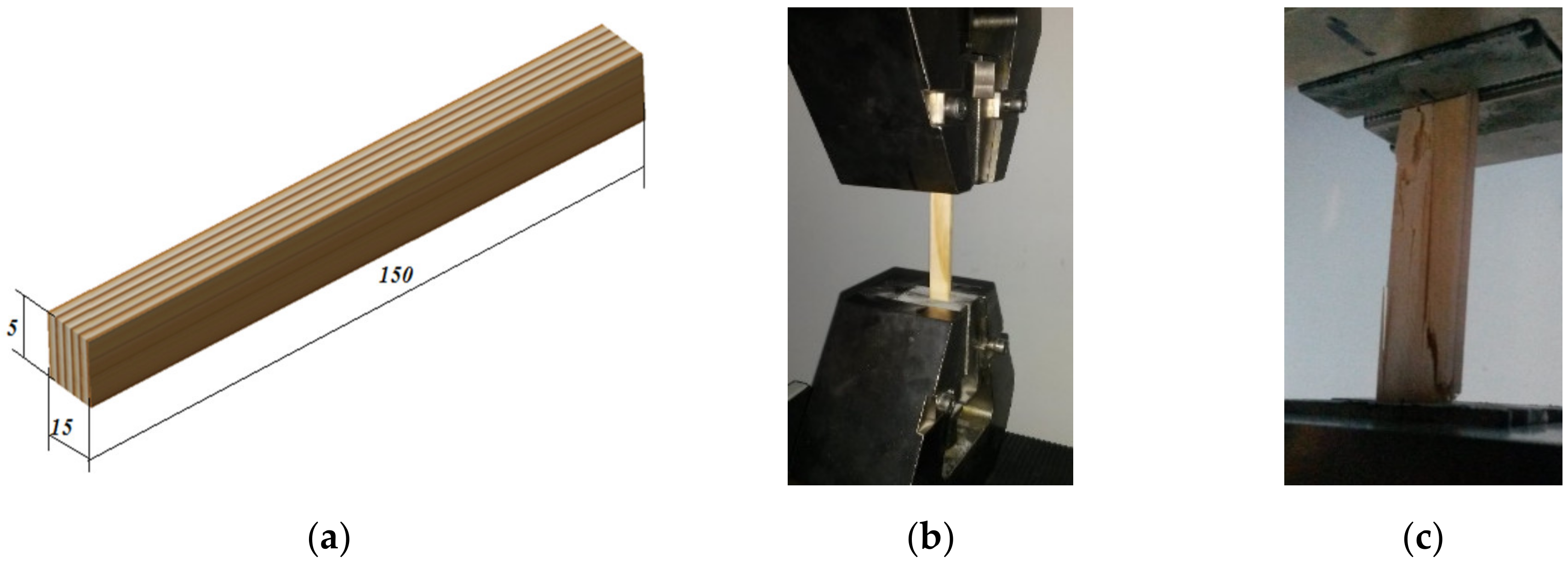
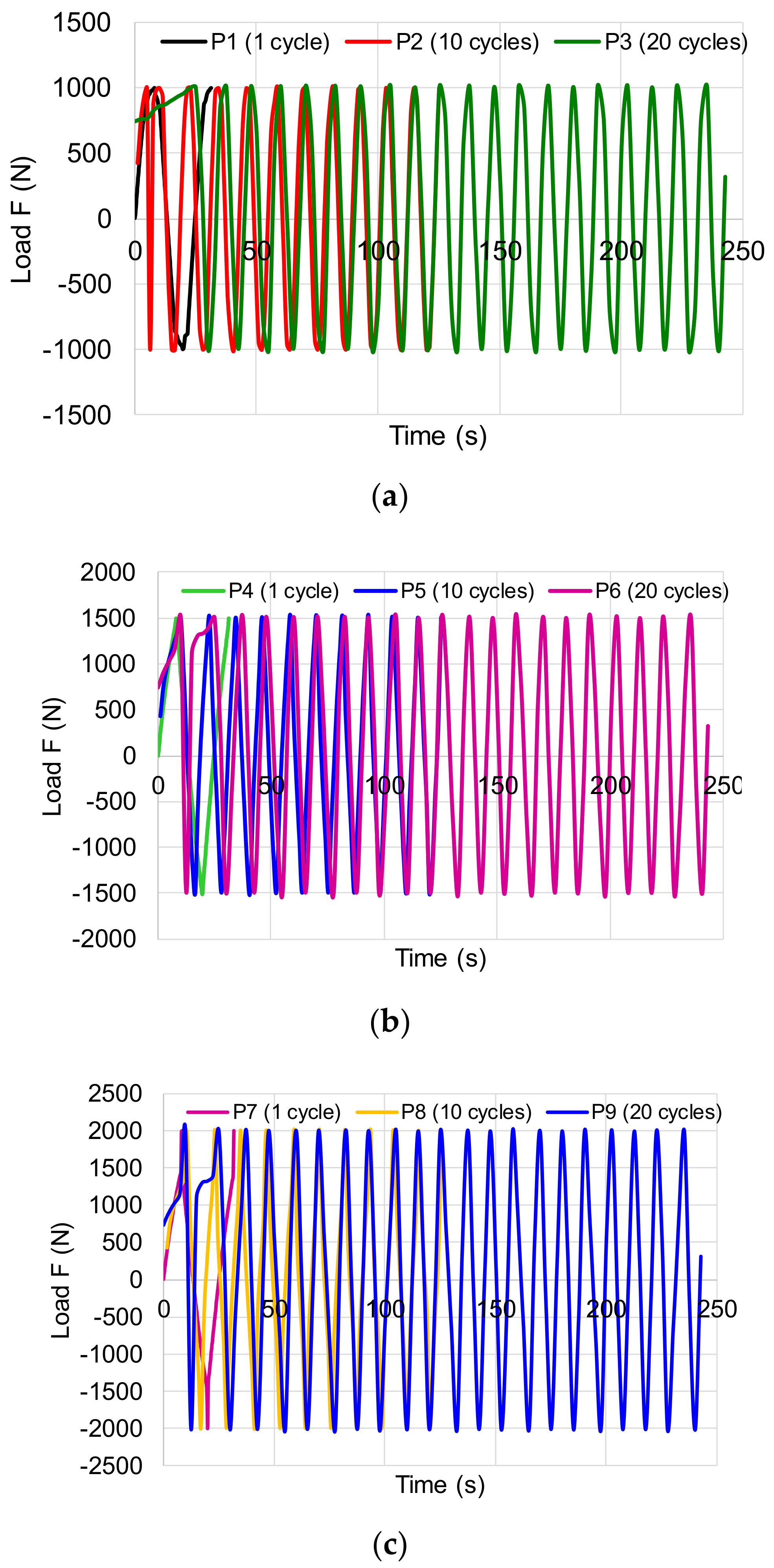



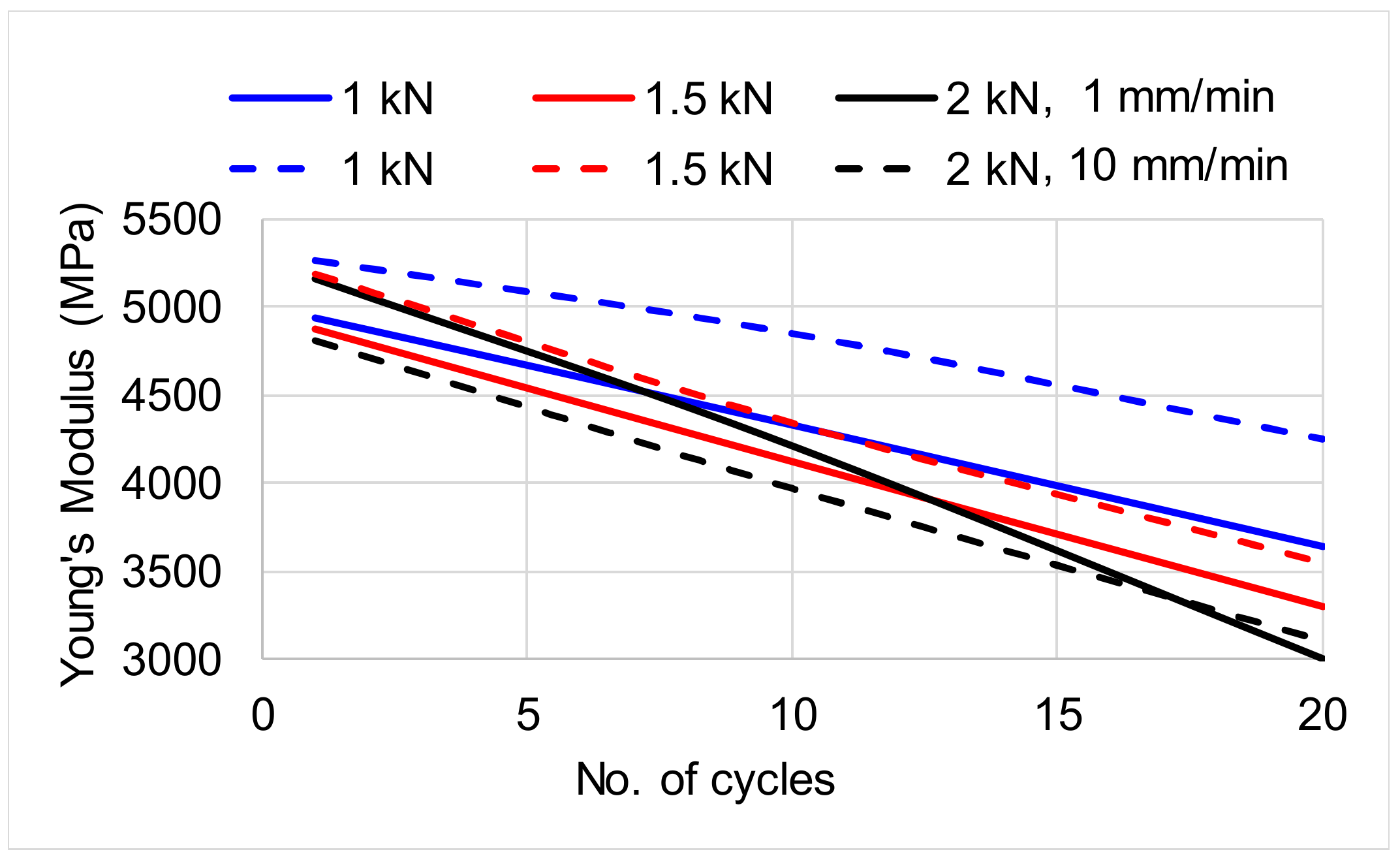
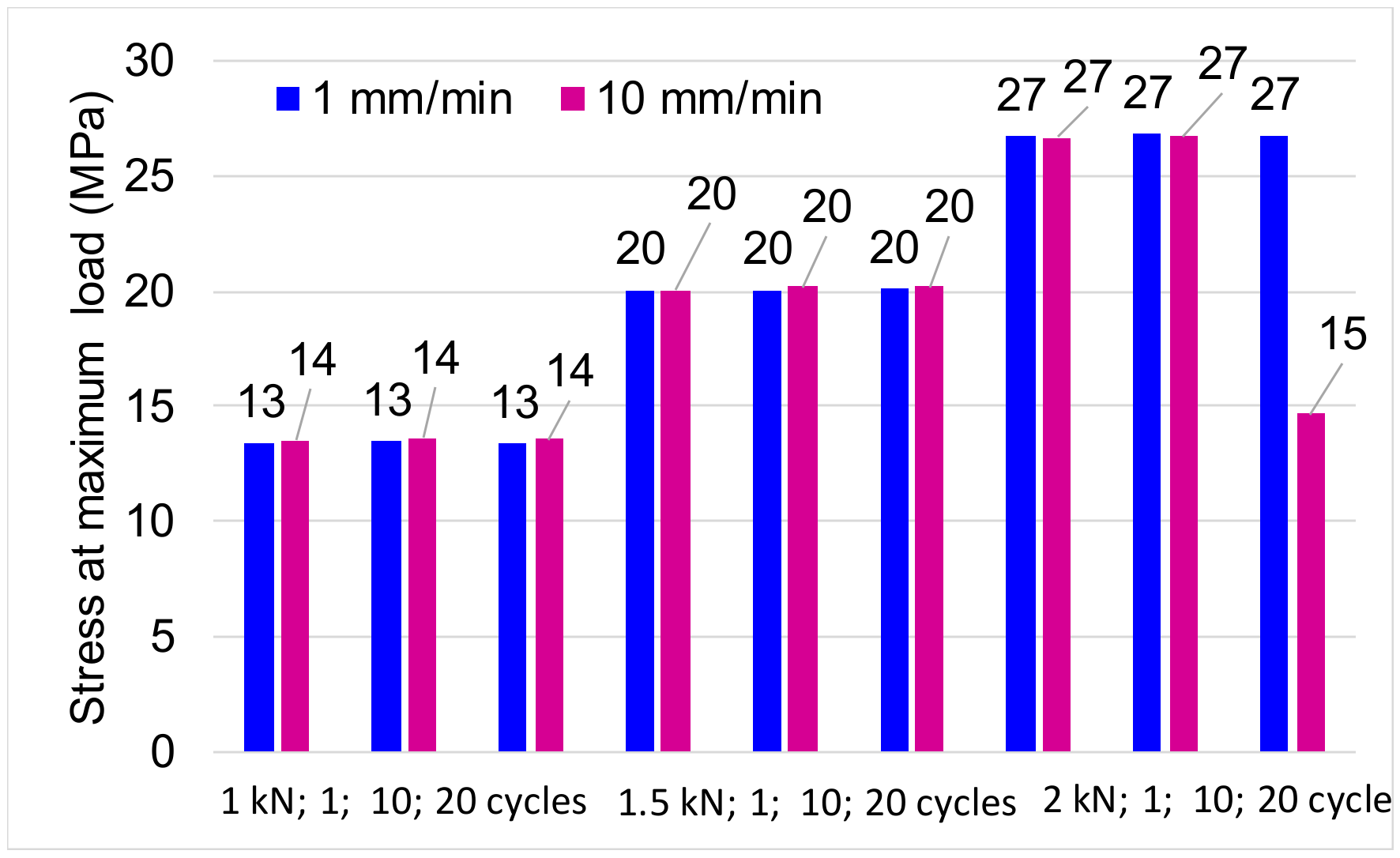
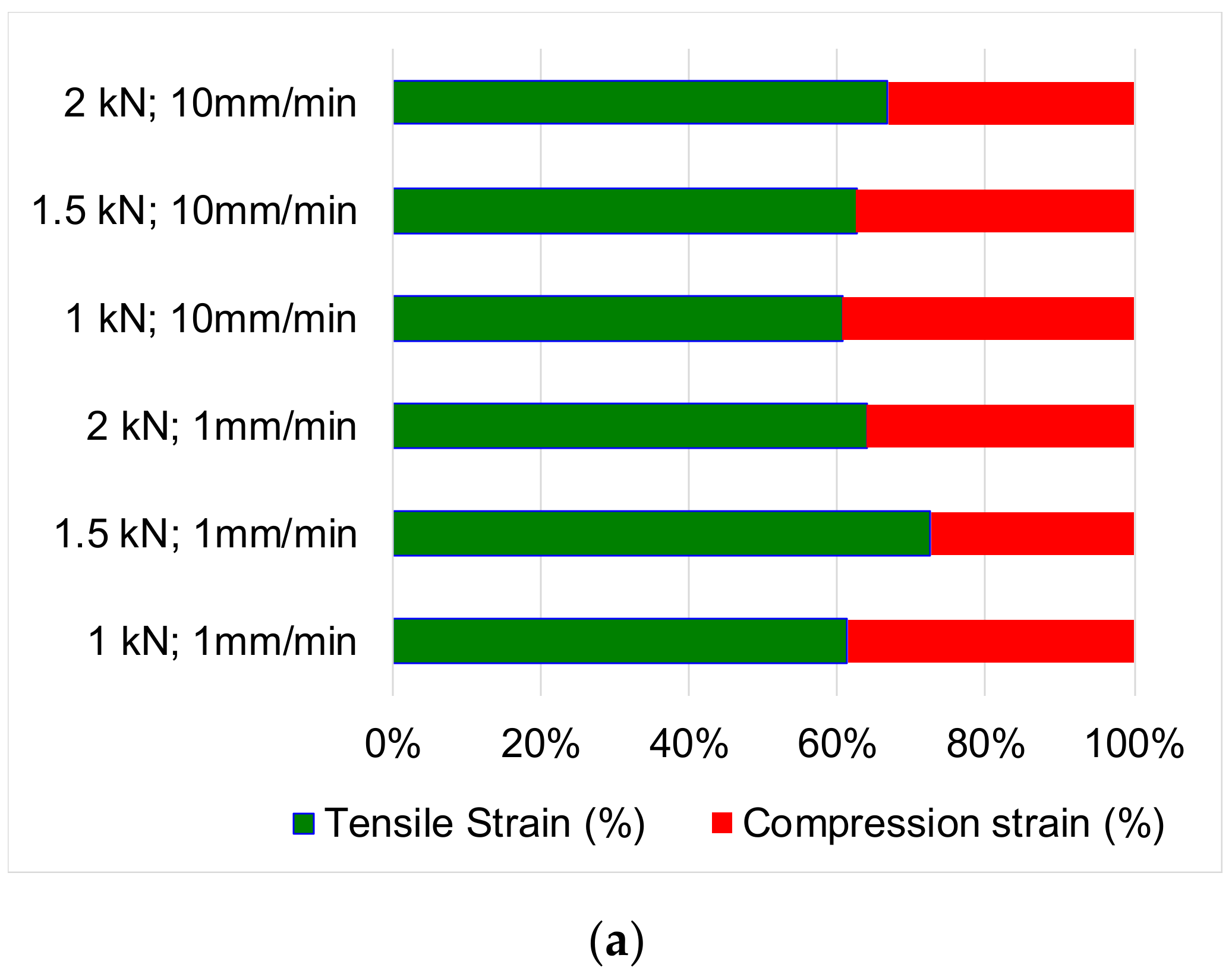

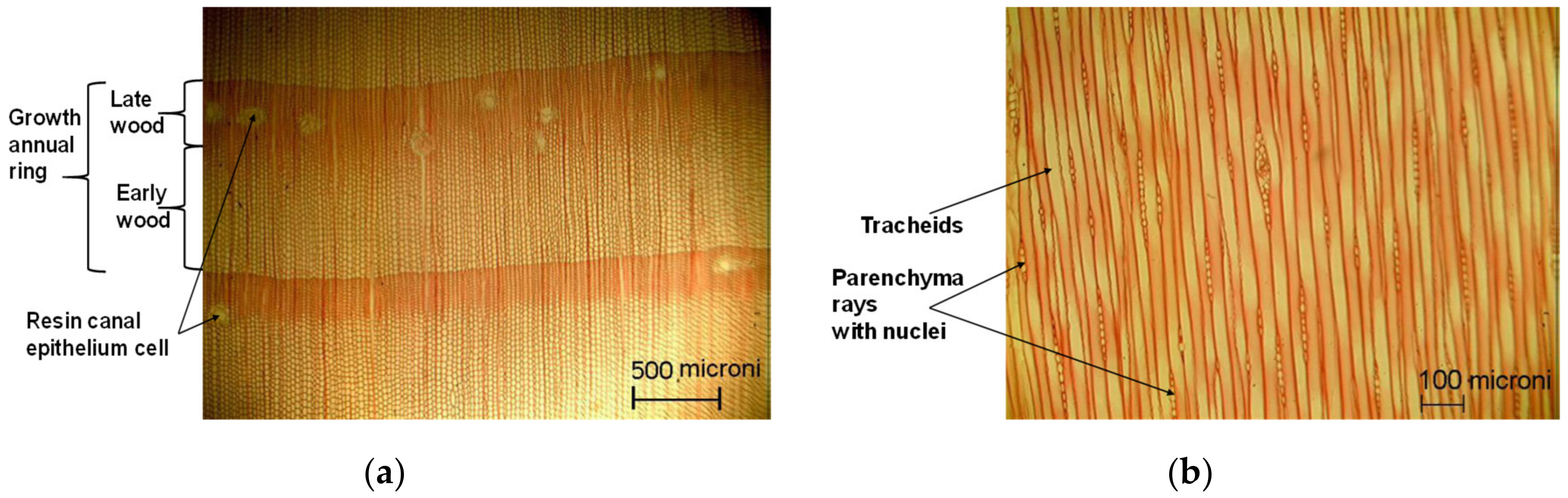


| Set of Tests | Sample | No of Cycles | Gauge Length (mm) | Speed (mm/min) | Width (mm) | Thickness (mm) | Area (mm2) | Limit of Tensile/ Compression Loading (kN) |
|---|---|---|---|---|---|---|---|---|
| A1 | P1 | 1 | 60 | 1 | 15 | 5 | 75 | ±1 |
| P2 | 10 | 60 | 1 | 15 | 5 | 75 | ±1 | |
| P3 | 20 | 60 | 1 | 15 | 5 | 75 | ±1 | |
| B1 | P4 | 1 | 60 | 1 | 5 | 5 | 75 | ±1.5 |
| P5 | 10 | 60 | 1 | 15 | 5 | 75 | ±1.5 | |
| P6 | 20 | 60 | 1 | 15 | 5 | 75 | ±1.5 | |
| C1 | P7 | 1 | 60 | 1 | 15 | 5 | 75 | ±2 |
| P8 | 10 | 60 | 1 | 15 | 5 | 75 | ±2 | |
| P9 | 20 | 60 | 1 | 15 | 5 | 75 | ±2 | |
| A10 | P10 | 1 | 60 | 10 | 15 | 5 | 75 | ±1 |
| P11 | 10 | 60 | 10 | 15 | 5 | 75 | ±1 | |
| P12 | 20 | 60 | 10 | 15 | 5 | 75 | ±1 | |
| B10 | P13 | 1 | 60 | 10 | 15 | 5 | 75 | ±1.5 |
| P14 | 10 | 60 | 10 | 15 | 5 | 75 | ±1.5 | |
| P15 | 20 | 60 | 10 | 15 | 5 | 75 | ±1.5 | |
| C10 | P16 | 1 | 60 | 10 | 15 | 5 | 75 | ±2 |
| P17 | 10 | 60 | 10 | 15 | 5 | 75 | ±2 | |
| P18 | 20 | 60 | 10 | 15 | 5 | 75 | ±2 |
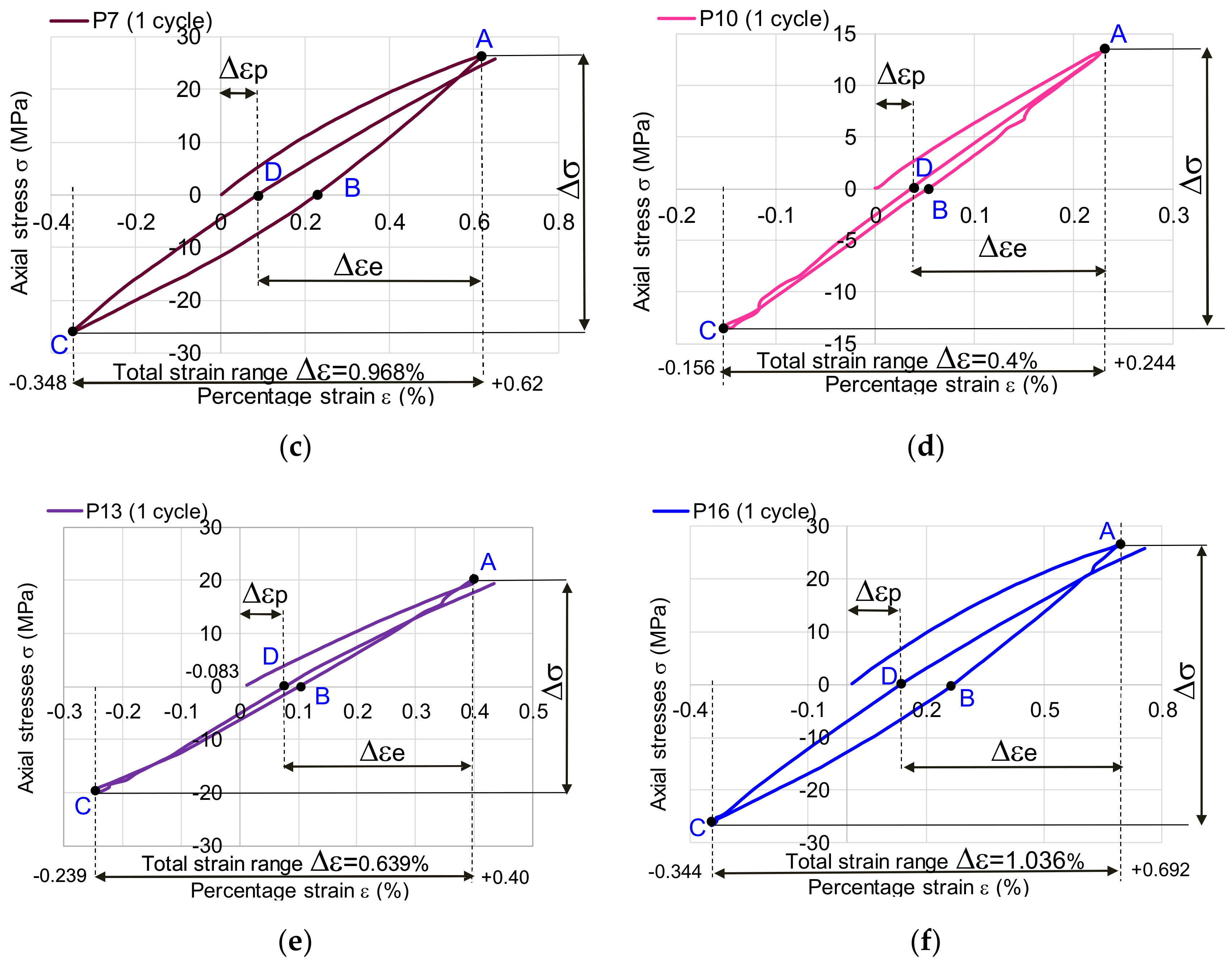
| Set of Tests | Δε = εt +εc (%) | Δεe (%) | Δεp (%) | εt (%) | εc (%) |
|---|---|---|---|---|---|
| A1 | 0.407 | 0.2042 | 0.0458 | 0.250 | 0.157 |
| B1 | 0.611 | 0.3422 | 0.1008 | 0.443 | 0.168 |
| C1 | 0.969 | 0.5368 | 0.0832 | 0.620 | 0.349 |
| A10 | 0.402 | 0.1982 | 0.0458 | 0.244 | 0.158 |
| B10 | 0.639 | 0.3212 | 0.0788 | 0.400 | 0.239 |
| C10 | 1.036 | 0.5566 | 0.1354 | 0.692 | 0.344 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanciu, M.D.; Teodorescu, H.D.; Vlase, S. Degradation of Mechanical Properties of Pine Wood Under Symmetric Axial Cyclic Loading Parallel to Grain. Polymers 2020, 12, 2176. https://doi.org/10.3390/polym12102176
Stanciu MD, Teodorescu HD, Vlase S. Degradation of Mechanical Properties of Pine Wood Under Symmetric Axial Cyclic Loading Parallel to Grain. Polymers. 2020; 12(10):2176. https://doi.org/10.3390/polym12102176
Chicago/Turabian StyleStanciu, Mariana D., Horațiu D. Teodorescu, and Sorin Vlase. 2020. "Degradation of Mechanical Properties of Pine Wood Under Symmetric Axial Cyclic Loading Parallel to Grain" Polymers 12, no. 10: 2176. https://doi.org/10.3390/polym12102176
APA StyleStanciu, M. D., Teodorescu, H. D., & Vlase, S. (2020). Degradation of Mechanical Properties of Pine Wood Under Symmetric Axial Cyclic Loading Parallel to Grain. Polymers, 12(10), 2176. https://doi.org/10.3390/polym12102176








