Characterizing Distributions of Tensile Strength and Crack Precursor Size to Evaluate Filler Dispersion Effects and Reliability of Rubber
Abstract
1. Introduction
2. Experimental Details
2.1. Materials, Mixing, and Curing
2.2. Tear Testing
2.3. Tensile Testing
2.4. Microscopy and Dispersion Measurements
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gent, A.N.; Lindley, P.B.; Thomas, A.G. Cut Growth and Fatigue of Rubbers. I. The Relationship Between Cut Growth and Fatigue. J. Appl. Polym. Sci. 1964, 8, 455–466. [Google Scholar] [CrossRef]
- Ellul, M.D. Mechanical Fatigue. In Engineering with Rubber—How to Design Rubber Components, 3rd ed.; Gent, A.N., Ed.; Carl Hanser Verlag: Munich, Germany, 2010; Chapter 6. [Google Scholar]
- Mars, W.V. Fatigue life prediction for elastomeric structures. Rubber Chem. Technol. 2007, 80, 481–503. [Google Scholar] [CrossRef]
- Huneau, B.; Masquelier, I.; Marco, Y.; Le Saux, V.; Noizet, S.; Schiel, C.; Charrier, P. Fatigue Crack Initiation in a Carbon Black-Filled Natural Rubber. Rubber Chem. Technol. 2016, 89, 126–141. [Google Scholar] [CrossRef]
- Hess, W.M.; Herd, C.R. Microstructure, Morphology and General Physical Properties. In Carbon Black: Science and Technology, 2nd ed.; Donnet, J.-B., Bansal, R.C., Wang, M.-J., Eds.; Marcel Dekker Inc., (CRC Press): New York, NY, USA, 1993; Chapter 3; pp. 160–161, “The particles of ball coke are formed from individual hydrocarbon droplets and range from <5 μm to >200 μm in size. The particles tend to be hollow with holes in the surface from the passage of internal gaseous materials, during carbonization.” . [Google Scholar]
- Choi, I.S.; Roland, C.M. Intrinsic Defects and the Failure Properties of cis-1,4-Polyisoprenes. Rubber Chem. Technol. 1996, 69, 591–599. [Google Scholar] [CrossRef]
- Ludwig, M.; Alshuth, T.; El Yaagoubi, M.; Juhre, D. Lifetime prediction of elastomers based on statistical occurrence of material defects. In Constitutive Models for Rubber IX; Marvalová, B., Petríková, I., Eds.; CRC Press, Taylor & Francis Group: London, UK, 2015; pp. 445–448. [Google Scholar]
- Ignatz-Hoover, F.; To, B. Effective Curative Dispersion for Uniform Mechanical Properties. In Proceedings of the Fall 178th Technical Meeting of the Rubber Division, ACS, Milwaukee, WI, USA, 12–14 October 2010; Paper #114. [Google Scholar]
- Ignatz-Hoover, F.; Robertson, C.G.; Basu, S.K.; Ludwig, M.; Alshuth, T. Silica Structure in Rubber: Characterization Using X-Ray Computed Tomography, Microscopy and Impact on Failure Properties. In Proceedings of the Deutsche Kautschuk-Tagung (DKT), Nürnberg, Germany, 29 June–2 July 2015. [Google Scholar]
- Wong, D.H.C.; Childress, A.; Ignatz-Hoover, F. Evaluation of Sulfur Dispersion Using Population Survival Analysis. In Proceedings of the 13th Fall Rubber Colloquium (KHK), Deutsches Institut für Kautschuktechnologie e. V. (DIK), Hannover, Germany, 6–8 November 2018. [Google Scholar]
- ASTM. ASTM D1514-15—Standard Test Method for Carbon Black—Sieve Residue; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Smith, A.P.; Aybar, T.L.; Magee, R.W.; Herd, C.R. Carbon Black Dispersion Measurement in Rubber Vulcanizates via Interferometric Microscopy. Rubber Chem. Technol. 2004, 77, 691–710. [Google Scholar] [CrossRef]
- ASTM. ASTM D2663-14—Standard Test Methods for Carbon Black Dispersion in Rubber (Test Method D—Microroughness Measurement with IFM); ASTM International: West Conshohocken, PA, USA, 2019. [Google Scholar]
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- Rinne, H. The Weibull Distribution: A Handbook; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2008. [Google Scholar]
- Peterlik, H.; Loidl, D. Bimodal strength distributions and flaw populations of ceramics and fibers. Eng. Fract. Mech. 2001, 68, 253–261. [Google Scholar] [CrossRef]
- Seshaiah, C.V.; Indhumathy, D. Analysis of Wind Speed at Sulur—A Bimodal Weibull and Weibull Distribution. Int. J. Latest Eng. Manag. Res. 2017, 2, 29–37. [Google Scholar]
- Inglis, C.E. Stresses in a plate due to the presence of cracks and sharp corners. Trans. Inst. Nav. Archit. 1913, 55, 219–241. [Google Scholar]
- Roland, C.M.; Smith, C.R. Defect Accumulation in Rubber. Rubber Chem. Technol. 1985, 58, 806–814. [Google Scholar] [CrossRef]
- Le Cam, J.-B.; Huneau, B.; Verron, E.; Gornet, L. Mechanism of Fatigue Crack Growth in Carbon Black Filled Rubber. Macromolecules 2004, 37, 5011–5017. [Google Scholar] [CrossRef]
- Zhang, H.; Scholz, A.K.; de Crevoisier, J.; Berghezan, D.; Narayanan, T.; Kramer, E.J.; Creton, C. Nanocavitation around a crack tip in a soft nanocomposite: A scanning microbeam small angle X-ray scattering study. J. Polym. Sci. Part B Polym. Phys. 2014, 53, 422–429. [Google Scholar] [CrossRef]
- Mars, W.V. Multiaxial fatigue crack initiation in rubber. Tire Sci. Technol. 2001, 29, 171–185. [Google Scholar] [CrossRef]
- Barbash, K.P.; Mars, W.V. Critical Plane Analysis of Rubber Bushing Durability under Road Loads. SAE Tech. Pap. 2016. [Google Scholar] [CrossRef]
- Mars, W.V.; Wei, Y.; Hao, W.; Bauman, M.A. Computing Tire Component Durability via Critical Plane Analysis. Tire Sci. Technol. 2019, 47, 31–54. [Google Scholar] [CrossRef]

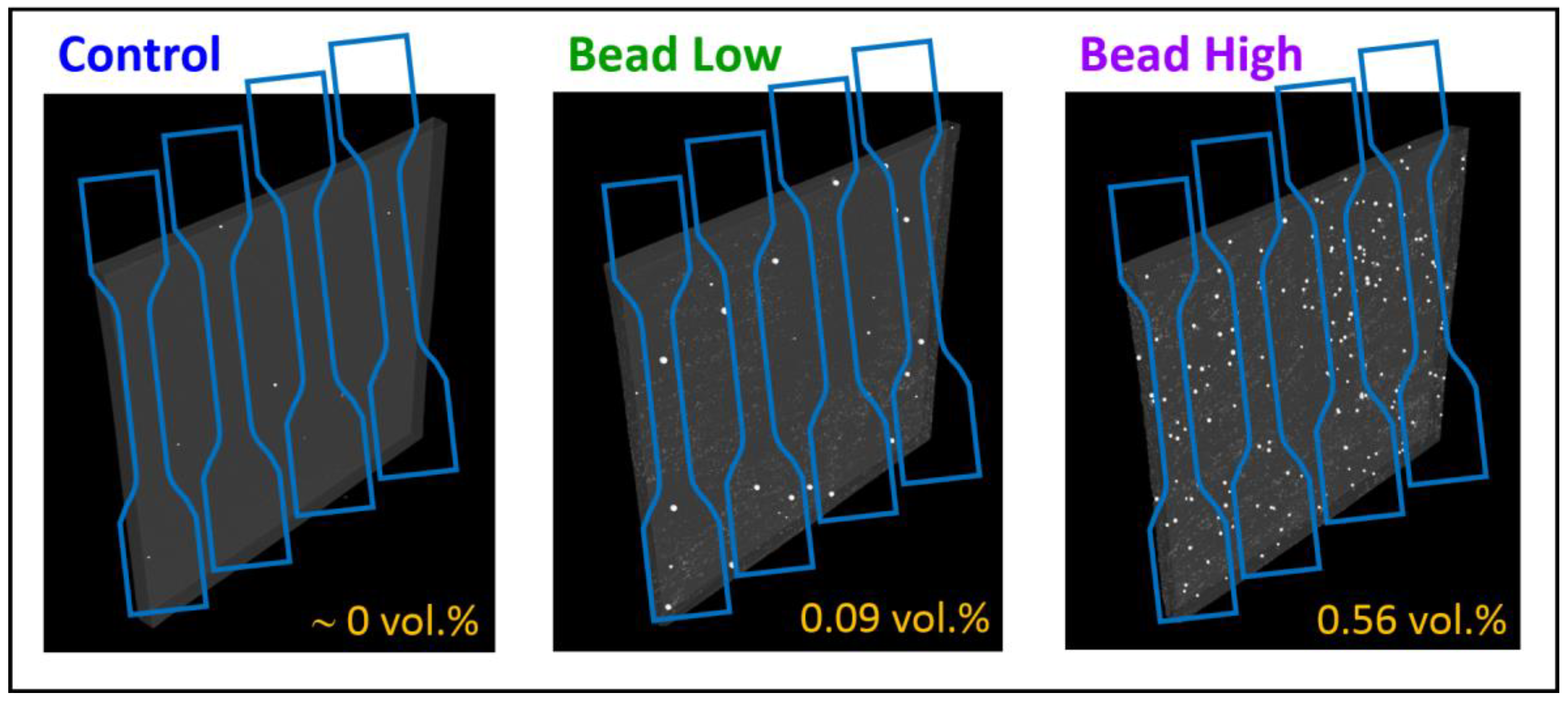

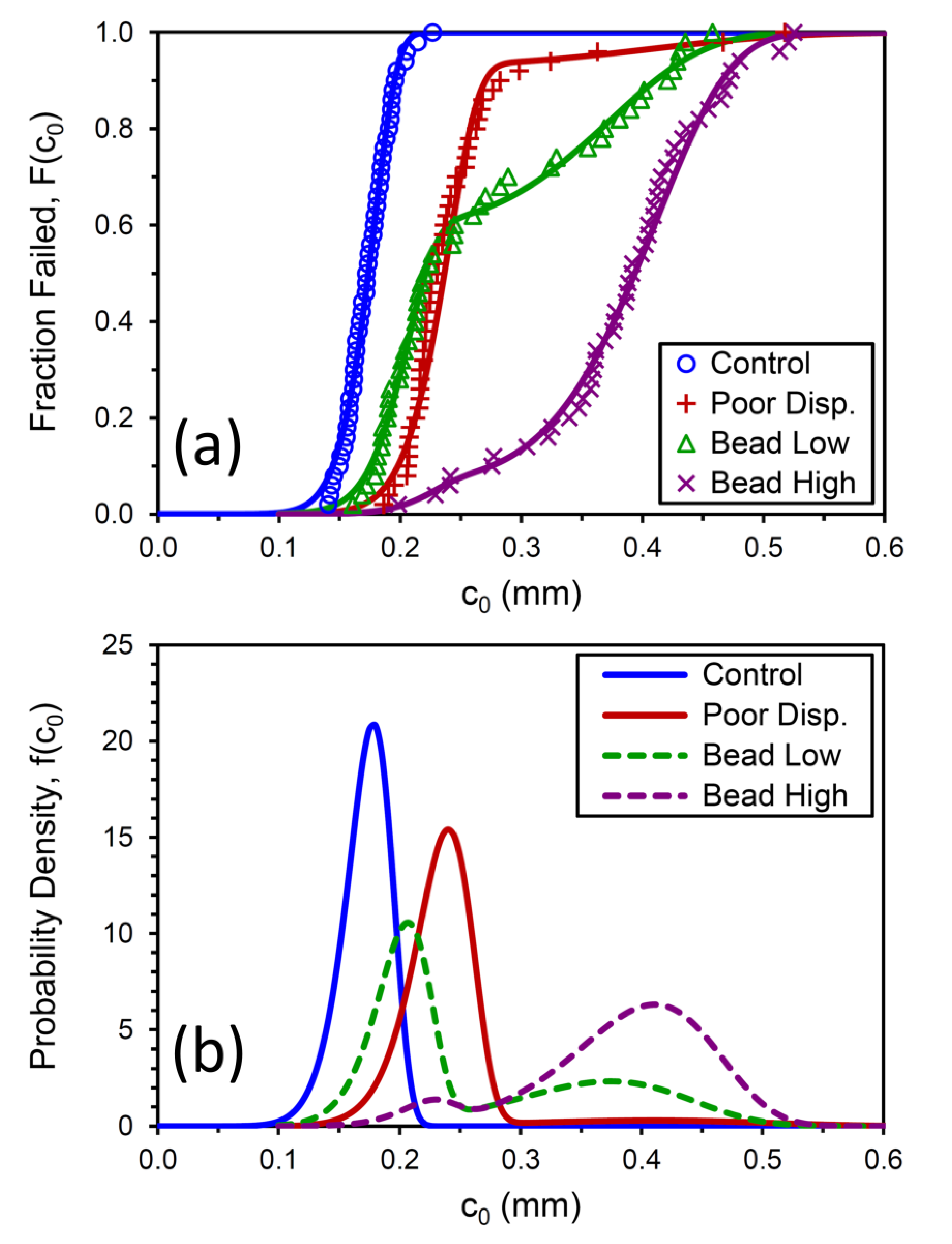

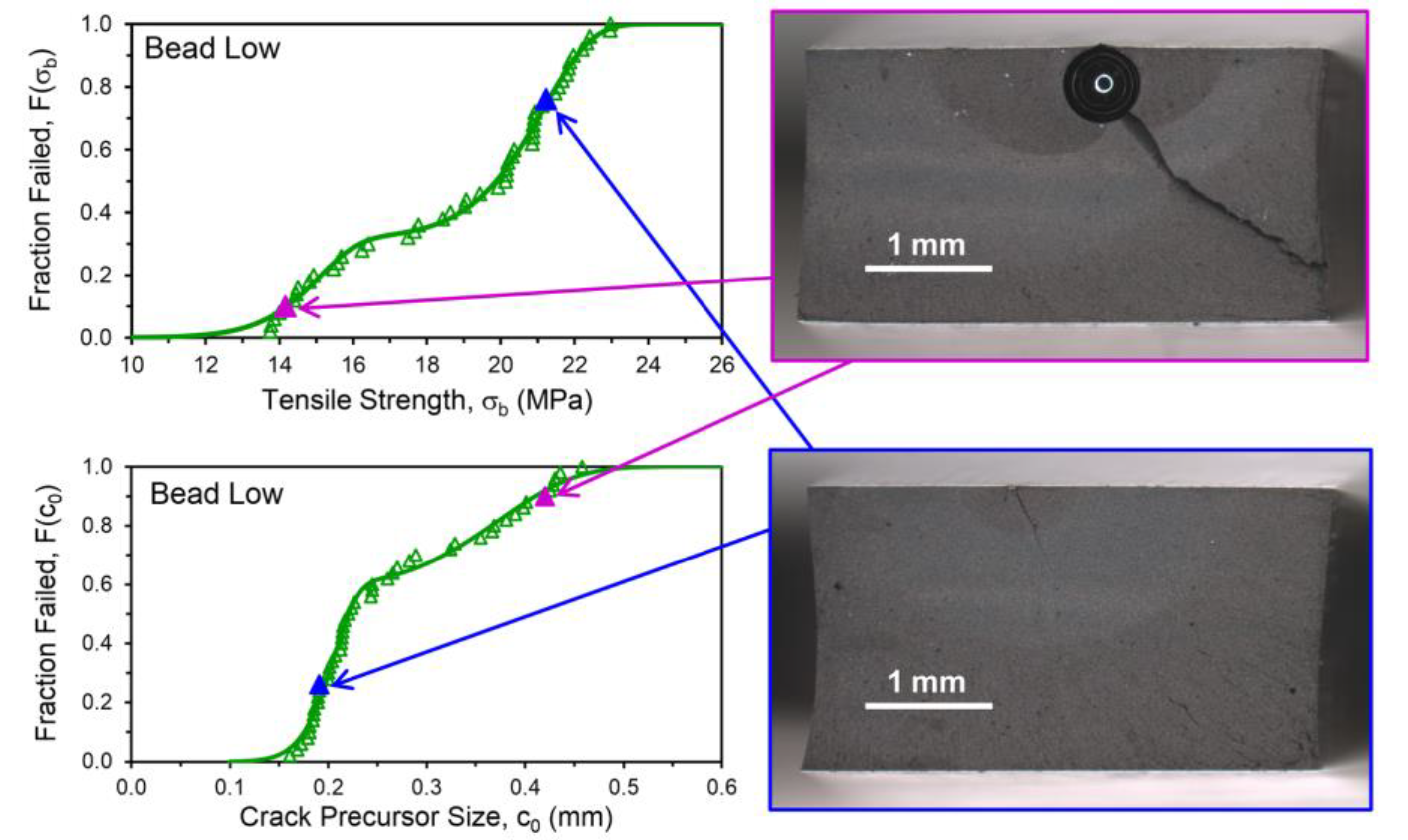
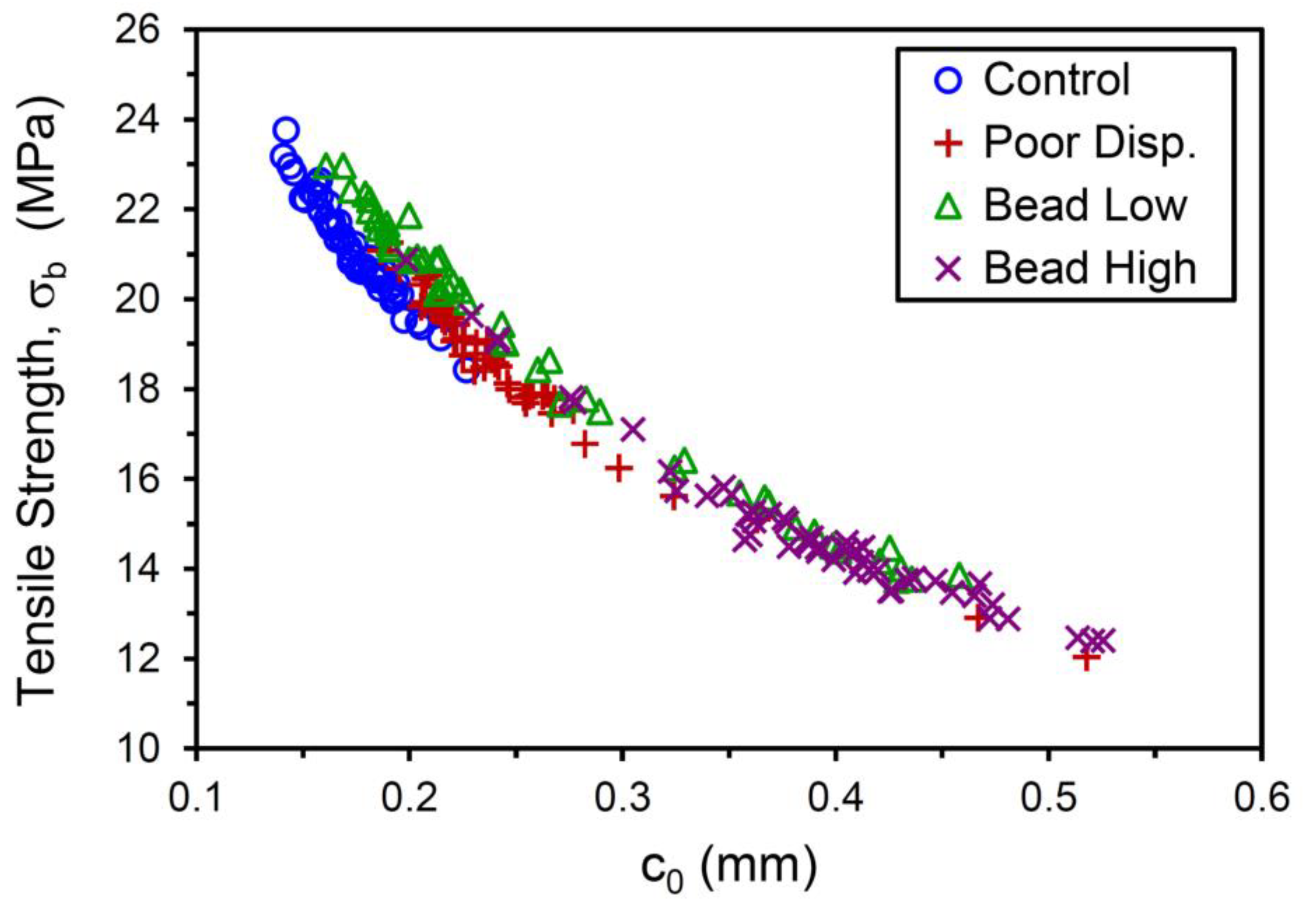
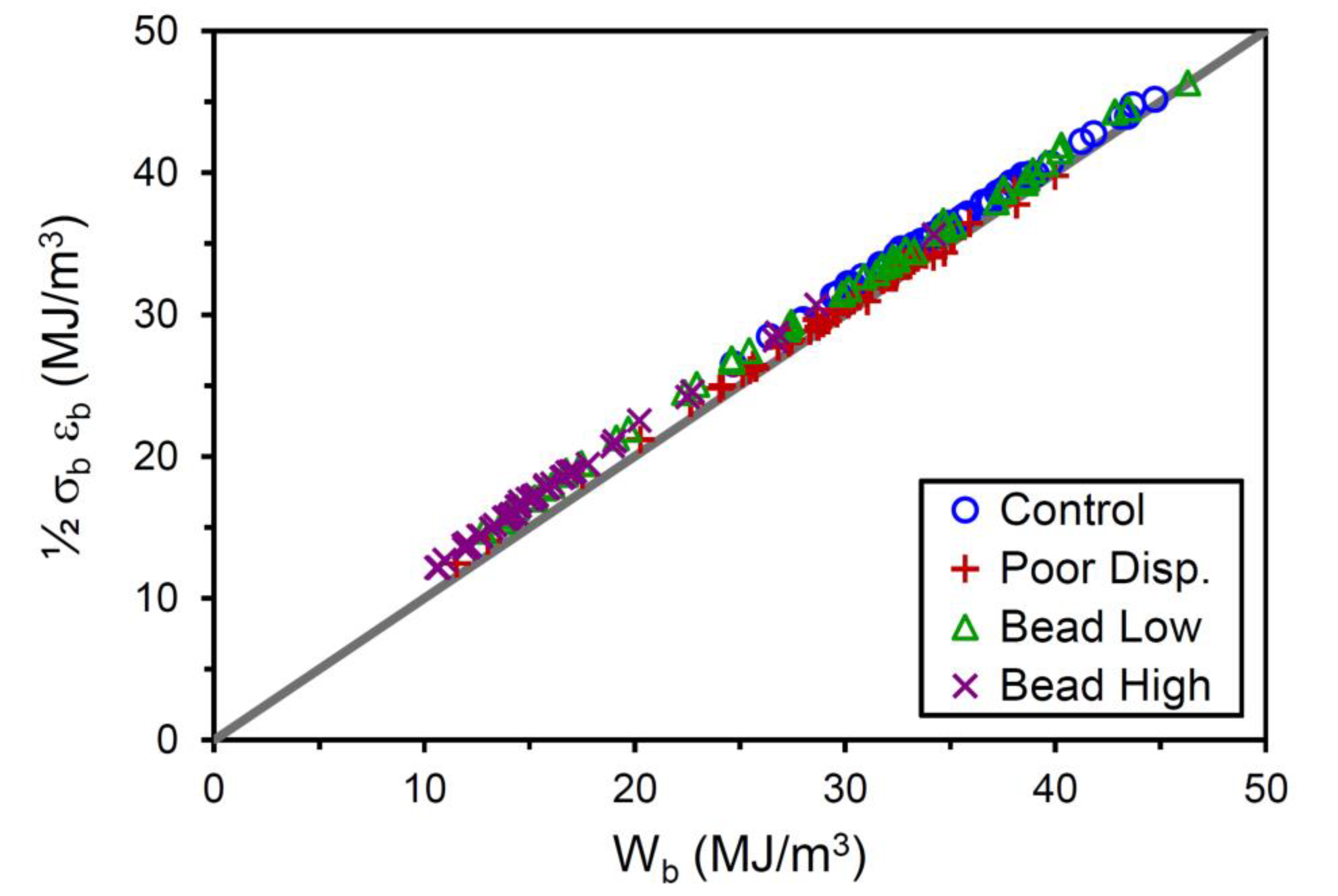
| Control | Poor Disp. | Bead Low | Bead High | ||
|---|---|---|---|---|---|
| Master Batch (Non-Productive) | SBR 1500 | 100 | 100 | 100 | 100 |
| N550 CB (0 ppm residue) | 50 | 30 | 50 | 50 | |
| Zinc Oxide | 2 | 2 | 2 | 2 | |
| Stearic Acid | 1 | 1 | 1 | 1 | |
| 6PPD A.O. | 1 | 1 | 1 | 1 | |
| Final Batch (Productive) | TBBS | 2 | 2 | 2 | 2 |
| Sulfur | 2 | 2 | 2 | 2 | |
| N550 CB (0 ppm residue) | 20 | ||||
| Two-Roll Mill | Glass Beads (d = 517 μm) | 0.09 | 0.72 |
| Control | Poor Disp. | Bead Low | Bead High | ||
|---|---|---|---|---|---|
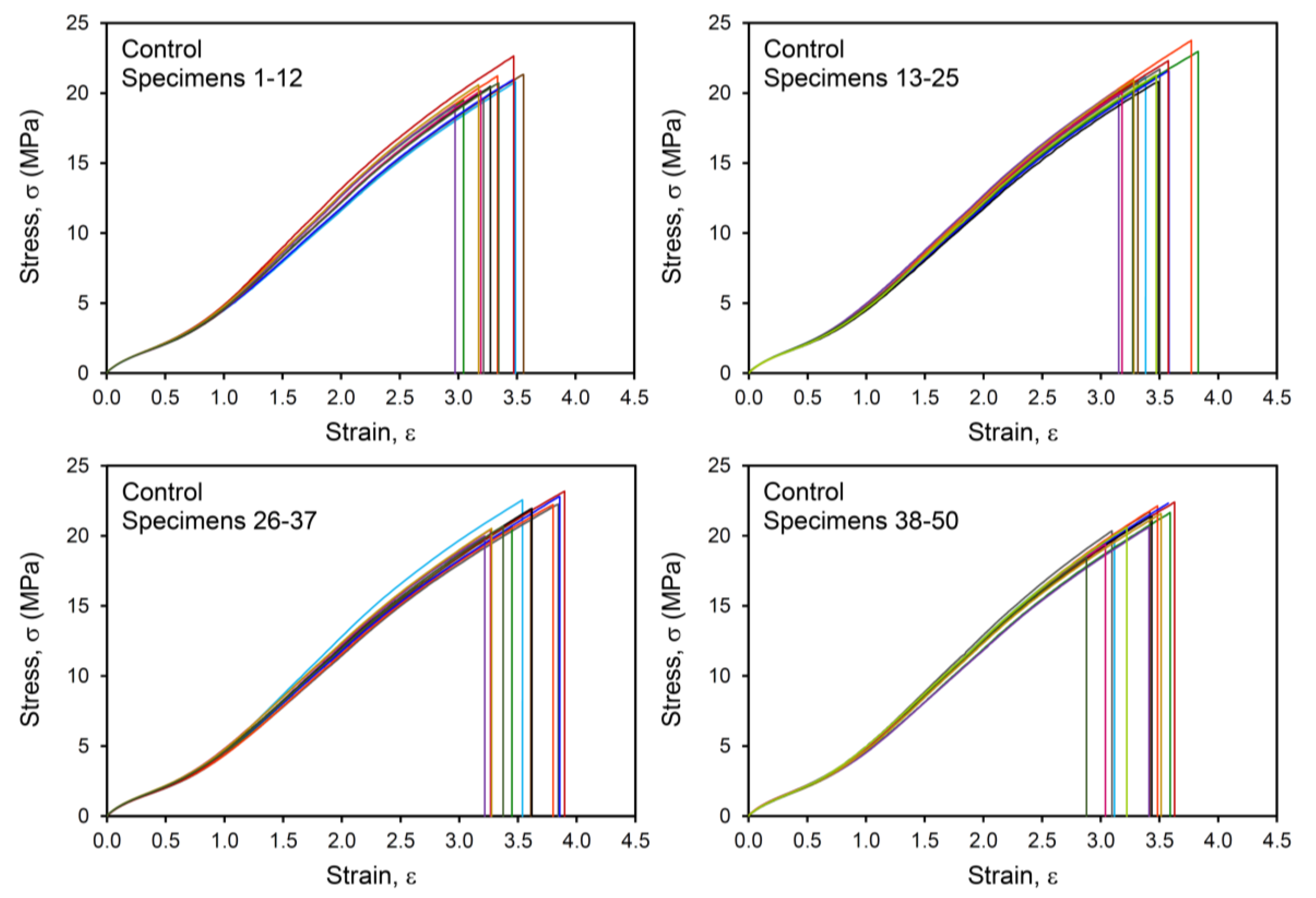
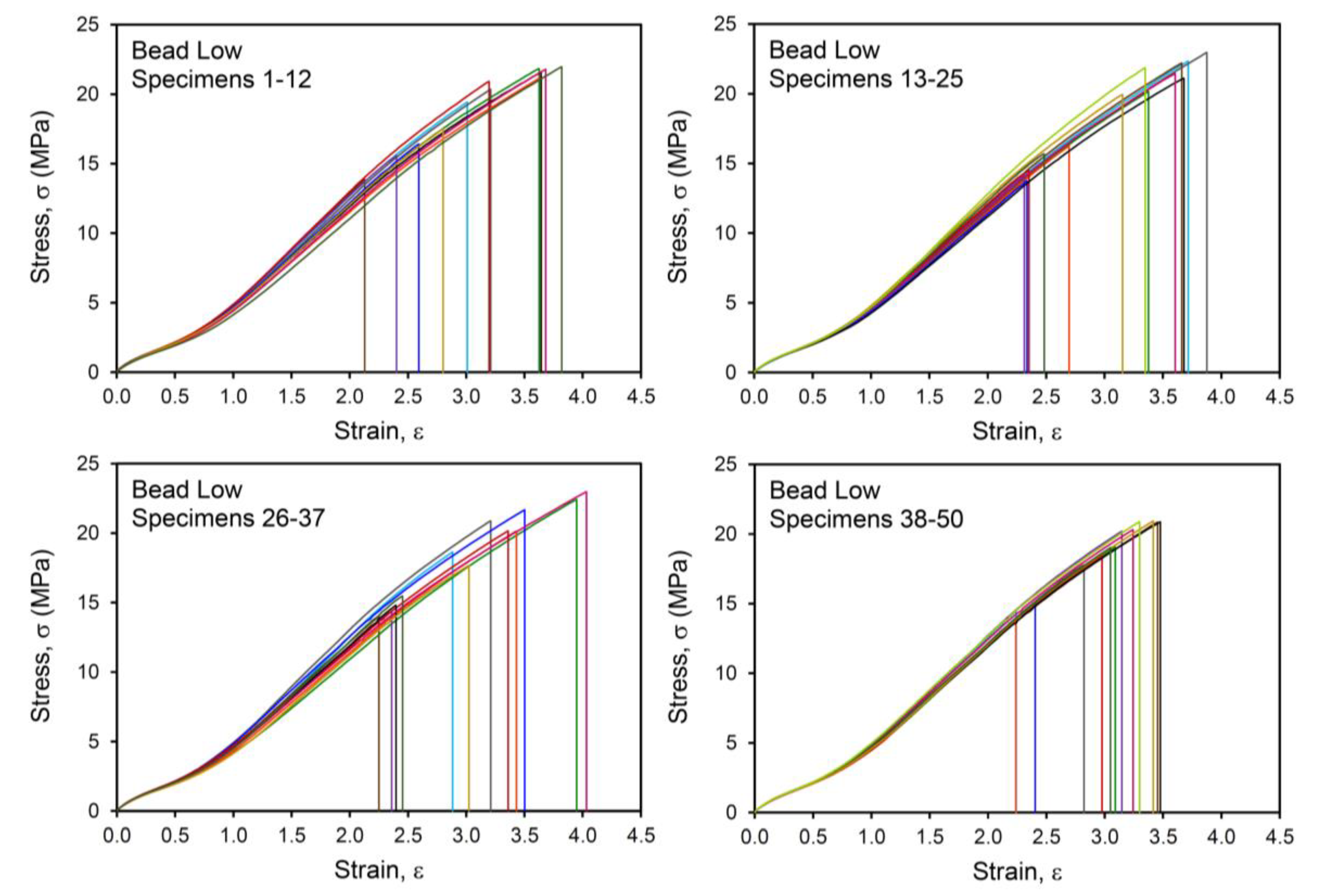
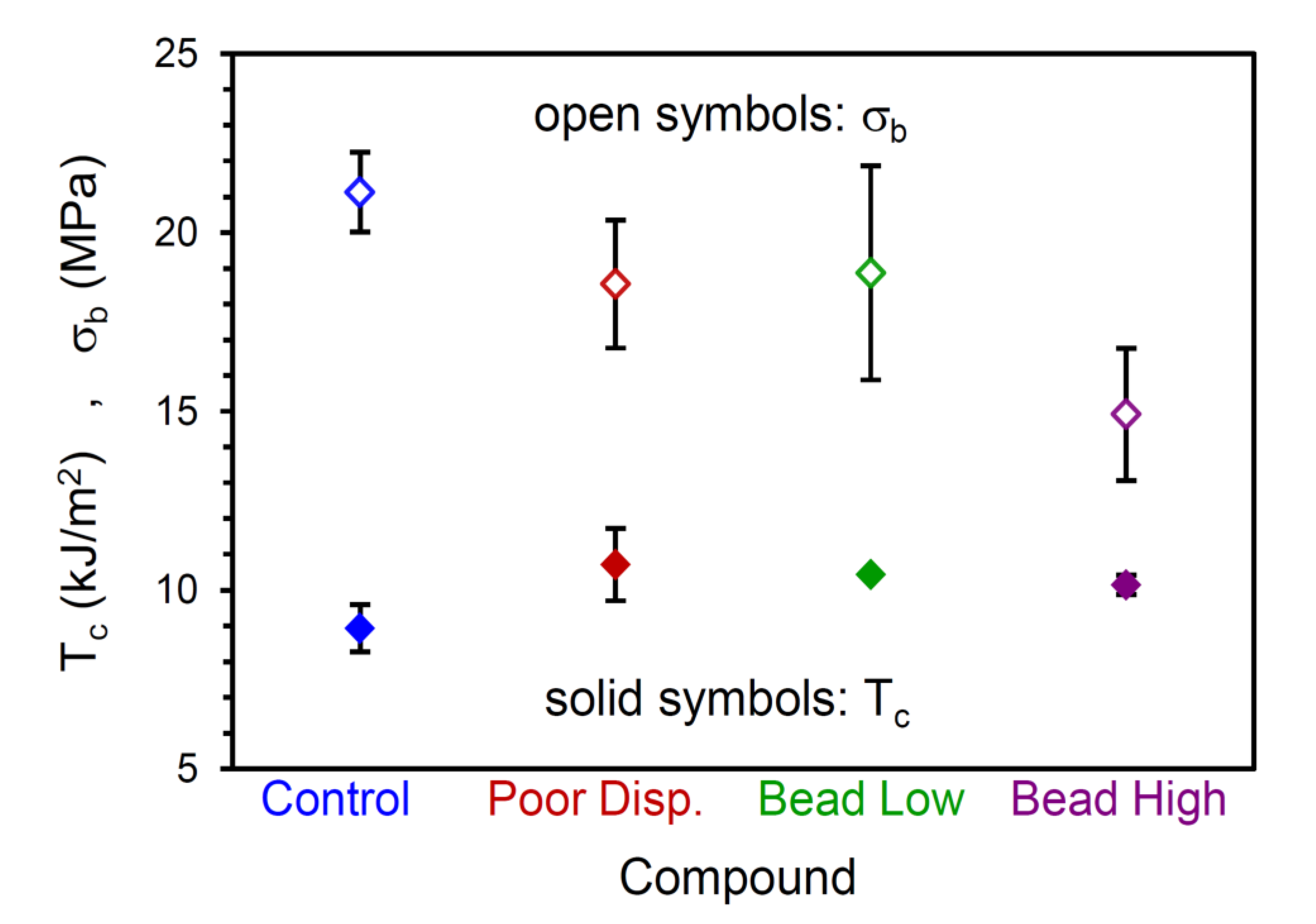
| Tensile Failure (no initial cut) | σb (MPa) | 21.13 ± 1.12 | 18.56 ± 1.79 | 18.87 ± 2.99 | 14.91 ± 1.85 |
| εb | 3.41 ± 0.24 | 3.23 ± 0.34 | 3.08 ± 0.54 | 2.39 ± 0.29 | |
| Wb (MJ/m3) | 34.74 ± 4.66 | 29.68 ± 5.73 | 28.23 ± 9.78 | 16.19 ± 4.73 | |
| Tear (initial cut) | Tc (kJ/m2) | 8.93 ± 0.66 | 10.71 ± 1.01 | 10.43 ± 0.02 | 10.15 ± 0.27 |
| Control | Poor Disp. | Bead Low | Bead High | |
|---|---|---|---|---|
| ϕ | 1 (unimodal) | 0.05306 | 0.3152 | 0.8709 |
| σb,s1 (MPa) | 21.51 | 12.84 | 15.15 | 14.66 |
| m1 | 21.82 | 10.07 | 14.98 | 16.82 |
| σb,s2 (MPa) | -- | 19.31 | 21.25 | 19.15 |
| m2 | -- | 18.83 | 17.34 | 19.37 |
| Control | Poor Disp. | Bead Low | Bead High | |
|---|---|---|---|---|
| ϕ | 1 (unimodal) | 0.9267 | 0.5859 | 0.06181 |
| c0,s1 (mm) | 0.1801 | 0.2424 | 0.2087 | 0.2280 |
| m1 | 10.18 | 10.85 | 9.884 | 10.75 |
| c0,s2 (mm) | -- | 0.4322 | 0.3865 | 0.4186 |
| m2 | -- | 4.646 | 5.812 | 7.576 |
| Control | Poor Disp. | Bead Low | Bead High | |
|---|---|---|---|---|
| IFM Dispersion Index [max. = 100] | 99.5 | 88.3 | 99.3 | 99.1 |
| Peak & Valley Area Percentage (%) | 0.17 | 3.84 | 0.23 | 0.31 |
| Number of Peaks & Valleys | 32 | 1021 | 34 | 57 |
| Mean Peak & Valley Diameter (μm) | 15.0 | 15.2 | 17.4 | 17.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robertson, C.G.; Tunnicliffe, L.B.; Maciag, L.; Bauman, M.A.; Miller, K.; Herd, C.R.; Mars, W.V. Characterizing Distributions of Tensile Strength and Crack Precursor Size to Evaluate Filler Dispersion Effects and Reliability of Rubber. Polymers 2020, 12, 203. https://doi.org/10.3390/polym12010203
Robertson CG, Tunnicliffe LB, Maciag L, Bauman MA, Miller K, Herd CR, Mars WV. Characterizing Distributions of Tensile Strength and Crack Precursor Size to Evaluate Filler Dispersion Effects and Reliability of Rubber. Polymers. 2020; 12(1):203. https://doi.org/10.3390/polym12010203
Chicago/Turabian StyleRobertson, Christopher G., Lewis B. Tunnicliffe, Lawrence Maciag, Mark A. Bauman, Kurt Miller, Charles R. Herd, and William V. Mars. 2020. "Characterizing Distributions of Tensile Strength and Crack Precursor Size to Evaluate Filler Dispersion Effects and Reliability of Rubber" Polymers 12, no. 1: 203. https://doi.org/10.3390/polym12010203
APA StyleRobertson, C. G., Tunnicliffe, L. B., Maciag, L., Bauman, M. A., Miller, K., Herd, C. R., & Mars, W. V. (2020). Characterizing Distributions of Tensile Strength and Crack Precursor Size to Evaluate Filler Dispersion Effects and Reliability of Rubber. Polymers, 12(1), 203. https://doi.org/10.3390/polym12010203







