Glass Transition Behaviors of Poly (Vinyl Pyridine)/Poly (Vinyl Phenol) Revisited
Abstract
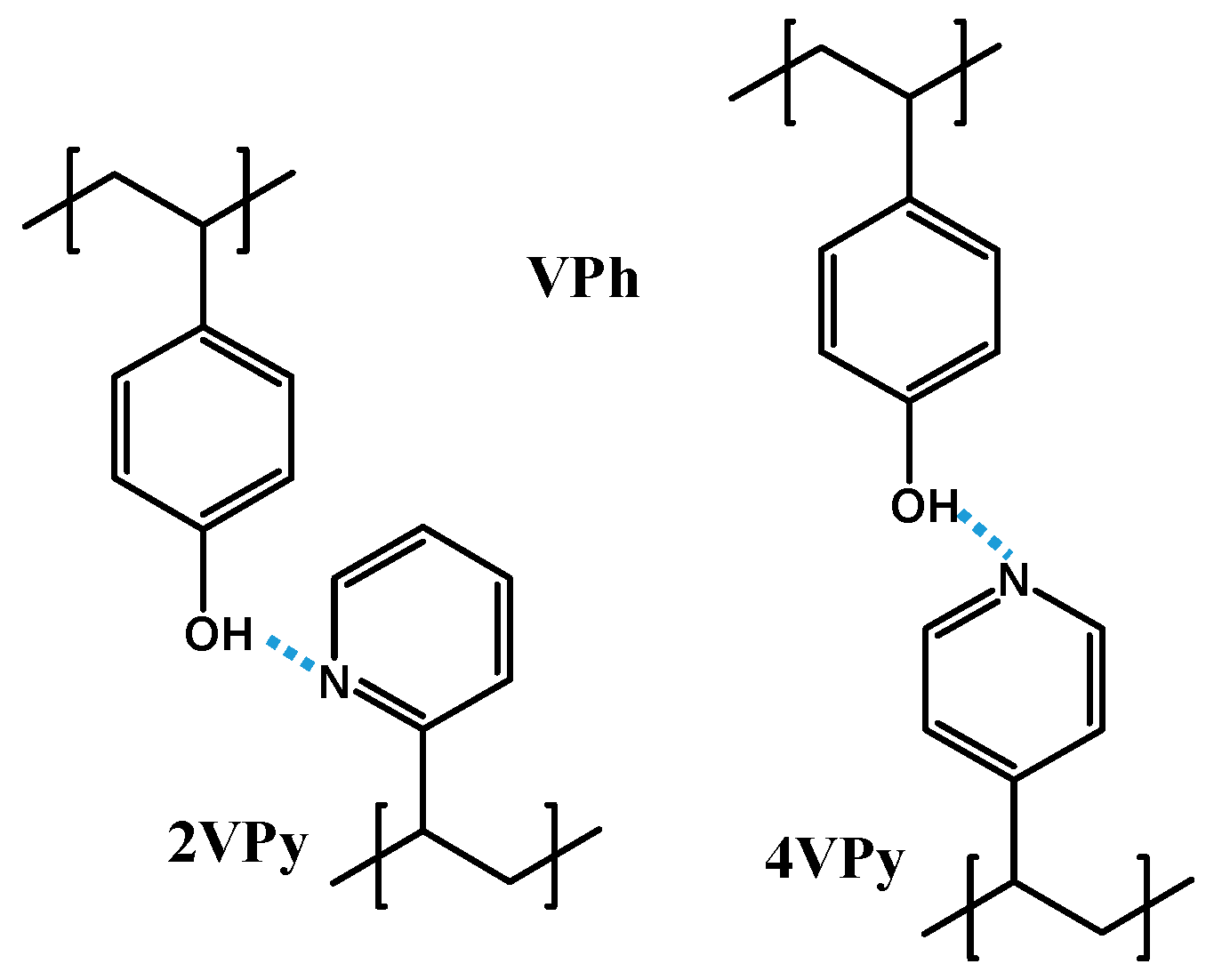
1. Introduction
2. Materials and Methods
3. Results and Discussion
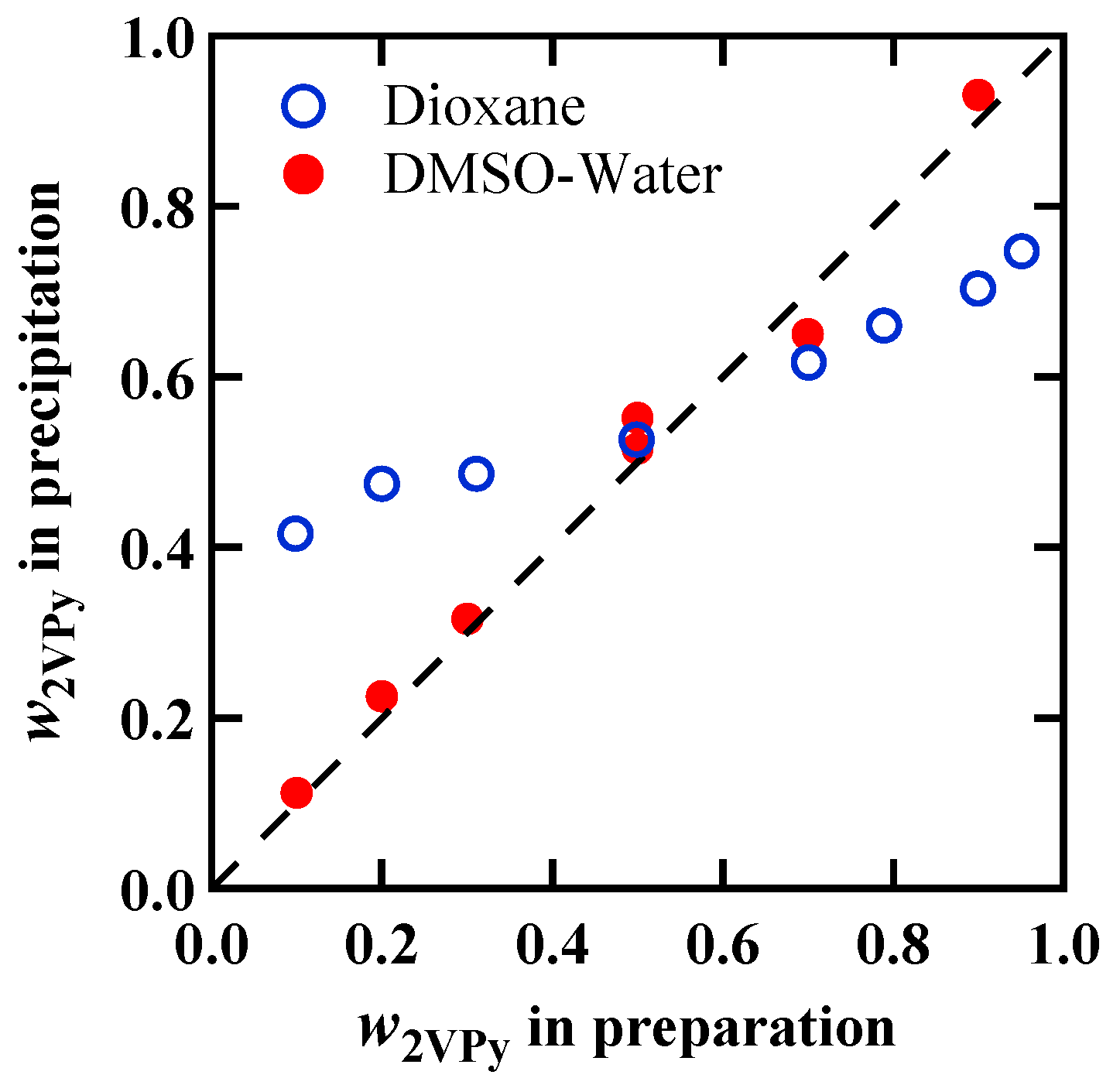
3.1. Weight Fractions in 2VPy/VPh Blend Obtained by Two Preparation Methods
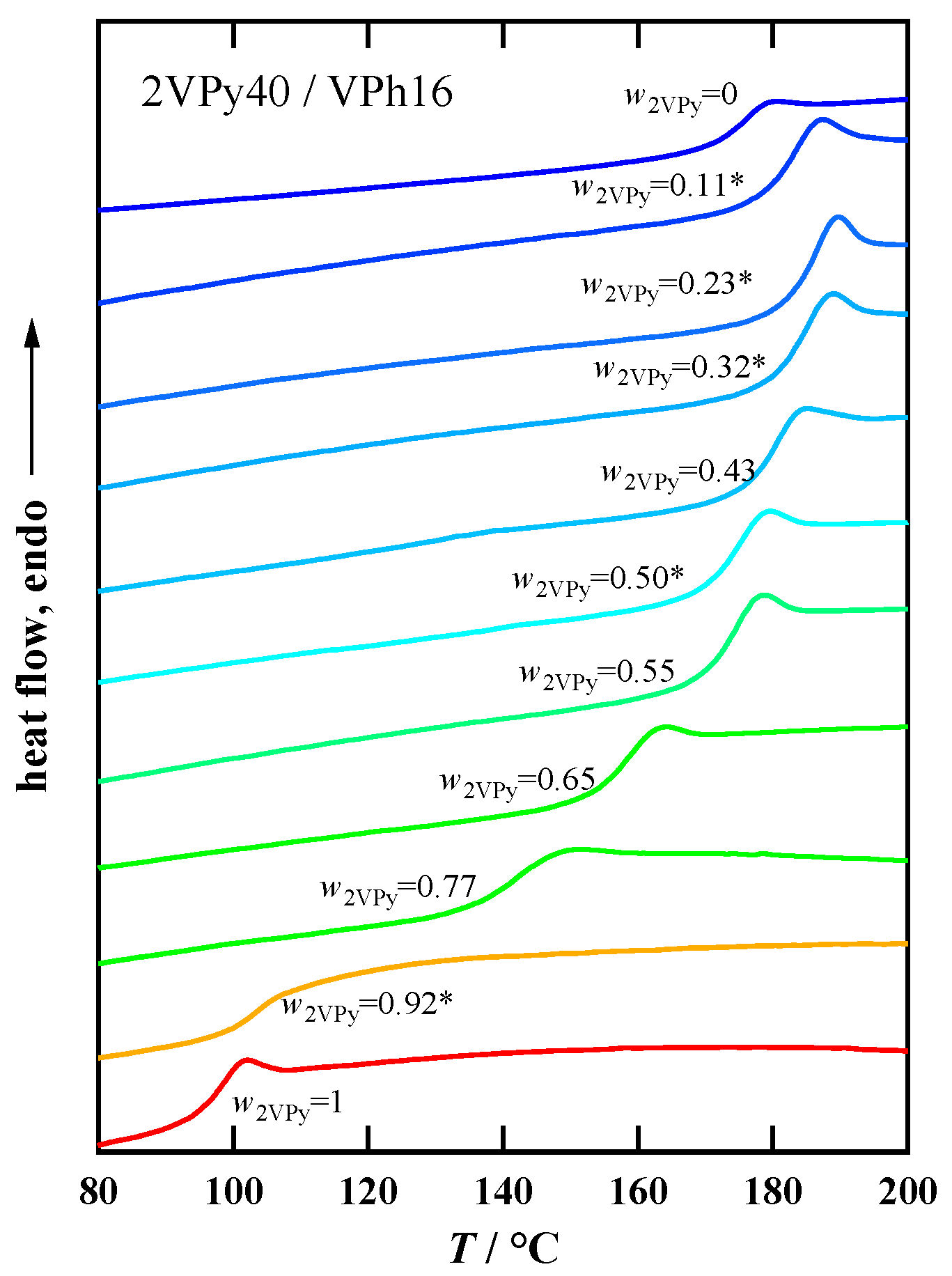
3.2. Glass Transition Behavior
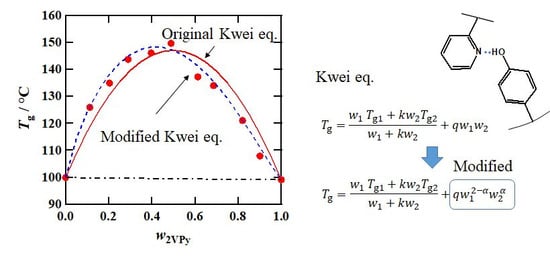
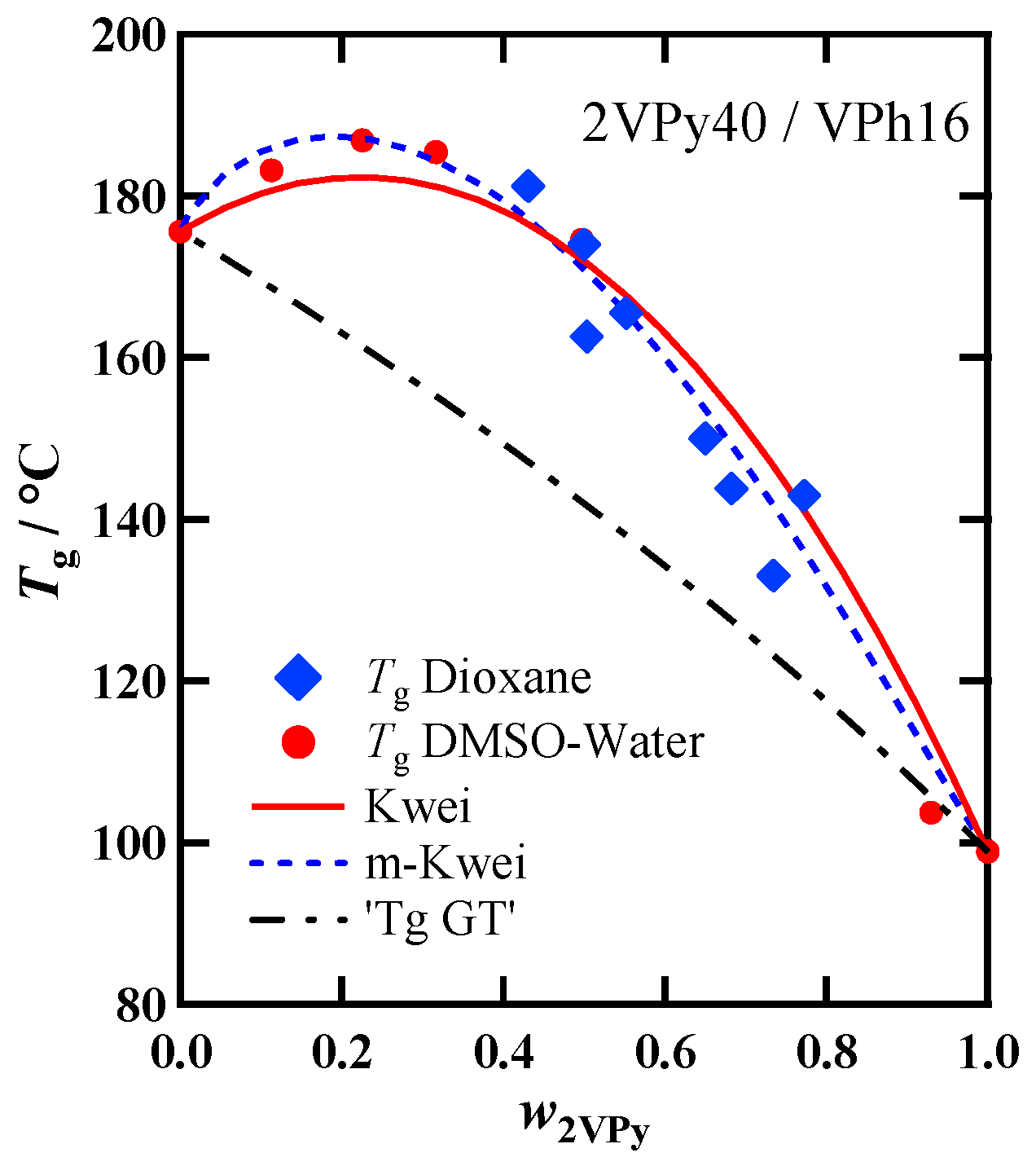
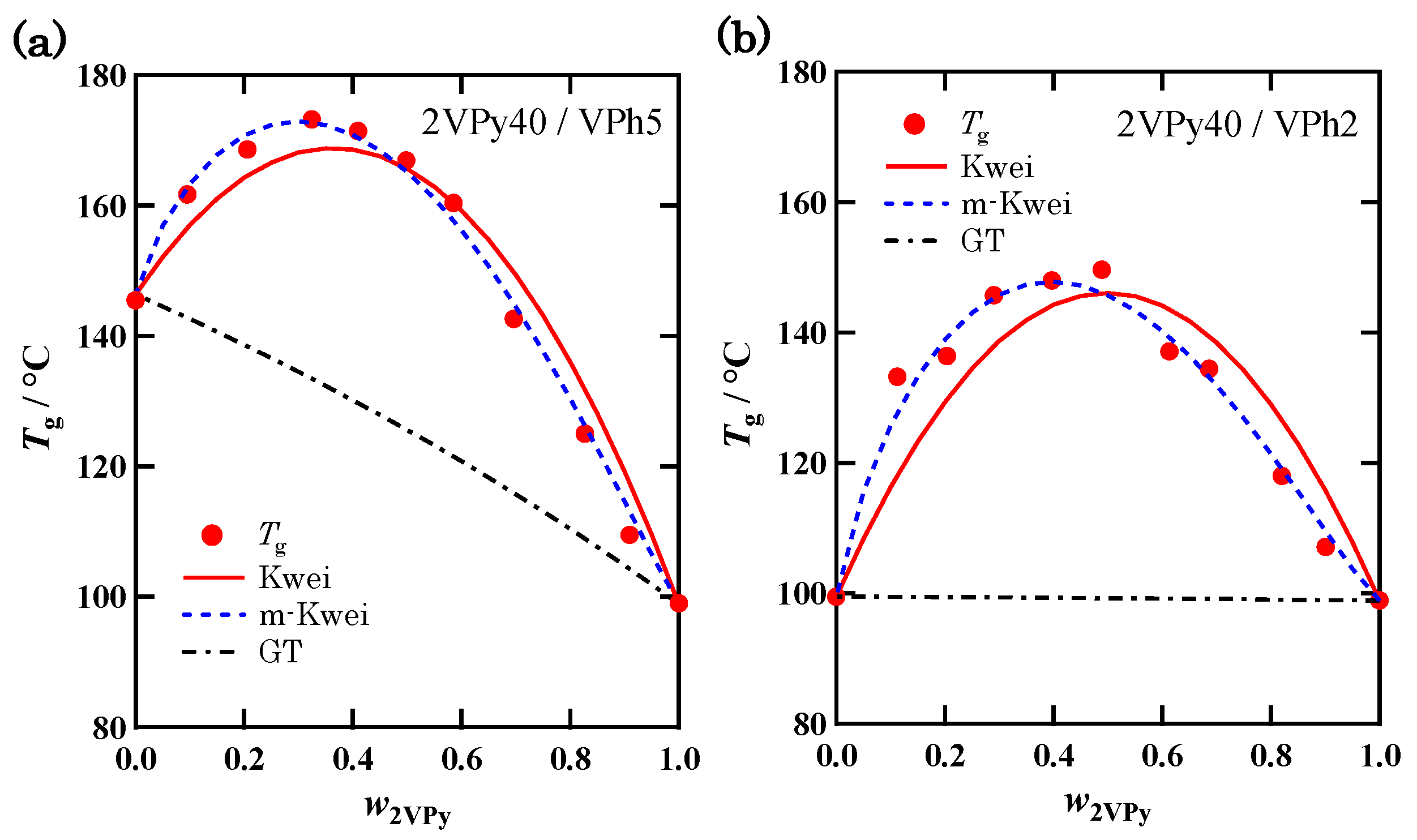
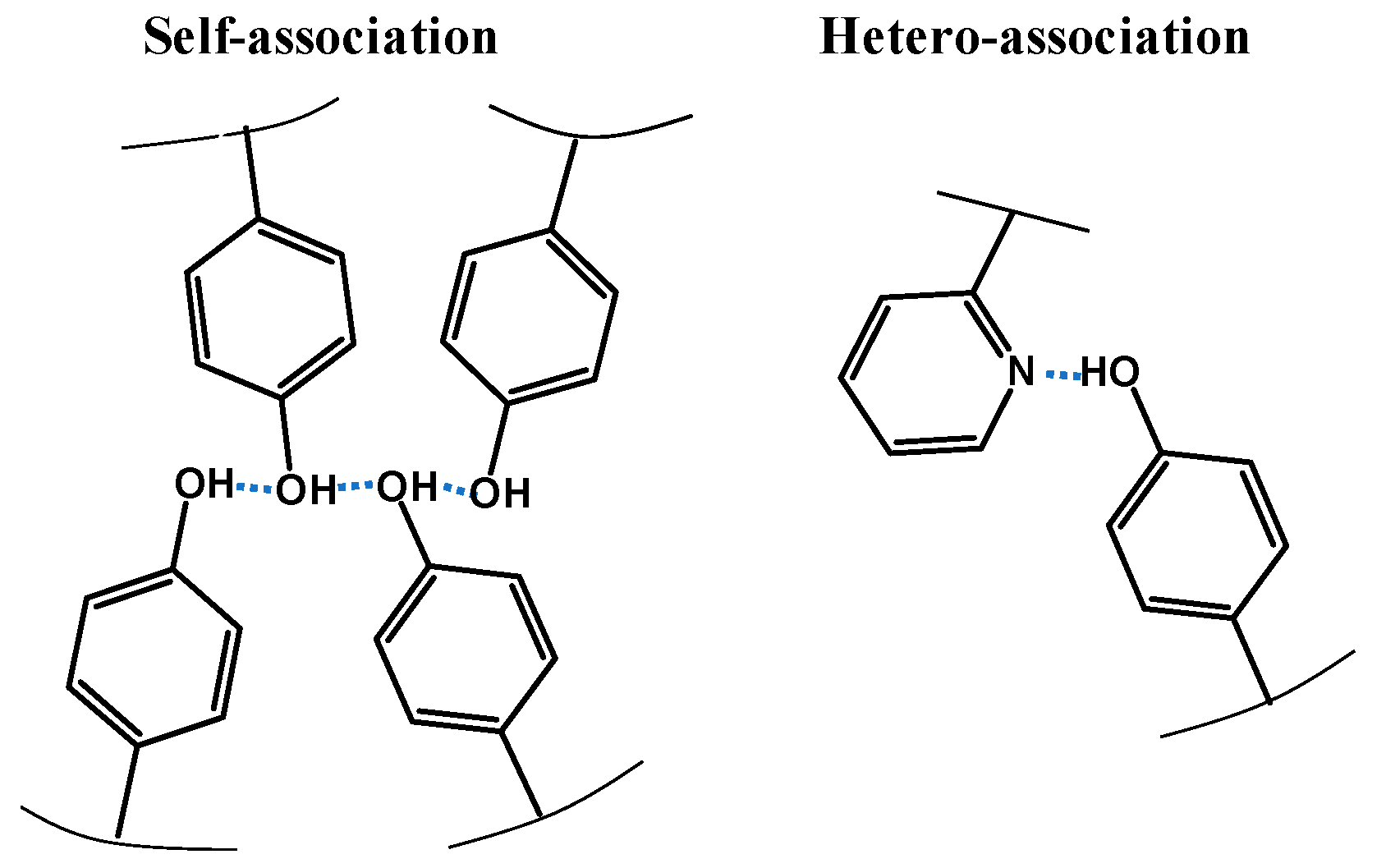
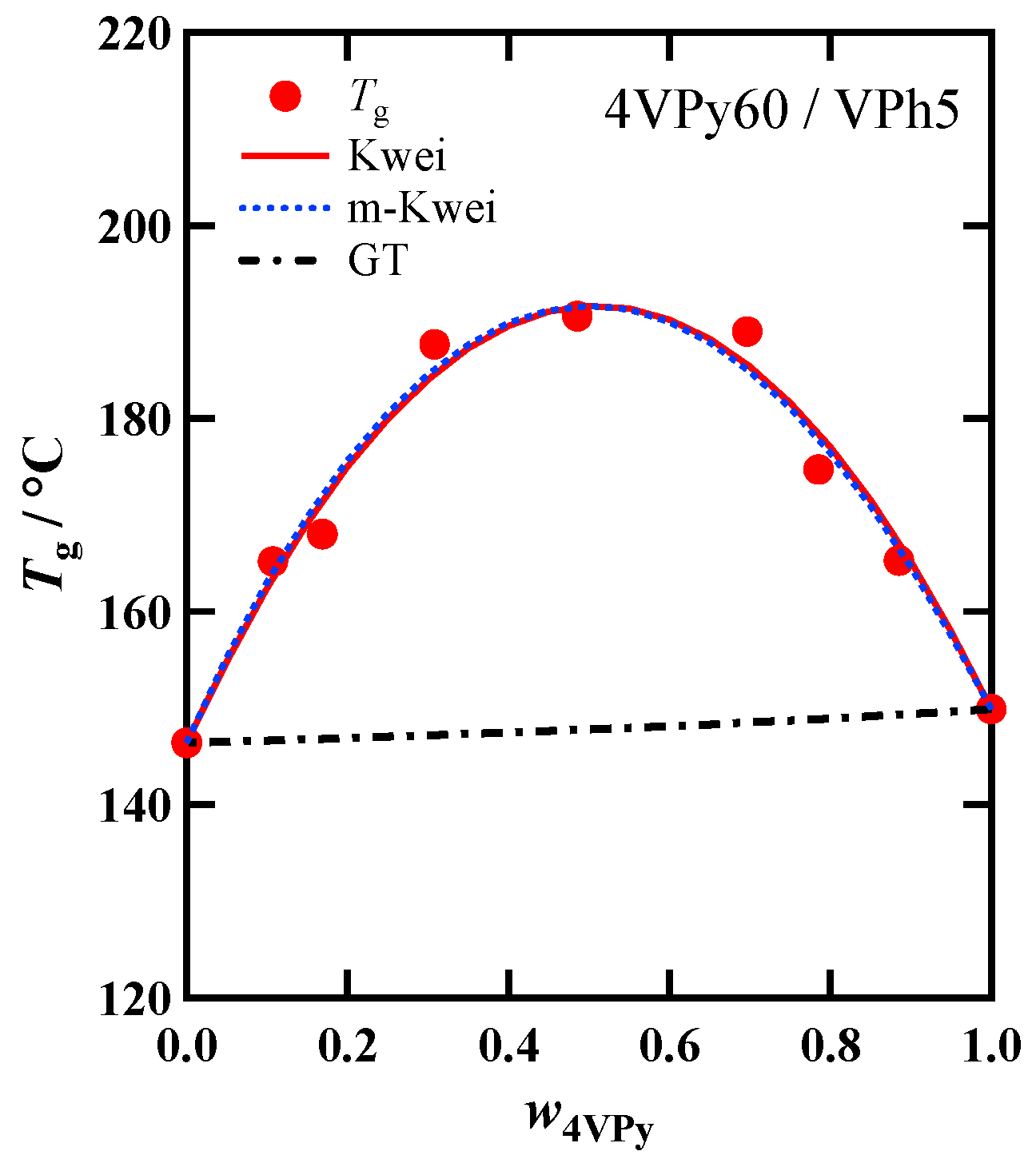
3.3. Composition Dependence of Tg
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Utracki, L.A.; Favis, B. Polymer Alloys and Blends; Marcel Dekker: New York, NY, USA, 1989; Volume 4. [Google Scholar]
- Mittal, V. Functional Polymer Blends: Synthesis, Properties, and Performance; CRC Press: Boca Rato, FL, USA, 2012. [Google Scholar]
- Hsu, W.Y.; Wu, S.H. Percolation Behavior in Morphology and Modulus of Polymer Blends. Polym. Eng. Sci. 1993, 33, 293–302. [Google Scholar] [CrossRef]
- Imagawa, A.; Qui, T.C. Structure-Property Relationship of Polymer Blends with Co-Continuous Structures Prepared by Photo-Cross-Linking. Macromolecules 1995, 28, 8388–8394. [Google Scholar] [CrossRef]
- Wu, S.H. Chain Entanglement and Melt Viscosity of Compatible Polymer Blends-Poly (Methyl Methacrylate) and Poly (Styrene Acrylonitrile). Polymer 1987, 28, 1144–1148. [Google Scholar] [CrossRef]
- Olabisi, O.; Robeson, L.; Shaw, M. Polymer-Polymer Miscibility; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Urakawa, O.; Ujii, T.; Adachi, K. Dynamic heterogeneity in a miscible poly (vinyl acetate)/poly (ethylene oxide) blend. J. Non Cryst. Solids 2006, 352, 5042–5049. [Google Scholar] [CrossRef]
- Jiang, M.; Li, M.; Xiang, M.L.; Zhou, H. Interpolymer complexation and miscibility enhancement by hydrogen bonding. Polym. Synth. Polym. Polym. Complexation 1999, 146, 121–196. [Google Scholar]
- Kuo, S.W. Hydrogen-bonding in polymer blends. J. Polym. Res. 2008, 15, 459–486. [Google Scholar] [CrossRef]
- Kuo, S.W. Hydrogen Bonding in Polymer Materials; Wiley-VCH: Weinheim, Germany, 2018. [Google Scholar]
- Urakawa, O.; Ikuta, H.; Nobukawa, S.; Shikata, T. Small-Angle Neutron Scattering Study on the Miscibility and Concentration Fluctuation of Hydrogen-Bonded Polymer Blends. J. Polym. Sci. Part B Polym. Phys. 2008, 46, 2556–2565. [Google Scholar] [CrossRef]
- Yang, Z.; Han, C.D. Rheology of miscible polymer blends with hydrogen bonding. Macromolecules 2008, 41, 2104–2118. [Google Scholar] [CrossRef]
- Cai, H.; Ait-Kadi, A.; Brisson, J. Dynamic rheological analysis of a miscible blend showing strong interactions. Polymer 2003, 44, 1481–1489. [Google Scholar] [CrossRef]
- Cai, H.J.; Ait-Kadi, A.; Brisson, J. Rheological quantification of molecular parameters: Application to a hydrogen bond forming blend. J. Appl. Polym. Sci. 2004, 93, 1623–1630. [Google Scholar] [CrossRef]
- Demeftahi, M.V.; Frechet, J.M.J. Study of the Compatibility of Blends of Polymers and Copolymers Containing Styrene, 4-Hydroxystyrene and 4-Vinylpyridine. Polymer 1988, 29, 477–482. [Google Scholar] [CrossRef]
- Kwei, T.K. The Effect of Hydrogen-Bonding on the Glass-Transition Temperatures of Polymer Mixtures. J. Polym. Sci. Polym. Lett. 1984, 22, 307–313. [Google Scholar] [CrossRef]
- Cesteros, L.C.; Meaurio, E.; Katime, I. Miscibility and Specific Interactions in Blends of Poly (Hydroxy Methacrylates) with Poly (Vinylpyridines). Macromolecules 1993, 26, 2323–2330. [Google Scholar] [CrossRef]
- Dai, J.; Goh, S.H.; Lee, S.Y.; Siow, K.S. Interpolymer Complexation between Poly (P-Vinylphenol) and Pyridine-Containing Polymers. Polym. J. 1994, 26, 905–911. [Google Scholar] [CrossRef]
- Bennour, S.; Metref, F.; Djadoun, S. Hydrogen-bonding interactions between poly (styrene-co-methacrylic acid) and poly (styrene-co-4-vinylpyridine). J. Appl. Polym. Sci. 2005, 98, 806–811. [Google Scholar] [CrossRef]
- Lee, L.T.; Woo, E.M.; Hou, S.S.; Forster, S. Miscibility with positive deviation in T-g-composition relationship in blends of poly (2-vinyl pyridine)-block-poly (ethylene oxide) and poly (p-vinyl phenol). Polymer 2006, 47, 8350–8359. [Google Scholar] [CrossRef]
- Haddadine-Rahmoun, N.; Amrani, F.; Arrighi, V.; Cowie, J.M.G. Interpolymer complexation in hydrolysed poly (styrene-co-maleicanhydride)/poly (styrene-co-4-vinylpyridine). Eur. Polym. J. 2008, 44, 821–831. [Google Scholar] [CrossRef]
- Chen, W.C.; Kuo, S.W.; Lu, C.H.; Jeng, U.S.; Chang, F.C. Self-Assembly Structures through Competitive Interactions of Crystalline-Amorphous Diblock Copolymer/Homopolymer Blends: Poly (epsilon-caprolactone-b-4-vinyl pyridine)/Poly (vinyl phenol). Macromolecules 2009, 42, 3580–3590. [Google Scholar] [CrossRef]
- Chen, S.C.; Kuo, S.W.; Jeng, U.S.; Su, C.J.; Chang, F.C. On Modulating the Phase Behavior of Block Copolymer/Homopolymer Blends via Hydrogen Bonding. Macromolecules 2010, 43, 1083–1092. [Google Scholar] [CrossRef]
- Tsai, S.C.; Lin, Y.C.; Lin, E.L.; Chiang, Y.W.; Kuo, S.W. Hydrogen bonding strength effect on self-assembly supramolecular structures of diblock copolymer/homopolymer blends. Polym. Chem. 2016, 7, 2395–2409. [Google Scholar] [CrossRef]
- Tseng, T.C.; Kuo, S.W. Hydrogen-Bonding Strength Influences Hierarchical Self-Assembled Structures in Unusual Miscible/Immiscible Diblock Copolymer Blends. Macromolecules 2018, 51, 6451–6459. [Google Scholar] [CrossRef]
- Tseng, T.C.; Kuo, S.W. Hierarchical Self-Assembled Structures from Diblock Copolymer Mixtures by Competitive Hydrogen Bonding Strength. Molecules 2018, 23. [Google Scholar] [CrossRef] [PubMed]
- Tseng, T.C.; Kuo, S.W. Hydrogen bonding induces unusual self-assembled structures from mixtures of two miscible disordered diblock copolymers. Eur. Polym. J. 2019, 116, 361–369. [Google Scholar] [CrossRef]
- Chen, S.C.; Kuo, S.W.; Liao, C.S.; Chang, F.C. Syntheses, Specific Interactions, and pH-Sensitive Micellization Behavior of Poly [vinylphenol-b-2-(dimethylamino) ethyl methacrylate] Diblock Copolymers. Macromolecules 2008, 41, 8865–8876. [Google Scholar] [CrossRef]
- Kuo, S.W.; Tung, P.H.; Chang, F.C. Syntheses and the study of strongly hydrogen-bonded poly (vinylphenol-b-vinylpyridine) diblock copolymer through anionic polymerization. Macromolecules 2006, 39, 9388–9395. [Google Scholar] [CrossRef]
- Gordon, M.; Taylor, J.S. Ideal Copolymers and the 2nd-Order Transitions of Synthetic Rubbers 1. Non-Crystalline Copolymers. J. Appl. Chem. 1952, 2, 493–500. [Google Scholar] [CrossRef]
- Wood, L.A. Glass Transition Temperatures of Copolymers. J. Polym. Sci. 1958, 28, 319–330. [Google Scholar] [CrossRef]
- Couchman, P.R. Compositional Variation of Glass-Transition Temperatures. 2. Application of Thermodynamic Theory to Compatible Polymer Blends. Macromolecules 1978, 11, 1156–1161. [Google Scholar] [CrossRef]
- Lin, A.A.; Kwei, T.K.; Reiser, A. On the Physical Meaning of the Kwei Equation for the Glass-Transition Temperature of Polymer Blends. Macromolecules 1989, 22, 4112–4119. [Google Scholar] [CrossRef]
- Urakawa, O.; Shimizu, A.; Fujita, M.; Tasaka, S.; Inoue, T. Memory effect in elastic modulus of a hydrogen-bonding polymer network. Polym. J. 2017, 49, 223–236. [Google Scholar] [CrossRef]
- Coleman, M.M.; Painter, P.C. Hydrogen bonded polymer blends. Prog. Polym. Sci. 1995, 20, 1–59. [Google Scholar] [CrossRef]
- Kuo, S.W.; Lin, C.L.; Chang, F.C. The study of hydrogen bonding and miscibility in poly (vinylpyridines) with phenolic resin. Polymer 2002, 43, 3943–3949. [Google Scholar] [CrossRef]
- Dobrosielska, K.; Wakao, S.; Takano, A.; Matsushita, Y. Nanophase-Separated Structures of AB Block Copolymer/C Homopolymer Blends with Complementary Hydrogen-Bonding Interactions. Macromolecules 2008, 41, 7695–7698. [Google Scholar] [CrossRef]
- Yasue, A.; Okada, Y.; Urakawa, O.; Inoue, T. Detailed Analysisi of Glass Transition Temperature on Polymer Blends with Hydorgen Bonding. J. Soc. Mater. Sci. Jpn. 2015, 64, 43–46. [Google Scholar] [CrossRef][Green Version]
- Sakaguchi, T.; Urakawa, O.; Adachi, K. Calorimetric Study of Dynamical Heterogeneity in Blends of Polyisoprene and Poly (vinylethylene). Macromolecules 2005, 38, 422–428. [Google Scholar] [CrossRef]
- Hirose, Y.; Urakawa, O.; Adachi, K. Dielectric study on the heterogeneous dynamics of miscible polyisoprene/poly (vinyl ethylene) blends: Estimation of the relevant length scales for the segmental relaxation dynamics. Macromolecules 2003, 36, 3699–3708. [Google Scholar] [CrossRef]
- Coleman, M.M.; Graf, J.F.; Painter, P.C. Specific Interactions and the Miscibility of Polymer Blends. In Specific Interactions and the Miscibility of Polymer Blends; Coleman, M.M., Graf, J.F., Painter, P.C., Eds.; Technomic Publishing Company, Inc.: Lancaster, PA, USA, 1991. [Google Scholar]
- Miwa, Y.; Shimada, S.; Urakawa, O.; Nobukawa, S. Origin of High Segmental Mobility at Chain Ends of Polystyrene. Macromolecules 2010, 43, 7192–7199. [Google Scholar] [CrossRef]
- Miwa, Y.; Udagawa, T.; Urakawa, O.; Nobukawa, S.; Kutsumizu, S. Rapid Stretching Vibration at the Polymer Chain End. ACS Macro Lett. 2014, 3, 126–129. [Google Scholar] [CrossRef]
- Miwa, Y.; Urakawa, O.; Doi, A.; Yamamoto, K.; Nobukawa, S. Glass Transition Temperature and beta Relaxation Temperature around Chain End of Polystyrene Determined by Site Specific Spin Labeling. J. Phys. Chem. B 2012, 116, 1282–1288. [Google Scholar] [CrossRef]
| Code | 103 Mw | Mw/Mn | Tg/°C | Cp/J °C−1 g−1 |
|---|---|---|---|---|
| VPh2 | 1.9 | 99.8 | 0.47 | |
| VPh5 | 4.5 | 1.8 | 146 | 0.44 |
| VPh16 (a) | 16 | 1.8 | 177 | 0.44 |
| 2VPy40 | 39 (b) | 1.03 | 99.0 | 0.34 |
| 4VPy60 | 60 (c) | 148 | 0.29 |
| Sample | q (Equation (1))/°C | q (Equation (3))/°C | α (Equation (3)) | |
|---|---|---|---|---|
| 2VPy40/VPh16 | 1.28 ± 0.1 | 120 ± 1 | 116 ± 1 | 1.19 ± 0.02 |
| 2VPy40/VPh5 | 1.28 ± 0.1 | 160 ± 1 | 158 ± 1 | 1.17 ± 0.02 |
| 2VPy40/VPh2 | 1.35 ± 0.1 | 187 ± 1 | 186 ± 1 | 1.18 ± 0.02 |
| n4VPy60/VPh5 | 1.52 ± 0.1 | 176 ± 1 | 176 ± 1 | 1.02 ± 0.02 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urakawa, O.; Yasue, A. Glass Transition Behaviors of Poly (Vinyl Pyridine)/Poly (Vinyl Phenol) Revisited. Polymers 2019, 11, 1153. https://doi.org/10.3390/polym11071153
Urakawa O, Yasue A. Glass Transition Behaviors of Poly (Vinyl Pyridine)/Poly (Vinyl Phenol) Revisited. Polymers. 2019; 11(7):1153. https://doi.org/10.3390/polym11071153
Chicago/Turabian StyleUrakawa, Osamu, and Ayaka Yasue. 2019. "Glass Transition Behaviors of Poly (Vinyl Pyridine)/Poly (Vinyl Phenol) Revisited" Polymers 11, no. 7: 1153. https://doi.org/10.3390/polym11071153
APA StyleUrakawa, O., & Yasue, A. (2019). Glass Transition Behaviors of Poly (Vinyl Pyridine)/Poly (Vinyl Phenol) Revisited. Polymers, 11(7), 1153. https://doi.org/10.3390/polym11071153