Janus Nanostructures from ABC/B Triblock Terpolymer Blends
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of SBM Bulk Films
2.3. Crosslinking of SBM Bulk Films
2.4. Transmission Electron Microscopy (TEM)
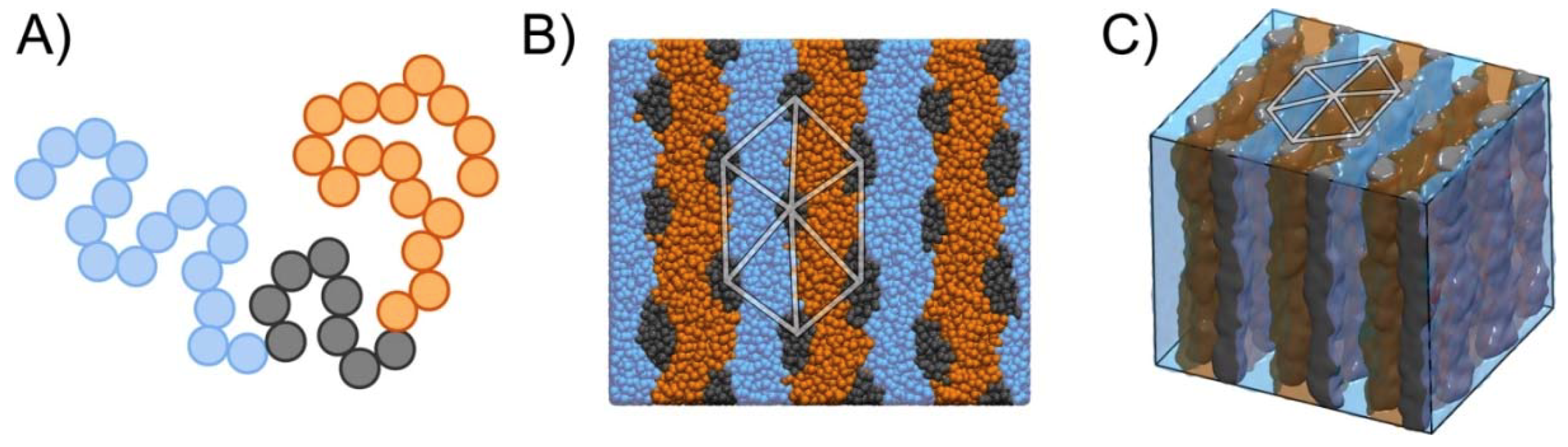
2.5. Simulation Model and Method
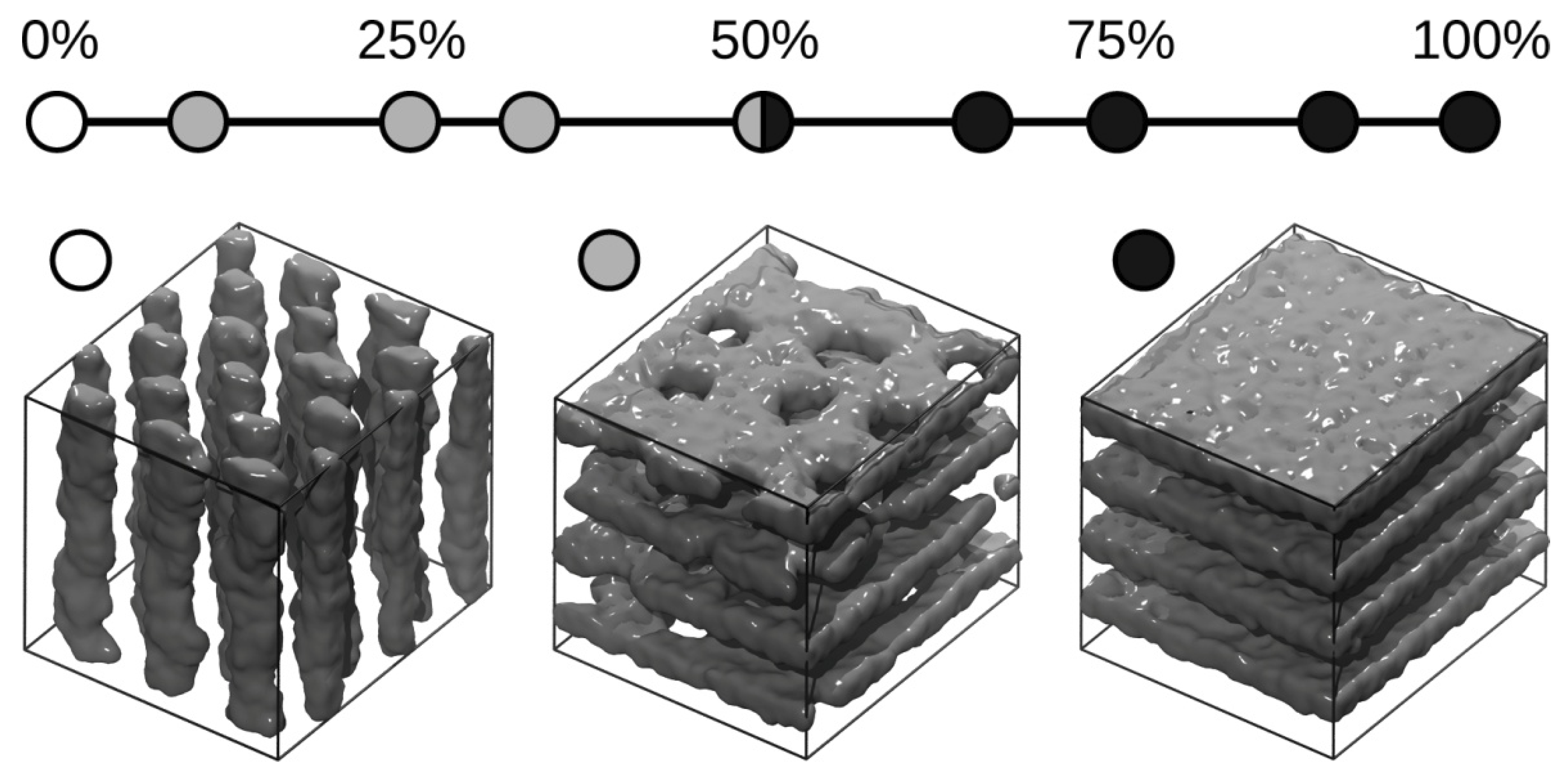
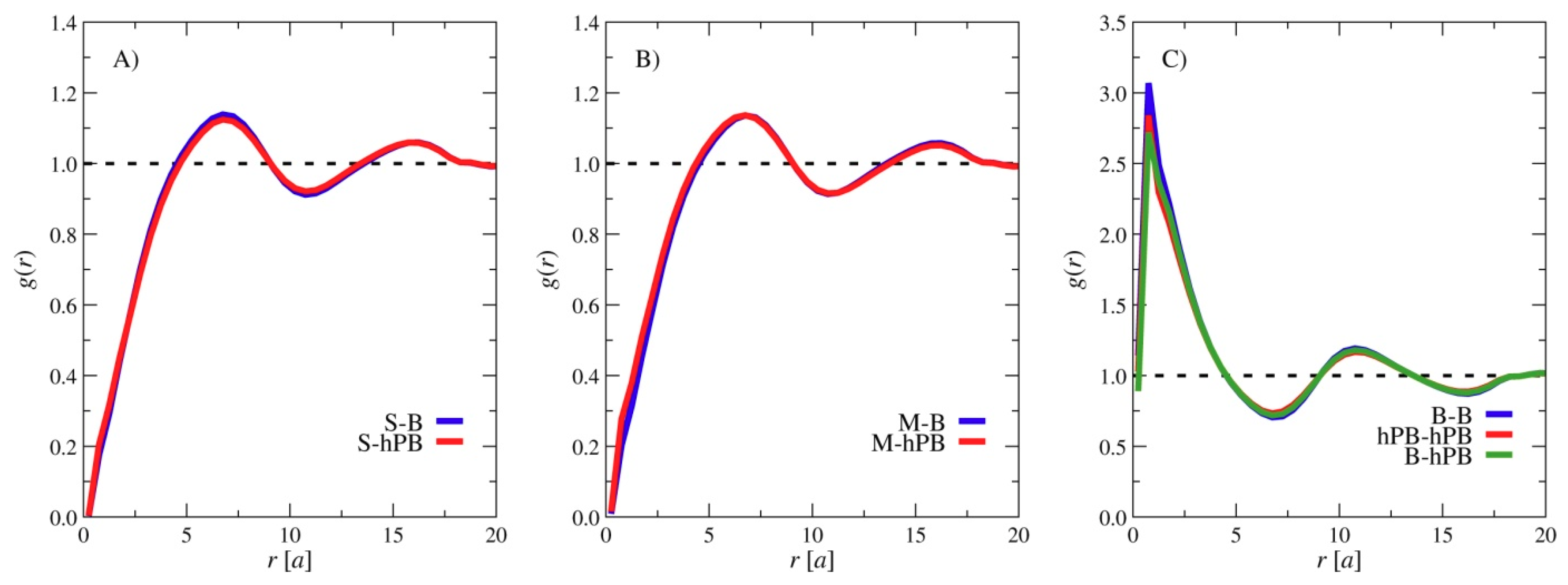
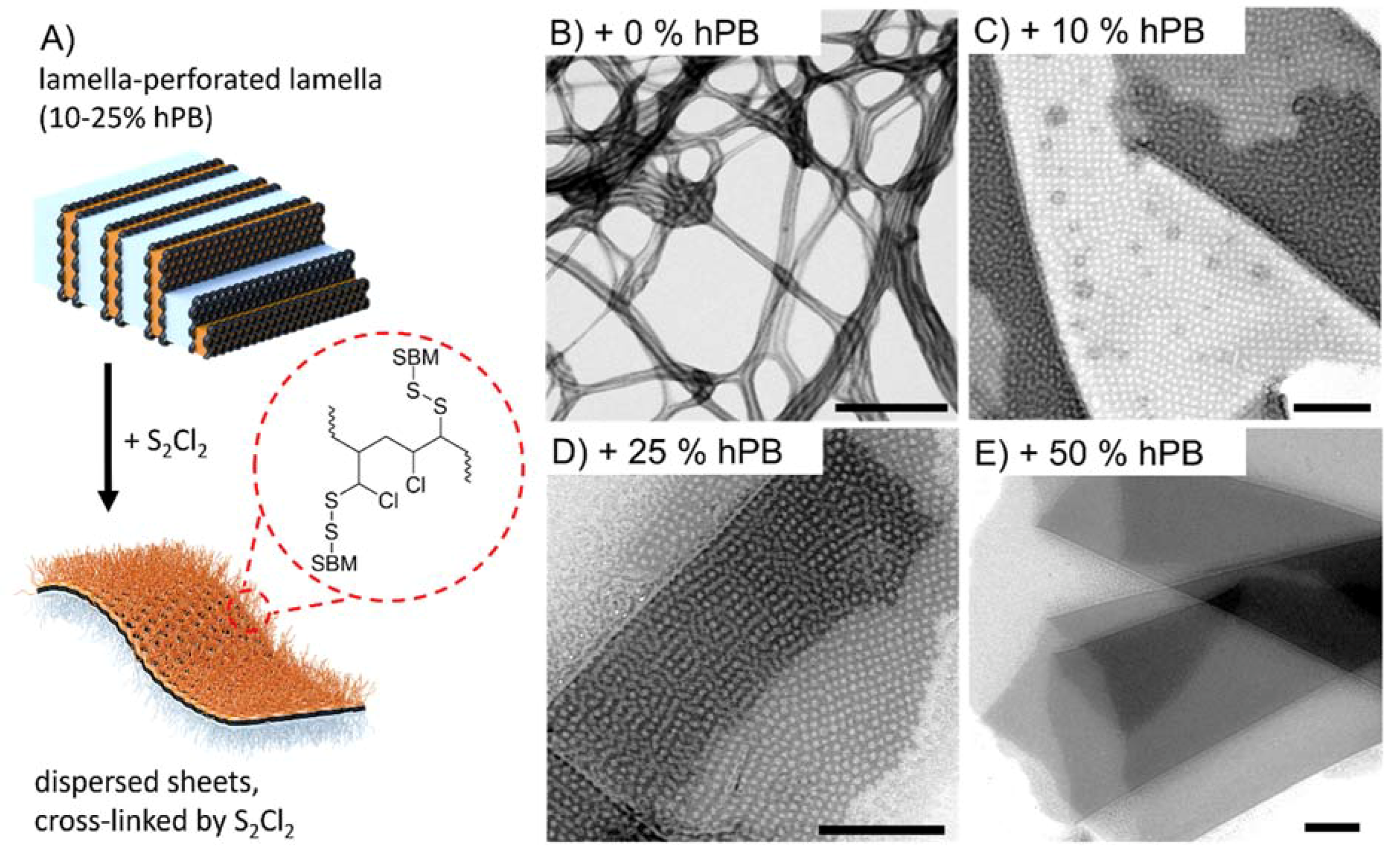
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abetz, V.; Simon, P.F.W. Phase behaviour and morphologies of block copolymers. In Advances in Polymer Science; Springer-Verlag: Berlin/Heidelberg, 2005; Volume 189, pp. 125–212. [Google Scholar]
- Schacher, F.H.; Rupar, P.A.; Manners, I. Functional Block Copolymers: Nanostructured Materials with Emerging Applications. Angew. Chemie Int. Ed. 2012, 51, 7898–7921. [Google Scholar] [CrossRef] [PubMed]
- Vukovic, I.; Brinke, G.T.; Loos, K. Block copolymer template-directed synthesis of well-ordered metallic nanostructures. Polymer 2013, 54, 2591–2605. [Google Scholar] [CrossRef]
- Crossland, E.J.W.; Kamperman, M.; Nedelcu, M.; Ducati, C.; Wiesner, U.; Smilgies, D.M.; Toombes, G.E.S.; Hillmyer, M.A.; Ludwigs, S.; Steiner, U.; et al. A bicontinuous double gyroid hybrid solar cell. Nano Lett. 2009, 9, 2807–2812. [Google Scholar] [CrossRef] [PubMed]
- Yoo, S.; Kim, J.-H.; Shin, M.; Park, H.; Kim, J.-H.; Lee, S.-Y.; Park, S. Hierarchical multiscale hyperporous block copolymer membranes via tunable dual-phase separation. Sci. Adv. 2015, 1, e1500101. [Google Scholar] [CrossRef] [PubMed]
- Abetz, V. Isoporous block copolymer membranes. Macromol. Rapid Commun. 2015, 36, 10–22. [Google Scholar] [CrossRef] [PubMed]
- Ludwigs, S.; Böker, A.; Voronov, A.; Rehse, N.; Magerle, R.; Krausch, G. Self-assembly of functional nanostructures from ABC triblock copolymers. Nat. Mater. 2003, 2, 744–747. [Google Scholar] [CrossRef]
- Marencic, A.P.; Register, R.A. Controlling Order in Block Copolymer Thin Films for Nanopatterning Applications. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 277–297. [Google Scholar] [CrossRef]
- Nikoubashman, A.; Davis, R.L.; Michal, B.T.; Chaikin, P.M.; Register, R.A.; Panagiotopoulos, A.Z. Thin films of homopolymers and cylinder-forming diblock copolymers under shear. ACS Nano 2014, 8, 8015–8026. [Google Scholar] [CrossRef]
- Stefik, M.; Guldin, S.; Vignolini, S.; Wiesner, U.; Steiner, U. Block copolymer self-assembly for nanophotonics. Chem. Soc. Rev. 2015, 44, 5076–5091. [Google Scholar] [CrossRef]
- Hannon, A.F.; Bai, W.; Alexander-Katz, A.; Ross, C.A. Simulation methods for solvent vapor annealing of block copolymer thin films. Soft Matter 2015, 11, 3794–3805. [Google Scholar] [CrossRef]
- Nikoubashman, A.; Register, R.A.; Panagiotopoulos, A.Z. Simulations of shear-induced morphological transitions in block copolymers. Soft Matter 2013, 9, 9960. [Google Scholar] [CrossRef]
- Abetz, V.; Boschetti-de-Fierro, A. Block Copolymers in the Condensed State. In Polymer Science: A Comprehensive Reference, 10 Volume Set; Elsevier: Amsterdam, The Netherlands, 2012; Volume 7, pp. 3–44. [Google Scholar]
- Bates, F.S.; Fredrickson, G.H. Block copolymers-designer soft materials. Phys. Today 1999, 52, 32–38. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, Z.-G. Morphology of ABC Triblock Copolymers. Macromolecules 1995, 28, 7215–7223. [Google Scholar] [CrossRef]
- Liu, M.; Li, W.; Qiu, F.; Shi, A.C. Theoretical study of phase behavior of frustrated ABC linear triblock copolymers. Macromolecules 2012, 45, 9522–9530. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, G.; Qiu, F.; Zhang, H.; Yang, Y.; Shi, A.-C. Discovering Ordered Phases of Block Copolymers: New Results from a Generic Fourier-Space Approach. Phys. Rev. Lett. 2008, 101, 028301. [Google Scholar] [CrossRef] [PubMed]
- Auschra, C.; Stadler, R. Synthesis of block copolymers with poly(methyl methacrylate): P(B-b-MMA), P(EB-b-MMA), P(S-b-B-b-MMA) and P(S-b-EB-b-MMA). Polym. Bull. 1993, 30, 257–264. [Google Scholar] [CrossRef]
- Beckmann, J.; Auschra, C.; Stadler, R. “Ball at the wall” — A new lamellar multiphase morphology in a polystyrene-block-polybutadiene-block-poly(methyl methacrylate) triblock copolymer. Macromol. Rapid Commun. 1994, 15, 67–72. [Google Scholar] [CrossRef]
- Stadler, R.; Auschra, C.; Beckmann, J.; Krappe, U.; Voigt-Martin, I.; Leibler, L. Morphology and Thermodynamics of Symmetric Poly(A-block-B-block-C) Triblock Copolymers. Macromolecules 1995, 28, 3080–3097. [Google Scholar] [CrossRef]
- Breiner, U.; Krappe, U.; Stadler, R. Evolution of the “knitting pattern” morphology in ABC triblock copolymers. Macromol. Rapid Commun. 1996, 17, 567–575. [Google Scholar] [CrossRef]
- Breiner, U.; Krappe, U.; Abetz, V.; Stadler, R. Cylindrical morphologies in asymmetric ABC triblock copolymers. Macromol. Chem. Phys. 1997, 198, 1051–1083. [Google Scholar] [CrossRef]
- Breiner, U.; Krappe, U.; Jakob, T.; Abetz, V.; Stadler, R. Spheres on spheres - A novel spherical multiphase morphology in polystyrene-block-polybutadiene-block-poly(methyl methacrylate) triblock copolymers. Polym. Bull. 1998, 40, 219–226. [Google Scholar] [CrossRef]
- Ludwigs, S.; Böker, A.; Abetz, V.; Müller, A.H.E.; Krausch, G. Phase behavior of linear polystyrene-block-poly(2-vinylpyridine)-block-poly(tert-butyl methacrylate) triblock terpolymers. Polymer 2003, 44, 6815–6823. [Google Scholar] [CrossRef]
- Löbling, T.I.; Hiekkataipale, P.; Hanisch, A.; Bennet, F.; Schmalz, H.; Ikkala, O.; Gröschel, A.H.; Müller, A.H.E. Bulk morphologies of polystyrene-block-polybutadiene-block-poly(tert-butyl methacrylate) triblock terpolymers. Polymer 2015, 72, 479–489. [Google Scholar] [CrossRef]
- Gobius du Sart, G.; Rachmawati, R.; Voet, V.; Alberda van Ekenstein, G.; Polushkin, E.; Brinke, G.T.; Loos, K. Poly(tert-butyl methacrylate-b-styrene-b-4-vinylpyridine) Triblock Copolymers: Synthesis, Interactions, and Self-Assembly. Macromolecules 2008, 41, 6393–6399. [Google Scholar] [CrossRef]
- Kumar, R.; Sides, S.W.; Goswami, M.; Sumpter, B.G.; Hong, K.; Wu, X.; Russell, T.P.; Gido, S.P.; Misichronis, K.; Rangou, S.; et al. Morphologies of ABC Triblock Terpolymer Melts Containing Poly(Cyclohexadiene): Effects of Conformational Asymmetry. Langmuir 2013, 29, 1995–2006. [Google Scholar] [CrossRef] [PubMed]
- Schacher, F.; Yuan, J.; Schoberth, H.G.; Müller, A.H.E. Synthesis, characterization, and bulk crosslinking of polybutadiene-block-poly(2-vinyl pyridine)-block-poly(tert-butyl methacrylate) block terpolymers. Polymer 2010, 51, 2021–2032. [Google Scholar] [CrossRef]
- Erhardt, R.; Böker, A.; Zettl, H.; Kaya, H.; Pyckhout-Hintzen, W.; Krausch, G.; Abetz, V.; Müller, A.H.E. Janus micelles. Macromolecules 2001, 34, 1069–1075. [Google Scholar] [CrossRef]
- Liu, Y.; Abetz, V.; Müller, A.H.E. Janus Cylinders. Macromolecules 2003, 36, 7894–7898. [Google Scholar] [CrossRef]
- Walther, A.; André, X.; Drechsler, M.; Abetz, V.; Müller, A.H.E. Janus discs. J. Am. Chem. Soc. 2007, 129, 6187–6198. [Google Scholar] [CrossRef]
- Wolf, A.; Walther, A.; Müller, A.H.E. Janus Triad: Three types of nonspherical, nanoscale Janus particles from one single triblock terpolymer. Macromolecules 2011, 44, 9221–9229. [Google Scholar] [CrossRef]
- Walther, A.; Müller, A.H.E. Janus Particles: Synthesis, Self-Assembly, Physical Properties, and Applications. Chem. Rev. 2013, 113, 5194–5261. [Google Scholar] [CrossRef] [PubMed]
- Walther, A.; Hoffmann, M.; Müller, A.H.E. Emulsion Polymerization Using Janus Particles as Stabilizers. Angew. Chemie Int. Ed. 2008, 47, 711–714. [Google Scholar] [CrossRef] [PubMed]
- Gröschel, A.H.; Löbling, T.I.; Petrov, P.D.; Müllner, M.; Kuttner, C.; Wieberger, F.; Müller, A.H.E. Janus Micelles as Effective Supracolloidal Dispersants for Carbon Nanotubes. Angew. Chemie Int. Ed. 2013, 52, 3602–3606. [Google Scholar] [CrossRef] [PubMed]
- Bahrami, R.; Löbling, T.I.; Gröschel, A.H.; Schmalz, H.; Müller, A.H.E.; Altstädt, V. The Impact of Janus Nanoparticles on the Compatibilization of Immiscible Polymer Blends under Technologically Relevant Conditions. ACS Nano 2014, 8, 10048–10056. [Google Scholar] [CrossRef] [PubMed]
- Walther, A.; Matussek, K.; Müller, A.H.E. Engineering nanostructured polymer blends with controlled nanoparticle location using Janus particles. ACS Nano 2008, 2, 1167–1178. [Google Scholar] [CrossRef] [PubMed]
- Binks, B.P.; Fletcher, P.D.I. Particles adsorbed at the oil-water interface: A theoretical comparison between spheres of uniform wettability and “Janus” particles. Langmuir 2001, 17, 4708–4710. [Google Scholar] [CrossRef]
- Glaser, N.; Adams, D.J.; Böker, A.; Krausch, G. Janus particles at liquid-liquid interfaces. Langmuir 2006, 22, 5227–5229. [Google Scholar] [CrossRef]
- Ruhland, T.M.; Gröschel, A.H.; Walther, A.; Müller, A.H.E. Janus cylinders at liquid-liquid interfaces. Langmuir 2011, 27, 9807–9814. [Google Scholar] [CrossRef]
- Ruhland, T.M.; Gröschel, A.H.; Ballard, N.; Skelhon, T.S.; Walther, A.; Müller, A.H.E.; Bon, S.A.F. Influence of janus particle shape on their interfacial behavior at liquid-liquid interfaces. Langmuir 2013, 29, 1388–1394. [Google Scholar] [CrossRef]
- Jiang, Y.; Löbling, T.I.; Huang, C.; Sun, Z.; Müller, A.H.E.; Russell, T.P. Interfacial Assembly and Jamming Behavior of Polymeric Janus Particles at Liquid Interfaces. ACS Appl. Mater. Interfaces 2017, 9, 33327–33332. [Google Scholar] [CrossRef]
- Jiang, S.; Göpfert, A.; Abetz, V. Novel morphologies of block copolymer blends via hydrogen bonding. Macromolecules 2003, 36, 6171–6177. [Google Scholar] [CrossRef]
- Hofman, A.H.; Terzic, I.; Stuart, M.C.A.; Ten Brinke, G.; Loos, K. Hierarchical Self-Assembly of Supramolecular Double-Comb Triblock Terpolymers. ACS Macro Lett. 2018, 7, 1168–1173. [Google Scholar] [CrossRef] [PubMed]
- Hiekkataipale, P.; Löbling, T.I.; Poutanen, M.; Priimagi, A.; Abetz, V.; Ikkala, O.; Gröschel, A.H. Controlling the shape of Janus nanostructures through supramolecular modification of ABC terpolymer bulk morphologies. Polymer 2016, 107, 456–465. [Google Scholar] [CrossRef]
- Izumi, Y.; Yamada, M.; Takano, A.; Matsushita, Y. A new periodic pattern with five-neighbored domain packing from ABC triblock terpolymer/B homopolymer blend. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 907–911. [Google Scholar] [CrossRef]
- Yu, X.; Luo, C.; Zhao, Q.; Yang, H.; Han, Y. Order-order transitions of a triblock copolymer with a homopolymer (ABC/A) blend film induced by saturated solvent vapor annealing. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 1030–1036. [Google Scholar] [CrossRef]
- Higuchi, T.; Sugimori, H.; Jiang, X.; Hong, S.; Matsunaga, K.; Kaneko, T.; Abetz, V.; Takahara, A.; Jinnai, H. Morphological control of helical structures of an ABC-type triblock terpolymer by distribution control of a blending homopolymer in a block copolymer microdomain. Macromolecules 2013, 46, 6991–6997. [Google Scholar] [CrossRef]
- Goldacker, T.; Abetz, V. Core-shell cylinders and core-shell gyroid morphologies via blending of lamellar ABC triblock and BC diblock copolymers. Macromolecules 1999, 32, 5165–5167. [Google Scholar] [CrossRef]
- Abetz, V.; Jiang, S.; Göpfert, A. Novel pattern formation in blends of asymmetric ABC triblock terpolymers. E-Polymers 2004, 4, 1–10. [Google Scholar] [CrossRef][Green Version]
- Jiang, S.; Göpfert, A.; Abetz, V. Novel Superlattices via Blending of Asymmetric Triblock Terpolymers with Diblock Copolymers. Macromol. Rapid Commun. 2003, 24, 932–937. [Google Scholar] [CrossRef]
- Goldacker, T.; Abetz, V. A new way to the “knitting pattern” via blending of ABC triblock copolymers. Macromol. Rapid Commun. 2002, 20, 415–418. [Google Scholar] [CrossRef]
- Matsushita, Y.; Suzuki, J.; Izumi, Y.; Matsuoka, K.; Takahashi, S.; Aoyama, Y.; Mihira, T.; Takano, A. Formation of undulated lamellar structure from ABC block terpolymer blends with different chain lengths. J. Chem. Phys. 2010, 133, 194901. [Google Scholar] [CrossRef] [PubMed]
- Asai, Y.; Yamada, K.; Yamada, M.; Takano, A.; Matsushita, Y. Formation of tetragonally-packed rectangular cylinders from ABC block terpolymer blends. ACS Macro Lett. 2014, 3, 166–169. [Google Scholar] [CrossRef]
- Asai, Y.; Takano, A.; Matsushita, Y. Creation of cylindrical morphologies with extremely large oblong unit lattices from ABC block terpolymer blends. Macromolecules 2015, 48, 1538–1542. [Google Scholar] [CrossRef]
- Steinhaus, A.; Chakroun, R.; Müllner, M.; Nghiem, T.-L.; Hildebrandt, M.; Gröschel, A.H. Confinement Assembly of ABC Triblock Terpolymers for the High-Yield Synthesis of Janus Nanorings. ACS Nano 2019, 13, 6269–6278. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.-C.; Hou, J.; Chen, V.; Xu, Z.-K. Janus Membranes: Exploring Duality for Advanced Separation. Angew. Chemie Int. Ed. 2016, 55, 13398–13407. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.G.; Louis, A.A.; Hansen, J.P.; Meijer, E.J. Accurate effective pair potentials for polymer solutions. J. Chem. Phys. 2001, 114, 4296–4311. [Google Scholar] [CrossRef]
- Likos, C.N. Effective interactions in soft condensed matter physics. Phys. Rep. 2001, 348, 267–439. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Groot, R.D.; Madden, T.J. Dynamic simulation of diblock copolymer microphase separation. J. Chem. Phys. 1998, 108, 8713–8724. [Google Scholar] [CrossRef]
- Español, P.; Warren, P. Statistical Mechanics of Dissipative Particle Dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Liu, D.; Zhong, C. Dissipative Particle Dynamics Simulation of Microphase Separation and Properties of Linear-Dendritic Diblock Copolymer Melts under Steady Shear Flow. Macromol. Rapid Commun. 2005, 26, 1960–1964. [Google Scholar] [CrossRef]
- Petrus, P.; Lísal, M.; Brennan, J.K. Self-Assembly of Lamellar- and Cylinder-Forming Diblock Copolymers in Planar Slits: Insight from Dissipative Particle Dynamics Simulations. Langmuir 2010, 26, 14680–14693. [Google Scholar] [CrossRef] [PubMed]
- Gavrilov, A.A.; Kudryavtsev, Y.V.; Chertovich, A.V. Phase diagrams of block copolymer melts by dissipative particle dynamics simulations. J. Chem. Phys. 2013, 139, 224901. [Google Scholar] [CrossRef] [PubMed]
- Schacher, F.H.; Sugimori, H.; Hong, S.; Jinnai, H.; Müller, A.H.E. Tetragonally perforated lamellae of polybutadiene-block-poly(2- vinylpyridine)-block-poly(tert-butyl methacrylate) (BVT) triblock terpolymers in the bulk: Preparation, cross-linking, and dissolution. Macromolecules 2012, 45, 7956–7963. [Google Scholar] [CrossRef]
- Kressler, J.; Higashida, N.; Shimomai, K.; Inoue, T.; Ougizawa, T. Temperature Dependence of the Interaction Parameter between Polystyrene and Poly(methyl methacrylate). Macromolecules 1994, 27, 2448–2453. [Google Scholar] [CrossRef]
- Ronca, G.; Russell, T.P. Concentration fluctuations of polystyrene-polybutadiene blends. Phys. Rev. B 1987, 35, 8566–8571. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Betthausen, E.; Dulle, M.; Hanske, C.; Müller, M.; Fery, A.; Förster, S.; Schacher, F.H.; Müller, A.H.E. Nanoporous sheets and cylinders via bulk templating of triblock terpolymer/homopolymer blends. Macromolecules 2014, 47, 6289–6301. [Google Scholar] [CrossRef]
- Breulmann, M.; Förster, S.; Antonietti, M. Mesoscopic surface patterns formed by block copolymer micelles. Macromol. Chem. Phys. 2000, 201, 204–211. [Google Scholar] [CrossRef]
- Peinemann, K.V.; Abetz, V.; Simon, P.F.W. Asymmetric superstructure formed in a block copolymer via phase separation. Nat. Mater. 2007, 6, 992–996. [Google Scholar] [CrossRef]
- Hahn, J.; Filiz, V.; Rangou, S.; Clodt, J.; Jung, A.; Buhr, K.; Abetz, C.; Abetz, V. Structure formation of integral-asymmetric membranes of polystyrene-block-Poly(ethylene oxide). J. Polym. Sci. Part B Polym. Phys. 2013, 51, 281–290. [Google Scholar] [CrossRef]
- Wang, Y.; Tong, L.; Steinhart, M. Swelling-induced morphology reconstruction in block copolymer nanorods: Kinetics and impact of surface tension during solvent evaporation. ACS Nano 2011, 5, 1928–1938. [Google Scholar] [CrossRef] [PubMed]
- Werber, J.R.; Osuji, C.O.; Elimelech, M. Materials for next-generation desalination and water purification membranes. Nat. Rev. Mater. 2016, 1, 16018. [Google Scholar] [CrossRef]




| Code | hPB added a | fSb | fBb | fMb | Thickness PB c |
|---|---|---|---|---|---|
| SBM-0 | 0 | 40 | 22 | 38 | 10.9 |
| SBM-10 | 10 | 39 | 24 | 37 | 15.0 |
| SBM-25 | 25 | 38 | 26 | 36 | 12.8 |
| SBM-50 | 50 | 36 | 30 | 34 | 12.6 |
| SBM-75 | 75 | 34 | 33 | 33 | 12.9 |
| SBM-100 | 100 | 33 | 36 | 31 | 14.6 |
| Interaction pairs | ||||
|---|---|---|---|---|
| S-M | 0.041 | 44.8 | 1.5 | 30.4 |
| S-B | 0.19 | 192 | 8.4 | 54.5 |
| B-M | 0.12 | 130 | 5.6 | 44.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steinhaus, A.; Srivastva, D.; Nikoubashman, A.; Gröschel, A.H. Janus Nanostructures from ABC/B Triblock Terpolymer Blends. Polymers 2019, 11, 1107. https://doi.org/10.3390/polym11071107
Steinhaus A, Srivastva D, Nikoubashman A, Gröschel AH. Janus Nanostructures from ABC/B Triblock Terpolymer Blends. Polymers. 2019; 11(7):1107. https://doi.org/10.3390/polym11071107
Chicago/Turabian StyleSteinhaus, Andrea, Deepika Srivastva, Arash Nikoubashman, and André H. Gröschel. 2019. "Janus Nanostructures from ABC/B Triblock Terpolymer Blends" Polymers 11, no. 7: 1107. https://doi.org/10.3390/polym11071107
APA StyleSteinhaus, A., Srivastva, D., Nikoubashman, A., & Gröschel, A. H. (2019). Janus Nanostructures from ABC/B Triblock Terpolymer Blends. Polymers, 11(7), 1107. https://doi.org/10.3390/polym11071107







