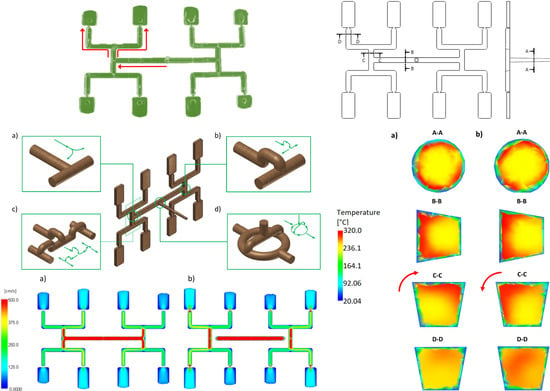
Simulation Studies on the Effect of Material Characteristics and Runners Layout Geometry on the Filling Imbalance in Geometrically Balanced Injection Molds
Abstract
:1. Introduction
2. Process Simulation
2.1. Simulation Program
2.2. Material
2.3. Procedure of Estimation of Filling Imbalance
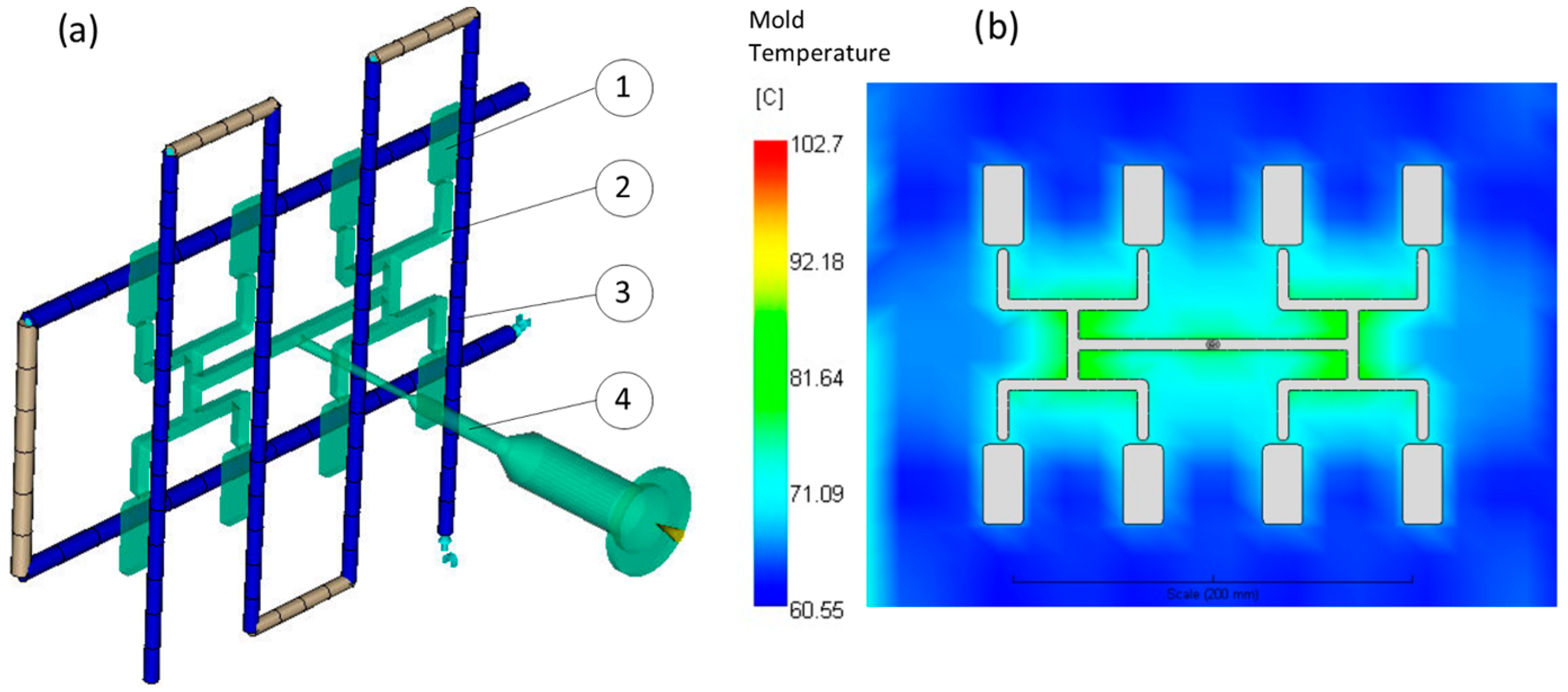
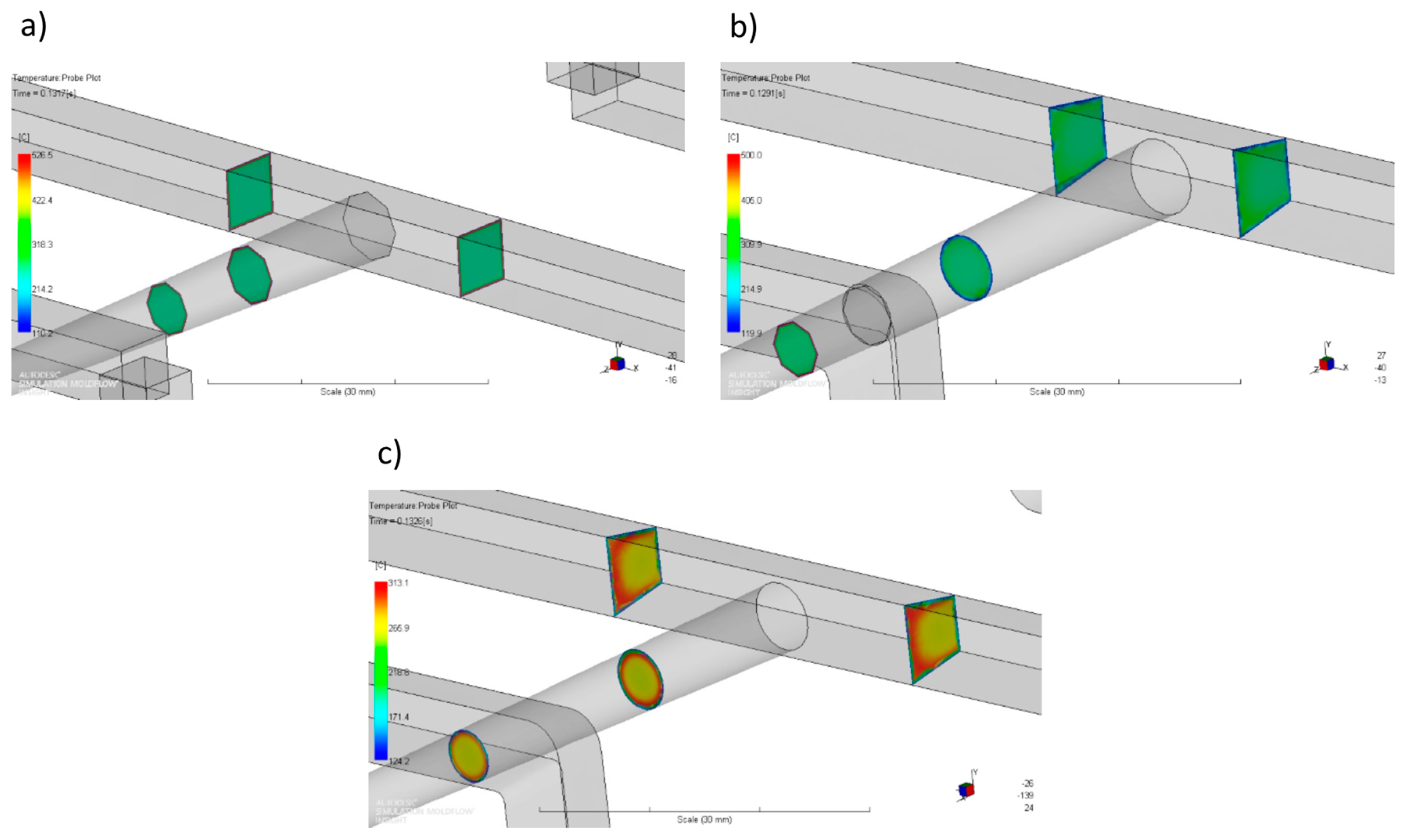
2.4. Simulation Technique
3. Results
3.1. Effect of Rheological Parameters
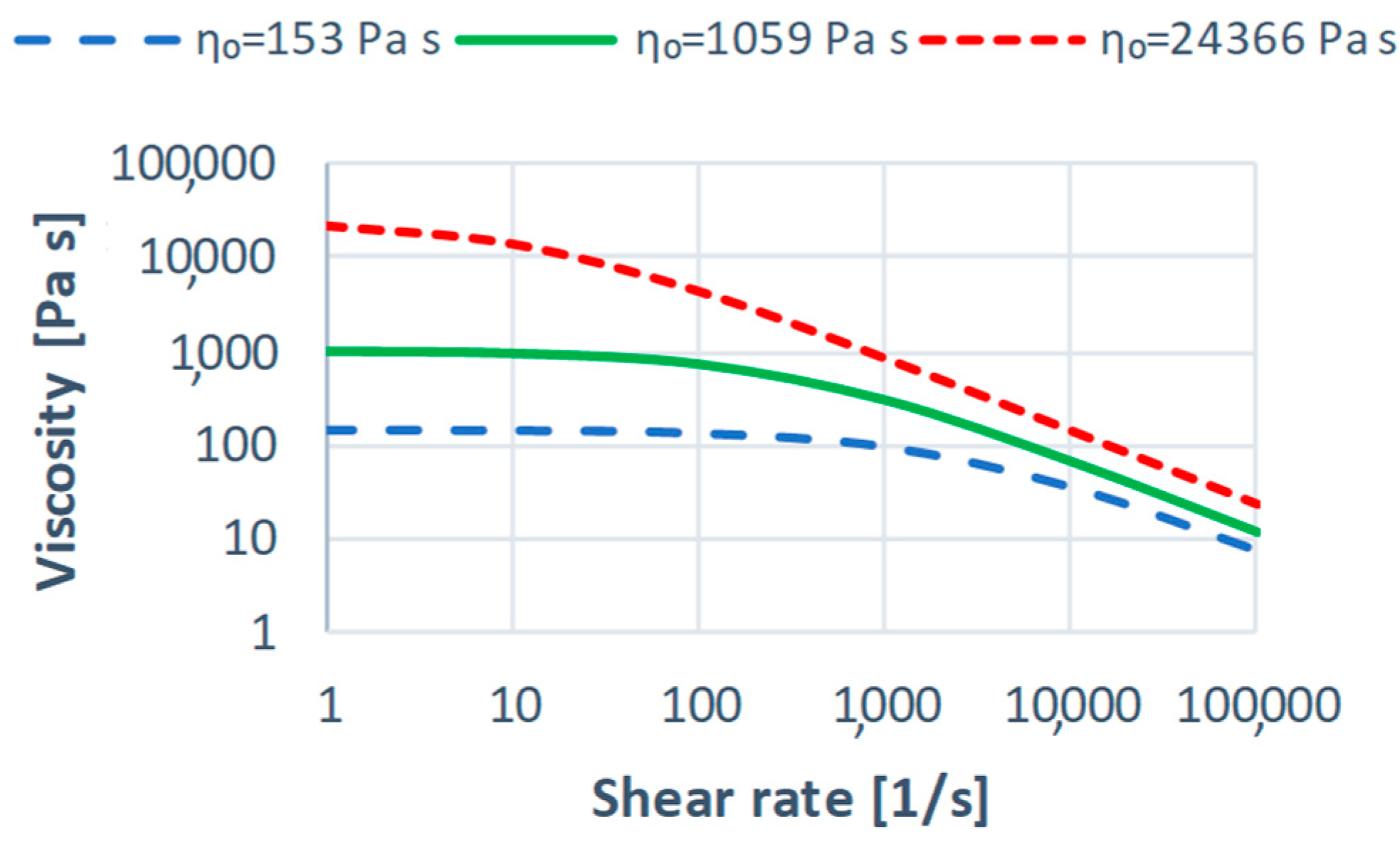
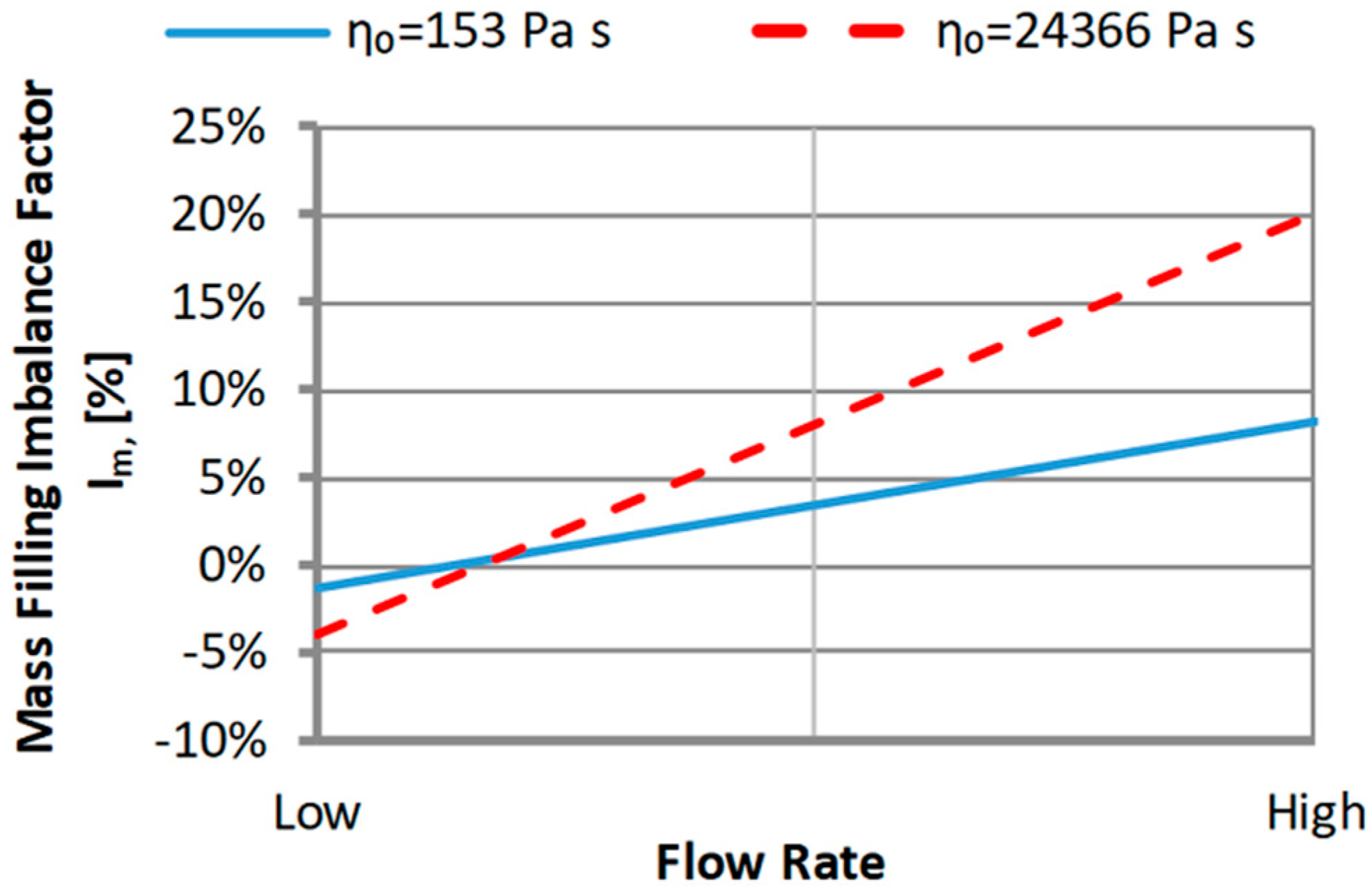
3.1.1. The Zero Shear Viscosity
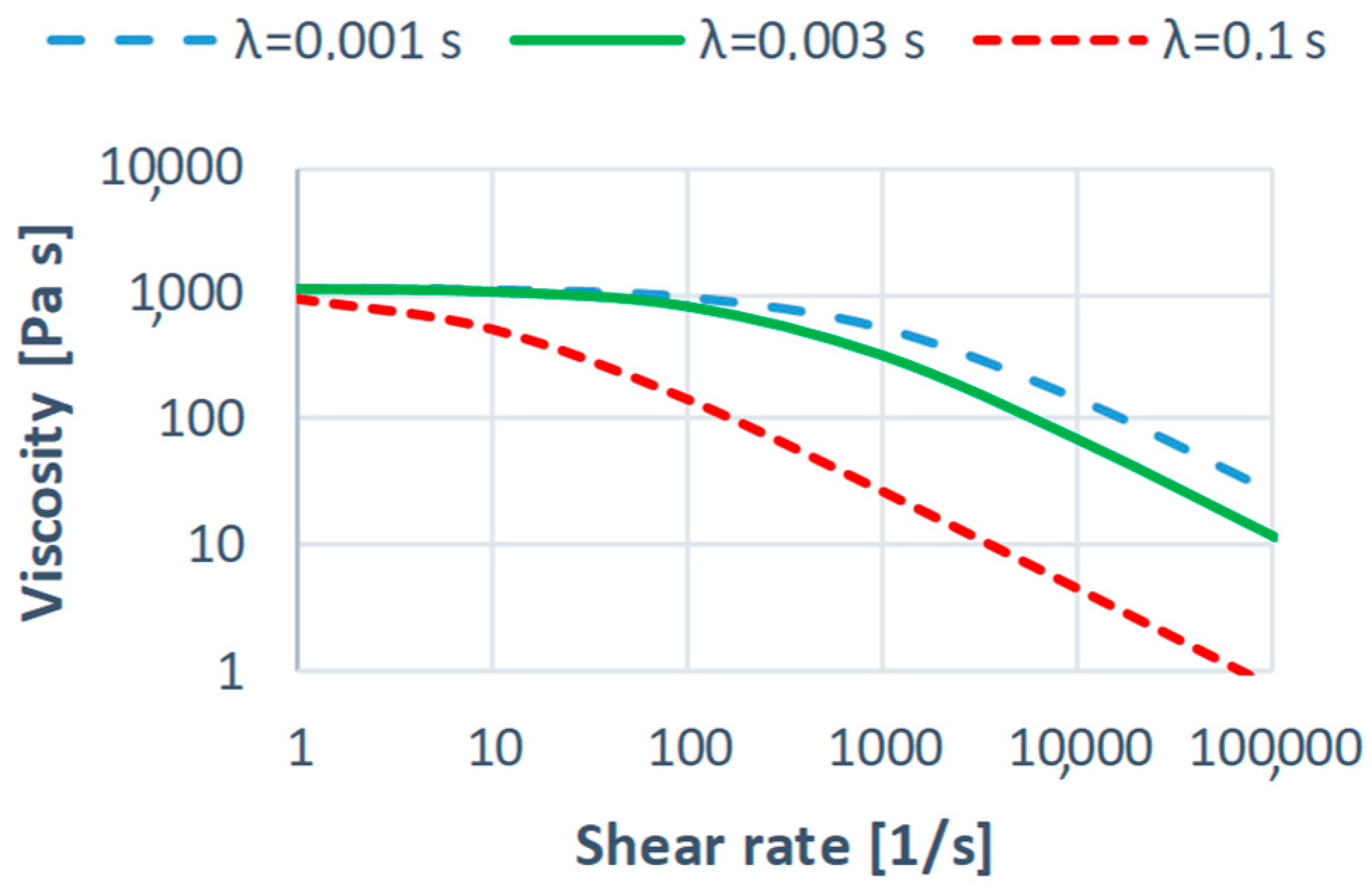
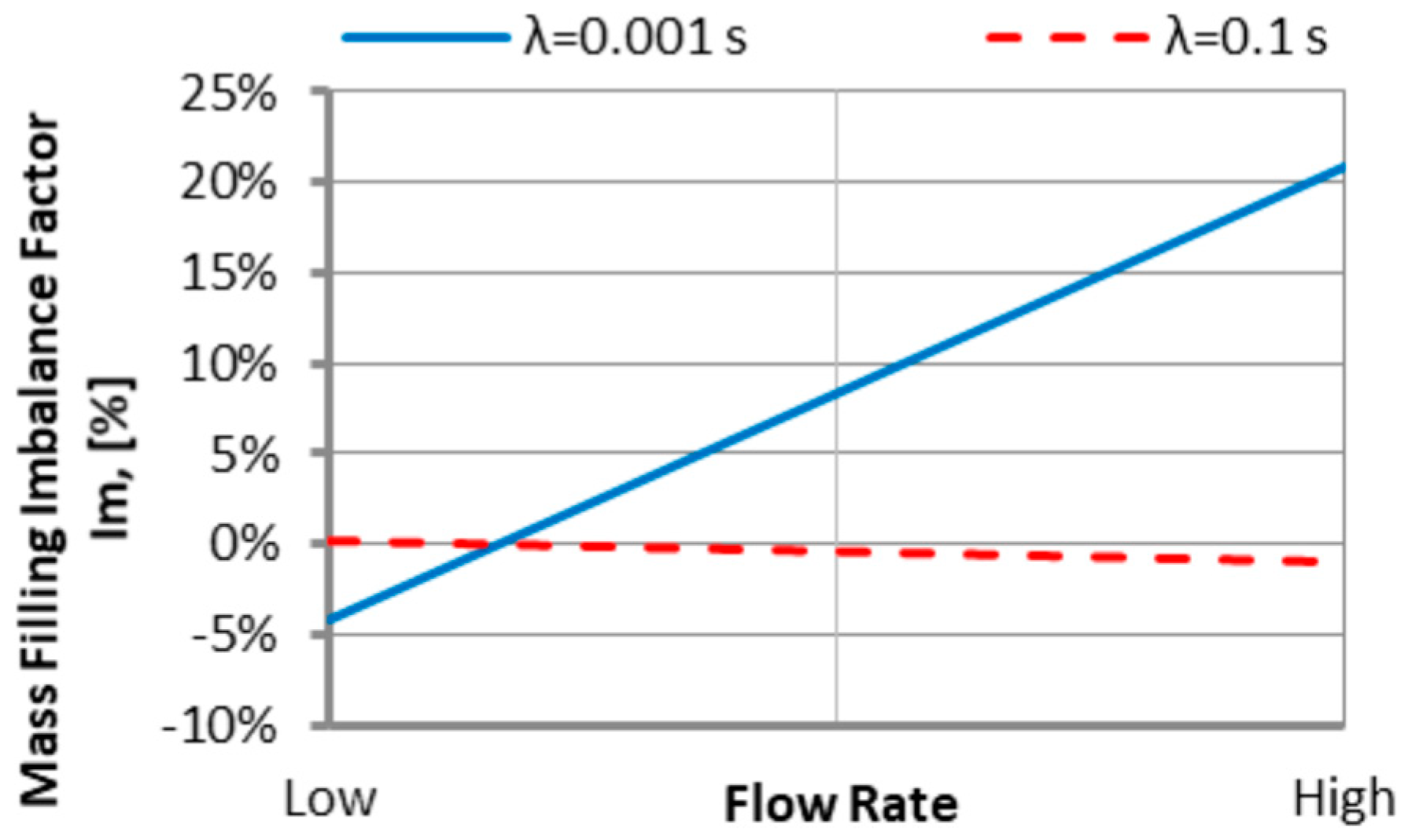
3.1.2. The Relaxation Time
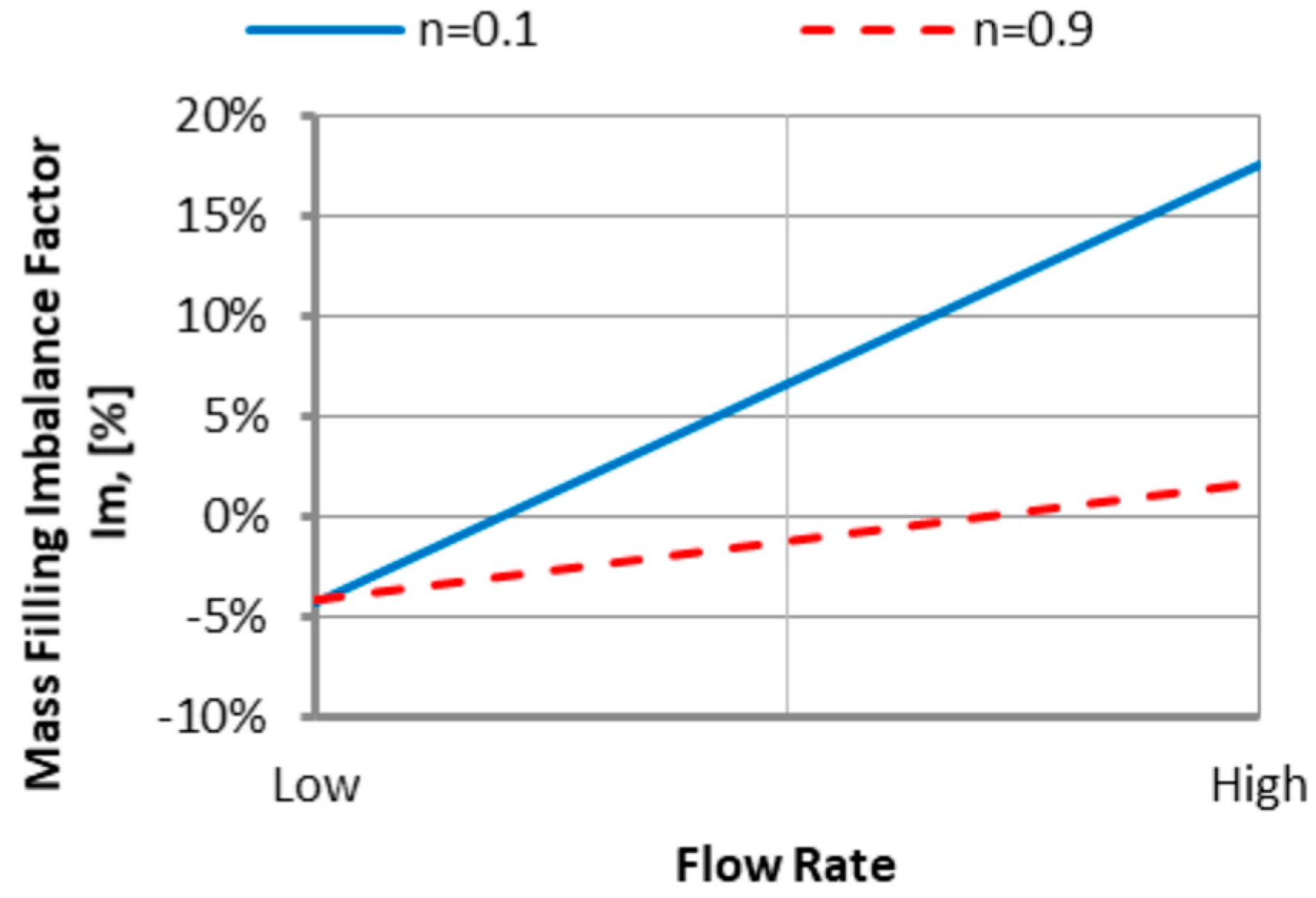
3.1.3. The Power Law Index
3.2. Effect of Thermal Parameters
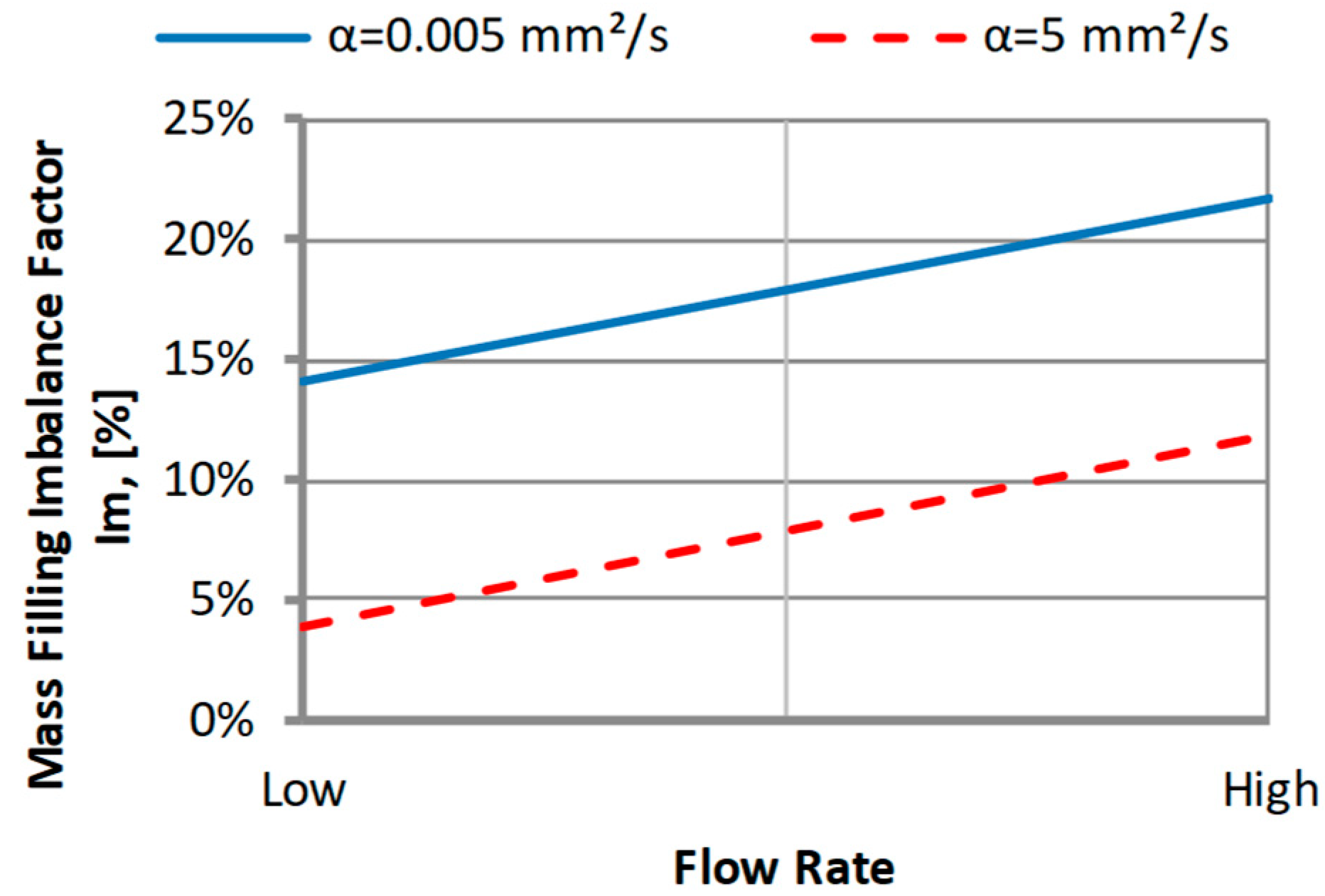
3.2.1. The Thermal Diffusivity
3.2.2. The Heat Transfer Coefficient
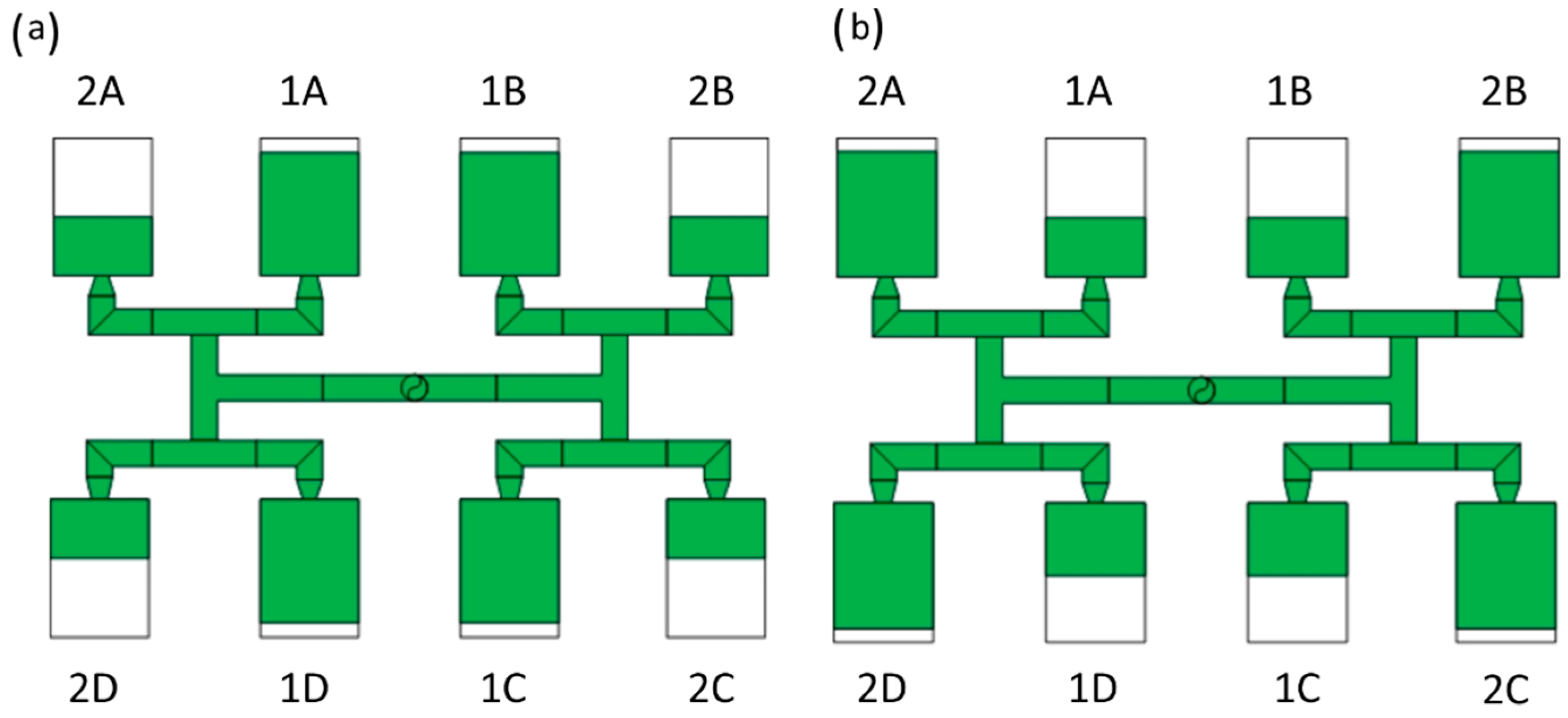
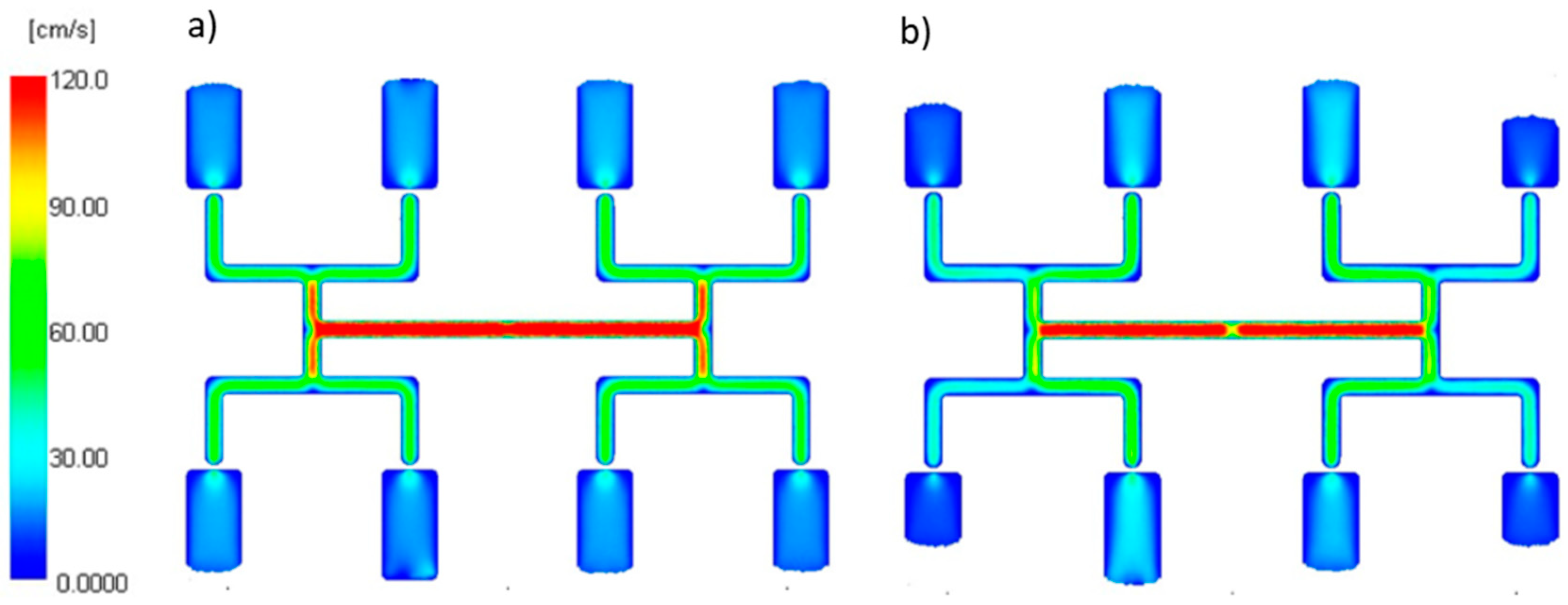
3.3. Geometry Effects
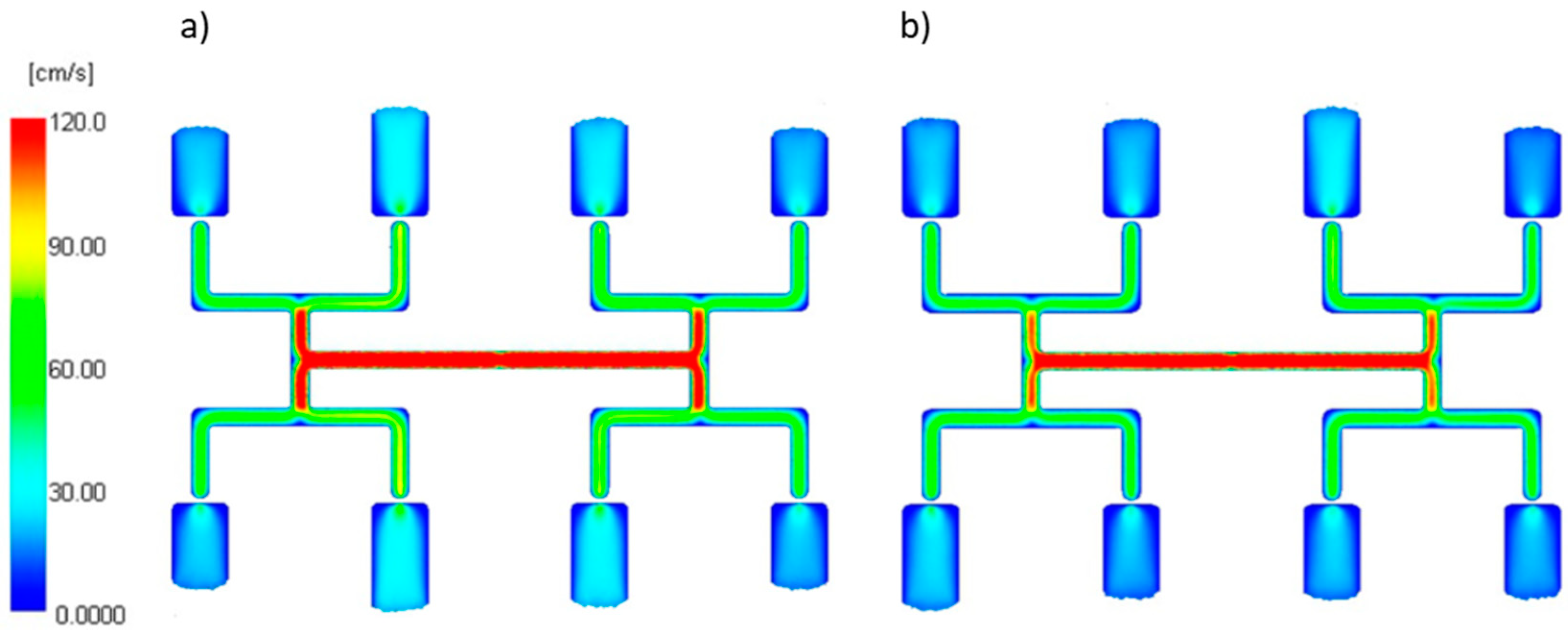
3.3.1. The Relaxation Time
3.3.2. The Thermal Diffusivity
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Wilczyński, K.; Narowski, P. Experimental and Theoretical Study on Filling Imbalance in Geometrically Balanced Injection Molds. Polym. Eng. Sci. 2019, 59, 599–604. [Google Scholar] [CrossRef]
- Beaumont, J.P. Runner and Gating Design Handbook, 2nd ed.; Hanser: Munich, Germany, 2004; ISBN 1569903476. [Google Scholar]
- Beaumont, J.P.; Young, J.H. Mold Filling Imbalances in Geometrically Balanced Runner Systems. J. Inject. Molding Technol. 1997, 1, 133–143. [Google Scholar] [CrossRef]
- Beaumont, J.P.; Young, J.H.; Jaworski, M.J. Mold Filling Imbalances in Geometrically Balanced Runner Systems. In Proceedings of the ANTEC; Society of Plastics Engineers: Atlanta, GA, USA, 1998; pp. 599–604. [Google Scholar]
- MeltFlipper—Patented Runner Design for Plastic Injection Molding. Available online: www.beaumontinc.com/meltflipper (accessed on 1 April 2019).
- Reifschneider, L.G. Documenting and Simulating Flow Segregation in Geometrically Balanced Runners. J. Inject. Molding Technol. 2001, 5, 208–223. [Google Scholar]
- Haylett, R.; Rhoades, A.M. True 3D Flow Analysis for Designing Hot and Cold Runners in Injection Molds. In Proceedings of the ANTEC; Society of Plastics Engineers: Dallas, TX, USA, 2001; pp. 47–52. [Google Scholar]
- Huang, T.C.; Huang, P.H.; Yang, S.Y.; Ko, T.Y. Improving Flow Balance During Filling a Multi-Cavity Mold with Modified Runner Systems. Int. Polym. Process. 2008, 23, 363–369. [Google Scholar] [CrossRef]
- Petzold, F.; Thornagel, M.; Manek, K. Complex Thermal Hot-Runner Balancing—A Method to Optimize Filling Pattern and Product Quality. In Proceedings of the ANTEC; Society of Plastics Engineers: Chicago, IL, USA, 2009; pp. 291–295. [Google Scholar]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Gaspar-Cunha, A. Using Multi-objective Evolutioary Algorithms for Optimization of the Cooling System in Polymer Injection Molding. Int. Polym. Process. 2012, 27, 213–223. [Google Scholar] [CrossRef]
- Rhee, B.O.; Park, H.P.; Lee, K. An Experimental Study of the Variable-Runner System. In Proceedings of the ANTEC; Society of Plastics Engineers: Charlotte, NC, USA, 2006; pp. 1113–1117. [Google Scholar]
- Rhee, B.O.; Lee, E.J.; Lee, Y.J.; Park, H.P.; Cha, B.S. Development of an Automated Runner-Valve System for the Filling Balance in Multi-Cavity Molds. In Proceedings of the ANTEC; Society of Plastics Engineers: Chicago, IL, USA, 2009; pp. 2078–2082. [Google Scholar]
- Schwenk, T.L. Uniform Mold Cavity Venting is Far More Critical to Balance Fill of Multi-Cavity Molds Then any Other Single Item. In Proceedings of the ANTEC; Society of Plastics Engineers: Chicago, IL, USA, 2009; pp. 2547–2550. [Google Scholar]
- Gadley, J.; Grumski, J. Understanding the Existence and Magnitude of Flow Induced Shear Imbalances in Liquid Silicone Rubbers. In Proceedings of the ANTEC; Society of Plastics Engineers: Boston, MA, USA, 2011; pp. 1781–1787. [Google Scholar]
- Bociąga, E.; Jaruga, T. Badania mikroskopowe przepływu tworzywa w kanałach 16-gniazdowej formy wtryskowej. Polimery 2006, 51, 843–851. [Google Scholar]
- Skiba, T.; Toomey, N. Material Warpage Response via Strategic Placement of High and Low Shear Laminates. In Proceedings of the ANTEC; Society of Plastics Engineers: Milwaukee, WI, USA, 2008; pp. 955–959. [Google Scholar]
- Glotzbach, M.; Haws, C. The Influence of Gate Design, Shear History, Processing Conditions, and Melt Rotation on Surface Defects in Molded Parts. In Proceedings of the ANTEC; Society of Plastics Engineers: Orlando, FL, USA, 2010; pp. 1382–1387. [Google Scholar]
- Slye, K.; Coulter, J.P.; Bekisli, B.; Skiba, T.; Beaumont, J.P. The Effect of Melt Rotation Technology on Particle Distribution during Injection Molding. In Proceedings of the ANTEC; Society of Plastics Engineers: Boston, MA, USA, 2011; pp. 1529–1533. [Google Scholar]
- Sun, S.; Hsu, C.; Huang, C.; Huang, K.; Tseng, S. Sandwich Injection Molding—Core Breakthrough and Flow Imbalance Studies. In Proceedings of the ANTEC; Society of Plastics Engineers: Cincinnati, OH, USA, 2013; pp. 1596–1600. [Google Scholar]
- Huang, C.T.; Yang, J.; Chang, R.Y. Dynamic penetration behavior of core-material in multi-cavity co-injection molding. In Proceedings of the ANTEC; Society of Plastics Engineers: Orlando, FL, USA, 2015; pp. 1695–1700. [Google Scholar]
- Li, Q.; Coulter, J.P.; Beaumont, J.P.; Rhoades, A.M. Effects of Melt Rotation on Resulting Localized Material Properties Throughout Injection Molded Polymeric Products. In Proceedings of the ANTEC; Society of Plastics Engineers: Las Vegas, NV, USA, 2014; Volume 2, pp. 1539–1546. [Google Scholar]
- Li, Q.; Beaumont, J.P.; Rhoades, A.M. Influences of Melt Rotation Technology on Polymeric Material Injection Molding Process and Final Product Properties. In Proceedings of the ANTEC; Society of Plastics Engineers: Orlando, FL, USA, 2015; pp. 1707–1714. [Google Scholar]
- Gim, J.S.; Tae, J.S.; Jeon, J.H.; Choi, J.H.; Rhee, B.O. Detection Method of Filling Imbalance in a Multi-Cavity Mold for Small Lens. Int. J. Precis. Eng. Manuf. 2015, 16, 531–535. [Google Scholar] [CrossRef]
- Li, Q.; Choo, S.R.; Coulter, J.P. An Investigation of Real-Time Monitoring of Shear Induced Cavity Filling Imbalances During Polymer Injection Molding. In Proceedings of the ANTEC; Society of Plastics Engineers: Indianapolis, IN, USA, 2016; pp. 1174–1181. [Google Scholar]
- White, C.W. Development of Filling Imbalances in Hot Runner Molds. In Proceedings of the ANTEC; Society of Plastics Engineers: New York, NY, USA, 1999; pp. 45–50. [Google Scholar]
- Spina, R.; Walach, P.; Schild, J.; Hopmann, C. Analysis of Lens Manufacturing with Injection Molding. Int. J. Precis. Eng. Manufact. 2012, 13, 2087–2095. [Google Scholar] [CrossRef]
- Matarrese, P.; Fontana, A.; Sorlini, M.; Diviani, L.; Maggi, A. Estimating Energy Consumption of Injection Moulding for Environmental-Driven Mould Design. J. Clean. Prod. 2017, 168, 1505–1512. [Google Scholar] [CrossRef]
- MOLDFLOW Plastic Injection and Compresion Mold Simulation. Available online: www.autodesk.com/products/moldflow (accessed on 1 April 2019).
- Cadmould® 3D-F: The Expert Software for Optimization of Part, Mold and Process. Available online: www.simcon-worldwide.com/en/products-and-services/injection-molding-simulation (accessed on 1 April 2019).
- Moldex3D Plastic Injection Molding Simulation Software. Available online: www.moldex3d.com (accessed on 1 April 2019).
- Wilczyński, K. System CADMOULD-3D komputerowego modelowania procesu wtryskiwania tworzyw sztucznych—symulacja fazy wypełniania formy. Polimery 1999, 44, 407–412. [Google Scholar]
- Cook, P.S.; Yu, H.; Kietzmann, C.V.; Costa, F.S. Prediction of Flow Imbalance in Geometrically Balanced Feed Systems. In Proceedings of the ANTEC; Society of Plastics Engineers: Boston, MA, USA, 2005; pp. 259–261. [Google Scholar]
- Chiang, G.; Chien, J.; Hsu, D.; Tsai, V.; Yang, A. True 3D CAE Visualization of Filling Imbalance in Geometry-Balanced Runners. In Proceedings of the ANTEC; Society of Plastics Engineers: Boston, MA, USA, 2005; pp. 55–59. [Google Scholar]
- Chien, J.C.; Huang, C.; Yang, W.; Hsu, D.C. True 3D CAE Visualization of “Intra-Cavity” Filling Imbalance in Injection. In Proceedings of the ANTEC; Society of Plastics Engineers: Charlotte, NC, USA, 2006; pp. 1153–1157. [Google Scholar]
- Hsu, C.; Lin, Y.; Chen, S.; Tsai, C.; Chang, C.; Yang, W.; Li, C.; Li, C.; City, C. Numerical Visualization of Melt Flow in Cold Runner and Hot Runner. In Proceedings of the ANTEC; Society of Plastics Engineers: Milwaukee, WI, USA, 2008; pp. 379–384. [Google Scholar]
- Wilczyński, K.; Nastaj, A.; Wilczyński, K.J. Symulacja komputerowa równoważenia przepływu w formach wtryskowych z układem “Melt FLIPPER”. Mechanik 2008, 327–330. [Google Scholar]
- Wilczyński, K.; Wilczyński, K.J.; Narowski, P. Badania symulacyjno-doœwiadczalne nierównomiernego wypełniania wielogniazdowych form wtryskowych zrównoważonych geometrycznie. Polimery 2015, 60, 56–66. [Google Scholar]
- Tadmor, Z. Fundamentals of Plasticating Extrusion. I. A Theoretical Model for Melting. Polym. Eng. Sci. 1966, 6, 185–190. [Google Scholar] [CrossRef]
- Tadmor, Z.; Duvdevani, I.; Klein, I. Melting in Plasticating Extuders Theory and Experiments. Polym. Eng. Sci. 1967, 7, 198–217. [Google Scholar] [CrossRef]
- Bawiskar, S.; White, J.L. Solids Conveying and Melting in a Starve Fed Self-Wiping Co-rotating Twin Screw Extruder. Int. Polym. Process. 1995, 10, 105–110. [Google Scholar] [CrossRef]
- Bawiskar, S.; White, J.L. Melting Model for Modular Self-Wiping Co-Rotating Twin Screw Extruders. Polym. Eng. Sci. 1998, 38, 727–740. [Google Scholar] [CrossRef]
- Wilczynski, K.; White, J.L. Melting Model for Intermeshing Counter-Rotating Twin-Screw Extruders. Polym. Eng. Sci. 2003, 43, 1715–1726. [Google Scholar] [CrossRef]
- Wilczynski, K.; Jiang, Q.; White, J.L. A Composite Model for Melting, Pressure and Fill Factor Profiles in a Metered Fed Closely Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Process. 2007, 22, 198–203. [Google Scholar] [CrossRef]
- Wilczyński, K.; Lewandowski, A. Modelowanie przepływu tworzyw w procesie wytłaczania dwuślimakowego przeciwbieżnego, Cz.2. Badania symulacyjne i doświadczalne. Polimery 2011, 56, 45–50. [Google Scholar]
- Wilczyński, K.; Nastaj, A.; Wilczyńśki, K.J. Melting Model for Starve Fed Single Screw Extrusion of Thermoplastics. Int. Polym. Process. 2013, 28, 34–42. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyńśki, K.J. A Composite Model for Starve Fed Single Screw Extrusion of Thermoplastics. Polym. Eng. Sci. 2014, 54, 2362–2374. [Google Scholar] [CrossRef]
- Potente, H.; Schulte, H.; Effen, N. Simulation of Injection Molding and Comparison with Experimental Values. Int. Polym. Process. 1993, 8, 224–235. [Google Scholar] [CrossRef]
- Steller, R.; Iwko, J. Polymer Plastication During Injection Molding. Int. Polym. Process. 2008, 23, 252–262. [Google Scholar] [CrossRef]
- Iwko, J.; Steller, R.; Wróblewski, R. Experimentally Verified Mathematical Model of Polymer Plasticization Process in Injection Molding. Polymers 2018, 10, 968. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Nóbrega, J.M.; Gaspar-Cunha, A. Modeling of Plasticating Injection Molding—Experimental Assessment. Int. Polym. Process. 2014, 29, 558–559. [Google Scholar] [CrossRef]
- Altınkaynak, A.; Gupta, M.; Spalding, M.A.; Crabtree, S.L. Melting in a Single Screw Extruder: Experiments and 3D Finite Element Simulations. Int. Polym. Process. 2011, 26, 182–196. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyńśki, K.J. Multipurpose Computer Model for Screw Processing of Plastics. Polym. Plast. Technol. Eng. 2012, 51, 626–633. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K. Uogólniony model uplastyczniania tworzyw polimerowych w procesie wytłaczania. Polimery 2018, 63, 444–452. [Google Scholar] [CrossRef]
- Tang, D.; Marchesini, F.H.; D’Hooge, D.R.; Cardon, L. Isothermal Flow of Neat Polypropylene Through a Slit Die and Its Die Swell: Bridging Experiments and 3D Numerical Simulations. J. Non-Newt. Fluid Mech. 2019, 266, 33–45. [Google Scholar] [CrossRef]
- STASA Steinbeis Angewandte Systemanalyse. Available online: www.stasa.de (accessed on 1 April 2019).
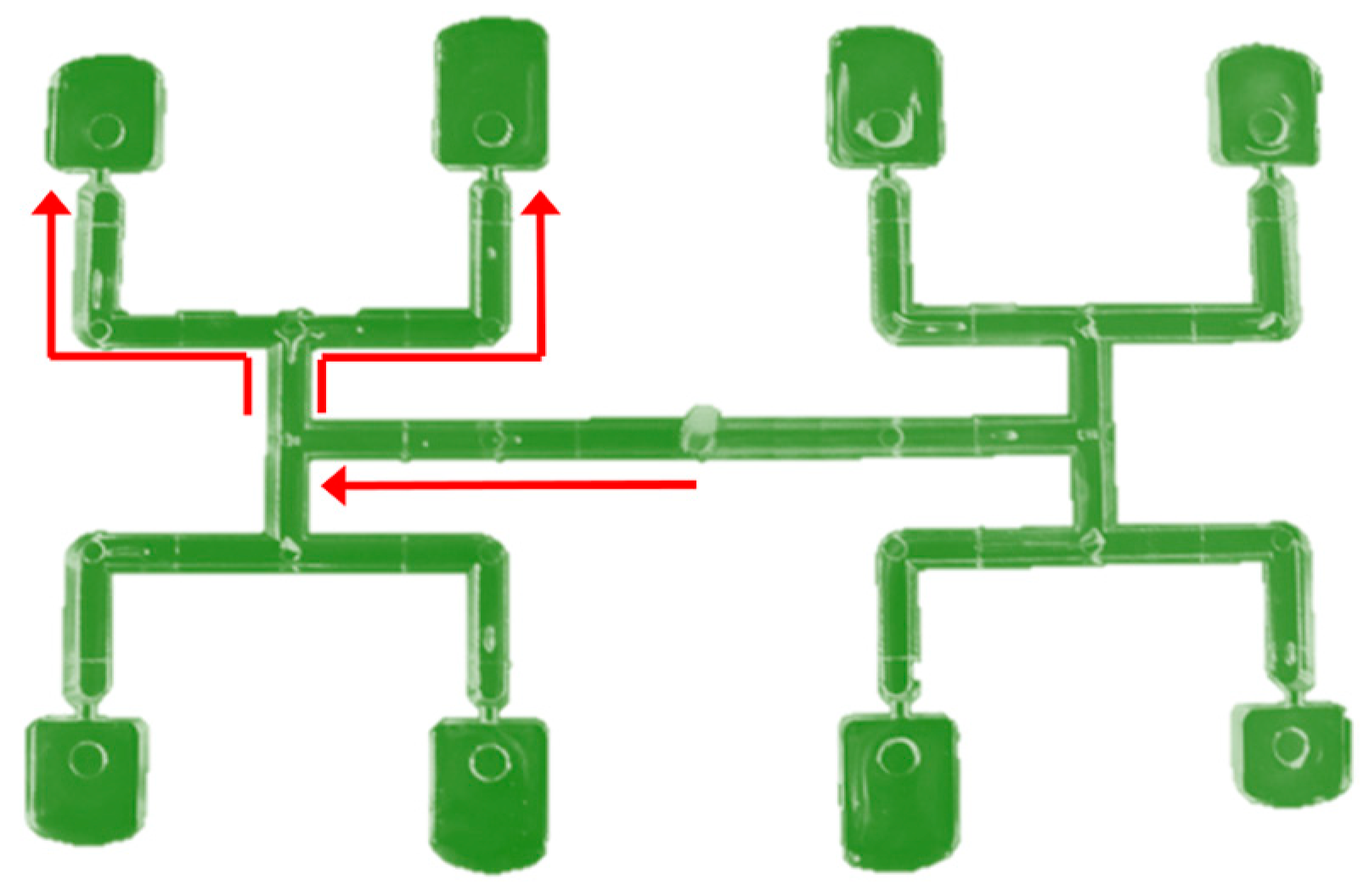


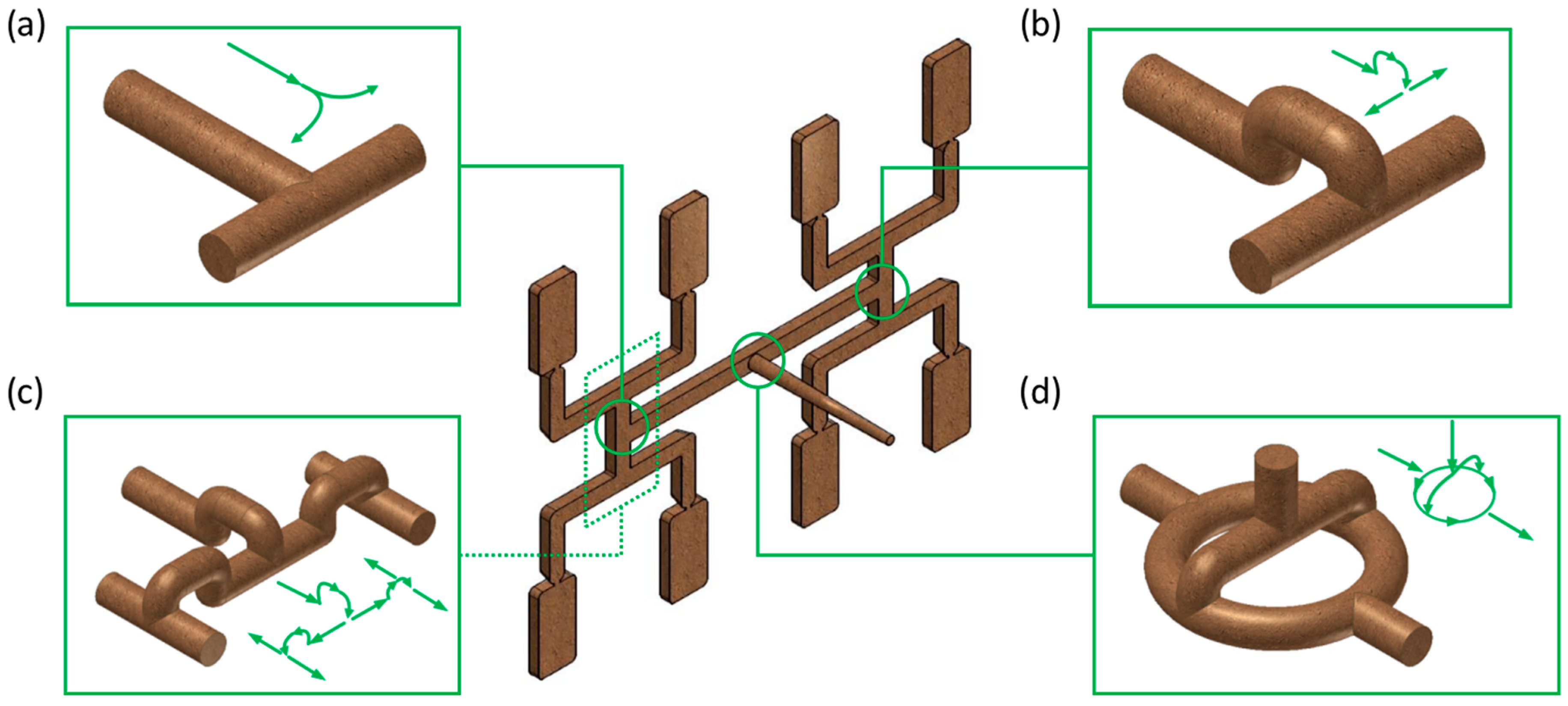
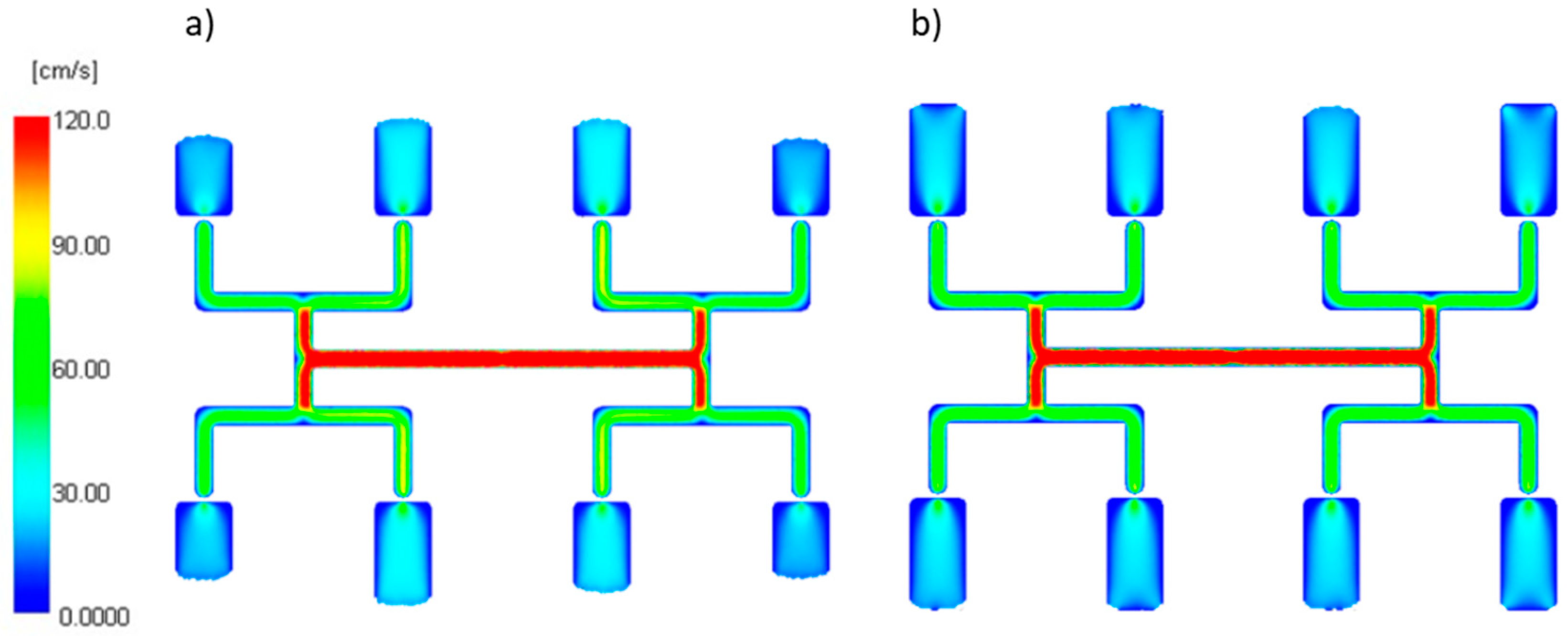
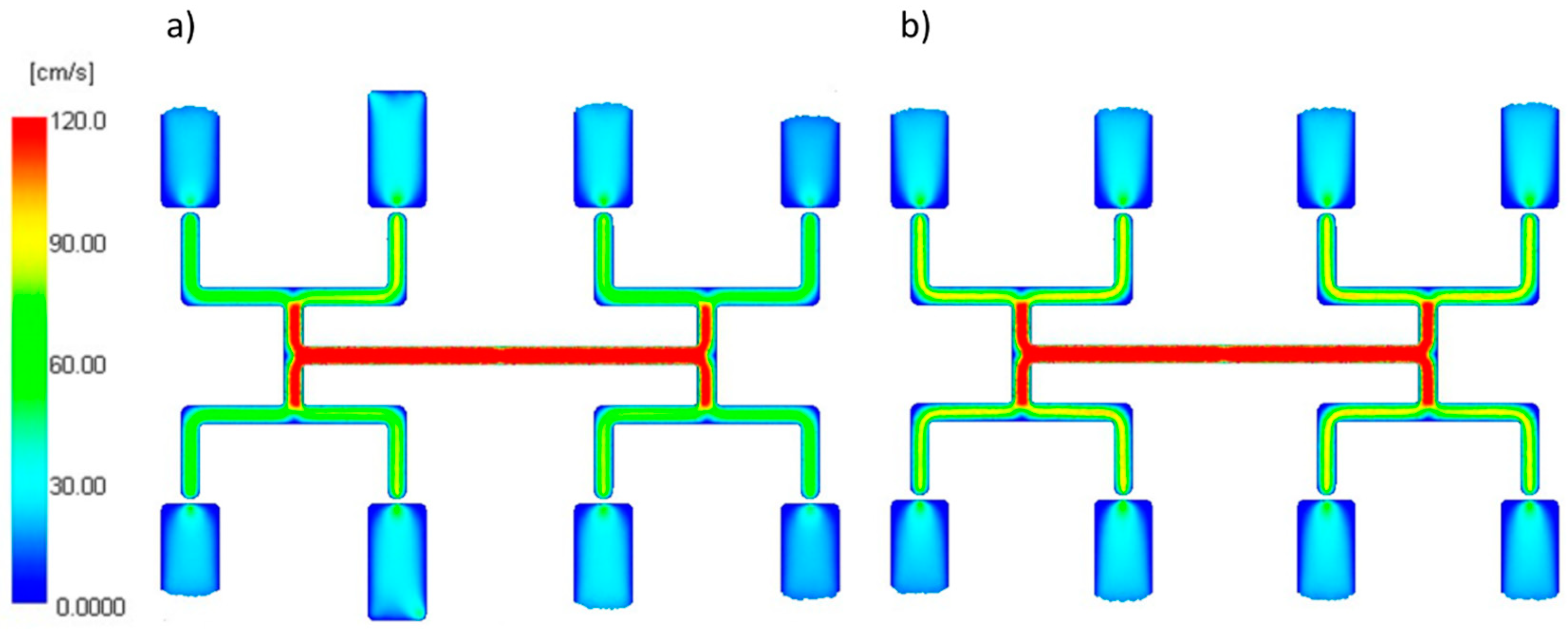
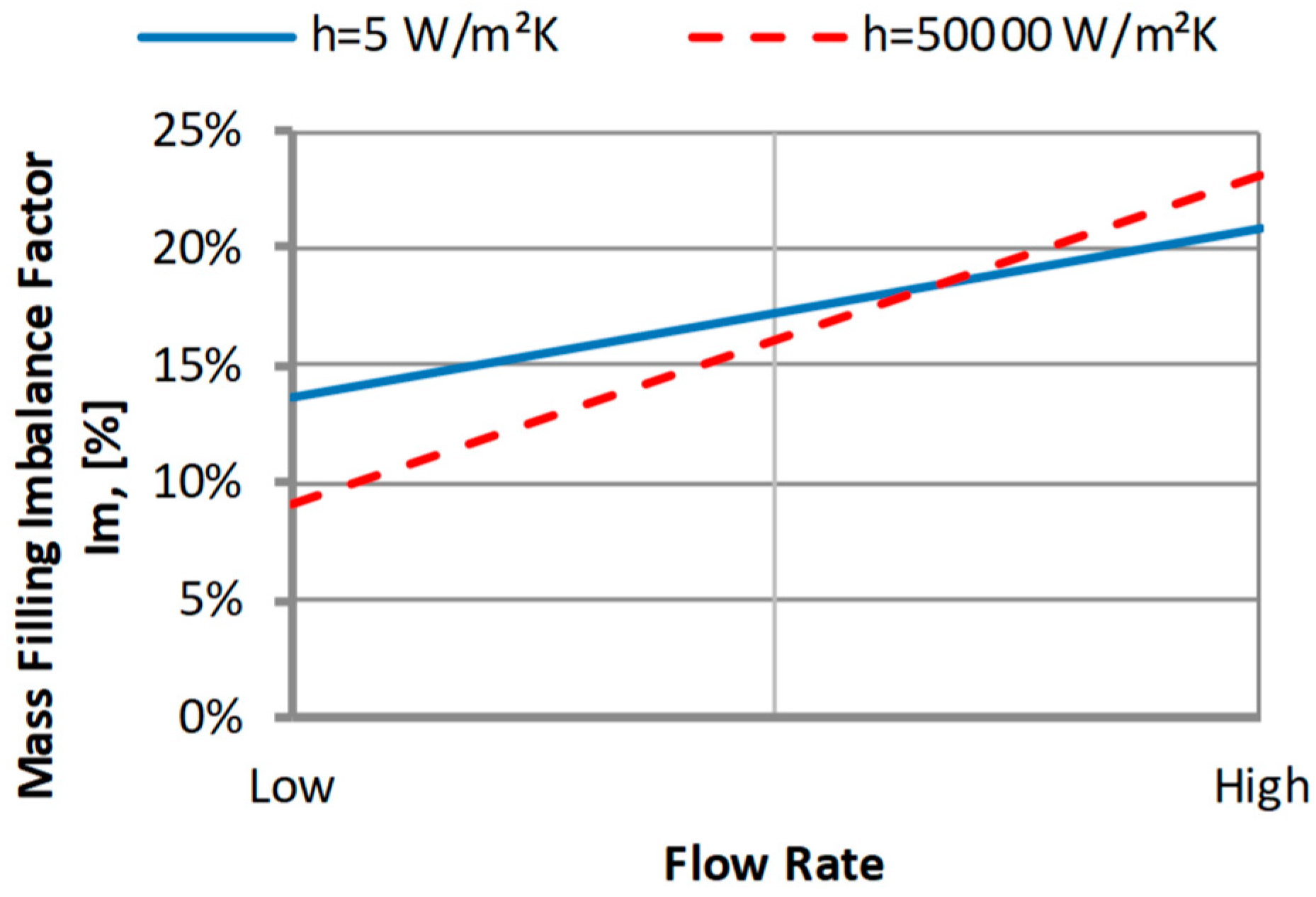
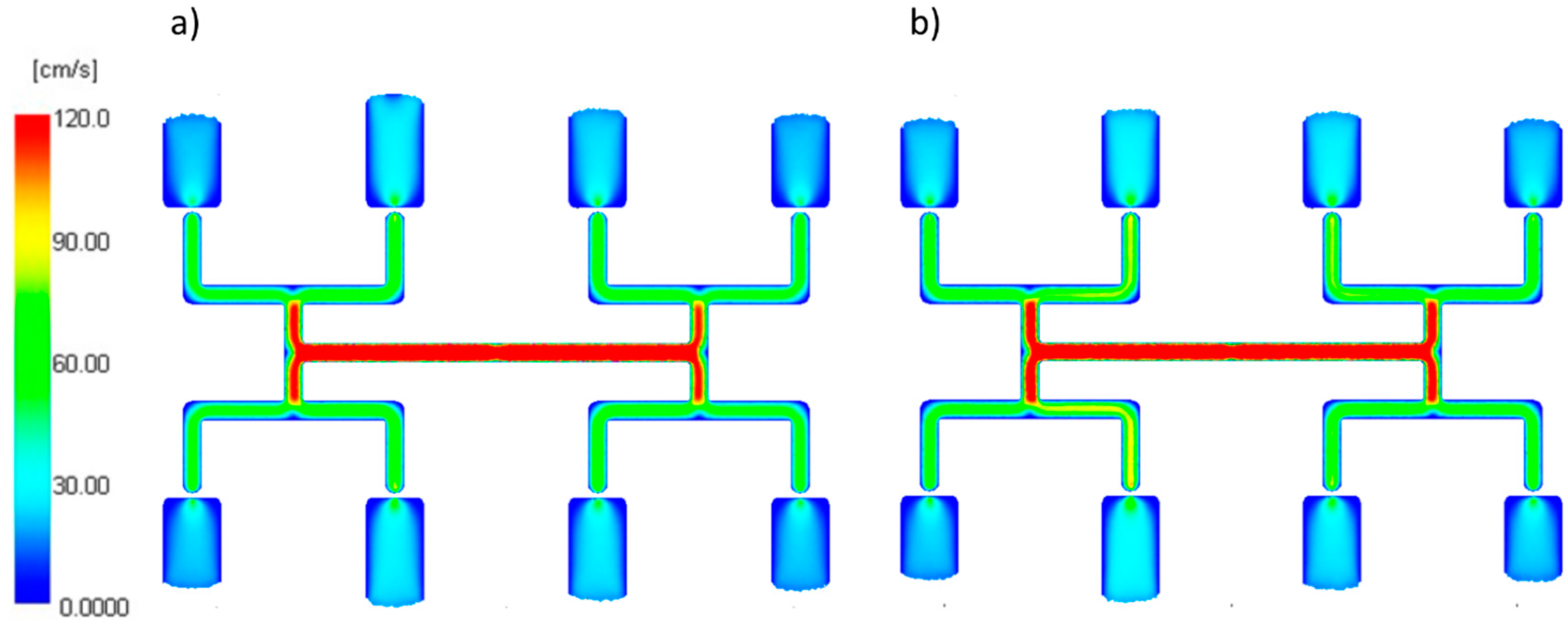
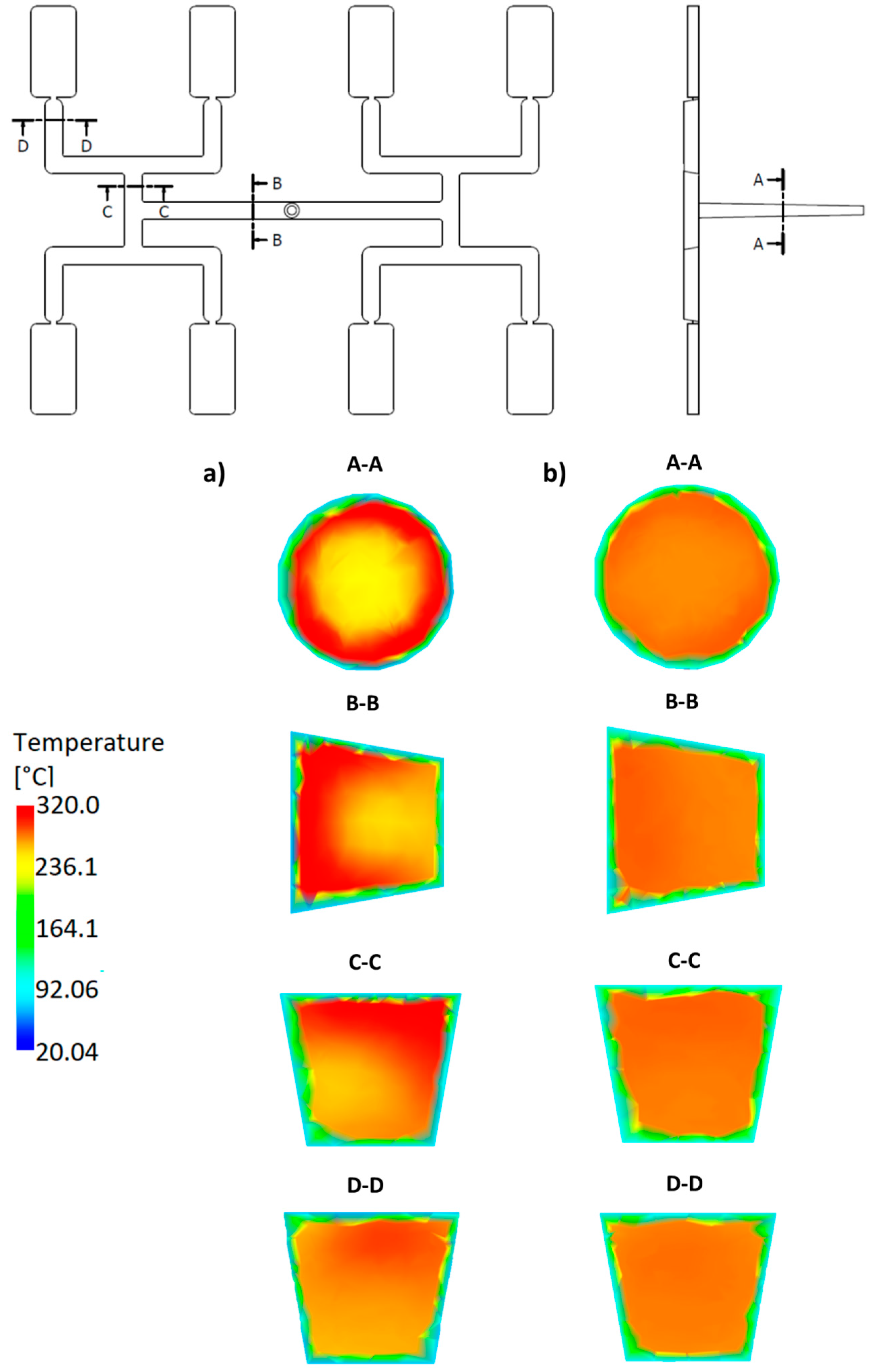
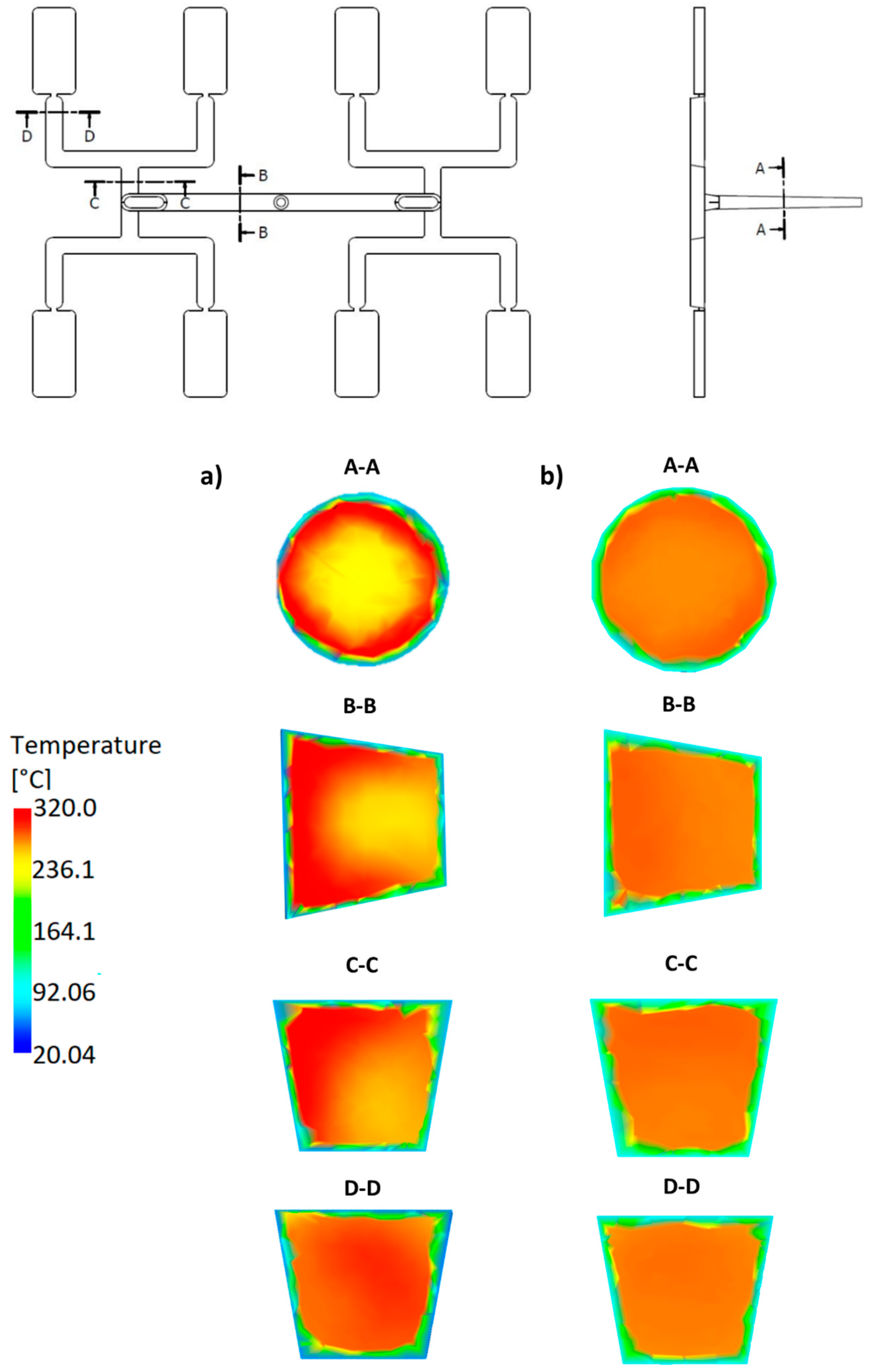
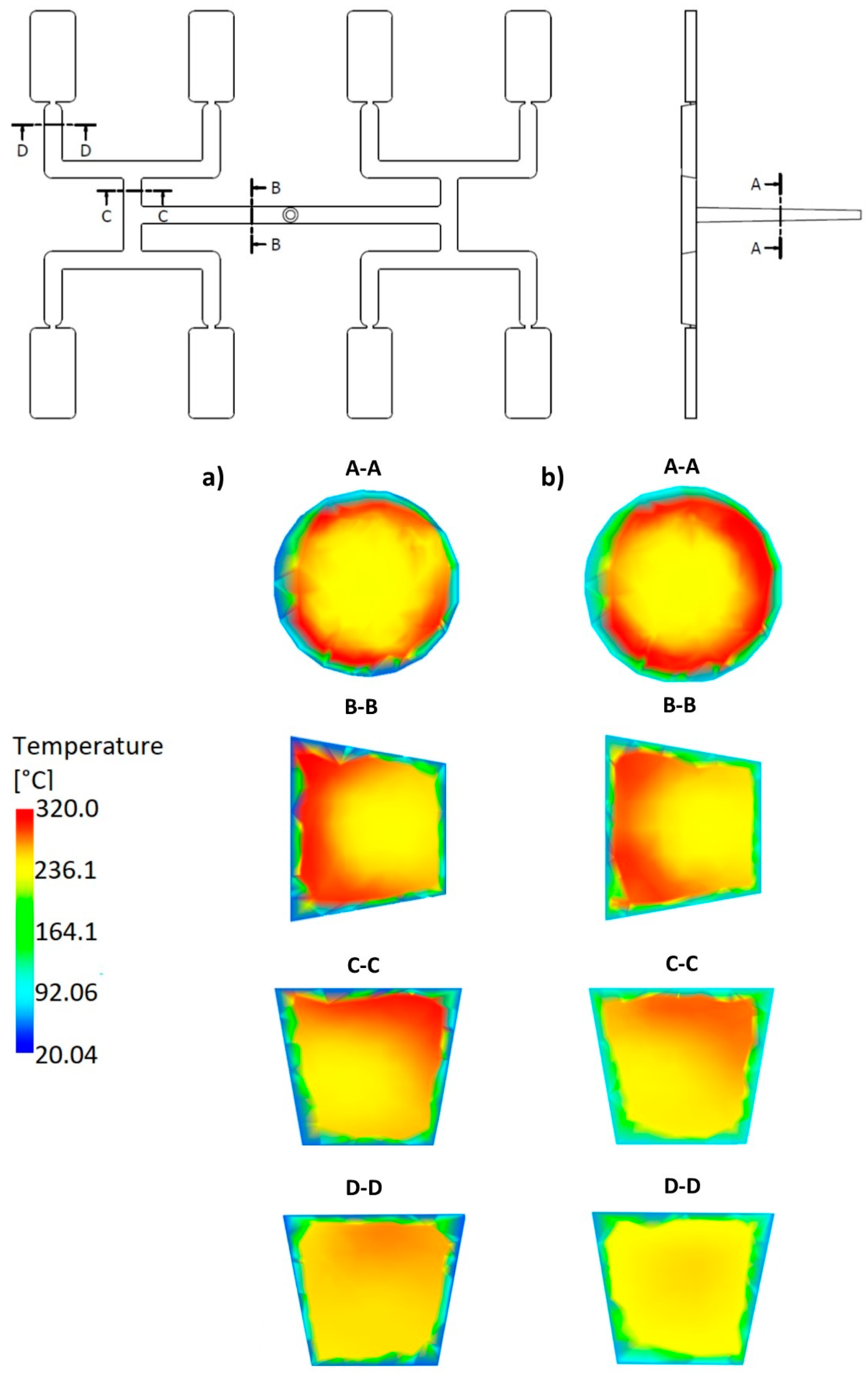
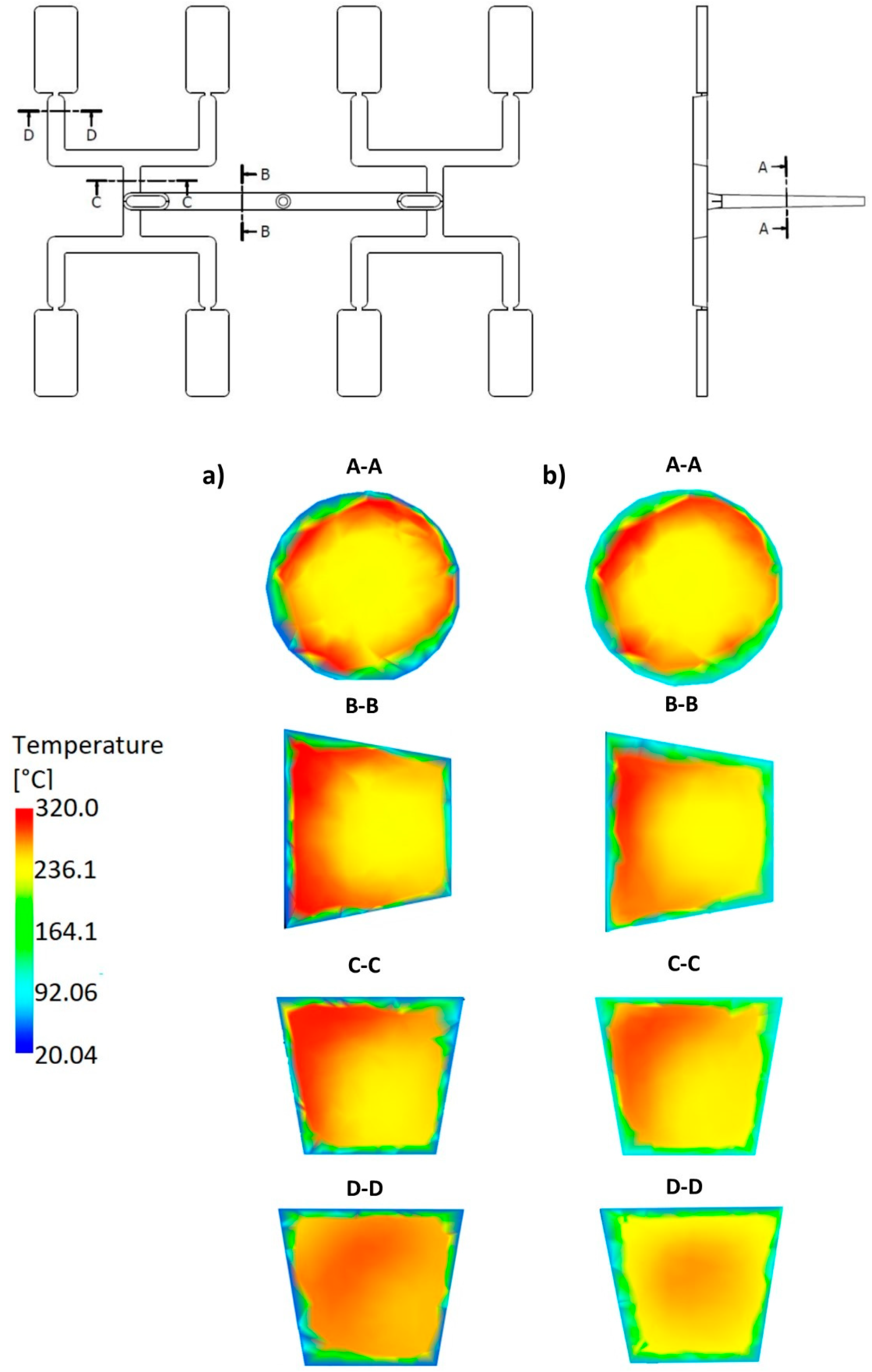
| Injection molding process parameters | |
| Mold temperature, Tmold | 63 °C |
| Coolant temperature, Tcool | 50 °C |
| Coolant Reynolds Number, Re | 90,000 |
| Melt temperature, Tmelt | 252 °C |
| Anmbient temperature, Tamb | 20 °C |
| Flow rate, Q | 5 cm3/s 500 cm3/s |
| Shear rate (at the wall, in the central runner), | 183.4 1/s 18,340 1/s |
| Injection/packing/cooling time, tcycle | 10 s |
| Mold opening time, topen | 5 s |
| Material and rheological properties | |
| Density | |
| - solid, ρs | 1204 kg/m3 |
| - melt, ρm | 1016 kg/m3 |
| MFI | 13 g/10 min (5 kg, 250 °C) |
| Heat capacity | |
| - melt, Cpm | 2110 J/(kg °C) |
| - solid, Cps | 1160 J/(kg °C) |
| Thermal conductivity - melt, km | 0.24 W/(m °C) |
| Melting temperature, Tm | 182 °C |
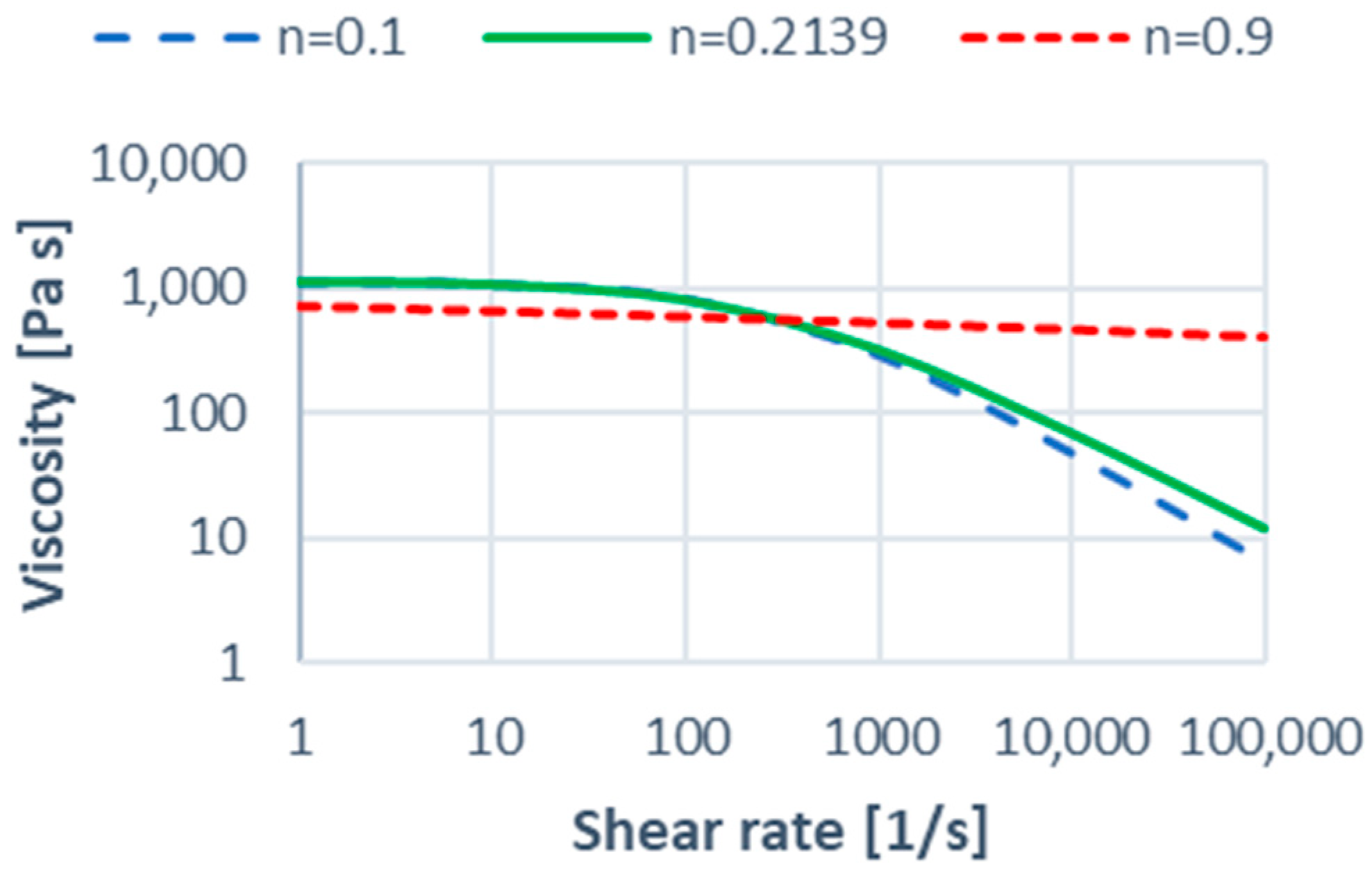
| Viscosity, η (Equation (1)) | |
| Zero viscosity, η0 (Equation (2)) | |
| - n | 0.2139 |
| - D1 | 5.32∙1023 Pa∙s |
| - τ* | 353,100 Pa |
| - A1 | 59.833 |
| - A2 | 51.6 K |
| - T* | 323 K |
| Effect of Process Parameters and Runners Layout on Filling Imbalance – Summary | ||||
|---|---|---|---|---|
| GS | G1 | G2 | G3 | |
| η0 ↗ | ↑ | ↓ | ↓ | ↑ |
| n ↗ | ↓ | ↑ | ↑ | ↓ |
| λ ↗ | ↓ | ↑ | ↑ | ↓ |
| ↗ | ↑ | ↓ | ↓ | ↑ |
| α ↗ | ↓ | ↑ | ↑ | ↓ |
| h ↗ | ↓ | ↑ | ↑ | ↓ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilczyński, K.; Narowski, P. Simulation Studies on the Effect of Material Characteristics and Runners Layout Geometry on the Filling Imbalance in Geometrically Balanced Injection Molds. Polymers 2019, 11, 639. https://doi.org/10.3390/polym11040639
Wilczyński K, Narowski P. Simulation Studies on the Effect of Material Characteristics and Runners Layout Geometry on the Filling Imbalance in Geometrically Balanced Injection Molds. Polymers. 2019; 11(4):639. https://doi.org/10.3390/polym11040639
Chicago/Turabian StyleWilczyński, Krzysztof, and Przemysław Narowski. 2019. "Simulation Studies on the Effect of Material Characteristics and Runners Layout Geometry on the Filling Imbalance in Geometrically Balanced Injection Molds" Polymers 11, no. 4: 639. https://doi.org/10.3390/polym11040639
APA StyleWilczyński, K., & Narowski, P. (2019). Simulation Studies on the Effect of Material Characteristics and Runners Layout Geometry on the Filling Imbalance in Geometrically Balanced Injection Molds. Polymers, 11(4), 639. https://doi.org/10.3390/polym11040639