Statistical Behaviors of Semiflexible Polymer Chains Stretched in Rectangular Tubes
Abstract
:1. Introduction
2. Materials and Methods
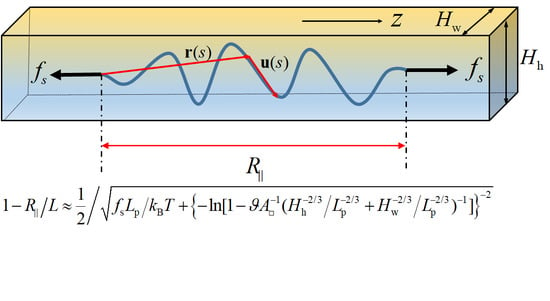
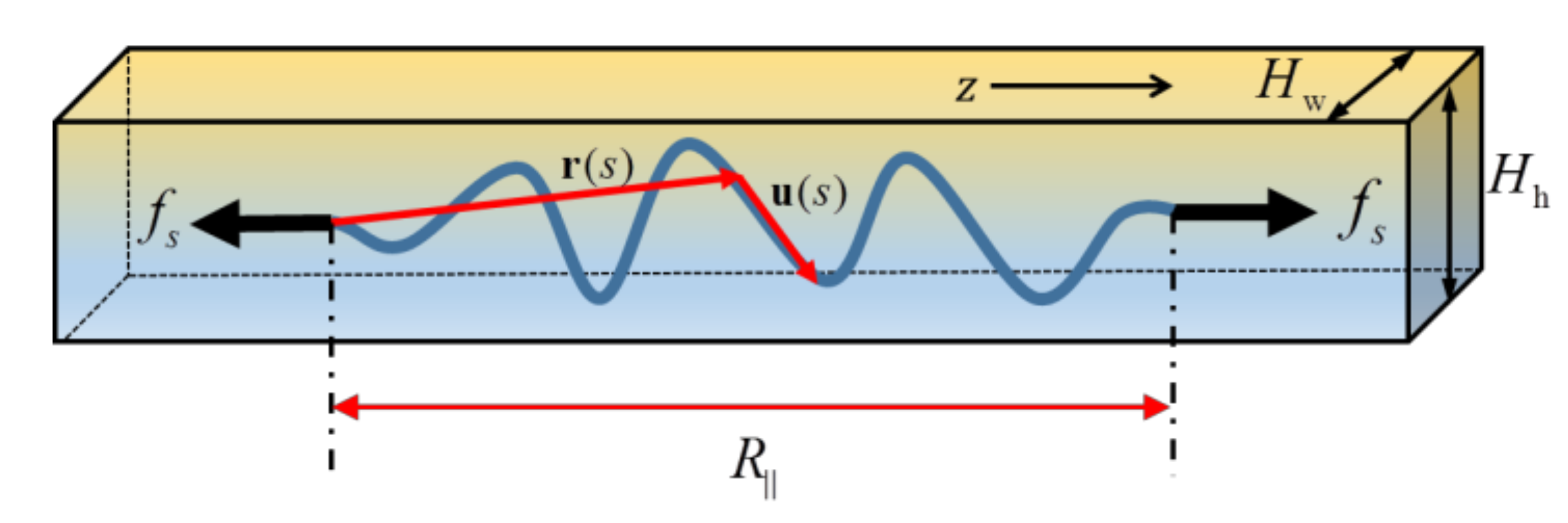
2.1. Model
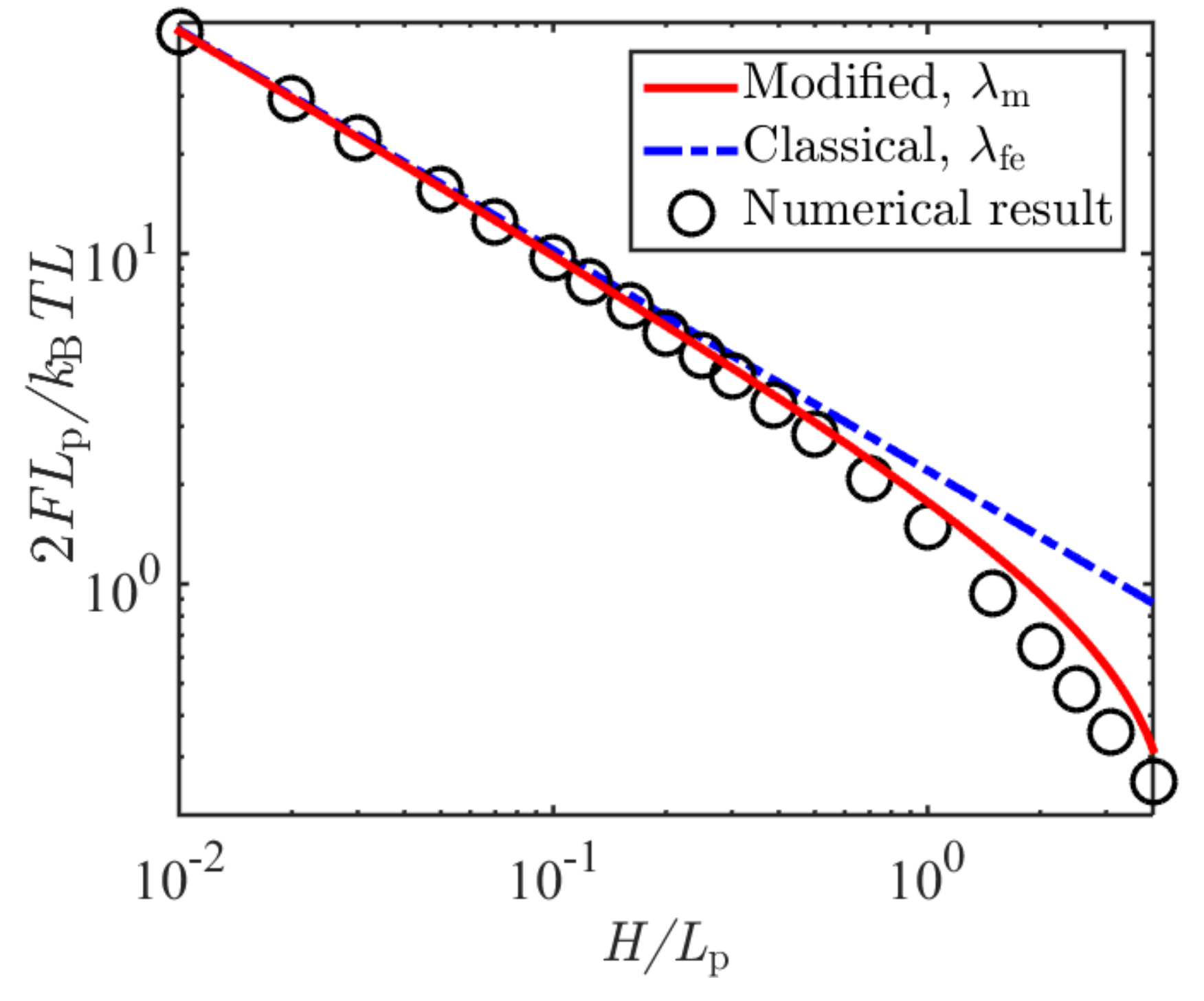
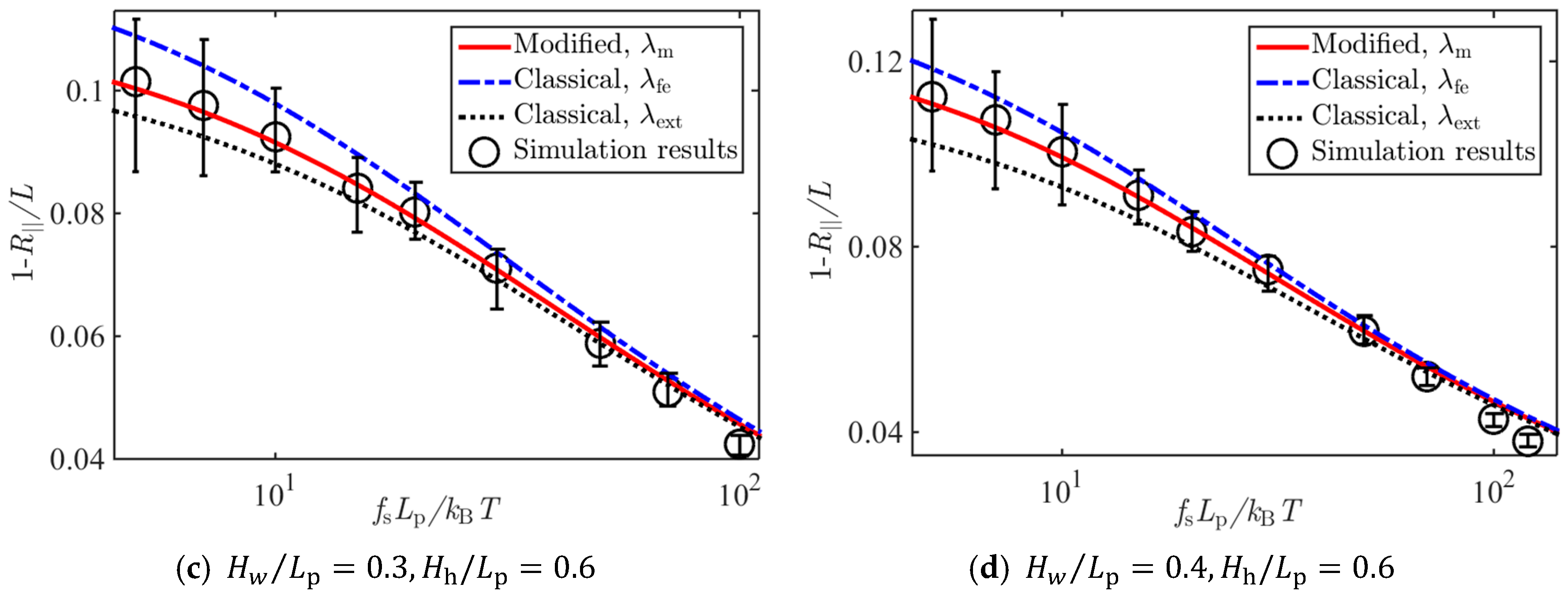
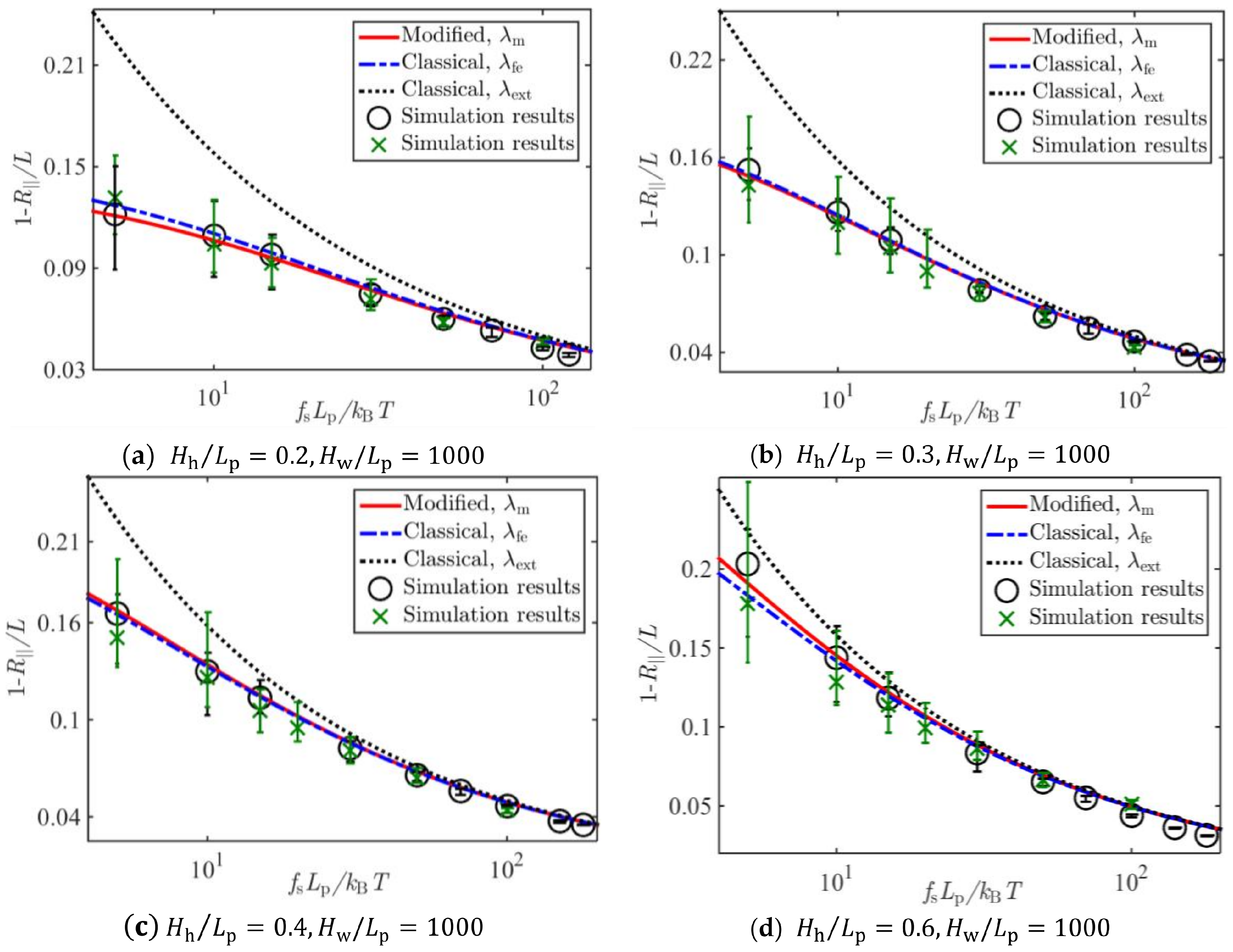
2.2. Numerical Verifications
2.2.1. Solutions to the Fokker–Planck Equation
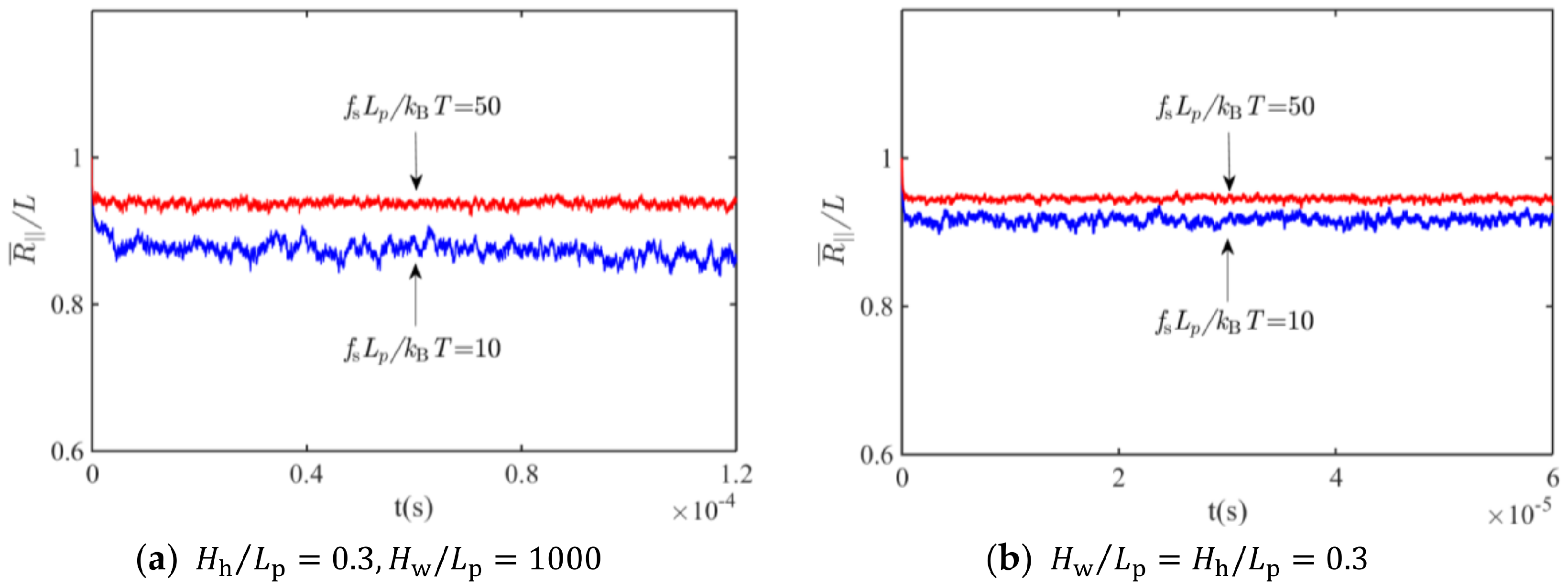
2.2.2. Brownian Dynamics Simulations (Appendix A)
3. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. The GBR Model for Brownian Dynamics Simulations
References
- Reisner, W.; Morton, K.J.; Riehn, R.; Wang, Y.M.; Yu, Z.; Rosen, M.; Sturm, J.C.; Chou, S.Y.; Frey, E.; Austin, R.H. Statics and dynamics of single DNA molecules confined in nanochannels. Phys. Rev. Lett. 2005, 94, 196101. [Google Scholar] [CrossRef] [PubMed]
- Reisner, W.; Pedersen, J.N.; Austin, R.H. DNA confinement in nanochannels: Physics and biological applications. Rep. Prog. Phys. 2012, 75, 106601. [Google Scholar] [CrossRef] [PubMed]
- Marko, J.F.; Siggia, E.D. Stretching DNA. Macromolecules 1995, 28, 8759–8770. [Google Scholar] [CrossRef]
- Dorfman, K.D.; King, S.B.; Olson, D.W.; Thomas, J.D.P.; Tree, D.R. Beyond gel electrophoresis: Microfluidic separations, fluorescence burst analysis, and DNA stretching. Chem. Rev. 2013, 113, 2584–2667. [Google Scholar] [CrossRef] [PubMed]
- Gorbunov, A.A.; Skvortsov, A.M. Statistical properties of confined macromolecules. Adv. Colloid Interfaces 1995, 62, 31–108. [Google Scholar] [CrossRef]
- Teraoka, I. Polymer solutions in confining geometries. Prog. Polym. Sci. 1996, 21, 89–149. [Google Scholar] [CrossRef]
- Choi, M.C. Direct Observation of Biaxial Confinement of a Semi-flexible Filament in a Channel. Macromolecules 2005, 38, 9882–9884. [Google Scholar] [CrossRef]
- Casassa, E.F. Equilibrium distribution of flexible polymer chains between a macroscopic solution phase and small voids. J. Polym. Sci. C Polym. Lett. 1967, 5, 773–778. [Google Scholar] [CrossRef]
- Daoud, M.; Gennes, P.G.D. Statistics of macromolecular solutions trapped in small pores. J. Phys. 1977, 38, 85–93. [Google Scholar] [CrossRef]
- Gennes, P.G.D. Scaling Concepts in Polymer Physics. Phys. Today 1980, 33, 51–54. [Google Scholar] [CrossRef]
- Kratky, O.; Porod, G. Röntgenuntersuchung gelöster Fadenmoleküle. Recl. Trav. Chim. Pays-Bas. 2015, 68, 1106–1122. [Google Scholar] [CrossRef]
- Odijk, T. The statistics and dynamics of confined or entangled stiff polymers. Macromolecules 1983, 16, 1340–1344. [Google Scholar] [CrossRef]
- Odijk, T. Theory of lyotropic polymer liquid crystals. Macromolecules 1986, 19, 2313–2329. [Google Scholar] [CrossRef]
- Odijk, T. Scaling theory of DNA confined in nanochannels and nanoslits. Phys. Rev. E 2008, 77, 060901. [Google Scholar] [CrossRef] [PubMed]
- Burkhardt, T.W. Free energy of a semiflexible polymer in a tube and statistics of a randomly-accelerated particle. J. Phys. A Gen. Phys. 1997, 30, L167–L172. [Google Scholar] [CrossRef]
- Burkhardt, T.W.; Yang, Y.; Gompper, G. Fluctuations of a long, semiflexible polymer in a narrow channel. Phys. Rev. E 2010, 82, 041801. [Google Scholar] [CrossRef] [PubMed]
- Bicout, D.J.; Burkhardt, T.W. Simulation of a semiflexible polymer in a narrow cylindrical pore. J. Phys. A Gen. Phys. 2001, 34, 5745–5750. [Google Scholar] [CrossRef]
- Yang, Y.; Burkhardt, T.W.; Gompper, G. Free energy and extension of a semiflexible polymer in cylindrical confining geometries. Phys. Rev. E 2007, 76, 011804. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Z.Y. Free Energy and Extension of a Wormlike Chain in Tube Confinement. Macromolecules 2013, 46, 9837–9844. [Google Scholar] [CrossRef]
- Dai, L.; Jones, J.J.; Van der, M.J.R.C.; Doyle, P.S. A systematic study of DNA conformation in slitlike confinement. Soft Matter 2012, 8, 2972–2982. [Google Scholar] [CrossRef]
- Chen, Y.L.; Graham, M.D.; De Pablo, J.J.; Randall, G.C.; Gupta, M.; Doyle, P.S. Conformation and dynamics of single DNA molecules in parallel-plate slit microchannels. Phys. Rev. E 2004, 70, 060901. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.K.; Fu, C.C.; Chen, Y.L.; Chen, Y.R.; Wei, P.K.; Kuan, C.H.; Fann, W.S. Static conformation and dynamics of single DNA molecules confined in nanoslits. Phys. Rev. E 2007, 76, 011806. [Google Scholar] [CrossRef] [PubMed]
- Tree, D.R.; Reinhart, W.F.; Dorfman, K.D. The Odijk regime in slits. Macromolecules 2014, 47, 3672–3684. [Google Scholar] [CrossRef]
- Chen, J.Z.Y.; Sullivan, D.E. Free energy of a wormlike polymer chain confined in a slit: Crossover between two scaling regimes. Macromolecules 2006, 39, 7769–7773. [Google Scholar] [CrossRef]
- Chen, Y.L.; Lin, P.; Chou, C.F. Generalized Force−Extension Relation for Wormlike Chains in Slit Confinement. Macromolecules 2010, 43, 10204–10207. [Google Scholar] [CrossRef]
- Dai, L.; van der Maarel, J.; Doyle, P.S. Extended de Gennes regime of DNA confined in a nanochannel. Macromolecules 2014, 47, 2445–2450. [Google Scholar] [CrossRef]
- Taloni, A.; Yeh, J.W.; Chou, C.F. Scaling Theory of Stretched Polymers in Nanoslits. Macromolecules 2013, 46, 7989–8002. [Google Scholar] [CrossRef]
- Odijk, T. Physics of tightly curved semiflexible polymer chains. Macromolecules 1993, 26, 6897–6902. [Google Scholar] [CrossRef]
- Wang, J.; Gao, H. Stretching a stiff polymer in a tube. J. Mater. Sci. 2007, 42, 8838–8843. [Google Scholar] [CrossRef]
- Li, R.; Wang, J. Stretching a Semiflexible Polymer in a Tube. Polymers 2016, 8, 328. [Google Scholar] [CrossRef]
- Chen, J.Z.Y. Theory of wormlike polymer chains in confinement. Prog. Polym. Sci. 2016, 54–55, 3–46. [Google Scholar] [CrossRef]
- Gao, J.; Tang, P.; Yang, Y.; Chen, J.Z.Y. Free energy of a long semiflexible polymer confined in a spherical cavity. Soft Matter 2014, 10, 4674–4685. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gao, H. A generalized bead-rod model for Brownian dynamics simulations of wormlike chains under strong confinement. J. Chem. Phys. 2005, 123, 084956. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gao, H. Brownian dynamics simulations of charged semiflexible polymers confined to curved surfaces. J. Mech. Behav. Biomed. 2011, 4, 174–179. [Google Scholar] [CrossRef] [PubMed]
- Abhiram, M.; Michael, Q.; Kevin, D. The backfolded odijk regime for wormlike chains confined in rectangular nanochannels. Polymers 2016, 8, 79. [Google Scholar]
- Yamakawa, H. Modern Theory of Polymer Solutions; Harper and Row: New York, NY, USA, 1971. [Google Scholar]
- Wang, J.; Li, R. Stretching strongly confined semiflexible polymer chain. Appl. Math. Mech.-Engl. 2014, 35, 1233–1238. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 14630–1472. [Google Scholar] [CrossRef]
- Ermak, D.L.; McCammon, J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar] [CrossRef]
- Peters, E.A.J.F.; Barenbrug, T.M. Efficient Brownian dynamics simulation of particles near walls. I. Reflecting and absorbing walls. Phys. Rev. E 2002, 66, 056701. [Google Scholar] [CrossRef]
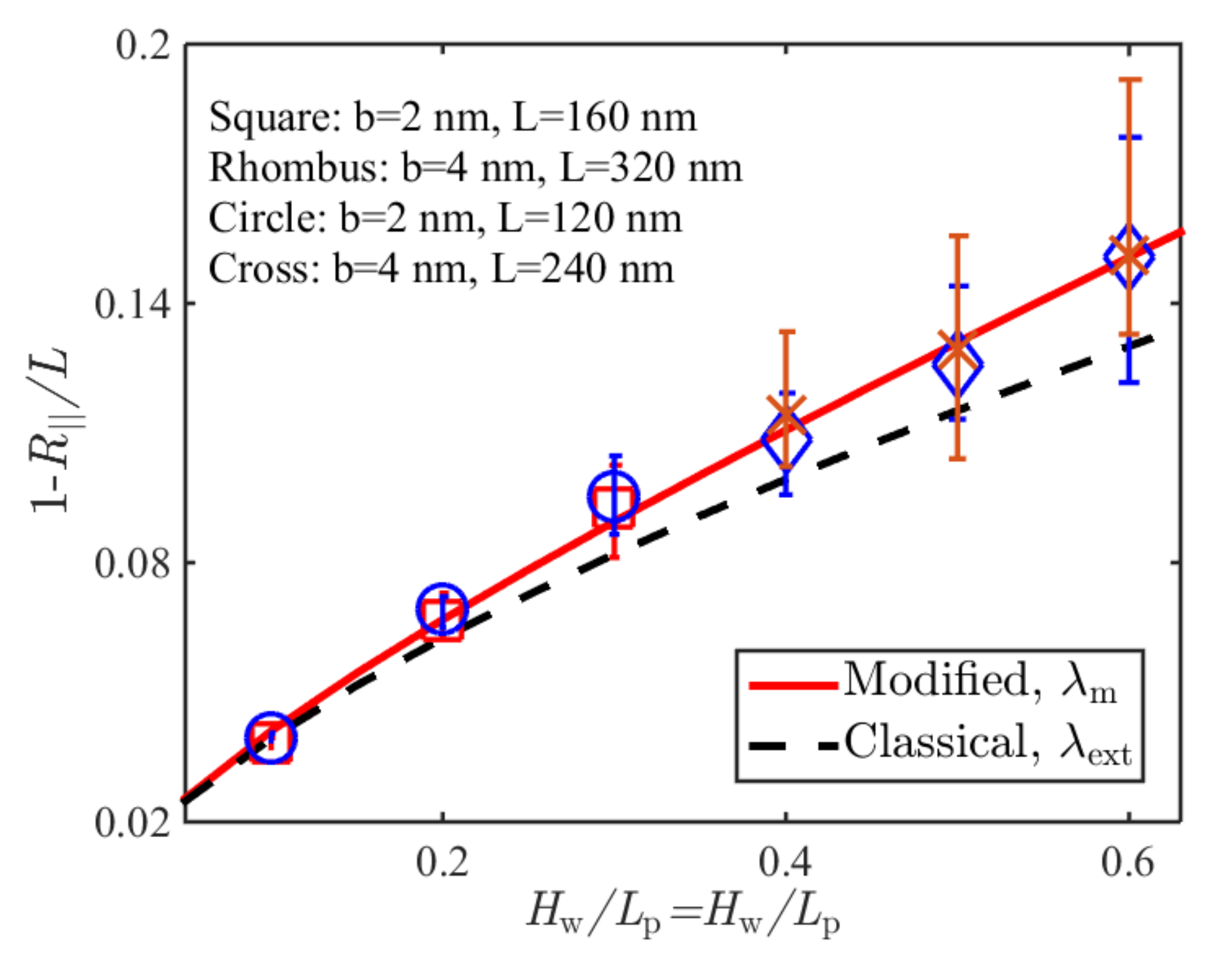
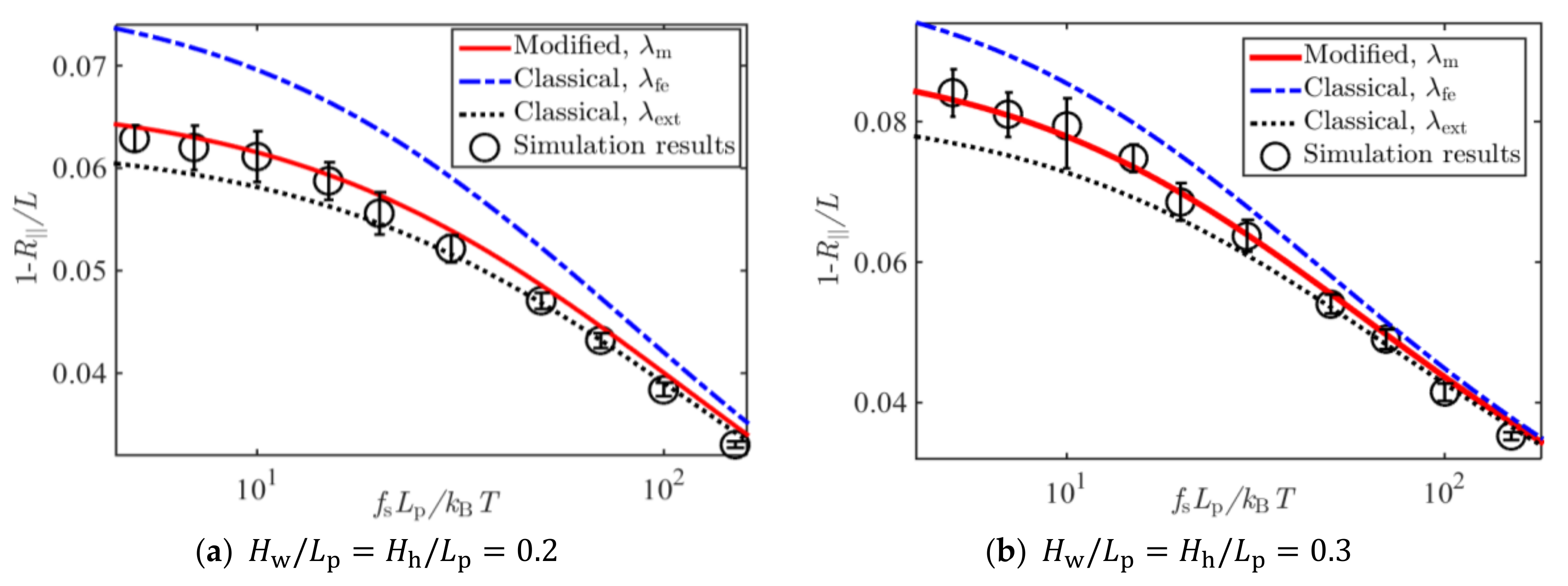
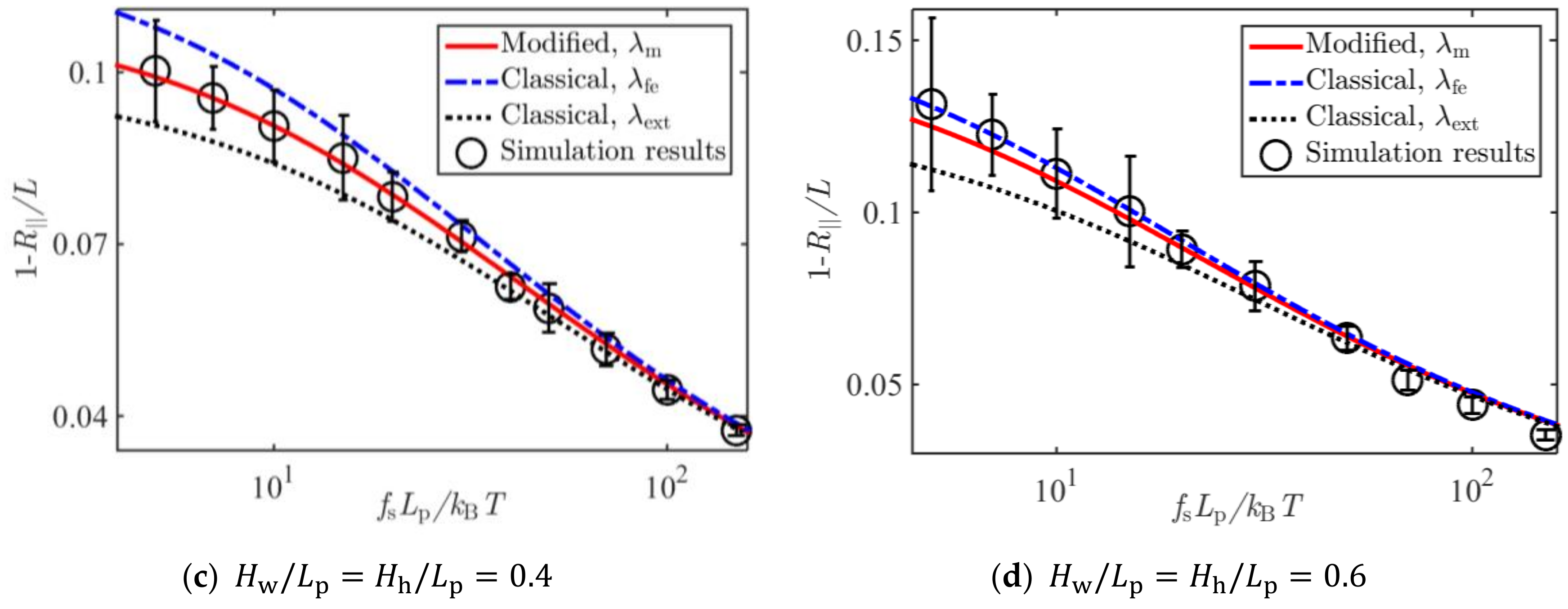
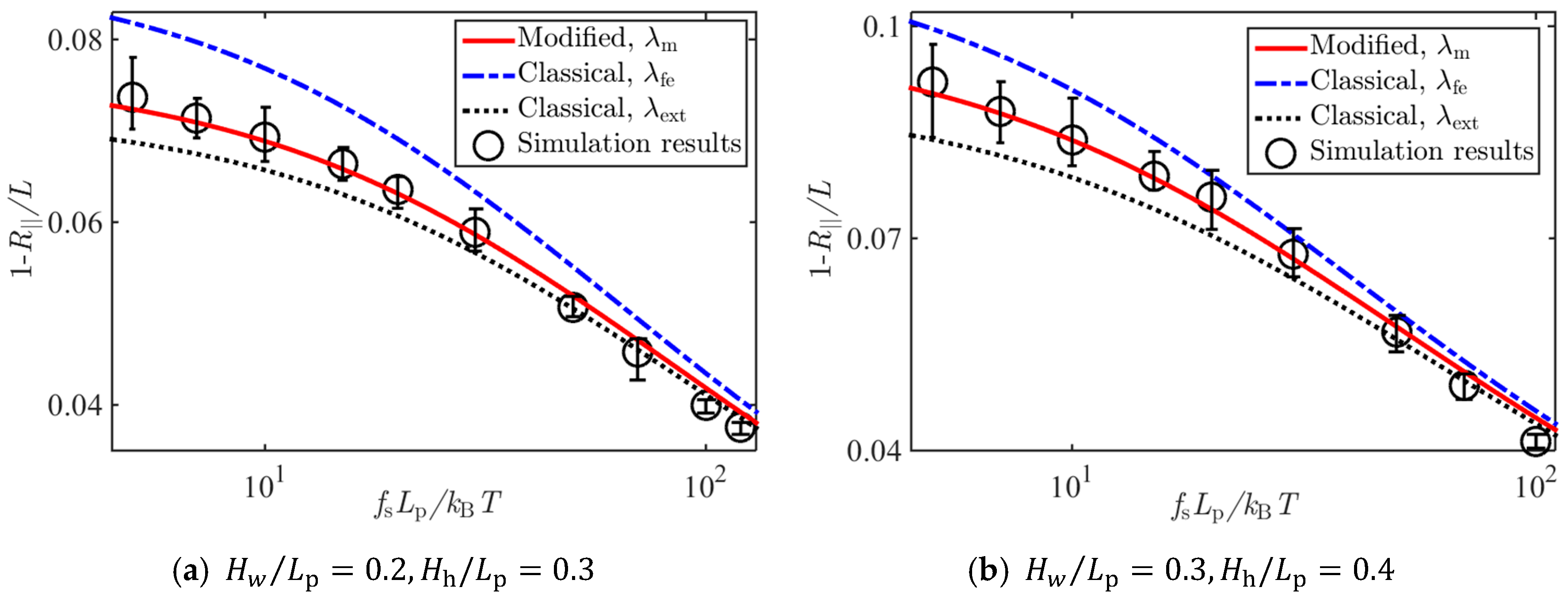
| 1.1036 [15] | -- |
| 1.108 ± 0.013 [17] | -- |
| 1.1038 ± 0.0006 [18] | 0.09137 ± 0.00007 [18] |
| 1.1032 ± 0.0001 [19] | 0.09143 ± 0.0001 [19] |
| Mark | Bead Radius | Bond Length | Time Step | Contour Length | Total Simulation Time | Total Trajectory Number |
|---|---|---|---|---|---|---|
| Square | 0.98 nm | 2 nm | 10 ps | 160 nm | 60 μs | 72 |
| Rhombus | 1.85 nm | 4 nm | 20 ps | 320 nm | 120 μs | 72 |
| Circle | 0.98 nm | 2 nm | 10 ps | 120 nm | 60 μs | 72 |
| Cross | 1.85 nm | 4 nm | 20ps | 240 nm | 120 μs | 72 |
| Confinement Size | Bead Radius | Bond Length | Time Step | Contour Length | Total Simulation Time | Total Trajectory Number |
|---|---|---|---|---|---|---|
| 0.2 | 1.85 nm | 4 nm | 10 ps | 120 nm | 60 μs | 120 |
| 0.3 | 1.85 nm | 4 nm | 10 ps | 120 nm | 60 μs | 120 |
| 0.4 | 1.85 nm | 4 nm | 20 ps | 600 nm | 120 μs | 120 |
| 0.6 | 1.85 nm | 4 nm | 20 ps | 600 nm | 120 μs | 120 |
| Confinement Size | Bead Radius | Bond Length | Time Step | Contour Length | Total Simulation Time | Total Trajectory Number |
|---|---|---|---|---|---|---|
| 0.2, 0.3 | 2 nm | 5 nm | 20 ps | 300 nm | 120 μs | 120 |
| 0.3, 0.4 | 1.85 nm | 4 nm | 20 ps | 200 nm | 120 μs | 120 |
| 0.3, 0.6 | 1.85 nm | 4 nm | 20 ps | 200 nm | 120 μs | 120 |
| 0.4, 0.6 | 2 nm | 5 nm | 20 ps | 300 nm | 120 μs | 120 |
| Confinement Size | Bead Radius | Bond Length | Time Step | Contour Length | Total Simulation Time | Total Trajectory Number |
|---|---|---|---|---|---|---|
| 0.2, 1000 | 2 nm | 5 nm | 15 ps | 200 nm | 90 μs | 120 |
| 0.3, 1000 | 2 nm | 5 nm | 20 ps | 150 nm | 120 μs | 120 |
| 0.4, 1000 | 1.85 nm | 4 nm | 25 ps | 400 nm | 150 μs | 120 |
| 0.6, 1000 | 1.85 nm | 4 nm | 20 ps | 400 nm | 120 μs | 120 |
| Confinement Size | Bead Radius | Bond Length | Time Step | Contour Length | Total Simulation Time | Total Trajectory Number |
|---|---|---|---|---|---|---|
| 0.2, 1000 | 1.85 nm | 4 nm | 20 ps | 240 nm | 120 μs | 120 |
| 0.3, 1000 | 1.85 nm | 4 nm | 20 ps | 240 nm | 120 μs | 120 |
| 0.4, 1000 | 2 nm | 5 nm | 25 ps | 500 nm | 150 μs | 120 |
| 0.6, 1000 | 2 nm | 5 nm | 25 ps | 500 nm | 120 μs | 120 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, K. Statistical Behaviors of Semiflexible Polymer Chains Stretched in Rectangular Tubes. Polymers 2019, 11, 260. https://doi.org/10.3390/polym11020260
Wang J, Li K. Statistical Behaviors of Semiflexible Polymer Chains Stretched in Rectangular Tubes. Polymers. 2019; 11(2):260. https://doi.org/10.3390/polym11020260
Chicago/Turabian StyleWang, Jizeng, and Kai Li. 2019. "Statistical Behaviors of Semiflexible Polymer Chains Stretched in Rectangular Tubes" Polymers 11, no. 2: 260. https://doi.org/10.3390/polym11020260
APA StyleWang, J., & Li, K. (2019). Statistical Behaviors of Semiflexible Polymer Chains Stretched in Rectangular Tubes. Polymers, 11(2), 260. https://doi.org/10.3390/polym11020260