Abstract
We investigated the statistical behaviors of semiflexible polymer chains, which were simultaneously subjected to force stretching and rectangular tube confinement. Based on the wormlike chain model and Odijk deflection theory, we derived a new deflection length, by using which new compact formulas were obtained for the confinement free energy and force–confinement–extension relations. These newly derived formulas were justified by numerical solutions of the eigenvalue problem associated with the Fokker–Planck governing equation and extensive Brownian dynamics simulations based on the so-called generalized bead-rod (GBR) model. We found that, compared to classical deflection theory, these new formulas were valid for a much more extended range of the confinement size/persistence length ratio and had no adjustable fitting parameters for sufficiently long semiflexible chains in the whole deflection regime.
1. Introduction
Statistical physics properties of single polymer chains can be significantly influenced or even determined by geometrical confinements and applied external forces [1,2,3,4]. A detailed understanding of the behaviors of polymers under such circumstances is still considered to be an unsolved problem in polymer physics after more than half a century. However, even so, advances in the study of geometrically and potentially constrained polymers are playing a role in the development of many existing nanotechnologies of genomics and materials science, etc. [5,6,7].
For polymers under confinement, the effects of constraints have usually been classified into three regimes (weak, moderate, and strong confinements), which are distinguished in terms of the comparison between the polymer’s unconfined radius of gyration and the Kuhn length of the typical confinement length scale. In the regime of weak confinement, Casassa [8] has discussed the free energy of ideal chains trapped in pores with different shapes based on the theory of diffusion. Then, de Gennes and his coworkers [9,10] developed the so-called blob model to describe the confinement of a long, flexible polymer. According to this model, the free energy of confinement is given by
Here, H is the length scale of confinement, is the Boltzmann constant, and T is the absolute temperature. is the radius of gyration of the unconfined polymer, N is the number of monomers, is of the order of the monomer-monomer separation, and v equals 1/2 for ideal polymers and approximately 3/5 for polymers with excluded volume. A widely used model of a polymer with bending energy is the wormlike chain (WLC) model, characterized by the contour length L and persistence length Lp, which was first proposed by Kratky and Porod in 1949 [11]. In the strong confinement regime, Odijk [12,13] has argued that polymer behavior can be interpreted in terms of statistically independent segments with deflection length . Based on this picture, he [12,13,14] obtained expressions of the confinement free energy, F, and the average extension of the chain, , in terms of as
where represent the free energy and extension-associated deflection lengths, respectively: [12] has been suggested for the confinement of a cylindrical tube with diameter D. For the confinement of a rectangular tube with height and width Hh and Hw, the deflection length associated with the free energy calculation has been suggested as [15,16]
In contrast, this deflection length associated with the average extension is given as
We note that Equations (4) and (5) have different expressions and prefactors. The prefactors in Equations (4) and (5) were determined by using various numerical techniques and theoretical derivations, such as the Monte Carlo simulations [17,18] and eigenvalue technique associated with the Fokker–Planck equations [15,19]. Examples of the determined prefactors are illustrated in Table 1. We can see that the prefactors and , respectively determined from free energy and extension, have an almost 10 times difference in quantity.

Table 1.
Prefactors of the Odijk deflection length scale.
In addition, a slit of separation H can be regarded as a rectangular tube with height Hh = H and infinite width . Statistical properties of polymer chains confined in the slit have been extensively studied [20,21,22,23,24,25] based on Monte Carlo simulations and eigenvalue analysis. The deflection length in a strong confinement regime has been confirmed to follow the Odijk scaling law,
Although the deflection length in Equation (5) can be viewed as the combination of that for two slits with heights Hh and Hw, respectively [15], it can be observed from Equations (4)–(6) that the deflection length in Equation (5) is not consistent with Equation (6) as .
Beyond the Odijk regime, Chen [24] numerically calculated the confinement free energy by treating the problem of a confined polymer as an eigenvalue problem. He also suggested an interpolating formula that can have very good agreement with that of the numerical calculations for polymers under both strong and weak confinements. In addition, an extended de Gennes regime [20,26,27] has also been identified based on the Monte Carlo simulations.
Interestingly, external forces can pose similar effects to the statistical behaviors of single polymer chains as geometrical confinements. For a polymer chain to be stretched by a sufficiently large force, , a deflection length also exists and can be expressed as [3,28] , where , so that the force-extension relation can be expressed as
Polymers in real microenvironments are usually subjected to both geometrical constraints and external forces. Wang and Gao [29] have revealed that the average extension of a strongly tube-confined and force-stretched polymer chain can be equivalent to that of an unconfined chain subjected to an effective stretching force. Li and Wang [30] later confirmed that this equivalence property is still valid for the tube-confined polymers in a much more extended Odijk regime. Therefore, for a semiflexible polymer chain in the deflection confinement regime, one can generally have
where one can set or as the normalized effective force due to the existence of strong confinement: For the confinements of rectangular tubes, , are given by Equations (4) and (5).
However, as shown above, Odijk deflection lengths based on free energy and extension are different. Then a critical question arises. Which deflection length should be used if the polymer chain is under both geometrical confinement and force stretching? Therefore, there are still open questions on how the Odijk length can be uniquely and precisely defined for polymer chains confined in rectangular tubes.
In this study, for semiflexible polymer chains confined in rectangular tubes and slits, we derived a modified deflection length, which was expected to be valid for a more extended range than the classical Odijk deflection length. This extended deflection length was directly used to quantitatively formulate both energy and extension. We will present numerical calculations based on the eigenvalue technique developed by Chen and coworkers [19,31,32] and Brownian dynamics simulations in terms of the generalized bead-rod (GBR) model [30,33,34] to justify our theoretical predictions.
2. Materials and Methods
2.1. Model
We first considered a WLC confined in a rectangular tube with width Hw and height Hh, as shown in Figure 1. We assumed that the tube was small so that the chain’s configurations with the so-called “hairpin” structures [14,35] rarely existed. This means statistical behaviors of the chain fell into the deflection regime. In order to obtain a universal deflection length scale, λ, to simultaneously characterize both the free energy and extension of the chain in terms of the ideas of de Gennes [9,10] and Odijk [12], the chain was assumed to behave like L/λ independent free segments, aligning one by one along the tube axis, so that the conformational free energy could still be scaled as Equation (1) and the average extension could be simply the sum of that for each free segment. On the other hand, when considering the average extension of the chain, the quantitative behavior of each segment should be in analogy with a free chain of effective contour length , in which the parameter c1 actually reflects the influence of two artificial ends of each such segment. For a free WLC segment of contour length , projection of the position vector of one end, r(s2), to the tangential vector of the other end, u(s1), can be given by [36]

Figure 1.
Schematic of a wormlike chain (WLC) confined in a rectangular tube and stretched by a force.
Then the average extension of the whole chain can be estimated as
in which is introduced as an unknown dimensionless factor. Equation (10) should reproduce Equation (3) in the deflection regime, which can determine and , so that eventually we have
For a tightly confined polymer in a channel with a rectangular cross-section, Burkhardt and Yang et al. [16,19] have derived that the confinement free energy of the polymer chain can be scaled by the average length of the tube occupied by the polymer, which is the average extension of the polymer chain, as follows:
Assuming that should satisfy Equations (2), (11), and (12), one has
or
where and . Equation (14) can be regarded as a new deflection length that fulfills both requirements for the free energy and statistics of geometrical quantities. We can see from Equation (14) that as long as , Taylor expansion of this equation yields the result in Equation (4). Inserting Equation (14) into Equation (2), and replacing by , we can obtain the confinement free energy as follows:
For the extension of the chain under both confinement and stretching force, as shown in Figure 1, Wang and Li [37] have suggested the force-extension relation shown in Equation (8), which now can be rewritten as
On the other hand, substituting Equation (5) into Equation (3), we can obtain the classical extension relation without stretching in the tight-confinement regime, , , as follows:
In the case of , Equation (16) in this regime can be reduced to
Equations (17) and (18) clearly agree in the special case () of a tube with a square cross-section. In terms of the aspect ratio , the right-hand side of Equation (17) is larger than the right-hand side of Equation (18) by the factor
The function has a single minimum at , corresponding to , and approaches in the limits and . Thus, Equation (18) only agrees with the classical strong confinement limit (17) if the cross-section of the tube is square or close to it.
2.2. Numerical Verifications
2.2.1. Solutions to the Fokker–Planck Equation
In order to verify the derived free energy expression, we considered the solutions to the Fokker–Planck equation, which can be used to describe the statistical behaviors of confined polymer chains. We first introduce to represent the probability that a polymer chain at arc length s has an end position vector r and an end unit tangential vector u. Then, we can have the partition function of the chain with contour length L as and the Fokker–Planck equation [31,32]
where
is the potential energy per unit length due to the confinement of a rectangular tube. As suggested by Chen [19,32], the solution of Equation (20) can be expanded into a series of eigenfunctions associated with negative exponential terms of eigenvalues. By noting that the chain is sufficiently long and that the high-order eigenvalues are large enough, then the solution can be approximated by the ground state eigenfunction and eigenvalue as follows:
Then the free energy can be written as
Comparing Equation (2) to Equation (23) gives
Chen and his coworkers [19,31,32] have proposed an iteration method to numerically determine the ground state eigenvalue and eigenfunction. In this study, we adopted this method to calculate the confinement free energy. As examples, we considered polymer chains confined in slits with different heights H. When using Chen’s method to calculate we set the tolerance error as . Figure 2 shows the comparison of the confinement free energy as a function of H/Lp obtained by numerical solutions of the ground state eigenvalue, Equation (15), and Equation (2) in terms of the classical Odijk length. It can be seen from Figure 2 that free energy based on the modified deflection length had a better agreement with the numerical results than that based on the classical one.
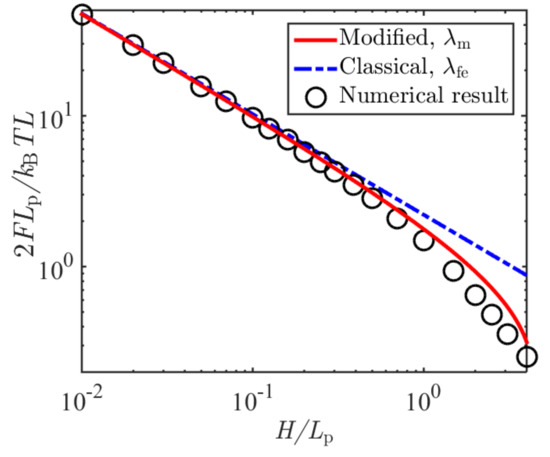
Figure 2.
Normalized confinement free energy as a function of the normalized slit height, predicted based on the classical and modified deflection lengths, and the solutions of the eigenvalue problem.
2.2.2. Brownian Dynamics Simulations (Appendix A)
We used the technique of statistical dynamics simulations to verify the derived force-extension relation on polymer chains subjected to both confinement of rectangular tubes and stretching of external forces. We performed the simulations by using our GBR model for Brownian dynamics of semiflexible polymer chains in confinements [33]. This model has been successfully applied to the quantitative analysis of statistical behaviors of polymers confined on spherical surfaces [34] and in cylindrical tubes [29,30] and subjected to stretching forces [29,30]. In this GBR model, we considered the polymer chain as a discrete WLC with N identical virtual beads of radius a at different positions }, where k = 1, 2, …, N, linked by N-1 rods with inextensible length b. The virtual beads are used to feel the hydrodynamic interactions, and angle changes of the adjacent rods are used to account for the bending deformation. As long as the position vectors of all N beads at the nth time step, denoted as = {, , …, }’, are obtained, the new position vector at the (n + 1)th time step, , can be calculated from [33,34]
where is the time step, is the Kronecker delta symbol, is the collective vector of internal and external forces, is a projection matrix (which together with sets the inextensible constraints), is the penalty displacement vector for the tube/slit walls, is the translational diffusion matrix determined through hydrodynamic interactions between beads, and is the vector of random force generated at each time step from a Gaussian distribution with zero mean and variance equal to
We performed Brownian dynamics simulations for WLCs confined in square tubes, rectangular tubes, and narrow slits of different sizes and subjected to various stretching forces. In all simulations, the chains were initially set in a straight configuration. Confinements and constant tensile forces were then applied during chain relaxation. At the nth time step, we recorded the end-to-end distance along the z axis, . For each simulation, we needed to keep the steady extension states lasting a sufficiently long enough time to generate enough numbers of different equilibrium configurations. For each case, average extension of the WLC was obtained by first averaging over time and then averaging over a large number of independent trajectories with different random seeds, which was then denoted as . For the simulation parameters, we should note that the contour length should be larger than (at least) two times the persistence length and much larger than the deflection length scale . As we were only interested in the equilibrium properties of the polymer chains, therefore specific values of the bead radius, the hydrodynamic interaction between beads, and time steps were not the key factors as long as sufficiently large numbers of different configurations of the polymer chain could be generated for averaging. In addition, the bond length should be selected to be much smaller than the deflection length scale and the persistence length. For all these Brownian dynamics simulations, we chose persistence length of the chain as Lp = 50 nm, the viscosity of water as , and the absolute temperature as . Simulation parameters on bead radius a, bond length b, time step , contour length L, total simulation time, and total number of different trajectories for the ensemble average are listed in Table 2, Table 3, Table 4, Table 5 and Table 6 for different chains in different confinements.

Table 2.
Simulation parameters for the confinement of square tubes without stretching force.

Table 3.
Simulation parameters for the confinement of square tubes.

Table 4.
Simulation parameters for the confinement of rectangular tubes.

Table 5.
Simulation parameters for the confinement of slits (circle).

Table 6.
Simulation parameters for the confinement of slits (cross).
Figure 3 shows convergence of the simulations for the evolution of the ensemble average of the extension, , for slit- and square tube-confined WLCs under stretching. It can be seen from Figure 3 that the equilibrium state could last a sufficiently long enough time to guarantee the effectiveness of time averaging.
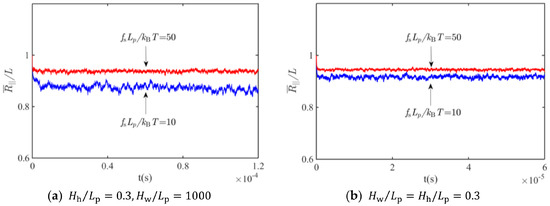
Figure 3.
Evolution of the extension for tube-confined WLCs under stretching: (a) Slit, ; (b) Square tube,.
Figure 4 shows the comparison of Brownian dynamics simulation results and corresponding theoretical predictions based on the classical deflection length as shown in Equation (17) and based on the modified deflection length in Equation (16) for the normalized average extension of the WLCs confined in square tubes of different sizes without stretching. Simulation parameters are listed in Table 2. It can be seen from Figure 4 that the prediction in terms of the modified deflection length agreed well with the simulation results, and could be reduced to that of the classical one at a tight confinement limit. For the case of a large Hw/Lp, the prediction in terms of the classical deflection length exhibited a large discrepancy with the simulation results.

Figure 4.
Comparison of Brownian dynamics simulations and theoretical predictions on the relative average extension of a WLC under confinements of square tubes.
Figure 5, Figure 6 and Figure 7 show the comparison of Brownian dynamics simulation results and corresponding theoretical predictions, based on Equation (8), associated with the classical deflection lengths in Equation (4), in Equation (5), and that based on Equation (17) associated with the present new deflection length in Equation (16), for the normalized average extension of the WLCs stretched by different forces and confined in square tubes, rectangular tubes, and slits of different sizes, respectively.
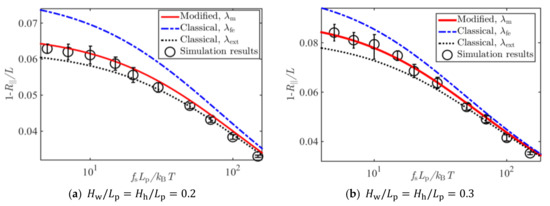
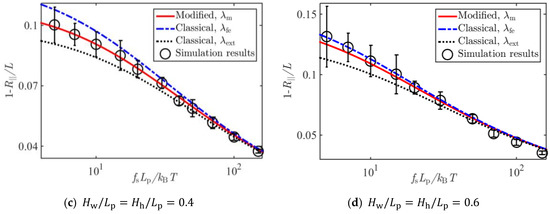
Figure 5.
Comparison of Brownian dynamics simulations and theoretical predictions on the relative average extension of a WLC under stretching and confinements of square tubes of sizes (a) , (b) , (c) , and (d) .
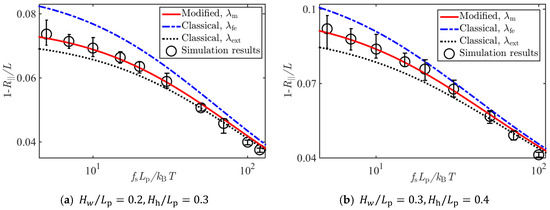
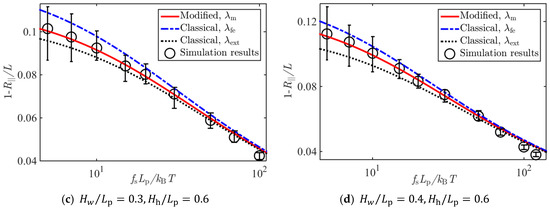
Figure 6.
Comparison of Brownian dynamics simulations and theoretical predictions on the relative average extension of a WLC under stretching forces and confinements of rectangular tubes with sizes (a) , (b) , (c) , and (d) .
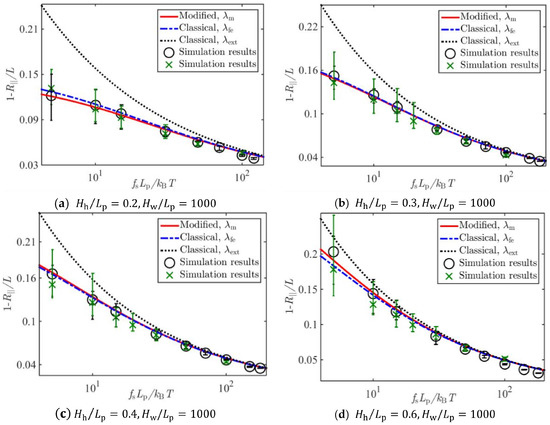
Figure 7.
Comparison of Brownian dynamics simulations and theoretical predictions on the relative average extension of a WLC under stretching forces and confinements of slits with sizes (a) , (b) , (c) , and (d) .
It can be seen from Figure 5, Figure 6 and Figure 7 that results based on the newly derived formula on the average extension of the confined WLC agreed with the simulation results very well, and those based on the classical deflection length showed an apparent discrepancy with the simulation results when the tube diameter became large or the stretching force was small.
3. Conclusions
Based on WLC theory and existing results on statistical properties of strongly confined polymers, we theoretically and numerically studied confinement free energy and force-confinement-extension relations of rectangular tube-confined semiflexible polymer chains under stretching in a deflection regime. We derived a modified deflection length without any adjustable parameters, which was valid for quantitative formulations of both free energy and geometrical extension. By using this deflection length scale, we obtained compact formulas on the confinement free energy and force-extension relation without any fitting parameters. Numerical analysis based on the eigenvalue problem of the governing Fokker–Planck equations and the GBR Brownian dynamics simulations justified these theoretical predictions to be valid for a much more extended range of the confinement/persistence length ratio than that based on the classical deflection length.
Author Contributions
J.W. and K.L. conceived and designed the study; K.L. performed the simulations; J.W. and K.L. analyzed the data; J.W. contributed reagents/materials/analysis tools; J.W. and K.L. wrote the paper.
Acknowledgments
The authors wish to thank Jeff Z. Y. Chen (Waterloo, Ontario, Canada) for help on solving the eigenvalue problem, and the anonymous reviewers whose comments have greatly improved this manuscript. This research is supported by grants from the National Natural Science Foundation of China (11472119) and the 111 Project (B14044). The National Supercomputing Center in Guangzhou provided the computational resources.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. The GBR Model for Brownian Dynamics Simulations
In the GBR model, a semiflexible chain is described as N identical virtual beads of radius a, which is connected by N−1 inextensible rods of length b. Each bead has a different position in a Cartesian coordinate system, , k = 1, 2, …, N, which is introduced for accounting hydrodynamic interactions between different chain segments. These segments are treated as hard rods, whose geometrical constraints are realized by the so-called linear constraint solver (LINCS) [33,38]. Evolution of chain configurations is characterized by a collective Brownian motion of N identical beads in solution. By denoting the time step, , and position vectors of all the beads at the current n , = {, , …, }’, then the position vectors at (n + 1) can be determined from the governing Langevin equation in terms of the first-order difference method as
where is the translational diffusion matrix consisting of 3 × 3 sub-blocks , j, k=1, 2, …, N, for which the Rotne–Prager tensor [39] is used to represent the hydrodynamic interactions between beads j and k. In a case where only equilibrium properties are interested, the sub-blocks can be simply set as
Such a simplification will not affect various average results in the equilibrium state as long as a sufficiently large number of different configurations can be generated. In Equation (A11), is the collective vector, including internal bending forces and external forces; and is the associated gradient matrix related to the N − 1 time-independent constraint equations for the inextensible rods
and
where is the length of the ith rod, and the dimensions of gradient matrix are . Vector consists of N − 1 Lagrange multipliers, so that can be regarded as collective constraint forces keeping the rod length constant. The vector represents random forces generated at each time step from a Gaussian distribution with zero mean and variance
where is the Kronecker delta symbol.
As is time-independent, the time derivative of Equation (A3) yields
Based on Equations (A1) and (A6), we can determine the Lagrange multipliers as
Inserting Equation (A7) into Equation (A1) and adding an additional term to suppress the accumulation of numerical errors, then the new position vector can be further expressed as
where , and is a projection matrix that sets the constraints.
For the confinement of a rectangular tube with width and height and , we used a semi-analytical technique proposed by Peters and Barenbrug [40] to treat the collective stochastic motion of N beads near the reflecting tube walls. Considering the jth bead with current position , we defined as the current distance of the jth bead from a wall. The bead can be viewed as close enough to the tube wall as long as
The influence of the tube wall on the movement of the jth bead in the next time step can be characterized by the random displacement , as derived by Peters and Barenbrug [40]:
where n is the unit normal vector of the tube wall, and is a random variable with first moment equal to 0. When , we set , implying that the bead is not sufficiently close to the wall. The stochastic displacements for all beads induced by the wall at the nth time step can be put in a 3N vector . Substituting into Equation (A8) leads to
If the chain is stretched by external forces, then the force vector in the above equation can be expressed as
where represents the internal forces on all beads due to bending deformation [33], and represents the tensile forces.
References
- Reisner, W.; Morton, K.J.; Riehn, R.; Wang, Y.M.; Yu, Z.; Rosen, M.; Sturm, J.C.; Chou, S.Y.; Frey, E.; Austin, R.H. Statics and dynamics of single DNA molecules confined in nanochannels. Phys. Rev. Lett. 2005, 94, 196101. [Google Scholar] [CrossRef] [PubMed]
- Reisner, W.; Pedersen, J.N.; Austin, R.H. DNA confinement in nanochannels: Physics and biological applications. Rep. Prog. Phys. 2012, 75, 106601. [Google Scholar] [CrossRef] [PubMed]
- Marko, J.F.; Siggia, E.D. Stretching DNA. Macromolecules 1995, 28, 8759–8770. [Google Scholar] [CrossRef]
- Dorfman, K.D.; King, S.B.; Olson, D.W.; Thomas, J.D.P.; Tree, D.R. Beyond gel electrophoresis: Microfluidic separations, fluorescence burst analysis, and DNA stretching. Chem. Rev. 2013, 113, 2584–2667. [Google Scholar] [CrossRef] [PubMed]
- Gorbunov, A.A.; Skvortsov, A.M. Statistical properties of confined macromolecules. Adv. Colloid Interfaces 1995, 62, 31–108. [Google Scholar] [CrossRef]
- Teraoka, I. Polymer solutions in confining geometries. Prog. Polym. Sci. 1996, 21, 89–149. [Google Scholar] [CrossRef]
- Choi, M.C. Direct Observation of Biaxial Confinement of a Semi-flexible Filament in a Channel. Macromolecules 2005, 38, 9882–9884. [Google Scholar] [CrossRef]
- Casassa, E.F. Equilibrium distribution of flexible polymer chains between a macroscopic solution phase and small voids. J. Polym. Sci. C Polym. Lett. 1967, 5, 773–778. [Google Scholar] [CrossRef]
- Daoud, M.; Gennes, P.G.D. Statistics of macromolecular solutions trapped in small pores. J. Phys. 1977, 38, 85–93. [Google Scholar] [CrossRef]
- Gennes, P.G.D. Scaling Concepts in Polymer Physics. Phys. Today 1980, 33, 51–54. [Google Scholar] [CrossRef]
- Kratky, O.; Porod, G. Röntgenuntersuchung gelöster Fadenmoleküle. Recl. Trav. Chim. Pays-Bas. 2015, 68, 1106–1122. [Google Scholar] [CrossRef]
- Odijk, T. The statistics and dynamics of confined or entangled stiff polymers. Macromolecules 1983, 16, 1340–1344. [Google Scholar] [CrossRef]
- Odijk, T. Theory of lyotropic polymer liquid crystals. Macromolecules 1986, 19, 2313–2329. [Google Scholar] [CrossRef]
- Odijk, T. Scaling theory of DNA confined in nanochannels and nanoslits. Phys. Rev. E 2008, 77, 060901. [Google Scholar] [CrossRef] [PubMed]
- Burkhardt, T.W. Free energy of a semiflexible polymer in a tube and statistics of a randomly-accelerated particle. J. Phys. A Gen. Phys. 1997, 30, L167–L172. [Google Scholar] [CrossRef]
- Burkhardt, T.W.; Yang, Y.; Gompper, G. Fluctuations of a long, semiflexible polymer in a narrow channel. Phys. Rev. E 2010, 82, 041801. [Google Scholar] [CrossRef] [PubMed]
- Bicout, D.J.; Burkhardt, T.W. Simulation of a semiflexible polymer in a narrow cylindrical pore. J. Phys. A Gen. Phys. 2001, 34, 5745–5750. [Google Scholar] [CrossRef]
- Yang, Y.; Burkhardt, T.W.; Gompper, G. Free energy and extension of a semiflexible polymer in cylindrical confining geometries. Phys. Rev. E 2007, 76, 011804. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Z.Y. Free Energy and Extension of a Wormlike Chain in Tube Confinement. Macromolecules 2013, 46, 9837–9844. [Google Scholar] [CrossRef]
- Dai, L.; Jones, J.J.; Van der, M.J.R.C.; Doyle, P.S. A systematic study of DNA conformation in slitlike confinement. Soft Matter 2012, 8, 2972–2982. [Google Scholar] [CrossRef]
- Chen, Y.L.; Graham, M.D.; De Pablo, J.J.; Randall, G.C.; Gupta, M.; Doyle, P.S. Conformation and dynamics of single DNA molecules in parallel-plate slit microchannels. Phys. Rev. E 2004, 70, 060901. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.K.; Fu, C.C.; Chen, Y.L.; Chen, Y.R.; Wei, P.K.; Kuan, C.H.; Fann, W.S. Static conformation and dynamics of single DNA molecules confined in nanoslits. Phys. Rev. E 2007, 76, 011806. [Google Scholar] [CrossRef] [PubMed]
- Tree, D.R.; Reinhart, W.F.; Dorfman, K.D. The Odijk regime in slits. Macromolecules 2014, 47, 3672–3684. [Google Scholar] [CrossRef]
- Chen, J.Z.Y.; Sullivan, D.E. Free energy of a wormlike polymer chain confined in a slit: Crossover between two scaling regimes. Macromolecules 2006, 39, 7769–7773. [Google Scholar] [CrossRef]
- Chen, Y.L.; Lin, P.; Chou, C.F. Generalized Force−Extension Relation for Wormlike Chains in Slit Confinement. Macromolecules 2010, 43, 10204–10207. [Google Scholar] [CrossRef]
- Dai, L.; van der Maarel, J.; Doyle, P.S. Extended de Gennes regime of DNA confined in a nanochannel. Macromolecules 2014, 47, 2445–2450. [Google Scholar] [CrossRef]
- Taloni, A.; Yeh, J.W.; Chou, C.F. Scaling Theory of Stretched Polymers in Nanoslits. Macromolecules 2013, 46, 7989–8002. [Google Scholar] [CrossRef]
- Odijk, T. Physics of tightly curved semiflexible polymer chains. Macromolecules 1993, 26, 6897–6902. [Google Scholar] [CrossRef]
- Wang, J.; Gao, H. Stretching a stiff polymer in a tube. J. Mater. Sci. 2007, 42, 8838–8843. [Google Scholar] [CrossRef]
- Li, R.; Wang, J. Stretching a Semiflexible Polymer in a Tube. Polymers 2016, 8, 328. [Google Scholar] [CrossRef]
- Chen, J.Z.Y. Theory of wormlike polymer chains in confinement. Prog. Polym. Sci. 2016, 54–55, 3–46. [Google Scholar] [CrossRef]
- Gao, J.; Tang, P.; Yang, Y.; Chen, J.Z.Y. Free energy of a long semiflexible polymer confined in a spherical cavity. Soft Matter 2014, 10, 4674–4685. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gao, H. A generalized bead-rod model for Brownian dynamics simulations of wormlike chains under strong confinement. J. Chem. Phys. 2005, 123, 084956. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gao, H. Brownian dynamics simulations of charged semiflexible polymers confined to curved surfaces. J. Mech. Behav. Biomed. 2011, 4, 174–179. [Google Scholar] [CrossRef] [PubMed]
- Abhiram, M.; Michael, Q.; Kevin, D. The backfolded odijk regime for wormlike chains confined in rectangular nanochannels. Polymers 2016, 8, 79. [Google Scholar]
- Yamakawa, H. Modern Theory of Polymer Solutions; Harper and Row: New York, NY, USA, 1971. [Google Scholar]
- Wang, J.; Li, R. Stretching strongly confined semiflexible polymer chain. Appl. Math. Mech.-Engl. 2014, 35, 1233–1238. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 14630–1472. [Google Scholar] [CrossRef]
- Ermak, D.L.; McCammon, J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar] [CrossRef]
- Peters, E.A.J.F.; Barenbrug, T.M. Efficient Brownian dynamics simulation of particles near walls. I. Reflecting and absorbing walls. Phys. Rev. E 2002, 66, 056701. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).