Complex Diffractive Optical Elements Stored in Photopolymers
Abstract
1. Introduction
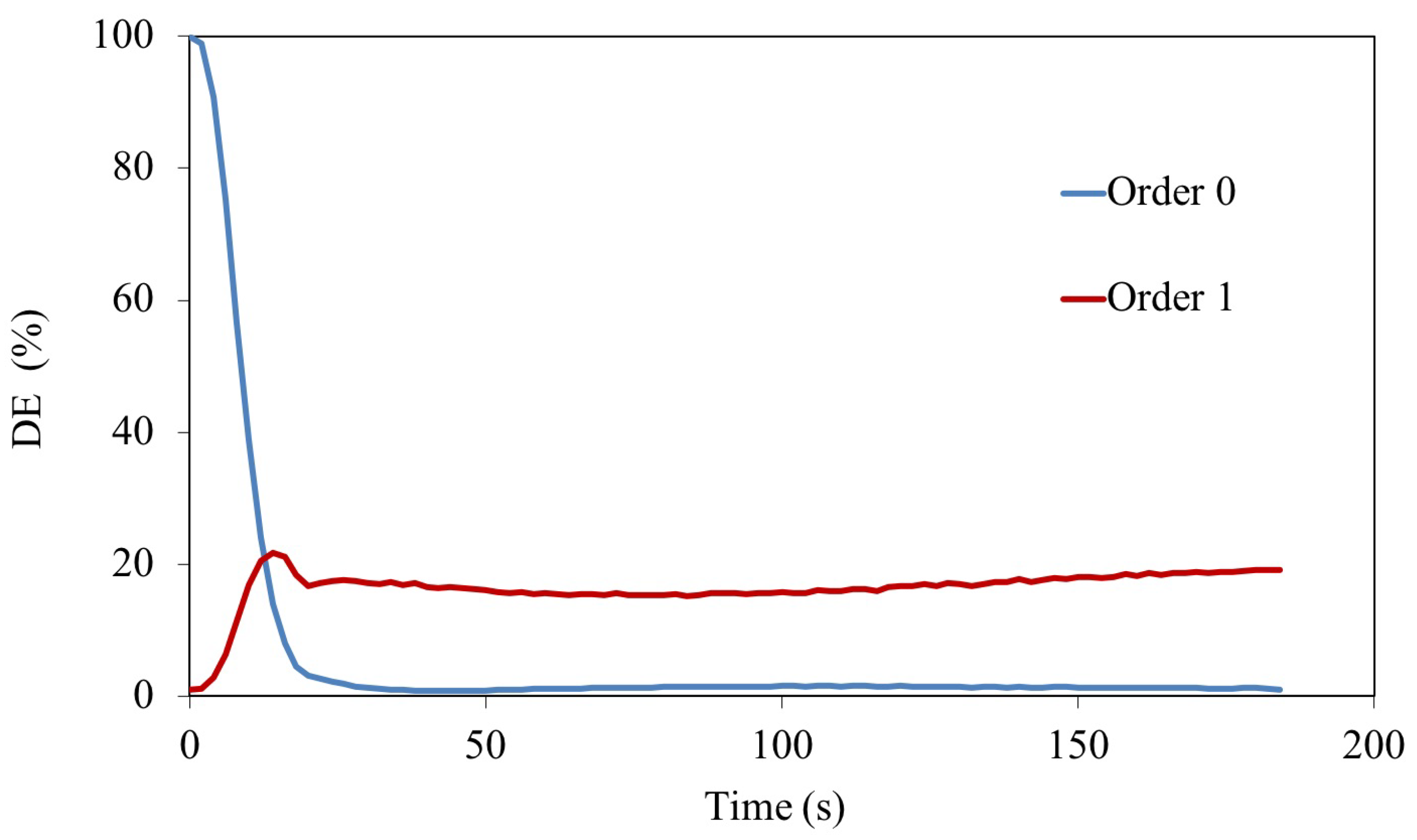
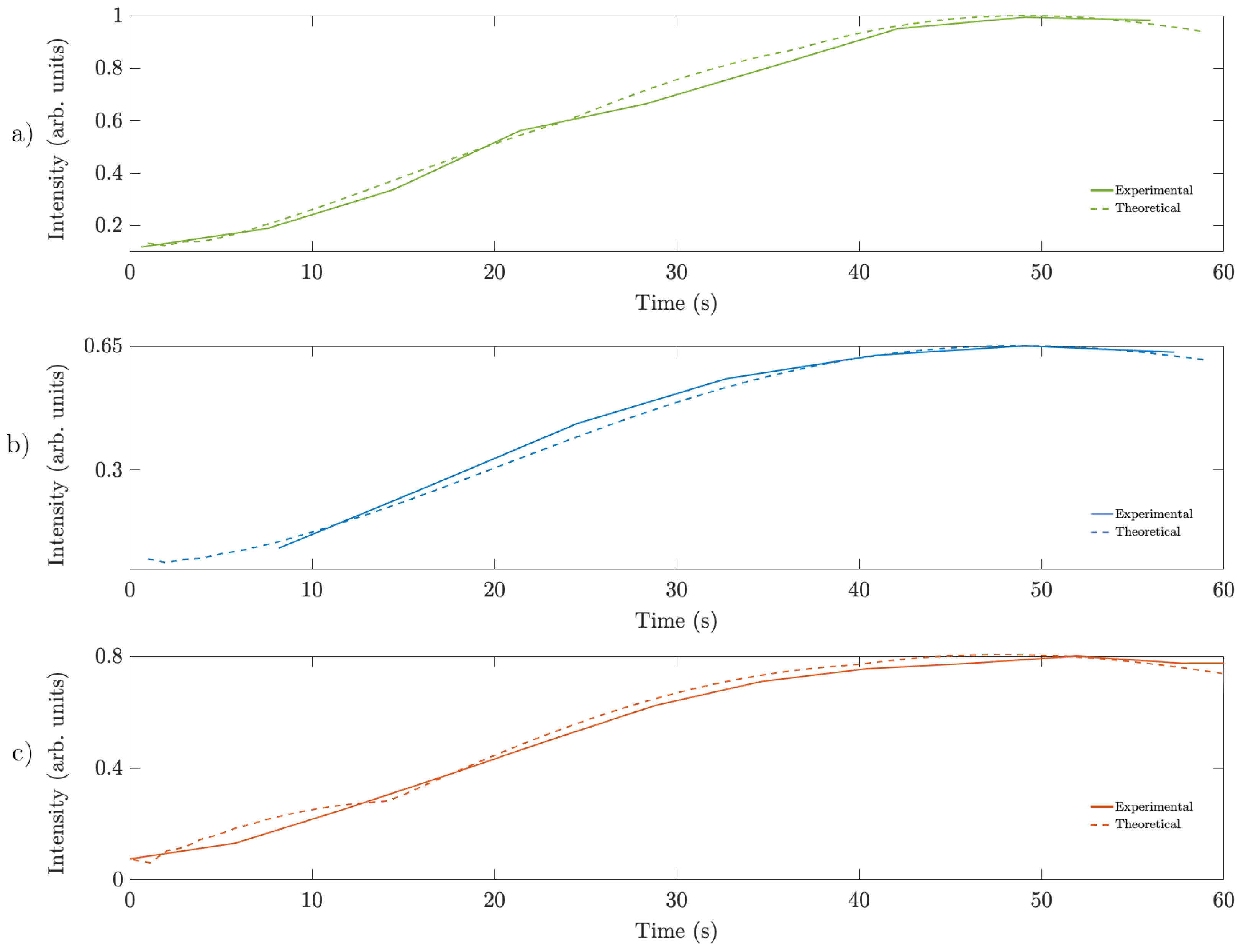
2. Diffusion Model
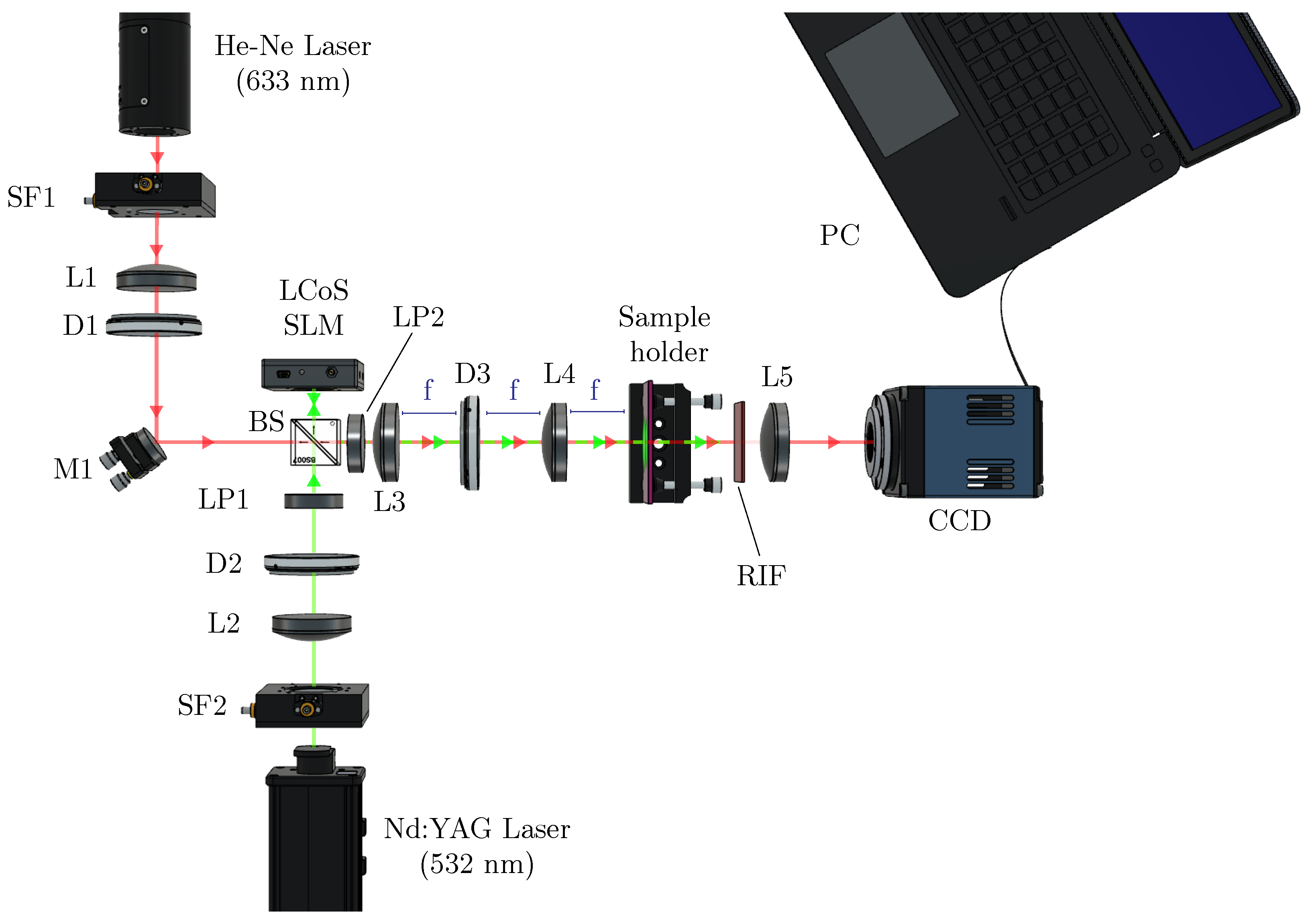
3. Experimental Setup
4. Results and Discussion
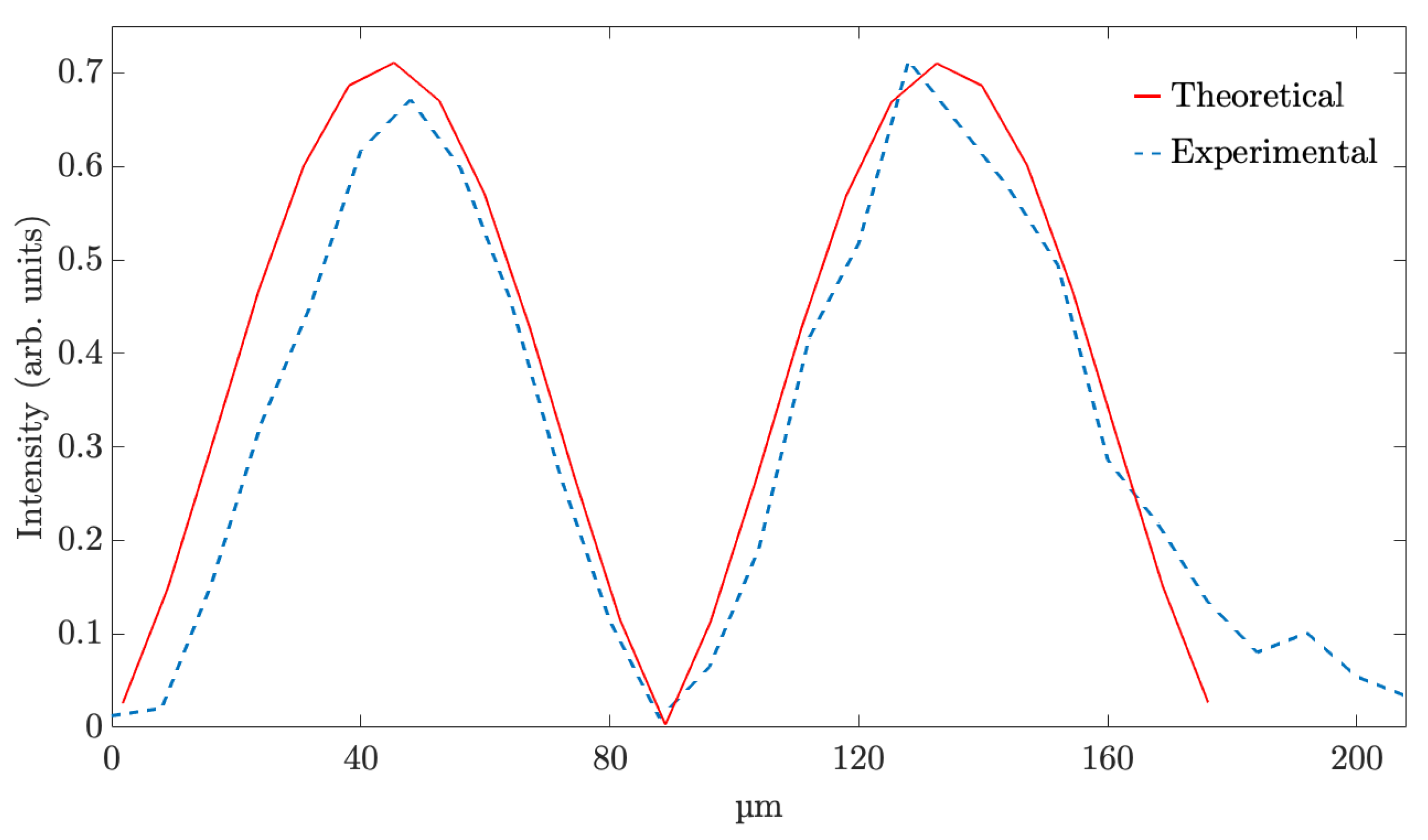
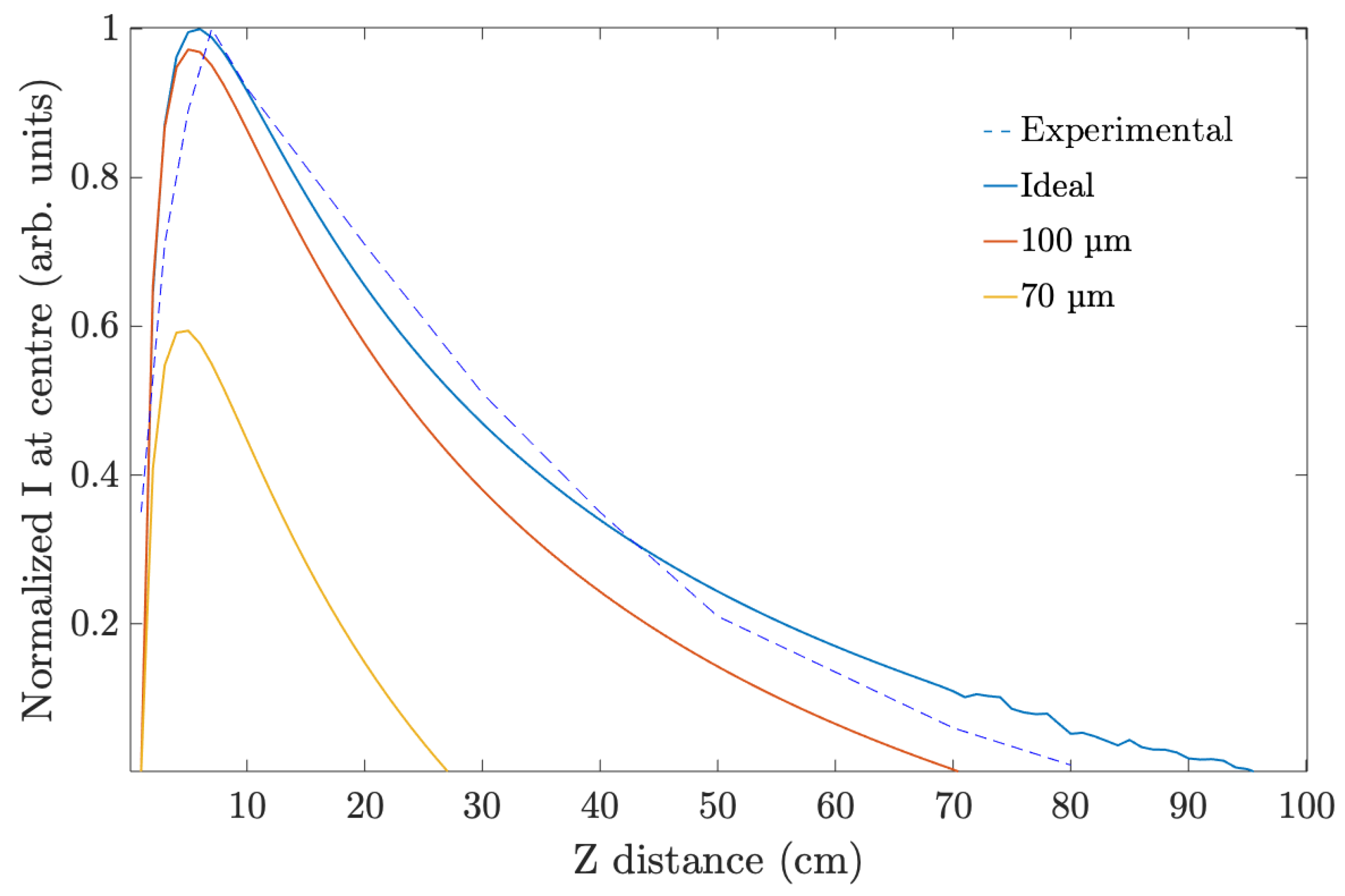
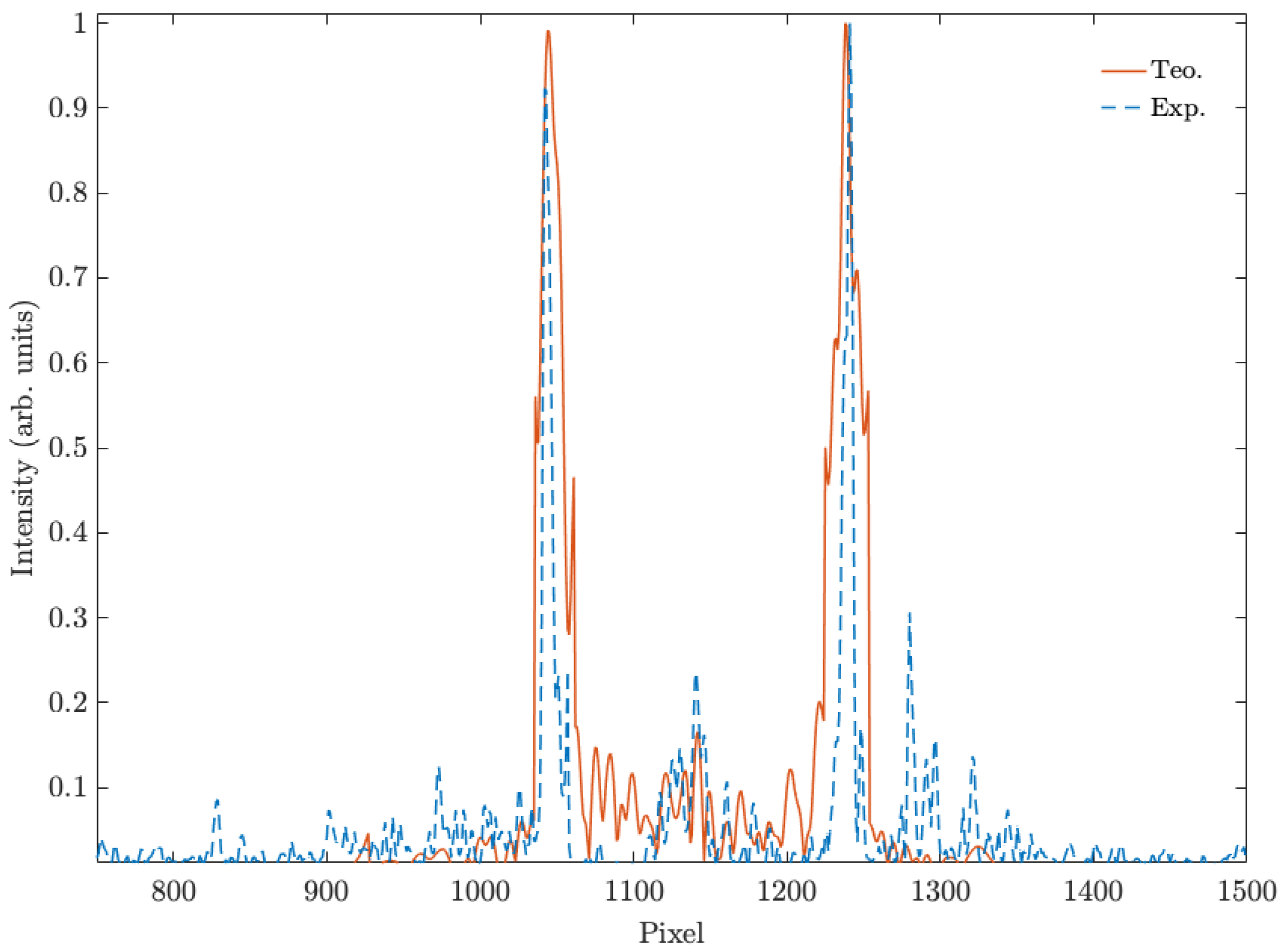
4.1. Fork Grating and Diffractive Axicon
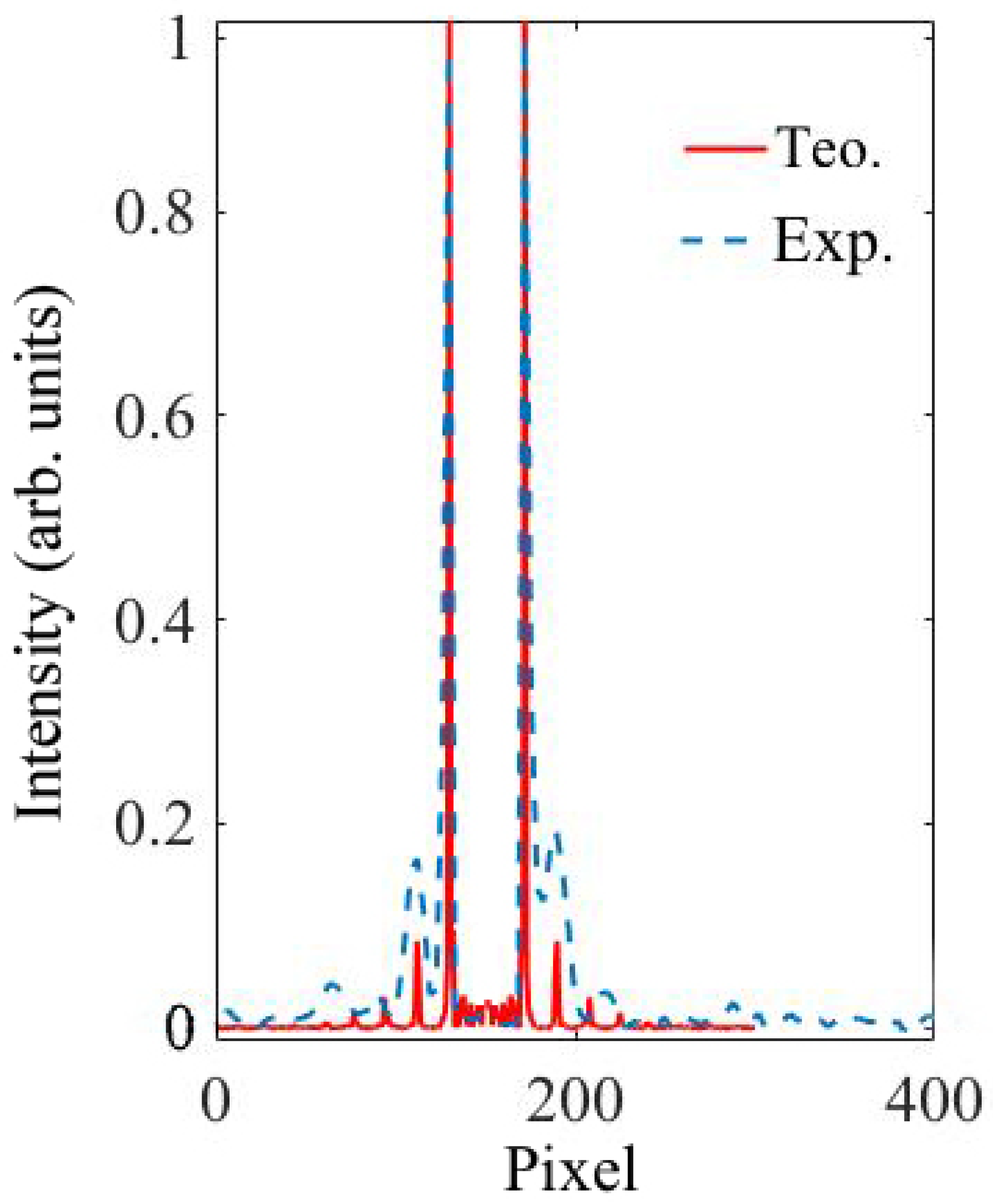
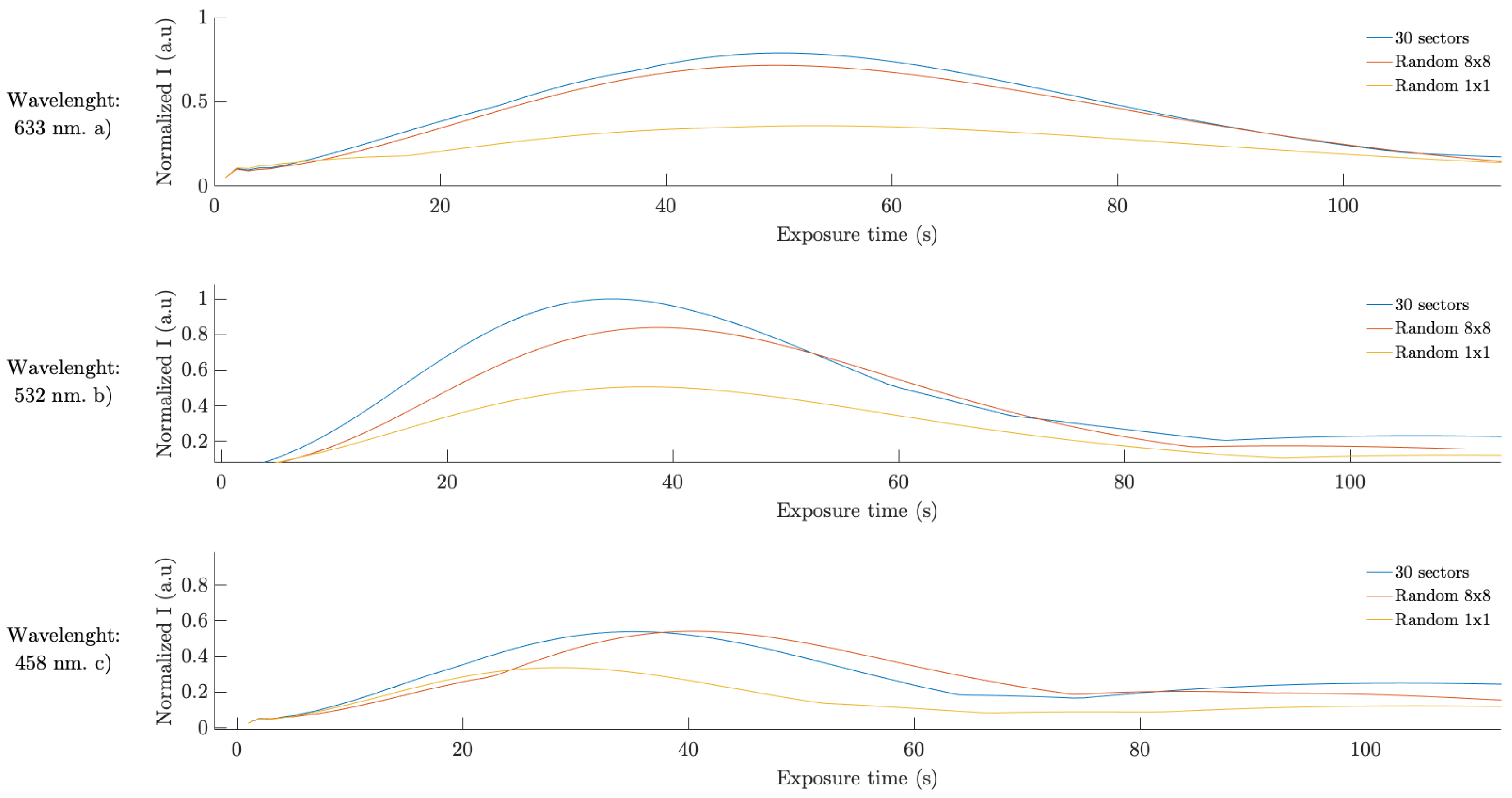
4.2. Achromatic Lenses
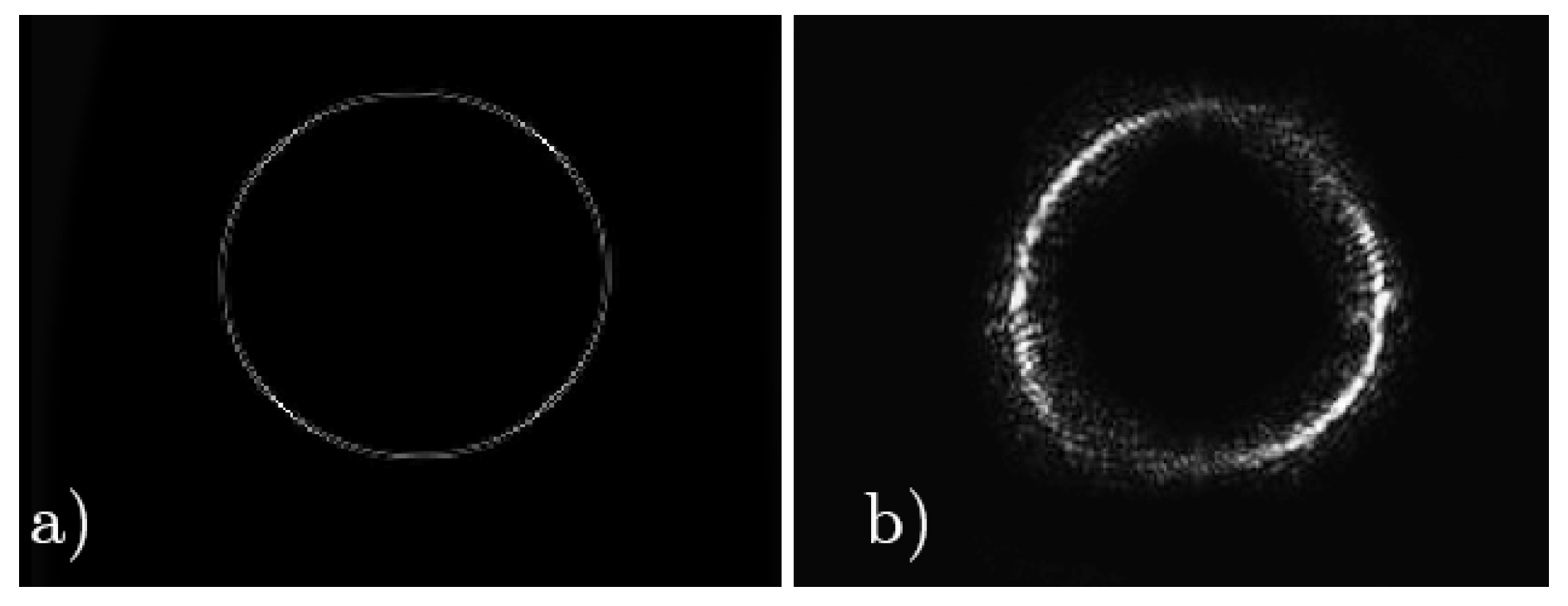
4.3. Helical Axicon
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Infusino, M.; Luca, A.D.; Barna, V.; Caputo, R.; Umeton, C. Periodic and aperiodic liquid crystal-polymer composite structures realized via spatial light modulator direct holography. Opt. Express 2012, 20, 23138–23143. [Google Scholar] [CrossRef] [PubMed]
- Miki, M.; Ohira, R.; Tomita, Y. Optical properties of electrically tunable two-dimensional photonic lattice structures formed in a holographic polymer-dispersed liquid crystal film: Analysis and experiment. Materials 2014, 7, 3677–3698. [Google Scholar] [CrossRef] [PubMed]
- Neipp, C.; Francés, J.; Martínez, F.; Fernández, R.; Ortuño, M.; Álvarez, A.S.; Bleda, S.G. Optimization of Photopolymer Materials for the Fabrication of a Holographic Waveguide. Polymers 2017, 9, 395. [Google Scholar] [CrossRef] [PubMed]
- Gallego, S.; Márquez, A.; Martínez, F.J.; Riquelme, M.; Fernández, R.; Pascual, I.; Beléndez, A. Linearity in the response of photopolymers as optical recording media. Opt. Express 2013, 21, 10995–11008. [Google Scholar] [CrossRef]
- Fernández, R.; Gallego, S.; Márquez, A.; Francés, J.; Martínez, F.J.; Beléndez, A. Influence of index matching on AA/PVA photopolymers for low spatial frequency recording. Appl. Opt. 2015, 54, 3132–3140. [Google Scholar] [CrossRef]
- Fernández, R.; Gallego, S.; Francés, J.; Pascual, I.; Beléndez, A. Characterization and comparison of different photopolymers for low spatial frequency recording. Opt. Mater. 2015, 44, 18–24. [Google Scholar] [CrossRef][Green Version]
- Fernández, R.; Gallego, S.; Márquez, A.; Francés, J.; Navarro-Fuster, V.; Beléndez, A. Blazed Gratings Recorded in Absorbent Photopolymers. Materials 2016, 9, 195. [Google Scholar] [CrossRef]
- Fernández, R.; Gallego, S.; Márquez, A.; Francés, J.; Navarro-Fuster, V.; Pascual, I. Diffractive lenses recorded in absorbent Photopolymers. Opt. Express 2016, 24, 1559–1572. [Google Scholar] [CrossRef]
- Andrés, P.; Climent, V.; Lancis, J.; Mínguez-Vega, G.; Tajahuerce, E.; Lohmann, A.W. All-incoherent dispersion-compensated optical correlator. Opt. Lett. 1999, 24, 1331–1333. [Google Scholar] [CrossRef]
- Carcole, E.; Millan, M.S.; Campos, J. Derivation of weighting coefficients for multiplexed phase-diffractive elements. Opt. Lett. 1995, 20, 2360. [Google Scholar] [CrossRef]
- Ben-eliezer, E.; Zalevsky, Z.; Marom, E. All-optical extended depth of field. J. Opt. A Pure Appl. Opt. 2003, 164, S164–S169. [Google Scholar] [CrossRef]
- Márquez, A.; Iemmi, C.; Campos, J.; Yzuel, M.J. Achromatic diffractive lens written onto a liquid crystal display. Opt. Lett. 2006, 31, 392. [Google Scholar] [CrossRef]
- Stoyanov, L.; Topuzoski, S.; Stefanov, I.; Janicijevic, L.; Dreischuh, A. Far field diffraction of an optical vortex beam by a fork-shaped grating. Opt. Commun. 2015, 350, 301–308. [Google Scholar] [CrossRef]
- Chen, S.; Cai, Y.; Li, G.; Zhang, S.; Cheah, K.W. Geometric metasurface fork gratings for vortex-beam generation and manipulation. Laser Photonics Rev. 2016, 10, 322–326. [Google Scholar] [CrossRef]
- Terhalle, B.; Langner, A.; Päivänranta, B.; Guzenko, V.A.; David, C.; Ekinci, Y. Generation of extreme ultraviolet vortex beams using computer generated holograms. Opt. Lett. 2011, 36, 4143–4145. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810. [Google Scholar] [CrossRef]
- Davidson, N. Dark optical traps for ultra-cold atoms. In Proceedings of the 19th Congress of the International Commission for Optics: Optics for the Quality of Life, Florence, Italy, 25–30 August 2002; Volume 4829, pp. 4822–4829. [Google Scholar]
- Leach, J.; Jack, B.; Romero, J.; Jha, A.K.; Yao, A.M.; Franke-Arnold, S.; Ireland, D.G.; Boyd, R.W.; Barnett, S.M.; Padgett, M.J. Quantum correlations in optical angle-orbital angular momentum variables. Science 2010, 329, 662–665. [Google Scholar] [CrossRef]
- Fürhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral interferometry. Opt. Lett. 2005, 30, 1953–1955. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- McLeod, J.H. Axicons and Their Uses. J. Opt. Soc. Am. 1960, 50, 166. [Google Scholar] [CrossRef]
- Yu, X.; Xie, Z.X.; Liu, J.H.; Zhang, Y.; Wang, H.B.; Zhang, Y. Optimization design of a diffractive axicon for improving the performance of long focal depth. Opt. Commun. 2014, 330, 1–5. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K. Generation of high-order Bessel beams by use of an axicon. Opt. Commun. 2000, 177, 297–301. [Google Scholar] [CrossRef]
- Lee, K.S.; Rolland, J.P. Bessel beam spectral-domain high-resolution optical coherence tomography with micro-optic axicon providing extended focusing range. Opt. Lett. 2008, 33, 1696. [Google Scholar] [CrossRef]
- Kuang, Z.; Perrie, W.; Edwardson, S.P.; Fearon, E.; Dearden, G. Ultrafast laser parallel microdrilling using multiple annular beams generated by a spatial light modulator. J. Phys. D Appl. Phys. 2014, 47, 115501. [Google Scholar] [CrossRef]
- Gallego, S.; Márquez, A.; Neipp, C.; Fernández, R.; Martínez, F.J.; Francés, J.; Ortuño, M.; Pascual, I.; Beléndez, A. Model of low spatial frequency diffractive elements recorded in photopolymers during and after recording. Opt. Mater. 2014, 38, 46–52. [Google Scholar] [CrossRef]
- Aubrecht, I.; Miler, M.; Koudela, I. Recording of holographic diffraction gratings in photopolymers: theoretical modelling and real-time monitoring of grating growth. J. Mod. Opt. 1998, 45, 1465–1477. [Google Scholar] [CrossRef]
- Kelly, J.R.; Gleeson, M.R.; Close, C.E.; O’Neill, F.T.; Sheridan, J.T.; Gallego, S.; Neipp, C. Temporal analysis of grating formation in photopolymer using the nonlocal polymerization-driven diffusion model. Opt. Express 2005, 13, 6990–7004. [Google Scholar] [CrossRef]
- Martínez, F.J.; Fernández, R.; Márquez, A.; Gallego, S.; Álvarez, M.L.; Pascual, I.; Beléndez, A. Exploring binary and ternary modulations on a PA-LCoS device for holographic data storage in a PVA/AA photopolymer. Opt. Express 2015, 23, 20459. [Google Scholar] [CrossRef]
- Gallego, S.; Ortuño, M.O.; Neipp, C.; Márquez, A.; Beléndez, A.; Pascual, I.; Kelly, J.V.; Sheridan, J.T. Physical and effective optical thickness of holographic diffraction gratings recorded in photopolymers. Opt. Express 2005, 13, 1939–1947. [Google Scholar] [CrossRef]
- Liu, Y.J.; Sun, X.W.; Wang, Q.; Luo, D. Electrically switchable optical vortex generated by a computer- generated hologram recorded in polymer-dispersed liquid crystals. Opt. Express 2007, 15, 16645–16650. [Google Scholar] [CrossRef] [PubMed]
- Fernández, R.; Navarro-Fuster, V.; Martínez, F.; Gallego, S.; Márquez, A.; Pascual, I.; Beléndez, A. Modeling diffractive lenses recording in environmentally friendly photopolymer. Polymers 2017, 9, 278. [Google Scholar] [CrossRef] [PubMed]
- Bentley, J.B.; Davis, J.A.; Bandres, M.A.; Gutiérrez-Vega, J.C. Generation of helical Ince-Gaussian beams with a liquid-crystal display. Opt. Lett. 2006, 31, 649–651. [Google Scholar] [CrossRef] [PubMed]
- Izdebskaya, Y.; Shvedov, V.; Volyar, A. Symmetric array of off-axis singular beams: spiral beams and their critical points. J. Opt. Soc. Am. A 2008, 25, 171–181. [Google Scholar] [CrossRef][Green Version]
- Razueva, E.; Abramochkin, E. Multiple-twisted spiral beams. J. Opt. Soc. Am. A 2019, 36, 1089–1097. [Google Scholar] [CrossRef]






| Tea (mL) | PVA (mL) (8% w/v) | AA (g) | BMA (g) | YE (0.8% w/v) (mL) |
|---|---|---|---|---|
| 2 | 25 | 0.84 | 0.25 | 0.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández, R.; Gallego, S.; Márquez, A.; Neipp, C.; Calzado, E.M.; Francés, J.; Morales-Vidal, M.; Beléndez, A. Complex Diffractive Optical Elements Stored in Photopolymers. Polymers 2019, 11, 1920. https://doi.org/10.3390/polym11121920
Fernández R, Gallego S, Márquez A, Neipp C, Calzado EM, Francés J, Morales-Vidal M, Beléndez A. Complex Diffractive Optical Elements Stored in Photopolymers. Polymers. 2019; 11(12):1920. https://doi.org/10.3390/polym11121920
Chicago/Turabian StyleFernández, Roberto, Sergi Gallego, Andrés Márquez, Cristian Neipp, Eva María Calzado, Jorge Francés, Marta Morales-Vidal, and Augusto Beléndez. 2019. "Complex Diffractive Optical Elements Stored in Photopolymers" Polymers 11, no. 12: 1920. https://doi.org/10.3390/polym11121920
APA StyleFernández, R., Gallego, S., Márquez, A., Neipp, C., Calzado, E. M., Francés, J., Morales-Vidal, M., & Beléndez, A. (2019). Complex Diffractive Optical Elements Stored in Photopolymers. Polymers, 11(12), 1920. https://doi.org/10.3390/polym11121920










