Correlations between Process Parameters and Outcome Properties of Laser-Sintered Polyamide
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
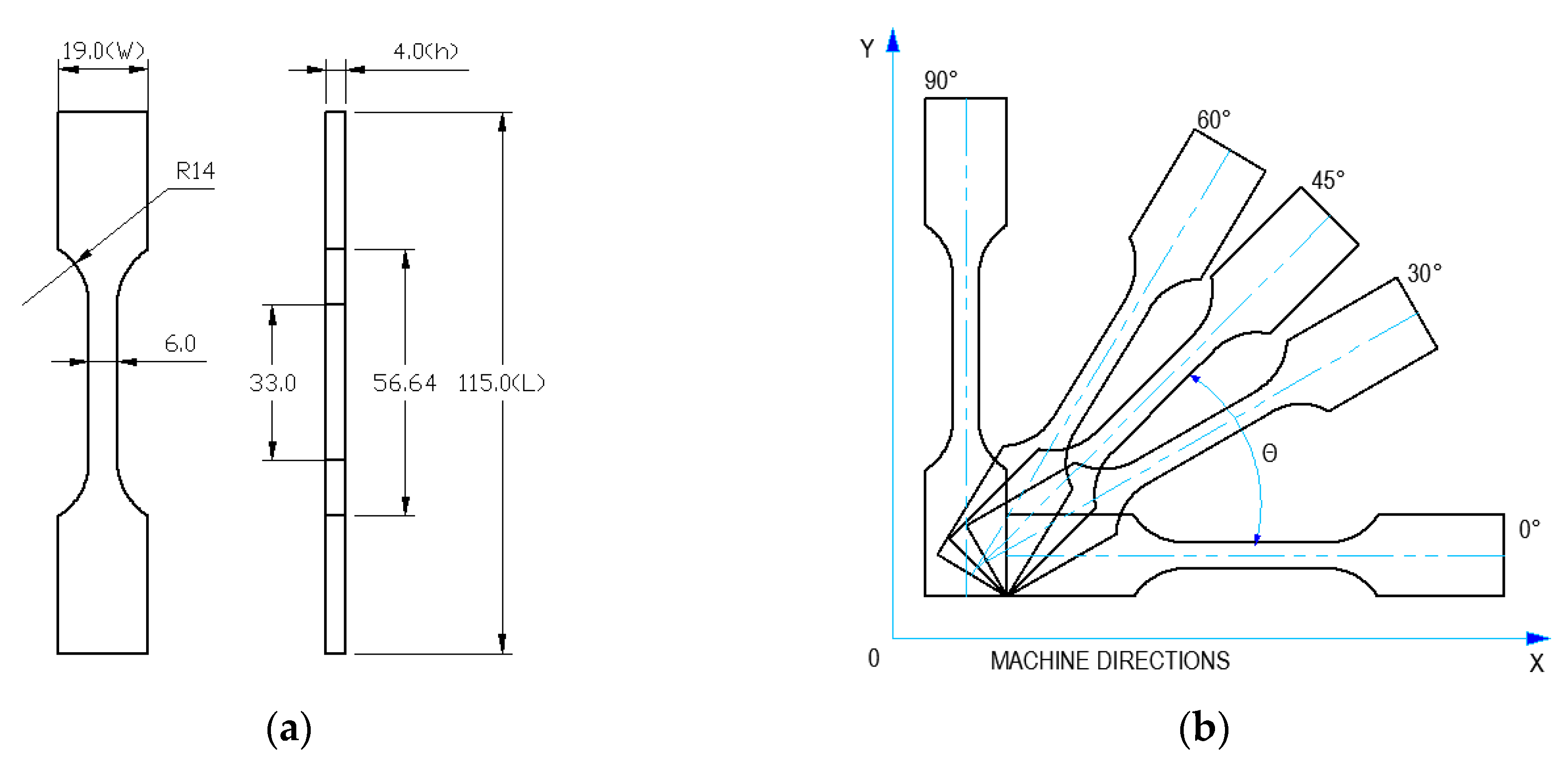
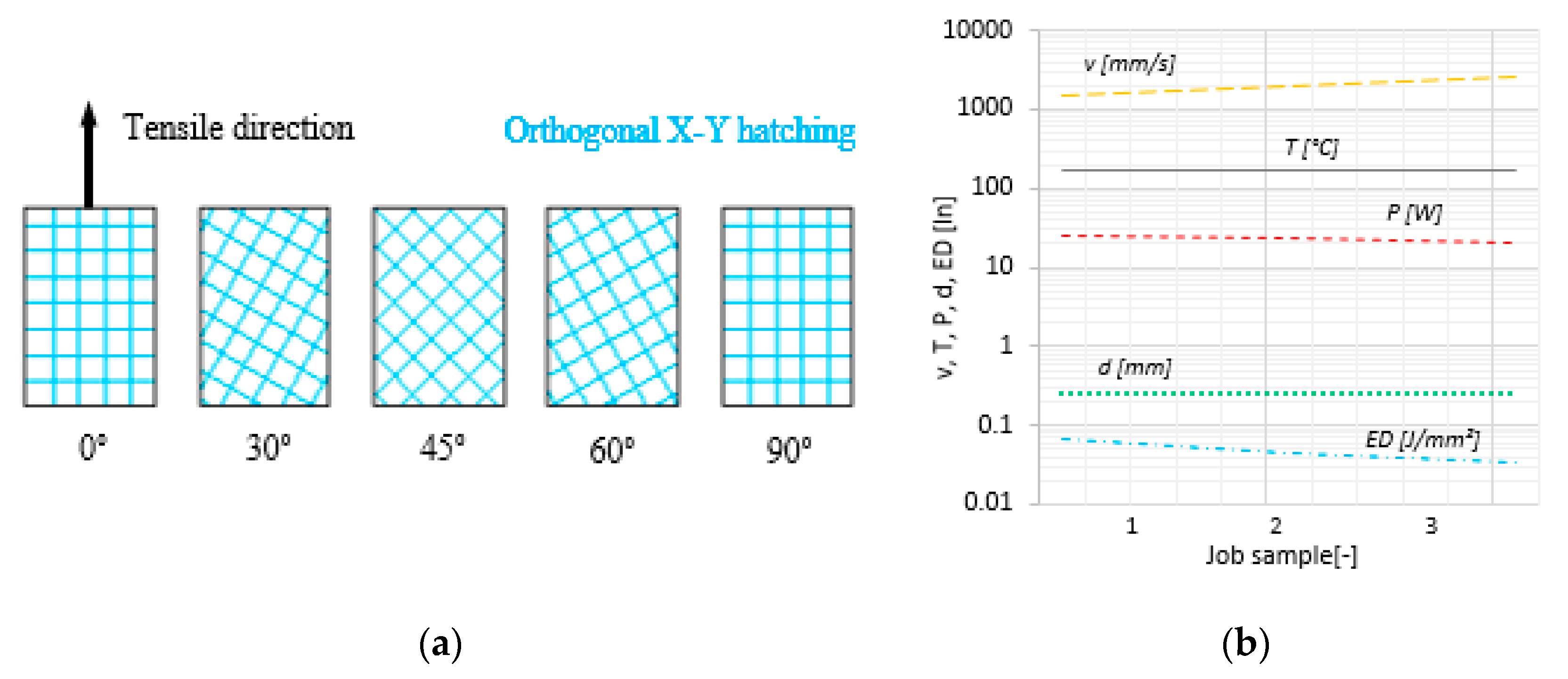
2.2.1. Process Parameter Setup
2.2.2. Formiga P100 Machine Setup
2.2.3. Measurements and Data Processing
2.2.4. Tensile Tests
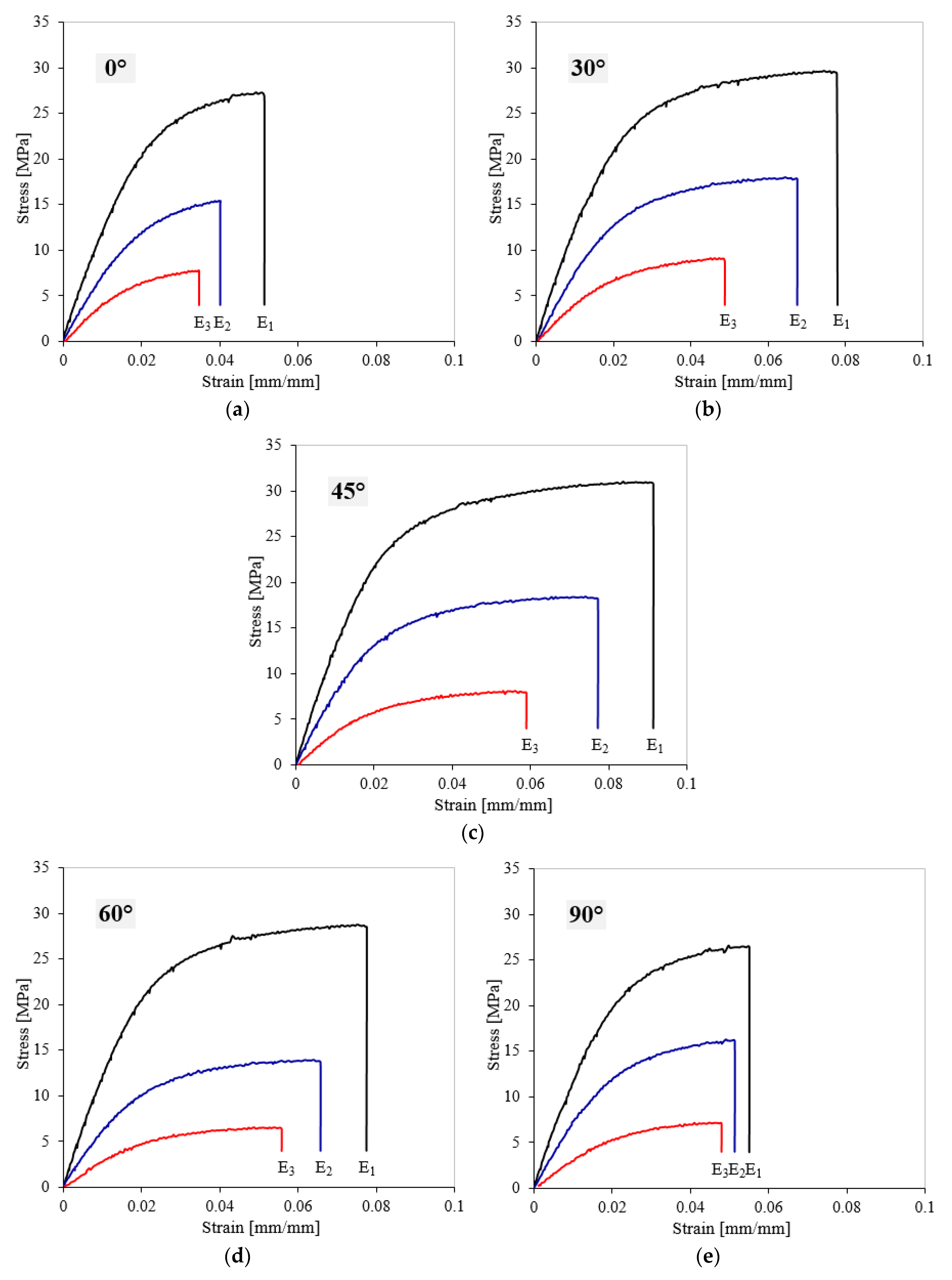
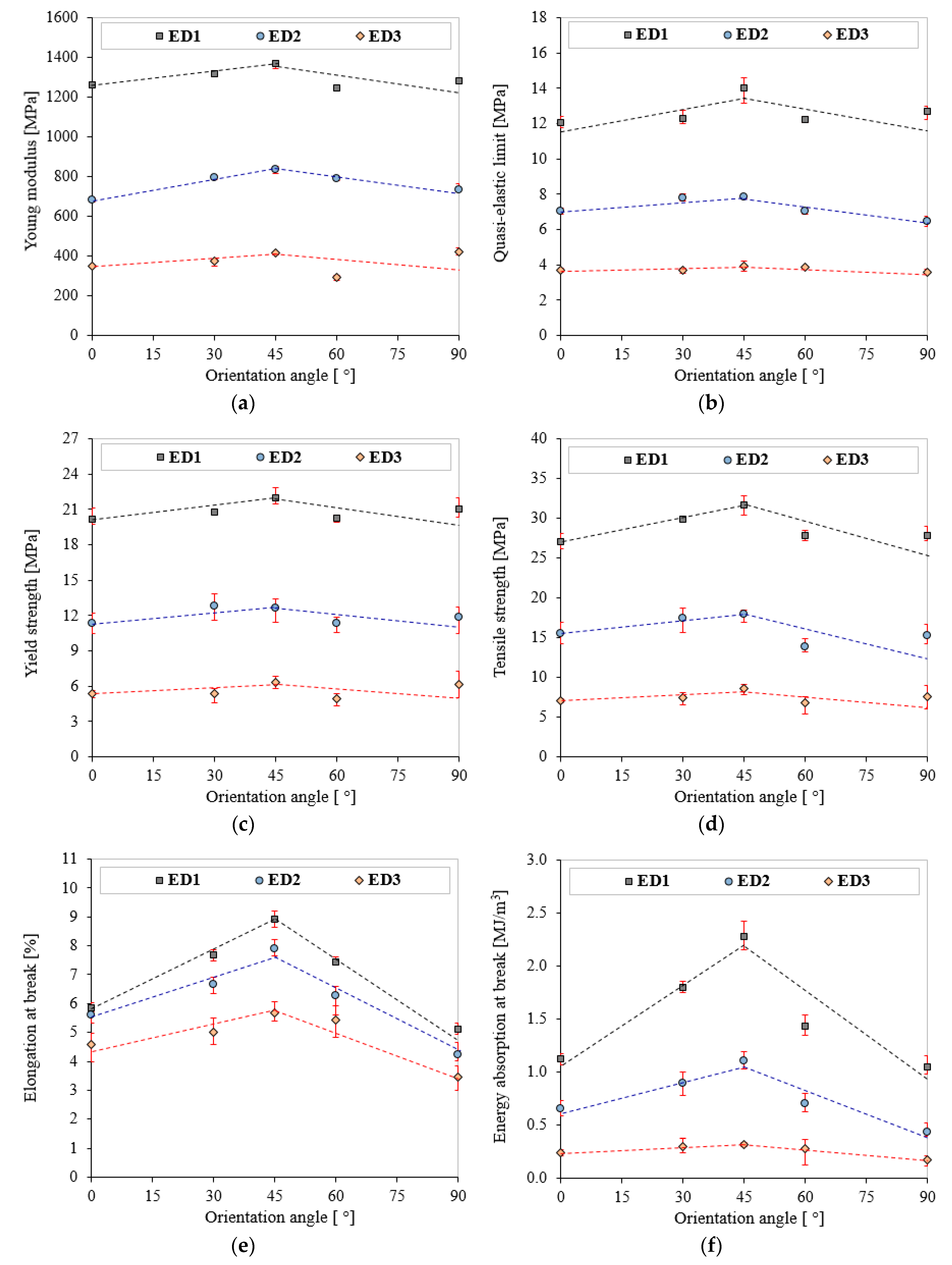
3. Results and Discussion
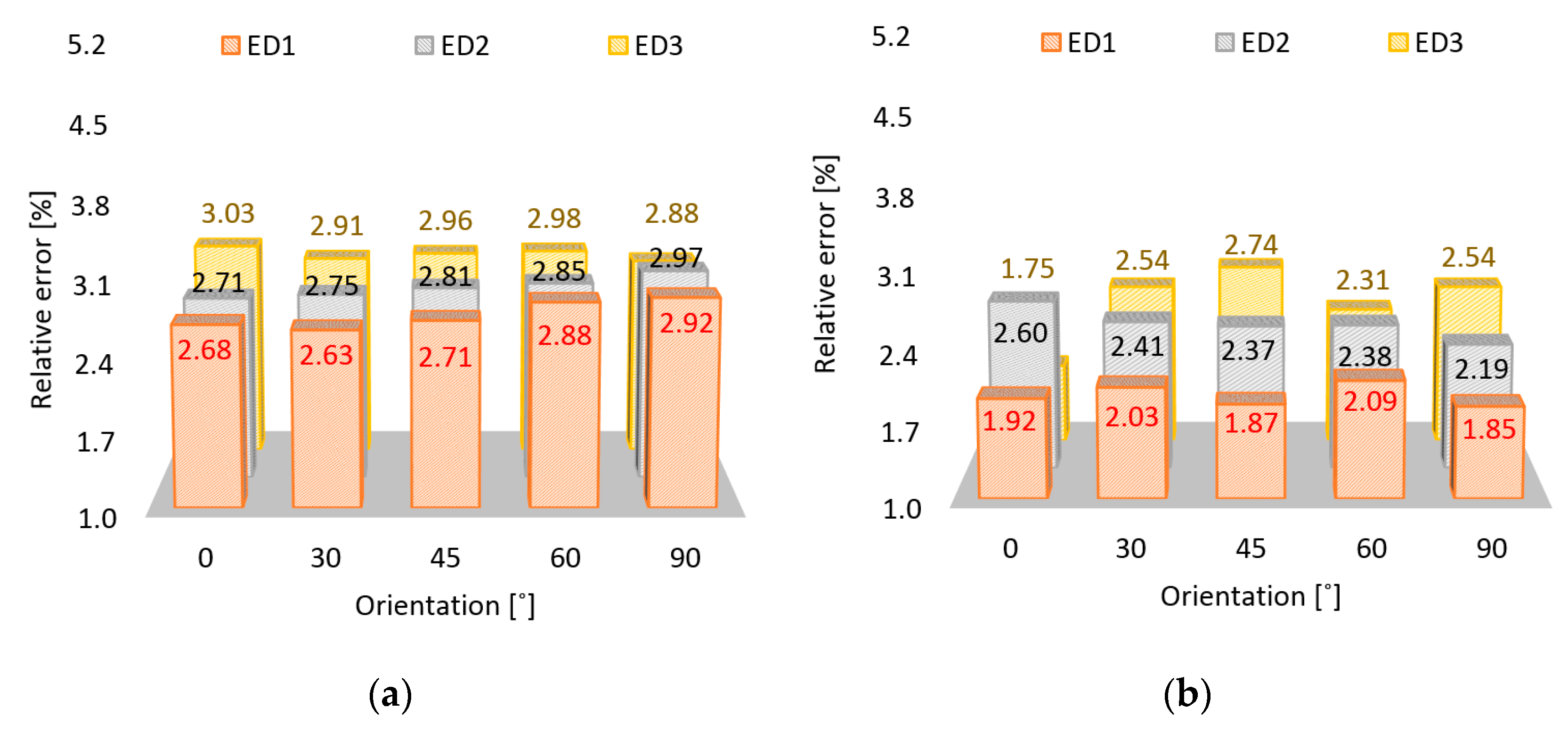
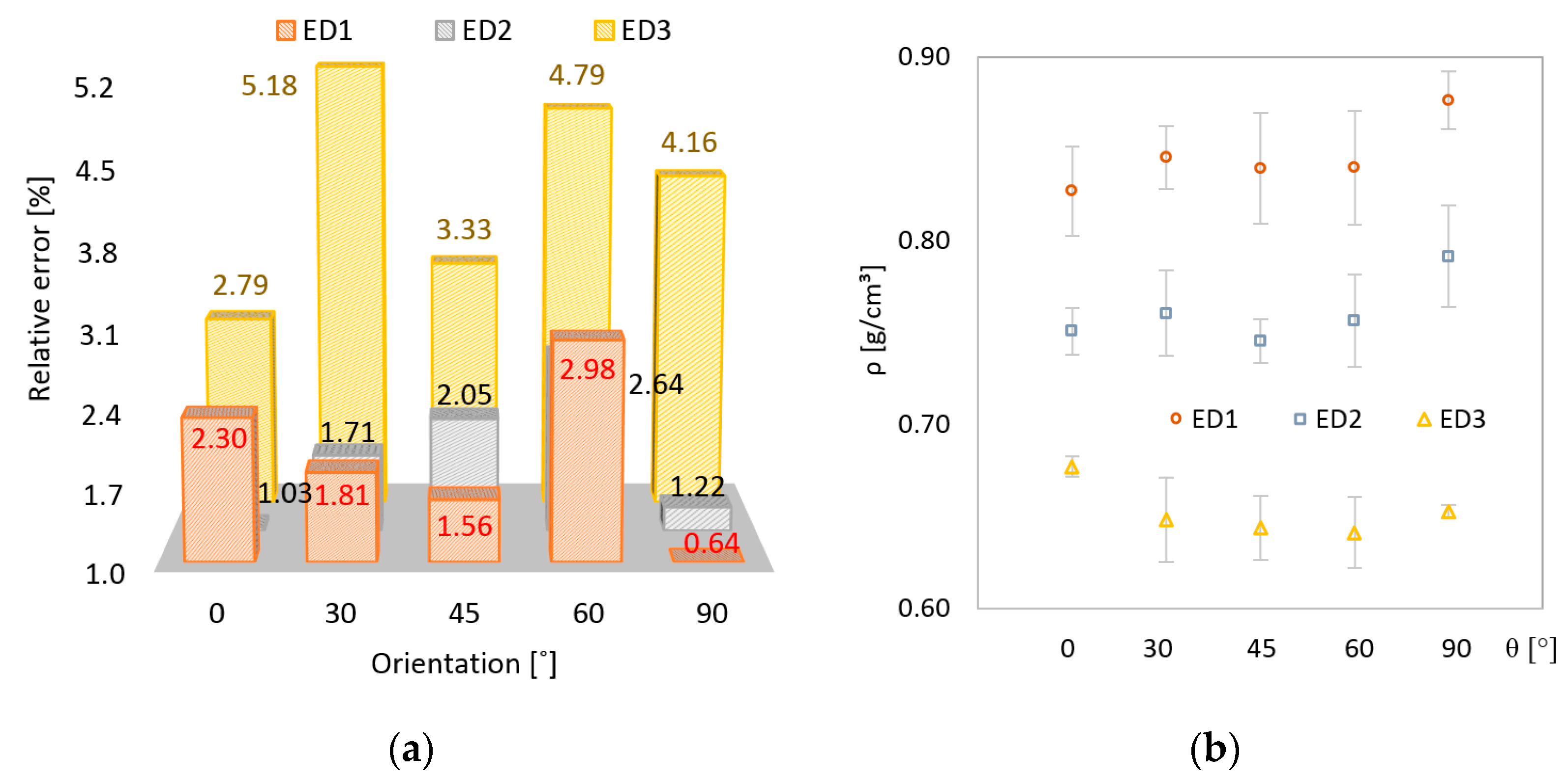
3.1. Geometric Properties
3.2. Tensile Properties
4. Conclusions
- The relative dimensional error for length (L), width (W), and thickness (H) ranged from 0.64% to 5.18%, with the larger error recorded for the lowest energy density (ED3).
- The largest variability was obtained for (H), measured along Z axis.
- The parameters L, ρ, and σm manifested positive linear correlations of 0.928, 0.974, and 0.998 with ED, respectively.
- Poor correlation with OA was determined for ρ and σm.
- The most promising tensile properties were obtained for ED1 at OA of 45°.
- One-way ANOVA analysis for L, ρ, and σm parameters showed statistically significant differences for ED1, ED2, and ED3 at every OA (p-value << 0.05).
Author Contributions
Funding
Conflicts of Interest
References
- Linul, E.; Vălean, C.; Linul, P.A. Compressive behavior of aluminum microfibers reinforced semi-rigid polyurethane foams. Polymers 2018, 10, 1298. [Google Scholar] [CrossRef] [PubMed]
- Nguyen-Tran, H.D.; Hoang, V.T.; Do, V.T.; Chun, D.M.; Yum, Y.J. Effect of multiwalled carbon nanotubes on the mechanical properties of Carbon Fiber-Reinforced Polyamide-6/Polypropylene composites for lightweight automotive parts. Materials 2018, 11, 429. [Google Scholar] [CrossRef] [PubMed]
- Aliha, M.R.M.; Linul, E.; Bahmani, A.; Marsavina, L. Experimental and theoretical fracture toughness investigation of PUR foams under mixed mode I + III loading. Polym. Test. 2018, 67, 75–83. [Google Scholar] [CrossRef]
- Linul, E.; Linul, P.A.; Vălean, C.; Marsavina, L.; Silaghi-Perju, D. Manufacturing and compressive mechanical behavior of reinforced Polyurethane Flexible (PUF) foams. In IOP Conference Series Materials Science Engineering; IOP Publishing: Bristol, UK, 2018; Volume 416, p. 012053. [Google Scholar]
- Chen, K.; Jia, M.; Sun, H.; Xue, P. Thermoplastic reaction injection pultrusion for continuous Glass Fiber-Reinforced Polyamide-6 composites. Materials 2019, 12, 463. [Google Scholar] [CrossRef] [PubMed]
- Linul, E.; Marsavina, L. Assesment of sandwich beams with rigid polyurethane foam core using failure-mode maps. Proc. Romanian Acad. Ser. A 2015, 16, 522–530. [Google Scholar]
- Salmoria, G.V.; Ahrens, C.H.; Klauss, P.; Paggi, R.A.; Oliveira, R.G.; Lago, A. Rapid manufacturing of polyethylene parts with controlled pore size gradients using Selective Laser Sintering. Mater. Res. 2007, 10, 211–214. [Google Scholar] [CrossRef]
- Pham, D.T.; Gault, R.S. A comparison of rapid prototyping technologies. Int. J. Mach. Tools Manuf. 1998, 38, 1257–1287. [Google Scholar] [CrossRef]
- Yeong, W.Y.; Chua, C.K. Implementing additive manufacturing for medical devices: A quality perspective. In Proceedings of the 6th International Conference on Advanced Research in Virtual and Rapid Prototyping, Leiria, Portugal, 1–5 October 2013; pp. 115–120. [Google Scholar]
- Es-Said, O.S.; Foyos, J.; Noorani, R.; Mendelson, M.; Marloth, R.; Pregger, B.A. Effect of layer orientation on mechanical properties of rapid prototyped samples. Mater. Manuf. Process. 2000, 15, 107–122. [Google Scholar] [CrossRef]
- Mousa, A.A. Experimental investigations of curling phenomenon in selective laser sintering process. Rapid Prototyp. J. 2006, 22, 405–415. [Google Scholar] [CrossRef]
- Griessbach, S.; Lach, R.; Grellmann, W. Structure–property correlations of laser sintered nylon 12 for dynamic dye testing of plastic parts. Polym. Test. 2010, 29, 1026–1030. [Google Scholar] [CrossRef]
- Lieneke, T.; Denzer, V.; Guido, A.; Adam, O.; Zimmer, D. Dimensional tolerances for additive manufacturing: Experimental investigation for Fused Deposition Modeling. Procedia CIRP 2016, 43, 286–291. [Google Scholar] [CrossRef]
- Kovácik, J.; Jerz, J.; Mináriková, N.; Marsavina, L.; Linul, E. Scaling of compression strength in disordered solids: Metallic foams. Frattura ed Integrita Strutturale 2016, 36, 55–62. [Google Scholar] [CrossRef]
- Dang, A.; Zhao, Z.; Tang, C.; Fang, C.; Kong, S.; Khan, M.; Li, T.; Zhao, T.; Li, H. Effect of Phenolic Resin on Micropores Development in Carbon Foam with High Performance. Materials 2019, 12, 1213. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Liu, C.; Coppola, B.; Barra, G.; Di Maio, L.; Incarnato, L.; Lafdi, K. Effect of porosity and crystallinity on 3D printed PLA properties. Polymers 2019, 11, 1487. [Google Scholar] [CrossRef]
- Pereira, A.B.; Fernandes, F.A.O.; de Morais, A.B.; Quintão, J. Mechanical strength of thermoplastic polyamide welded by Nd:YAG Laser. Polymers 2019, 11, 1381. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, L.; Fuh, J.Y.H.; Lee, H.P. Effect of porosity on mechanical properties of 3D printed polymers: Experiments and micromechanical modeling based on X-ray computed tomography analysis. Polymers 2019, 11, 1154. [Google Scholar] [CrossRef]
- Feng, L.; Wang, Y.; Wei, Q. PA12 powder recycled from SLS for FDM. Polymers 2019, 11, 727. [Google Scholar] [CrossRef]
- Hesse, N.; Dechet, M.A.; Bonilla, J.S.G.; Lübbert, C.; Roth, S.; Bück, A.; Schmidt, J.; Peukert, W. Analysis of tribo-charging during powder spreading in Selective Laser Sintering: Assessment of polyamide 12 powder ageing effects on charging behavior. Polymers 2019, 11, 609. [Google Scholar] [CrossRef]
- Pilipović, A.; Brajlih, T.; Drstvenšek, I. Influence of processing parameters on tensile properties of SLS polymer product. Polymers 2018, 10, 1208. [Google Scholar] [CrossRef]
- Dizon, J.R.C.; Espera, A.H.; Chen, Q.; Advincula, R.C. Mechanical characterization of 3D-printed polymers. Addit. Manuf. 2018, 20, 44–67. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Susmel, L. A material length scale–based methodology to assess static strength of notched additively manufactured polylactide (PLA). Fatigue Fract. Eng. Mater. Struct. 2018, 41, 2071–2098. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Berto, F. Fatigue strength of notched specimens made of Ti-6Al-4V produced by Selected Laser Melting technique. Procedia Struct. Integr. 2019, 13, 74–78. [Google Scholar] [CrossRef]
- Solberg, K.; Torgersen, J.; Berto, F. Fatigue behaviour of additively manufactured inconel 718 produced by Selective Laser Melting. Procedia Struct. Integr. 2018, 13, 1762–1767. [Google Scholar] [CrossRef]
- Arab, A.; Sktani, Z.D.I.; Zhou, Q.; Ahmad, Z.A.; Chen, P. Effect of MgO addition on the mechanical and dynamic properties of zirconia toughened alumina (ZTA) ceramics. Materials 2019, 12, 2440. [Google Scholar] [CrossRef]
- Stoia, D.I.; Linul, E.; Marsavina, L. Influence of manufacturing parameters on mechanical properties of porous materials by Selective Laser Sintering. Materials 2019, 12, 871. [Google Scholar] [CrossRef]
- Mengqi, Y.; Bourell, D. Orientation effects for laser sintered polyamide optically translucent parts. Rapid Prototyp. J. 2016, 22, 97–103. [Google Scholar]
- Galantucci, M.; Bodi, I.; Kacani, J.; Lavecchi, F. Analysis of dimensional performance for a 3D open-source printer based on fused deposition modeling technique. Procedia CIRP 2015, 28, 82–87. [Google Scholar] [CrossRef]
- Guido, A.O.A.; Detmar, Z. On design for additive manufacturing: Evaluating geometrical limitations. Rapid Prototyp. J. 2015, 21, 662–670. [Google Scholar]
- Goodridge, R.D.; Tuck, C.J.; Hague, R.J.M. Laser sintering of polyamides and other polymers. Prog. Mater. Sci. 2012, 57, 229–267. [Google Scholar] [CrossRef]
- ISO 13320. Particle Size Analysis—Laser Diffraction Methods, International Organization for Standardization; ISO: Geneva, Switzerland, 2009; p. 51. [Google Scholar]
- ISO 60. Plastics—Determination of Apparent Density of Material that can be Poured from a Specified Funnel, International Organization for Standardization; ISO: Geneva, Switzerland, 1977; p. 2. [Google Scholar]
- ISO 11357-1. Plastics—Differential Scanning Calorimetry (DSC)—Part 1: General Principles, International Organization for Standardization; ISO: Geneva, Switzerland, 2016; p. 33. [Google Scholar]
- ISO 306. Plastics—Thermoplastic Materials—Determination of Vicat Softening Temperature (VST), International Organization for Standardization; ISO: Geneva, Switzerland, 2004. [Google Scholar]
- ISO 10993-1. Biological Evaluation of Medical Devices—Part 1: Evaluation and Testing within a Risk Management Process; ISO: Geneva, Switzerland, 2018; p. 41. [Google Scholar]
- EOS GmbH Product Information. Available online: www.eos.info/material-p (accessed on 9 November 2018).
- ISO 527-1. Plastics-Determination of Tensile Properties—part 1: General Principles. International Organization for Standardization; ISO: Geneva, Switzerland, 2012; p. 23. [Google Scholar]
- Toth-Tascau, M.; Raduta, A.; Stoia, D.I.; Locovei, C. Influence of the energy density on the porosity of Polyamide parts in SLS process. In Proceedings of the 4th International Conference on Advanced Materials and Structures, Timisoara, Romania, 27–28 October 2011; pp. 400–405. [Google Scholar]
- Pilipović, A.; Valentan, B.; Šercer, M. Influence of SLS processing parameters according to the new mathematical model on flexural properties. Rapid Prototyp. J. 2016, 22, 258–268. [Google Scholar] [CrossRef]
- Ilkgün, Ö. Effects of Production Parameters on Porosity and Hole Properties in Laser Sintering Rapid Prototyping Process. Master’s Thesis, The Graduate School of Natural and Applied Sciences of Middle East Technical University, Ankara, Turkey, 2005. [Google Scholar]
- Rajak, D.K.; Pagar, D.D.; Menezes, P.L.; Linul, E. Fiber reinforced polymer composites: Manufacturing, properties, and applications. Polymers 2019, 11, 1667. [Google Scholar] [CrossRef] [PubMed]
- García Plaza, E.; López, P.J.N.; Torija, M.Á.C.; Muñoz, J.M.C. Analysis of PLA geometric properties processed by FFF additive manufacturing: Effects of process parameters and plate-extruder precision motion. Polymers 2019, 11, 1581. [Google Scholar] [CrossRef] [PubMed]
- Linul, E.; Marsavina, L. Prediction of fracture toughness for open cell polyurethane foams by finite element micromechanical analysis. Iran. Polym. J. 2011, 20, 736–746. [Google Scholar]
- Movahedi, N.; Linul, E. Quasi-static compressive behavior of the ex-situ aluminum-alloy foam-filled tubes under elevated temperature conditions. Mater. Lett. 2017, 206, 182–184. [Google Scholar] [CrossRef]
- Linul, E.; Serban, D.A.; Voiconi, T.; Marsavina, L.; Sadowski, T. Energy-absorption and efficiency diagrams of rigid PUR foams. Key Eng. Mater. 2014, 601, 246–249. [Google Scholar] [CrossRef]
- Movahedi, N.; Linul, E.; Marsavina, L. The temperature effect on the compressive behavior of closed-cell aluminum-alloy foams. J. Mater. Eng. Perform. 2018, 27, 99–108. [Google Scholar] [CrossRef]
- Linul, E.; Marsavina, L.; Vălean, C.; Bănică, R. Static and dynamic mode I fracture toughness of rigid PUR foams under room and cryogenic temperatures. Eng. Fract. Mech. 2019. [Google Scholar] [CrossRef]
- Rebollar, E.; Perez, S.; Hernandez, M.; Domingo, C.; Martin, M.; Ezquerra, T.A.; Garcia-Ruiz, J.P.; Castillejo, M. Physicochemical modifications accompanying UV laser induced surface structures on poly (ethylene terephthalate) and their effect on adhesion of mesenchymal cells. Phys. Chem. Chem. Phys. 2014, 16, 17551–17559. [Google Scholar] [CrossRef]
- Rodriguez-Rodriguez, A.; Rebollar, E.; Soccio, M.; Ezquerra, T.A.; Rueda, D.R.; Garcia-Ramos, J.V.; Castillejo, M.; Garcia-Gutierrez, M.C. Laser-Induced Periodic Surface Structures on Conjugated Polymers: Poly(3-hexylthiophene). Macromolecules 2015, 48, 4024–4031. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Rodriguez, A.; Gutiérrez-Fernández, E.; Garcia-Gutierrez, M.C.; Nogales, A.; Ezquerra, T.A.; Rebollar, E. Synergistic Effect of Fullerenes on the Laser-Induced Periodic Surface Structuring of Poly (3-Hexyl Thiophene). Polymers 2019, 11, 190. [Google Scholar] [CrossRef]

| Code | P [W] | v [mm/s] | ED [J/mm2] | d [mm] | h [mm] | T [°C] | Tr [°C] | t [mm] | SF [%] |
|---|---|---|---|---|---|---|---|---|---|
| E1 | 25 | 1500 | 0.067 | 0.15 | |||||
| E2 | 23 | 2000 | 0.046 | 0.25 | 169.5 | 159 | 0.1 | 2.3 | |
| E3 | 21 | 2500 | 0.034 |
| Parameter | Orientation Angle | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 30° | 45° | 60° | 90° | |||||||
| ED | SS | p-value | SS | p-value | SS | p-value | SS | p-value | SS | p-value | |
| BG | 0.5170 | 8 × 10−5 | 0.2737 | 1 × 10−4 | 0.2072 | 1 × 10−4 | 0.0618 | 4 × 10−3 | 0.0282 | 1 × 10−2 | |
| WG | 0.1362 | 0.0775 | 0.0598 | 0.0417 | 0.0276 | ||||||
| Parameter | Orientation Angle | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 30° | 45° | 60° | 90° | |||||||
| ED | SS | p-value | SS | p-value | SS | p-value | SS | p-value | SS | p-value | |
| BG | 0.0337 | 8 × 10−5 | 0.0585 | 8 × 10−5 | 0.0574 | 9 × 10−5 | 0.0596 | 2 × 10×4 | 0.0764 | 1 × 10−5 | |
| WG | 0.0015 | 0.0027 | 0.0027 | 0.0039 | 0.0020 | ||||||
| Orientation Angle α [°] | Young’s Modulus E [MPa] | Quasi-elastic Limit σe [MPa] | Yield Strength σc [MPa] | Tensile Strength σm [MPa] | Elongation at Break εb [%] | Energy Absorption Wb [MJ/m3] |
|---|---|---|---|---|---|---|
| 0 | 1253.9 | 12.21 | 19.86 | 26.70 | 5.59 | 1.15 |
| 1271.4 | 11.79 | 19.70 | 26.21 | 5.86 | 1.06 | |
| 1276.1 | 12.11 | 20.45 | 27.73 | 5.98 | 1.18 | |
| 1266.8 | 12.43 | 21.10 | 28.14 | 5.87 | 1.14 | |
| 1252.5 | 11.89 | 19.84 | 26.54 | 5.96 | 1.08 | |
| 30 | 1222.8 | 12.37 | 19.66 | 27.32 | 7.28 | 1.55 |
| 1266.2 | 12.82 | 21.03 | 28.98 | 7.46 | 1.70 | |
| 1264.8 | 12.59 | 20.63 | 28.75 | 7.77 | 1.77 | |
| 1229.5 | 11.95 | 19.79 | 26.58 | 6.24 | 1.05 | |
| 1263.4 | 11.37 | 19.93 | 27.69 | 8.48 | 1.11 | |
| 45 | 1375.3 | 14.07 | 22.33 | 32.16 | 8.93 | 2.38 |
| 1364.8 | 14.00 | 22.19 | 32.25 | 9.07 | 2.35 | |
| 1370.5 | 13.82 | 21.74 | 30.98 | 8.79 | 2.18 | |
| 1356.7 | 13.91 | 21.74 | 31.32 | 8.94 | 2.25 | |
| 1374.3 | 14.18 | 22.07 | 31.54 | 8.79 | 2.22 | |
| 60 | 1222.8 | 12.37 | 19.66 | 27.32 | 7.28 | 1.55 |
| 1266.2 | 12.82 | 21.03 | 28.98 | 7.46 | 1.70 | |
| 1264.8 | 12.59 | 20.63 | 28.75 | 7.77 | 1.77 | |
| 1229.5 | 11.95 | 19.79 | 26.58 | 6.24 | 1.05 | |
| 1263.4 | 11.37 | 19.93 | 27.69 | 8.48 | 1.11 | |
| 90 | 1273.7 | 12.31 | 21.76 | 28.71 | 5.34 | 1.15 |
| 1282.2 | 12.26 | 20.65 | 27.14 | 5.25 | 1.05 | |
| 1276.7 | 13.01 | 20.62 | 27.18 | 4.96 | 0.98 | |
| 1291.3 | 12.89 | 21.96 | 28.98 | 4.94 | 1.03 | |
| 1278.7 | 12.96 | 20.32 | 27.35 | 5.13 | 1.02 |
| Orientation Angle α [°] | Young’s Modulus E [MPa] | Quasi-elastic Limit σe [MPa] | Yield Strength σc [MPa] | Tensile Strength σm [MPa] | Elongation at Break εb [%] | Energy Absorption Wb [MJ/m3] |
|---|---|---|---|---|---|---|
| 0 | 674.98 | 7.21 | 10.43 | 14.29 | 5.76 | 0.59 |
| 693.32 | 6.86 | 12.23 | 16.91 | 5.48 | 0.73 | |
| 674.39 | 7.07 | 10.9 | 15.13 | 5.71 | 0.67 | |
| 674.15 | 6.84 | 10.92 | 14.93 | 5.47 | 0.65 | |
| 692.49 | 7.16 | 12.03 | 16.38 | 5.53 | 0.64 | |
| 30 | 804.77 | 7.73 | 12.83 | 16.79 | 6.76 | 0.93 |
| 792.98 | 8.04 | 13.81 | 18.41 | 6.77 | 1.00 | |
| 784.55 | 7.66 | 12.76 | 18.21 | 6.46 | 0.87 | |
| 797.62 | 7.61 | 13.11 | 17.06 | 6.89 | 0.92 | |
| 799.66 | 7.89 | 11.61 | 16.82 | 6.35 | 0.77 | |
| 45 | 836.94 | 7.68 | 12.88 | 18.04 | 8.21 | 1.20 |
| 849.08 | 7.92 | 13.18 | 19.18 | 8.10 | 1.08 | |
| 837.14 | 8.01 | 13.15 | 17.90 | 7.72 | 1.12 | |
| 836.20 | 7.75 | 12.04 | 18.24 | 7.26 | 1.03 | |
| 826.66 | 7.82 | 11.89 | 16.11 | 8.22 | 1.10 | |
| 60 | 781.20 | 7.11 | 11.79 | 14.26 | 6.22 | 0.62 |
| 800.66 | 7.08 | 12.14 | 13.83 | 6.45 | 0.70 | |
| 806.64 | 7.03 | 10.11 | 13.95 | 6.02 | 0.71 | |
| 771.67 | 6.92 | 11.82 | 14.51 | 6.56 | 0.69 | |
| 800.60 | 6.94 | 10.75 | 12.94 | 6.04 | 0.78 | |
| 90 | 736.41 | 6.49 | 12.07 | 15.45 | 4.01 | 0.42 |
| 721.53 | 6.73 | 10.46 | 14.33 | 4.15 | 0.52 | |
| 737.56 | 6.38 | 11.33 | 14.19 | 4.01 | 0.41 | |
| 722.98 | 6.52 | 12.55 | 15.77 | 4.43 | 0.44 | |
| 763.34 | 6.19 | 12.68 | 16.68 | 4.64 | 0.40 |
| Orientation Angle α [°] | Young’s Modulus E [MPa] | Quasi-elastic Limit σe [MPa] | Yield Strength σc [MPa] | Tensile Strength σm [MPa] | Elongation at Break εb [%] | Energy Absorption Wb [MJ/m3] |
|---|---|---|---|---|---|---|
| 0 | 347.09 | 3.58 | 5.30 | 7.29 | 4.98 | 0.26 |
| 350.12 | 3.79 | 5.01 | 6.86 | 3.97 | 0.26 | |
| 349.14 | 3.67 | 5.33 | 7.19 | 4.81 | 0.24 | |
| 350.57 | 3.76 | 5.42 | 7.22 | 4.25 | 0.21 | |
| 344.46 | 3.65 | 5.60 | 6.82 | 4.88 | 0.23 | |
| 30 | 358.74 | 3.76 | 4.82 | 7.04 | 4.88 | 0.31 |
| 380.32 | 3.78 | 4.76 | 5.98 | 5.49 | 0.37 | |
| 370.57 | 3.54 | 5.61 | 7.88 | 4.60 | 0.24 | |
| 381.04 | 3.77 | 5.73 | 8.05 | 4.76 | 0.29 | |
| 383.39 | 3.62 | 5.80 | 8.14 | 5.29 | 0.29 | |
| 45 | 428.82 | 3.98 | 6.69 | 9.17 | 5.70 | 0.29 |
| 413.28 | 3.91 | 6.82 | 9.28 | 3.85 | 0.16 | |
| 428.56 | 3.93 | 6.30 | 8.40 | 6.35 | 0.37 | |
| 419.73 | 3.95 | 6.36 | 8.59 | 6.50 | 0.40 | |
| 393.71 | 3.98 | 5.60 | 7.77 | 5.91 | 0.35 | |
| 60 | 294.71 | 3.85 | 5.41 | 7.28 | 5.22 | 0.27 |
| 296.92 | 3.93 | 5.16 | 7.17 | 5.85 | 0.31 | |
| 296.65 | 4.11 | 5.03 | 6.96 | 5.35 | 0.27 | |
| 281.21 | 3.56 | 4.35 | 6.01 | 5.18 | 0.29 | |
| 294.73 | 3.94 | 4.79 | 6.58 | 5.58 | 0.27 | |
| 90 | 405.36 | 3.61 | 6.29 | 7.98 | 3.84 | 0.20 |
| 441.70 | 3.52 | 6.47 | 7.77 | 3.46 | 0.18 | |
| 418.94 | 3.49 | 5.04 | 6.02 | 3.01 | 0.11 | |
| 412.91 | 3.53 | 5.45 | 6.77 | 3.51 | 0.15 | |
| 436.97 | 3.75 | 7.30 | 9.03 | 3.49 | 0.21 |
| Parameter | Orientation Angle | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 30° | 45° | 60° | 90° | |||||||
| ED | SS | p-value | SS | p-value | SS | p-value | SS | p-value | SS | p-value | |
| BG | 1006.7 | 2 × 10−13 | 1045.2 | 6 × 10-13 | 1340.3 | 3 × 10−14 | 1148.5 | 3 × 10−14 | 1055.4 | 3 × 10−12 | |
| WG | 7.6139 | 9.8336 | 7.6750 | 6.5014 | 12.9031 | ||||||
| Outcome Parameter | Technological Parameters | |||
|---|---|---|---|---|
| Energy Density (ED) | Orientation Angle | |||
| OA (at ED1) | OA (at ED1) | OA (at ED1) | ||
| Length (L) | 0.9285 | −0.7640 | −0.8412 | 0.4529 |
| Density (ρ) | 0.9744 | 0.5480 | 0.5021 | −0.4415 |
| Tensile strength (σm) | 0.9988 | 0.1307 | −0.2569 | 0.0730 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stoia, D.I.; Marşavina, L.; Linul, E. Correlations between Process Parameters and Outcome Properties of Laser-Sintered Polyamide. Polymers 2019, 11, 1850. https://doi.org/10.3390/polym11111850
Stoia DI, Marşavina L, Linul E. Correlations between Process Parameters and Outcome Properties of Laser-Sintered Polyamide. Polymers. 2019; 11(11):1850. https://doi.org/10.3390/polym11111850
Chicago/Turabian StyleStoia, Dan Ioan, Liviu Marşavina, and Emanoil Linul. 2019. "Correlations between Process Parameters and Outcome Properties of Laser-Sintered Polyamide" Polymers 11, no. 11: 1850. https://doi.org/10.3390/polym11111850
APA StyleStoia, D. I., Marşavina, L., & Linul, E. (2019). Correlations between Process Parameters and Outcome Properties of Laser-Sintered Polyamide. Polymers, 11(11), 1850. https://doi.org/10.3390/polym11111850








