Modeling the Stiffness of Coupled and Uncoupled Recycled Cotton Fibers Reinforced Polypropylene Composites
Abstract
1. Introduction
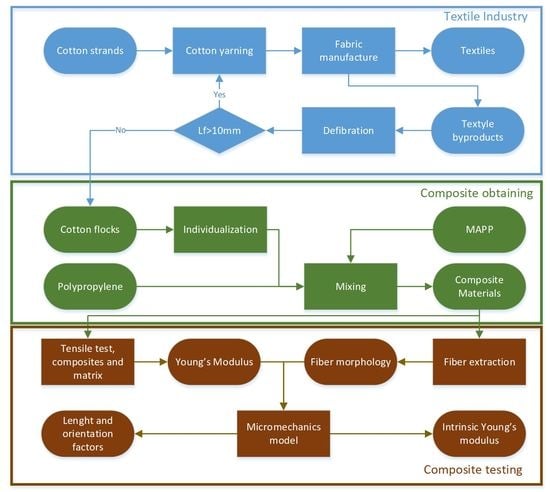
2. Materials and methods
2.1. Materials
2.2. Cotton Flocks Treatment and Composites Preparation
2.3. Composite and Standard Specimen Preparation
2.4. Mechanical Test
2.5. Morphologic Analysis of the Reinforcements
3. Results and Discussion
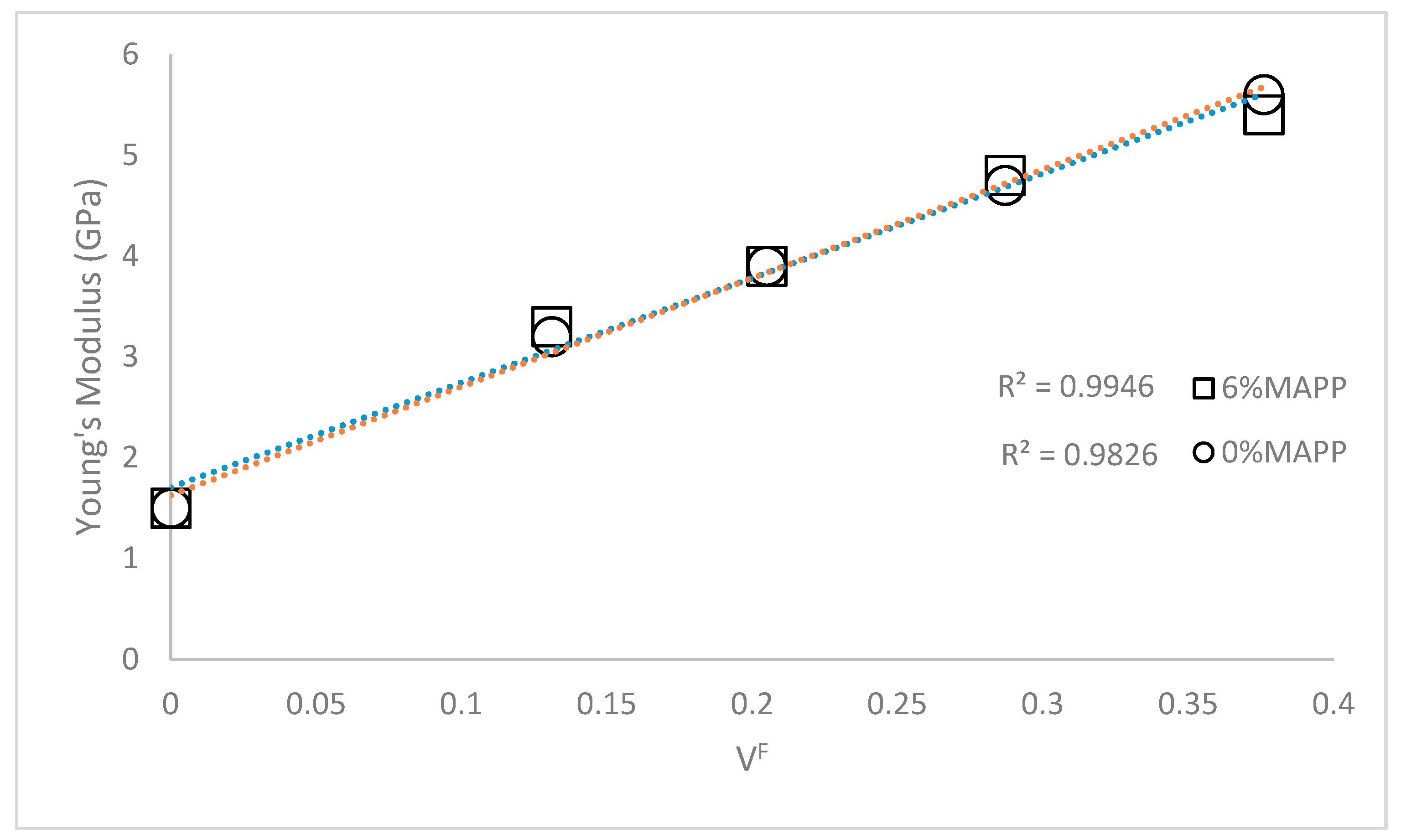
3.1. Young’s Modulus of the Composites
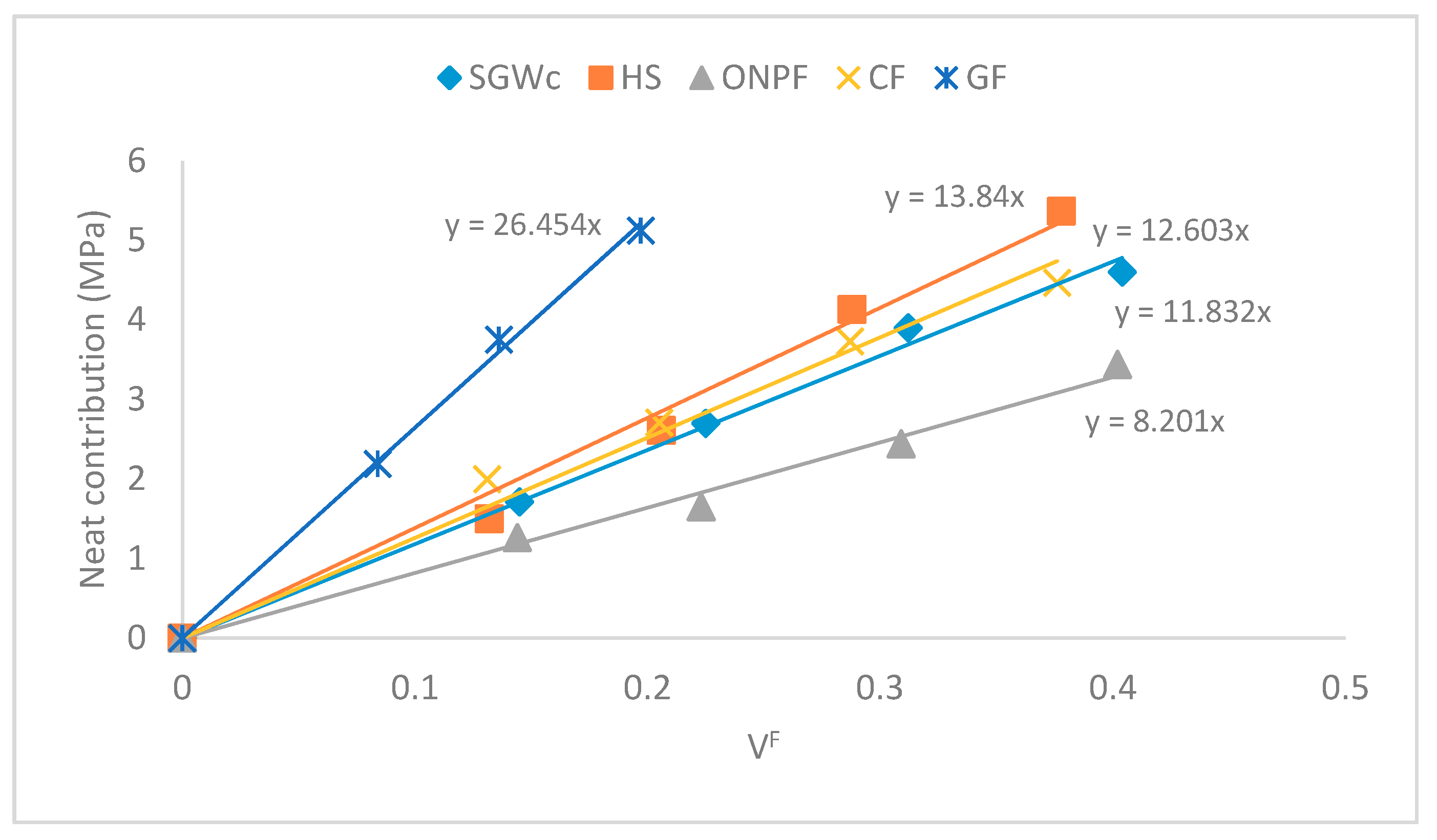
3.2. Neat Contribution of the Reinforcements
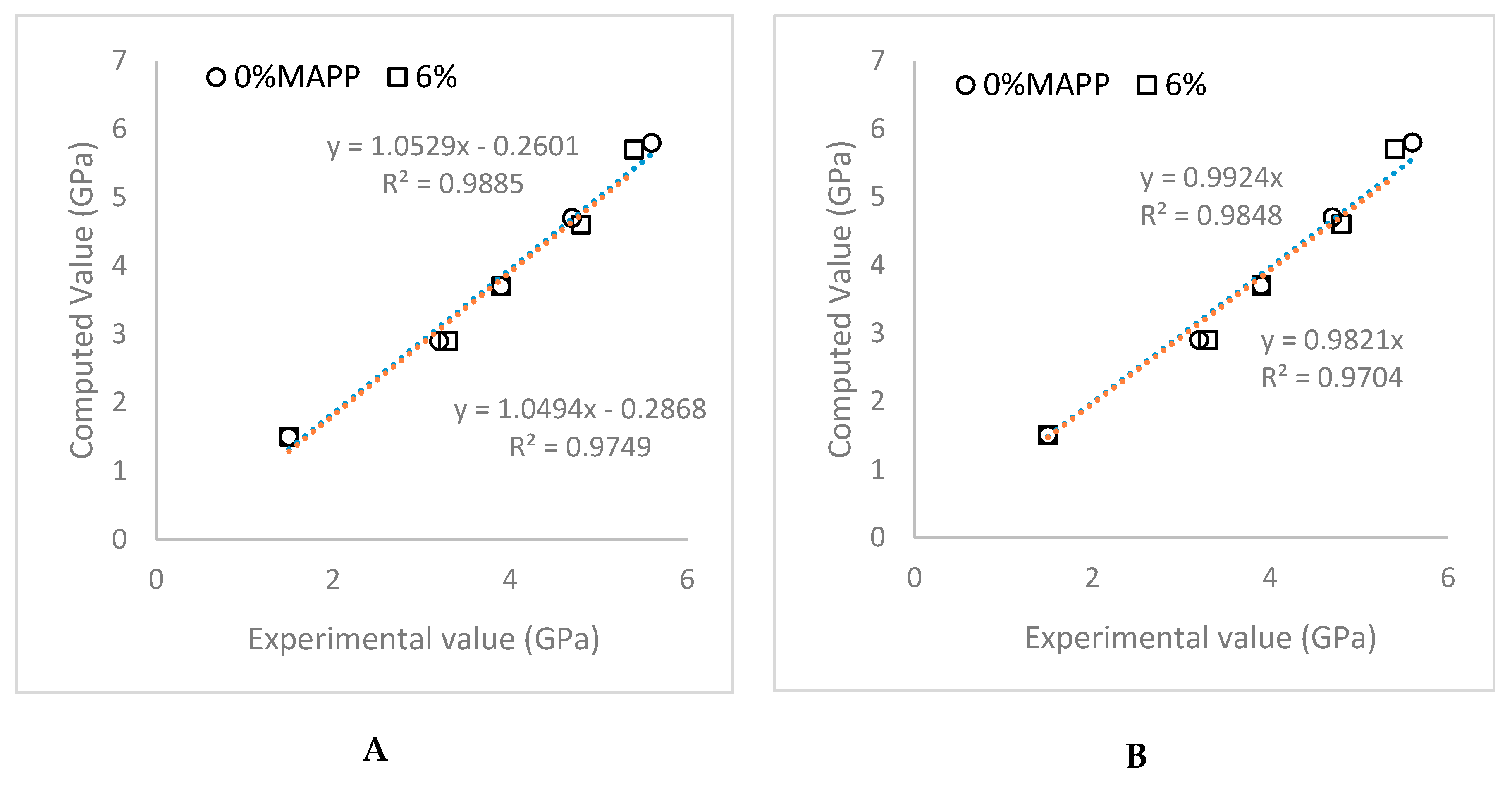
3.3. Micromechanics Analysis of the Young’s Modulus
3.4. Effect of the Morphology of the Reinforcements
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Anastas, P.T.; Warner, J. Green Chemistry: Theory and Practice; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Schumann, A. Plastics-the Environmentally Friendly Design Material. ATZ Heavy Duty Worldw. 2019, 12, 74. [Google Scholar] [CrossRef]
- Ferreira, F.V.; Pinheiro, I.F.; Mariano, M.; Cividanes, L.S.; Costa, J.C.; Nascimento, N.R.; Kimura, S.P.; Neto, J.C.; Lona, L.M. Environmentally friendly polymer composites based on PBAT reinforced with natural fibers from the amazon forest. Polym. Compos. 2019. [Google Scholar] [CrossRef]
- Reixach, R.; Espinach, F.X.; Franco-Marquès, E.; Ramirez de Cartagena, F.; Pellicer, N.; Tresserras, J.; Mutjé, P. Modeling of the tensile moduli of mechanical, thermomechanical, and chemi-thermomechanical pulps from orange tree pruning. Polym. Compos. 2013, 34, 1840–1846. [Google Scholar] [CrossRef]
- Serrano, A.; Espinach, F.X.; Tresserras, J.; del Rey, R.; Pellicer, N.; Mutje, P. Macro and micromechanics analysis of short fiber composites stiffness: The case of old newspaper fibers-polypropylene composites. Mater.Des. 2014, 55, 319–324. [Google Scholar] [CrossRef]
- Espinach, F.X.; Chamorro-Trenado, M.A.; Llorens, J.; Tresserras, J.; Pellicer, N.; Vilaseca, F.; Pèlach, A. Study of the Flexural Modulus and the Micromechanics of Old Newspaper Reinforced Polypropylene Composites. BioResources 2019, 14, 3578–3593. [Google Scholar]
- Serra, A.; Tarrés, Q.; Llop, M.; Reixach, R.; Mutjé, P.; Espinach, F.X. Recycling dyed cotton textile byproduct fibers as polypropylene reinforcement. Text. Res. J. 2019, 89, 2113–2125. [Google Scholar] [CrossRef]
- Petrucci, R.; Nisini, E.; Puglia, D.; Sarasini, F.; Rallini, M.; Santulli, C.; Minak, G.; Kenny, J. Tensile and fatigue characterisation of textile cotton waste/polypropylene laminates. Compos. Pt B-Eng. 2015, 81, 84–90. [Google Scholar] [CrossRef]
- Kallel, T.K.; Taktak, R.; Guermazi, N.; Mnif, N. Mechanical and structural properties of glass fiber-reinforced polypropylene (PPGF) composites. Polym. Compos. 2018, 39, 3497–3508. [Google Scholar] [CrossRef]
- Thomason, J.; Jenkins, P.; Yang, L. Glass Fibre Strength—A Review with Relation to Composite Recycling. Fibers 2016, 4, 18. [Google Scholar] [CrossRef]
- Espinach, F.X.; Julian, F.; Verdaguer, N.; Torres, L.; Pelach, M.A.; Vilaseca, F.; Mutje, P. Analysis of tensile and flexural modulus in hemp strands/polypropylene composites. Compos. Pt. B-Eng. 2013, 47, 339–343. [Google Scholar] [CrossRef]
- Vilaseca, F.; Valadez-Gonzalez, A.; Herrera-Franco, P.J.; Pelach, M.A.; Lopez, J.P.; Mutje, P. Biocomposites from abaca strands and polypropylene. Part I: Evaluation of the tensile properties. Bioresource Technol. 2010, 101, 387–395. [Google Scholar] [CrossRef] [PubMed]
- Mishra, R.; Behera, B.; Militky, J. Recycling of Textile Waste Into Green Composites: Performance Characterization. Polym. Compos. 2014, 35, 1960–1967. [Google Scholar] [CrossRef]
- Lopez, J.P.; Mutje, P.; Pelach, M.A.; El Mansouri, N.E.; Boufi, S.; Vilaseca, F. Analysis of the tensile modulus of PP composites reinforced with Stone grounwood fibers from softwood. BioResources 2012, 7, 1310–1323. [Google Scholar] [CrossRef]
- Espinach, F.X.; Mendez, J.A.; Granda, L.A.; Pelach, M.A.; Delgado-Aguilar, M.; Mutje, P. Bleached kraft softwood fibers reinforced polylactic acid composites, tensile and flexural strengths. In Natural Fibre-Reinforced Biodegradable and Bioresorbable Polymer Composites; Lau, A., Ed.; Woodhead Publishing Limited: Cambridge, UK, 2017. [Google Scholar]
- Araújo, R.S.; Rezende, C.C.; Marques, M.F.V.; Ferreira, L.C.; Russo, P.; Emanuela Errico, M.; Avolio, R.; Avella, M.; Gentile, G. Polypropylene-based composites reinforced with textile wastes. J. Appl. Polym. Sci. 2017, 134, 45060. [Google Scholar] [CrossRef]
- Monteiro, S.N.; Lopes, F.P.D.; Barbosa, A.P.; Bevitori, A.B.; Da Silva, I.L.A.; Da Costa, L.L. Natural Lignocellulosic Fibers as Engineering Materials-An Overview. Metall. Mater. Trans. A-Phys. Metall. Mater. Sci. 2011, 42, 2963–2974. [Google Scholar] [CrossRef]
- Reddy, N.; Yang, Y.Q. Properties and potential applications of natural cellulose fibers from the bark of cotton stalks. Bioresource Technol. 2009, 100, 3563–3569. [Google Scholar] [CrossRef]
- De Silva, R.; Byrne, N. Utilization of cotton waste for regenerated cellulose fibres: Influence of degree of polymerization on mechanical properties. Carbohyd. Polym. 2017, 174, 89–94. [Google Scholar] [CrossRef]
- Serra, A.; Tarrés, Q.; Claramunt, J.; Mutjé, P.; Ardanuy, M.; Espinach, F. Behavior of the interphase of dyed cotton residue flocks reinforced polypropylene composites. Compos. Pt. B-Eng. 2017, 128, 200–207. [Google Scholar] [CrossRef]
- Ryu, C.; Phan, A.N.; Sharifi, V.N.; Swithenbank, J. Combustion of textile residues in a packed bed. Exp. Therm. Fluid Sci. 2007, 31, 887–895. [Google Scholar] [CrossRef]
- Jha, M.K.; Kumar, V.; Maharaj, L.; Singh, R.J. Studies on leaching and recycling of zinc from rayon waste sludge. Ind. Eng. Chem. Res. 2004, 43, 1284–1295. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Franciszczak, P.; Osman, Z.; Elbadawi, M. Polypropylene biocomposites reinforced with softwood, abaca, jute, and kenaf fibers. Ind. Crop. Prod. 2015, 70, 91–99. [Google Scholar] [CrossRef]
- Lopez, J.P.; Boufi, S.; El Mansouri, N.E.; Mutje, P.; Vilaseca, F. PP composites based on mechanical pulp, deinked newspaper and jute strands: A comparative study. Compos. Pt. B-Eng. 2012, 43, 3453–3461. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Mamun, A.A.; Faruk, O. Abaca fibre reinforced PP composites and comparison with jute and flax fibre PP composites. Express Polym. Lett. 2007, 1, 755–762. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Gassan, J. Composites reinforced with cellulose based fibres. Prog. Polym. Sci. 1999, 24, 221–274. [Google Scholar] [CrossRef]
- Rogovina, S.; Prut, E.; Berlin, A. Composite Materials Based on Synthetic Polymers Reinforced with Natural Fibers. Polym. Sci. Ser. A 2019, 61, 417–438. [Google Scholar] [CrossRef]
- Faruk, O.; Bledzki, A.K.; Fink, H.P.; Sain, M. Progress report on natural fiber reinforced composites. Macromol. Mater. Eng. 2014, 299, 9–26. [Google Scholar] [CrossRef]
- Hirsch, T. Modulus of elasticity of concrete affected by elastic moduli of cement paste matrix and aggregate. J. Am. Concr. Inst. 1962, 59, 427–451. [Google Scholar] [CrossRef]
- Halpin, J.C.; Tsai, S.W. Effects of Environmental Factors on Composite Materials; Technical Report AFML-TR-67-423; National Institute of Occupational Safety and Health: Cincinnati, OH, USA, 1969.
- Halpin, J.C.; Pagano, N.J. The Laminate Approximation for Randomly Oriented Fibrous Composites. J. Compos. Mater. 1969, 3, 720–724. [Google Scholar] [CrossRef]
- Granda, L.A.; Espinach, F.X.; Mendez, J.A.; Tresserras, J.; Delgado-Aguilar, M.; Mutje, P. Semichemical fibres of Leucaena collinsii reinforced polypropylene composites: Young’s modulus analysis and fibre diameter effect on the stiffness. Compos. Pt. B-Eng. 2016, 92, 332–337. [Google Scholar] [CrossRef]
- Tarrés, Q.; Vilaseca, F.; Herrera-Franco, P.J.; Espinach, F.X.; Delgado-Aguilar, M.; Mutjé, P. Interface and micromechanical characterization of tensile strength of bio-based composites from polypropylene and henequen strands. Ind. Crop. Prod. 2019, 132, 319–326. [Google Scholar] [CrossRef]
- Julian, F.; Mendez, J.A.; Espinach, F.X.; Verdaguer, N.; Mutje, P.; Vilaseca, F. Bio-based composites from stone groundwood applied to new product development. BioResources 2012, 7, 5829–5842. [Google Scholar] [CrossRef]
- Oliver-Ortega, H.; Chamorro-Trenado, M.À.; Soler, J.; Mutjé, P.; Vilaseca, F.; Espinach, F.X. Macro and micromechanical preliminary assessment of the tensile strength of particulate rapeseed sawdust reinforced polypropylene copolymer biocomposites for its use as building material. Constr. Build. Mater. 2018, 168, 422–430. [Google Scholar] [CrossRef]
- Serrano, A.; Espinach, F.X.; Tresserras, J.; Pellicer, N.; Alcala, M.; Mutje, P. Study on the technical feasibility of replacing glass fibers by old newspaper recycled fibers as polypropylene reinforcement. J. Clean. Prod. 2014, 65, 489–496. [Google Scholar] [CrossRef]
- Shah, D.U.; Nag, R.K.; Clifford, M.J. Why do we observe significant differences between measured and ‘back-calculated’ properties of natural fibres? Cellulose 2016, 23, 1481–1490. [Google Scholar] [CrossRef]
- Facca, A.G.; Kortschot, M.T.; Yan, N. Predicting the elastic modulus of natural fibre reinforced thermoplastics. Compos. Pt. A-Appl. Sci. 2006, 37, 1660–1671. [Google Scholar] [CrossRef]
- Serrano, A.; Espinach, F.X.; Julian, F.; del Rey, R.; Mendez, J.A.; Mutje, P. Estimation of the interfacial shears strength, orientation factor and mean equivalent intrinsic tensile strength in old newspaper fiber/polypropylene composites. Compos. Pt. B-Eng. 2013, 50, 232–238. [Google Scholar] [CrossRef]
- Vallejos, M.E.; Espinach, F.X.; Julian, F.; Torres, L.; Vilaseca, F.; Mutje, P. Micromechanics of hemp strands in polypropylene composites. Compos. Sci. Technol. 2012, 72, 1209–1213. [Google Scholar] [CrossRef]
- Krenchel, H. Fibre Reinforcement; Akademisk Forlag: Copenhagen, Denmark, 1964. [Google Scholar]
- Del Rey, R.; Serrat, R.; Alba, J.; Perez, I.; Mutje, P.; Espinach, F.X. Effect of Sodium Hydroxide Treatments on the Tensile Strength and the Interphase Quality of Hemp Core Fiber-Reinforced Polypropylene Composites. Polymers 2017, 9, 377. [Google Scholar] [CrossRef]
- Reixach, R.; Franco-Marquès, E.; El Mansouri, N.-E.; de Cartagena, F.R.; Arbat, G.; Espinach, F.X.; Mutjé, P. Micromechanics of Mechanical, Thermomechanical, and Chemi-Thermomechanical Pulp from Orange Tree Pruning as Polypropylene Reinforcement: A Comparative Study. BioResources 2013, 8, 3231–3246. [Google Scholar] [CrossRef]
- Fukuda, H.; Kawata, K. On Young’s modulus of short fibre composites. Fibre Sci. Technol. 1974, 7, 207–222. [Google Scholar] [CrossRef]
- Espinach, F.X.; Julián, F.; Alcalà, M.; Tresserras, J.; Mutjé, P. High stiffness performance alpha-grass pulp fiber reinforced thermoplastic starch-based fully biodegradable composites. BioResources 2013, 9, 738–755. [Google Scholar] [CrossRef]
- Thomason, J.L. The influence of fibre length and concentration on the properties of glass fibre reinforced polypropylene: 5. Injection moulded long and short fibre PP. Compos. Pt. A-Appl. Sci. 2002, 33, 1641–1652. [Google Scholar] [CrossRef]
- Lopez, J.P.; Mendez, J.A.; Espinach, F.X.; Julian, F.; Mutje, P.; Vilaseca, F. Tensile Strength characteristics of Polypropylene composites reinforced with Stone Groundwood fibers from Softwood. BioResources 2012, 7, 3188–3200. [Google Scholar] [CrossRef]
| 0%MAPP | 6%MAPP | ||||
|---|---|---|---|---|---|
| WF | VF | EtC (GPa) | σtC (MPa) | EtC (GPa) | σtC (MPa) |
| 0 | 0 | 1.5 ± 0.1 | 27.6 ± 0.5 | 1.5 ± 0.1 | 27.6 ± 0.5 |
| 20% | 0.131 | 3.2 ± 0.1 | 35.0 ± 0.5 | 3.3 ± 0.1 | 41.7 ± 0.7 |
| 30% | 0.205 | 3.9 ± 0.2 | 38.2 ± 0.8 | 3.9 ± 0.1 | 47.1 ±0.7 |
| 40% | 0.287 | 4.7 ± 0.2 | 41.7 ± 0.8 | 4.8 ± 0.2 | 53.6 ± 1.0 |
| 50% | 0.376 | 5.6 ± 0.2 | 45.4 ± 1.1 | 5.4 ± 0.2 | 58.3 ± 1.2 |
| SGW | HS | ONPF | GF | |
|---|---|---|---|---|
| 20% | 2.7 ± 0.1 | 2.8 ± 0.1 | 2.8 ± 0.1 | 4.1 ± 0.1 |
| 30% | 3.5 ± 0.1 | 3.8 ± 0.1 | 3.8 ± 0.1 | 5.7 ± 0.1 |
| 40% | 4.3 ± 0.1 | 5.2 ± 0.1 | 4.2 ± 0.1 | 7.7 ± 0.1 |
| 50% | 5.2 ± 0.1 | 6.3 ± 0.1 | 5.3 ± 0.1 | - |
| VF | EtF (GPa) | ƞe | ƞl | ƞo | αo |
|---|---|---|---|---|---|
| 0.131 | 31.48 | 0.52 | 0.89 | 0.58 | 48.8 |
| 0.205 | 28.06 | 0.47 | 0.89 | 0.53 | 53.3 |
| 0.287 | 26.48 | 0.45 | 0.89 | 0.51 | 55.1 |
| 0.376 | 25.46 | 0.45 | 0.90 | 0.49 | 56.2 |
| Mean | 27.87 ± 2.63 | 0.47 ± 0.03 | 0.89 ± 0.01 | 0.53 ± 0.04 | 53.3 ± 3.3 |
| Experimental | Tsai-Pagano | Error (GPa) | Error (%) | |||||
|---|---|---|---|---|---|---|---|---|
| VF | 0% MAPP | 6% MAPP | 0% MAPP | 6% MAPP | 0% MAPP | 6% MAPP | 0% MAPP | 6% MAPP |
| 0.131 | 3.2 | 3.3 | 2.9 | 2.9 | 0.3 | 0.4 | 9.4 | 12.1 |
| 0.205 | 3.9 | 3.9 | 3.7 | 3.7 | 0.2 | 0.2 | 5.1 | 5.1 |
| 0.287 | 4.7 | 4.8 | 4.7 | 4.6 | 0 | 0.2 | 0 | 4.2 |
| 0.376 | 5.6 | 5.4 | 5.8 | 5.7 | –0.2 | –0.3 | –3.6 | –5.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serra, A.; Tarrés, Q.; Chamorro, M.-À.; Soler, J.; Mutjé, P.; Espinach, F.X.; Vilaseca, F. Modeling the Stiffness of Coupled and Uncoupled Recycled Cotton Fibers Reinforced Polypropylene Composites. Polymers 2019, 11, 1725. https://doi.org/10.3390/polym11101725
Serra A, Tarrés Q, Chamorro M-À, Soler J, Mutjé P, Espinach FX, Vilaseca F. Modeling the Stiffness of Coupled and Uncoupled Recycled Cotton Fibers Reinforced Polypropylene Composites. Polymers. 2019; 11(10):1725. https://doi.org/10.3390/polym11101725
Chicago/Turabian StyleSerra, Albert, Quim Tarrés, Miquel-Àngel Chamorro, Jordi Soler, Pere Mutjé, Francesc X. Espinach, and Fabiola Vilaseca. 2019. "Modeling the Stiffness of Coupled and Uncoupled Recycled Cotton Fibers Reinforced Polypropylene Composites" Polymers 11, no. 10: 1725. https://doi.org/10.3390/polym11101725
APA StyleSerra, A., Tarrés, Q., Chamorro, M.-À., Soler, J., Mutjé, P., Espinach, F. X., & Vilaseca, F. (2019). Modeling the Stiffness of Coupled and Uncoupled Recycled Cotton Fibers Reinforced Polypropylene Composites. Polymers, 11(10), 1725. https://doi.org/10.3390/polym11101725