Thiol–Ene Photopolymerization: Scaling Law and Analytical Formulas for Conversion Based on Kinetic Rate and Thiol–Ene Molar Ratio
Abstract
1. Introduction
2. Materials and Methods
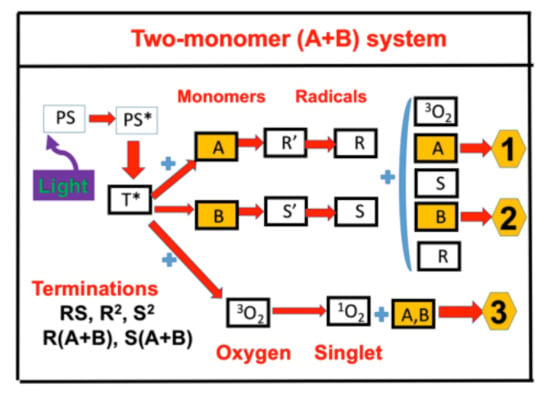
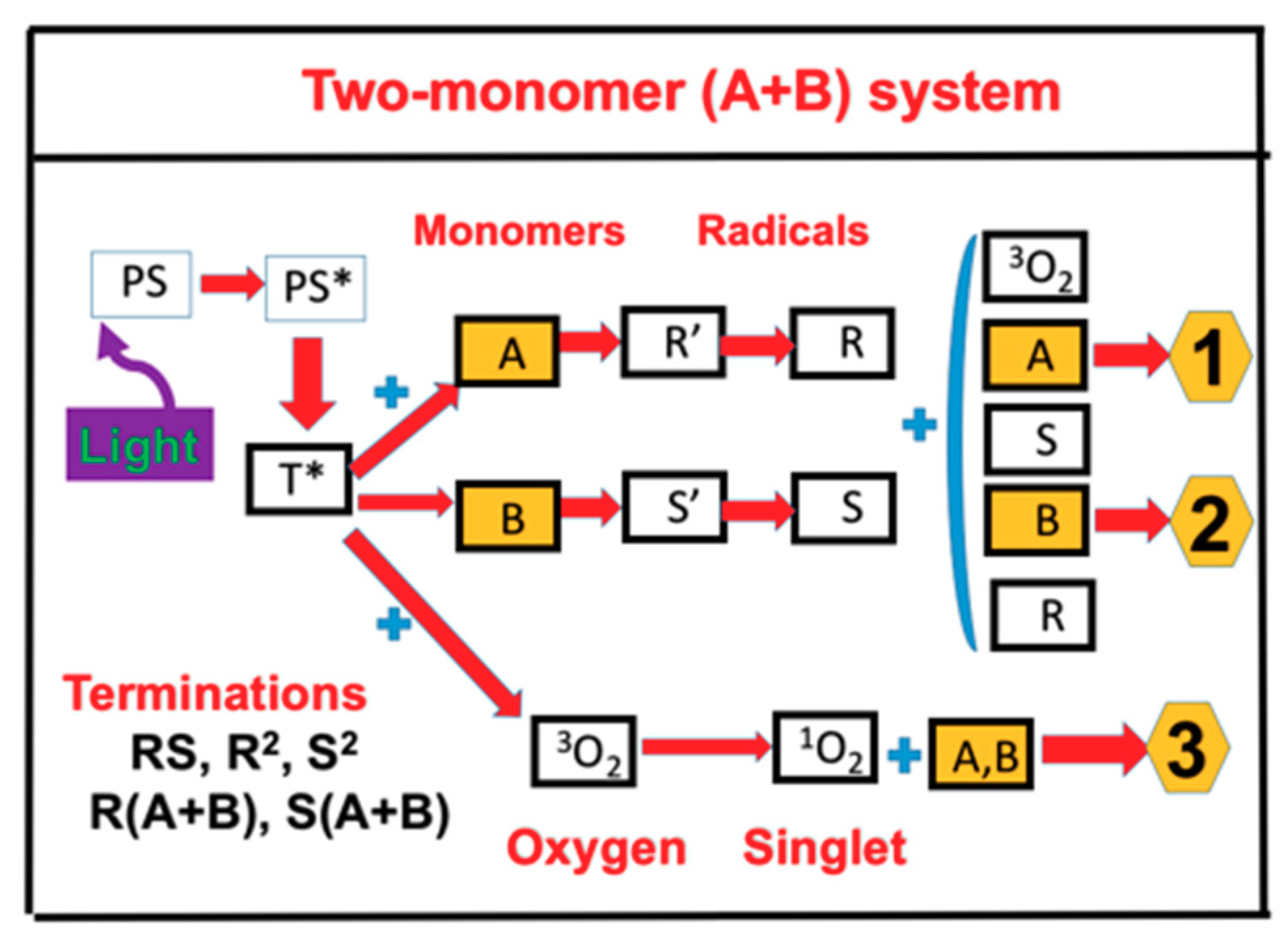
2.1. Photochemical Kinetics
2.2. Analytical Formulas for Efficacy
2.3. The Second-Order Solution
2.4. Effects of Viscosity and Homopolymerization
2.5. Dynamic Light Intensity
2.6. Gelation Time
2.7. Crosslink Depth
3. Results and Discussion
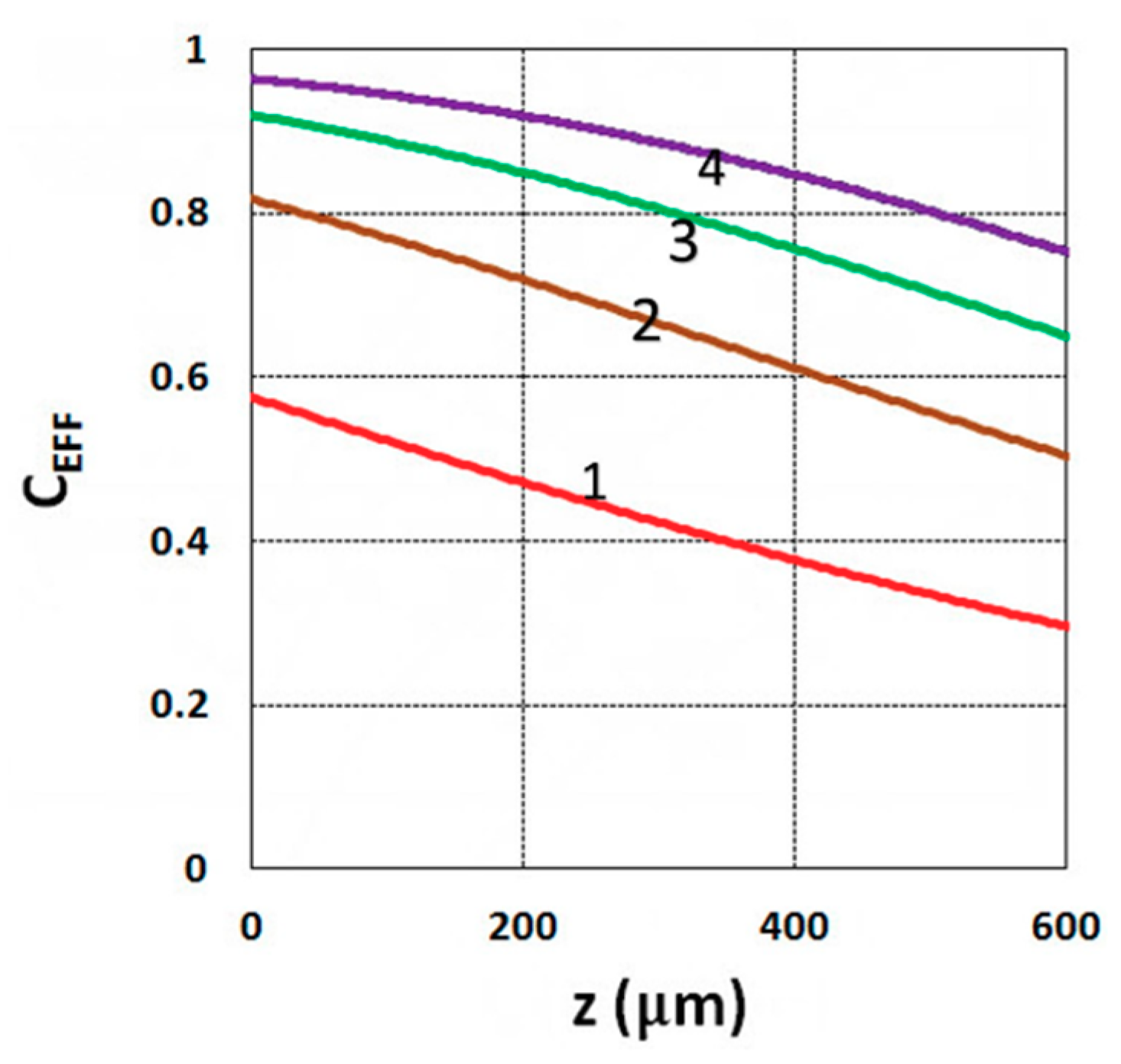
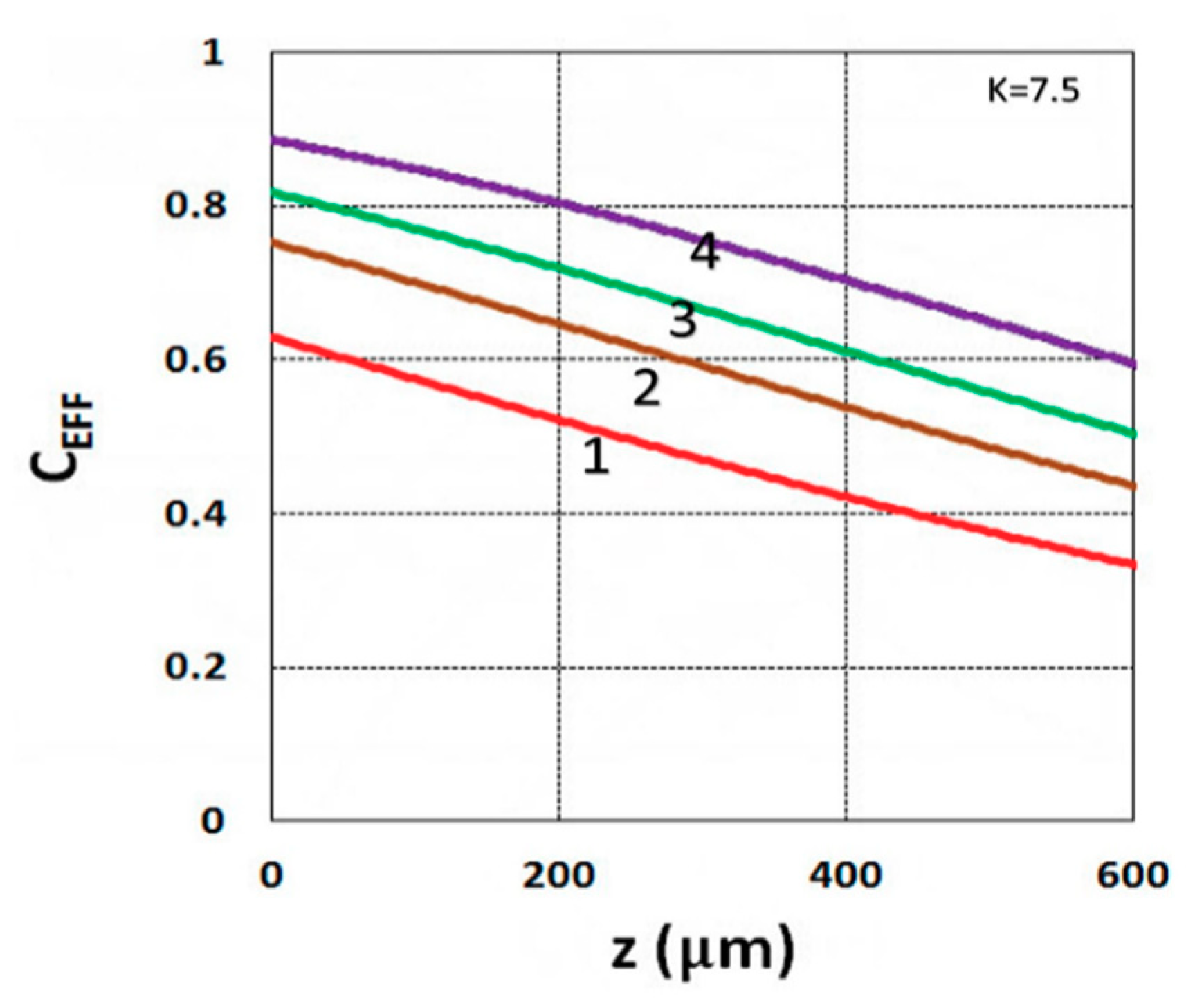
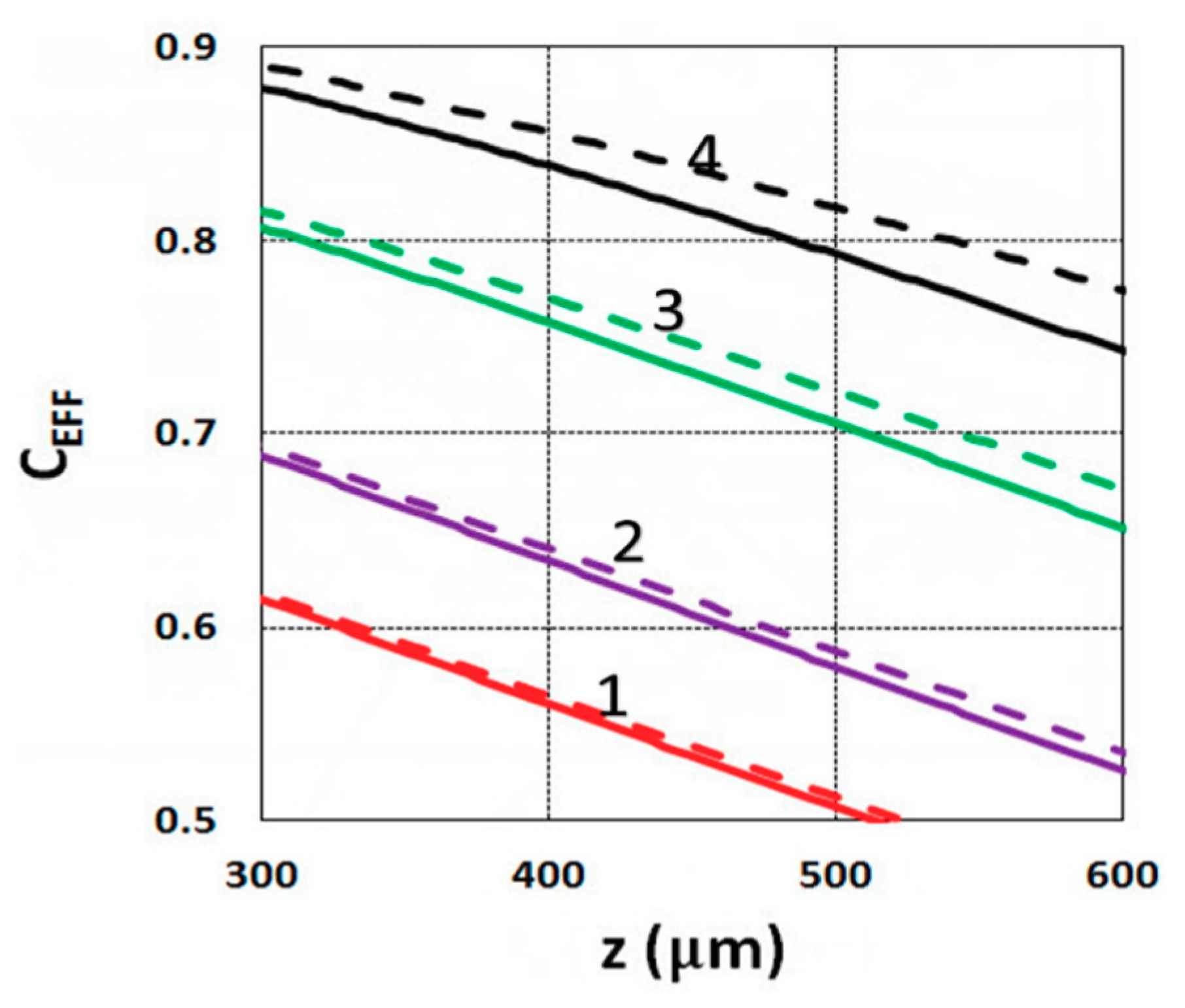
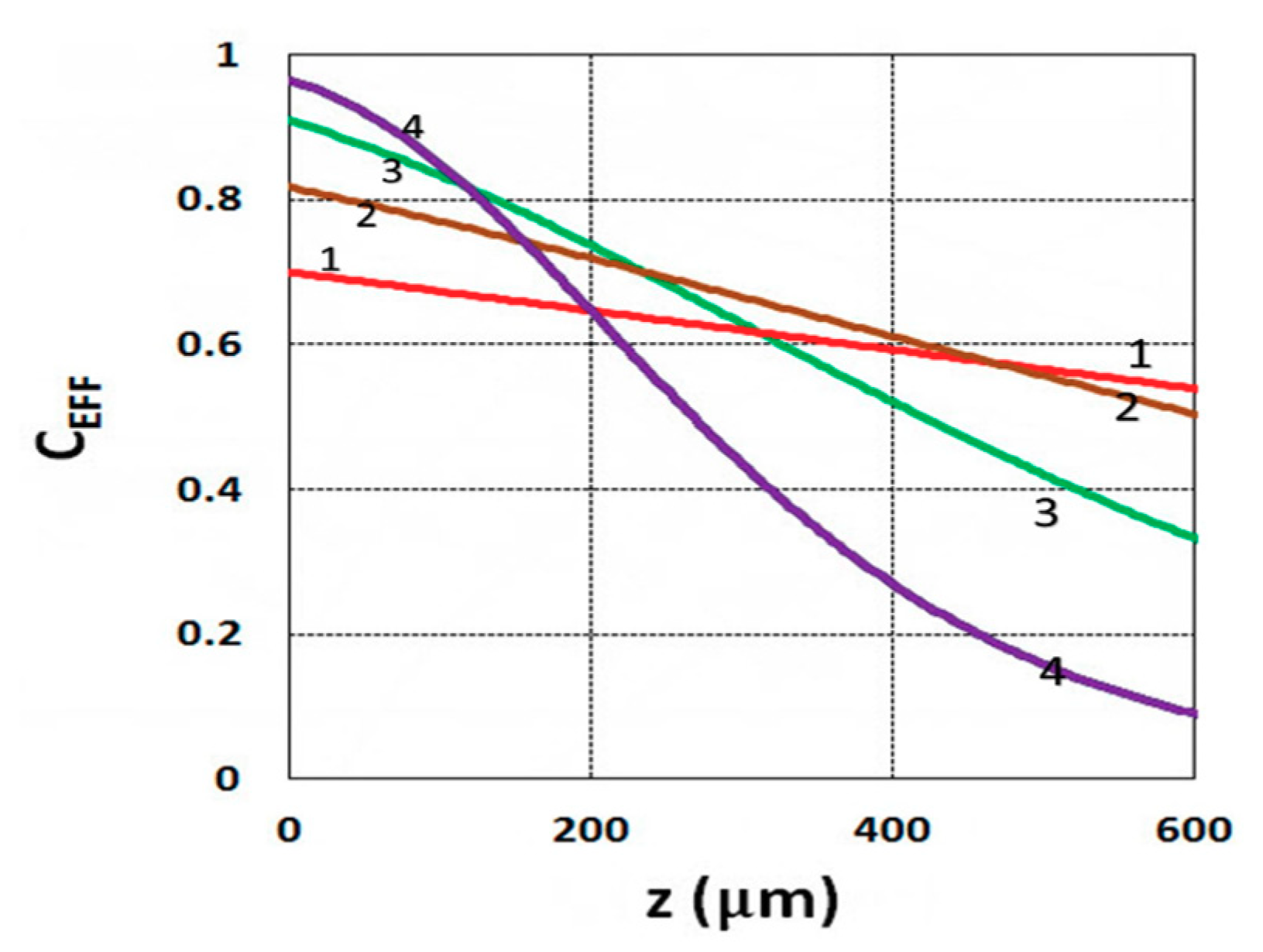
3.1. Efficacy Spatial Profiles
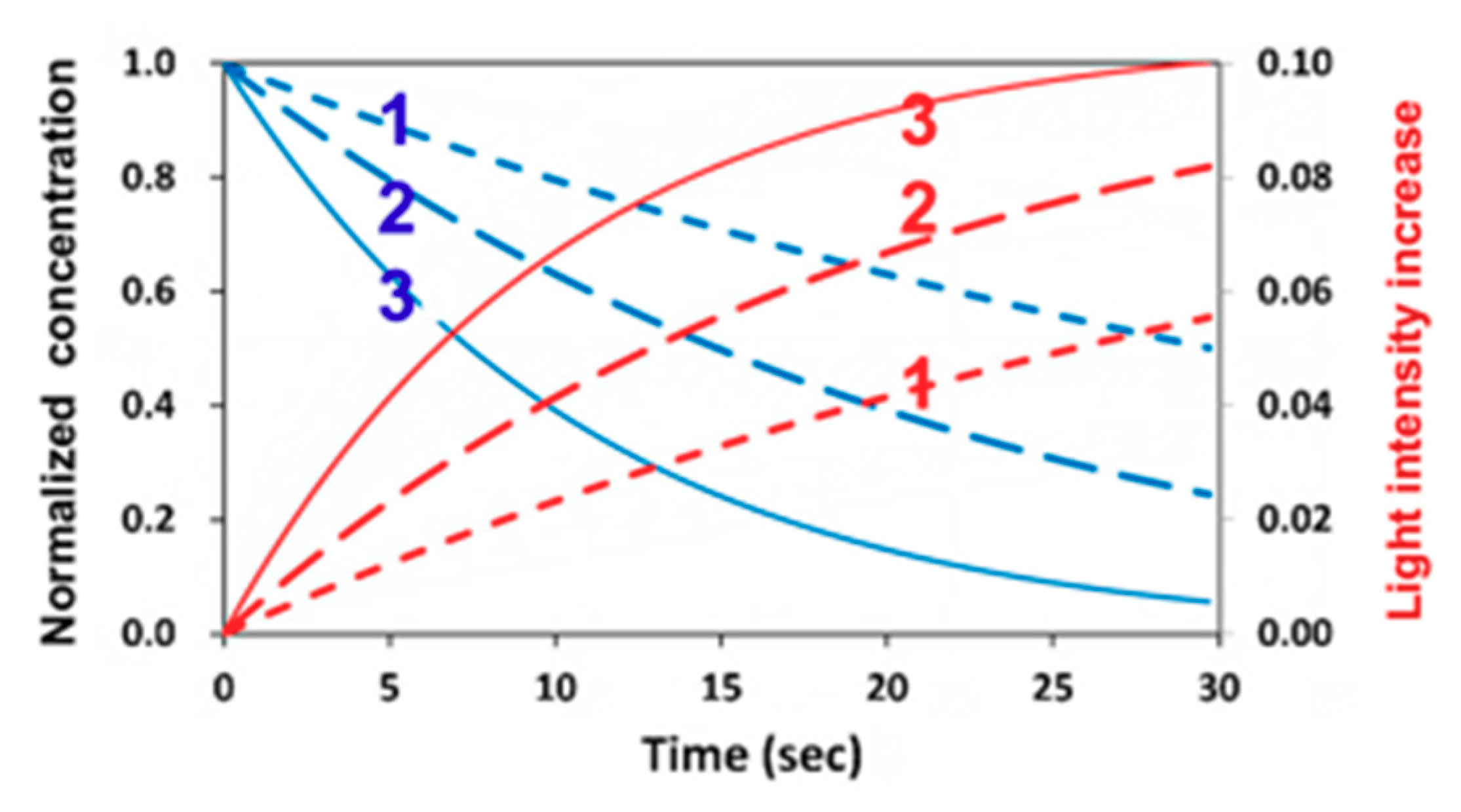
3.2. Dynamic Profiles of the Light Intensity
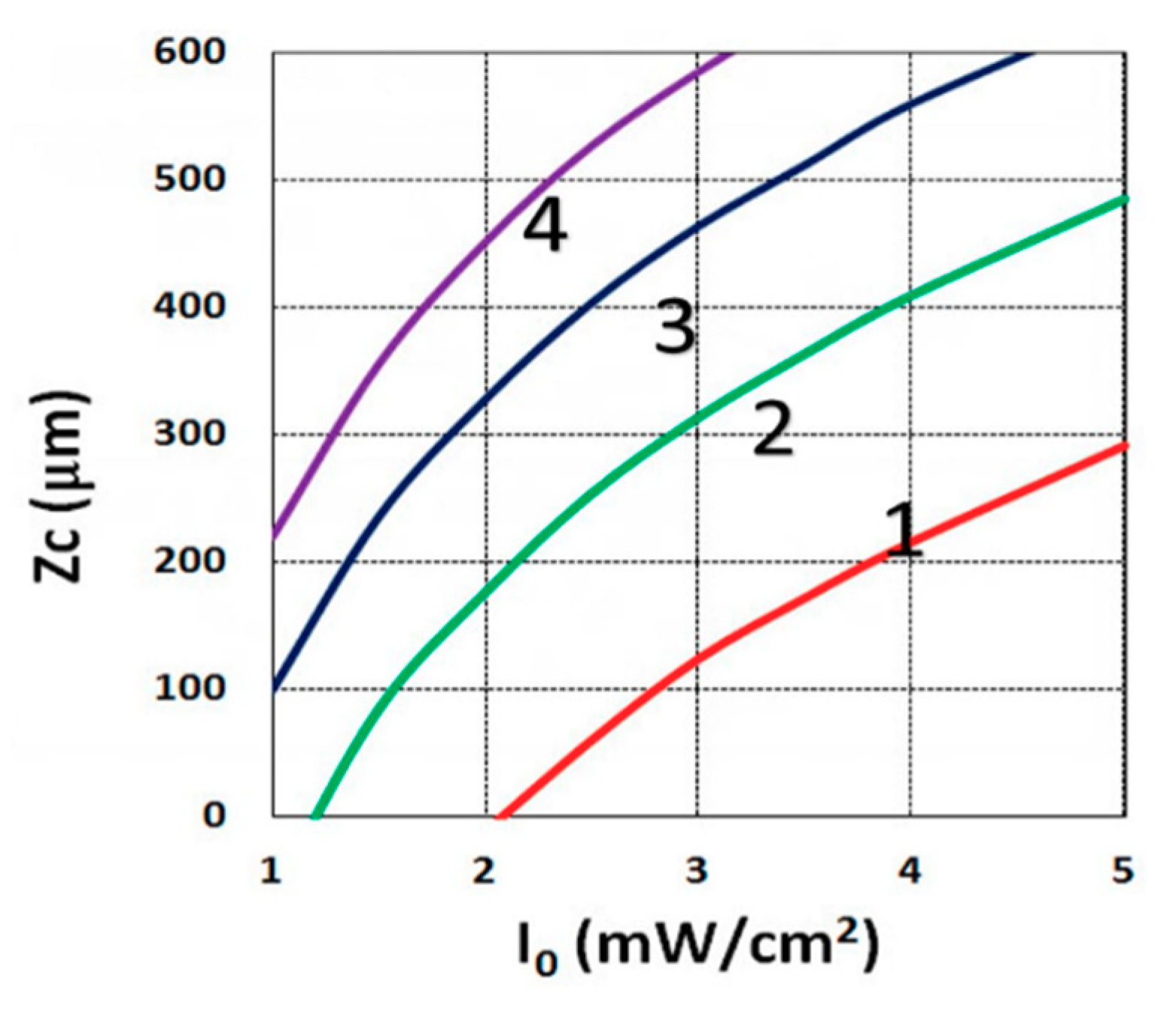
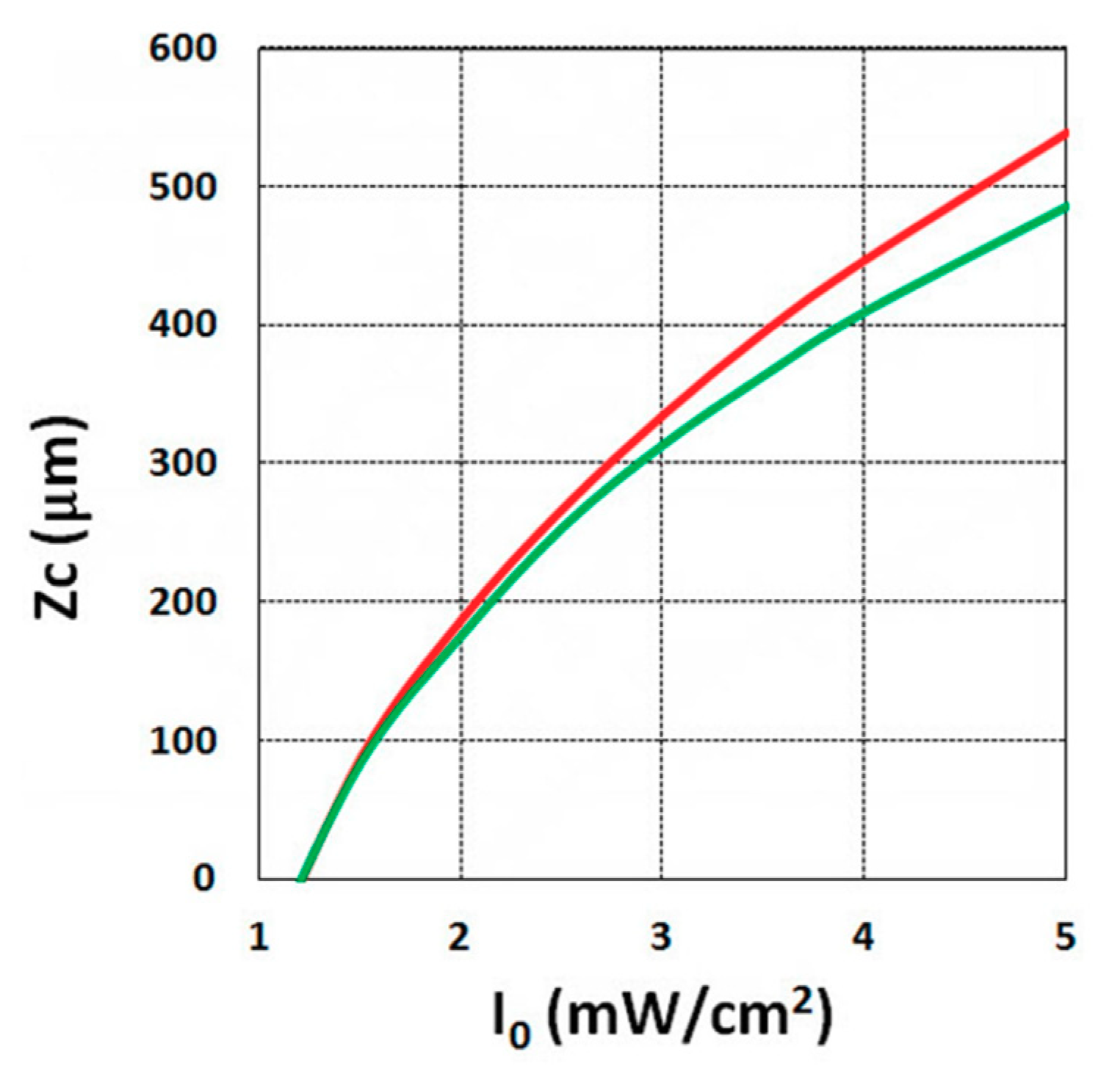
3.3. Crosslink Depth Profiles
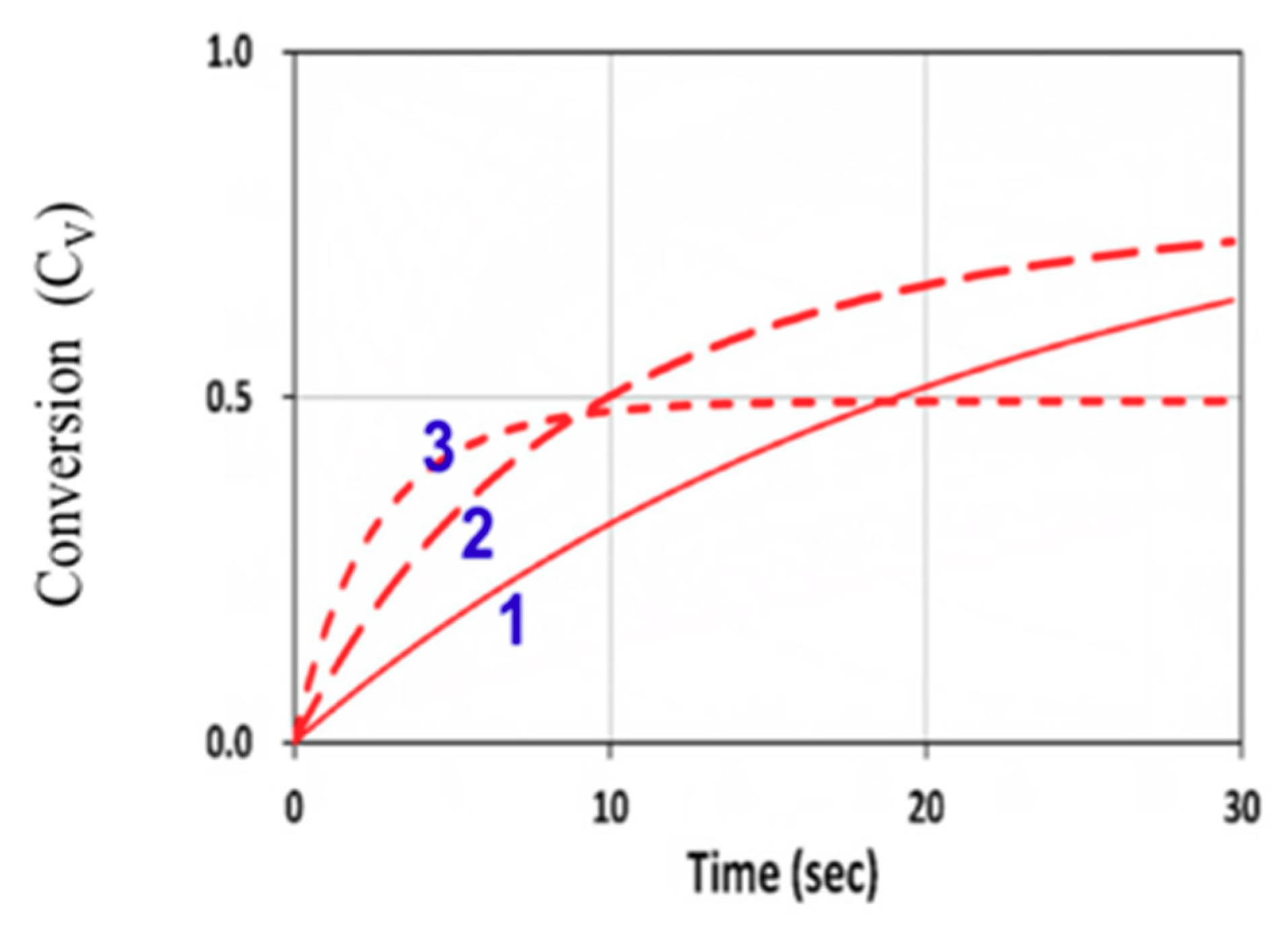
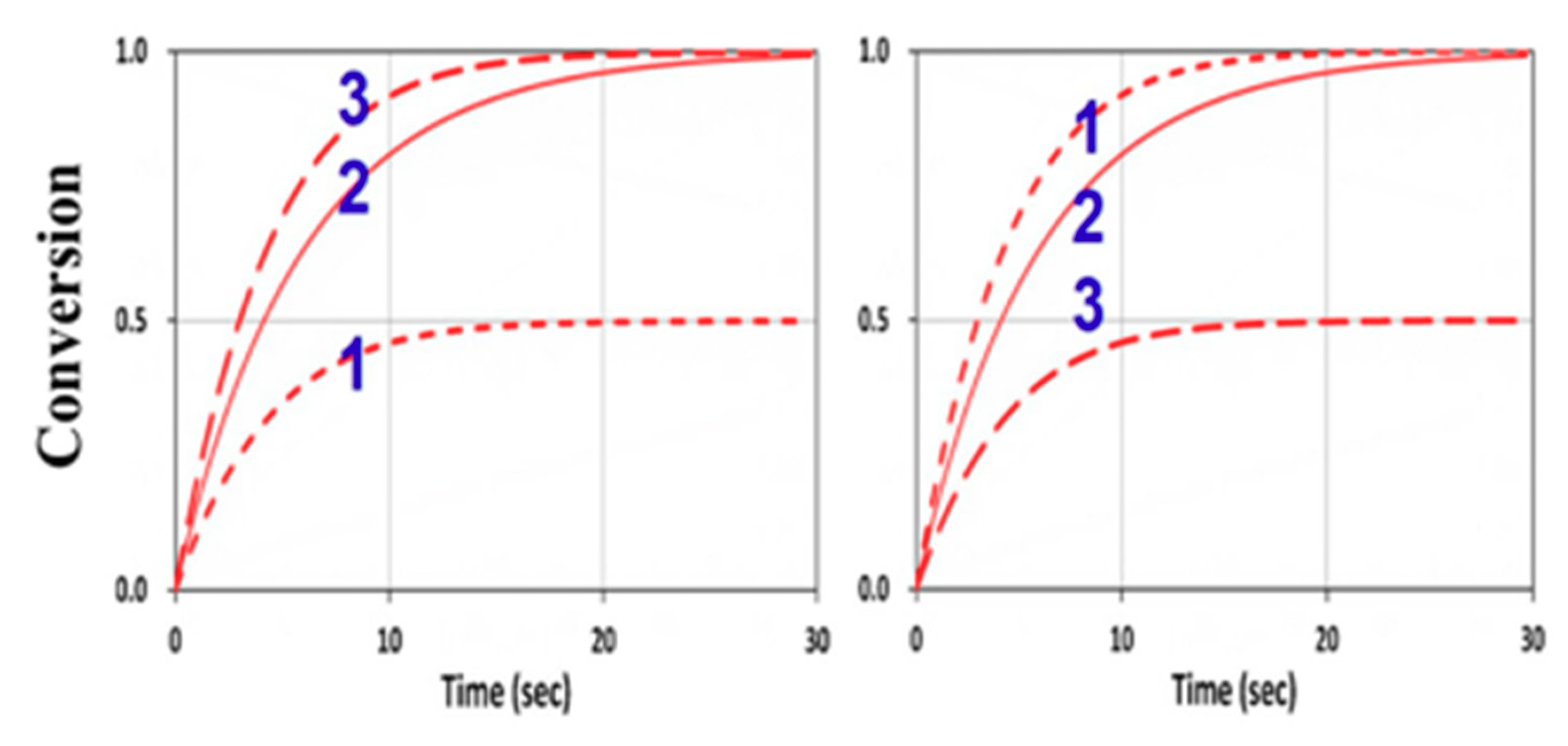
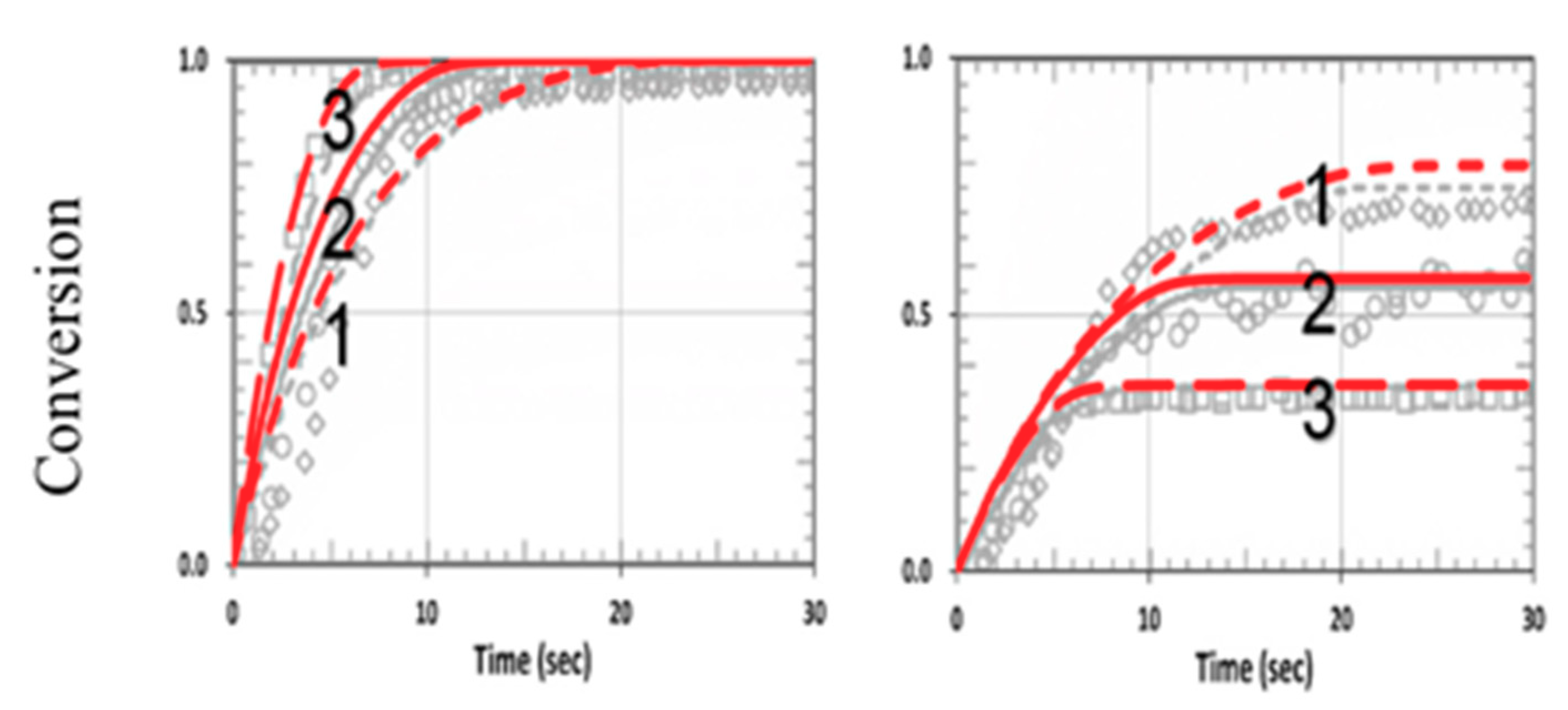
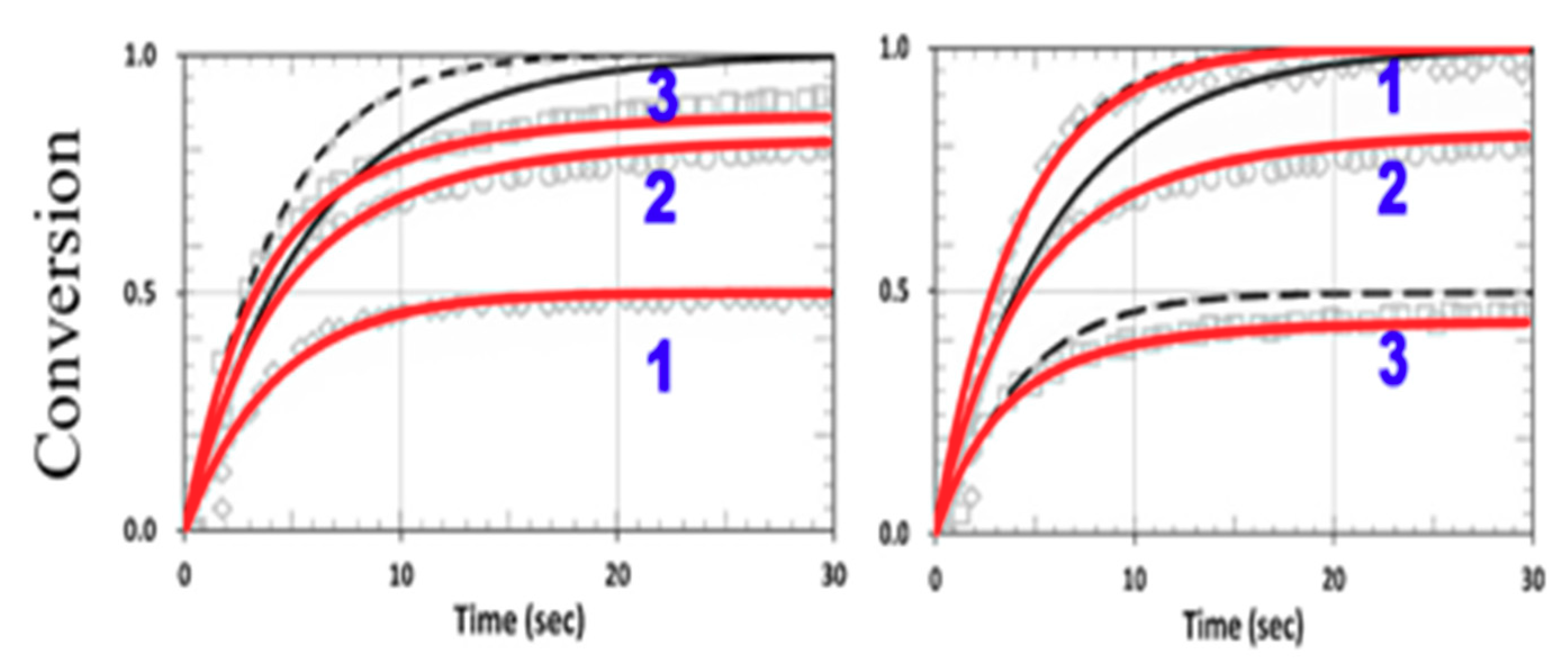
3.4. Numerical Results of Conversion
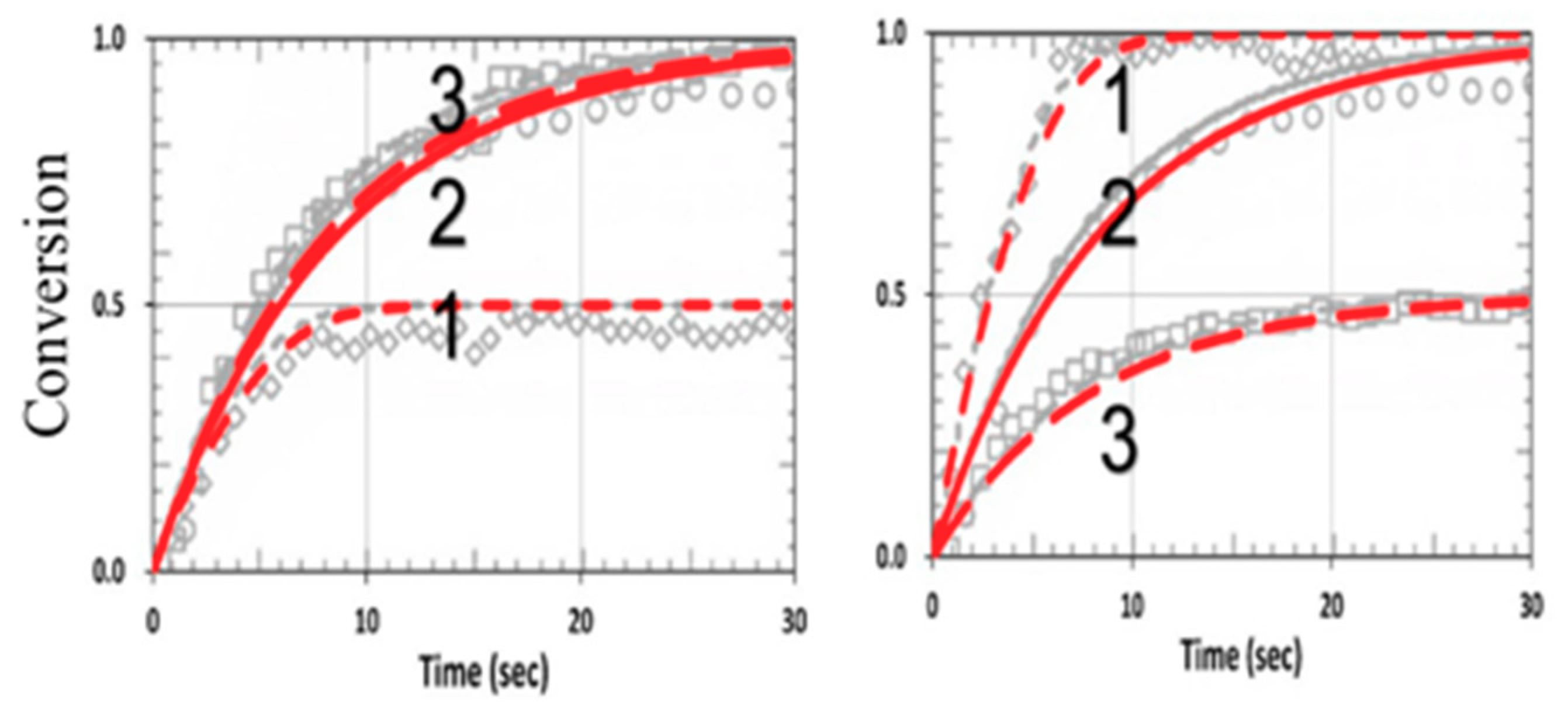
3.5. Analysis of Measured Data
3.6. General Features of Conversion Efficacy
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fouassier, J.P. Photoinitiation, Photo-Polymerization, and Photocuring: Fundamentals and Applications; Hanser Gardner Publications: Munich, Germany, 1995. [Google Scholar]
- Odian, G. Principles of Polymerization, 4th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Chen, F.M.; Shi, S. Principles of Tissue Engineering, 4th ed.; Elsevier: New York, NY, USA, 2014. [Google Scholar]
- Hafezi, F.; Randleman, J.B. (Eds.) Corneal Collagen Cross-Linking, 2nd ed.; SLACK: Thorofare, NJ, USA, 2016. [Google Scholar]
- Wohlers, T.; Caffrey, T. Wohlers Report 2016: 3D Printing and Additive Manufacturing State of the Industry; Annual Worldwide Progress Report; Wohlers Associates, Inc.: Fort Collins, CO, USA, 2016. [Google Scholar]
- Chen, F.H.; Pathreeker, S.B.; Hosein, I.D. Synthesis of Micropillar Arrays via Photopolymerization: An In Situ Study of Light-Induced Formation, Growth Kinetics, and the Influence of Oxygen Inhibition. Macromolecules 2017, 50, 5767–5778. [Google Scholar] [CrossRef]
- Cabral, J.T.; Hudson, S.D.; Harrison, C.; Douglas, J.F. Frontal Photopolymerization for Microfluidic Applications. Langmuir 2004, 20, 10020–10029. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, A.K.; Bowman, C.N. Modeling the effect of oxygen on photopolymerization kinetics. Macromol. Theory Simul. 2006, 15, 176–182. [Google Scholar] [CrossRef]
- Dendukuri, D.; Panda, P.; Haghgooie RKim, J.M.; Hatton, T.A.; Doyle, P.S. Modeling of Oxygen-Inhibited Free Radical Photopolymerization in a PDMS Microfluidic Device. Macromolecules 2008, 41, 8547–8556. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Theory of molecular size distribution and gel formation in branched polymers II. general cross linking. J. Chem. Phys. 2004, 12, 125. [Google Scholar] [CrossRef]
- Alvankarian, J.; Majlis, B.Y. Exploiting the Oxygen Inhibitory Effect on UV Curing in Microfabrication: A Modified Lithography Technique. PLoS ONE 2015, 10, e0119658. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhao, Z.; Hamel, C.M.; Mu, X.; Kuang, X.; Guo, Z.; Qi, H.J. Evolution of material properties during free radical photopolymerization. J. Mechan. Phys. Solid. 2018, 112, 25–49. [Google Scholar] [CrossRef]
- Lin, J.T. Efficacy S-formula and kinetics of oxygen-mediated (type-II) and non-oxygen-mediated (type-I) corneal cross-linking. Ophthalmol. Res. 2018, 8, 1–11. [Google Scholar] [CrossRef]
- Lin, J.T.; Wang, K.C. Analytic formulas and numerical simulations for the dynamics of thick and non-uniform polymerization by a UV light. J. Polym. Res. 2016, 23, 53. [Google Scholar] [CrossRef]
- Lin, J.T.; Cheng, D.C. Modeling the efficacy profiles of UV-light activated corneal collagen crosslinking. PLoS ONE 2017, 12, e0175002. [Google Scholar] [CrossRef]
- Lin, J.T.; Liu, H.W.; Chen, K.T.; Cheng, D.C. Modeling the optimal conditions for improved efficacy and crosslink depth of photo-initiated polymerization. Polymers 2019, 11, 217. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.T.; Lin, J.T.; Liu, H.W. Enhancing radical-mediated photopolymerization efficacy and crosslink depth: Kinetic modeling of a two-monomer system. Res. Med. Eng. Sci. 2019, 8, 853–860. [Google Scholar]
- Cramer, N.B.; Reddy, S.K.; O’Brien, A.K.; Bowman, C.N. Thiol-ene photopolymerization mechanism and rate limiting step for various vinyl functional group chemistries. Macromolecules 2003, 36, 7964–7969. [Google Scholar] [CrossRef]
- Cramer, N.B.; Bowman, C.N. Thiol-X Click Chemistries in Polymer and Materials Science; Lowe, A.B., Bowman, C.N., Eds.; RSC Publishing: Cambridge, UK, 2013; p. 318. [Google Scholar]
- Reddy, S.K.; Cramer, N.B.; Bowman, C.N. Thiol-Vinyl Mechanisms. 2. Kinetic Modeling of Ternary Thiol-Vinyl Photopolymerizations. Macromolecules 2006, 39, 3681–3687. [Google Scholar] [CrossRef]
- Okay, O.; Bowman, C.N. Kinetic modeling of thiol-ene reactions with both step and chain growth aspects. Macromol. Theory Simul. 2005, 14, 267–277. [Google Scholar] [CrossRef]
- Claudino, M.; Jonsson, M.; Johansson, M. Thiol-ene coupling kinetics of D-limonene: a versatile ’non-click’ free-radical reaction involving a natural terpene. RSC Adv. 2013, 3, 11021–11034. [Google Scholar] [CrossRef]
- Li, Y.; Su, H.; Feng, X.; Wang, Z.; Guo, K.; Wesdemiotis, C.; Fu, Q.; Cheng, S.Z.D.; Zhang, W.-B. Thiol-Michael “click” Chemistry: Another Efficient Tool for Head Functionalization of Giant Surfactants. Polym. Chem. 2014, 5, 6151–6162. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Podgoŕski, M.; Xi, W.; Shah, P.; Stansbury, J.; Bowman, C.N. Monodispersity/Narrow Polydispersity Cross-Linked Microparticles Prepared by Step-Growth Thiol-Michael Addition Dispersion Polymerizations. Macromolecules 2015, 48, 8461–8470. [Google Scholar] [CrossRef]
- Zhang, X.; Xi, W.; Wang, C.; Podgoŕski, M.; Bowman, C.N. Visible-Light-Initiated Thiol-Michael Addition Polymerizations with Coumarin-Based Photobase Generators: Another Photoclick Reaction Strategy. ACS Macro Lett. 2016, 5, 229–233. [Google Scholar] [CrossRef]
- Claudino, M.; Zhang, X.; Alim, M.D.; Podgoŕski, M.; Bowman, C.N. Mechanistic Kinetic Modeling of Thiol-Michael Addition Photopolymerizations via Photocaged “superbase” Generators: An Analytical Approach. Macromolecules 2016, 49, 8061–8074. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Sinha, J.; Podgoŕski, M.; Zhang, X.; Claudino, M.; Bowman, C.N. Mechanistic Modeling of the Thiol-Michael Addition Polymerization Kinetics: Structural Effects of the Thiol and Vinyl Monomers. Macromolecules 2018, 51, 5979–5988. [Google Scholar] [CrossRef]
- Esposito Corcione, C.; Greco, A.; Maffezzoli, A. Photopolymerization kinetics of an epoxy based resin for setereolithography by calorimetric analysis. J. Therm. Anal. Calorim. 2003, 72, 687–693. [Google Scholar] [CrossRef]
- Esposito Corcione, C.; Frigione, M. UV-cured siloxane-modified acrylic coatings containing birifrangent calcarenitic stone particles: Photo-calorimetric analysis and surface properties. Prog. Org. Coat. 2011, 72, 522–527. [Google Scholar] [CrossRef]
- Esposito Corcione, C.; Frigione, M. Factors Influencing Photo-Curing Kinetics of Novel UV Cured Siloxane-Modified Acrylic Coatings: Oxygen Inhibition and Composition. Thermochim. Acta 2012, 534, 21–27. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.-T.; Cheng, D.-C.; Lin, J.-T.; Liu, H.-W. Thiol–Ene Photopolymerization: Scaling Law and Analytical Formulas for Conversion Based on Kinetic Rate and Thiol–Ene Molar Ratio. Polymers 2019, 11, 1640. https://doi.org/10.3390/polym11101640
Chen K-T, Cheng D-C, Lin J-T, Liu H-W. Thiol–Ene Photopolymerization: Scaling Law and Analytical Formulas for Conversion Based on Kinetic Rate and Thiol–Ene Molar Ratio. Polymers. 2019; 11(10):1640. https://doi.org/10.3390/polym11101640
Chicago/Turabian StyleChen, Kuo-Ti, Da-Chuan Cheng, Jui-Teng Lin, and Hsia-Wei Liu. 2019. "Thiol–Ene Photopolymerization: Scaling Law and Analytical Formulas for Conversion Based on Kinetic Rate and Thiol–Ene Molar Ratio" Polymers 11, no. 10: 1640. https://doi.org/10.3390/polym11101640
APA StyleChen, K.-T., Cheng, D.-C., Lin, J.-T., & Liu, H.-W. (2019). Thiol–Ene Photopolymerization: Scaling Law and Analytical Formulas for Conversion Based on Kinetic Rate and Thiol–Ene Molar Ratio. Polymers, 11(10), 1640. https://doi.org/10.3390/polym11101640