Thermoconductive Thermosetting Composites Based on Boron Nitride Fillers and Thiol-Epoxy Matrices
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
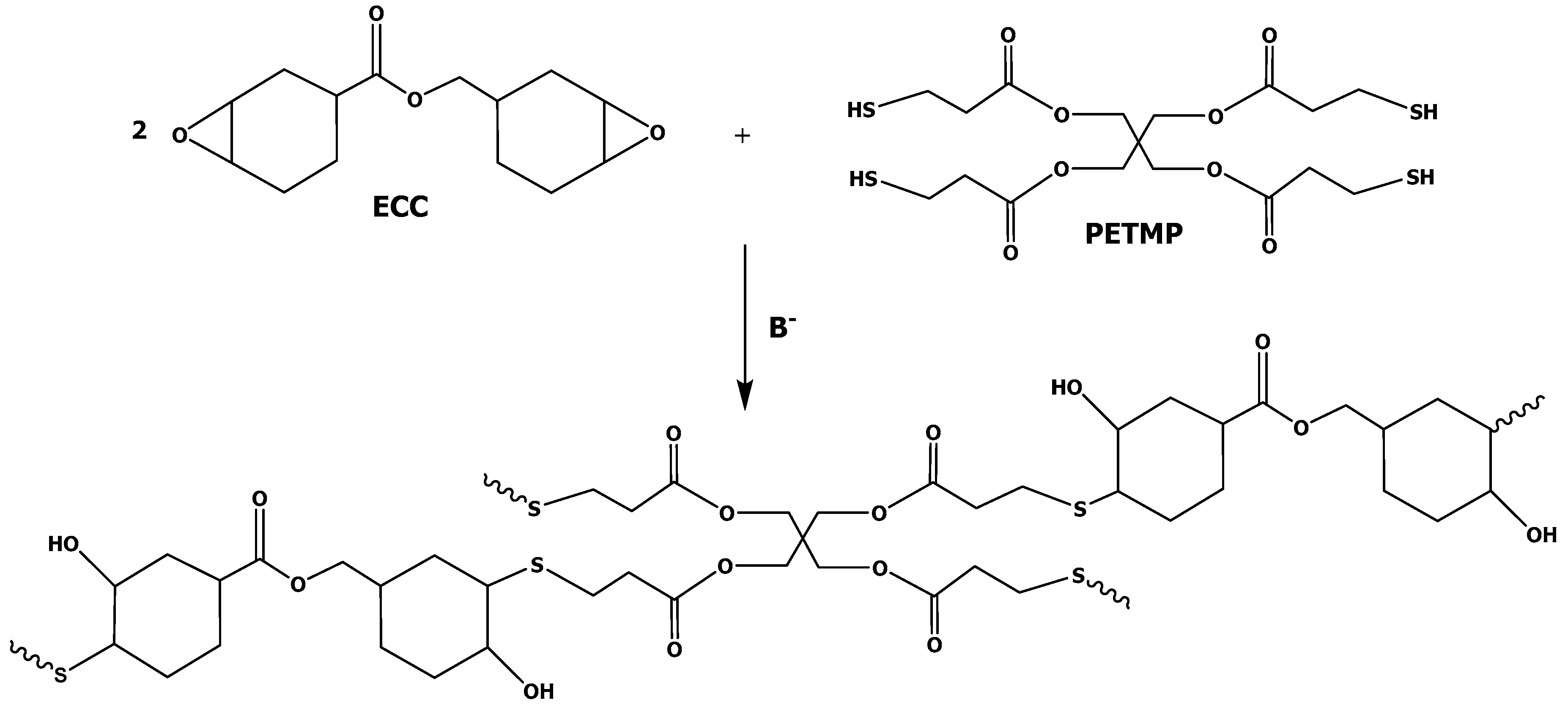
2.2. Sample Preparation
2.3. Characterization Techniques
3. Results and Discussion
3.1. Study of the Curing Process
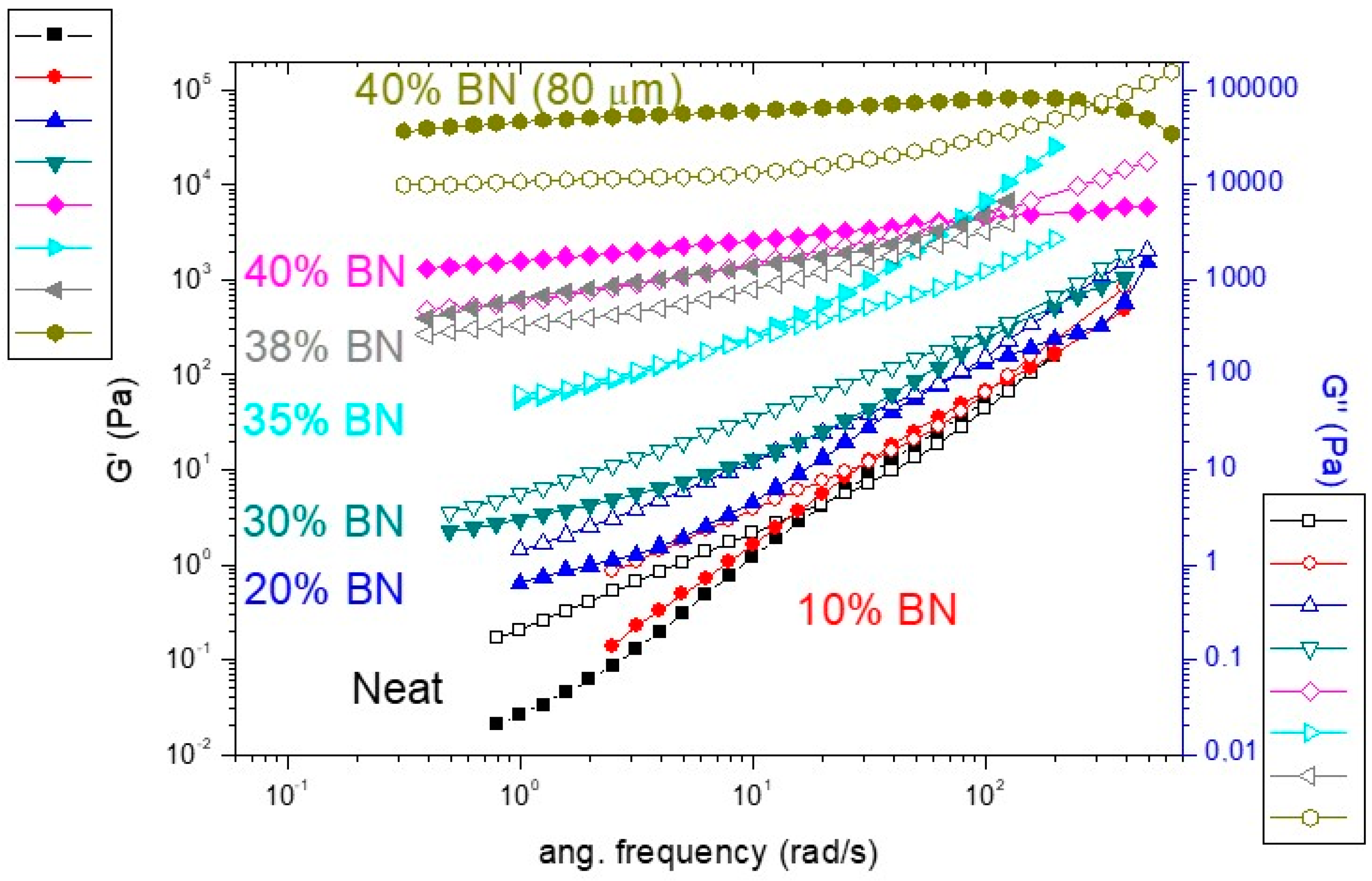
3.2. Rheological Study of the BN Formulations
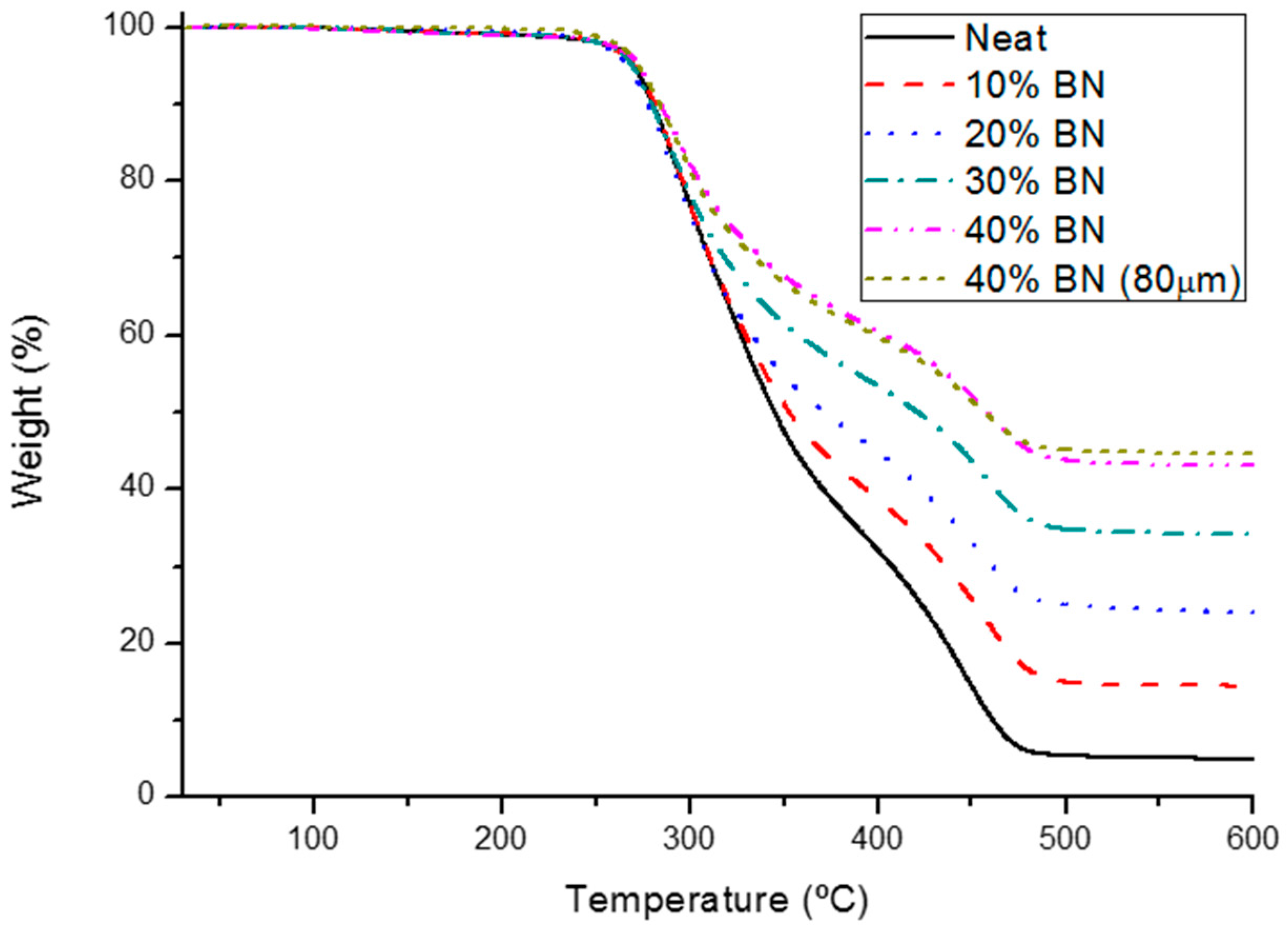
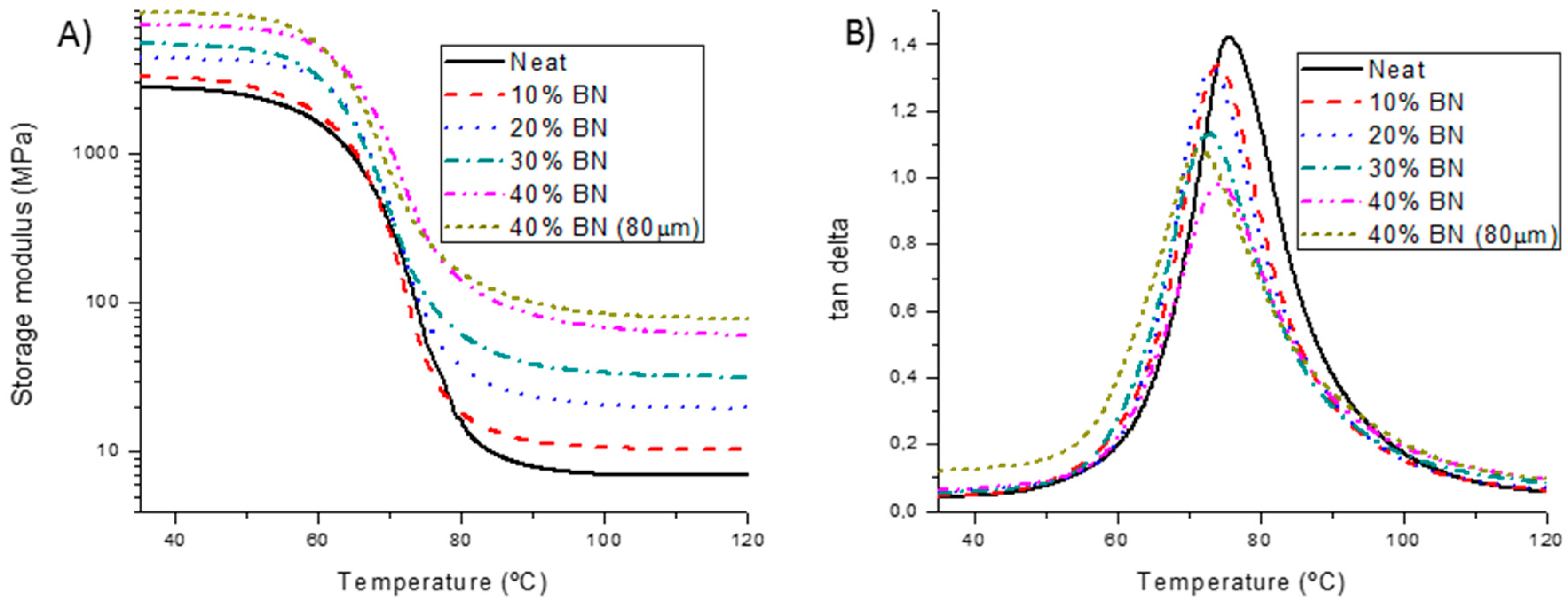
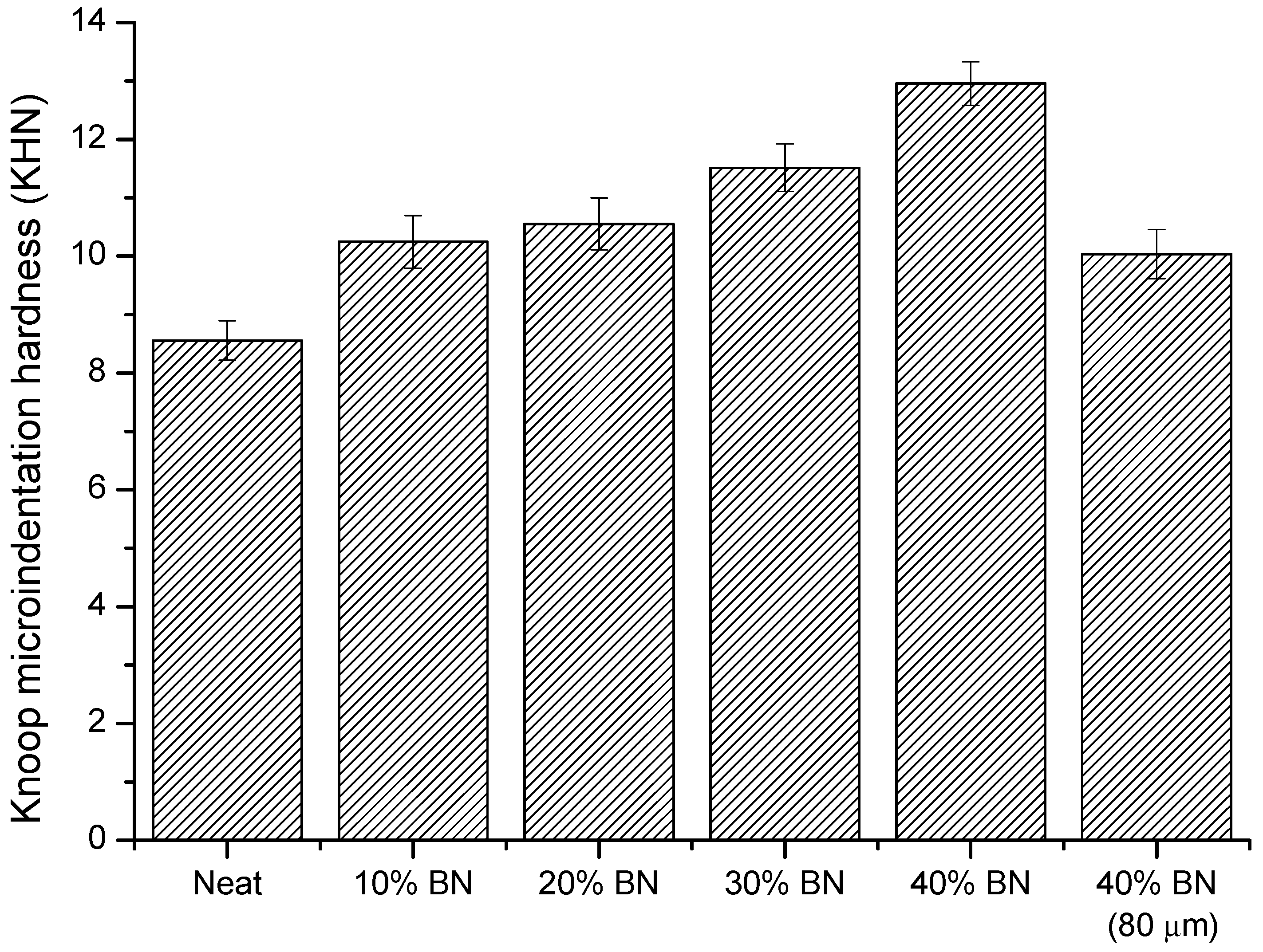
3.3. Thermal and Mechanical Characterization of BN Composites
3.4. Morphology Inspection of BN Composites
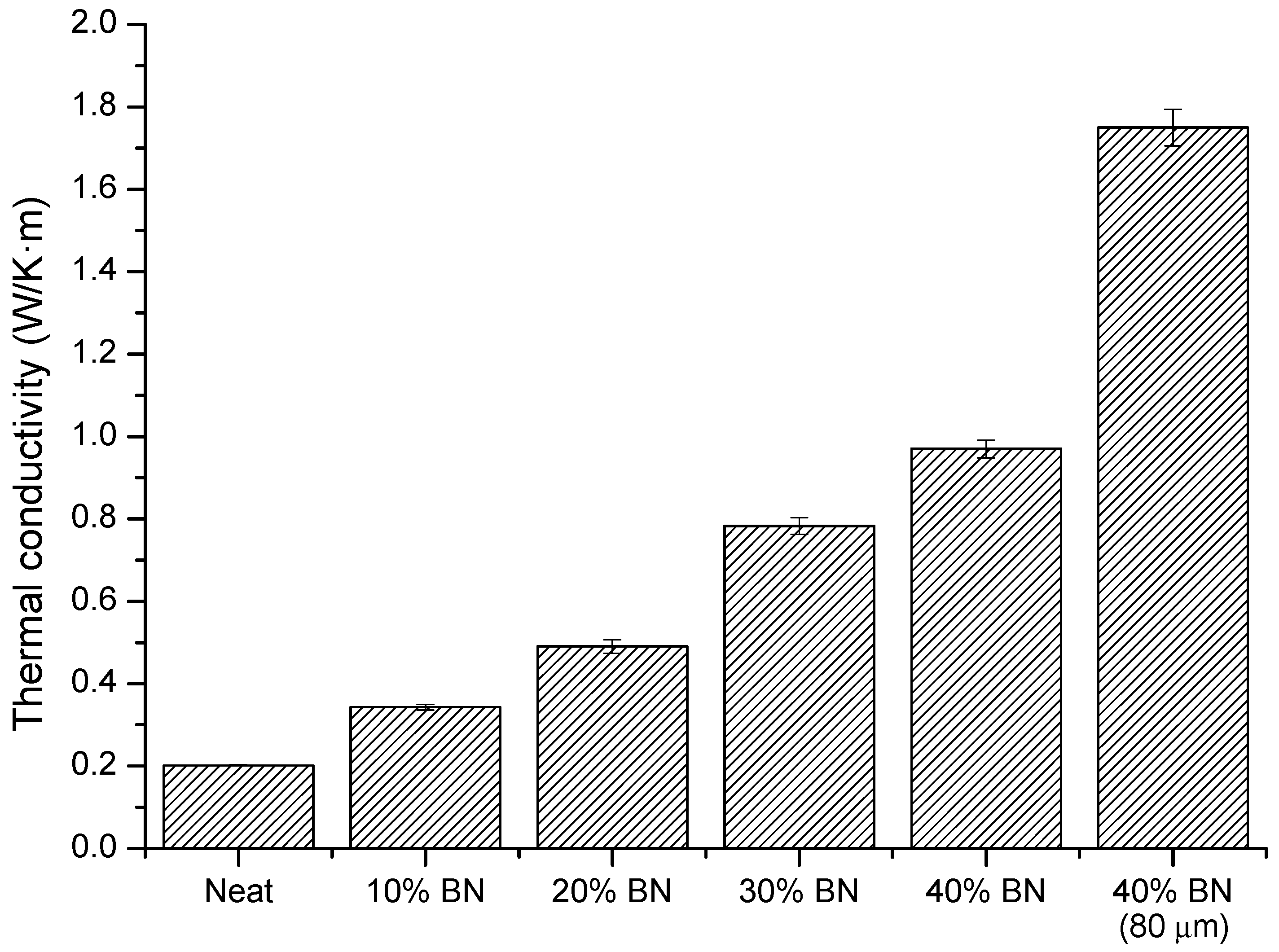
3.5. Thermal Conductivity of BN Composites
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer: Fundamentals and Application, 5th ed.; McGraw-Hill: New York, NY, USA, 2015; ISBN 978-0073398181. [Google Scholar]
- Zhang, S.; Zhao, D. (Eds.) Aerospace Materials Handbook; CRC Press: Boca Raton, FL, USA, 2013; ISBN 9781439873298. [Google Scholar]
- Burger, N.; Laachachi, A.; Ferriol, M.; Lutz, M.; Toniazzo, V.; Ruch, D. Review of thermal conductivity in composites: Mechanisms, parameters and theory. Prog. Polym. Sci. 2016, 61, 1–28. [Google Scholar] [CrossRef]
- Gaska, K.; Rybak, A.; Kapusta, C.; Sekula, R.; Siwek, A. Enhanced thermal conductivity of epoxy–matrix composites with hybrid fillers. Polym. Adv. Technol. 2015, 26, 26–31. [Google Scholar] [CrossRef]
- Song, W.-L.; Wang, P.; Cao, L.; Anderson, A.; Meziani, M.J.; Farr, A.J.; Sun, Y.-P. Polymer/Boron Nitride Nanocomposite Materials for Superior Thermal Transport Performance. Angew. Chem. Int. Ed. 2012, 51, 6498–6501. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Ginzburg, V.V.; Yang, J.; Yang, Y.; Liu, W.; Huang, Y.; Du, L.; Chen, B. Thermal conductivity of polymer-based composites: Fundamentals and Applications. Prog. Polym. Sci. 2016, 59, 41–85. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef] [PubMed]
- Golberg, D.; Bando, Y.; Huang, Y.; Terao, T.; Mitome, M.; Tang, C.C.; Zhi, C.Y. Boron Nitride Nanotubes and Nanosheets. ACS Nano 2010, 4, 2979–2993. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.T.; Bresnehan, M.S.; Robinson, J.A.; Haque, M.A. Thermal conductivity of ultra-thin chemical vapor deposited hexagonal boron nitride films. Appl. Phys. Lett. 2014, 104, 013113. [Google Scholar] [CrossRef]
- Li, A.; Zhang, C.; Zhang, Y.-F. Thermal Conductivity of Graphene-Polymer Composites: Mechanisms, Properties, and Applications. Polymers 2017, 9, 437. [Google Scholar] [CrossRef]
- Yu, J.; Huang, X.; Wu, C.; Wu, X.; Wang, G.; Jiang, P. Interfacial modification of boron nitride nanoplatelets for epoxy composites with improved thermal properties. Polymer 2012, 53, 471–480. [Google Scholar] [CrossRef]
- Seyhan, A.T.; Göncü, Y.; Durukan, O.; Akay, A.; Ay, N. Silanization of boron nitride nanosheets (BNNSs) through microfluidization and their use for producing thermally conductive and electrically insulating polymer nanocomposites. J. Solid State Chem. 2017, 249, 98–107. [Google Scholar] [CrossRef]
- Fang, L.; Wu, C.; Qian, R.; Xie, L.; Yang, K.; Jiang, P. Nano–micro structure of functionalized boron nitride and aluminum oxide for epoxy composites with enhanced thermal conductivity and breakdown strength. RSC Adv. 2014, 4, 21010–21017. [Google Scholar] [CrossRef]
- Kim, K.; Kim, M.; Hwang, Y.; Kim, J. Chemically modified boron nitride epoxy terminated dimethylsiloxane composite for improving the thermal conductivity. Ceram. Int. 2014, 40, 2047–2056. [Google Scholar] [CrossRef]
- Hutchinson, J.M.; Román, F.; Cortés, P.; Calventus, Y. Epoxy composites filled with boron nitride and aluminium nitride for improved thermal conductivity. Polimery 2017, 62, 764–770. [Google Scholar] [CrossRef]
- Guzmán, D.; Mateu, B.; Fernández-Francos, X.; Ramis, X.; Serra, A. Novel thermal curing of cycloaliphatic resins by thiol–epoxy click process with several multifunctional thiols. Polym. Int. 2017, 66, 1697–1707. [Google Scholar] [CrossRef]
- Guzmán, D.; Ramis, X.; Fernández-Francos, X.; Serra, A. New catalysts for diglycidyl ether of bisphenol A curing based on thiol-epoxy click reaction. Eur. Polym. J. 2014, 59, 377–386. [Google Scholar] [CrossRef]
- Guzmán, D.; Ramis, X.; Fernández-Francos, X.; Serra, A. Enhancement in the glass transition temperature in latent thiol-epoxy click cured thermosets. Polymers 2015, 7, 680–694. [Google Scholar] [CrossRef]
- Isarn, I.; Gamardella, F.; Massagués, L.; Fernández-Francos, X.; Serra, A.; Ferrando, F. New epoxy composite thermosets with enhanced thermal conductivity and high Tg obtained by cationic homopolymerization. Polym. Compos. 2018. [Google Scholar] [CrossRef]
- Pascault, J.P.; Sauterau, H.; Verdu, J.; Williams, R.J.J. Thermosetting Polymers; Marcel Dekker: New York, NY, USA, 2002; ISBN 0-8247-0670-6. [Google Scholar]
- Isarn, I.; Massagués, L.; Ramis, X.; Serra, A.; Ferrando, F. New BN-epoxy composites obtained by thermal latent cationic curing with enhanced thermal conductivity. Compos. Part A 2017, 103, 35–47. [Google Scholar] [CrossRef]
- Carreau, P.J.; De Kee, D.C.R.; Chhabra, R.P. Rheology of Polymeric Systems: Principles and Applications; Hanser Publishers: Münich, Germany, 1997; ISBN 978-1569902189. [Google Scholar]
- Laun, H.M. Rheological properties of aqueous polymer dispersion. Angew. Makromol. Chem. 1984, 123/124, 335–359. [Google Scholar] [CrossRef]
- Jouault, N.; Vallat, P.; Dalmas, F.; Said, S.; Jestin, J.; Boué, F. Well-dispersed fractal aggregates as filler in polymer-silica nanocomposites: Long-range effects in rheology. Macromolecules 2009, 42, 2031–2040. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: New York, NY, USA, 1980; ISBN 0-471-048941-1. [Google Scholar]
- De Gennes, P.G. Scaling theory of polymer adsorption. J. Phys. 1976, 37, 1445–1452. [Google Scholar] [CrossRef]
- Zhang, Q.; Rastogi, S.; Chen, D.; Lippits, D.; Lemstra, P.J. Low percolation threshold in single-walled carbon nanotube/high density polyethylene composites prepared by melt processing technique. Carbon 2006, 44, 778–785. [Google Scholar] [CrossRef]
- Hassanabadi, H.M.; Wilhelm, M.; Rodrigue, D. A rheological criterion to determine the percolation threshold in polymer nano-composites. Rheol. Acta 2014, 53, 869–882. [Google Scholar] [CrossRef]
- Ng, H.; Manas-Zloczower, I. Chemorheology of unfilled and filled epoxy-resins. Polym. Eng. Sci. 1993, 33, 211–216. [Google Scholar] [CrossRef]
- Hamerton, I. Recent Developments in Epoxy Resins; Smithers Rapra Technology: Shawbury, UK, 1996; Volume 8, ISBN 978-1859570838. [Google Scholar]
- Huang, X.; Jiang, P.; Tanaka, T. A review of dielectric polymer composites with high thermal conductivity. IEEE Electr. Insul. Mag. 2011, 27, 8–16. [Google Scholar] [CrossRef]
- Teng, C.-C.; Ma, C.-C.M.; Chiou, K.-C.; Lee, T.-M.; Shih, Y.-F. Synergetic effect of hybrid boron nitride and multi-walled carbon nanotubes on the thermal conductivity of epoxy composites. Mater. Chem. Phys. 2011, 126, 722–728. [Google Scholar] [CrossRef]
- Pak, S.Y.; Kim, H.M.; Kim, S.Y.; Youn, J.R. Synergistic improvement of thermal conductivity of thermoplastic composites with mixed boron nitride and multi-walled carbon nanotube fillers. Carbon 2012, 50, 4830–4838. [Google Scholar] [CrossRef]
- Chiang, T.H.; Hsieh, T.-E. A study of Encapsulation Resin Containing Hexagonal Boron Nitride (hBN) as Inorganic Filler. J. Inorg. Organomet. Polym. Mater. 2006, 16, 175–183. [Google Scholar] [CrossRef]
- Yu, J.; Mo, H.; Jiang, P. Polymer/boron nitride nanosheet composite with high thermal conductivity and sufficient dielectric strength. Polym. Adv. Technol. 2015, 26, 514–520. [Google Scholar] [CrossRef]
- Lindsay, L.; Broido, D.A. Enhanced thermal conductivity and isotope effect in single-layer hexagonal boron nitride. Phys. Rev. B 2011, 84, 155421–155426. [Google Scholar] [CrossRef]
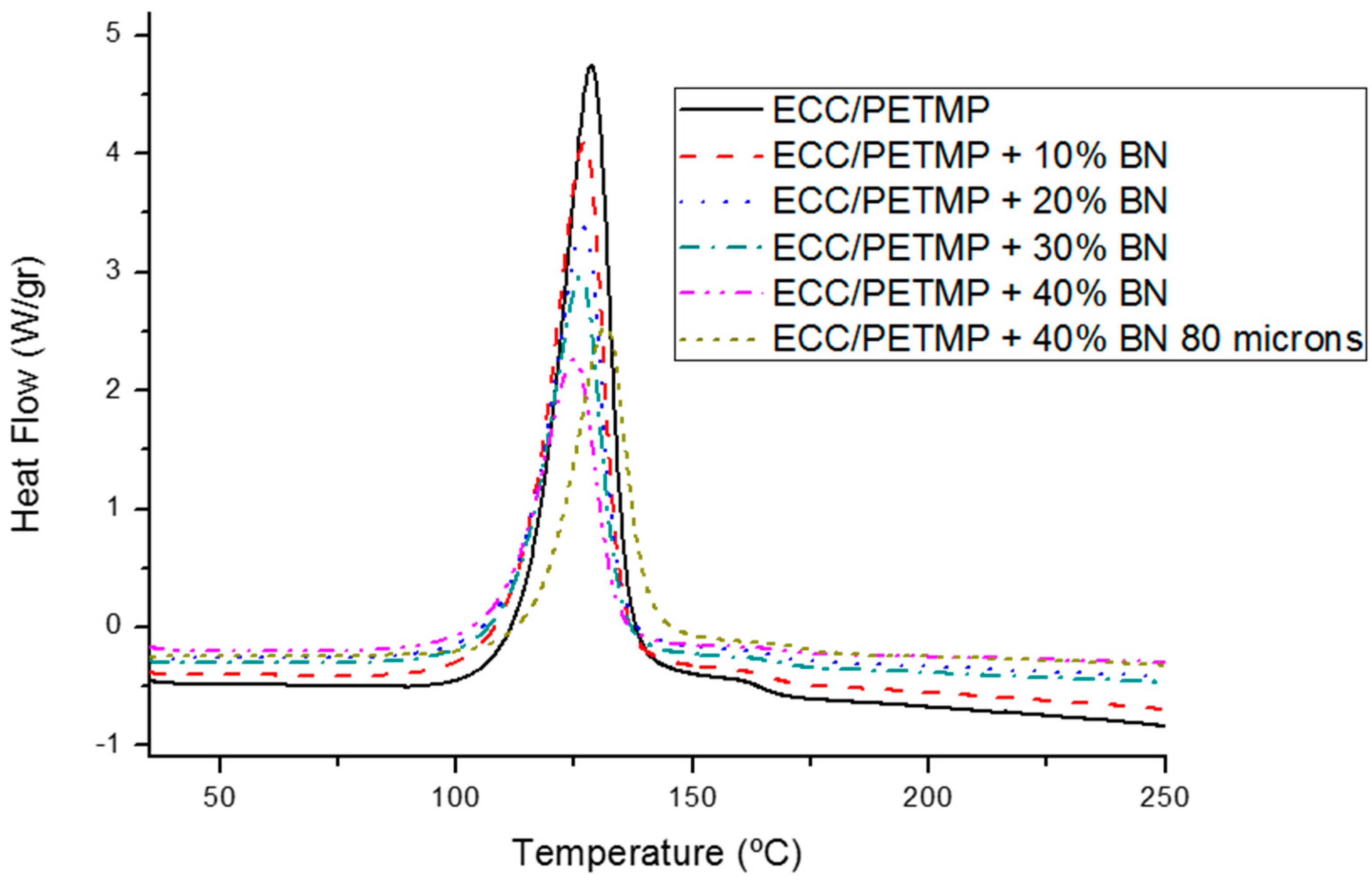



| BN (wt. %) | Tmax a (°C) | Δh b (J/g) | Δh b (kJ/ee) | Tg c (°C) |
|---|---|---|---|---|
| 0 | 127 | 479 | 120 | 58 |
| 10 | 126 | 436 | 121 | 58 |
| 20 | 126 | 376 | 118 | 57 |
| 30 | 125 | 337 | 121 | 57 |
| 40 | 124 | 272 | 114 | 57 |
| 40 (80 µm) | 131 | 276 | 116 | 58 |
| BN (wt. %) | G′slope a (Low Freq.) | G″slope a (Low Freq.) | tgel b (Min.) | xgel c (%) |
|---|---|---|---|---|
| 0 | 1.81 | 1.02 | 16.3 | 59 |
| 10 | 1.77 | 1.06 | 17.8 | 62 |
| 20 | 1.34 | 0.99 | 18.3 | 60 |
| 30 | 0.62 | 0.84 | 18.4 | 55 |
| 35 | 0.57 | 0.66 | - | - |
| 38 | 0.36 | 0.27 | - | - |
| 40 | 0.22 | 0.24 | 19.5 | 55 |
| 40 (80 µm) | 0.11 | 0.08 | - | - |
| BN (wt. %) | BN (vol %) | T2% a (°C) | Char Yield b (%) | CTEglass c (10−6·K−1) | CTErubber c (10−6·K−1) |
|---|---|---|---|---|---|
| 0 | 0 | 249 | 5.0 | 69 | 195 |
| 10 | 6.0 | 250 | 14.4 | 68 | 192 |
| 20 | 12.8 | 249 | 24.0 | 66 | 166 |
| 30 | 20.2 | 250 | 34.2 | 67 | 157 |
| 40 | 28.2 | 252 | 43.0 | 55 | 134 |
| 40 (80 µm) | 27.4 | 259 | 44.7 | 43 | 135 |
| BN (wt. %) | Young’s Modulus a (GPa) | Ttan δ b (°C) | E’rubber c (MPa) | Peakarea d | FWHM e (°C) |
|---|---|---|---|---|---|
| 0 | 2.3 | 75 | 6.9 | 1.37 | 13.7 |
| 10 | 2.4 | 74 | 10.4 | 1.28 | 14.6 |
| 20 | 3.6 | 73 | 19.6 | 1.27 | 14.8 |
| 30 | 4.5 | 73 | 31.9 | 1.13 | 16.0 |
| 40 | 5.6 | 74 | 61.2 | 0.90 | 16.8 |
| 40 (80 µm) | 4.0 | 71 | 78.5 | 0.88 | 19.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isarn, I.; Ramis, X.; Ferrando, F.; Serra, A. Thermoconductive Thermosetting Composites Based on Boron Nitride Fillers and Thiol-Epoxy Matrices. Polymers 2018, 10, 277. https://doi.org/10.3390/polym10030277
Isarn I, Ramis X, Ferrando F, Serra A. Thermoconductive Thermosetting Composites Based on Boron Nitride Fillers and Thiol-Epoxy Matrices. Polymers. 2018; 10(3):277. https://doi.org/10.3390/polym10030277
Chicago/Turabian StyleIsarn, Isaac, Xavier Ramis, Francesc Ferrando, and Angels Serra. 2018. "Thermoconductive Thermosetting Composites Based on Boron Nitride Fillers and Thiol-Epoxy Matrices" Polymers 10, no. 3: 277. https://doi.org/10.3390/polym10030277
APA StyleIsarn, I., Ramis, X., Ferrando, F., & Serra, A. (2018). Thermoconductive Thermosetting Composites Based on Boron Nitride Fillers and Thiol-Epoxy Matrices. Polymers, 10(3), 277. https://doi.org/10.3390/polym10030277







