Abstract
The development of a highly oriented fiber morphology by effect of tensile deformation of stereodefective isotactic polypropylene (iPP) samples, starting from the unoriented γ form, is studied by following the transformation in real time during stretching through wide angle X-ray scattering (WAXS) measurements. In the stretching process, after yielding, the initial γ form transforms into the mesomorphic form of iPP through mechanical melting and re-crystallization. The analysis of the scattering invariant measured in the WAXS region highlights that the size of the mesomorphic domains included in the well oriented fiber morphology obtained at high deformations increases through a process which involves the coalescence of the small fragments formed by effect of tensile stress during lamellar destruction with the domain of higher dimensions.
1. Introduction
The structural and morphological transformations of isotactic polypropylene (iPP) by effect of stretching have been widely studied [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. These studies are mainly concerned with iPP samples synthesized by Ziegler-Natta (ZN) heterogeneous catalyst systems [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. In general, ZN-iPP crystallizes from the melt in the α form, which shows high rigidity, and breaks at low deformations before yielding [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,21]. Therefore, the key to probing the mechanical response of iPP, in the α form up to high deformations, generally consists in crystallizing iPP from the melt at high cooling rates, to obtain more easily deformable samples, due to formation of thin lamellar crystals or of the mesophase [1,2,3,4,5,6,7,8,9,10,14].
More recently, the deformation behavior of metallocene-made iPP samples with a uniform distribution of stereodefects has been also studied [16,17,18,19,20]. These samples contain only one kind of stereo-defects, namely isolated rr triads, at concentrations in the range 0.5–11 mol % [16]. They crystallize from the melt as mixtures of the α and γ forms [22]. In particular, the relative amount of γ form increases with increasing the concentration of rr defects. Simultaneously, the values of the melting temperature and the degree of crystallinity decrease from 160 to 84 °C, and from 70% to 40%, respectively, and also the values of Young modulus decrease, from 200 to 19 MPa [16,18,22]. However, in spite of the relatively high values of melting temperature, crystallinity and Young modulus, these samples show high ductility, with values of deformation at break increasing with increasing the concentration of defects [16,18,22]. They define a class of materials with properties which can be finely tuned by introducing the tailored amount of rr defects in the reactor step [17,22]. Typically, properties of stiff-plastic materials with high melting temperatures are achieved at low defect concentrations, whereas at intermediate rr concentrations, the samples show properties of flexible-materials melting in the temperature range 115–120 °C, and achieve properties of elastomeric materials with high strength due to the high crystallinity (higher than 40%), melting at 80–110 °C, at high concentration of rr defects [22]. This behavior is clearly different from that of ZN-iPP, for which, the γ form may be obtained only at high pressures and in low molecular mass fractions [23].
The study of the structural and morphological transitions occurring by effect of stretching in metallocene-made iPP samples was studied both at unit cell and lamellar length scales, by performing wide (WAXS) and small (SAXS) angle X-ray scattering measurements [16,17,18,19,20]. In particular, WAXS analysis show that during the transformation of the initially isotropic spherulitic morphology into a well oriented fiber morphology by effect of stretching, the initial crystalline α and/or γ forms transform into a well-oriented mesophase [16,17,18,19,20], as in Ziegler-Natta iPP [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. The transformation into mesophase is gradual and starts occurring at deformations higher than the yielding point, that is concomitant with lamellar fragmentation (mechanical melting) and successive recrystallization into fibrils [17,18,19,20,24,25]. The critical strain at which the phase transition starts occurring depends on the stability of the crystal blocks initially present in the sample and the entanglement density of the amorphous phase [17,18,19,20,24,25]. SAXS analysis, instead, reveals that the main events occurring at low deformations are interlamellar separation and lamellar reorientation [19,20,26,27,28,29]. With increasing the deformation, chevron-like textures develop, followed by fragmentation of lamellae, and cavitation [19,20,29,30,31,32,33,34]. The fibrillary morphology obtained upon lamellar fragmentation is characterized by rod-like entities consisting of mesomorphic elongated aggregates separated by amorphous regions, placed at uncorrelated longitudinal and lateral distances [19].
In this paper, we focus on an aspect often neglected in performing the analysis of the WAXS data collected in real time during tensile deformation, that is the behavior of the scattering invariant defined in the WAXS region as a function of deformation. The analysis is illustrated in the case of two stereodefective metallocene iPP samples and has allowed highlighting a process of coalescence of mesomorphic fragments included in the well oriented fibers obtained at high deformations with consequent formation of larger domains.
2. Materials and Methods
Samples, synthesized using single site organometallic catalysts activated with methylalumoxane as described in ref. [35], are analyzed. The samples are characterized by molecular mass of ≈120 and ≈210 kg/mol, a polydispersity index close to two and a concentration of stereo-defects consisting solely of isolated rr triads equal to 5.92 and 11.01 mol % [22]. The samples show high level of crystallinity (≈40–55%), relatively high melting temperature, glass transition temperature around 0 °C, and crystallize from the melt almost completely in the γ form [22]. The main characteristics of these samples are shown in Table 1.

Table 1.
Molecular mass (Mv), melting temperature (Tm) and content of rr triads of iPP samples prepared by metallocene catalysts as described in ref. [22] a.
Specimens of rectangular shape and initial gauge length l0 of 3.0 mm, width w0 of 1.6 mm, and thickness t0 of 0.25 mm were cut from films obtained by melting the samples in a hot press up to reach a temperature 20–30 °C higher than the melting temperature determined in the DSC scans, using only a small pressure, and by cooling the melt to room temperature while fluxing cold water in the refrigerating system of the press (average cooling rate ≈ 10 °C/min).
The stretching experiments are performed at 25 °C while collecting in situ bidimensional WAXS patterns using the high flux available at the Synchrotron Radiation Source in Daresbury (Cheshire, UK, beam-line 16.1). The applied deformation rate is 2.36 mm/min, the wavelength of incident radiation is λ = 1.4 Å, and the WAXS images are collected at a rate of 1 frame/5 s. The size of the primary X-ray beam at the sample position is 0.1 × 0.1 mm2. The strong reflections of the unoriented film specimens are used to determine the correct beam center coordinates and the sample to detector distance. Roughly, the transmission factor is determined measuring the intensity of the direct beam (using an attenuator) in absence of the sample, and in presence of the sample, before stretching, and at the end of stretching experiment. In no case the sample was brought to the rupture. Raw WAXS data are reduced and analyzed using the home made software XESA [36]. In the experiments, the X-ray beam is incident on the central region of the specimens. In this way, the structural changes occurring by effect of mere uniaxial deformation with negligible shear components may be probed. The equatorial profiles are obtained by radial integration of WAXS intensity along arcs in slices spanning an angle of ±20° with respect to the horizontal axis (equator) of the bidimensional WAXS images. We checked that in the stretching conditions adopted for the in situ WAXS measurements, the samples experience uniform deformation. We found that the thickness t decreases according to a power law t = t0 (l0/l)ν, with ν comprised between 0.4 and 0.5, depending on the deformation, l being the gauge length of the deformed specimens [19,20]. In the calculation we set, for the sake of simplicity, ν ≈ 0.5, in the whole deformation range, as expected for ideal rubbery materials [37].
3. Results
The stress-strain curves and representative WAXS images collected in situ during stretching of compression-moulded specimens of the samples iPP-5.9 and iPP-11.0 are shown in Figure 1. The equatorial profiles extracted from the bidimensional WAXS images collected at relevant deformations are reported in Figure 2. The initial compression-moulded samples are crystallized from the melt in the γ form almost completely (patterns a of Figure 1) [19,20].
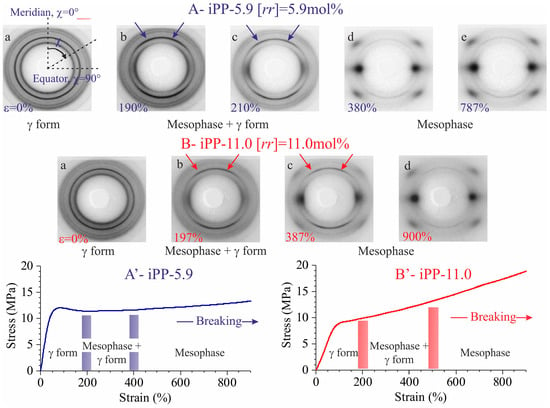
Figure 1.
Stress strain curves (A’,B’) and bidimensional WAXS patterns of the sample iPP-5.9 (A) and iPP-11.0 (B) at the indicated deformations. The critical values of deformation marking the beginning (εstart), and the complete (εend) transformation of the initial γ form into mesophase are indicated by the vertical bold lines in (A’,B’). The stretching direction is vertical. Arrows in b and c indicate the polarization of the (008)γ reflection of γ form, off the equator (horizontal direction) and off the meridian (vertical direction), defined in the image a of part A of the figure, occurring at low deformations, due to orientation of the crystals of the γ form with chain axes nearly perpendicular to the stretching direction (vide infra). The azimuthal angle χ is defined in the image a of part A.
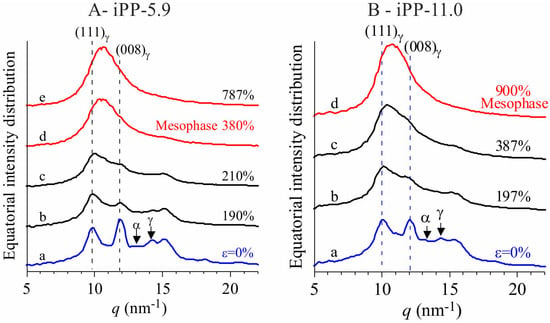
Figure 2.
Equatorial profiles extracted from the bidimensional WAXS images of Figure 1 for the samples iPP-5.9 (A) and iPP-11.0 (B). The relevant reflections of α and γ forms are indicated.
The WAXS images indicate that the γ form gradually transforms into the mesomorphic form of iPP by effect of deformation [16,17,18,19,20]. The transformation into mesophase starts at deformation εstart ≈ 200% and is complete at εend ≈ 400–500% (Figure 1 and Figure 2). In all cases a highly oriented fibrillary morphology is obtained already at the deformations marking the end of transition [19,20].
The textural transformations of the initially isotropically oriented morphology into a well-oriented fiber morphology is indicated by the change in distribution of intensity of the reflections along the azimuthal angle χ defined in the image a of Figure 1A. This is particularly evident for the changes in the azimuthal spreading of intensity at q ≈ 10 nm−1, corresponding to the reflection (111)γ of γ form at low deformations (images a–c of Figure 1 and curves a of Figure 2), and to the tail of the mesomorphic halo centered at q ≈ 11 nm−1 at high deformations (images d–e of Figure 1A, d of Figure 1B, curves d–e of Figure 2A, and d of Figure 2B). In fact, as shown in Figure 3, the azimuthal intensity distribution at q ≈ 10 nm−1 is uniform for the undeformed samples (curves a of Figure 3) and becomes polarized on the equator with increasing the deformation (curves b–e of Figure 3A and b–d of Figure 3B).
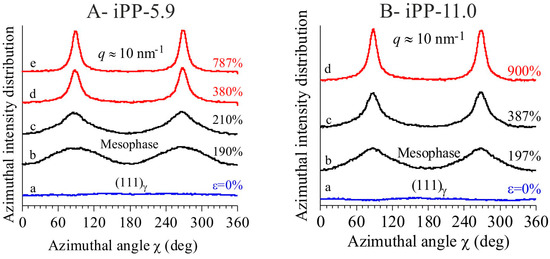
Figure 3.
Azimuthal profiles of intensity centered in the q region around 10 nm−1, extracted from the bidimensional WAXS images of Figure 1 for the samples iPP-5.9 (A) and iPP-11.0 (B).
The intensity at q ≈ 12 nm−1 relative to the (008)γ reflections of γ form (curves a of Figure 2), instead, at low deformations is polarized on a layer line off the equator (horizontal direction) and off the meridian (vertical direction), as indicated by the arrows in the images b, c of Figure 1, and only when the transformation into the mesophase is complete, that is, at deformations higher than εend, the intensity at q ≈ 12 nm−1 becomes polarized on the equator [19,20]. This indicates that part of the crystals of the initial γ form tend to become oriented at low deformations with the chain axes nearly perpendicular to the stretching direction, as shown in Figure 4, instead than parallel as in the standard fiber morphology [16,38]. It is worth noting that for the perpendicular chain axis orientation of γ form, the polarization of the (111)γ (at q ≈ 10 nm−1) reflection occurs on the equator [39].
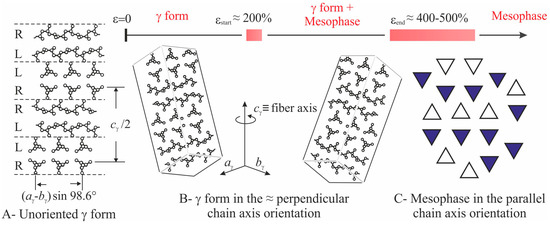
Figure 4.
Structural model of γ form (A), scheme of the perpendicular chain axis orientation of γ crystals (B) and of mesomorphic domains of iPP (C), as they develop by effect of stretching, starting from unoriented specimens.
4. Data Analysis and Discussion
The change of orientation of crystals by stretching is quantitatively analyzed using the azimuthal intensity at q ≈ 10 nm−1 of Figure 3. A numerical descriptor O that plays the role of an orientation order parameter is introduced from the calculation of the orientation function <P2> [40]. In general, for uniaxially symmetric materials (such as fibers) the orientation function for a direction normal (pole) to any given {hkl} family of planes <P2(cosχ)> with respect to a preferred direction (fiber axis) is defined as:
where <cosχ> is the average cosine of the angle χ that the poles make with the preferred direction and denotes the second order Legendre polynomial of argument <cosχ>. The values of <cosχ>, in turn, are calculated from the azimuthal intensity distribution of the hkl reflection as [40]:
According to Equation (1), <P2> = 1 corresponds to an ideal case of perfect alignment of the poles in the preferential direction, <P2> = 0 corresponds to isotropic case and <P2> = −0.5 corresponds to an ideal case of perfect perpendicular orientation.
In our case, the order parameter is calculated considering the degree of polarization of the intensity at q ≈ 10 nm−1 on the equator, with respect to the fiber axis. This would correspond to values of the orientation function <P2>exp ranging from zero at zero deformation (completely isotropic case) to values less than zero with increasing the deformation. The parameter O is calculated by comparing the experimental values of <P2>exp at q ≈ 10 nm−1 with that of an ideal model characterized by an extremely narrow equatorial polarization of intensity at this q (that is <P2>id = −0.5) as:
According to Equation (3), the values of O are positive and range from zero (fully isotropic case) to 1 (fully oriented case).
Since the polarization intensity on the equator at q ≈ 10 nm−1 originates from the perpendicular chain axis orientation of the residual γ form crystals at low and moderate deformations and from the parallel chain axis orientation of the already transformed mesomorphic domains at moderate and high deformations, the value of the parameter O represents a measure of the average degree of orientation of the chain axes with respect to the fiber axis only at high deformations, that is, after complete transformation of the original crystals of γ form into the mesophase, whereas at lower deformation, the values of O represents a measure of the average degree of orientation of the residual crystals of γ form in the perpendicular chain axis orientation, and of the transformed mesomorphic domains in the parallel chain axis orientation. The so obtained values of the parameter O derived for the iPP samples are reported in Figure 5A.
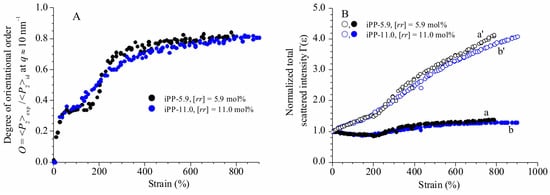
Figure 5.
Orientation parameter O (A) and total WAXS scattered intensity (invariant) normalized for the integrated intensity of the unoriented sample Γ(ε) (B) as a function of strain, for the samples iPP-5.9 (○, ●) and iPP-11.0 (○, ●). The parameter O is calculated from the azimuthal intensity distribution at q ≈ 10 nm−1 in the bi-dimensional WAXS images of Figure 1, corresponding to the reflection (111)γ of γ form at low deformations, to the tail of the mesomorphic halo centered at q ≈ 11 nm−1 at high deformations. It represents a measure of the average degree of orientation of the chain axes with respect to the fiber axis at high deformations (>εend), and to the average degree of orientation of the residual crystals of γ form in the perpendicular chain axis orientation, and of the transformed mesomorphic domains in the parallel chain axis orientation at deformations lower than εend. In (B), the curves a’ and b’ (open symbols) are obtained by multiplying the curves a and b (full symbols) by the factor t0/t = (l/l0)1/2 to account for the thickness contraction (see Experimental section).
The evolution of orientational order O with deformation (Figure 5A) of the two samples follows a common trend involving different steps. For deformations ε lower than 100%, a steep increment of the orientational order occurs, due to orientation of the crystals in the γ form with chains axes perpendicular to stretching direction. In the deformation range between 100 and ≈150–200%, the values of O reach a quasi-plateau of 0.30–0.4. This indicates that at low deformations, changes in azimuthal intensity distribution of (111)γ reflections of γ forms essentially probe small reorientation of the lamellar crystals along the pathway toward the fibrillary morphology, due to lamellar rotations [26,27,40]. The leading deformation mechanisms in the first plateau region, instead, correspond to interlamellar shear, that is slip of the crystalline lamellae parallel to each other, and/or interlamellar separation [26,27,28,41,42]. At this stage, no phase transitions occur and all movements are assisted by the shear deformation of the compliant interlamellar amorphous phase. Successively, starting from deformations close to the critical strain at which transformation into mesophase starts (εstart ≈ 200%, Figure 1 and Figure 4), the orientational order O increases again up to reach a final plateau value of ≈0.8 at high deformations (Figure 5A). This indicates that after lamellar breaking, further deformation induces collective shear process, up to reach destruction of the preexisting crystals (mechanical melting) and successive recrystallization with formation of fibrils including mesomorphic aggregates [24,25].
A further quantitative descriptor of the changes at WAXS length scale is obtained using the ratio Γ(ε) = Q(ε)/Q(0) between the total WAXS intensity Q(ε) at deformation ε and the total scattered intensity Q(0) at ε = 0. For samples exhibiting uniaxial symmetry (fibers), the total scattered intensity in the WAXS region Q(ε) can be calculated from the WAXS intensity collected on a bidimensional detector (Figure 1) by integrating all over the sampled reciprocal space, that is between qmin = 3 nm−1 and qmax = 22 nm−1, using Equation (4):
In Equation (4), it is implicitly assumed a uniform distribution of intensity along circles of radius q sinχ because of the cylindrical symmetry of the fibers. Moreover, the intensity, at any q, was subtracted for the background contribution (Bk(q)) estimated from the equation of the straight line subtending the radially averaged profiles extracted from the bi-dimensional diffraction images. The ratio of the total scattered intensity and the integrated intensity of the unoriented sample gives the normalized value of the total scattered intensity:
Equation (4) corresponds to a reduced scattering invariant [43]. The values of the parameter Γ(ε) are reported in Figure 5B as a function of deformation before (curves a, b) and after (curves a’, b’) correction for the thickness contraction.
Also in this case, we observe that the change of the parameter Γ(ε) with deformation follows a common trend for the two samples (Figure 5B). In particular, before correction for the thickness contraction, Γ(ε) decreases with increasing deformation up to ε ≈ 200%, then increases for further increment of deformation, up to reach a quasi-plateau at values close to 1.3–1.4 (curves a, b of Figure 5B). The decrease in Γ(ε) values of Figure 5B at deformations lower than 200% can be attributed to a decrease in the sample thickness. In fact, after correction for this effect only an increase of Γ(ε) with the deformation is observed (curves a’, b’ of Figure 5B). In particular, we use a correction factor equal to t0/t to account for the thickness contraction, by setting t0/t = (l/l0)ν with ν = 0.5 (see Section 2). Therefore, curves a, b and a’, b’ of Figure 5B illustrate the change of the parameter Γ(ε) with increasing the deformation, in the limiting cases of no thickness contraction (Poisson’s ratio = 0, curves a, b) and in the rubbery limit of thickness contraction, corresponding to Poisson’s ratio ν = 0.5 (curves a’, b’). The invariant is expected to change with deformation according to a behavior in between these two limiting cases.
After correction for the thickness contraction, the values of the WAXS reduced scattering invariant experience a remarkable increase with increasing the deformation, reaching values up to ≈4 times higher than those of the undeformed state. The remarkable increase of invariant with increasing deformation holds also after taking into account the absorption, since the correction of the scattered intensity for the transmission factor would decrease the values of the parameter Γ(ε) at most by a factor of 1.1.
The increase of the total scattering intensity in the WAXS region by a factor 1.3–1.4 in the hypothesis of no thickness contraction, and a factor ≈4 in the hypothesis of thickness contraction according to the rubbery limit is unexpected. In fact, for a multi-phases system (in our case three phases, γ form, mesophase and amorphous component), the measured WAXS intensity Iε(q,χ) can be written as a linear combination of the scattering intensities from each phase:
where Iεi(q,χ) are the scattering intensities of the γ form (phase i = 1), mesophase (phase i = 2) and amorphous component (phase i = 3) and xi(ε) are the corresponding mass fractions. Therefore, also the total WAXS reduced invariant Q(ε) (Equation (4)) is a linear combination of the contribution from components Qi(ε).
Each term of the invariant Qi(ε), in turn, is proportional to the following quantities [44,45]:
where ρi and Niε, are the electron density and the number of domains of phase i with average volume of coherence equal to Viε,. The Niε domains contribute additively to the scattering, whereas the coherent (elastic) scattering occurs only within each domain. The density of γ form, mesophase and amorphous phase in isotactic polypropylene are 0.939, 0.91 and 0.854 g/cm3 [46] and the corresponding values of electron density are 323, 313 and 294 electrons/nm3 respectively. Based on previous analyses [16,17,18], the total degree of crystallinity, due to the γ form and mesophase contributions, apparently, does not greatly change during deformation (x1(ε) + x2(ε) ≈ 0.50, see Table 1). Therefore, in the hypothesis that also the total volume of the coherently scattering crystalline domains does not change by effect of deformation (N1ε V1ε, + N2ε V2ε, = cost.), the scattering invariant is expected to remain constant or to slightly decrease with increasing the deformation, since the γ form transforms into the mesophase with slightly lower electron density.
The tendency of the scattering invariant to increase at deformations lower than εstart marking the beginning of transformation of the initial γ form into mesophase, may be due to local “densification” of the amorphous intralamellar phase by effect of stretching, since the intralamellar amorphous phase experiences compressive forces in the direction parallel or perpendicular to the layers, depending on the orientation, perpendicular or parallel to the stretching direction, respectively, of the lamellar stacks in which the amorphous layers are embedded [2,20]. At deformations higher than εstart, marking also the beginning of lamellar destruction, we hypothesize that the increase of invariant may be due to a slight increase of the size of coherent domains located in the mesomorphic aggregates, leading to a remarkable increase of their average volumes V2ε, even though the total number of these domains N2ε does not necessarily change. This increase may involve the incorporation of isolated chains, or groups of 2–3 chains located at the boundaries of adjacent domains, into close neighboring larger domains through small movements and/or rotations facilitated by deformation, as shown in the model of Figure 6.
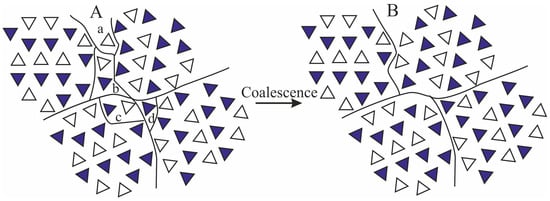
Figure 6.
Model of coalescence of mesomorphic domains separated at the boundaries by isolated groups of 1–2 chains (sub-domains a–d) in a completely different arrangement (A) with formation of larger mesomorphic domains (B). By effect of stretching, the sub-domains a–d coalesce with close-neighbors mesomorphic domains.
Moreover, considering that the mesophase originates from the breaking of crystals of γ form through a process of mechanical melting and re-crystallization, and that the lamellar crystals of γ form are not characterized by chain folding because of the non-parallel arrangement of the chains (Figure 4A) [47], the size of the coherent domains in a mesomorphic aggregate may easily increase by effect of stretching also in the direction parallel to the chain axes, through incorporation of monomeric units located at the boundaries with the amorphous phase. We calculate that, on average, an increase of the coherent length by a factor of 1.1–1.6 along the three orthogonal directions x, y and z of a domain, leads to an increase of volume by a factor 1.13–1.63 ≈ 1.3–4. As shown in the model of Figure 6, the increase of the coherent length of the mesomorphic domains by incorporation (coalescence) of the isolated sub-domains a-d within the mesomorphic domains, does not necessarily lead to a decrease of the number of domains N2ε. As a consequence, the total scattering intensity increases by effect of deformation, because the product (N2εV2ε) increases due to coalescence phenomena of the kind depicted in Figure 6.
On the other hand, the fact that the crystallinity index measured from the radially averaged WAXS profiles as the ratio between the area of the crystalline phase (Ac) and the total area of the diffraction profile (Atot) does not apparently change (see Figure 7A), is due to the fact that Ac is often overestimated in this procedure, as it is obtained by the difference of Atot and the diffraction area from the amorphous component (approximated in Figure 7A by the diffraction profile of an atactic polypropylene, curve b). In other terms, the crystallinity calculated from the radially averaged WAXS curves according to the procedure of Figure 7A, includes not only the Bragg contribution, but also diffuse scattering located in the diffraction region between the amorphous halo and the Bragg peaks (Figure 7A). Instead, in the experimental value of the scattering invariant, the diffuse scattering terms makes a contribution, which is at least one order of magnitude lower than the Bragg component. Diffuse scattering arises from the presence of disorder and its contribution to the scattering intensity is proportional to the fluctuations of the structure factor f (per monomeric unit), given by the term <f 2> − <f>2, which represent the difference between the average square (<f 2>) and the square of average (<f>2) of f [48]. Therefore, the higher the local structure factor deviates from the average value <f> because of the presence of disorder, the higher the fluctuations, and the higher the diffuse scattering. By effect of coalescence of the small sub-domains into the large domains, the diffuse scattering decreases and the interference term (Bragg-like contribution) increases. The WAXS invariant increases, because the diffuse scattering term is always lower than the Bragg term.
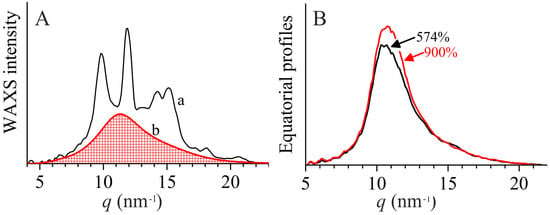
Figure 7.
(A) Radially averaged WAXS profile of the undeformed sample iPP-5.9, extracted from the bidimensional WAXS image a of Figure 1A (a) and underlying amorphous contribution, approximated by the diffraction profile of an atactic polypropylene (b). (B) Equatorial profiles extracted from the bidimensional WAXS images of Figure 1B, of the sample iPP-11.0 stretched at 574 and 900% deformations. The diffraction curves are subtracted for the background contribution, approximated as a straight line subtending the whole profiles.
In order to probe the effective increase of the size of the mesomorphic domains by effect of stretching, we compare in Figure 7B the equatorial profiles of the sample iPP-11.0 stretched at 574 and 900% deformations. The curves are not corrected for the thickness contraction, but only for the transmission factor. Yet, it is evident that at 900% deformation the equatorial peak of the mesophase becomes narrower than that at 574% deformation, confirming the increase of the lateral size of the mesomorphic domains. It is worth noting that the maximum is shifted toward slightly higher q values at 900% deformation, indicating that the average correlation distance between the chain axes within the mesomorphic domains decreases, producing increase of electron density. Therefore, the increase of the scattering invariant is not only due to coarsening, but also to increase of electron density (densification).
5. Conclusions
The structural transformations occurring by effect of stretching in stereo-irregular isotactic polypropylene samples are studied in situ during deformation by collecting WAXS patterns. The metallocene-made iPP samples selected in this study show high ductility, allowing achieving high deformations before breaking.
WAXS analysis reveals that the crystals of γ form tend to assume a nearly perpendicular chain axis orientation instead than parallel to the stretching direction at low deformations. At ≈200% deformation (εstart) the γ form starts transforming into the mesomorphic form of iPP, and at 400–500% deformation (εend), the transformation is almost complete. The stress induced phase transition of the γ form into the mesophase occurs after the beginning of lamellar fragmentation, concomitant with destruction of the crystalline blocks (mechanical melting) and re-crystallization in fibrillary entities containing mesomorphic aggregates. At the end of transformation into mesophase, a fibrillary morphology develops with a high degree of orientational order of the chain axes parallel to the stretching direction. We show that the chains extracted from the original crystals re-crystallize forming aggregates of mesomorphic domains responsible for the coherent elastic scattering (Bragg-like contribution) which include at the boundaries isolated chains or groups of 2–3 chains, which contribute to diffuse scattering. The coalescence process of these chains with the larger mesomorphic domains, increases the volume of coherence of the mesomorphic domains. Since the number of coherent domains does not decrease, the WAXS scattering invariant increases by effect of coalescence during deformation, even if the sampled q region is narrow. Coalescence starts concomitant with the process of lamellar destruction, and beginning of transformation of the initial γ form into the mesophase and, after complete transformation into the mesomorphic form, continues facilitated by the mechanical stress field.
Acknowledgments
Paul Sotta, from CNRS/Solvay-France, is acknowledged for the useful discussions.
Author Contributions
Finizia Auriemma and Claudio De Rosa conceived the experiments. Finizia Auriemma wrote the manuscript. Simona Esposito, Geoffrey Robert Mitchell, Rocco Di Girolamo and Miriam Scoti performed the experiments. Geoffrey Robert Mitchell developed the program for data analysis. Finizia Auriemma, Simona Esposito and Anna Malafronte performed the data analysis.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peterlin, A. Molecular model of drawing polyethylene and polypropylene. J. Mater. Sci. 1971, 6, 490–508. [Google Scholar] [CrossRef]
- Aboulfaraj, M.; G’Sell, C.; Ulrich, B.; Dahoun, A. In situ observation of the plastic deformation of polypropylene spherulites under uniaxial tension and simple shear in the scanning electron microscope. Polymer 1995, 36, 731–742. [Google Scholar] [CrossRef]
- Ran, S.; Zong, X.; Fang, D.; Hsiao, B.S.; Chu, B.; Phillips, R.A. Structural and morphological studies of isotactic polypropylene fibers during heat/draw deformation by in situ synchrotron SAXS/WAXS. Macromolecules 2001, 34, 2569–2578. [Google Scholar] [CrossRef]
- Zuo, F.; Keum, J.K.; Chen, X.M.; Hsiao, B.S.; Chen, H.Y.; Lai, S.Y.; Wevers, R.; Li, J. The Role of Interlamellar Chain Entanglement in Deformation-Induced Structure Changes during Uniaxial Stretching of Isotactic Polypropylene. Polymer 2007, 48, 6867–6880. [Google Scholar] [CrossRef]
- Pawlak, A.; Galeski, A. Cavitation during Tensile Deformation of Polypropylene. Macromolecules 2008, 41, 2839–2851. [Google Scholar] [CrossRef]
- Ma, Z.; Shao, C.; Wang, X.; Zhao, B.; Li, X.; An, H.; Yan, T.; Li, Z.; Li, L. Critical stress for drawing-induced α-crystal-mesophase transition in isotactic polypropylene. Polymer 2009, 50, 2706–2715. [Google Scholar] [CrossRef]
- Liu, Y.P.; Hong, Z.H.; Bai, L.G.; Tian, N.; Ma, Z.; Li, X.Y.; Chen, L.; Hsiao, B.S.; Li, L. A Novel Way to Monitor the Sequential Destruction of Parent-Daughter Crystals in Isotactic Polypropylene under Uniaxial Tension. J. Mater. Sci. 2014, 49, 3016–3024. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, Y.T.; Chen, R.; Zhao, J.Y.; Jiang, Z.Y.; Men, Y.F. Cavitation in lsotactic Polypropylene at Large Strains during Tensile Deformation at Elevated Temperatures. Macromolecules 2015, 48, 5799–5806. [Google Scholar] [CrossRef]
- Krajenta, A.; Rozanski, A. The Influence of Cavitation Phenomenon on Selected Properties and Mechanisms Activated During Tensile Deformation of Polypropylene. J. Polym. Sci. Part B 2016, 54, 1853–1868. [Google Scholar] [CrossRef]
- Kang, J.; Yuan, S.; Hong, Y.-L.; Chen, W.; Kamimura, A.; Otsubo, A.; Miyoshi, M. Unfolding of Isotactic Polypropylene under Uniaxial Stretching. ACS Macro Lett. 2016, 5, 65–68. [Google Scholar] [CrossRef]
- Lezak, E.; Bartczak, Z.; Galeski, A. Plastic Deformation of the γ Phase in Isotactic Polypropylene in Plane-Strain Compression. Macromolecules 2006, 39, 4811–4819. [Google Scholar] [CrossRef]
- Caelers, H.; Govaert, L.; Peters, G. The prediction of mechanical performance of isotactic polypropylene on the basis of processing conditions. Polymer 2016, 83, 116–128. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, R.; Zhao, J.; Jiang, Z.; Men, Y. Stretching Temperature Dependency of Fibrillation Process in Isotactic Polypropylene. J. Phys. Chem. B 2017, 121, 6969–6978. [Google Scholar] [CrossRef] [PubMed]
- Caelers, H.J.M.; Troisi, E.M.; Govaert, L.E.; Peters, G.W.M. Deformation-Induced Phase Transitions in iPP Polymorphs. Polymers 2017, 9, 547. [Google Scholar] [CrossRef]
- Xu, W.; Martin, D.; Arruda, E. Finite strain response, microstructural evolution and β→α phase transformation of crystalline isotactic polypropylene. Polymer 2005, 46, 455–470. [Google Scholar] [CrossRef]
- De Rosa, C.; Auriemma, F.; De Lucia, G.; Resconi, L. From stiff plastic to elastic polypropylene: Polymorphic transformations during plastic deformation of metallocene-made isotactic polypropylene. Polymer 2005, 46, 9461–9475. [Google Scholar] [CrossRef]
- De Rosa, C.; Auriemma, F. Structural-mechanical phase diagram of isotactic polypropylene. J. Am. Chem. Soc. 2006, 128, 11024–11025. [Google Scholar] [CrossRef] [PubMed]
- De Rosa, C.; Auriemma, F. Stress-induced phase transitions in metallocene-made isotactic polypropylene. Lect. Notes Phys. 2007, 714, 345–371. [Google Scholar]
- Auriemma, F.; De Rosa, C.; Di Girolamo, R.; Malafronte, A.; Scoti, M.; Mitchell, G.R.; Esposito, S. Deformation of Stereoirregular Isotactic Polypropylene across Length Scales: Influence of Temperature. Macromolecules 2017, 50, 2856–2870. [Google Scholar] [CrossRef]
- Auriemma, F.; De Rosa, C.; Di Girolamo, R.; Malafronte, A.; Scoti, M.; Mitchell, G.R.; Esposito, S. Relationship Between Molecular Configuration and Stress-Induced Phase Transitions. In Controlling the Morphology of Polymers; Mitchell, G.R., Tojeira, A., Eds.; Springer: Berlin, Germany, 2016; pp. 287–327. [Google Scholar]
- De Rosa, C.; Auriemma, F. The deformability of polymers: The role of disordered mesomorphic crystals and stress-induced phase transformations. Angew. Chem. Int. Ed. 2012, 51, 1207–1211. [Google Scholar] [CrossRef] [PubMed]
- De Rosa, C.; Auriemma, F.; Di Capua, A.; Resconi, L.; Guidotti, S.; Camurati, I.; Nifant’ev, I.E.; Laishevtsev, I.P. Structure-property correlations in polypropylene from metallocene catalysts: Stereodefective, regioregular isotactic polypropylene. J. Am. Chem. Soc. 2004, 126, 17040–17049. [Google Scholar] [CrossRef] [PubMed]
- Mezghani, K.; Phillips, P. The γ-phase of high molecular weight isotactic polypropylene: III. The equilibrium melting point and the phase diagram. Polymer 1998, 39, 3735–3744. [Google Scholar] [CrossRef]
- Hiss, R.; Hobeika, S.; Lynn, C.; Strobl, G. Network Stretching, Slip Processes, and Fragmentation of Crystallites during Uniaxial Drawing of Polyethylene and Related Copolymers. A Comparative Study. Macromolecules 1999, 32, 4390–4403. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Tang, Y.J.; Rieger, J.; Enderle, H.F.; Lilge, D.; Roth, S.V.; Gehrke, R.; Wu, Z.H.; Li, Z.H.; Men, Y.F. Structural Evolution of Tensile Deformed High-Density Polyethylene at Elevated Temperatures: Scanning Synchrotron Small- and Wide-Angle X-Ray Scattering Studies. Polymer 2009, 50, 4101–4111. [Google Scholar] [CrossRef]
- Bowden, P.B.; Young, R.J. Deformation mechanisms in crystalline polymers. J. Mater. Sci. 1974, 9, 2034–2051. [Google Scholar] [CrossRef]
- Lin, L.; Argon, A.S. Structure and plastic deformation of polyethylene. J. Mater. Sci. 1994, 29, 294–323. [Google Scholar] [CrossRef]
- Schultz, J.M. Polymer Materials Science; Prentice Hall: Englewood Cliffs, NJ, USA, 1974. [Google Scholar]
- Galeski, A. Strength and toughness of crystalline polymer systems. Prog. Polym. Sci. 2003, 28, 1643–1699. [Google Scholar] [CrossRef]
- Pawlak, A.; Galeski, A. Plastic deformation of crystalline polymers: The role of cavitation and crystal plasticity. Macromolecules 2005, 38, 9688–9697. [Google Scholar] [CrossRef]
- Pawlak, A.; Galeski, A. Cavitation and morphological changes in polypropylene deformed at elevated temperatures. J. Polym. Sci. Part B 2010, 48, 1271–1280. [Google Scholar] [CrossRef]
- Pawlak, A. Cavitation during tensile deformation of isothermally crystallized polypropylene and high-density polyethylene. Colloid Polym. Sci. 2013, 291, 773–787. [Google Scholar] [CrossRef] [PubMed]
- Read, D.; Duckett, R.; Sweeney, J.; Mcleish, T. The chevron folding instability in thermoplastic elastomers and other layered material. J. Phys. D Appl. Phys. 1999, 32, 2087–2099. [Google Scholar] [CrossRef]
- Krumova, M.; Henning, S.; Michler, G. Chevron morphology in deformed semicrystalline polymers. Philos. Mag. 2006, 86, 1689–1712. [Google Scholar] [CrossRef]
- Nifant’ev, I.E.; Laishevtsev, I.P.; Ivchenko, P.V.; Kashulin, I.A.; Guidotti, S.; Piemontesi, F.; Camurati, I.; Resconi, L.; Klusener, P.A.A.; Rijsemus, J.J.H.; et al. C1-symmetric heterocyclic zirconocenes as catalysts for propylene polymerization, 1: Ansa-zirconocenes with linked dithienocyclopentadienyl-substituted cyclopentadienyl ligands. Macromol. Chem. Phys. 2004, 205, 2275–2291. [Google Scholar] [CrossRef]
- Mitchell, G.R. XESA Reference Manual; Institute Polytechnic Leira: Leiria, Portugal, 2016. [Google Scholar]
- Nitta, K.-H.; Yamana, M. Rheology; De Vicente, J., Ed.; InTech: London, UK, 2012; ISBN 978-953-51-0187-1. Available online: http://www.intechopen.com/books/rheology/poisson-s-ratio-and-mechanical-nonlinearity-undertensile-deformation (accessed on 7 February 2018).
- Geddes, A.J.; Parker, K.D.; Atkins, E.D.T.; Beighton, E. “Cross-β” conformation in proteins. J. Mol. Biol. 1968, 32, 343–358. [Google Scholar] [CrossRef]
- Auriemma, F.; De Rosa, C. Stretching Isotactic Polypropylene: From “cross-β” to Crosshatches, from α Form to γ Form. Macromolecules 2006, 39, 7635–7647. [Google Scholar] [CrossRef]
- Alexander, L.E. X-ray Diffraction Methods in Polymer Science; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Humbert, S.; Lame, O.; Chenal, J.; Rochas, C.; Vigier, G. Small strain behavior of polyethylene: In situ SAXS measurements. J. Polym. Sci. B 2010, 48, 1535–1542. [Google Scholar] [CrossRef]
- Séguéla, R. Dislocation approach to the plastic deformation of semicrystalline polymers: Kinetic aspects for polyethylene and polypropylene. J. Polym. Sci. B 2002, 40, 593–601. [Google Scholar] [CrossRef]
- Roe, R.-J. Methods of X-ray and Neutron Scattering in Polymer Science; Oxford University Press: New York, NY, USA, 2000; ISBN-10 0195113217. [Google Scholar]
- Krogh-Moe, J. A Method for Converting Experimental X-ray Intensities to an Absolute Scale. Acta Cryst. 1956, 9, 951–953. [Google Scholar] [CrossRef]
- Norman, N. The Fourier Transform Method for Normalizing Intensities. Acta Cryst. 1957, 10, 370–373. [Google Scholar] [CrossRef]
- Brandrup, J.; Immergut, E.H. (Eds.) Polymer Handbook, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Meille, S.V.; Brückner, S. Non-parallel chains in crystalline g-isotactic polypropylene. Nature 1989, 340, 455–457. [Google Scholar] [CrossRef]
- De Rosa, C.; Auriemma, F. Crystals and Crystallinity in Polymers: Diffraction Analysis of Ordered and Disordered Crystals; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).