Calibration of a Cohesive Model for Fracture in Low Cross-Linked Epoxy Resins
Abstract
1. Introduction
2. Mechanical Response of the Epoxy Resin RTM: Experiments and Modeling
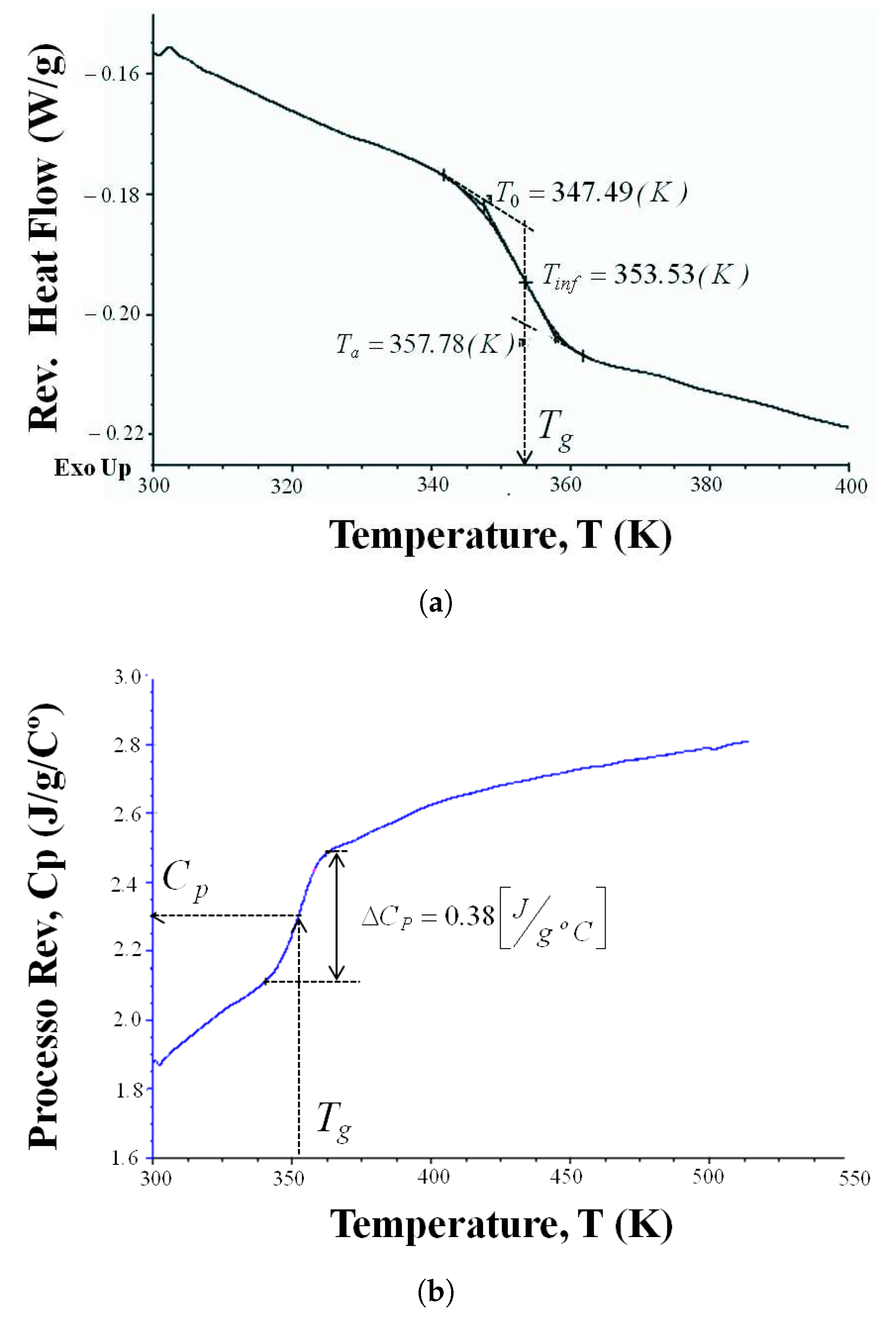
2.1. Preparation of the Material and Characterization
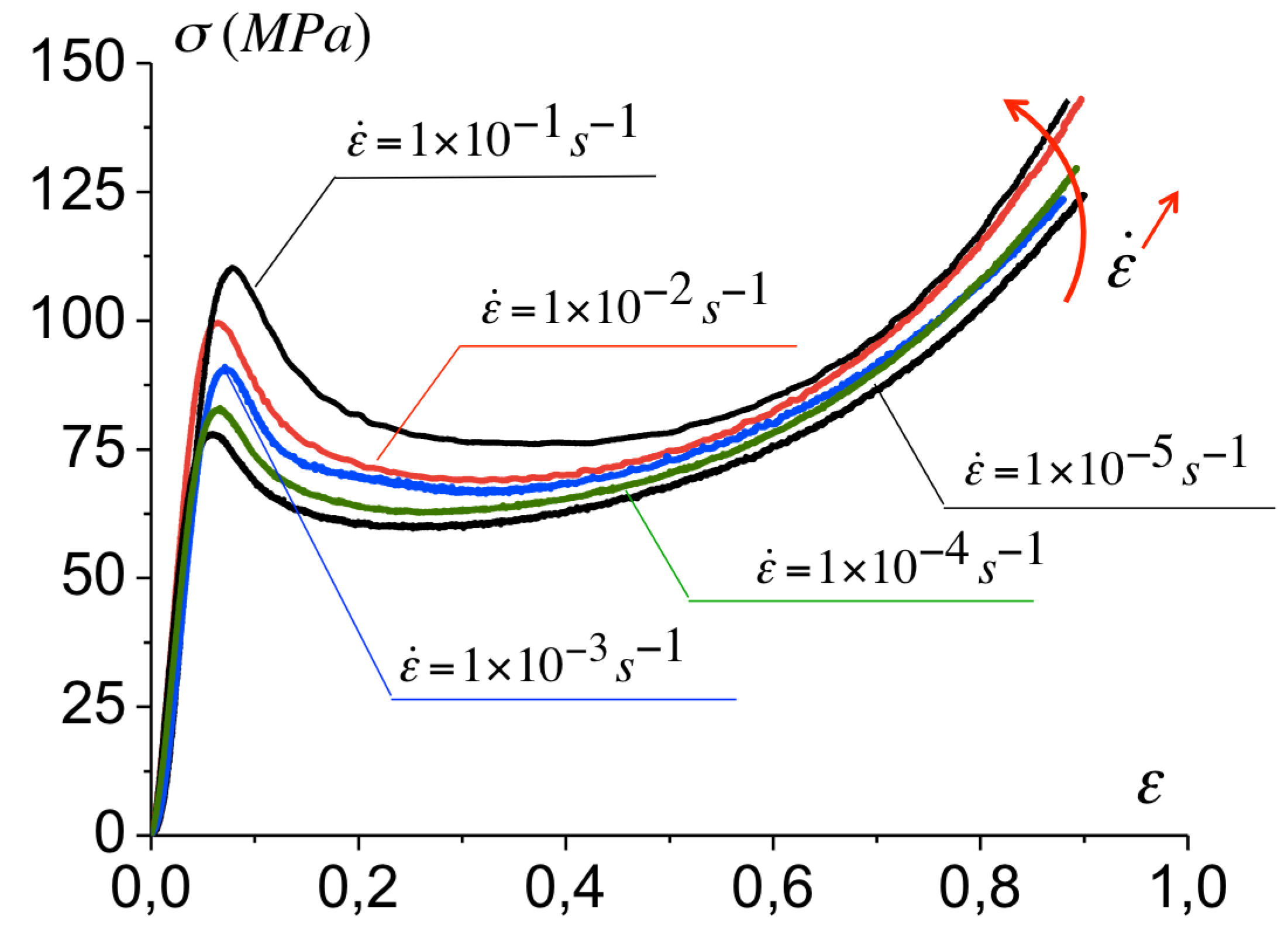
2.2. Mechanical Response under Uniaxial Compression
2.3. Constitutive Model for the Epoxy Resin RTM
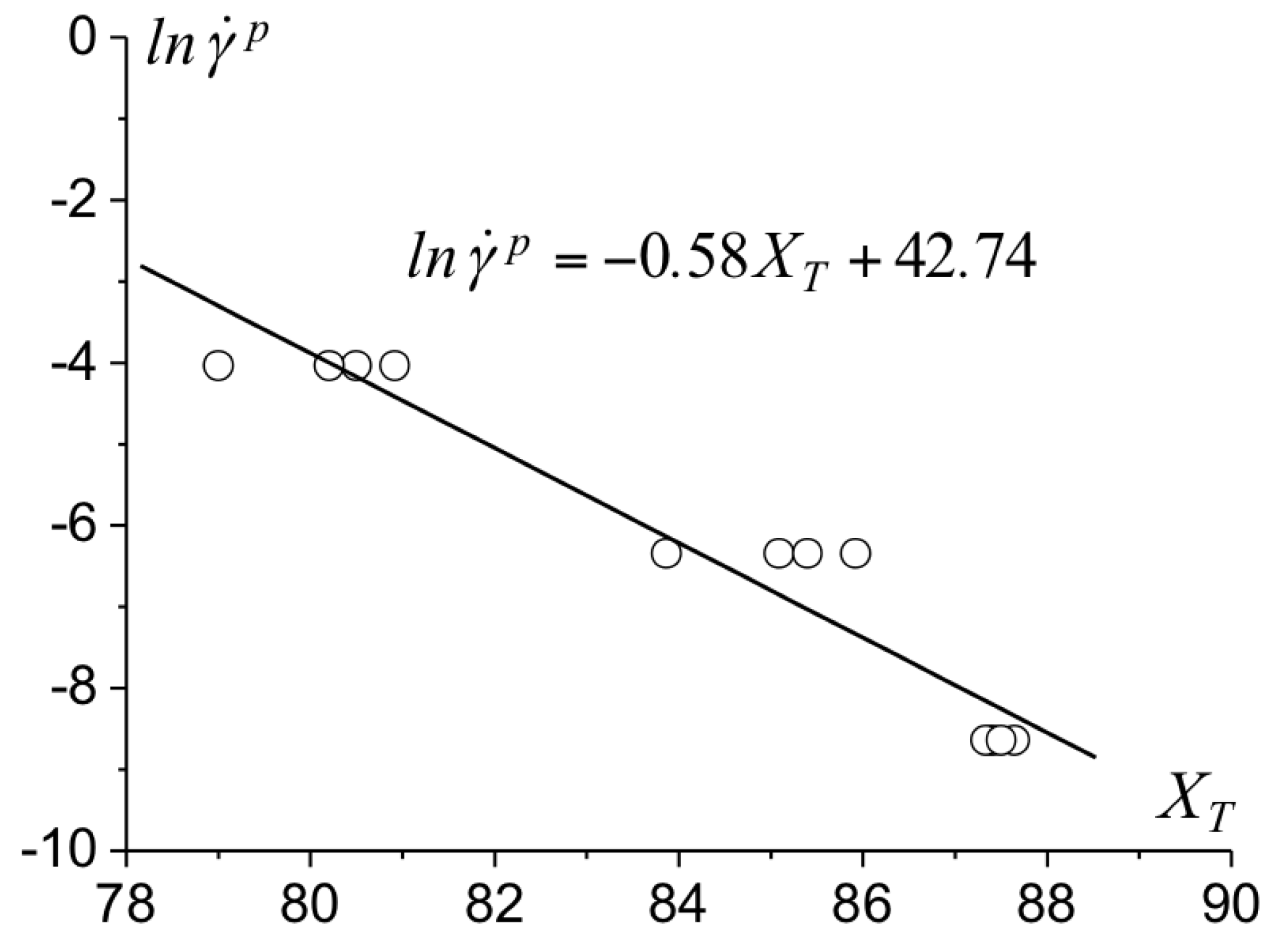
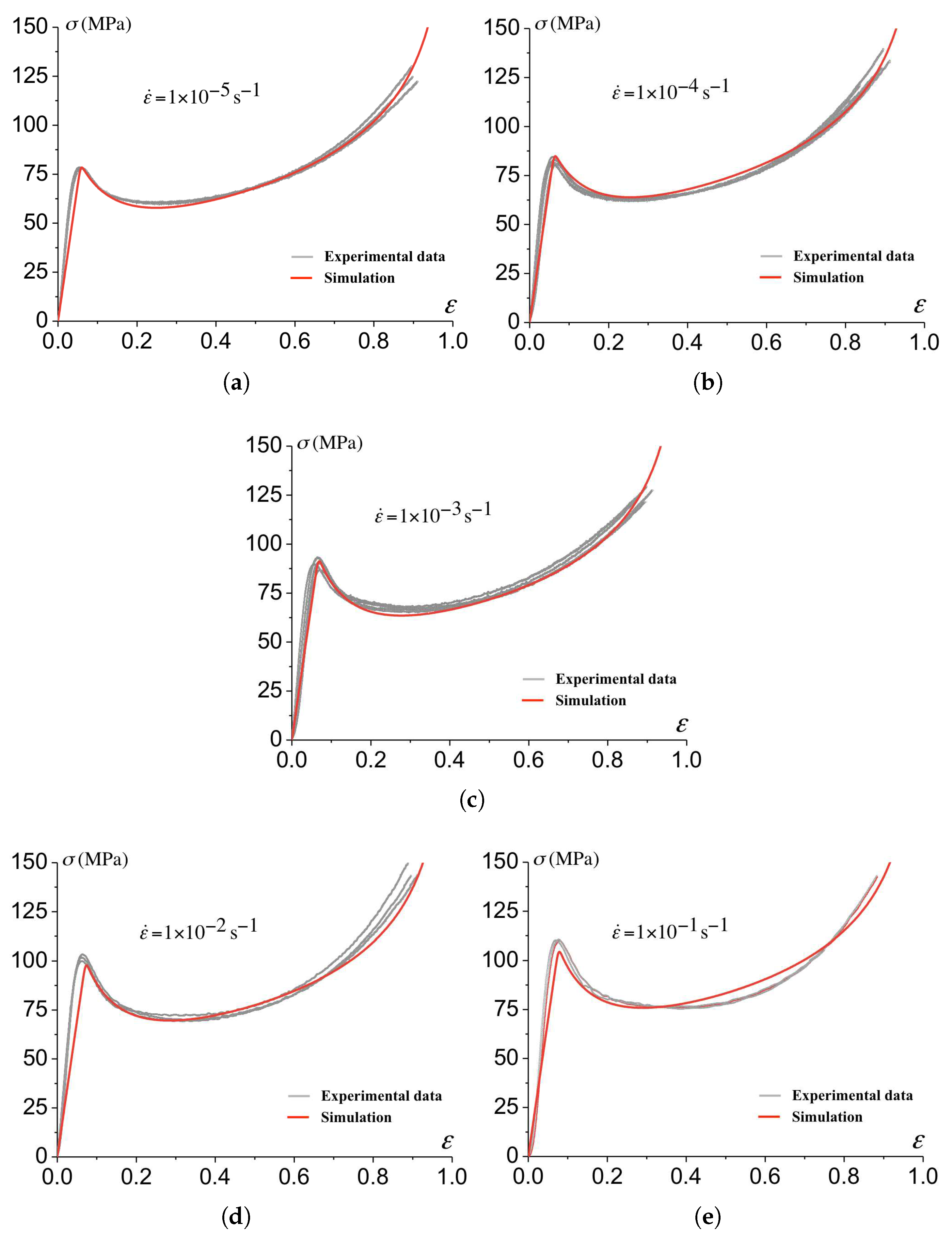
2.4. Identification of Bulk Parameters for the Epoxy Resin
3. Modeling of the Fracture Process with a Rate-Dependent Cohesive Model: Fracture Tests, Experiments and Simulations
3.1. Preparation of the Samples
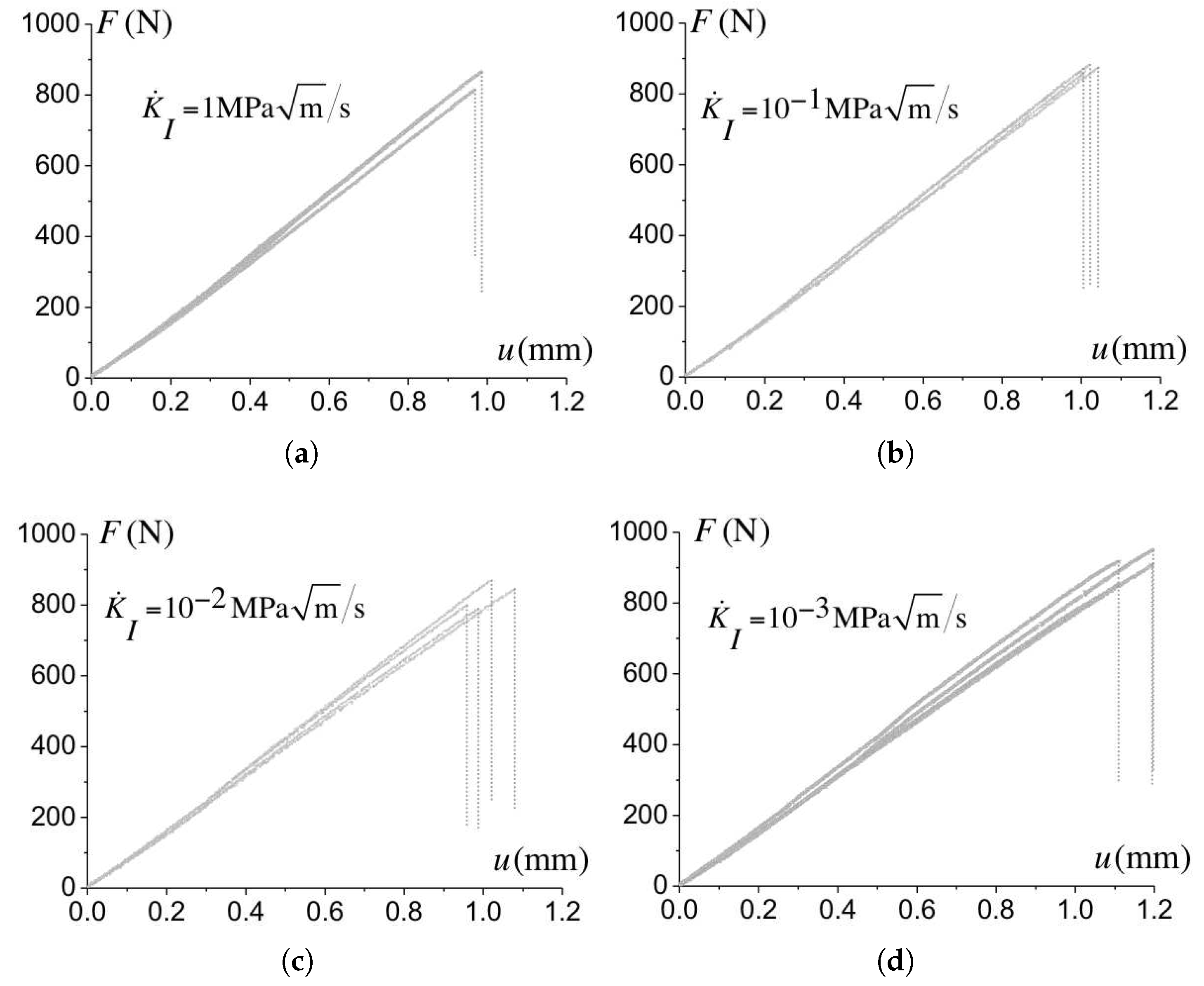
3.2. Fracture Response under Mode I
3.3. Rate-Dependent Cohesive Zone Model for Failure in Epoxy Resin
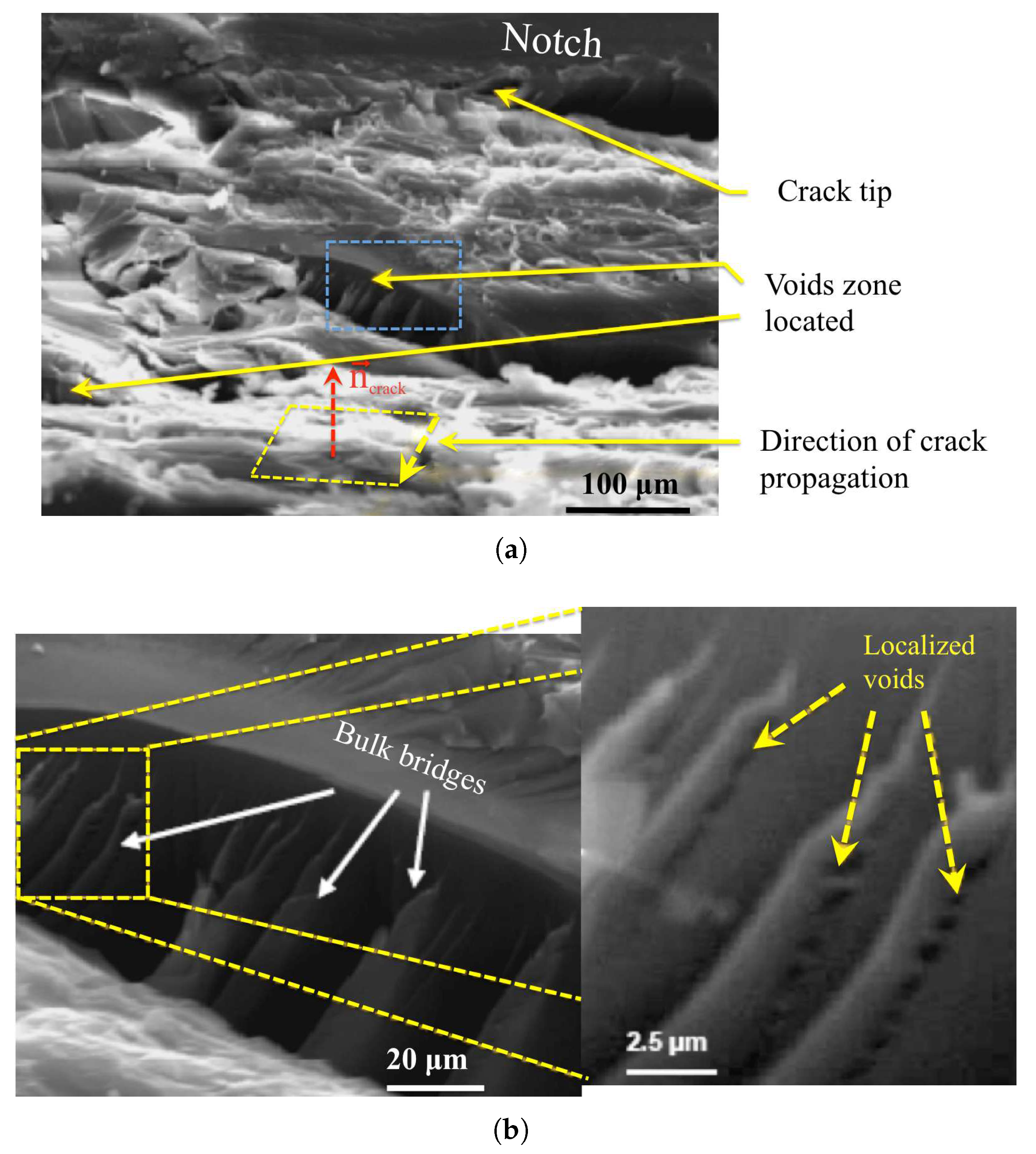
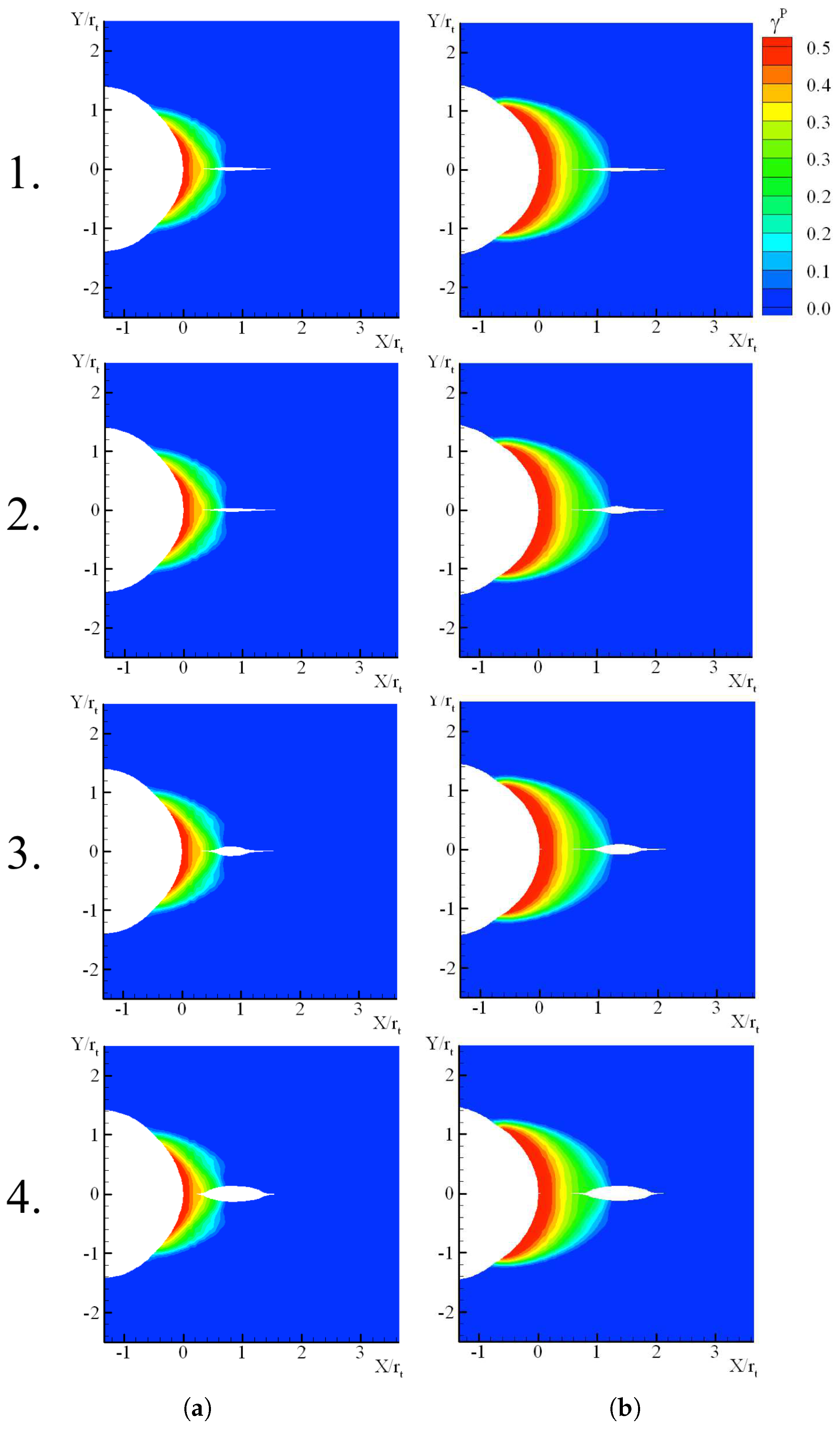
3.4. Description of the Failure Process in Low Cross-Link Epoxy
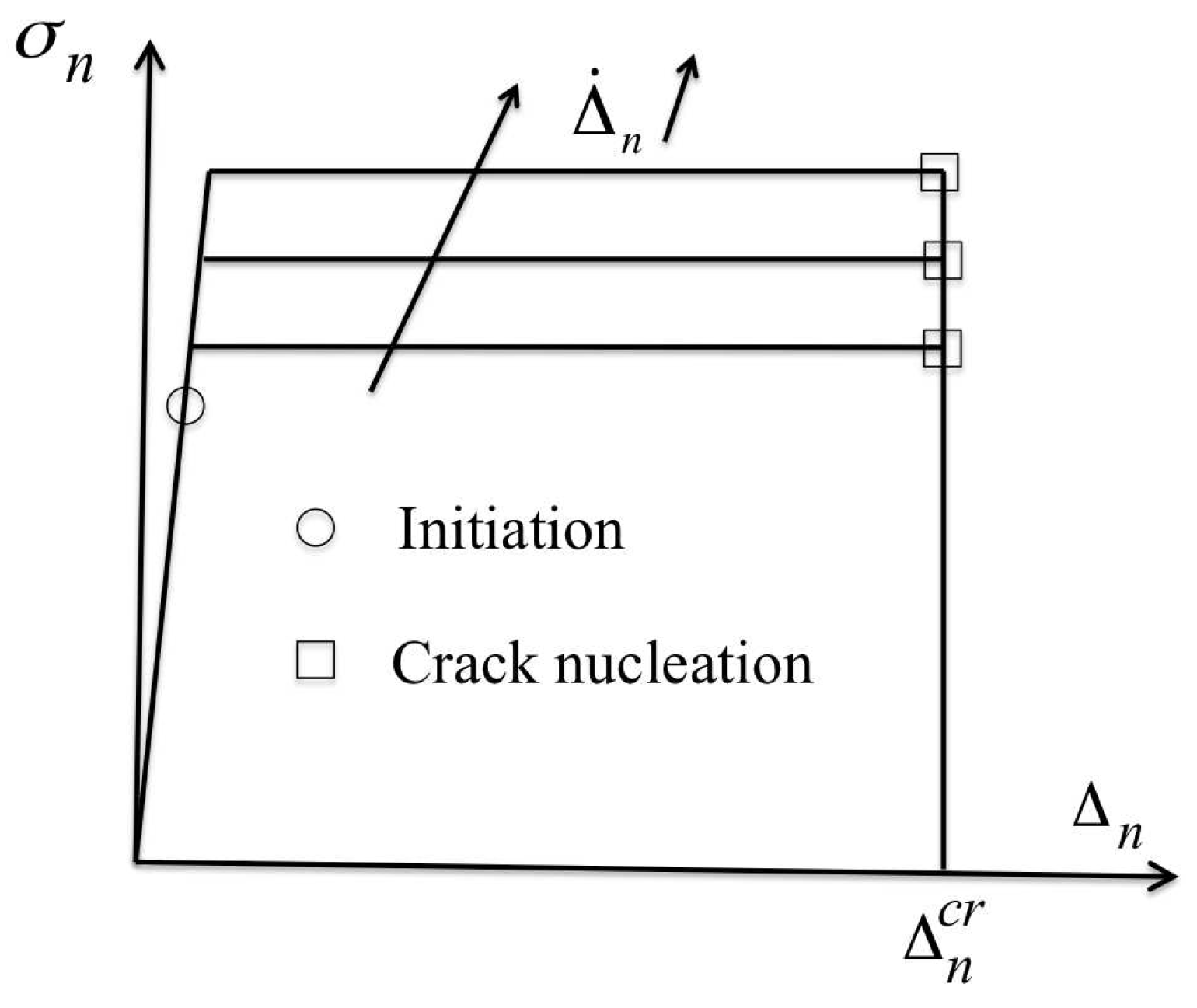
3.4.1. Initiation
3.4.2. Damage Zone and Cohesive Thickening
3.4.3. Crack Nucleation
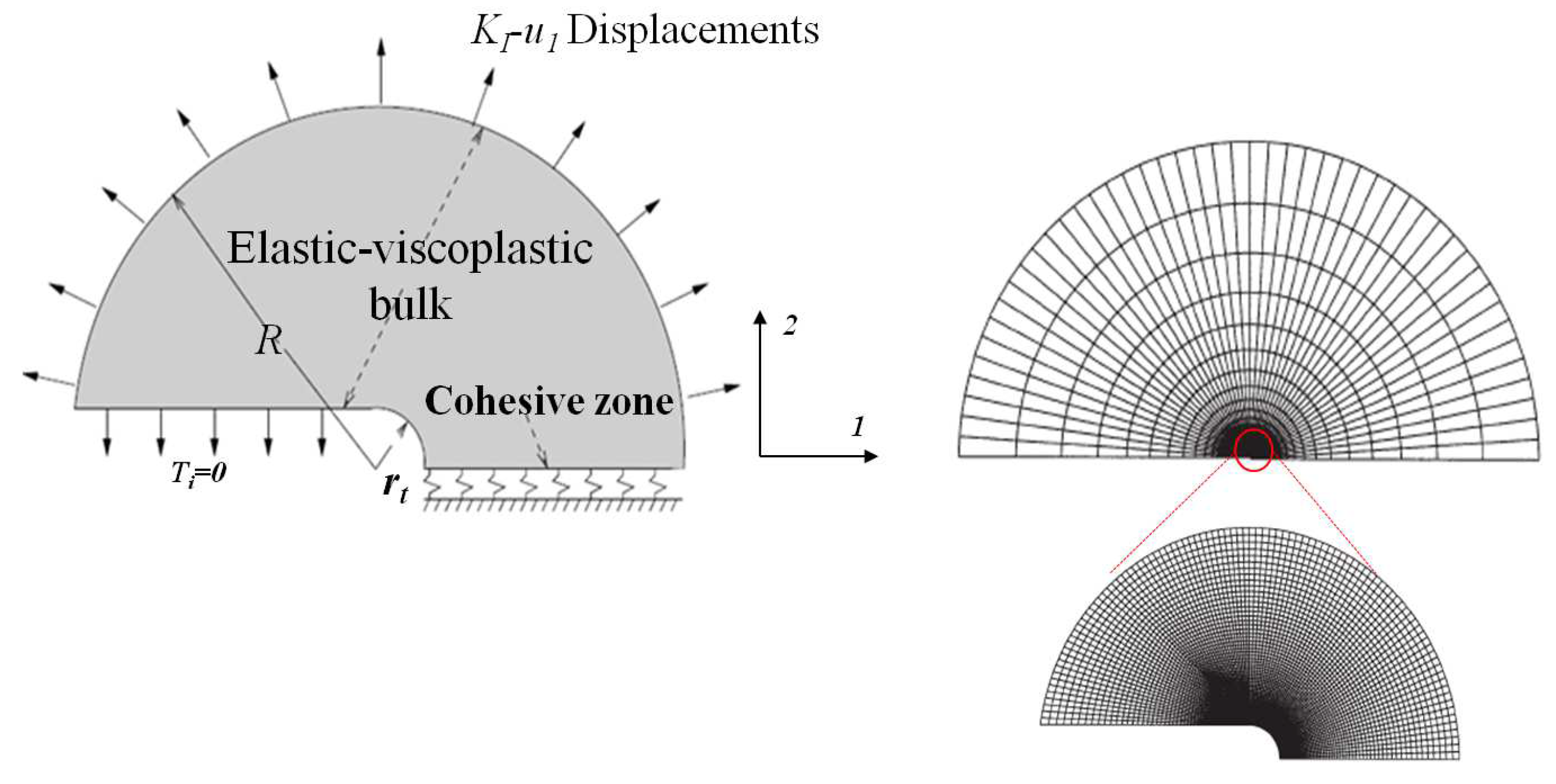
3.5. Problem Formulation for Mode I Fracture
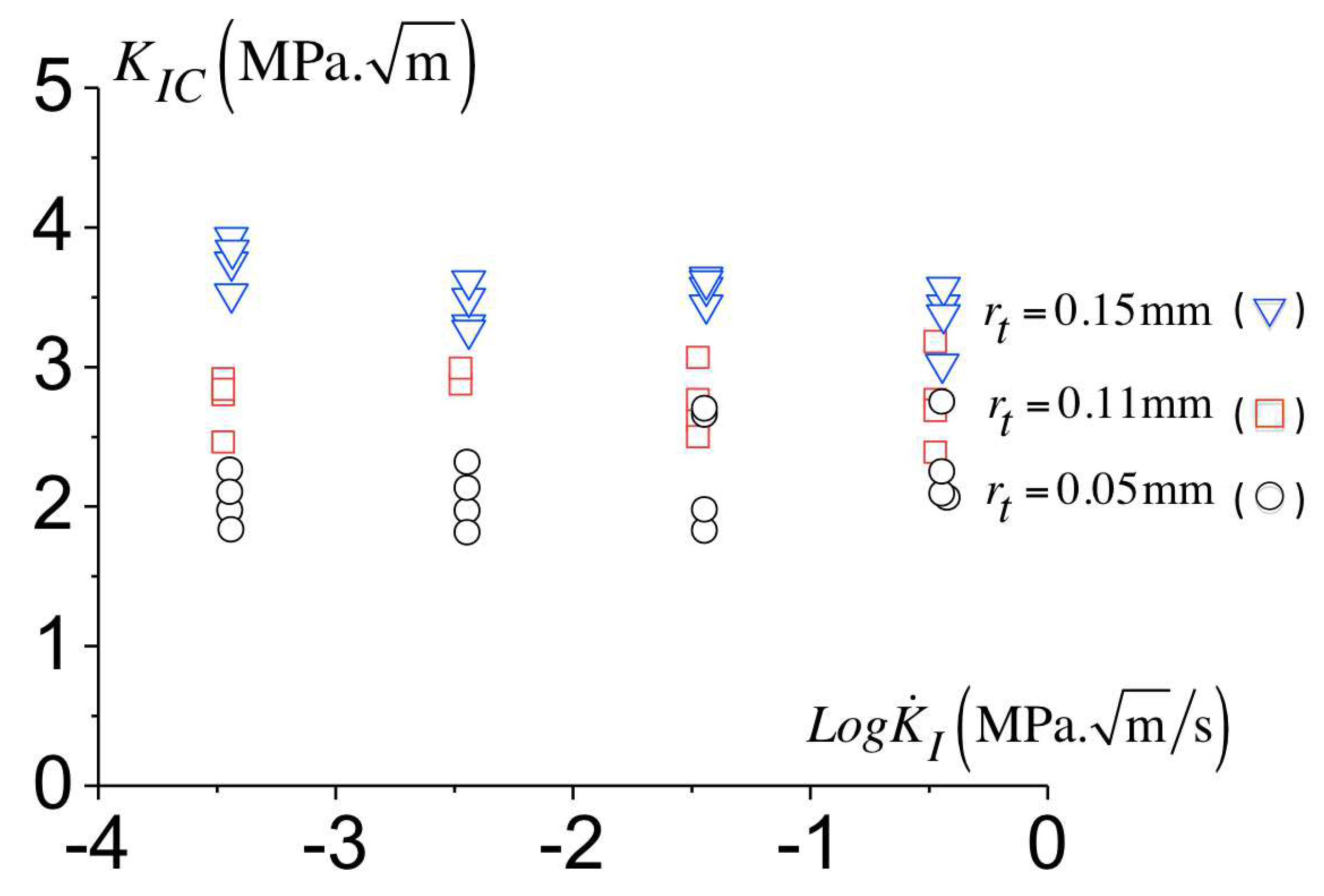
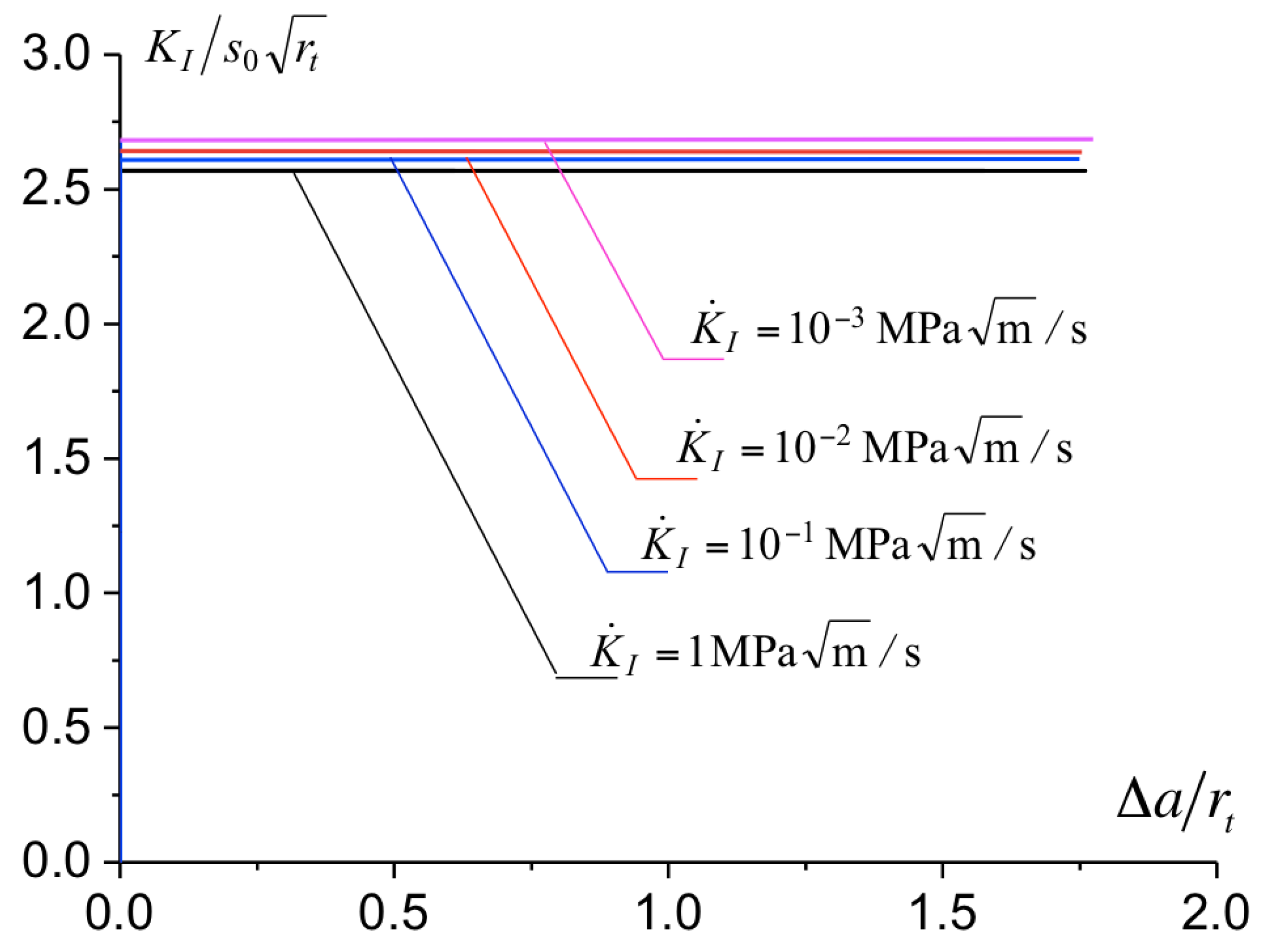
3.6. Calibration of the Cohesive Model
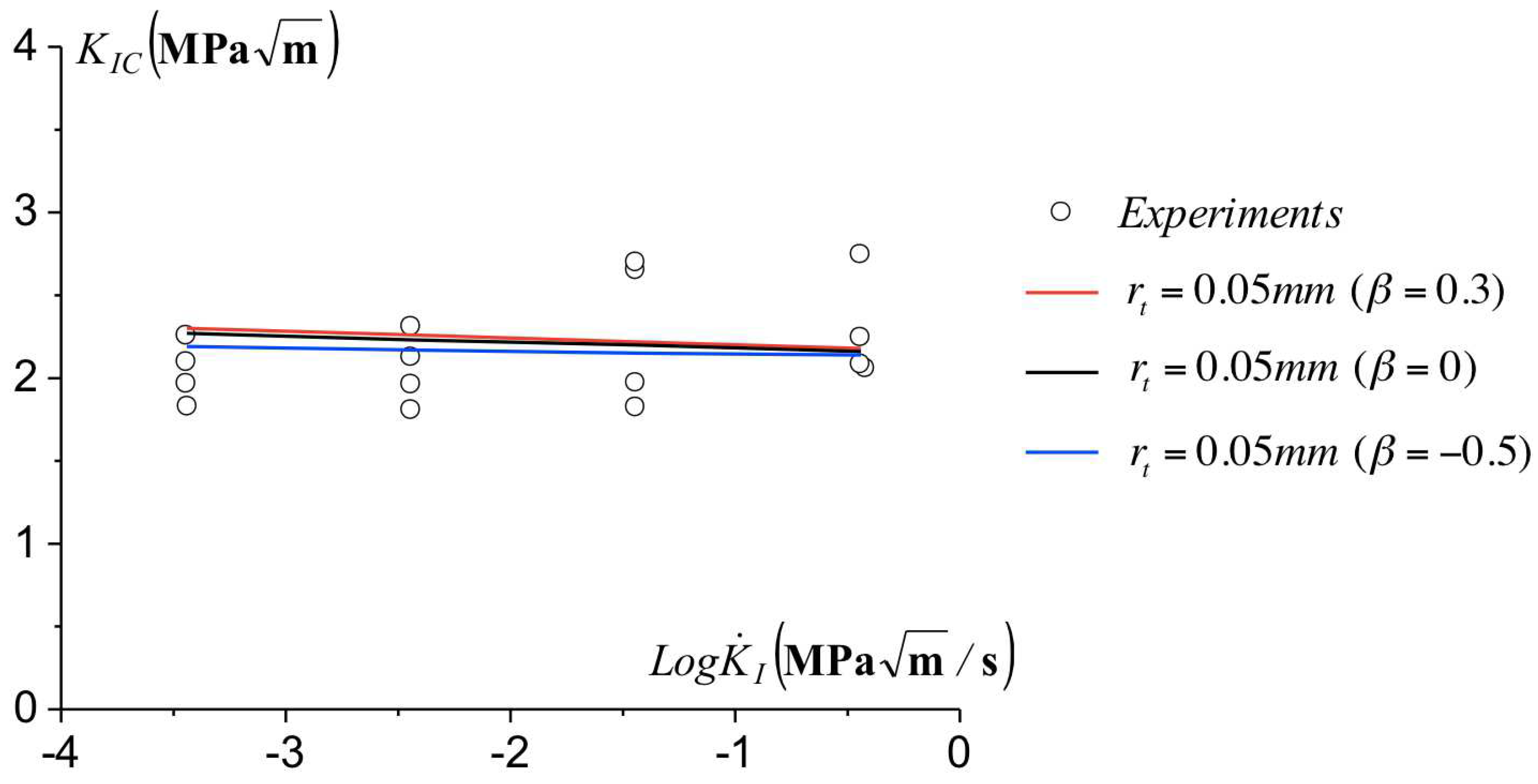
3.7. Influence of the T-Stress on the Toughness
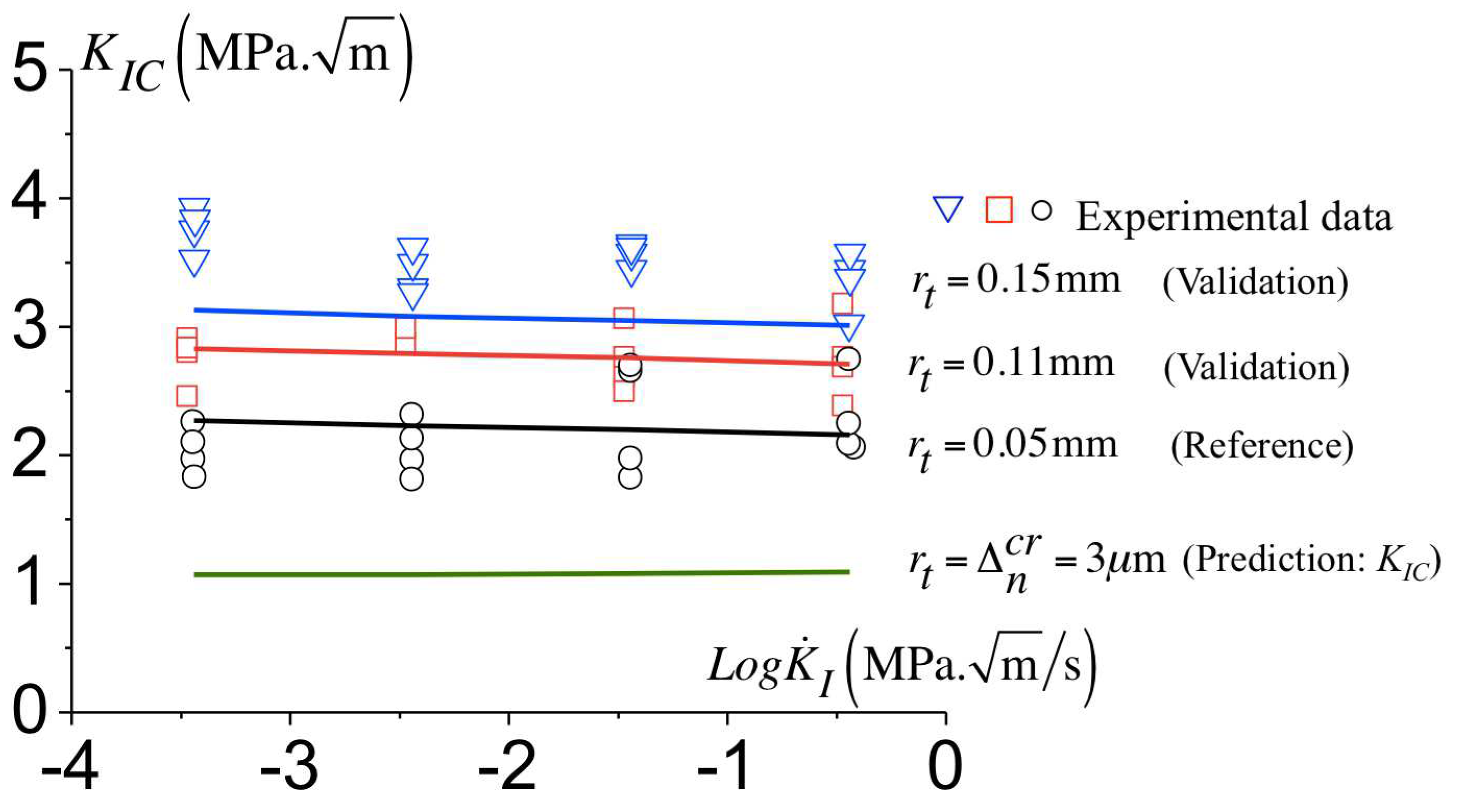
3.8. Validation
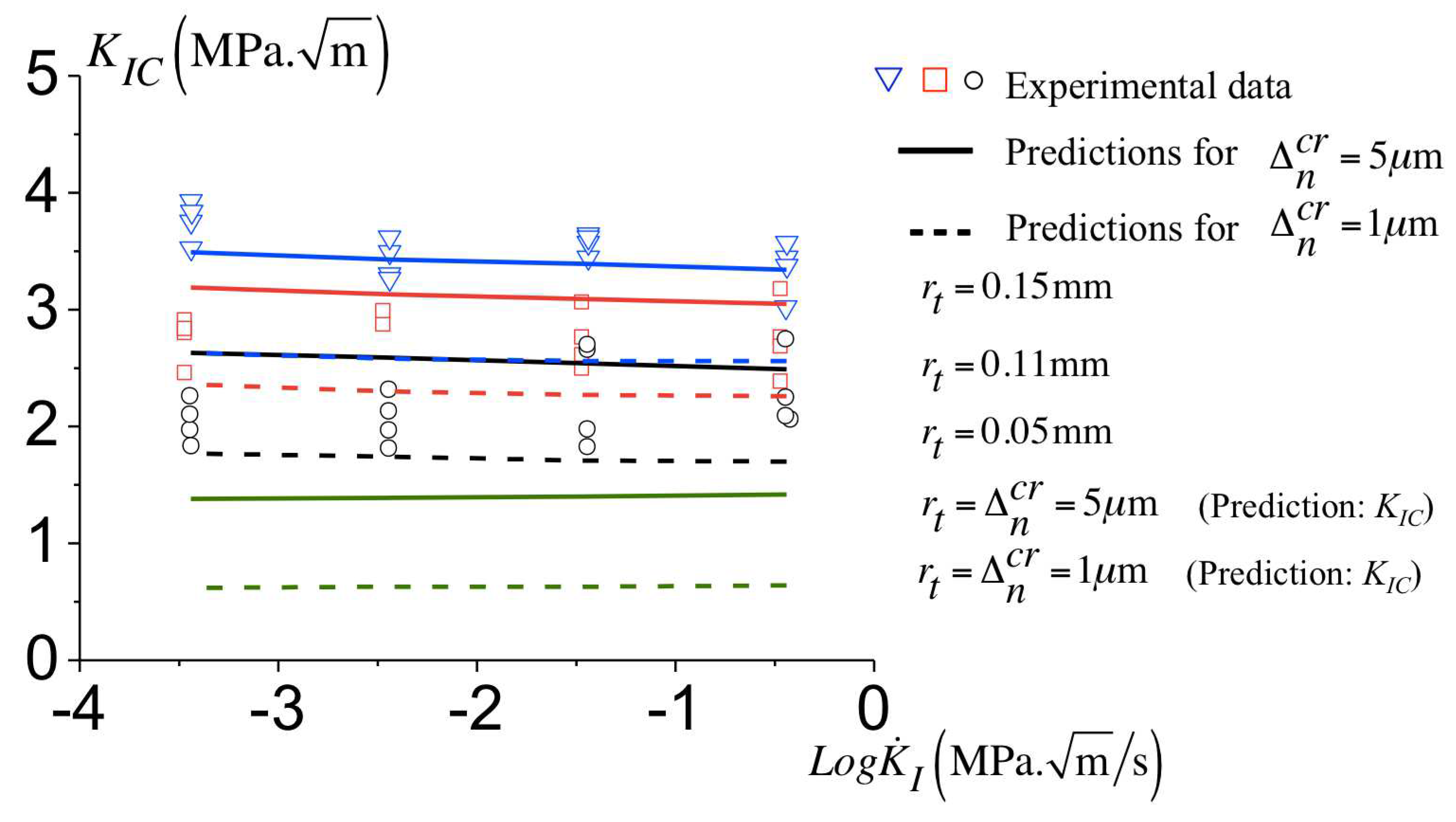
3.9. Influence of the Critical Opening, on the Failure’s Predictions
4. Discussion and Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Golding, J.H. RTM with epoxy resins for aerospace composites. Reinf. Plast. 1990, 34, 18–23. [Google Scholar]
- Kinloch, A. Mechanics and mechanisms of fracture of thermosetting epoxy polymers. In Epoxy Resins and Composites I; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Lilley, J.; Holloway, D.G. Crazing in epoxy resins. Philos. Mag. 1973, 28, 215–220. [Google Scholar] [CrossRef]
- Pascault, J.P.; Sautereau, H.; Verdu, J.; Williams, R.J. Thermosetting Polymers, 1st ed.; Plastics Engineering; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Kanchanomai, C.; Rattananon, S.; Soni, M. Effects of loading rate on fracture behavior and mechanism of thermoset epoxy resin. Polym. Test. 2005, 24, 886–892. [Google Scholar] [CrossRef]
- Estevez, R.; Tijssens, M.; der Giessen, E.V. Modeling of the competition between shear yielding and crazing in glassy polymers. J. Mech. Phys. Solids 2000, 48, 2585–2617. [Google Scholar] [CrossRef]
- Saad-Gouider, N.; Estevez, R.; Olagnon, C.; Séguéla, R. Calibration of a viscoplastic cohesive zone for crazing in PMMA. Eng. Fract. Mech. 2006, 73, 2503–2522. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C.; Jayachandran, R. Effects of strain rate, temperature and thermomechanical coupling on the finite strain deformation of glassy polymers. Mech. Mater. 1995, 19, 193–212. [Google Scholar] [CrossRef]
- Boyce, M.C.; Parks, D.M.; Argon, A.S. Large inelastic deformation of glassy polymers. part I: Rate dependent constitutive model. Mech. Mater. 1988, 7, 15–33. [Google Scholar] [CrossRef]
- Wu, P.D.; van der Giessen, E. On improved network models for rubber elasticity and their applications to orientation hardening in glassy polymers. J. Mech. Phys. Solids 1993, 41, 427–456. [Google Scholar] [CrossRef]
- Poulain, X.; Benzerga, A.; Goldberg, R. Finite-strain elasto-viscoplastic behavior of an epoxy resin: Experiments and modeling in the glassy regime. Int. J. Plast. 2014, 62, 138–161. [Google Scholar] [CrossRef]
- Argon, A.S. A theory for the low-temperature plastic deformation of glassy polymers. Philos. Mag. 1973, 28, 839–865. [Google Scholar] [CrossRef]
- Haward, R.N.; Thackray, G. The Use of a Mathematical Model to Describe Isothermal Stress-Strain Curves in Glassy Thermoplastics. Proc. R. Soc. Lond. A 1968, 302, 453–472. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook, 3rd ed.; ASME Press: New York, NY, USA, 2000. [Google Scholar]
- Ishikawa, M.; Ikuo, N.; Hiroyuki, O. Criterion for craze nucleation in polycarbonate. J. Polym. Sci. Polym. Phys. Ed. 1977, 15, 1791–1804. [Google Scholar] [CrossRef]
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: Oxford, UK, 1950; Volume 11. [Google Scholar]
- Lai, J.; der Giessen, E. A numerical study of crack–tip plasticity in glassy polymers. Mech. Mater. 1997, 25, 183–197. [Google Scholar] [CrossRef]
- Yee, A.F.; Pearson, R.A. Toughening mechanisms in elastomer–modified epoxies. J. Mater. Sci. 1986, 21, 2462–2474. [Google Scholar] [CrossRef]
- Tijssens, M.; van der Giessen, E.; Sluys, L. Modeling of crazing using a cohesive surface methodology. Mech. Mater. 2000, 32, 19–35. [Google Scholar] [CrossRef]
- Wu, P.D.; van der Giessen, E. Computational aspects of localized deformations in amorphous glassy polymers. Eur. J. Mech. A Solids 1996, 15, 799–823. [Google Scholar]
- Döll, W. Optical interference measurements and fracture mechanics analysis of crack tip craze zones. In Crazing in Polymers; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar] [CrossRef]
- Larsson, S.; Carlsson, A. Influence of non-singular stress terms and specimen geometry on small-scale yielding at crack tips in elastic-plastic materials. J. Mech. Phys. Solids 1973, 21, 263–277. [Google Scholar] [CrossRef]
- Rice, J. Limitations to the small scale yielding approximation for crack tip plasticity. J. Mech. Phys. Solids 1974, 22, 17–26. [Google Scholar] [CrossRef]
- Leevers, P.; Radon, J. Inherent stress biaxiality in various fracture specimen geometries. Int. J. Fract. 1982, 19, 311–325. [Google Scholar] [CrossRef]
- Zamanian, M.; Mortezaei, M.; Salehnia, B.; Jam, J. Fracture toughness of epoxy polymer modified with nanosilica particles: Particle size effect. Eng. Fract. Mech. 2013, 97, 193–206. [Google Scholar] [CrossRef]
- Dittanet, P.; Pearson, R.A. Effect of silica nanoparticle size on toughening mechanisms of filled epoxy. Polymer 2012, 53, 1890–1905. [Google Scholar] [CrossRef]
- Liang, Y.; Pearson, R. Toughening mechanisms in epoxy-silica nanocomposites (ESNs). Polymer 2009, 50, 4895–4905. [Google Scholar] [CrossRef]
- Chen, Q.; Chasiotis, I.; Chen, C.; Roy, A. Nanoscale and effective mechanical behavior and fracture of silica nanocomposites. Compos. Sci. Technol. 2008, 68, 3137–3144. [Google Scholar] [CrossRef]
- Chen, C.; Justice, R.S.; Schaefer, D.W.; Baur, J.W. Highly dispersed nanosilica–epoxy resins with enhanced mechanical properties. Polymer 2008, 49, 3805–3815. [Google Scholar] [CrossRef]
- Castrillo, P.D.; Olmos, D.; González-Benito, J. Novel polymer composites based on a mixture of preformed nanosilica-filled poly(methyl methacrylate) particles and a diepoxy/diamine thermoset system. J. Appl. Polym. Sci. 2009, 111, 2062–2070. [Google Scholar] [CrossRef]


| Parameter | Notation | Value |
|---|---|---|
| Elastic | (MPa) | 1395 |
| 0.38 | ||
| Viscoplastic | (MPa) | 140 |
| A(K/MPa) | 173 | |
| (s) | 3.6 | |
| Softening | (MPa) | 114 |
| h (MPa) | 648 | |
| Hardening | (MPa) | 14 |
| N | 2.7 |
| Parameters | Initiation | Thickening | Crack | ||
|---|---|---|---|---|---|
| (MPa) | (MPa) | (K/MPa) | (mm/s) | (m) | |
| Reference | 50 | 140 | 173 | 10 | 3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres, D.; Guo, S.; Villar, M.-P.; Araujo, D.; Estevez, R. Calibration of a Cohesive Model for Fracture in Low Cross-Linked Epoxy Resins. Polymers 2018, 10, 1321. https://doi.org/10.3390/polym10121321
Torres D, Guo S, Villar M-P, Araujo D, Estevez R. Calibration of a Cohesive Model for Fracture in Low Cross-Linked Epoxy Resins. Polymers. 2018; 10(12):1321. https://doi.org/10.3390/polym10121321
Chicago/Turabian StyleTorres, Dery, Shu Guo, Maria-Pilar Villar, Daniel Araujo, and Rafael Estevez. 2018. "Calibration of a Cohesive Model for Fracture in Low Cross-Linked Epoxy Resins" Polymers 10, no. 12: 1321. https://doi.org/10.3390/polym10121321
APA StyleTorres, D., Guo, S., Villar, M.-P., Araujo, D., & Estevez, R. (2018). Calibration of a Cohesive Model for Fracture in Low Cross-Linked Epoxy Resins. Polymers, 10(12), 1321. https://doi.org/10.3390/polym10121321





