Theoretical Evaluation of the Influence of Molecular Packing Mode on the Intramolecular Reorganization Energy of Oligothiophene Molecules
Abstract
:1. Introduction
2. Materials and Methods
2.1. Molecular Dynamics of the Packing Modes
2.2. QM and QM/MM Calculations of Reorganization Energy
3. Results
3.1. Packing Mode of Different Length and Different Substituted P3AT
3.2. Different Conformations from QM, MD, and QM/MM Simulations
3.3. Molecular Packing Influences on the Reorganization Energy
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shuai, Z.; Geng, H.; Xu, W.; Liao, Y.; André, J.M. From charge transport parameters to charge mobility in organic semiconductors through multiscale simulation. Chem. Soc. Rev. 2014, 43, 2662–2679. [Google Scholar] [CrossRef] [PubMed]
- Dang, M.T.; Hirsch, L.; Wantz, G. P3HT:PCBM, Best seller in polymer photovoltaic research. Adv. Mater. 2011, 23, 3597–3602. [Google Scholar] [CrossRef] [PubMed]
- Kleinschmidt, A.T.; Root, S.E.; Lipomi, D.J. Poly(3-hexylthiophene) (P3HT): Fruit fly or outlier in organic solar cell research? J. Mater. Chem. A 2017, 5, 11396–11400. [Google Scholar] [CrossRef]
- Bauer, D.; Von Schütz, J.U.; Wolf, H.C.; Hünig, S.; Sinzger, K.; Kremer, R.K. Alloyed deuterated copper-DCNQI salts: Phase transitions and reentry of conductivity, giant hysteresis effects, and coexistence of metallic and semiconducting modes. Adv. Mater. 1993, 5, 829–834. [Google Scholar] [CrossRef]
- Yang, X.; Wang, L.; Wang, C.; Long, W.; Shuai, Z. Influences of crystal structures and molecular sizes on the charge mobility of organic semiconductors: Oligothiophenes. Chem. Mater. 2008, 20, 3205–3211. [Google Scholar] [CrossRef]
- Ling, M.M.; Erk, P.; Gomez, M.; Koenemann, M.; Locklin, J.; Bao, Z. Air-Stable n-Channel Organic Semiconductors Based on Perylene Diimide Derivatives without Strong Electron Withdrawing Groups. Adv. Mater. 2007, 19, 1123–1127. [Google Scholar] [CrossRef]
- McCullough, R.D.; Lowe, R.D.; Jayaraman, M.; Anderson, D.L. Design, synthesis, and control of conducting polymer architectures: Structurally homogeneous poly (3-alkylthiophenes). J. Org. Chem. 1993, 58, 904–912. [Google Scholar] [CrossRef]
- Li, Y.F.; He, Y.J.; Zhou, W. Materials and Devices for Polymer Solar Cells; Chemical Industry Press: Beijing, China, 2013; pp. 20–30. ISBN 978-7-122-16890-0. [Google Scholar]
- Marcus, R.A. Electron transfer reactions in chemistry. Theory and experiment. Rev. Mod. Phys. 1993, 65, 599. [Google Scholar] [CrossRef]
- Malagoli, M.; Brédas, J.L. Density functional theory study of the geometric structure and energetics of triphenylamine-based hole-transporting molecules. Chem. Phys. Lett. 2000, 327, 13–17. [Google Scholar] [CrossRef]
- Nan, G.J.; Shi, Q.; Shuai, Z.G.; Li, Z.S. Influences of molecular packing o the charge mobility of organic semiconductor: From quantum charge transfer rate theory beyond the first-order perturbation. Phys. Chem. Chem. Phys. 2011, 13, 9736–9746. [Google Scholar] [CrossRef] [PubMed]
- Schutt, T.C.; Hegde, G.A.; Bharadwaj, V.S.; Johns, A.J.; Maupin, C.M. Impact of Water-Dilution on the Biomass Solvation Properties of the Ionic Liquid 1-Methyltriethoxy-3-Ethylimidazolium Acetate. J. Phys. Chem. B 2017, 121, 843–853. [Google Scholar] [CrossRef] [PubMed]
- Bharadwaj, V.S.; Eagan, N.M.; Wang, N.M.; Liberatore, M.W.; Maupin, C.M. Molecular Simulations of Fatty-Acid Methyl Esters and Representative Biodiesel Mixtures. ChemPhysChem 2015, 16, 2810–2817. [Google Scholar] [CrossRef] [PubMed]
- Bhatta, R.S.; Yimer, Y.Y.; Perry, D.S.; Tsige, M. Improved Force Field for Molecular Modeling of Poly(3-hexylthiophene). J. Phys. Chem. B 2013, 117, 10035–10045. [Google Scholar] [CrossRef] [PubMed]
- Alexiadis, O.; Mavrantzas, V.G. All-Atom Molecular Dynamics Simulation of Temperature Effects on the Structural, Thermodynamic, and Packing Properties of the Pure Amorphous and Pure Crystalline Phases of Regioregular P3HT. Macromolecules 2013, 46, 2450–2467. [Google Scholar] [CrossRef]
- Li, H.; Duan, L.; Zhang, D.; Qiu, Y. Influence of Molecular Packing on Intramolecular Reorganization Energy: A Case Study of Small Molecules. J. Phys. Chem. C 2014, 118, 14848–14852. [Google Scholar] [CrossRef]
- Van Bolhuis, F.; Wynberg, H.; Havinga, E.E.; Meijer, E.W.; Staring, E.G. The X-ray structure and MNDO calculations of α-terthienyl: A model for polythiophenes. Synth. Met. 1989, 30, 381–389. [Google Scholar] [CrossRef]
- Porzio, W.; Destri, S.; Mascherpa, M.; Brückner, S. Structural aspects of oligothienyl series from X-ray powder diffraction data. Acta Polym. 1993, 44, 266–272. [Google Scholar] [CrossRef]
- Azumi, R.; Goto, M.; Honda, K.; Matsumoto, M. Conformation and packing of odd-numbered α-oligothiophenes in single crystals. Bull. Chem. Soc. Jpn. 2003, 76, 1561–1567. [Google Scholar] [CrossRef]
- Prosa, T.J.; Winokur, M.J.; Moulton, J.; Smith, P.; Heeger, A.J. X-ray structural studies of poly (3-alkylthiophenes): An example of an inverse comb. Macromolecules 1992, 25, 4364–4372. [Google Scholar] [CrossRef]
- Mårdalen, J.; Samuelsen, E.J.; Gautun, O.R.; Carlsen, P.H. X-ray scattering from oriented poly (3-alkylthiophenes). Synth. Met. 1992, 48, 363–380. [Google Scholar] [CrossRef]
- Tashiro, K.; Kobayashi, M.; Kawai, T.; Yoshino, K. Crystal structural change in poly (3-alkyl thiophene) s induced by iodine doping as studied by an organized combination of X-ray diffraction, infrared/Raman spectroscopy and computer simulation techniques. Polymer 1997, 38, 2867–2879. [Google Scholar] [CrossRef]
- Yang, S.Y.; Zhao, L.; Duan, Y.A.; Geng, Y.; Su, Z.M. The influence of molecular solid packings on the photoluminescence and carrier transport properties for two bow-shaped thiophene compounds: A theoretical study. Theor. Chem. Acc. 2013, 132, 1377. [Google Scholar] [CrossRef]
- Zhu, L.L.; Zhang, B.; Zhou, K.X.; Yao, J.X.; Dai, S.Y. Molecular Dynamics of the Assembly Modes of the Oligothiophene Polymers with Different Chain Lengths. In Key Engineering Materials; Trans Tech Publications: Zurich, Switzerland, 2017; Volume 727, pp. 476–481. [Google Scholar] [CrossRef]
- Accelrys Software Inc. Materials Studio Release Notes; Release 6.1; Accelrys Software Inc.: San Diego, CA, USA, 2012; Available online: http://accelrys.com/products/collaborative-science/biovia-materials-studio/ (accessed on 26 December 2017).
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D. 01; Gaussian, Inc.: Wallingford, CT, USA, 2009. Available online: http://gaussian.com/glossary/g09/ (accessed on 26 December 2017).
- Besler, B.H.; Merz, K.M.; Kollman, P.A. Atomic charges derived from semiempirical methods. J. Comput. Chem. 1990, 11, 431–439. [Google Scholar] [CrossRef]
- Fox, T.; Kollman, P.A. Application of the RESP methodology in the parametrization of organic solvents. J. Phys. Chem. B 1998, 102, 8070–8079. [Google Scholar] [CrossRef]
- Case, D.A.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, H.; Goetz, A.W.; Greene, D.; Homeyer, N.; et al. AMBER 2017; University of California: San Francisco, CA, USA, 2017; Available online: http://ambermd.org/ (accessed on 26 December 2017).
- Hagler, A.T.; Lifson, S.; Dauber, P. Consistent force-field studies of inter-molecular forces in hydrogen-bonded crystals. 2. Benchmark for the objective comparison of alternative force-fields. J. Am. Chem. Soc. 1979, 101, 5122–5130. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Berendsen, H.J.; Postma, J.V.; van Gunsteren, W.F.; DiNola, A.R.H.J.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Roe, D.R.; Cheatham, T.E., III. PTRAJ and CPPTRAJ: Software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef] [PubMed]
- Petrenko, A.; Stein, M. Molecular reorganization energy as a key determinant of J-band formation in J-aggregates of polymethine dyes. J. Chem. Phys. A 2015, 119, 6773–6780. [Google Scholar] [CrossRef] [PubMed]
- Dapprich, S.; Komáromi, I.; Byun, K.S.; Morokuma, K.; Frisch, M.J. A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. J. Mol. Struct. THEOCHEM 1999, 461, 1–21. [Google Scholar] [CrossRef]
- Fichou, D.; Bachet, B.; Demanze, F.; Billy, I.; Horowitz, G.; Garnier, F. Growth and structural characterization of the Quasi–2D single crystal of α-octithiophene. Adv. Mater. 1996, 8, 500–504. [Google Scholar] [CrossRef]
- Colle, R.; Grosso, G.; Ronzani, A.; Zicovich-Wilson, C.M. Structure and X-ray spectrum of crystalline poly (3-hexylthiophene) from DFT-van der Waals calculations. Phys. Stat. Solidi B 2011, 248, 1360–1368. [Google Scholar] [CrossRef]
- Liu, Y.F.; Krug, K.; Lee, Y.L. Self-organization of two-dimensional poly (3-hexylthiophene) crystals on Au (111) surfaces. Nanoscale 2013, 5, 7936–7941. [Google Scholar] [CrossRef] [PubMed]
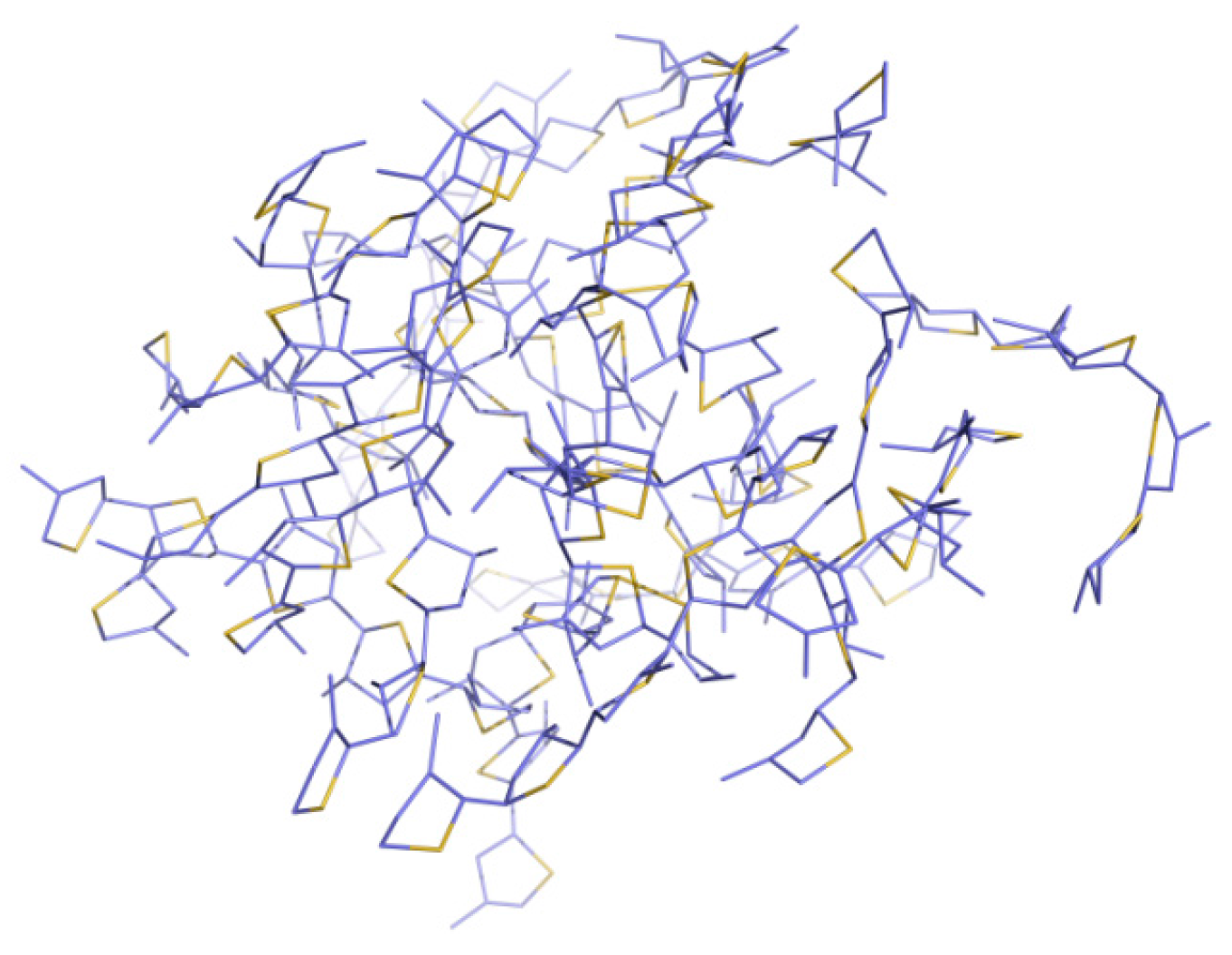

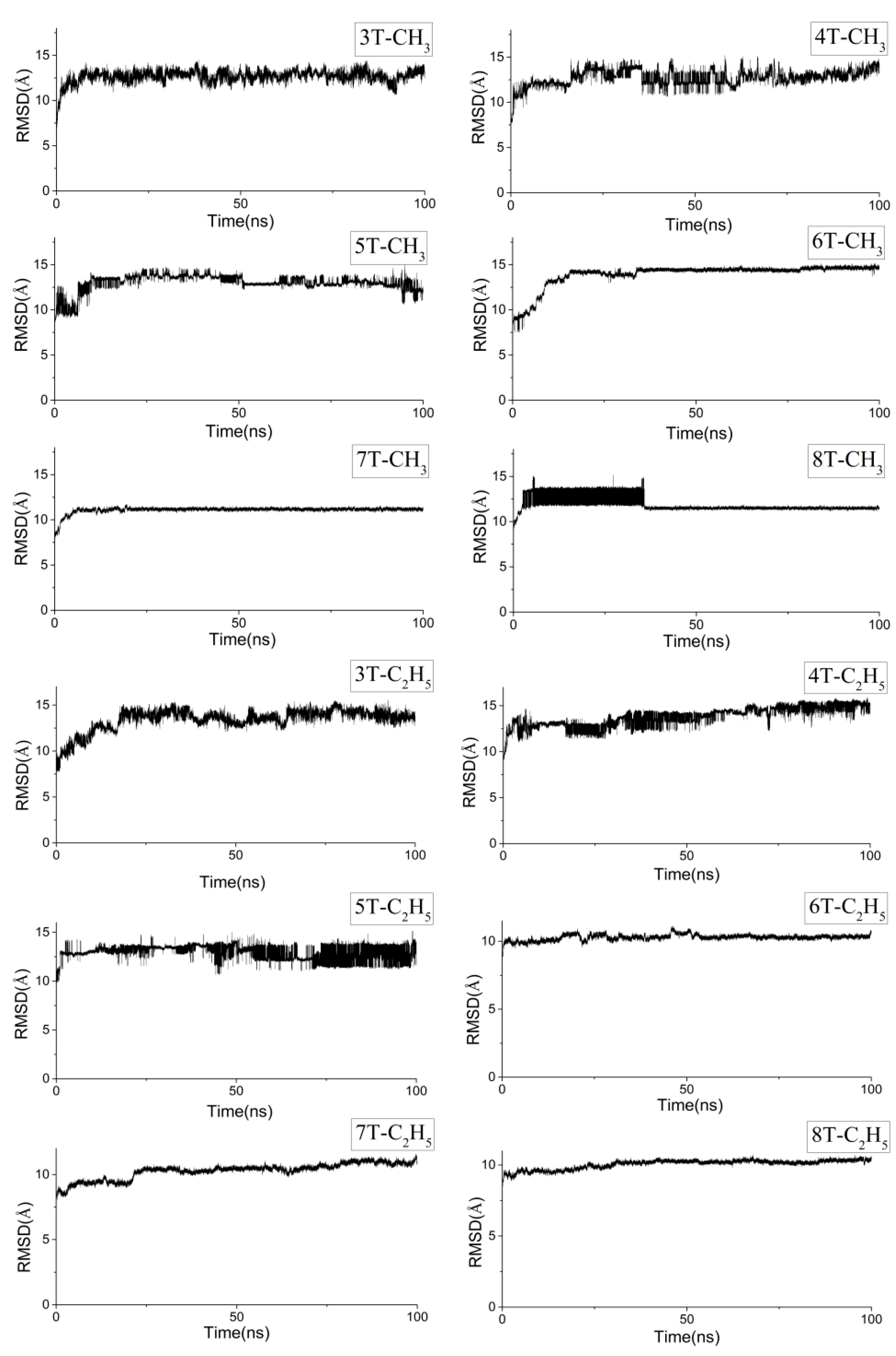


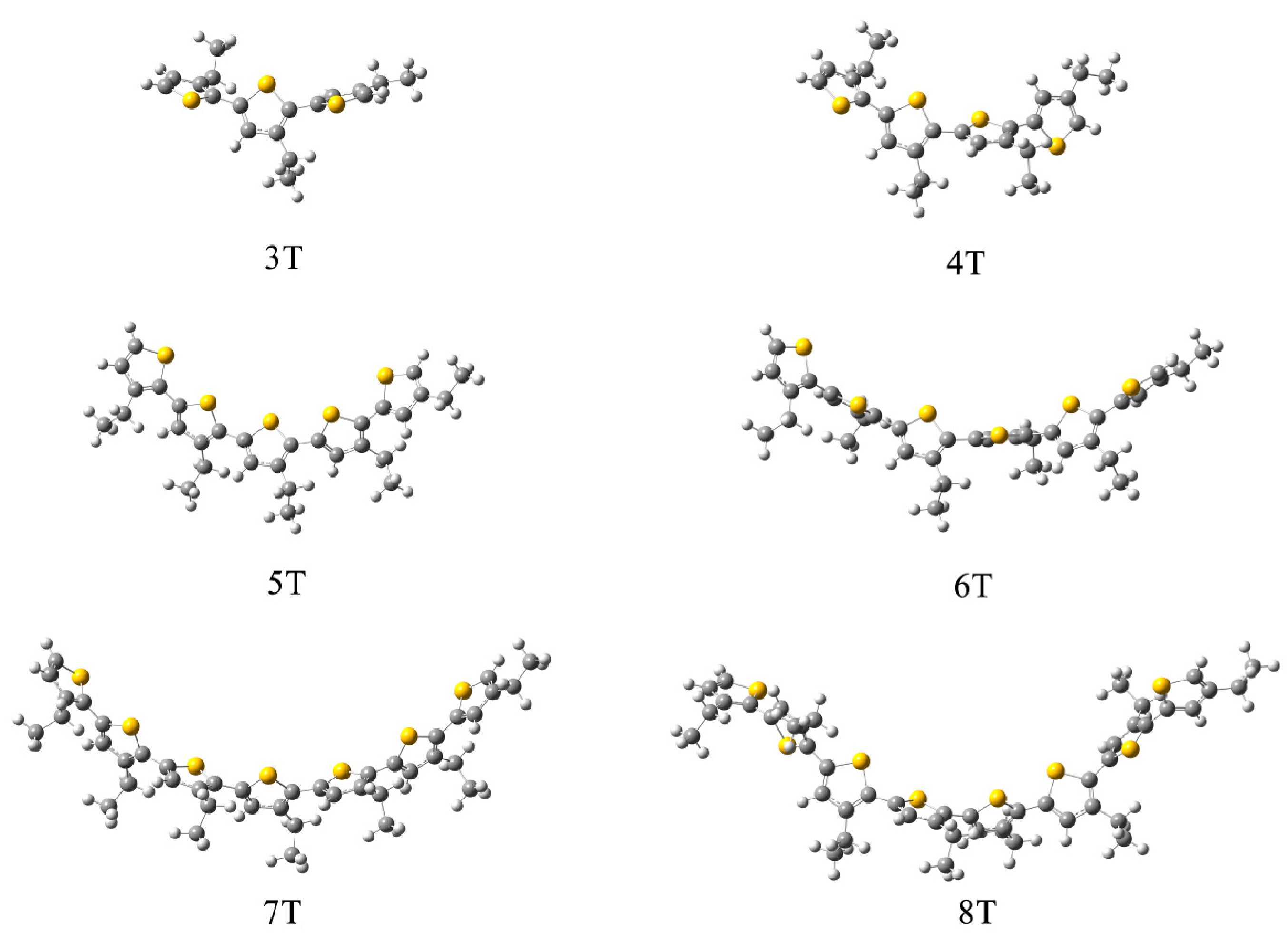
| System | Method | Curvature | Torsion Angles (°) |
|---|---|---|---|
| 3T | QM | 0.03294 | 148.67 |
| QM/MM | 0.02813 | 167.12 | |
| 4T | QM | 0.02964 | 149.18 |
| QM/MM | 0.01035 | 177.91 | |
| 5T | QM | 0.03098 | 149.44 |
| QM/MM | 0.00430 | 172.87 | |
| 6T | QM | 0.02898 | 149.59 |
| QM/MM | 0.00581 | 174.99 | |
| 7T | QM | 0.02886 | 149.70 |
| QM/MM | 0.00629 | 173.62 | |
| 8T | QM | 0.02687 | 149.82 |
| QM/MM | 0.00008 | 175.74 | |
| 3T-Met | QM | 0.07136 | 121.25 |
| QM/MM | 0.02417 | 173.65 | |
| 4T-Met | QM | 0.07259 | 122.07 |
| QM/MM | 0.00758 | 174.32 | |
| 5T-Met | QM | 0.04749 | 121.89 |
| QM/MM | 0.01285 | 173.24 | |
| 6T-Met | QM | 0.07427 | 122.25 |
| QM/MM | 0.00400 | 172.40 | |
| 7T-Met | QM | 0.03871 | 122.52 |
| QM/MM | 0.00010 | 174.62 | |
| 8T-Met | QM | 0.07546 | 122.32 |
| QM/MM | 0.00854 | 176.07 | |
| 3T-Eth | QM | 0.12960 | 115.31 |
| QM/MM | 0.01145 | 176.30 | |
| 4T-Eth | QM | 0.14049 | 118.29 |
| QM/MM | 0.02314 | 169.33 | |
| 5T-Eth | QM | 0.15070 | 123.05 |
| QM/MM | 0.05283 | 174.91 | |
| 6T-Eth | QM | 0.09435 | 111.82 |
| QM/MM | 0.00714 | 154.58 | |
| 7T-Eth | QM | 0.09893 | 111.98 |
| QM/MM | 0.01247 | 173.33 | |
| 8T-Eth | QM | 0.10528 | 114.23 |
| QM/MM | 0.01983 | 174.78 |
| System | Non- | Methyl- λQM/MM (kcal/mol) | Ethyl- λQM/MM (kcal/mol) | |
|---|---|---|---|---|
| λQM (kcal/mol) | λQM/MM (kcal/mol) | |||
| 3T | 10.148 | 9.849 | 12.144 | 13.444 |
| 4T | 9.479 | 7.680 | 12.143 | 13.015 |
| 5T | 9.067 | 7.455 | 10.862 | 11.074 |
| 6T | 8.539 | 6.867 | 10.097 | 10.247 |
| 7T | 8.029 | 6.945 | 9.734 | 8.593 |
| 8T | 7.558 | 6.086 | 7.084 | 7.474 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Xu, Y.; Zhu, L.; Zhou, S.; Liao, Y.; Zhou, K.; Yao, J.; Dai, S. Theoretical Evaluation of the Influence of Molecular Packing Mode on the Intramolecular Reorganization Energy of Oligothiophene Molecules. Polymers 2018, 10, 30. https://doi.org/10.3390/polym10010030
Zhang B, Xu Y, Zhu L, Zhou S, Liao Y, Zhou K, Yao J, Dai S. Theoretical Evaluation of the Influence of Molecular Packing Mode on the Intramolecular Reorganization Energy of Oligothiophene Molecules. Polymers. 2018; 10(1):30. https://doi.org/10.3390/polym10010030
Chicago/Turabian StyleZhang, Bing, Yingxue Xu, Lilin Zhu, Shijie Zhou, Yinjie Liao, Kaixuan Zhou, Jianxi Yao, and Songyuan Dai. 2018. "Theoretical Evaluation of the Influence of Molecular Packing Mode on the Intramolecular Reorganization Energy of Oligothiophene Molecules" Polymers 10, no. 1: 30. https://doi.org/10.3390/polym10010030
APA StyleZhang, B., Xu, Y., Zhu, L., Zhou, S., Liao, Y., Zhou, K., Yao, J., & Dai, S. (2018). Theoretical Evaluation of the Influence of Molecular Packing Mode on the Intramolecular Reorganization Energy of Oligothiophene Molecules. Polymers, 10(1), 30. https://doi.org/10.3390/polym10010030






