Dielectric Properties of Chiral Ferroelectric Liquid Crystalline Compounds with Three Aromatic Rings Connected by Ester Groups
Abstract
:1. Introduction
2. Experimental
2.1. Materials
2.2. Dielectric Spectroscopy Measurements
3. Results and Discussions
3.1. Phase Behaviour
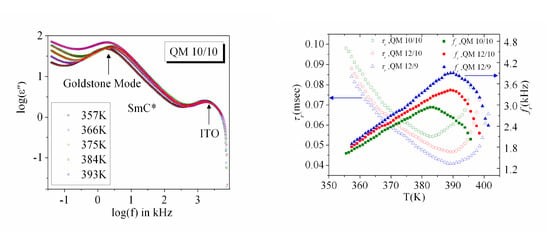
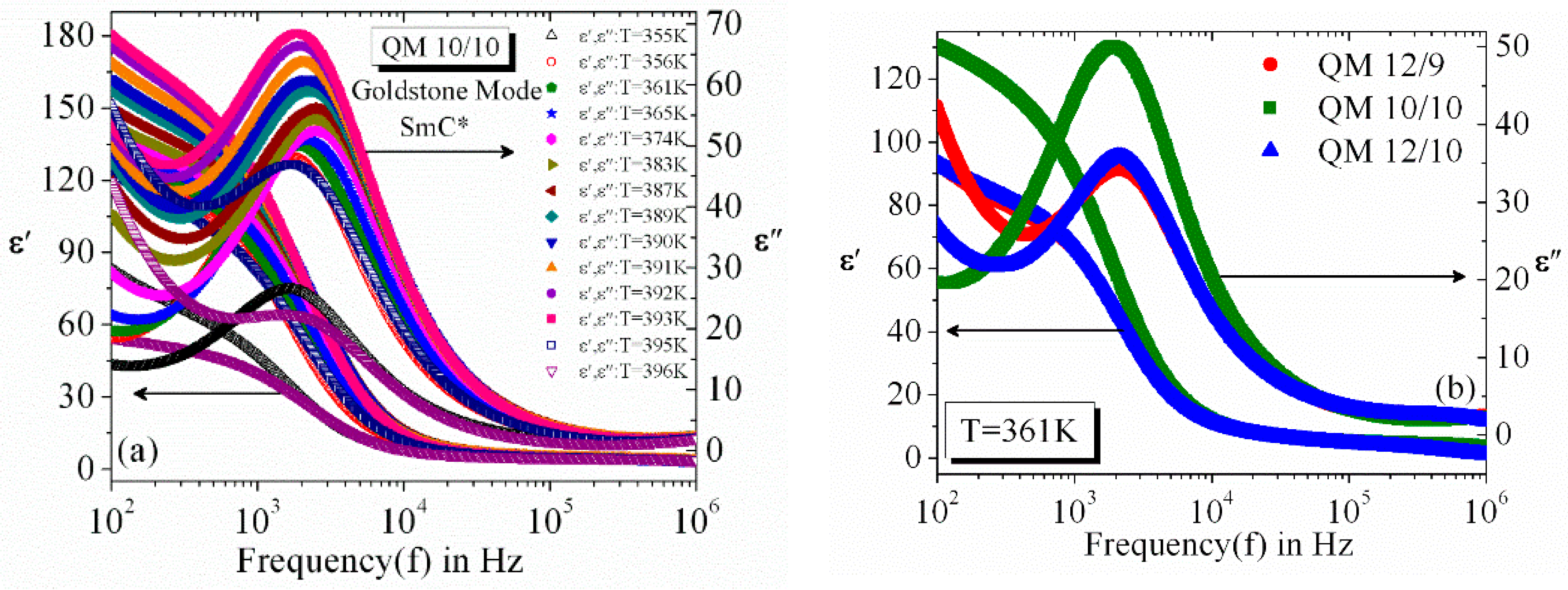
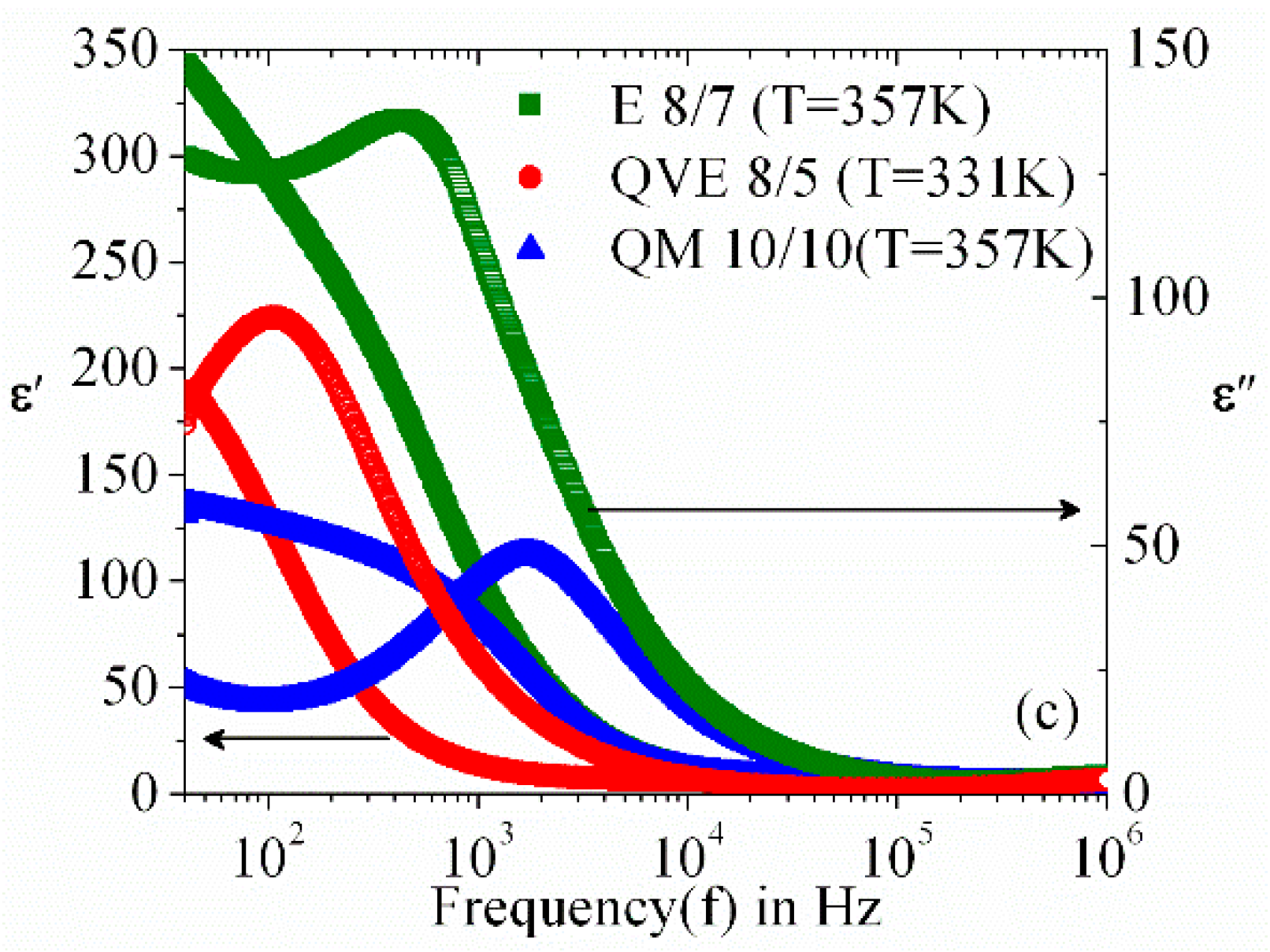
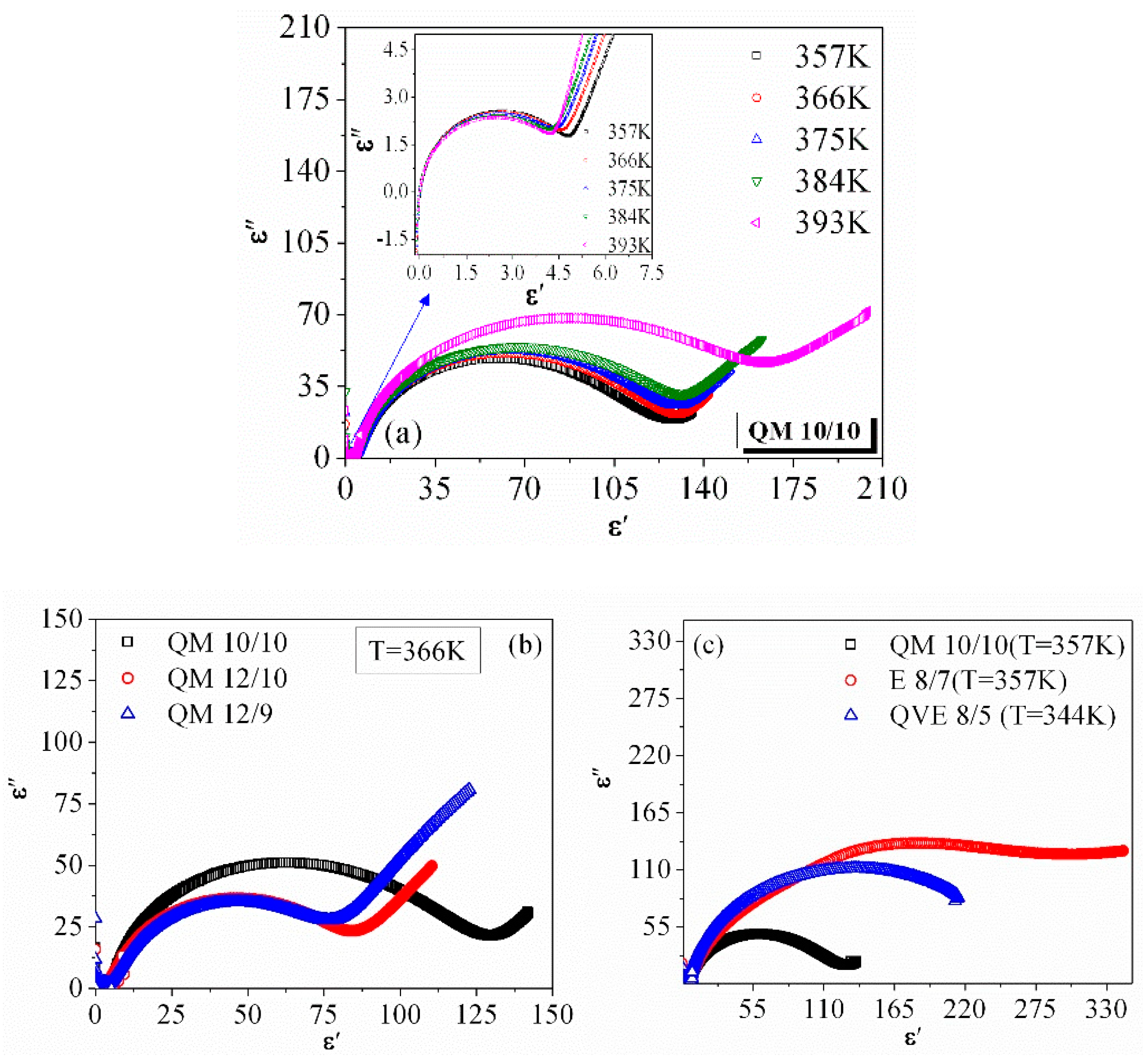
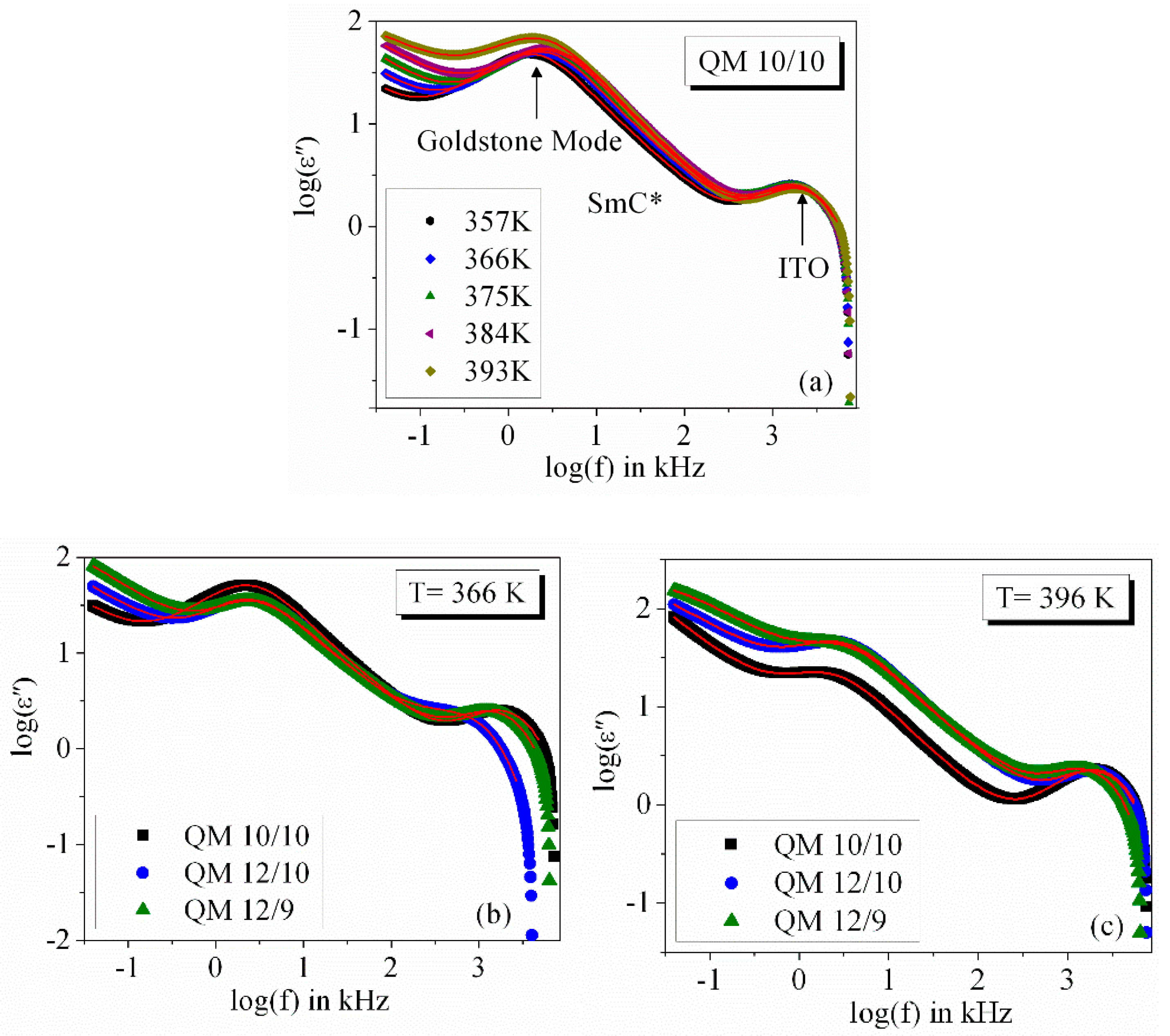
3.2. Frequency Dispersion of Complex Permittivity
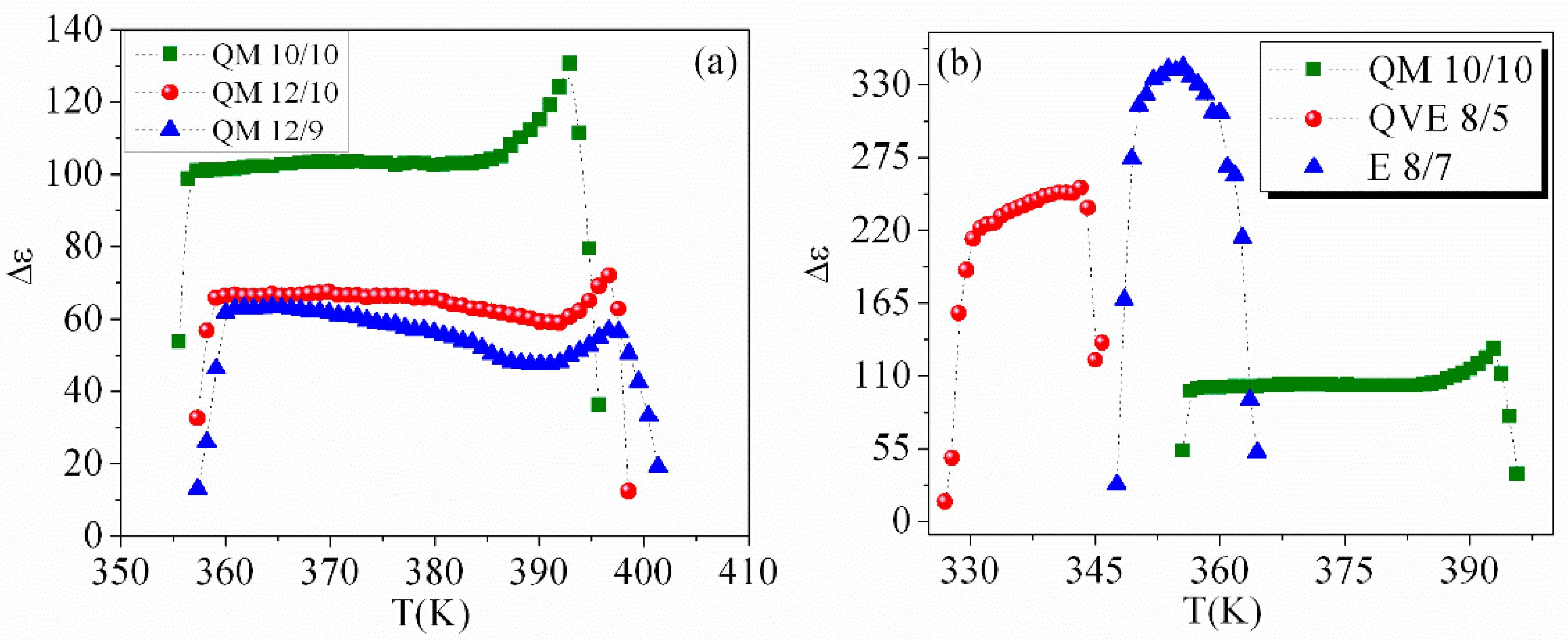
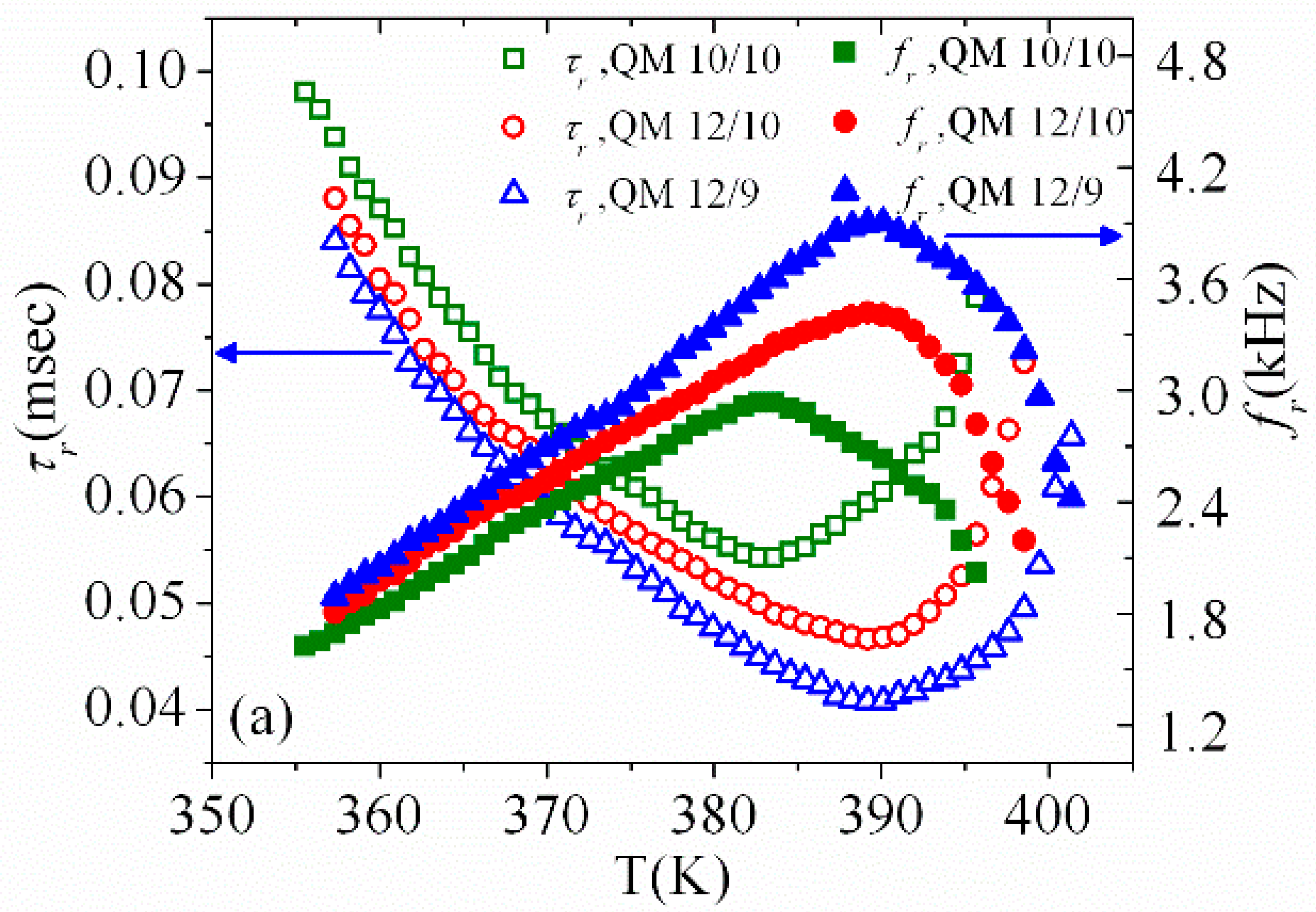
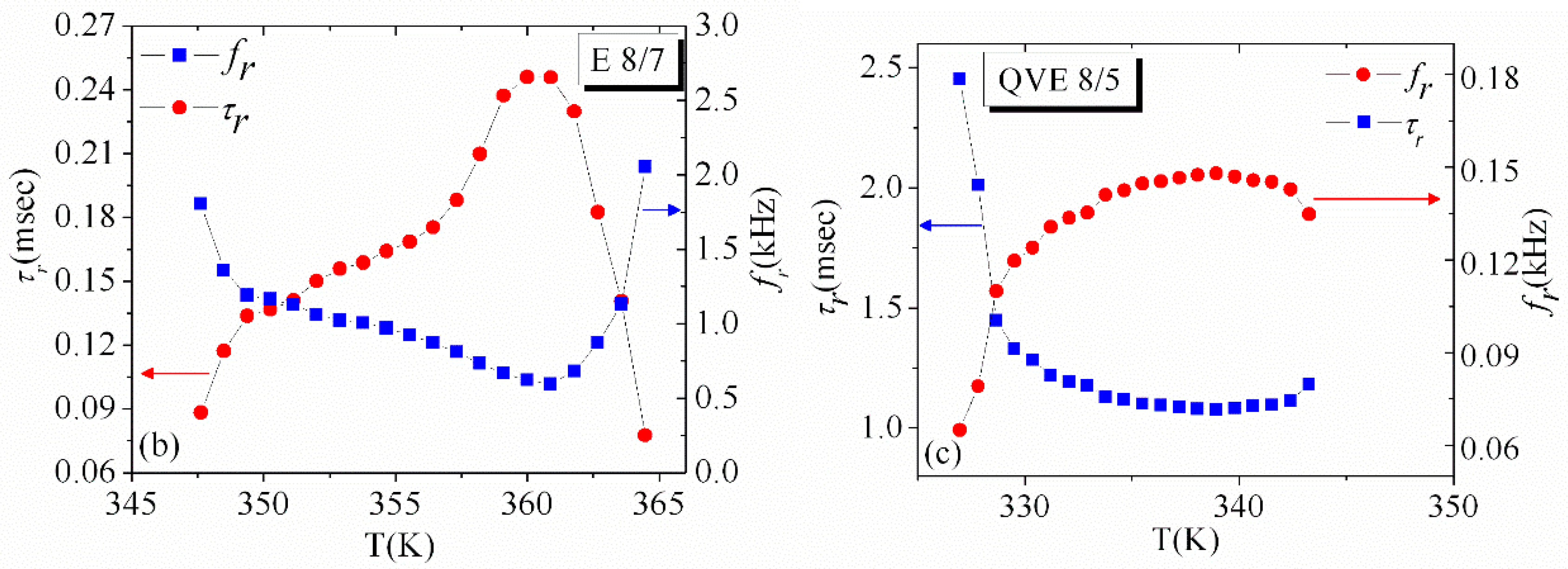
3.3. Temperature Dependence of Dielectric Strength and Relaxation Frequency
4. Summary of the Results and Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Palffy-Muhoray, P.; Cao, W.; Moreira, M.; Taheri, B.; Munoz, A. Photonics and lasing in liquid crystal materials. Philos. Trans. R. Soc. A 2006, 364, 2747–2761. [Google Scholar] [CrossRef] [PubMed]
- Fratalocchi, A.; Asquini, R.; Assanto, G. Integrated electro-optic switch in liquid crystals. Opt. Exp. 2005, 13, 32–37. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Yang, B.; Zhang, T.; Ji, L.; Wang, Y. Study on a Lateral-Electrical-Field Pixel Architecture for FLC Spatial Light Modulator with Continuously Tunable Grayscales. IEEE Trans. Electron Dev. 2003, 50, 1694–1697. [Google Scholar] [CrossRef]
- Scheffer, T.J.; Nehring, J. A new highly multiplexable liquid crystal display. Appl. Phys. Lett. 1984, 45, 1021–1023. [Google Scholar] [CrossRef]
- Kato, T.; Mizoshita, N.; Kishimoto, K. Functional liquid-crystalline assemblies: Self-organized soft materials. Angew. Chem. Int. Ed. 2006, 45, 38–68. [Google Scholar] [CrossRef] [PubMed]
- Hird, M.; Goodby, J.W.; Hindmarsh, P.; Lewis, R.A.; Toyne, K.J. The design, synthesis and structure property relationships of ferroelectric and antiferroelectric liquid crystal materials. Ferroelectrics 2002, 276, 219–237. [Google Scholar] [CrossRef]
- Kaspar, M.; Hamplova, V.; Pakhomov, S.A.; Bubnov, A.; Guittard, F.; Sverenyak, H.; Stibor, I.; Vanek, P.; Glogarova, M. New series of ferroelectric liquid crystals with four ester groups. Liq. Cryst. 1998, 24, 599–605. [Google Scholar] [CrossRef]
- Bubnov, A.; Novotna, V.; Hamplova, V.; Kaspar, M.; Glogarova, M. Effect of multilactate chiral part of the liquid crystalline molecule on mesomorphic behavior. J. Mol. Struct. 2008, 892, 151–157. [Google Scholar] [CrossRef]
- Brombach, F.; Neudorfl, M.J.; Blunk, D. The chiral pool as valuable natural source: New chiral mesogens made from lactic acid. Mol. Cryst. Liq. Cryst. 2011, 542, 62–74. [Google Scholar] [CrossRef]
- Lagerwall, T.S. Ferroelectric and Antiferroelectric Liquid Crystals; Wiley-VCH: New York, NY, USA, 1999. [Google Scholar]
- Takahashi, T.; Furue, H.; Shikada, M.; Matsuda, N.; Miyama, T.; Kobayashi, S. Preliminary study of field sequential full color liquid crystal display using polymer stabilized ferroelectric liquid crystal display. Jpn. J. Appl. Phys. 1999, 38, L534–L536. [Google Scholar] [CrossRef]
- Bahadur, B. Liquid Crystals: Applications and Uses; World Scientific: Singapore, 1990; Volume 1. [Google Scholar]
- Lagerwall, J.P.F.; Giesselmann, F. Current topics in smectic liquid crystal research. ChemPhysChem 2006, 7, 20–45. [Google Scholar] [CrossRef] [PubMed]
- Clark, N.A.; Lagerwall, S.T. Submicrosecondbistable electro-optic switching in liquid crystals. Appl. Phys. Lett. 1980, 36, 899–901. [Google Scholar] [CrossRef]
- Malik, P.; Raina, K.K.; Bubnov, A.; Prakash, C. Dielectric spectroscopy of a high-polarization ferroelectric liquid crystal. Phase Transit. 2006, 79, 889–898. [Google Scholar] [CrossRef]
- Barman, B.; Das, B.; Das, M.K.; Hamplová, V.; Bubnov, A. Effect of molecular structure on dielectric and electro-optic properties of chiral liquid crystals based on lactic acid derivatives. J. Mol. Liq. 2019, 283, 472–781. [Google Scholar] [CrossRef]
- Bubnov, A.; Domenici, V.; Hamplova, V.; Kaspar, M.; Veracini, C.A.; Glogarova, M. Orientational and structural properties of ferroelectric liquid crystal with a broad temperature range in the SmC* phase by 13C NMR, X-ray scattering and dielectric spectroscopy. J. Phys. 2009, 21, 035102. [Google Scholar]
- Ray, T.D.; Kundu, S.; Nayek, P.; Majumder, T.P.; Roy, S.K.; Haase, W. Dielectric and electro-optic behavior of pure ferroelectric liquid crystal material and the isomeric mixtures. Curr. Appl. Phys. 2009, 9, 605–609. [Google Scholar]
- Hemine, J.; Legrand, N.; Isaert, A.; Kaaouachi, E.; Nguyen, H.T. Structural, electro-optical and dielectric characterizations of ferroelectric liquid crystals showing the SmC*–SmA*–N* phase sequence. Physica B 2007, 390, 34–39. [Google Scholar] [CrossRef]
- Stojanović, M.; Bubnov, A.; Obadović, D.Z.; Hamplová, V.; Kašpar, M.; Cvetinov, M. Effect of the chiral chain length on structuraland phase properties of ferroelectric liquid crystals. Phase Transit. 2011, 84, 380–390. [Google Scholar] [CrossRef]
- Bubnov, A.; Pakhomov, S.; Kašpar, M.; Hamplová, V.; Glogarová, M. Synthesis and dielectric properties of new liquid crystalline substances with a lactate chiral group. Mol. Cryst. Liq. Cryst. Sci. Technol. 1999, 328, 317–324. [Google Scholar] [CrossRef]
- George, A.K.; Al-Hinai, M.; Carboni, C.; Al-Harthi, S.H.; Potukuchi, D.M.; Naciri, J. Dielectric response in the smectic A and smectic C* phases of a ferroelectric liquid crystal, 12CN5(R*). Mol. Cryst. Liq. Cryst. 2004, 409, 343–353. [Google Scholar] [CrossRef]
- Blinc, R.; Zeks, B. Dynamics of helicoidal ferroelectric smectic-C liquid crystals. Phys. Rev. A 1978, 18, 740. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Dhar, R.; Agrawal, V.K.; Lee, H.S.; Dabrowski, R. Switching and electrical properties of ferro-and antiferroelectric phases of MOPB(H)PBC. Liq. Cryst. 2008, 35, 1101–1108. [Google Scholar] [CrossRef]
- Filipic, C.; Carlsson, T.; Levstik, A.; Zeks, B.; Blink, R.; Gouda, F.; Lagerwall, S.T.; Skarp, K. Dielectric properties near the smectic-C*-smectic-A phase transition of some ferroelectric liquid-crystalline systems with a very large spontaneous polarization. Phys. Rev. A 1988, 38, 5833. [Google Scholar] [CrossRef] [PubMed]
- Levstik, A.; Carlsson, T.; Filipic, C.; Levstik, I.; Zeks, B. Goldstone mode and soft mode at the smectic-A—smectic-C* phase transition studied by dielectric relaxation. Phys. Rev. A 1987, 35, 3527. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, T.; Zeks, B. Generalized Landau model of ferroelectric liquid crystals. Phys. Rev. A 1984, 36, 1484. [Google Scholar] [CrossRef]
- Hiller, S.; Biradar, A.M.; Wrobel, S.; Haase, W. Dielectric behavior at the smectic-C*-chiral-nematic phase transition of a ferroelectric liquid crystal. Phys. Rev. E 1996, 53, 641. [Google Scholar] [CrossRef] [PubMed]
- Wrobel, S.; Hasse, W.; Pfeiffer, M.; Geelhar, T. Dielectric relaxation processes in a model ferroelectric liquid crystal. Mol. Cryst. Liq. Cryst. 1992, 212, 335–343. [Google Scholar] [CrossRef]
- Rozanski, S.A.; Thoen, J. Collective and antiferroelectric dielectric modes in a highly tilted three-ring ester. Liq. Cryst. 2007, 34, 519–526. [Google Scholar] [CrossRef]
- Glogarová, M.; Novotná, V.; Bubnov, A. Dielectric response of ferroelectric liquid crystals in samples of finite thickness. Ferroelectrics 2018, 532, 20–27. [Google Scholar] [CrossRef]
- Jasiurkowska-Delaporte, M.; Rozwadowski, T.; Juszyńska-Gałązka, E. Kinetics of Non-Isothermal and Isothermal Crystallization in a Liquid Crystal with Highly Ordered Smectic Phase as Reflected by Differential Scanning Calorimetry, Polarized Optical Microscopy and Broadband Dielectric Spectroscopy. Crystals 2019, 9, 205. [Google Scholar] [CrossRef]
- Pakhomov, S.; Kaspar, M.; Hamplova, V.; Bubnov, A.; Sverenyak, H.; Glogarova, M.; Stibor, I. Synthesis and mesomorphic properties of (S)-lactic acid derivatives containing several ester linkages in the core. Ferroelectrics 1998, 212, 341–348. [Google Scholar] [CrossRef]
- Bubnov, A.; Kaspar, M.; Novotna, V.; Hamplova, V.; Glogarova, M.; Kapernaum, N.; Giesselmann, F. Effect of lateral methoxy substitution on mesomorphic and structural properties of ferroelectric liquid crystals. Liq. Cryst. 2008, 35, 1329–1337. [Google Scholar] [CrossRef]
- Vajda, A.; Kaspar, M.; Hamplova, V.; Pakhomov, S.A.; Vanek, P.; Bubnov, A.; Csorba, K.F.; Éber, N. Synthesis and liquid crystalline properties of (S)-[4-n-Alkyloxy-benzoyloxyphenyl]-4′-[(2-nalkyloxy)propionyloxy]benzoate. Mol. Cryst. Liq. Cryst. 2001, 365, 569–580. [Google Scholar] [CrossRef]
- Gouda, F.; Skarp, K.; Lagerwall, S.T. Dielectric studies of the soft mode and Goldstone mode in ferroelectric liquid crystals. Ferroelectrics 1991, 113, 165–206. [Google Scholar] [CrossRef]
- Hill, N.; Vaughan, W.E.; Price, A.H.; Davies, M. Dielectric Properties and Molecular Behaviour; Van Nostrand Reinhold: New York, NY, USA, 1969. [Google Scholar]
- Bottcher, C.J.F.; Bordewijk, P. Theory of Electric Polarization, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1978; Volume 2. [Google Scholar]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Pandey, A.S.; Dhar, R.; Pandey, M.B.; Achalkumar, A.S.; Yelamaggad, C.V. Dielectric spectroscopy of unsymmetrical liquid crystal dimers showing wide temperature range TGBA and TGBC* phases. Liq. Cryst. 2009, 36, 13–19. [Google Scholar] [CrossRef]
- Havriliak, S., Jr.; Negami, S. A Complex plane analysis of α-dispersions in some polymer systems. J. Polym. Sci. C 1966, 14, 99. [Google Scholar] [CrossRef]
- Kundu, K.S.; Yagihara, S.; Yoshizawa, A. Dielectric spectroscopy of a smectic liquid crystal. Liq. Cryst. 2007, 34, 981–986. [Google Scholar] [CrossRef]
- Ghosh, S.; Nayek, P.; Roy, K.S.; Majumder, T.P.; Dabrowski, R. Dielectric relaxation spectroscopy and electro-optical studies of a new, partially fluorinated orthoconic antiferroelectric liquid crystal material exhibiting V-shaped switching. Liq. Cryst. 2010, 37, 369–375. [Google Scholar] [CrossRef]
- Shenoy, D.; Lavarello, A.; Naciri, J.; Shashidhar, R. Influence of annealing on the dielectric properties of a ferroelectric liquid crystal. Ferroelectrics 2002, 278, 161–166. [Google Scholar] [CrossRef]
- Shukla, R.K.; Raina, K.K.; Hamplová, V.; Kašpar, M.; Bubnov, A. Dielectric behaviour of the composite system: Multiwall carbon nanotubes dispersed in ferroelectric liquid crystal. Phase Transit. 2011, 84, 850–857. [Google Scholar] [CrossRef]
- Mishra, A.; Weglowska, D.; Dabrowski, R.; Dhar, R. Relaxation phenomena of a highly tilted ferroelectric liquid crystalline material (S)-(+)-4′-(3-pentanoyloxy prop-1-oxy)biphenyl-4-yl-4-(1-methylheptyloxy)benzoates. Liq. Cryst. 2015, 42, 1543–1549. [Google Scholar]
- Pandey, M.B.; Dhar, R.; Dabrowski, R. Dielectric spectroscopy of a newly synthesized chlorinated analogue of MHPOBC antiferroelectric liquid crystals. Ferroelectrics 2006, 343, 83–100. [Google Scholar] [CrossRef]
- Kaur, S.; Dierking, I.; Gleeson, H.F. Dielectric spectroscopy of Polymer Stabilized Ferroelectric Liquid Crystals. Eur. Phys. J. E 2009, 30, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Dwivedi, A.; Dhar, R.; Dabrowski, R. Dielectric Spectroscopy of Para-, Ferro-, and Anti-Ferro-Electric Phases of (S)-(+)-(1-Methylheptyloxycarbonyl) Phenyl 4′-(6-Perfluoropentanoyloxyhex-1-Oxy) Biphenyl-4-Carboxylate. Soft Mater. 2009, 7, 54–65. [Google Scholar] [CrossRef]
- Dhar, R.; Singh, S.; Das, I.M.L.; Dabrowski, R. Thermodynamic and dielectric studies of liquid crystalline compound (S)-(+)-4-(1-methylheptyloxycarbonyl) phenyl 4′-(6-octanoyloxyhex-1-oxy) biphenyl-4-carboxylate. Phase Trans. 2009, 82, 251–265. [Google Scholar] [CrossRef]
- Gupta, S.K.; Singh, D.P.; Manohar, R. Enhancement of Dielectric and Electro-Optical Properties in SWCNT Dispersed Ferroelectric Liquid Crystals. Ferroelectrics 2014, 468, 84–91. [Google Scholar] [CrossRef]
- Perkowski, P. Dielectric spectroscopy of liquid crystals, theoritical model of ITO electrodes influence on dielectric measurements. Opto-Electron. Rev. 2009, 17, 180–186. [Google Scholar] [CrossRef]
- Wojciechowski, M.; Gromiec, L.A.; Bak, G.W. Dielectric characteristics of chiral smectic C subphases in liquid crystal MHPOPB. J. Mol. Liq. 2006, 124, 7–12. [Google Scholar] [CrossRef]
- Manohar, R.; Yadav, S.P.; Pandey, K.K.; Srivastava, A.K.; Misra, A.K. Comparative study of dielectric and electro-optical properties of pure and polymer ferroelectric liquid crystal composites. J. Polym. Res. 2011, 18, 435–441. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Manohar, R.; Shukla, J.P.; Biradar, A.M. Dielectric relaxation of dye-doped ferroelectric liquid crystal mixture: A comparative study of Smectic C* and Smectic A phase. Jpn. J. Appl. Phys. 2007, 46, 1100–1105. [Google Scholar] [CrossRef]
- Pandey, M.B.; Dhar, R.; Dabrowski, R. Electrical characteristics of wide temperature range phase. Mol. Cryst. Liq. Cryst. 2009, 509, 363–377. [Google Scholar] [CrossRef]
- Kurp, K.; Tykarska, M.; Salamon, P.; Czerwinski, M.; Bubnov, A. Design of functional multicomponent liquid crystalline mixtures with nano-scale pitch fulfilling deformed helix ferroelectric mode demands. J. Mol. Liq. 2019, 290, 111329. [Google Scholar] [CrossRef]
- Fitas, J.; Marzec, M.; Szymkowiak, M.; Jaworska-Gołąb, T.; Deptuch, A.; Tykarska, M.; Kurp, K.; Żurowska, M.; Bubnov, A. Mesomorphic, electro-optic and structural properties of binary liquid crystalline mixtures with ferroelectric and antiferroelectric liquid crystalline behavior. Phase Trans. 2018, 91, 1017–1026. [Google Scholar] [CrossRef]
- Fitas, J.; Marzec, M.; Kurp, K.; Żurowska, M.; Tykarska, M.; Bubnov, A. Electro-optic and dielectric properties of new binary ferroelectric and antiferroelectric liquid crystalline mixtures. Liq. Cryst. 2017, 44, 1468–1476. [Google Scholar] [CrossRef]
- Bubnov, A.; Podoliak, N.; Hamplová, V.; Tomašková, P.; Havlíček, J.; Kašpar, M. Eutectic behaviour of binary mixtures composed by two isomeric lactic acid derivatives. Ferroelectrics 2016, 495, 105–115. [Google Scholar] [CrossRef]
- Kurp, K.; Czerwiński, M.; Tykarska, M.; Bubnov, A. Design of advanced multicomponent ferroelectric liquid crystalline mixtures with sub-micrometer helical pitch. Liq. Cryst. 2017, 44, 748–756. [Google Scholar] [CrossRef]
- Sreenilayam, S.P.; Brabazon, D.; Panarin, Y.P. Fast ferroelectric liquid crystal based optical switch: Simulation and experiments. Crystals 2019, 9, 388. [Google Scholar] [CrossRef]
- Dabrowski, R.; Kula, P.; Herman, J. High Birefringence Liquid Crystals. Crystals 2013, 3, 443–482. [Google Scholar] [CrossRef]
 | ||||||
| Compound | n | m | X | Y | Z | Ref. |
| QM10/10 | 10 | 10 | -O- | -COO- | H | [35] |
| QM12/9 | 12 | 9 | -O- | -COO- | H | [35] |
| QM12/10 | 12 | 10 | -O- | -COO- | H | [35] |
| E8/7 | 8 | 7 | -OCO- | -OCO- | H | [33] |
| E6/10 | 6 | 10 | -OCO- | -OCO- | H | [33] |
| E10/10 | 10 | 10 | -OCO- | -OCO- | H | [33] |
| E8/12 | 8 | 12 | -OCO- | -OCO- | H | [33] |
| QVE8/5 | 8 | 5 | -O- | -OCO- | OCH3 | [34] |
| COMP | m.p. | c.p. | Ph | Ph | Ph | Ph | |||
|---|---|---|---|---|---|---|---|---|---|
| QM10/10 | 373.1 | 404.6 | Cr | 355.6 | SmC* | 397.8 | N* | 403.9 | Iso |
| [+42.4] | [+2.1] | [−37.7] | [−8.1] | [−1.9] | |||||
| QM12/9 | 374 | 404.5 | Cr | 357.8 | SmC* | 401.3 | N* | 403.6 | Iso |
| [+39.5] | [+1.5] | [−32.4] | [−8.6] | [−1.9] | |||||
| QM12/10 | 373.5 | 402.2 | Cr | 356.7 | SmC* | 399.9 | N* | 401.2 | Iso |
| [+42.0] | [+7.5] | [−37.5] | [−8.7] | [−1.4] | |||||
| E8/7 | 367.1 | 382.3 | Cr | 336.5 | SmC* | 369.5 | SmA* | 380.6 | Iso |
| [+42.2] | [+5.3] | [−34.6] | [−0.5] | [−5.2] | |||||
| E6/10 | 367.6 | 381.6 | Cr | 336.8 | SmC* | 365.7 | SmA* | 379.8 | Iso |
| [+43.8] | [+5.3] | [−36.9] | [−0.2] | [−5.6] | |||||
| E10/10 | 365.0 | 381.6 | Cr | 343.5 | SmC* | 375.1 | SmA* | 380.6 | Iso |
| [+78.6] | [+6.3] | [−67.0] | [−0.4] | [−6.2] | |||||
| E8/12 | 360.1 | 378.3 | Cr | 336.7 | SmC* | 368.7 | SmA* | 377.8 | Iso |
| [+76.5] | [+6.2] | [−35.4] | [−0.3] | [−6.0] | |||||
| QVE8/5 | 355.3 | 365.4 | Cr | 318.1 | SmC* | 346.8 | N* | 363.9 | Iso |
| [+38.9] | [+1.2] | [−27.8] | [−1.5] | [−1.0] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, M.K.; Barman, B.; Das, B.; Hamplová, V.; Bubnov, A. Dielectric Properties of Chiral Ferroelectric Liquid Crystalline Compounds with Three Aromatic Rings Connected by Ester Groups. Crystals 2019, 9, 473. https://doi.org/10.3390/cryst9090473
Das MK, Barman B, Das B, Hamplová V, Bubnov A. Dielectric Properties of Chiral Ferroelectric Liquid Crystalline Compounds with Three Aromatic Rings Connected by Ester Groups. Crystals. 2019; 9(9):473. https://doi.org/10.3390/cryst9090473
Chicago/Turabian StyleDas, Malay Kumar, Barnali Barman, Banani Das, Věra Hamplová, and Alexey Bubnov. 2019. "Dielectric Properties of Chiral Ferroelectric Liquid Crystalline Compounds with Three Aromatic Rings Connected by Ester Groups" Crystals 9, no. 9: 473. https://doi.org/10.3390/cryst9090473
APA StyleDas, M. K., Barman, B., Das, B., Hamplová, V., & Bubnov, A. (2019). Dielectric Properties of Chiral Ferroelectric Liquid Crystalline Compounds with Three Aromatic Rings Connected by Ester Groups. Crystals, 9(9), 473. https://doi.org/10.3390/cryst9090473