Abstract
The present work explains simulation and experimental investigation of the most significant performance parameters of a ferroelectric liquid crystal (FLC) optical switch. The measurements were carried out with commercially available FLC mixture (θ = 22.5°), having a very fast response time within the range of 1–10 μs. The best achieved cross talk was ~19 dB, which is an exact match with the theoretical result.
1. Introduction
With the rapid pace in technological advances and the widespread deployment of optical networks over the past few years, fiber-optic communications have a significant role due to their higher bandwidth and greater reliability than copper cables [1,2]. The demand for unlimited band width encourages the generation of novel technologies to make networks much faster, more reliable, and more scalable [3,4]. In transparent optical networks, bit-error-rate (BER) largely depends on intensity of cross-talk. To achieve low BER (10−9), required cross-talk is <−30 dB [5]. For a high bit rate transmission, optical switches are essential and this transmission must be matched with the switching capacity. All-optic switch fabrics allow switching directly in to the optical domain to avoid electronic bottlenecks. The high cross-talk and slow response time are, therefore, serious issues to be overcome in the fast growing communication networks. Development of power-efficient, low cross-talk, and much faster optical switches is crucial in tackling this problem. The optical switch performance can be assessed by measurement of the transparency to bit rate and data format, scalability, insertion loss, and cross-talk. In photonic switches, to control the properties of optical signals, it is most effective to use materials such as LiNbO3 [6], semiconductor optical amplifiers (SOA) [7,8,9], liquid crystal (LC) [10,11], etc., which can change their refractive index upon photo irradiation. Among the materials, LCs exhibit large optical anisotropy, and a large change in refractive index by changing their alignment, which is obviously advantageous for photonic applications [12,13]. Due to the permanent electrical dipole moment, molecules can take up a certain mean relative orientation in the LC phase. It is possible via the application of suitable electric field across a LC cell to act on the orientation of molecules, and thereby alter the optical properties of the material [14,15,16,17,18,19,20]. LC optical switches are based on the change of polarization state of incident light by LC as a result of an external electric field. The change of polarization with polarization-selective beam splitters offers optical space switching.
LC based optical switches exhibits attractive characteristics, such as low power consumption, no moving parts, low voltage driving, free space switching, fast response time, and cost efficiency [21,22,23,24,25]. The operating range of conventional nematic LC switches is in the order of 1–100 ms, which limits network speed and shows slightly excessive cross-talk [26,27]. Unpowered nematic switches may quickly become disordered and fail to direct signals according to the most recently selected path, which means they do not have a memory and numerous stability states. Ferroelectric liquid crystals (FLCs) discovered by Mayer in 1975 [28] have become a subject for intensive research and have observed increasing high technology applications for displays and data processing. In 1998, Riza et al. reported a low cross-talk highly scalable 2 × 2 ferroelectric liquid crystal (FLC) switch for all-optical fiber networks [29]. The evolution of FLC switches in fiber networks deliver much faster response times (τ) and have a memory capability such that optical signals will be directed along a pre-selected path until the switch position is actively changed.
The purpose of present work is the simulation and experimental investigation of the most important performance parameters of FLC modulator. The molecular tilt angle (θ) of a KCFLC 10R sample shows 22.5°. The cell thickness was optimized to get a better contrast ratio as cross-talk = 10 log (1/K), where K is the contrast ratio. For optimal FLC parameters, the best achieved cross-talk obtained at room temperature was ~19 dB. The response time as a function of voltage showed very good results (<10 μs).
2. Experiments
The experiments were conducted using the commercial smectic mixture KCFLC 10R from Kingston Chemicals Limited. The mesophases and transition temperatures while cooling down from isotropic phase were SmC* 62 °C, SmA* 97 °C, N* 107 °C Iso. The homogeneously aligned cells of thicknesses varying from 2 μm to 25 μm were used for the measurements. The cell thickness was estimated by transmittance measurements using Avaspec-2048 spectrometer (Avantes, Louisville, USA). The RN-1175 polymer (Nissan Chemicals, Tokyo, Japan) is used to obtain perfect homogeneous alignment. This thermo aligning polymer aligns nematic [30,31,32] and ferroelectric [33,34,35,36] LC molecules homogenously in cells. The spin coated (3000 rpm, 30 s) Indium Tin Oxide (ITO) glass substrates were baked at 250 °C for an hour to generate planar alignment by evaporating excess solvent. The FLC cells were rubbed anti-parallel and sealed with epoxy on two sides.
The molecular tilt angle (θ) was measured by rotating a microscopic stage between +θ and −θ by the application of electric fields. The contrast ratio is the property, which determines the quality of a device, and was measured using stabilized He-Ne laser emitting at a wavelength (λ) of 632.8 nm. The transmitted light intensity was captured by a photo detector and output signal was recorded on a dual-trace storage oscilloscope (Tektronix, Model TDS 2014). A square wave signal was applied to the sample at a driving frequency 110 Hz, which was obtained from a function generator (Agilent, Model 33120A). Figure 1 shows the schematic of the experimental set-up used for FLC physical parameter measurements.
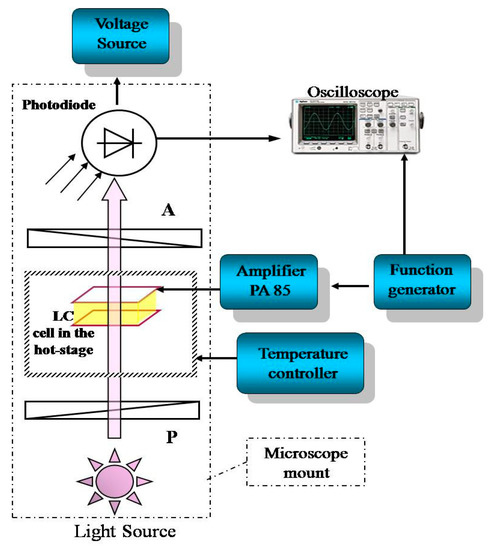
Figure 1.
Schematic representation of the implemented electro-optic measurement technique.
Cell Thickness Optimization
A wedge FLC cell (Figure 2a) was made of glass plates coated with RN1175 polymer and rubbed in an antiparallel direction to achieve a well-aligned planar configuration. The plates were glued with spacers of 1 μm along one edge and 30 μm along the opposite edge. The orientation of LC molecules imposed by the glass substrates was parallel to the boundaries and to the wedge edge.
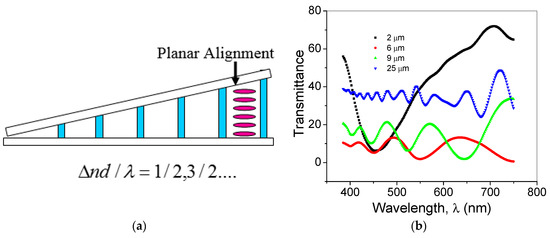
Figure 2.
(a) Schematic of the wedge shaped cell and (b) graph showing the wavelength dependent transmittance of cells of different thicknesses.
The wedge cell was placed on a hot stage under crossed polarized states and the light transmission through the cell was measured using an Avaspec spectrometer, which provides accuracy of wavelength better than 10%. The empty cell thickness (Figure 2b) was measured from the interference fringes reflected from both glass substrates, and is calculated as
where and are the wavelengths of two minima or maxima and n is the number of fringes. In the vicinity of each fringe, the cell is the same as a system of flat cells and the thickness varies slowly from one edge to the other edge.
3. Optical Switching in FLC Modulator
Optical switching was performed in the smectic C* (SmC*) mesophase. The center of mass of the LC molecules in this phase is randomly distributed in the equally spaced smectic layers. The molecular director (n) is tilted with an angle θ/2 with respect to the normal to the smectic layers and the phase is optically biaxial. The possible states of molecules in SmC* phase is depicted in Figure 3.
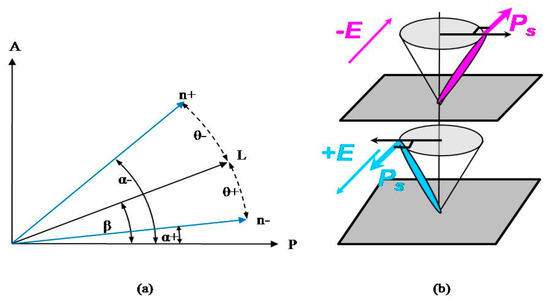
Figure 3.
(a) Representation of two possible states of molecules in SmC* mesophase under crossed polarizers and (b) its polarization-dependent orientations. Note: A = analyzer; P = polarizer
From Figure 3a it is obvious that , where θ is the molecular tilt angle. In order to measure θ, one must find out the position (i.e., β angle) of minimum transmittance which occurs at α = 0. There are two angular positions (of β) for such minimum, first β = θ gives a minimum for negative state, i.e., , and the second β = −θ gives a minimum for positive state, i.e., . Therefore, by measuring the angular positions of rotation stage of polarizing optical microscope which correspond to the negative and positive minimums we can determine 2θ.
In sufficiently thin samples, a homogeneously polarized ferroelectric state can be switched under the application of an electric field. FLC acts as a dielectric in a transparent capacitor. The applied voltages across the capacitor plates produce linear electro-optical switching of the polarization and tilt and also principal optical axis switching. The optical axis for an FLC is determined by n and the molecule can be switched between two stable states with a relative angle θ. Two molecular orientations are possible with respect to the polarization in the SmC* phase, and can be seen in Figure 3b. The net spontaneous polarization (P) appears in the direction perpendicular to the smectic layer plane. The switching can be easily observed between crossed polarizers. Due to the birefringence of the cell, the ordinary and extraordinary waves travel at different speeds through the cell and interfere at the output. The molecules can be switched by the application of electric field in the direction perpendicular to the surface. When the direction of spontaneous polarization is reversed by the external electric field then the optical axis therefore changes its orientation by twice the tilt angle.
3.1. Principle of Operation
Binary Switch
The principle of operation is that the birefringent plate at the input port manipulates the polarization states to the desired ones. The most important element in the binary switch is FLC, in conjunction with the lateral beam splitters (LBS). In the absence of the electric field, the input signal passes through the FLC cell and polarization beam splitter with the same polarization. The schematics of optical switching through the FLC cell and the LBS are shown in Figure 4.
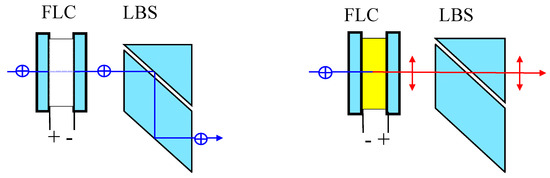
Figure 4.
Schematics of possible switching through the ferroelectric liquid crystal (FLC) binary switch which consist of lateral beam splitters (LBS) and FLC material.
Through the application of an electric field, FLC molecules rotate the polarizations of the signal passing through it. With the sufficient electric field, optical signal polarizations rotate to the orthogonal ones and the LBS passes the signal to the other output port. The principle of basic switch matrix mechanism is reported by Alex et al. in 2007 [37]. In this study, we are introducing a faster FLC instead of a twist nematic (TN) LC. In general, the optical parameters of FLCs are worse than in nematics but the main source for cross-talk is non-ideal beam splitters, and this problem can be fixed by the insertion of final cross-talk removal stages. In this case, the optical parameters of LC-SLM (liquid crystal special light modulator) are not important and FLCs may be used for fast matrix switch.
3.2. Simulation of Switch Performance Parameters
In multimode optical switching, the most challenging problem is the attainment of low cross-talk and faster response time. For the potential application of a FLC switch, the most significant performance parameter cross-talk (ratio of power leaked through the wrong output to the right one) is characterized theoretically and experimentally. Low crosstalk indicates high signal quality or small signal interference. The light transmittance through the FLC material between the crossed and parallel polarized state can be expressed as:
where θ is the tilt angle and π∙Δn∙d/λ is the optical retardation, in which Δn is the refractive index anisotropy, d is FLC layer thickness, and λ is the wavelength. T+ and T− are the maximum and minimum transmitted light intensity, which depend on the phase shift introduced by the FLC material. The superscripts (±) correspond to the polarity of applied voltage and subscripts (+ and ||) represent the crossed and parallel polarizer geometry. Therefore, the transmittance between parallel polarizers complements , so that:
From the transmittance measurements, it is possible to calculate the contrast ratio as:
The K+ and K||‘ are the contrast ratio of both crossed and parallel polarized states. As cross-talk is 10 log (1/K), we have simulated the cross-talk (CT) using Equations (5a) and (5b), also shown in Figure 5.
and Δn(T) of crossed and parallel polarized states.
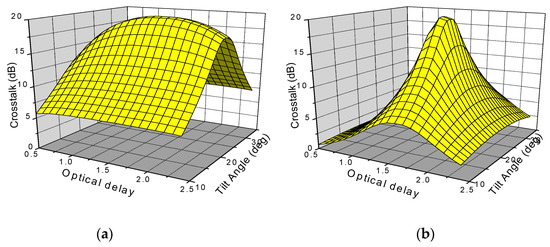
Figure 5.
Simulated cross talk as a function of temperature dependent parameters θ (T) and Δn (T) of (a) crossed and (b) parallel polarised states.
Figure 5 reveals the possible conditions for better cross-talk in both crossed and parallel polarized states. In the former state () this depends only on molecular tilt angle, but in the parallel polarized state it depends on birefringence in addition to the molecular tilt angle (). The simulation clearly explains the cell thickness dependencies of cross-talk. As FLC optical switching is wavelength-dependent, it implies certain restrictions for wavelength division multiplexing (WDM) applications. Nevertheless, this effect is not as strong as the other cross-talk factors.
4. Results and Discussions
Electro-Optic Measurements
The KCFLC 10R material under study exhibits an optimal molecular tilt angle of 22.5° at room temperature (Figure 6a). The molecular tilt angle as a function of temperature (Figure 6a) is measured in a 6 µm cell using the application of an external field. While cooling down from isotropic temperature, θ exhibits optimal angle at room temperature. The phase transition to the ferroelectric phase θ is considered as the primary order parameter, and it is the angle between the smectic layer and the principal director n.
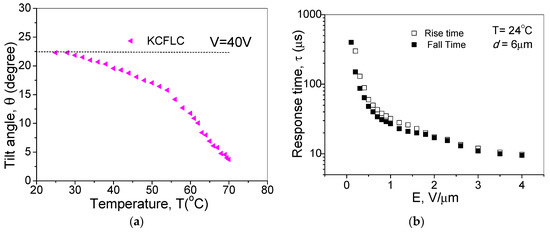
Figure 6.
(a) Temperature-dependent molecular tilt angle (θ) and (b) the electric field-dependent response time (τ) for the KCFLC 10R sample in a planar aligned cell with cell thickness of 6 μm. The measurement was performed at 24 °C.
The switching time of FLC material under investigation has been characterized as a function of an applied electric field, shown in Figure 6b. Fast response time is one of the important peculiarities of FLCs together with bi-stability when compared to conventional nematic LC switches. At room temperature, the 6 μm cell exhibits much faster switching time (<10 μs for 4 V/μm) and it shows an increasing trend of response time with an increasing electric field. LC shutters are limited by the switching time to rotate the LC director under the application of electric field and the recovery time after the field is removed. While the recovery time is entirely dependent upon the properties of LC, switching time also depends on the applied field. For optical systems, as with flat panel displays, both switching and recovery times are important, but for recording one time images only the switching time is more important than recovery time.
The contrast ratio (K) as a function of temperature in crossed and parallel polarized-state measured at room temperature is depicted in Figure 7. The measurements were performed by KCFLC 10R material with a cone angle of 45° to obtain the maximum contrast.
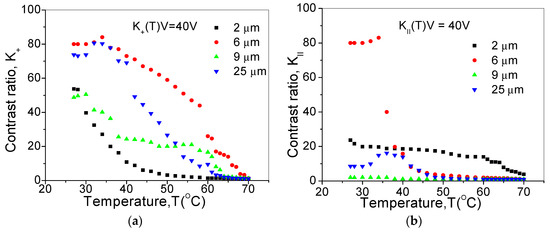
Figure 7.
Temperature dependent contrast ratio of SmC* phase (K) in (a) crossed and (b) parallel polarized states. Measurements are carried out by the application of 40 V in planar-aligned cells filled with KCFLC 10R material, in a cooling process.
Experimentally, it is convenient to express the cross-talk in terms of measured K and the results in Figure 7 shows maximum contrast is achieved with 6 µm cell for both crossed and parallel polarized states. The calculated cross-talk in both polarized states is 19 dB. The simulated results were confirmed by experiments with a FLC binary switch. When compared to all other optical switches, LC-based switches exhibit slightly excessive cross-talk because of the cross-talk sources, two of which are from FLCs and two from beam splitters. This is evident in the schematic shown in Figure 8.
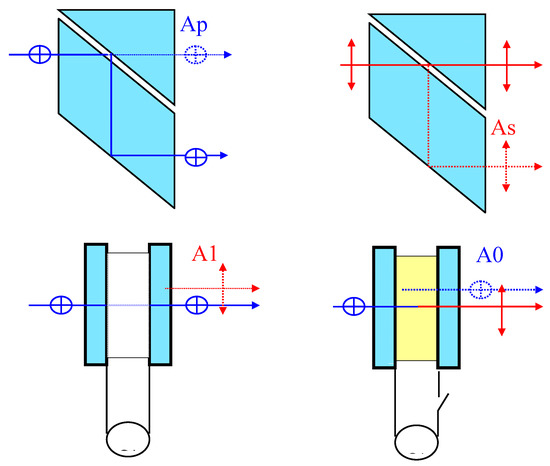
Figure 8.
Different cross talk sources: two are from FLCs and two from lateral beam splitters (LBSs).
Here, Ap and As are the cross-talk sources of passed and shifted signals by LBS and A1 (due to the depolarization of the light beam passed through the switched FLC state) and A0 (which shows how closely the light rotates at 90° while passing through the FLC material) are from the FLCs. The measured cross-talk of the FLC binary switch is presented in Table 1.

Table 1.
Measured cross-talk of FLC binary optical switch.
It can clearly be seen in Table 1 that the main cross-talk in the binary FLC switching stage under study is from the beam splitter (Ap). In ideal conditions, the vertically polarized light must completely pass straightforward through the LBS (see Figure 4), however practically some part of the beam is reflected from the air split and is shifted by the beam splitter (As), as can be seen in Figure 8. Similarly, some part of the horizontally polarized light (Ap) passes straight forward through the LBS. The values obtained from the LBS are As ~19 dB and Ap ~27 dB, and from the FLC are A1 ~21 dB and A0 ~19 dB. The main source of cross-talk in FLC is the imperfect alignment of LC molecules. In one of the previous work, Fracasso et al. developed a free-space switch based on the FLC material [38]. Cross-talk in the developed 1 × 14 single-stage switch varies from −21 dB to −45 dB in between the addressed and non-addressed fibers with the switching time only in the order of sub-millisecond. In another work, Yulia et al. demonstrated a fast 2 × 2 free-space photonic switch exhibiting cross-talk of −33 dB [39]. This switch was based on FLC exhibiting switching times in the order of microseconds. In this study, the obtained crosstalk of approximately −19 dB can be modified to obtain better results by introducing cross-talk cleaning stages to the final switching stage.
5. Conclusions
In summary, the feasibility of a free space fast optical switch concept was studied theoretically and experimentally using FLC material. Even if they have the disadvantage of slightly excessive cross-talk, LC switches offer large electro-optic effects over a short distance, are very reliable, and also their optical performance is satisfactory. The switching speed of the FLC material under study, KCFLC 10R, is much faster (<10 µs) than conventional non-mechanical switches. For optimal FLC parameters at fixed temperature, the best achieved crosstalk measured was approximately −19 dB. The use of cross-talk removal stages helps to reduce cross talk to better than −30 dB. The main idea of a faster FLC matrix switch is to use conventional LCD technology to perform parallel switching in optical channels, without disturbing each other. Due to the faster response time and reliability, FLC modulators are attractive for scientific research and have many potential applications in optical communication networks.
Author Contributions
The experiment was designed by S.P.S. The result analysis was performed by Y.P.P. and S.P.S. Additionally, S.P.S., Y.P.P., and D.B. were responsible for interpretation of results and writing the paper.
Funding
This work is supported by Strand-1 project funded by Science Foundation Ireland and Dublin Institute of Technology’s Fiosraigh Post Graduate Research program.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fujiwara, M.; Goodman, M.; O’Mahony, M.; Tonguz, O.; Willner, A. Guest Editorial Multiwavelength Optical Technology and Networks. J. Light. Technol. 1996, 14, 932. [Google Scholar] [CrossRef]
- Cruz, R.L.; Hill, G.R.; Kellner, A.L.; Ramaswamy, R.; Sasaki, G.H.; Yamabayashi, Y. Guest Editorial Optical Networks. IEEE J. Select. Areas Commun. 1996, 14, 761. [Google Scholar] [CrossRef]
- Ollier, E. Optical MEMS devices based on moving waveguides. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 155. [Google Scholar] [CrossRef]
- Wang, X.; Howley, B.; Chen, M.; Chen, R. 4×4 Nonblocking Polymeric Thermo-Optic Switch Matrix Using the Total Internal Reflection Effect. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 997. [Google Scholar] [CrossRef]
- Ho, K.P.; Liaw, S.K. Demultiplexer Crosstalk Rejection Requirements for Hybrid WDM System with Analog and Digital Channels. IEEE Photon. Technol. Lett. 1998, 10, 737. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Zhang, M.; Chen, K. Broadband 2×2 lithium niobate electro-optic switch based on a Mach–Zehnder interferometer with counter-tapered directional couplers. Appl. Opt. 2017, 56, 8164. [Google Scholar] [CrossRef]
- Stephens, M.F.C.; Asghari, M.; Penty, R.V.; White, I.H. Demonstration of ultrafast all-optical wavelength conversion utilizing birefringence in semiconductor optical amplifiers. IEEE Photon. Technol. Lett. 1997, 9, 449. [Google Scholar] [CrossRef]
- Banchi, L.; Presi, M.; D’Errico, A.; Contestabile, G.; Ciaramella, E. All-optical 10 and 40 Gbit/s RZ-to-NRZ format and wavelength conversion using semiconductor optical amplifiers. J. Lightwave Technol. 2010, 28, 32. [Google Scholar] [CrossRef]
- Nolting, H.P.; Gravert, M.; Bachmann, M.; Renaud, M. Crosstalk Reduced Digital Optical Switch with Single Electrode Designed for InP. Opt. Amplif. Appl. 1996, 6, 637. [Google Scholar]
- Shigeto, K.; Seiiti, S.; Yoshie, T.; Noriyoshi, Y. Ferroelectric liquid crystal driving method for optical switching devices in communication networks. Ferroelectrics 1993, 149, 159. [Google Scholar]
- Panarin, Y.; Sreenilayam, S. FLC based matrix optical switch. In Proceedings of the International Conference on Photonics in Switching, Pisa, Italy, 15–19 September 2009. [Google Scholar]
- Schadt, M.; Seiberle, H.; Schuster, A. Optical patterning of multi-domain liquid-crystal displays with wide viewing angles. Nature 1996, 381, 212. [Google Scholar] [CrossRef]
- Saito, I.; Ono, H.; Kawatsuki, N. Photorefractive Bragg diffraction in high- and low-molar-mass liquid crystal mixtures. Appl. Phys. Lett. 1998, 72, 1942. [Google Scholar]
- Sreenilayam, S.P.; Panarin, Y.P.; Vij, J.K.; Lehmann, A.; Poppe, M.; Tschierske, C. Development of ferroelectricity in the smectic phases of 4-cyanoresorcinol derived achiral bent-core liquid crystals with long terminal alkyl chains. Phys. Rev. Mater. 2017, 1, 035604. [Google Scholar] [CrossRef]
- Sreenilayam, S.P.; Panarin, Y.P.; Vij, J.K.; Panov, V.P.; Lehmann, A.; Poppe, M.; Prehm, M.; Tschierske, C. Spontaneous helix formation in non-chiral bent-core liquid crystals with fast linear electro-optic effect. Nat. Commun. 2016, 7, 11369. [Google Scholar] [CrossRef]
- Panarin, Y.P.; Sreenilayam, S.P.; Vij, J.K.; Lehmann, A.; Tschierske, C. A fast linear electro-optical effect in a non-chiral bent-core liquid crystal. J. Mater. Chem. C 2017, 5, 12585. [Google Scholar] [CrossRef]
- Vij, J.K.; Panarin, Y.P.; Sreenilayam, S.P.; Alaasar, M.; Tschierske, C. Investigation of the heliconical smectic SmCSPFhel phase in achiral bent-core mesogens derived from 4-cyanoresorcinol. Phys. Rev. Mater. 2019, 3, 045603. [Google Scholar] [CrossRef]
- Srivastava, A.; Hu, W.; Chigrinov, V.; Kiselev, A.; Lu, Y.Q. Fast switchable grating based on orthogonal photo alignments of ferroelectric liquid crystals. Appl. Phys. Lett. 2012, 101, 031112. [Google Scholar] [CrossRef]
- Chigrinov, V.; Manohar, R.; Srivastava, A.; Pozhidaev, E.P. Single walled carbon nano-tube, ferroelectric liquid crystal composites: Excellent diffractive tool. Appl. Phys. Lett. 2011, 99, 201106. [Google Scholar]
- Sreenilayam, S.P.; Agra-Kooijman, D.M.; Panov, V.P.; Swaminathan, V.; Vij, J.K.; Panarin, Y.P.; Kocot, A.; Panov, A.; Rodriguez-Lojo, D.; Stevenson, P.J. Phase behavior and characterization of heptamethyltrisiloxane-based de Vries smectic liquid crystal by electro-optics, x rays, and dielectric spectroscopy. Phys. Rev. E 2017, 95, 032701. [Google Scholar] [CrossRef]
- Larsen, T.T.; Bjarklev, A.; Sparre, D.H.; Broeng, J. Optical devices based on liquid crystal photonic bandgap fibres. Optics Express 2003, 11, 2589. [Google Scholar] [CrossRef]
- Soref, R.A.; McMahon, D.H. Calcite 2×2 optical bypass switch controlled by liquid-crystal cells. Opt. Lett. 1982, 7, 186. [Google Scholar] [CrossRef]
- Fuji, Y. Low-Crosstalk 1×2 Optical Switch Composed of Twisted Nematic Liquid Crystal Cells. IEEE. Photon. Lett. 1993, 5, 206. [Google Scholar] [CrossRef]
- Pozhidaev, E.P.; Chigrinov, V.G.; Du, T. Fast Switching Bistable Ferroelectric Liquid Crystal Switches as a New Optical Elements for Photonics Applications. In Proceedings of the 14th OptoElectronics and Communications Conference, Vienna, Austria, 13–17 July 2009. [Google Scholar] [CrossRef]
- Chigrinov, V.G. Liquid Crystal Applications in Photonics. In Proceedings of the Photonics West Conference, San Jose, CA, USA, 25–28 January 2009. [Google Scholar]
- Soref, R.A. Low-cross-talk 2×2 optical switch. Opt. Lett. 1981, 6, 275. [Google Scholar] [CrossRef]
- Shankar, N.; Morris, J.; Yakymyshyn, C.; Pollock, C. A 2×2 fiber optic switch using chiral liquid crystals. IEEE Photon. Technol. Lett. 1990, 2, 147. [Google Scholar] [CrossRef]
- Meyer, R.; Liebert, L.; Strzelecki, L.; Keller, P. Ferroelectric liquid crystals. J. Phys. Lett. 1975, 36, 69. [Google Scholar] [CrossRef]
- Riza, N.; Yuan, S. Low optical interchannel crosstalk, fast switching speed, polarisation independent 2×2 fibre optic switch using ferroelectric liquid crystals. Electron. Lett. 1998, 34, 1341. [Google Scholar] [CrossRef]
- Sreenilayam, S.P.; Panov, V.P.; Vij, J.K.; Shanker, G. The NTB phase in an achiral asymmetrical bent-core liquid crystal terminated with symmetric alkyl chains. Liq. Cryst. 2017, 44, 244. [Google Scholar] [CrossRef]
- Sreenilayam, S.P.; Panarin, Y.P.; Vij, J.K.; Torgova, S.I.; Lehmann, A.; Tschierske, C. Flexoelectric polarization studies in bent-core nematic liquid crystals. Phys. Rev. E 2015, 92, 022502. [Google Scholar] [CrossRef]
- Torgova, S.; Sreenilayam, S.P.; Panarin, Y.P.; Francescangeli, O.; Vita, F.; Vij, J.K.; Pozhidaev, E.; Minchenko, M.; Ferrero, C.; Strigazzi, A. Short bent-core molecules: X-ray, polarization, dielectricity, texture and electro-optics investigations. Phys. Chem. Chem. Phys. 2017, 19, 22946. [Google Scholar] [CrossRef]
- Sreenilayam, S.P.; Rodriguez-Lojo, D.; Panov, V.P.; Swaminathan, V.; Vij, J.K.; Panarin, Y.P.; Gorecka, E.; Panov, A.; Stevenson, P.J. Design and investigation of de Vries liquid crystals based on 5-phenyl-pyrimidine and( R, R )2,3-epoxyhexoxy backbone. Phys. Rev. E 2017, 96, 042701. [Google Scholar] [CrossRef]
- Swaminathan, V.; Panov, V.P.; Panarin, Y.P.; Sreenilayam, S.P.; Vij, J.K.; Panov, A.; Rodriguez-Lojo, D.; Stevenson, P.J.; Gorecka, E. The effect of chiral doping in achiral smectic liquid crystals on the de Vries characteristics: Smectic layer thickness, electro-optics and birefringence. Liq. Cryst. 2018, 45, 513. [Google Scholar] [CrossRef]
- Sreenilayam, S.P.; Panarin, Y.P.; Vij, J.K.; Lehmann, A.; Tschierske, C. Physical Properties of SmAb Phase in an Achiral Bent–Core Smectic Liquid Crystal. Ferroelectrics 2012, 431, 196. [Google Scholar] [CrossRef]
- Sreenilayam, S.P.; Rodriguez-Lojo, D.; Agra-Kooijman, D.M.; Vij, J.K.; Panov, V.P.; Panov, A.; Fisch, M.R.; Kumar, S.; Stevenson, P.J. de Vries liquid crystals based on a chiral 5-phenylpyrimidine benzoate core with a tri- and tetra-carbosilane backbone. Phys. Rev. Mater. 2018, 2, 025603. [Google Scholar] [CrossRef]
- Alex, V.; Dubtsov, A.; Panarin, Y.; Wilkinson, T. Optical Performance of Non-blocking 4×4 Optical Switch: Simulation and Experiment. Euro. Disp. 2007, S9-3, 161. [Google Scholar]
- Fracasso, B.; de Bougrenet de la Tocnaye, J.L.; Noirie, L.; Razzak, M.; Danniel, E. Performance Assessment of a Liquid Crystal Multichannel Photonic Spaceswitch. In Photonics in Switching (Technical Digest); Academic Press: Cambridge, MA, USA, 2001; p. 24. [Google Scholar]
- Yuliya, S.; Gerald, F.; Qian, W. Fast free-space photonic switch based on a ferroelectric liquid crystal. Proc. SPIE 2006, 6185, 618518. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).