Ferroelectric Liquid Crystals: Physics and Applications
Abstract
:1. Introduction
2. Operation Principle of Electrooptic Modes in FLCs
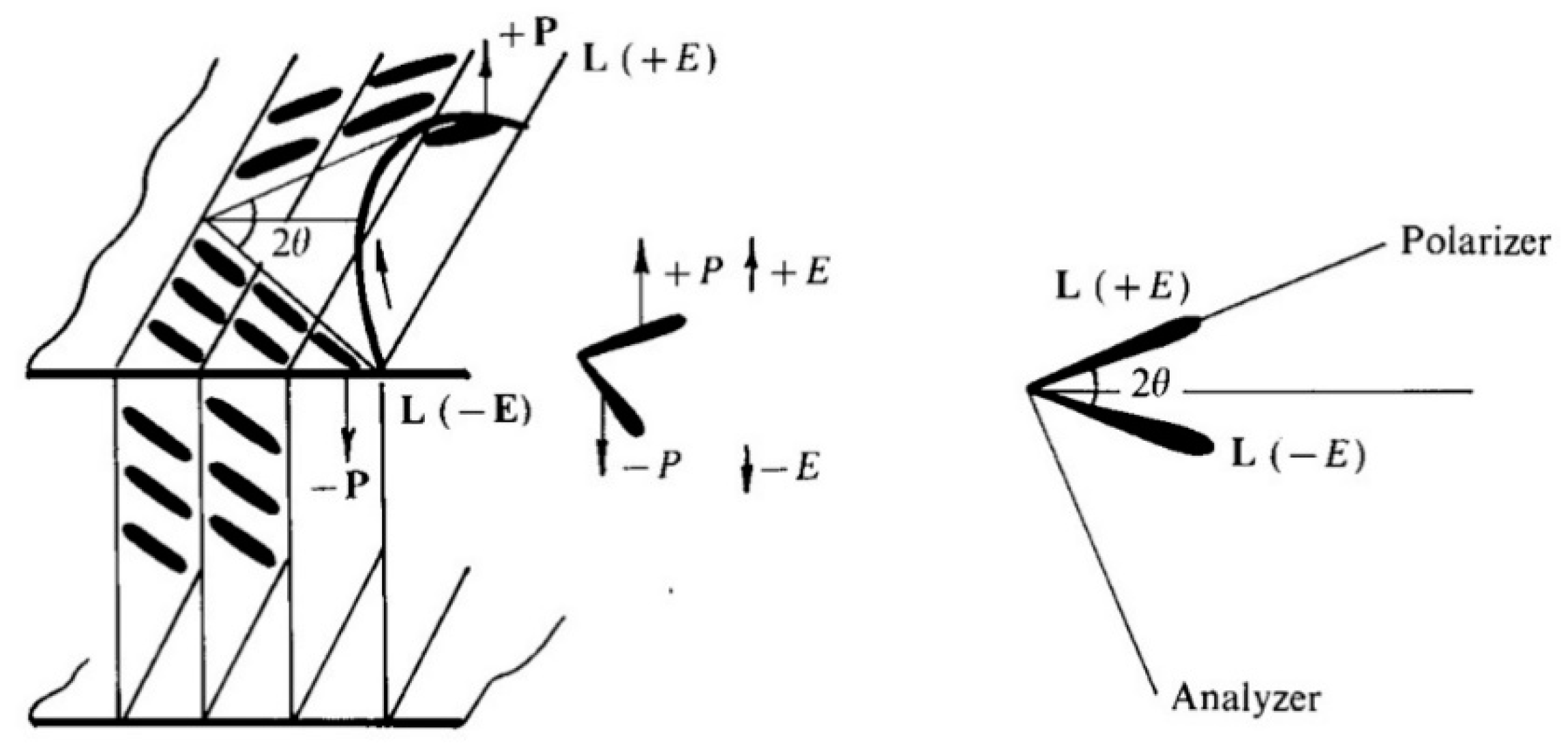
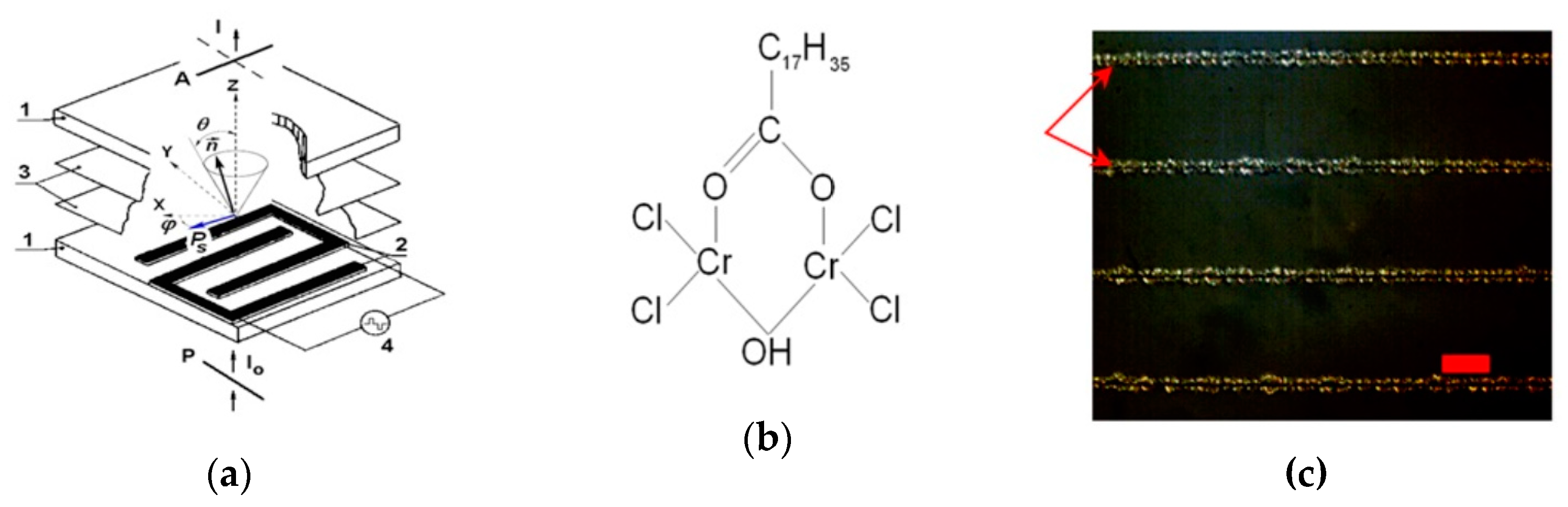
2.1. Surface Stabilized FLC (SSFLC) Mode
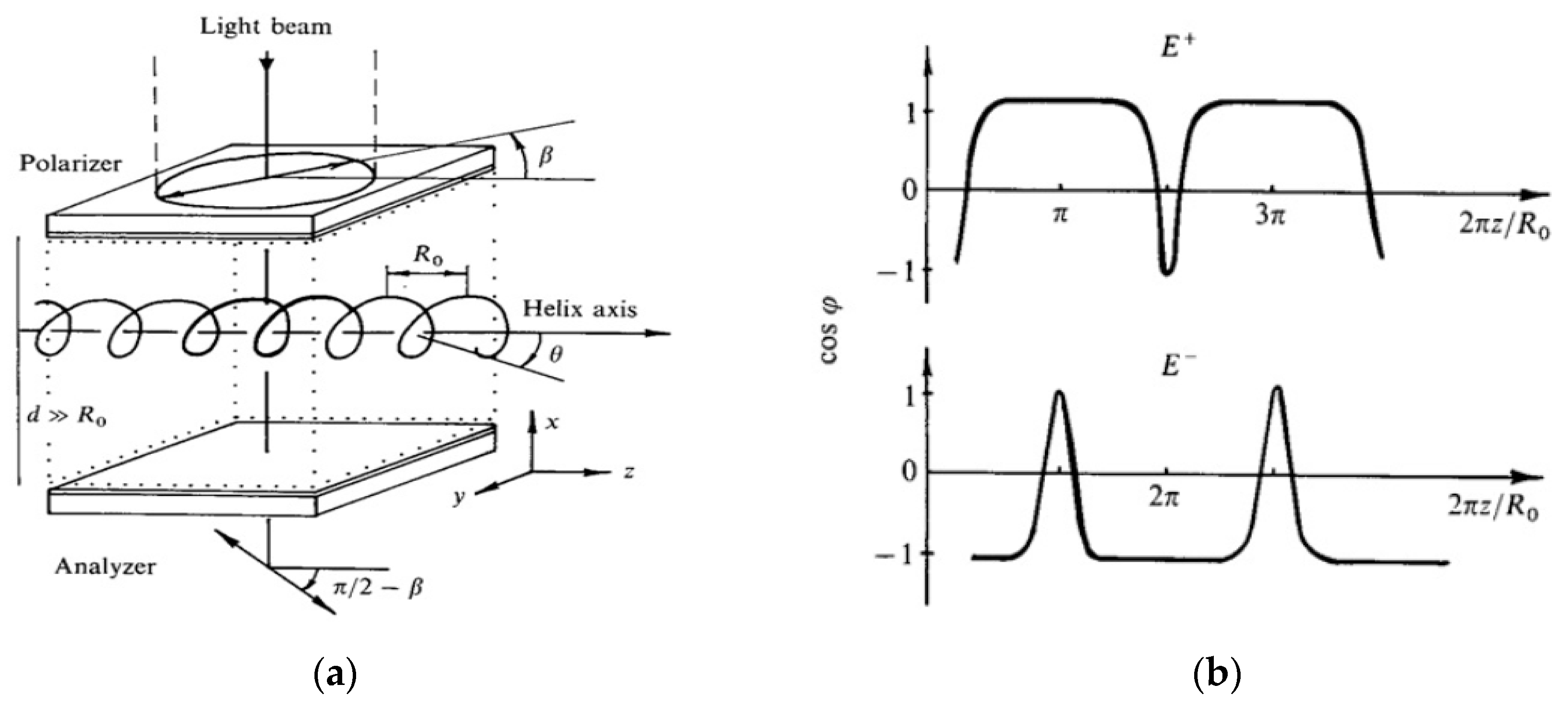
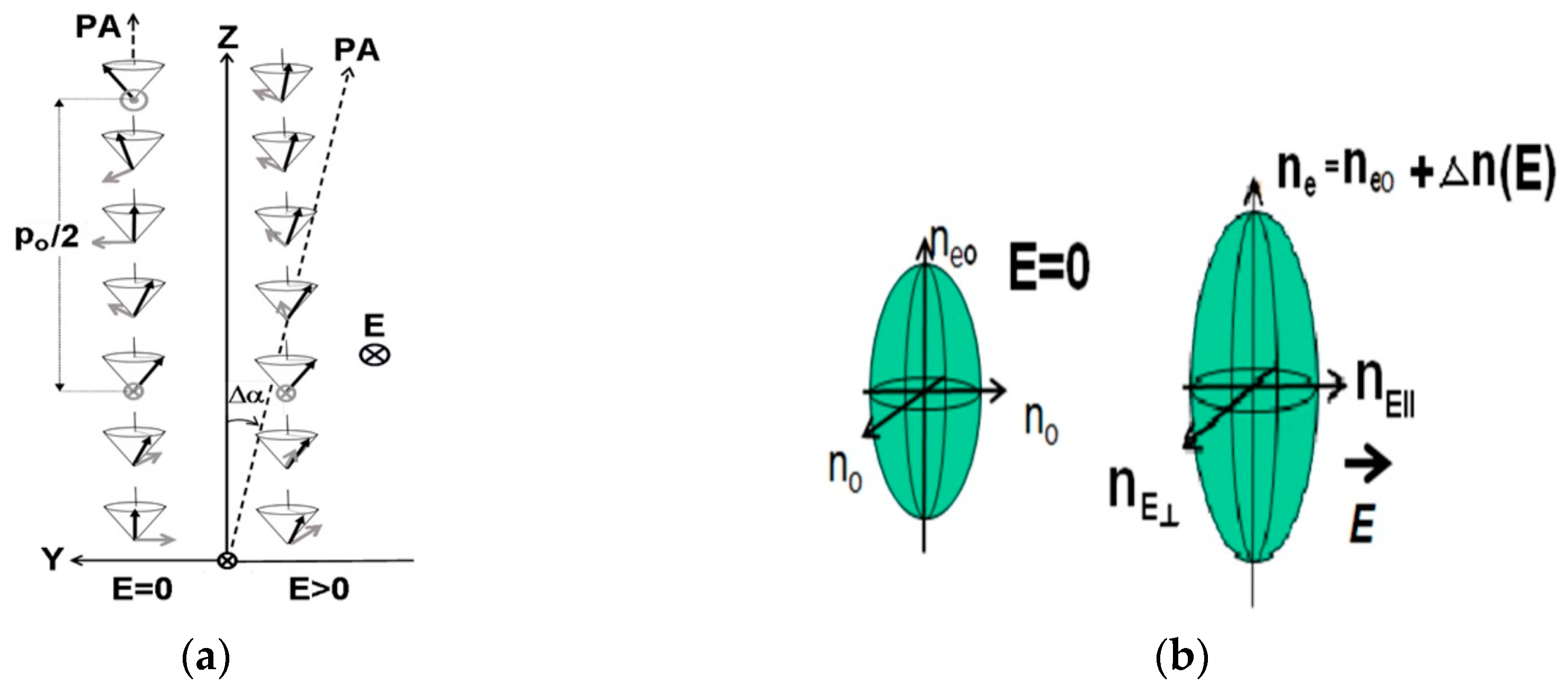
2.2. Deformed Helix Ferroelectric (DHF) Mode
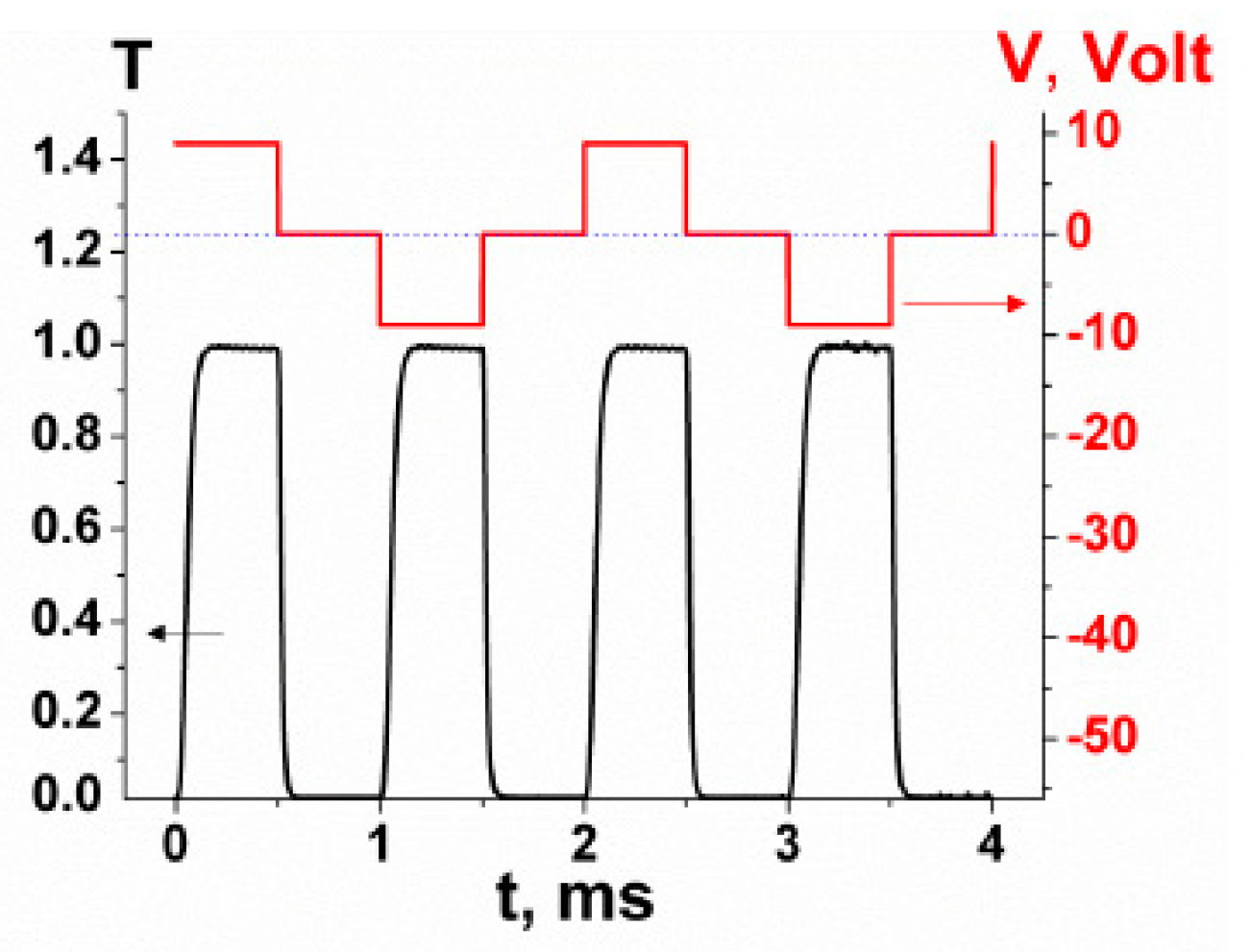
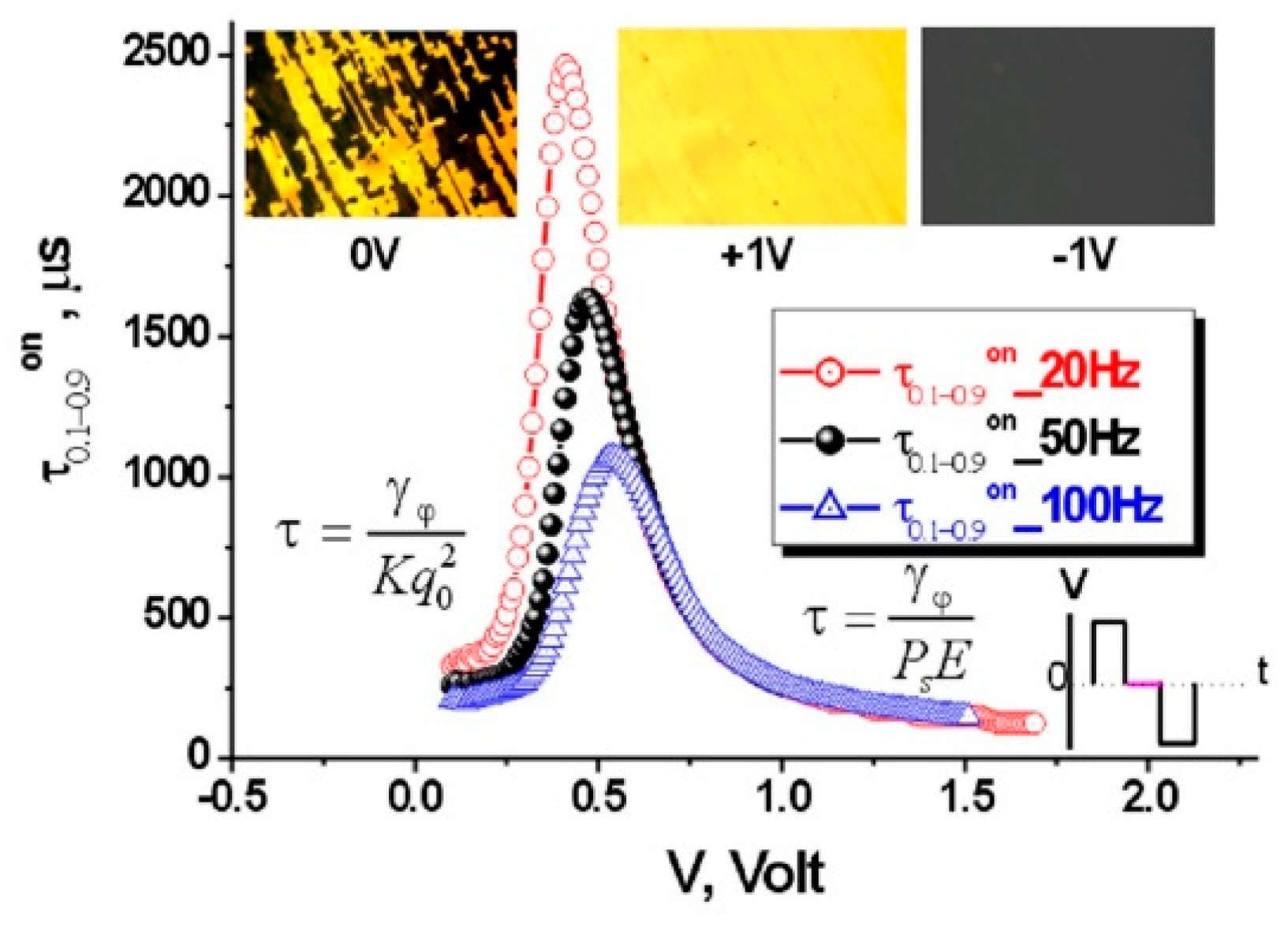
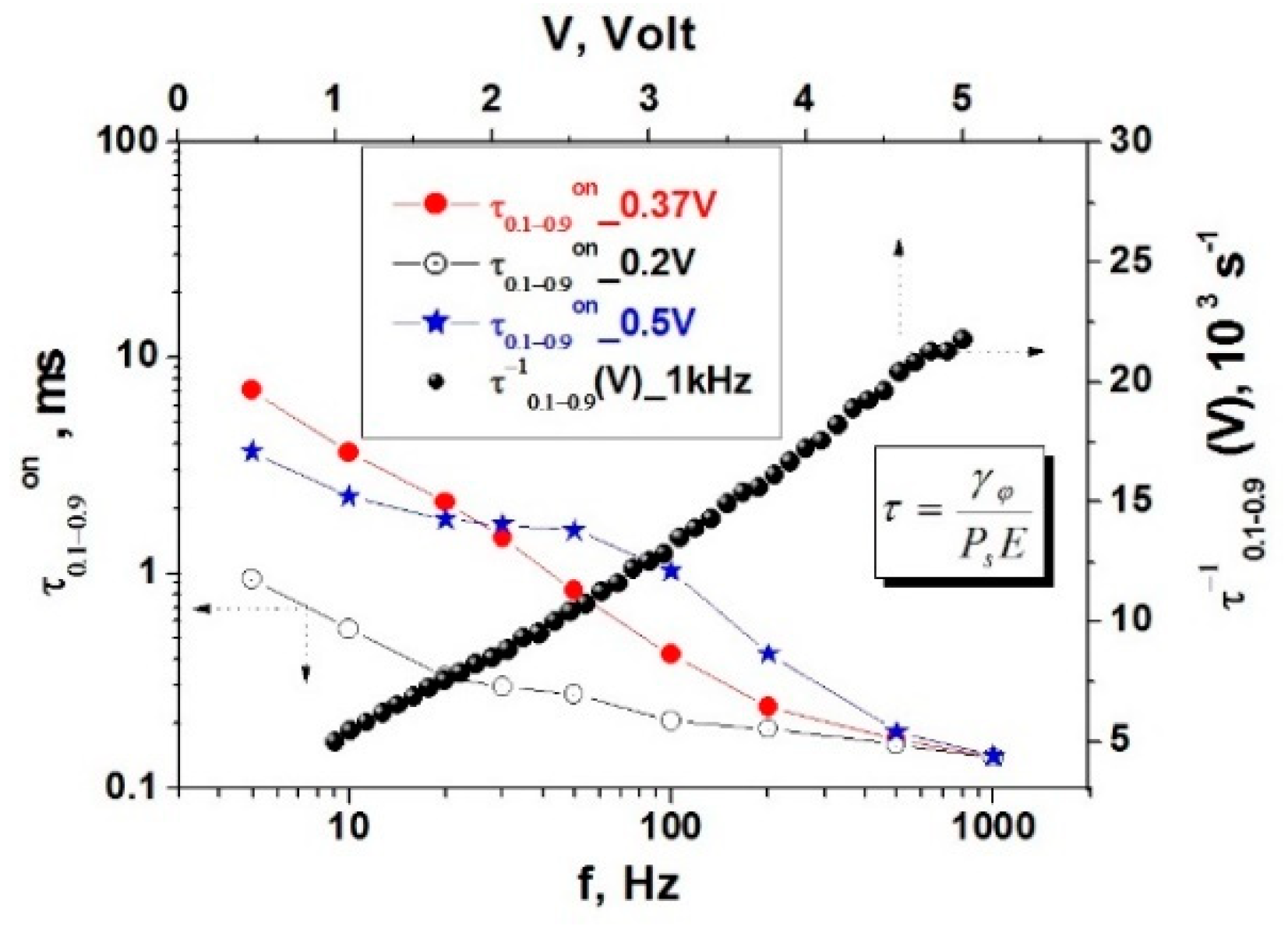
2.3. Electrically Suppressed Helix (ESH) Mode
3. Electrooptic Effects of FLC Modes and Their Applications
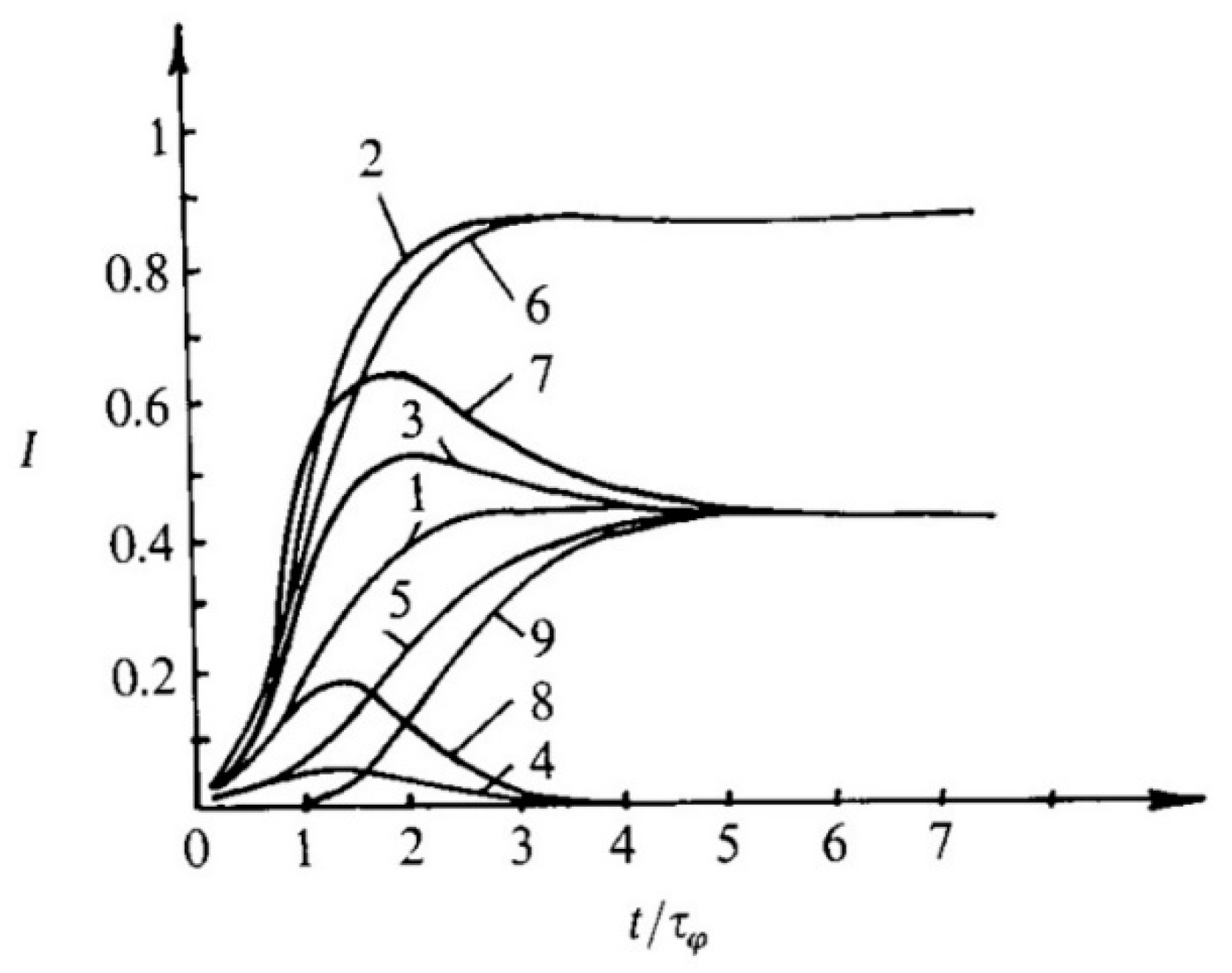
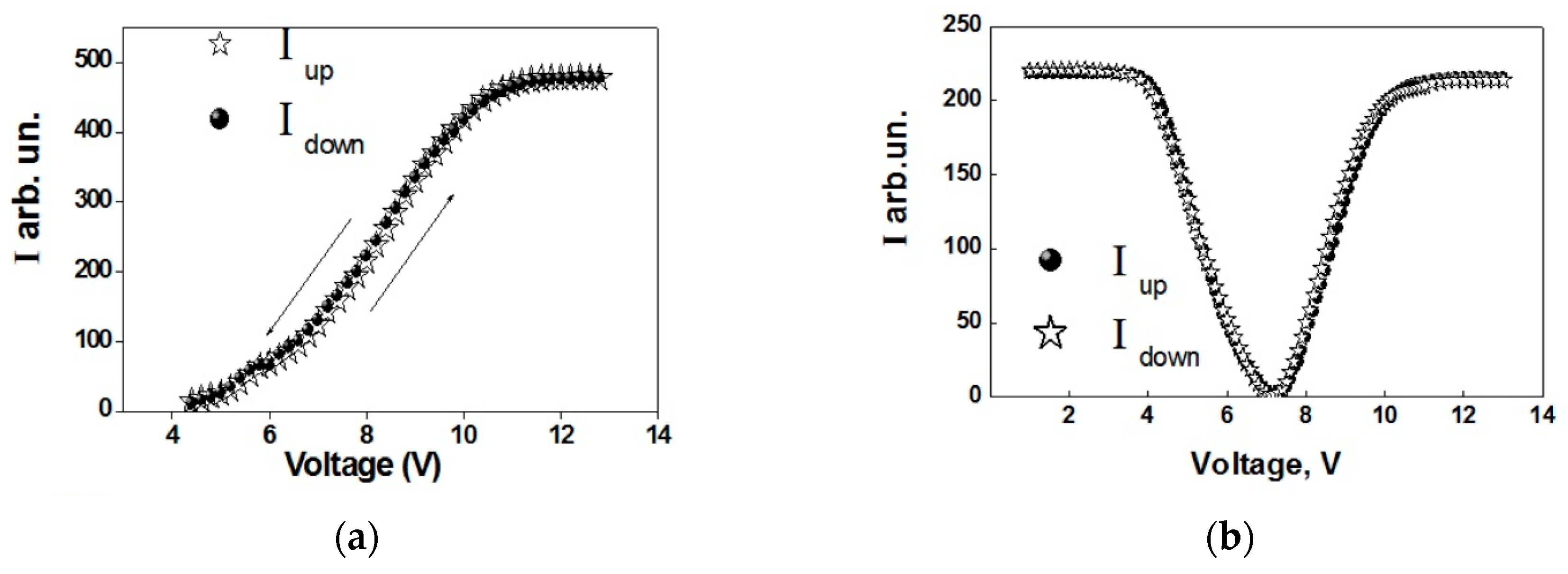
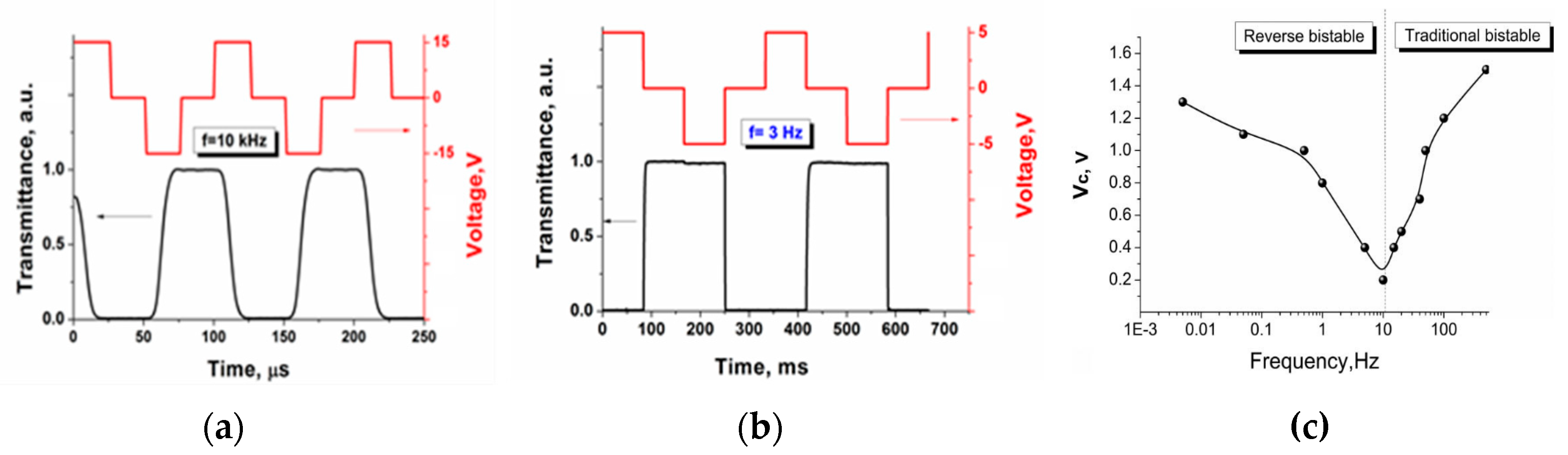
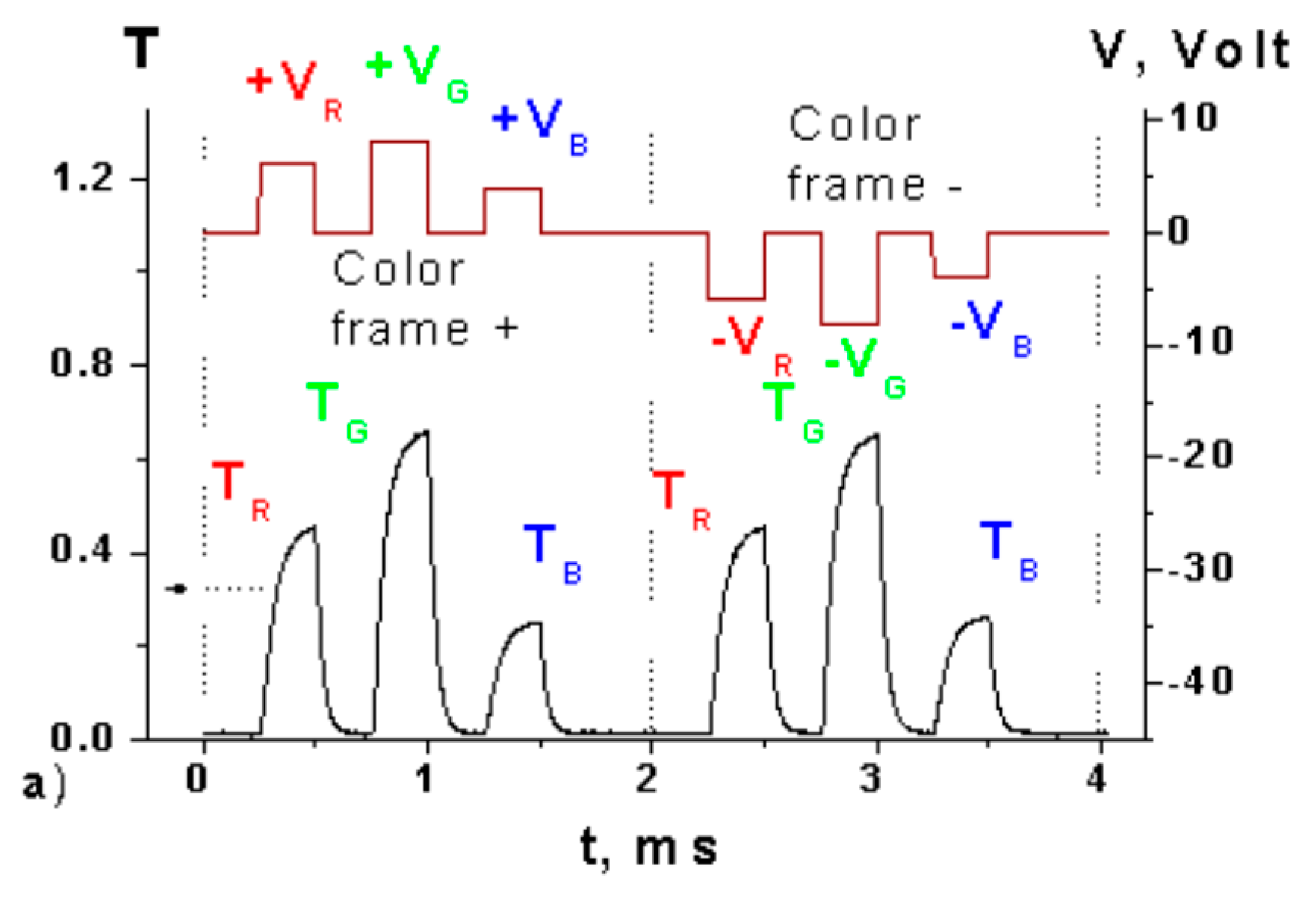
3.1. Bi- and Multi-Stable Switching
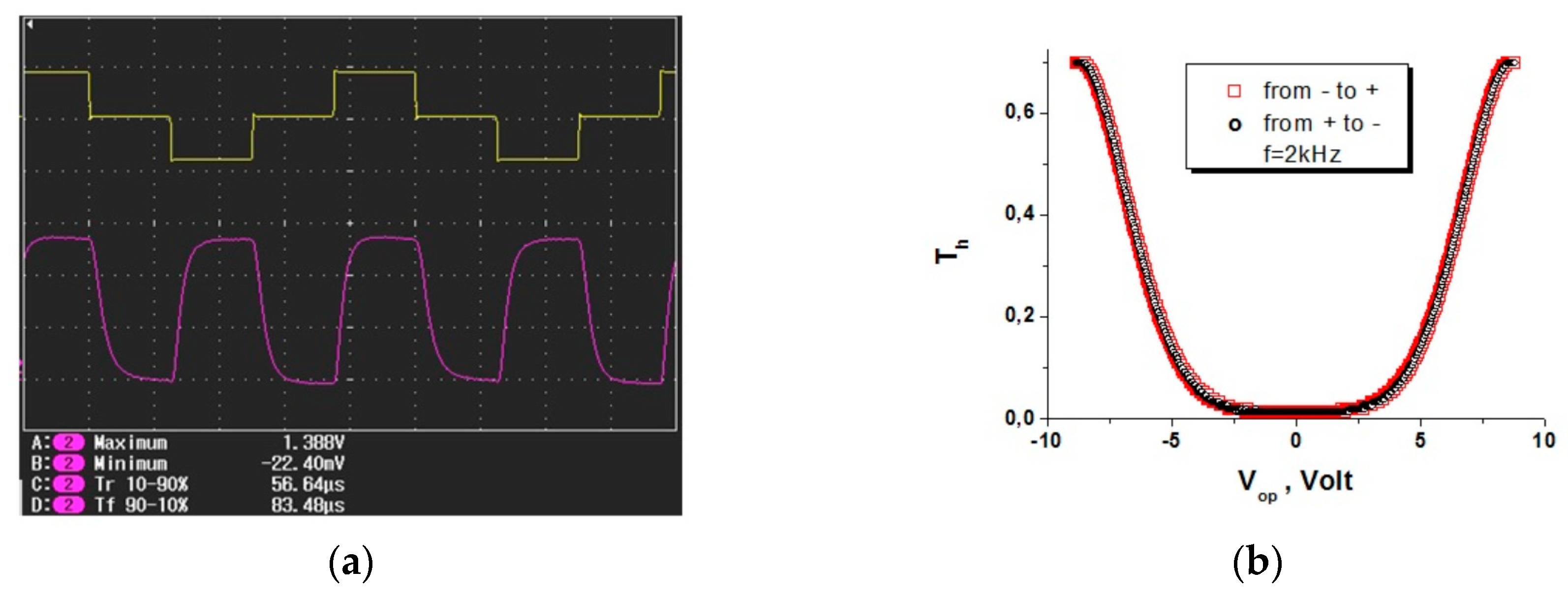
3.2. V-Shape Electrooptic Response
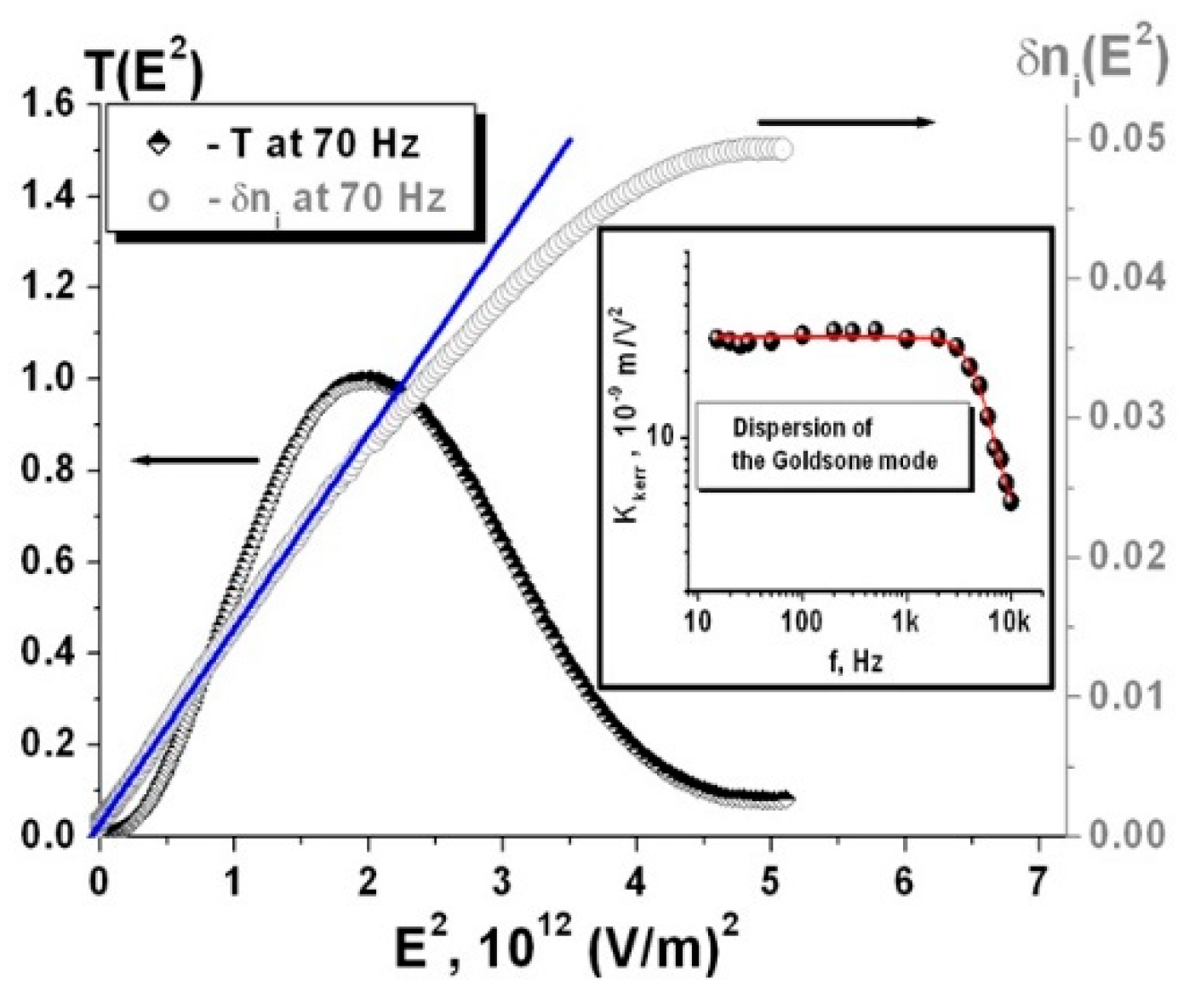
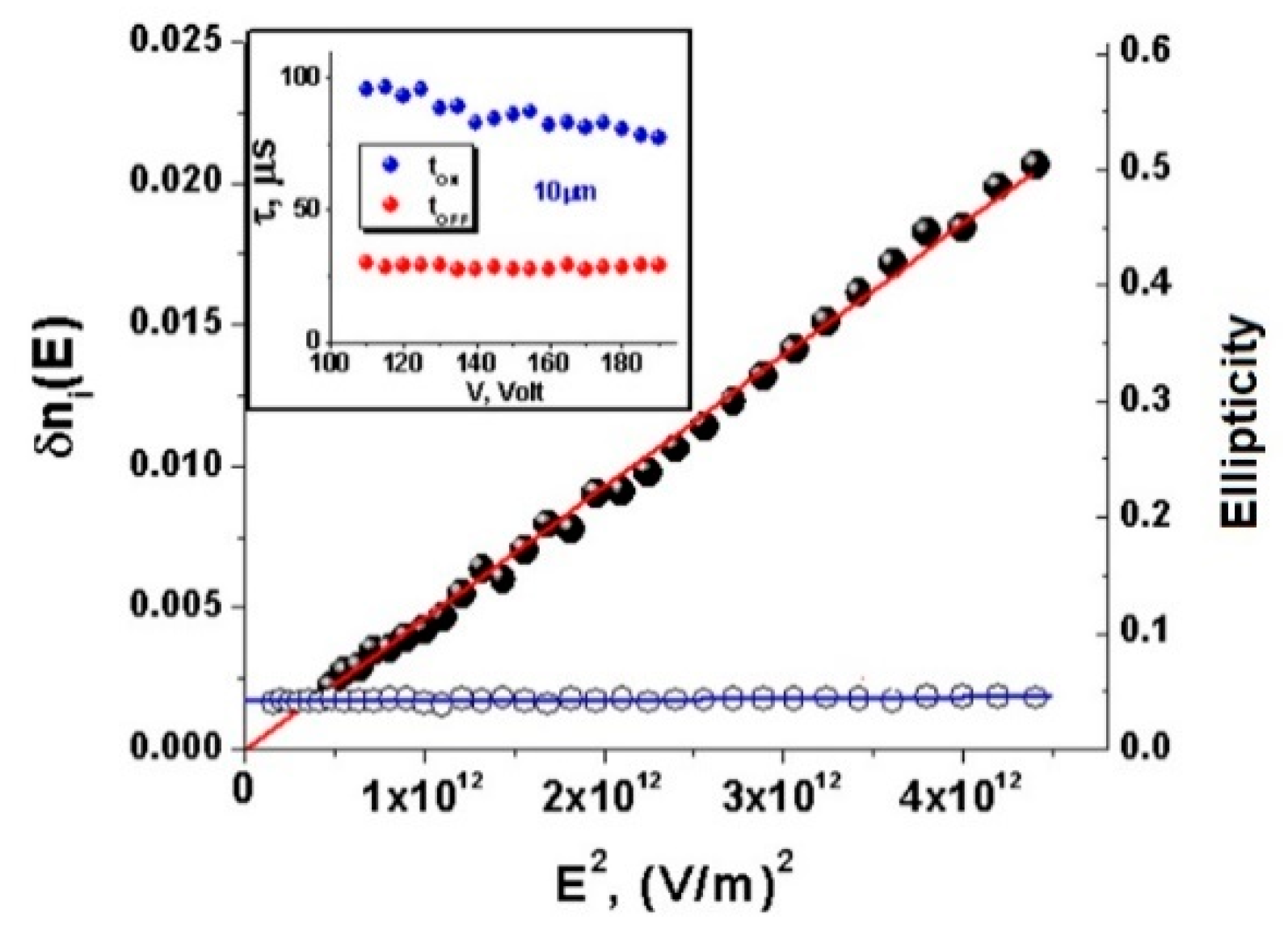
3.3. Orientational “Kerr Effect”
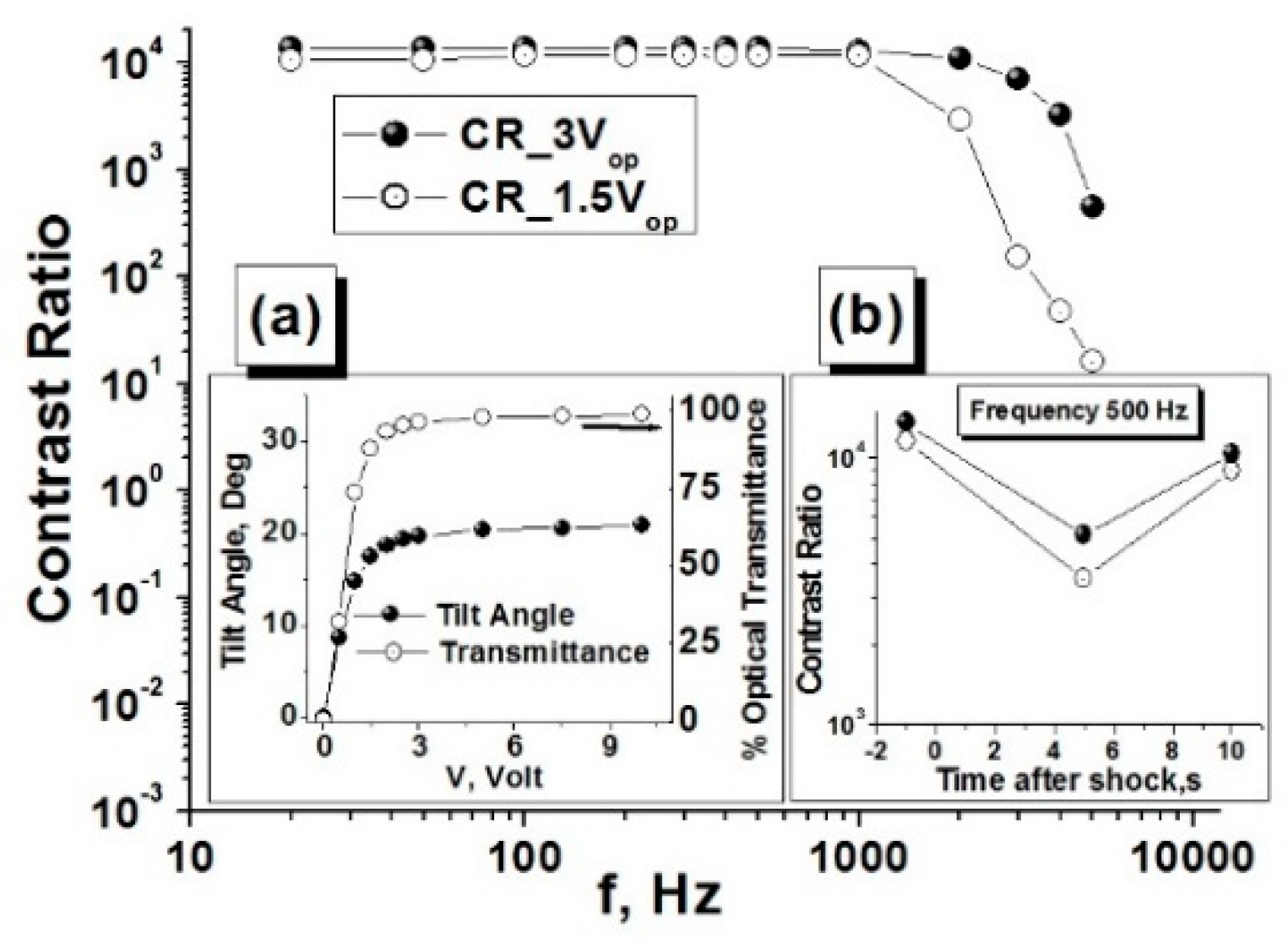
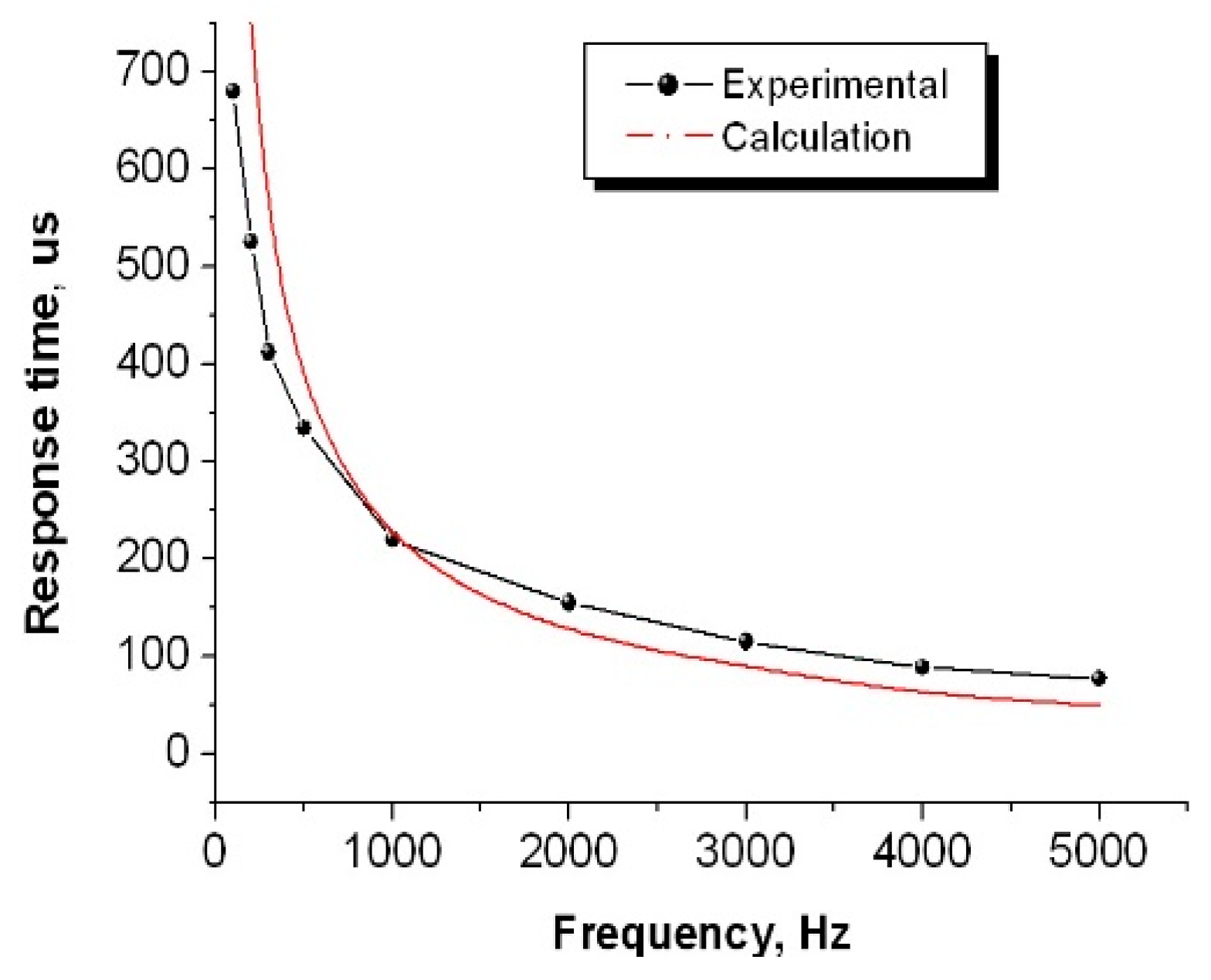
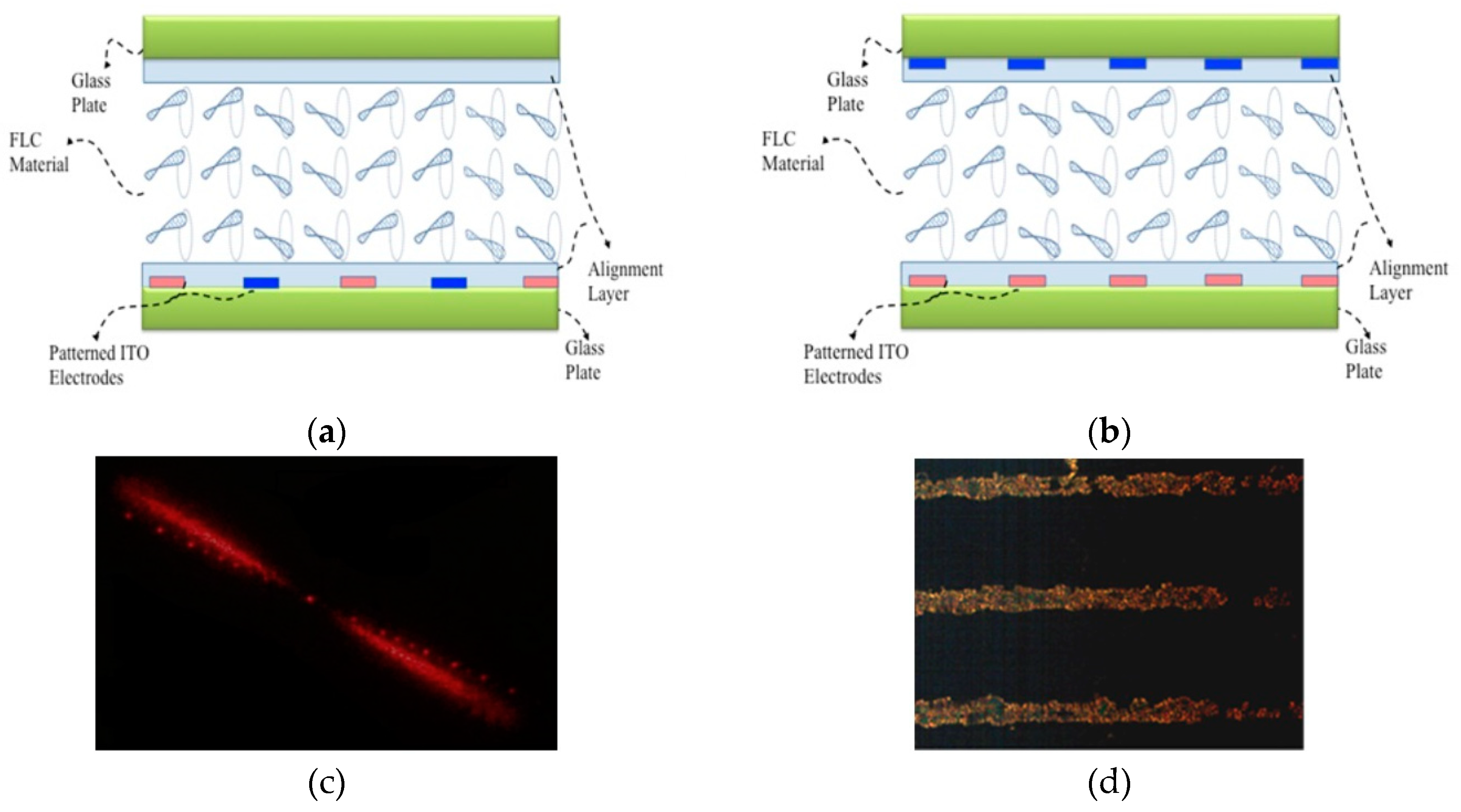
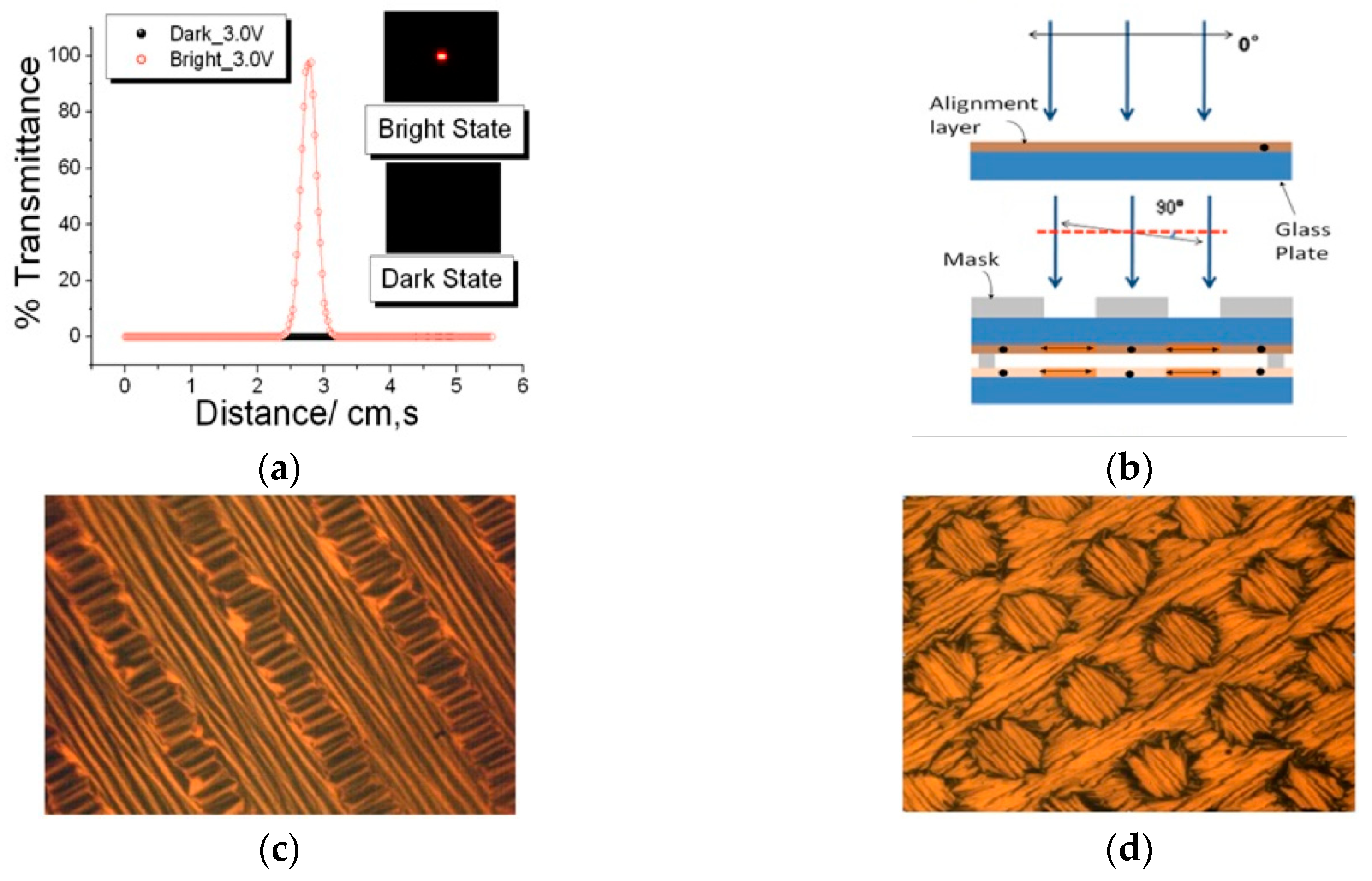
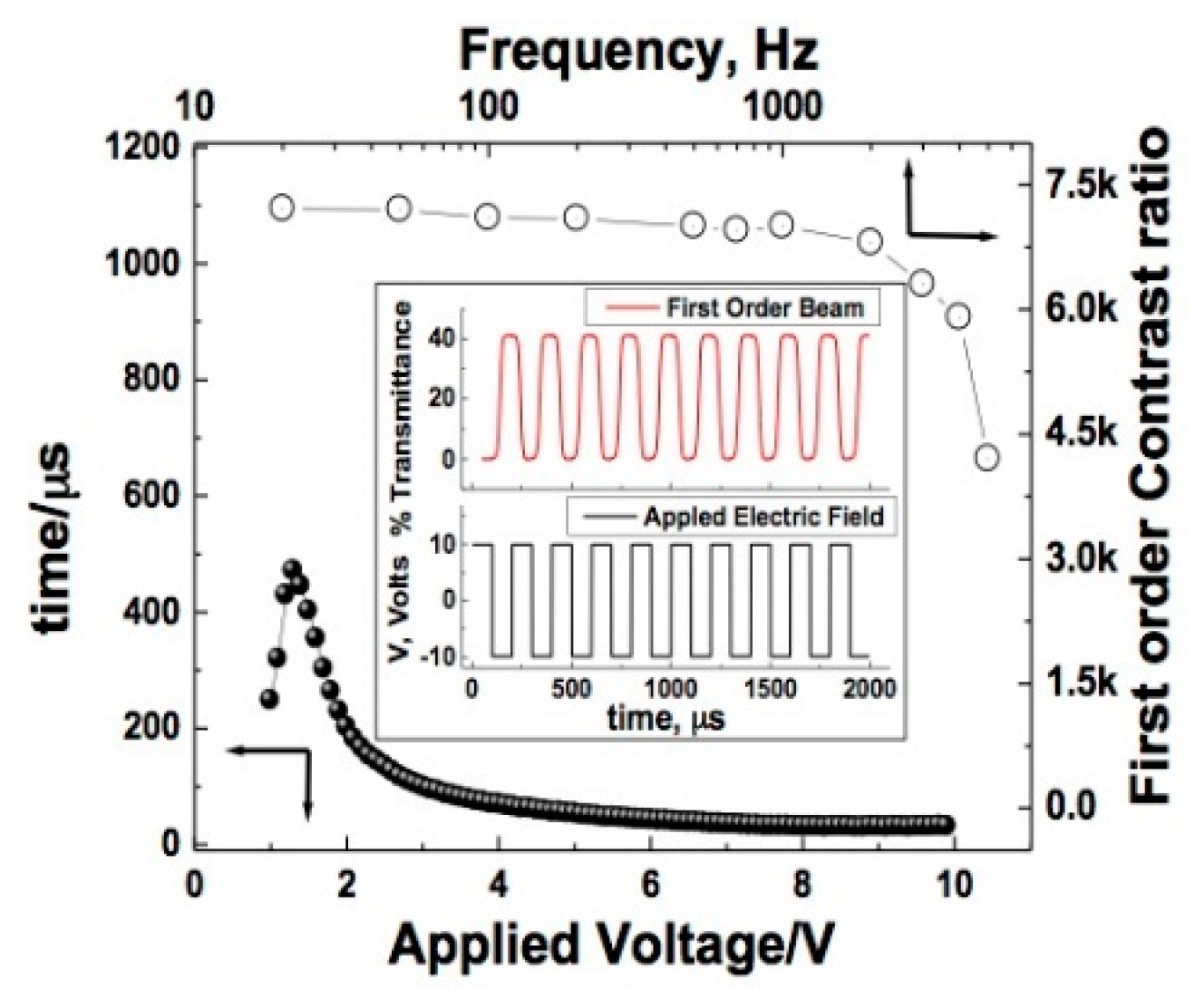
3.4. Fast Shutter with High Contrast Ratio
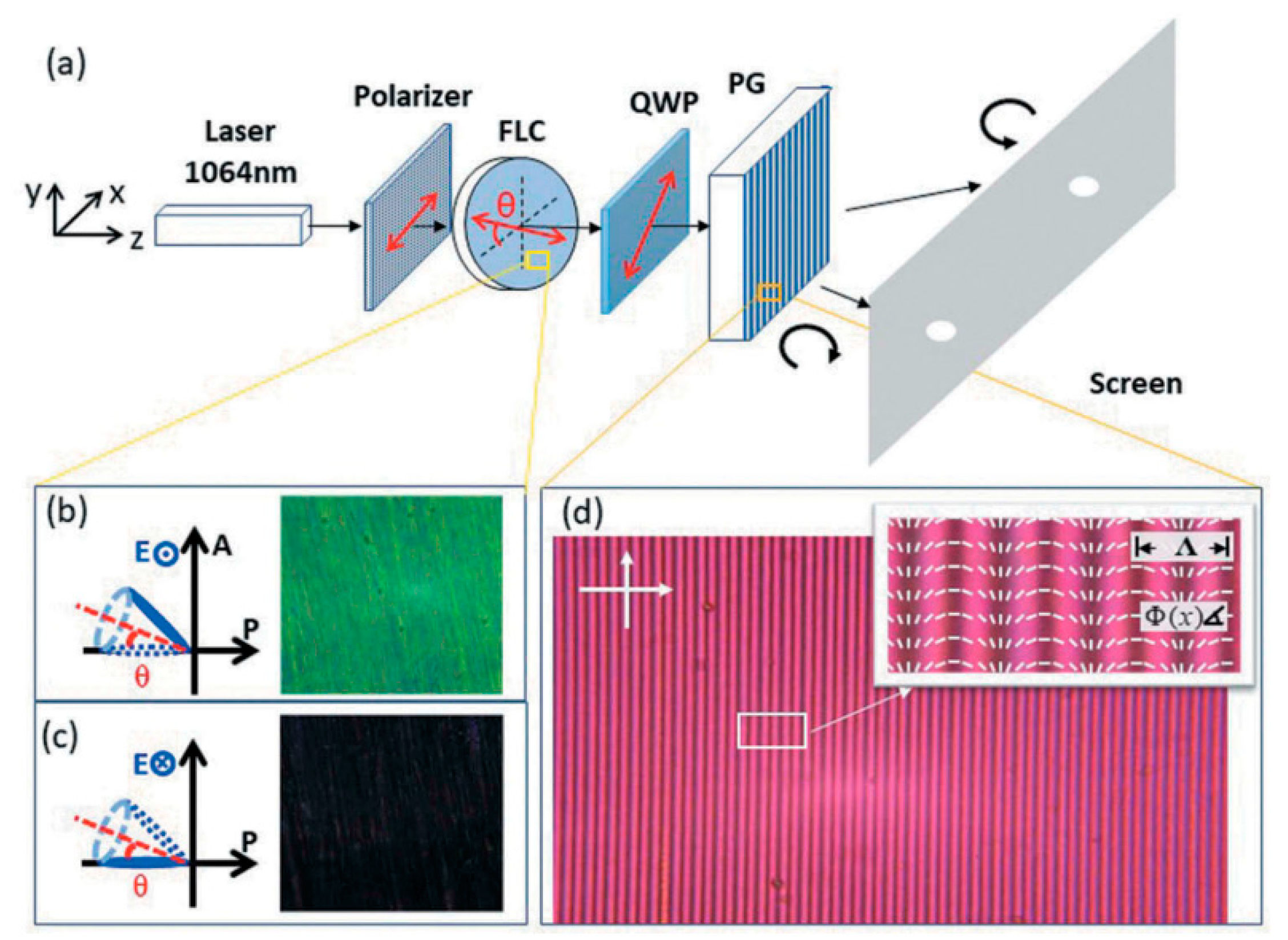
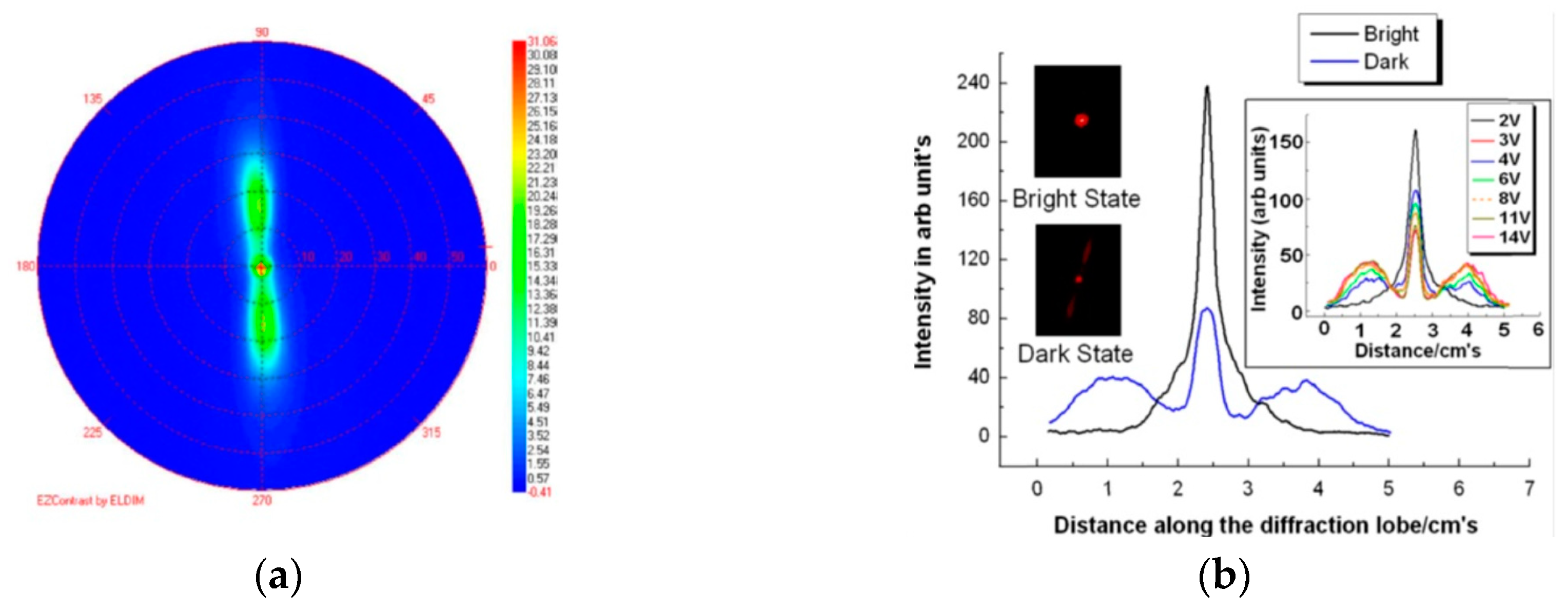
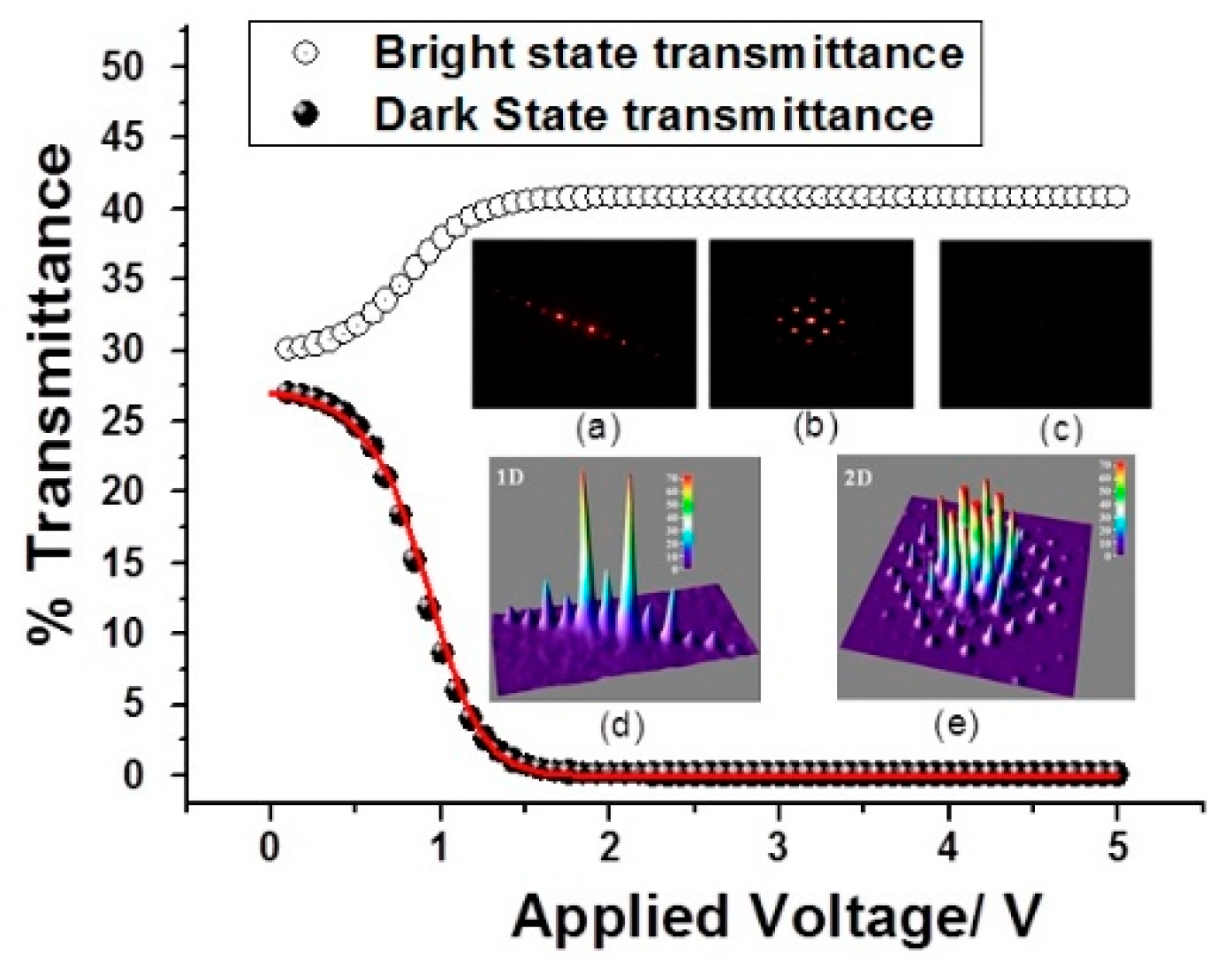
3.5. Fast Switching Gratings
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tan, G.; Lee, Y.H.; Zhan, T.; Yang, J.; Liu, S.; Zhao, D.; Wu, S.T. Foveated imaging for near-eye displays. Opt. Express 2018, 26, 25076. [Google Scholar] [CrossRef] [PubMed]
- Song, D.H.; Kim, J.W.; Kim, K.-H.; Rho, S.J.; Lee, H.; Kim, H.; Yoon, T.H. Ultrafast switching of randomly-aligned nematic liquid crystals. Opt. Express 2012, 20, 11659. [Google Scholar] [CrossRef] [PubMed]
- Akahashi, T.T.; Urue, H.F.; Hikada, M.S.; Atsuda, N.M. Preliminary Study of Field Sequential Fullcolor Liquid Crystal Display using Polymer Stabilized Ferroelectric Liquid Crystal Display. Jpn. J. Appl. Phys. 1999, 38, 534–536. [Google Scholar] [CrossRef]
- Castles, F.; Morris, S.M.; Gardiner, D.J.; Malik, Q.M.; Coles, H.J. Ultra-fast-switching flexoelectric liquid-crystal display with high contrast. J. Soc. Inf. Disp. 2010, 18, 128. [Google Scholar] [CrossRef]
- Packham, C.; Escuti, M.; Ginn, J.; Oh, C.; Quijano, I.; Boreman, G. Polarization Gratings: A Novel Polarimetric Component for Astronomical Instruments. Publ. Astron. Soc. Pacific 2010, 122, 1471–1482. [Google Scholar] [CrossRef] [Green Version]
- He, Z.; Gou, F.; Chen, R.; Yin, K.; Zhan, T.; Wu, S.T. Liquid Crystal Beam Steering Devices: Principles, Recent Advances, and Future Developments. Crystals 2019, 9, 292. [Google Scholar] [CrossRef]
- Andreev, A.; Andreeva, T.; Kompanets, I.; Zalyapin, N. Helix-Free Ferroelectric Liquid Crystals: Electro Optics and Possible Applications. Appl. Sci. 2018, 8, 2429. [Google Scholar] [CrossRef]
- Hofmann, U.; Janes, J.; Quenzer, H.J. High-Q MEMS resonators for laser beam scanning displays. Micromachines 2012, 3, 509–528. [Google Scholar] [CrossRef]
- Wu, T.; Sher, C.W.; Lin, Y.; Lee, C.F.; Liang, S.; Lu, Y.; Huang Chen, S.W.; Guo, W.; Kuo, H.C.; Chen, Z. Mini-LED and Micro-LED: Promising Candidates for the Next Generation Display Technology. Appl. Sci. 2018, 8, 1557. [Google Scholar] [CrossRef]
- Chen, H.-S.; Lin, Y.-H.; Srivastava, A.K.; Chigrinov, V.G.; Chang, C.-M.; Wang, Y.-J. A large bistable negative lens by integrating a polarization switch with a passively anisotropic focusing element. Opt. Express 2014, 22, 13138. [Google Scholar] [CrossRef] [PubMed]
- Kotova, S.P.; Patlan, V.V.; Samagin, S.A. Tunable liquid-crystal focusing device. 2. Experiment. Quantum Electron. 2011, 41, 65–70. [Google Scholar] [CrossRef]
- Wang, L.; Lin, X.W.; Hu, W.; Shao, G.H.; Chen, P.; Liang, L.J.; Jin, B.B.; Wu, P.H.; Qian, H.; Lu, Y.N.; et al. Broadband tunable liquid crystal terahertz waveplates driven with porous graphene electrodes. Light Sci. Appl. 2015, 4, e253. [Google Scholar] [CrossRef]
- Hisakado, Y.; Kikuchi, H.; Nagamura, T.; Kajiyama, T. Large electro-optic Kerr effect in polymer-stabilized liquid-crystalline blue phases. Adv. Mater. 2005, 17, 96–98. [Google Scholar] [CrossRef]
- Ren, H.; Lin, Y.H.; Fan, Y.H.; Wu, S.T. Polarization-independent phase modulation using a polymer-dispersed liquid crystal. Appl. Phys. Lett. 2005, 86, 1–3. [Google Scholar] [CrossRef]
- Zhu, J.L.; Ni, S.B.; Song, Y.; Zhong, E.W.; Wang, Y.J.; Chen, C.P.; Ye, Z.; He, G.; Wu, D.Q.; Song, X.L.; et al. Improved Kerr constant and response time of polymer-stabilized blue phase liquid crystal with a reactive diluent. Appl. Phys. Lett. 2013, 102, 071104. [Google Scholar] [CrossRef]
- Chigrinov, V.G.; Baikalov, V.A.; Pozhidaev, E.P.; Blinov, L.M.; Beresnev, L.A.; Allagulov, A.I. Flexoelectric polarization of a ferroelectric smectic liquid crystal. Sov. Phys. JETP 1985, 61, 1193. [Google Scholar]
- Kim, S.H.; Shi, L.; Chien, L.C. Fast flexoelectric switching in a cholesteric liquid crystal cell with surface-localized polymer network. J. Phys. D. Appl. Phys. 2009, 42, 195102. [Google Scholar] [CrossRef]
- Clark, N.A.; Lagerwall, S.T. Submicrosecond bistable electro-optic switching in liquid crystals. Appl. Phys. Lett. 1980, 36, 899–901. [Google Scholar] [CrossRef]
- Lagerwall, S.T. Ferroelectric and antiferroelectric liquid crystals. Ferroelectrics 2004, 301, 15–45. [Google Scholar] [CrossRef]
- Chigrinov, V.G. Liquid Crystal Devices: Physics and Applications; Artech-House: Boston, London, 1999. [Google Scholar]
- Chigrinov, V.G.; Kozenkov, V.M.; Kwok, H.S. Photoalignment of Liquid Crystalline Materials: Physics and Applications; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Pozhidaev, E.; Chigrinov, V.; Huang, D.; Zhukov, A.; Ho, J.; Kwok, H.S. Photoalignment of ferroelectric liquid crystals by azodye layers. Jpn. J. Appl. Physics 2004, 43, 5440–5444. [Google Scholar] [CrossRef]
- Guo, Q.; Srivastava, A.K.; Pozhidaev, E.P.; Chigrinov, V.G.; Kwok, H. Optimization of alignment quality of ferroelectric liquid crystals by controlling anchoring energy. Appl. Phys. Express 2014, 7, 021701. [Google Scholar] [CrossRef]
- Panarin, Y.; Pozhidaev, E.; Chigrinov, V. Dynamics of controlled birefringence in an electric field deformed helical structure of a ferroelectric liquid crystal. Ferroelectrics 1991, 114, 181–186. [Google Scholar] [CrossRef]
- Pozhidaev, E.P. Electrooptical properties of deformed-helix ferroelectric liquid crystal display cells. Proc. SPIE 2001, 4511, 92–99. [Google Scholar]
- Beresnev, L.A.; Chigrinov, V.G.; Dergachev, D.I.; Pozhidaev, E.P.; Funfschilling, J.; Schadt, M. Deformed helix ferroelectric liquid crystal display: A new electrooptic mod in ferroelectric chiral smectic C liquid crystal. Liq. Cryst. 1989, 5, 1171–1177. [Google Scholar] [CrossRef]
- Presnyakov, V.; Liu, Z.; Chigrinov, V.G. Fast optical retarder using deformed-helical ferroelectric liquid crystals. Proc. SPIE 2005, 5970, 59701K. [Google Scholar]
- Chigrinov, V.G.; Kwok, H.S. Photoalignment of liquid crystals: applications to fast response ferroelectric liquid crystals and rewritable photonic devices. Proc. Liquid Cryst. Sci. Technol. 2013, 4, 199–226. [Google Scholar]
- Pozhidaev, E.; Chigrinov, V.; Hegde, G.; Xu, P. Multistable electro-optical modes in ferroelectric liquid crystals. J. Soc. Inf. Disp. 2009, 17, 53–59. [Google Scholar] [CrossRef]
- Guo, Q.; Brodzeli, Z.; Pozhidaev, E.P.; Fan, F.; Chigrinov, V.G.; Kwok, H.S.; Silvestri, L.; Ladouceur, F. Fast electro-optical mode in photo-aligned reflective deformed helix ferroelectric liquid crystal cells. Opt. Lett. 2012, 37, 2343–2345. [Google Scholar] [CrossRef]
- Pozhidaev, E.; Chigrinov, V. Fast Photo-Aligned V-shape Ferroelectric LCD Based on DHF Mode. SID Symp. Dig. Tech. Pap. 2010, 41, 387. [Google Scholar] [CrossRef]
- Hegde, G.; Xu, P.; Pozhidaev, E.; Chigrinov, V.; Kwok, H.S. Electrically controlled birefringence colours in deformed helix ferroelectric liquid crystals. Liq. Cryst. 2008, 35, 1137–1144. [Google Scholar] [CrossRef]
- Pozhidaev, E.P.; Minchenko, M.; Molkin, V.; Torgova, S.; Srivastava, A.K.; Chigrinov, V.; Kwok, H.S.; Vashenko, V.; Krivoshey, A. High Frequency Low Voltage Shock-Free Ferroelectric Liquid Crystal: A New Electro-Optical Mode with Electrically Suppressed Helix. In Proceedings of the 31th International Display Research Conference EuroDisplay, Arcachon, France, 19–22 September 2011. [Google Scholar]
- Pozhidaev, E.P.; Chigrinov, V.G. Bistable and multistable states in ferroelectric liquid crystals. Crystallogr. Reports 2006, 51, 1030–1040. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, X.; Zhao, H.; Chigrinov, V.G. Reverse bistable effect in ferroelectric liquid crystal devices with ultra-fast switching at low driving voltage. Opt. Lett. 2015, 40, 2413–2416. [Google Scholar] [CrossRef] [PubMed]
- Chigrinov, V.G.; Kwok, H.S.; Yakovlev, D.; Simonenko, G.V.; Tsoi, V.I. LCD Optimization and Modeling. J. SID 2004, 12, 183–187. [Google Scholar] [CrossRef]
- Kiselev, A.D.; Pozhidaev, E.P.; Chigrinov, V.G.; Kwok, H.S. Polarization-gratings approach to deformed-helix ferroelectric liquid crystals with subwavelength pitch. Phys. Rev. E 2011, 83, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Chigrinov, V.; Pozhidaev, E.; Srivastava, A.; Qi, G.; Fan, F.; Ma, Y.; Lastochkin, A.; Kwok, H.S. Novel Photoaligned Fast Ferroelectric Liquid Crystal Display. In Proceedings of the LCT6-1, IDW’11 Conference, Nagoya, Japan, 7–9 December 2011. [Google Scholar]
- Pozhidaev, E.P.; Kiselev, A.D.; Chigrinov, V.G.; Srivastava, A.K.; Minchenko, M.V.; Kotova, S.P. Orientational Kerr-effect in Ferroelectric Liquid Crystals. In Proceedings of the 24th International Liquid Crystal Conference, Mainz, Germany, 19–24 August 2012. [Google Scholar]
- Pozhidaev, E.P.; Kiselev, A.D.; Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.S.; Minchenko, M.V. Orientational Kerr effect and phase modulation of light in deformed-helix ferroelectric liquid crystals with subwavelength pitch. Phys. Rev. E 2013, 87, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, Y.; Yan, J.; Liu, Y.; Cui, J.; Wang, Q.; Wu, S.T. Polymer-stabilized blue phase liquid crystal with a negative Kerr constant. Opt. Mater. Express 2012, 2, 1135. [Google Scholar] [CrossRef]
- Guo, Q.; Xu, L.; Sun, J.; Yang, X.; Liu, H.; Yan, K.; Zhao, H.; Chigrinov, V.G.; Kwok, H.S. Fast switching beam steering based on ferroelectric liquid crystal phase shutter and polarisation grating. Liq. Cryst. 2019, 46, 1383–1388. [Google Scholar] [CrossRef]
- Srivastava, A.K.; de Bougrenet de la Tocnaye, J.L.; Dupont, L. Liquid Crystal Active Glasses for 3D Cinema. J. Disp. Technol. 2010, 6, 522–530. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Pozhidaev, E.P.; Chigrinov, V.G.; Manohar, R. Single walled carbon nano-tube, ferroelectric liquid crystal composites: Excellent diffractive tool. Appl. Phys. Lett. 2011, 99, 1–4. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.S. Ferroelectric Liquid Crystal Gratings. In Proceedings of the Liquid Crystals Photonic Workshop, Hong Kong, China, 9–11 December 2012. [Google Scholar]
- Woltman, S.J.; Eakin, J.N.; Crawford, G.P.; Žumer, S. Electro-optical investigations of holographic-polymer-dispersed ferroelectric liquid crystals. J. Opt. Soc. Am. A 2007, 24, 3789. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Hu, W.; Chigrinov, V.G.; Kiselev, A.D.; Lu, Y.Q. Fast switchable grating based on orthogonal photo alignments of ferroelectric liquid crystals. Appl. Phys. Lett. 2012, 101, 031112. [Google Scholar] [CrossRef]
- Ma, Y.; Sun, J.; Srivastava, A.K.; Guo, Q.; Chigrinov, V.G.; Kwok, H.S. Optically rewritable ferroelectric liquid-crystal grating. Europhys. Lett. 2013, 102, 24005. [Google Scholar] [CrossRef]
- Hu, W.; Srivastava, A.; Xu, F.; Sun, J.T.; Lin, X.W.; Cui, H.Q.; Chigrinov, V.; Lu, Y.-Q. Liquid crystal gratings based on alternate TN and PA photoalignment. Opt. Express 2012, 20, 5384. [Google Scholar] [CrossRef] [PubMed]
- Beresnev, L.A.; Loseva, M.V.; Chernova, N.I.; Kononov, S.G.; Adomenas, P.V.; Pozhidaev, E.P. Ferroelectric domains in liquid crystal. JETP Lett. 1990, 51, 516–521. [Google Scholar]
- Wang, X.Q.; Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.S. Switchable Fresnel lens based on micropatterned alignment. Opt. Lett. 2013, 38, 1775. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Wang, X.Q.; Chigrinov, V.G.; Kwok, H.S. Liquid Crystal Fresnel Lens. Filled USPTO Application. U.S. Patent No. US 61/958742, August 2013. [Google Scholar]
- Shteyner, E.A.; Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.S.; Afanasyev, A.D. Submicron-scale liquid crystal photo-alignment. Soft Matter 2013, 9, 5160–5165. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Yan, K.; Chigrinov, V.; Zhao, H.; Tribelsky, M. Ferroelectric Liquid Crystals: Physics and Applications. Crystals 2019, 9, 470. https://doi.org/10.3390/cryst9090470
Guo Q, Yan K, Chigrinov V, Zhao H, Tribelsky M. Ferroelectric Liquid Crystals: Physics and Applications. Crystals. 2019; 9(9):470. https://doi.org/10.3390/cryst9090470
Chicago/Turabian StyleGuo, Qi, Kexin Yan, Vladimir Chigrinov, Huijie Zhao, and Michael Tribelsky. 2019. "Ferroelectric Liquid Crystals: Physics and Applications" Crystals 9, no. 9: 470. https://doi.org/10.3390/cryst9090470
APA StyleGuo, Q., Yan, K., Chigrinov, V., Zhao, H., & Tribelsky, M. (2019). Ferroelectric Liquid Crystals: Physics and Applications. Crystals, 9(9), 470. https://doi.org/10.3390/cryst9090470






