Synthesis, Characterization, and Crystal Structure Determination of a New Lithium Zinc Iodate Polymorph LiZn(IO3)3
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Sample Characterization
2.3. Density-Functional Theory Calculations
3. Results and Discussion
3.1. Morphology and Composition
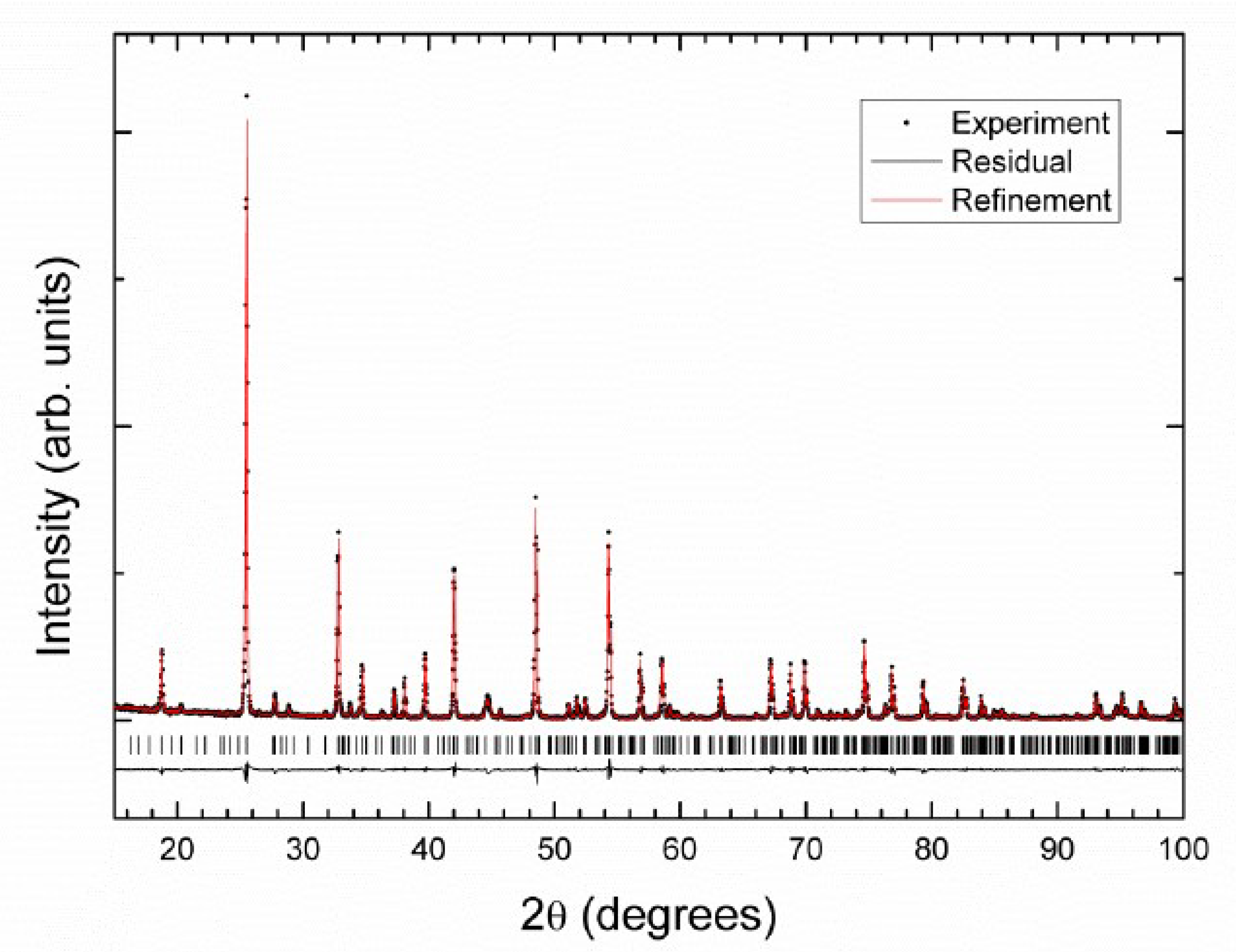
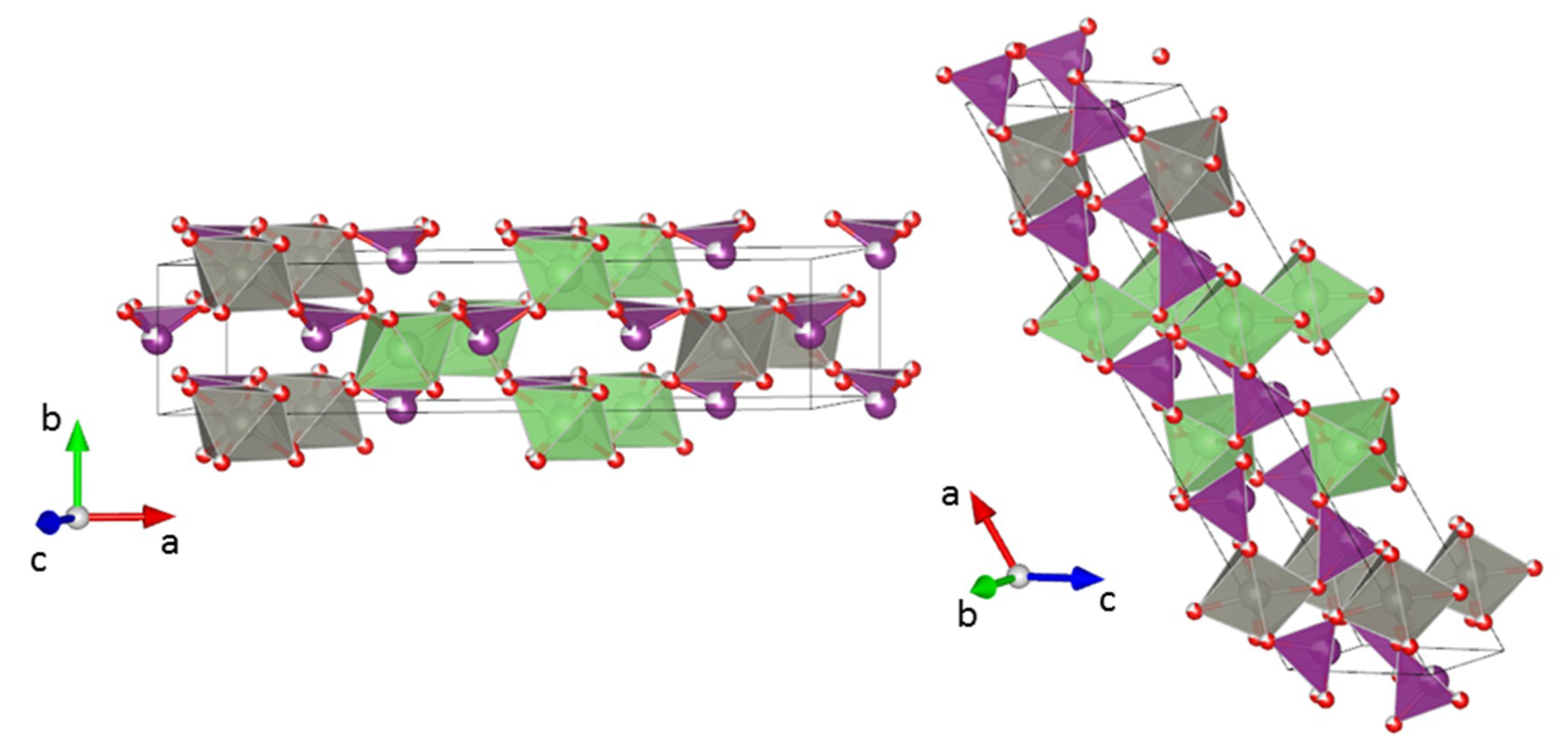
3.2. Crystal Structure
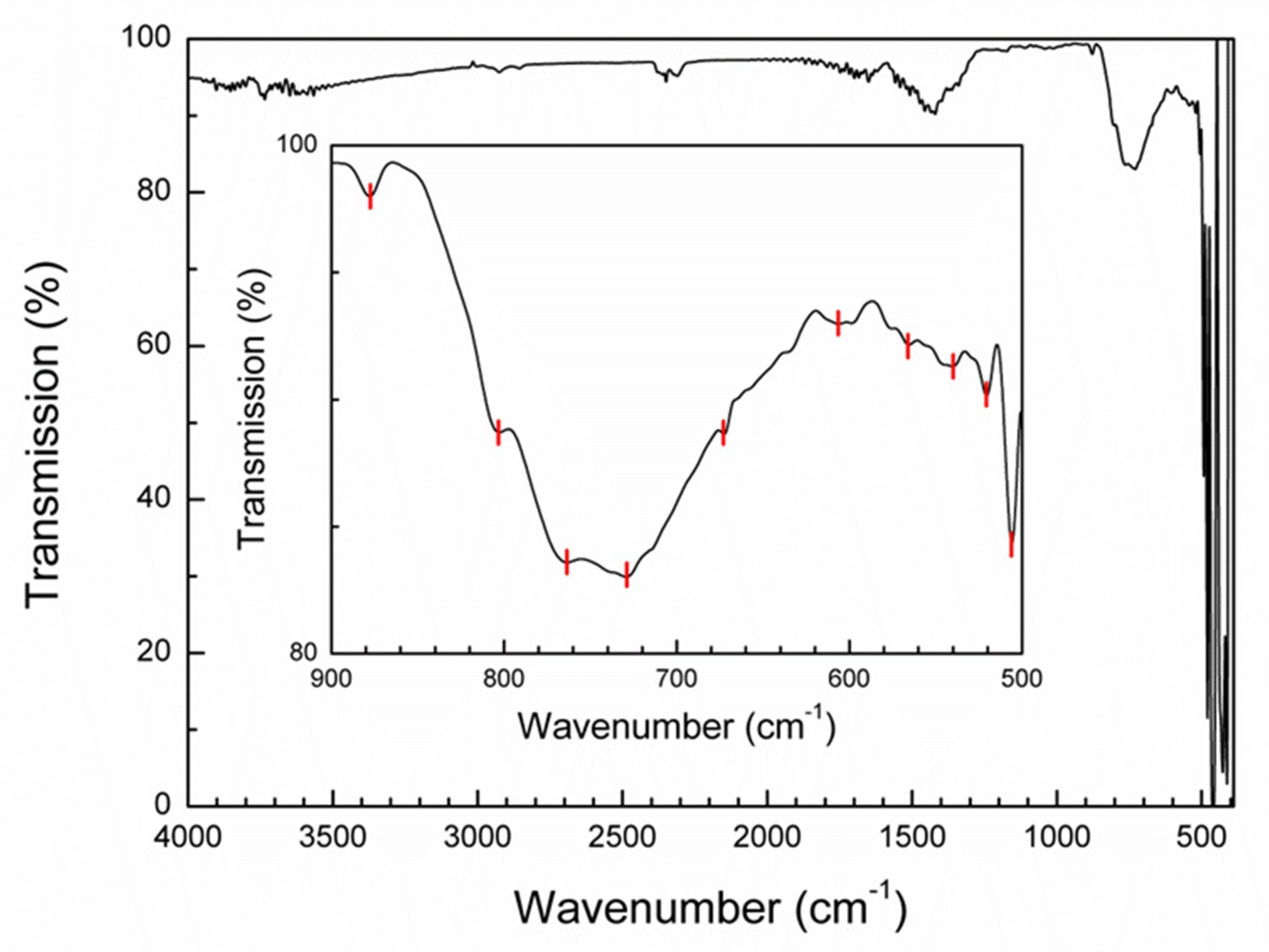
3.3. FTIR Spectroscopy
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guo, S.P.; Chi, Y.; Guo, G.C. Recent achievements on middle and far-infrared second-order nonlinear optical materials. Coord. Chem. Rev. 2017, 335, 44–57. [Google Scholar] [CrossRef]
- Xiao, L.; Zhenbo, Y.; Yao, J.Y.; Lin, Z.S.; Hu, Z.G. A new cerium iodate infrared nonlinear optical material with a large second-harmonic generation response. J. Mater. Chem. C 2017, 5, 2130–2134. [Google Scholar] [CrossRef]
- Reshak, A.H.; Auluck, S. LiMoO3(IO3), a novel molybdenyl iodate with strong second-order optical nonlinearity. J. Alloy. Compd. 2016, 660, 32–38. [Google Scholar] [CrossRef]
- Ngo, N.; Kalachnikova, K.; Assefa, Z.; Haire, R.G.; Sykora, R.E. Synthesis and structure of In(IO3)3 and vibrational spectroscopy of M(IO3)3 (M = Al, Ga, In). J. Solid State Chem. 2006, 179, 3824–3830. [Google Scholar] [CrossRef]
- Pathania, D.; Sharma, G.; Mu, N.; Vishal, P. A biopolymer-based hybrid cation exchanger pectin cerium(IV) iodate: Synthesis, characterization, and analytical applications. Desalin. Water Treat. 2016, 57, 468–475. [Google Scholar] [CrossRef]
- Biggs, K.R.; Gomme, R.A.; Graham, J.T.; Ogden, J.S. Characterization of molecular alkali metal iodates by mass spectrometry and matrix isolation IR spectroscopy. J. Phys. Chem. 1992, 96, 9738–9741. [Google Scholar] [CrossRef]
- Stahl, K.; Szafranski, M. A neutron powder diffraction study of HIO3 and DIO3. Acta Cryst. C 1992, 48, 1571–1574. [Google Scholar] [CrossRef]
- Keve, E.T.; Abrahams, S.C.; Bernstein, J.L. Pyroelectric ammonium iodate, a potential ferroelastic: crystal structure. J. Chem. Phys. 1971, 54, 2556–2563. [Google Scholar] [CrossRef]
- Kumar, R.A.; Babu, D.R.; Vizhi, R.E.; Vijayan, N.; Bhagavannarayana, G. Synthesis, growth and optical studies of Mn: α-LiIO3 single crystal. Adv. Mater. Res. 2012, 584, 3–7. [Google Scholar] [CrossRef]
- Bushiri, M.J.; Kochuthresia, T.C.; Vaidyan, V.K.; Gautier-Luneau, I. Raman scattering structural studies of nonlinear optical M(IO3)3 (M = Fe, Ga, α-In) and linear optical β-In(IO3)3. J. Nonlin. Opt. Phys. Mater. 2014, 23, 1450039. [Google Scholar] [CrossRef]
- Mugnier, Y.; Galez, C.; Crettez, J.M.; Bourson, P.; Opagiste, C.; Bouillot, J. Low-frequency relaxation phenomena in α-LiIO3: The nature and role of defects. J. Solid State Chem. 2002, 168, 76–84. [Google Scholar] [CrossRef]
- Kochuthresia, T.C.; Gautier-Luneau, I.; Vaidyan, V.K.; Bushiri, M.J. Raman and FTIR spectral investigations of twinned M(IO3)2 (M = Mn, Ni, Co, and Zn) crystals. J. Appl. Spectrosc. 2016, 82, 941–946. [Google Scholar] [CrossRef]
- Hermet, P. First-principles based analysis of the piezoelectric response in α-LiIO3. Comput. Mater. Science 2017, 138, 199–203. [Google Scholar]
- Peter, S.; Pracht, G.; Lange, N.; Lutz, H.D. Zinkiodate–schwingungsspektren (IR, Raman) und kristallstruktur von Zn(IO3)2·2H2O. Z. Anorg. Allg. Chem. 2000, 626, 208–215. [Google Scholar] [CrossRef]
- Hector, A.L.; Henderson, S.J.; Levason, W.; Webster, M. Hydrothermal synthesis of rare earth iodates from the corresponding periodates: Structures of Sc(IO3)3, Y(IO3)3·2H2O, La(IO3)3·1/2H2O and Lu(IO3)3·2H2O. Z. Anorg. Allg. Chem. 2002, 628, 198–202. [Google Scholar] [CrossRef]
- Bentria, B.; Benbertal, D.; Bagieu-Beucher, M.; Mosset, A.; Zaccaro, J. Crystal engineering strategy for quadratic nonlinear optics. Part II: Hg(IO3)2. Solid State Sci. 2003, 5, 359–365. [Google Scholar] [CrossRef]
- Galez, C.; Mugnier, Y.; Bouillot, J.; Lambert, Y.; le Dantec, R. Synthesis and characterisation of Fe(IO3)3 nanosized powder. J. Alloys Compd. 2006, 416, 261–264. [Google Scholar] [CrossRef]
- Bentria, B.; Benbertal, D.; Hebboul, Z.; Bagieu-Beucher, M.; Mosset, A. Polymorphism of anhydrous cadmium iodate structure of ε-Cd(IO3)2. Z. Anorg. Allg. Chem. 2005, 631, 894–901. [Google Scholar] [CrossRef]
- Sun, C.F.; Hu, C.L.; Xu, X.; Ling, J.B.; Hu, T.; Kong, F.; Long, X.F.; Mao, J.G. BaNbO(IO3)5: A new polar material with a very large SHG response. J. Am. Chem. Soc. 2009, 131, 9486–9487. [Google Scholar] [CrossRef]
- Lan, Y.C.; Chen, X.L.; Xie, A.Y.; Jiang, P.Z.; Lin, C.L. Synthesis, thermal and magnetic properties of new metal iodate: (LiFe1/3)(IO3)2. J. Cryst. Growth 2002, 240, 526–530. [Google Scholar] [CrossRef]
- Bonacina, L.; Mugnier, Y.; Courvoisier, F.; le Dantec, R.; Extermann, J.; Lambert, Y.; Boutou, V.; Wolf, C.G.J.-P. Polar Fe(IO3)3 nanocrystals as local probes for nonlinear microscopy. Appl. Phys. B 2007, 87, 399–403. [Google Scholar] [CrossRef]
- Taouti, M.B. Synthèses et Caractérisations Structurales D’iodates Métalliques, Matériaux Lasers Convertisseurs de Fréquences. Ph. D. Thesis, Université Joseph-Fourier, Grenoble, France, 2008. [Google Scholar]
- Sheng, T.D.; Ming, F.Z.; Xiu, L.W. Invesigation of the pseudo-binary system LilO3-Zn(IO3)2. Acta Phys. Sin. 1981, 30, 234–241. [Google Scholar]
- Kraus, W.; Nolze, G. POWDER CELL: A program for the representation and manipulation of crystal structures and calculation of the resulting X-ray powder patterns. J. Appl. Cryst. 1996, 29, 301–303. [Google Scholar] [CrossRef]
- Rodriguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Physical B 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Garg, A.B.; Errandonea, D. High-pressure powder x-ray diffraction study of EuVO4. J. Solid State Chem. 2015, 226, 147–153. [Google Scholar] [CrossRef]
- Caglioti, G.; Paoletti, A.; Ricci, F.P. Choice of collimators for a crystal spectrometer for neutron diffraction. Nucl. Instrum. 1958, 3, 223–228. [Google Scholar] [CrossRef]
- Liang, J.K.; Wang, C.G. Diffusion of lithium in intercalated compound LixTiO2. Acta Chim. Sin. 1982, 40, 969–976. [Google Scholar]
- Phanon, D.; Bentria, B.; Jeanneau, E.; Benbertal, D.; Mosset, A.; Luneau, I.G. Crystal structure of M(IO3)2 metal iodates, twinned bypseudo-merohedry, with MII: MgII, MnII, CoII, NiII and ZnII. Z. Kristallogr. Cryst. Mater. 2006, 221, 635–642. [Google Scholar] [CrossRef]
- Crettez, J.M.; Coquet, E.; Pannetier, J.; Bouillot, J.; Floch, M.D. Neutron structure refinement of gamma- and beta-lithium: Comparison between alpha, gamma, and beta phases. J. Solid State Chem. 1985, 56, 133–147. [Google Scholar] [CrossRef]
- Errandonea, D.; Santamaria-Perez, D.; Martinez-Garcia, D.; Gomis, O.; Shukla, R.; Achary, S.N.; Tyagi, A.K.; Popescu, C. Pressure impact on the stability and distortion of the crystal structure of CeScO3. Inorg. Chem. 2017, 56, 8363–8371. [Google Scholar] [CrossRef]
- Benmakhlouf, A.; Errandonea, D.; Bouchenafa, M.; Maabed, S.; Bouhemadou, A.; Bentabet, A. New pressure-induced polymorphic transitions of anhydrous magnesium sulfate. Dalton Trans. 2017, 46, 5058–5068. [Google Scholar] [CrossRef] [PubMed]
- Freccero, R.; Solokha, P.; Proserpio, D.M.; Saccone, A.; de Negri, S. Lu5Pd4Ge8 and Lu3Pd4Ge4: Two more germanides among polar intermetallics. Crystals 2018, 8, 205. [Google Scholar] [CrossRef]
- van Troeye, B.; Gillet, Y.; Poncé, S.; Gonze, X. First-principles characterization of the electronic and optical properties of hexagonal LiIO3. Opt. Mater. 2014, 36, 1494–1501. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Für Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.W.; Kim, S.B.; Ok, K.M. ZnIO3(OH): A new layered non-centrosymmetric polar iodate–hydrothermal synthesis, crystal structure, and second-harmonic generating (SHG) properties. Dalton Trans. 2012, 41, 8348–8353. [Google Scholar] [CrossRef] [PubMed]
- Černý, R. Crystal structures from powder diffraction: Principles, difficulties and progress. Crystals 2017, 7, 142. [Google Scholar] [CrossRef]
- Gomis, O.; Sans, J.A.; Lacomba-Perales, R.; Errandonea, D.; Meng, Y.; Chervin, J.C.; Polian, A. Complex high-pressure polymorphism of barium tungstate. Phys. Rev. B 2012, 86, 054121. [Google Scholar] [CrossRef]
- Gomis, O.; Lavina, B.; Rodríguez-Hernández, P.; Muñoz, A.; Errandonea, R.; Errandonea, D.; Bettinelli, M. High-pressure structural, elastic, and thermodynamic properties of zircon-type HoPO4 and TmPO4. J. Phys. Condens. Matter 2017, 29, 095401. [Google Scholar] [CrossRef]
- Tobby, B.H. R factors in Rietveld analysis: How good is good enough? Powder Diffr. 2006, 21, 67–70. [Google Scholar] [CrossRef]
- Errandonea, D.; Kumar, R.S.; Gomis, O.; Manjon, F.J.; Ursaki, V.V.; Tiginyanu, I.M. X-ray diffraction study on pressure-induced phase transformations and the equation of state of ZnGa2Te4. J. Appl. Phys. 2013, 114, 233507. [Google Scholar] [CrossRef]
- Bouillot, J.; Coquet, E.; Pannetier, J.; Crettez, J.M. Neutron powder diffraction studies of LiIO3 and (HIO3, 2LiIO3). Physica B + C 1986, 136, 493–497. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F.J. VESTA: A three-dimensional visualization system for electronic and structural analysis. Appl. Cryst. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Robinson, K.F.; Gibbs, G.V.; Ribbe, P.H. Quadratic elongation: A quantitative measure of distortion in coordination polyhedral. Science 1971, 172, 567–570. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.K.; Rao, G.H.; Zhang, Y.M. Polymorphism phase transition and the relative stability of various phases in the LiIO3 crystal. Phys. Rev. B 1989, 39, 459–466. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.L.; Mao, J.G. Recent advances on second-order NLO materials based on metal iodates. Coord. Chem. Rev. 2015, 288, 1–17. [Google Scholar] [CrossRef]
- Mugnier, Y.; Galez, C.; Crettez, J.M.; Bouillot, P.B.J. Dielectric characterization and ionic conductivity of α-LiIO3 crystals related to the growth conditions. Sol. State Comm. 2000, 115, 619–623. [Google Scholar] [CrossRef]
- Errandonea, D.; Muñoz, A.; Rodríguez-Hernández, P.; Gomis, O.; Achary, S.N.; Popescu, C.; Patwe, S.J.; Tyagi, A.K. High-pressure crystal structure, lattice vibrations, and band structure of BiSbO4. Inorg. Chem. 2016, 55, 4958–4969. [Google Scholar] [CrossRef] [PubMed]
- Garg, A.B.; Errandonea, D.; Pellicer-Porres, J.; Martinez-Garcia, D.; Kesari, S.; Rao, R.; Popescu, C.; Bettinelli, M. LiCrO2 under pressure: In-situ structural and vibrational studies. Crystals 2019, 9, 2. [Google Scholar] [CrossRef]
- Errandonea, D.; Ruiz-Fuertes, J. A brief review of the effects of pressure on wolframite-type oxides. Crystals 2018, 8, 71. [Google Scholar] [CrossRef]
- Zhang, W.W.; Cui, Q.L.; Pan, Y.W.; Dong, S.S.; Liu, J.; Zou, G.T. High-pressure x-ray diffraction study of LiIO3 to 75 GPa. J. Phys. Condens. Matter 2002, 14, 10579–10582. [Google Scholar] [CrossRef]
- Cafferty, M.S. Absorption of LiIO3 in the infrared for the ordinary direction of propagation. Infr. Phys. Techn. 1994, 35, 801–804. [Google Scholar] [CrossRef]
- Crettez, J.M.; Gard, R.; Remoissenet, M. Near and far infrared investigations from α and β lithium iodate crystals. Solid State Commun. 1972, 11, 951–954. [Google Scholar] [CrossRef]
- Pimenta, M.A.; Oliveira, M.A.S.; Boursond, P.; Crettez, J.M. Raman study of crystals. J. Phys. Condens. Matter 1997, 9, 7903–7912. [Google Scholar] [CrossRef]
- Nassau, K.; Shiever, J.W.; Prescott, B.E. Transition metal iodates. I. Preparation and characterization of the 3d iodates. J. Solid State Chem. 1973, 7, 186–204. [Google Scholar] [CrossRef]
- Crettez, J.M.; Misset, J.P.; Coquet, E. Vibrations and force constants of the hexagonal lithium iodate crystal. J. Chem. Phys. 1979, 70, 4194–4198. [Google Scholar] [CrossRef]
- Joulaud, C.; Mugnier, Y.; Djanta, G.; Dubled, M.; Marty, J.C.; Galez, C.; Wolf, J.P.; Bonacina, L.; le Dante, R. Characterization of the nonlinear optical properties of nanocrystals by Hyper Rayleigh scattering. J. Nanobiotechnol. 2013, 11, S8. [Google Scholar] [CrossRef] [PubMed]

| Atom | Wyckoff Position | x | y | z | Occupation |
|---|---|---|---|---|---|
| Li | 2a | 0.13073 | 0.93865 | 0.02872 | 1 |
| Zn | 2a | 0.62218 | 0.91685 | 0.00530 | 1 |
| I1 | 2a | 0.03618 | 0.97718 | 0.33248 | 0.75 |
| I2 | 2a | 0.53645 | 0.95209 | 0.33300 | 0.75 |
| I3 | 2a | 0.30300 | 0.97387 | 0.33483 | 0.75 |
| I4 | 2a | 0.79086 | 0.98644 | 0.32689 | 0.75 |
| O1 | 2a | 0.45968 | 0.17690 | 0.33564 | 0.75 |
| O2 | 2a | 0.95849 | 0.20846 | 0.28041 | 0.75 |
| O3 | 2a | 0.10713 | 0.16625 | 0.67254 | 0.75 |
| O4 | 2a | 0.60797 | 0.15273 | 0.65619 | 0.75 |
| O5 | 2a | 0.05892 | 0.18401 | 0.08682 | 0.75 |
| O6 | 2a | 0.54373 | 0.16225 | 0.03871 | 0.75 |
| O7 | 2a | 0.38252 | 0.19763 | 0.66145 | 0.75 |
| O8 | 2a | 0.86320 | 0.20816 | 0.63333 | 0.75 |
| O9 | 2a | 0.22246 | 0.15968 | 0.31462 | 0.75 |
| O10 | 2a | 0.70911 | 0.14574 | 0.29944 | 0.75 |
| O11 | 2a | 0.30225 | 0.17019 | 0.03227 | 0.75 |
| O12 | 2a | 0.78937 | 0.19692 | 0.01147 | 0.75 |
| Bond | Distance | Bond | Distance | Bond | Distance |
|---|---|---|---|---|---|
| Zn–O | 2.1087(5) Å | I1–O | 1.9571(5) Å | I3–O | 1.9249(5) Å |
| 2.1391(5) Å | 1.9634(5) Å | 1.9596(5) Å | |||
| 2.1789(5) Å | 1.9758(5) Å | 2.0833(5) Å | |||
| 2.1828(5) Å | 2.4729(5) Å | 2.4011(5) Å | |||
| 2.1834(0) Å | 2.5285(5) Å | 2.5406(5) Å | |||
| 2.2154(0) Å | 2.6350(5) Å | 2.7273(5) Å | |||
| Li–O | 2.0903(5) Å | I2–O | 1.9450(5) Å | I4–O | 1.9037(5) Å |
| 2.1310(5) Å | 2.0061(5) Å | 1.9702(5) Å | |||
| 2.1351(5) Å | 2.0484(5) Å | 2.0161(5) Å | |||
| 2.1626(5) Å | 2.1952(5) Å | 2.5582(5) Å | |||
| 2.1648(5) Å | 2.2619(5) Å | 2.7049(5) Å | |||
| 2.2487(5) Å | 2.3999(5) Å | 2.7772(5) Å |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hebboul, Z.; Galez, C.; Benbertal, D.; Beauquis, S.; Mugnier, Y.; Benmakhlouf, A.; Bouchenafa, M.; Errandonea, D. Synthesis, Characterization, and Crystal Structure Determination of a New Lithium Zinc Iodate Polymorph LiZn(IO3)3. Crystals 2019, 9, 464. https://doi.org/10.3390/cryst9090464
Hebboul Z, Galez C, Benbertal D, Beauquis S, Mugnier Y, Benmakhlouf A, Bouchenafa M, Errandonea D. Synthesis, Characterization, and Crystal Structure Determination of a New Lithium Zinc Iodate Polymorph LiZn(IO3)3. Crystals. 2019; 9(9):464. https://doi.org/10.3390/cryst9090464
Chicago/Turabian StyleHebboul, Zoulikha, Christine Galez, Djamal Benbertal, Sandrine Beauquis, Yannick Mugnier, Abdelnour Benmakhlouf, Mohamed Bouchenafa, and Daniel Errandonea. 2019. "Synthesis, Characterization, and Crystal Structure Determination of a New Lithium Zinc Iodate Polymorph LiZn(IO3)3" Crystals 9, no. 9: 464. https://doi.org/10.3390/cryst9090464
APA StyleHebboul, Z., Galez, C., Benbertal, D., Beauquis, S., Mugnier, Y., Benmakhlouf, A., Bouchenafa, M., & Errandonea, D. (2019). Synthesis, Characterization, and Crystal Structure Determination of a New Lithium Zinc Iodate Polymorph LiZn(IO3)3. Crystals, 9(9), 464. https://doi.org/10.3390/cryst9090464






