All-Optical Ultra-Fast Graphene-Photonic Crystal Switch
Abstract
:1. Introduction
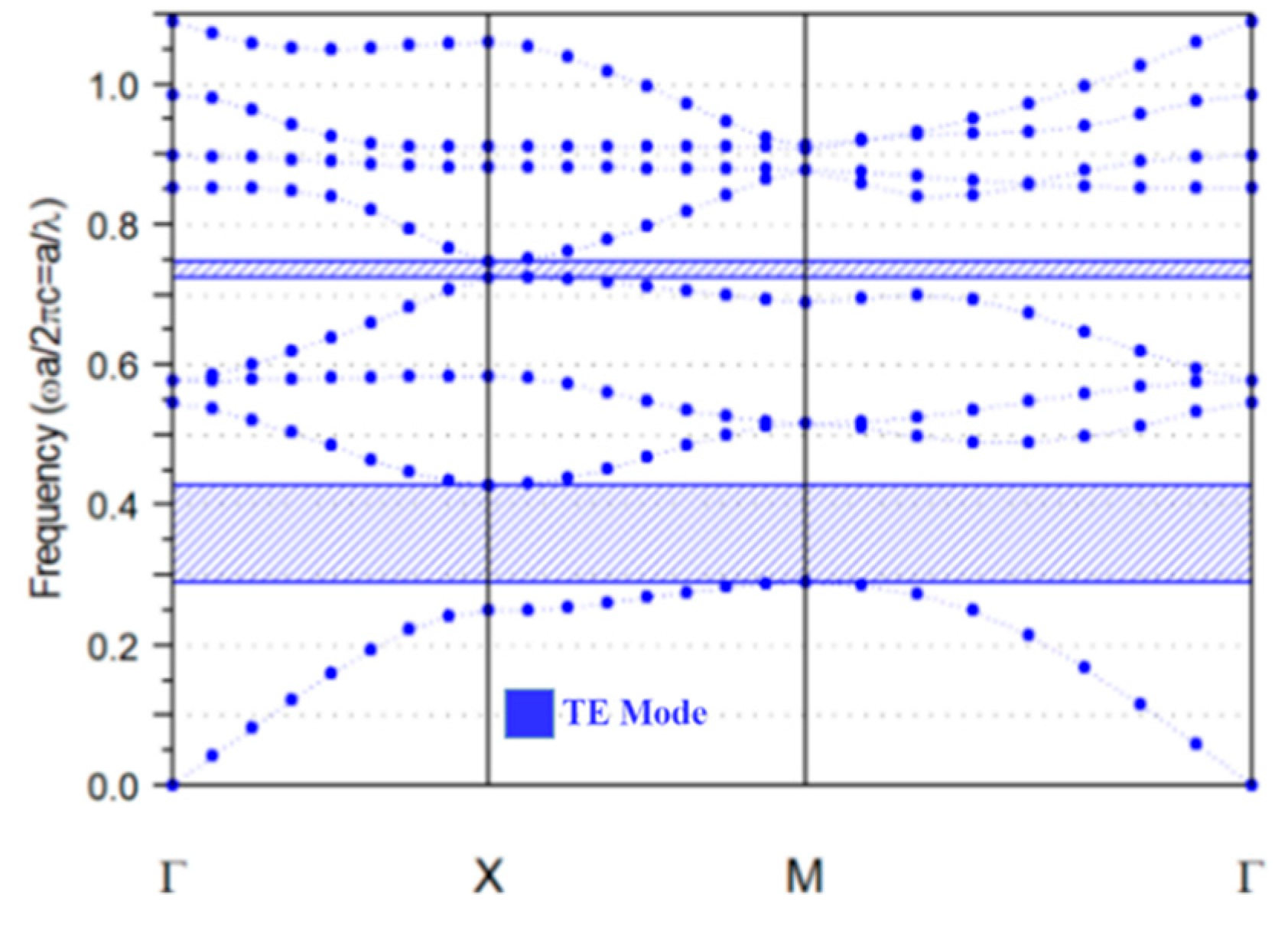
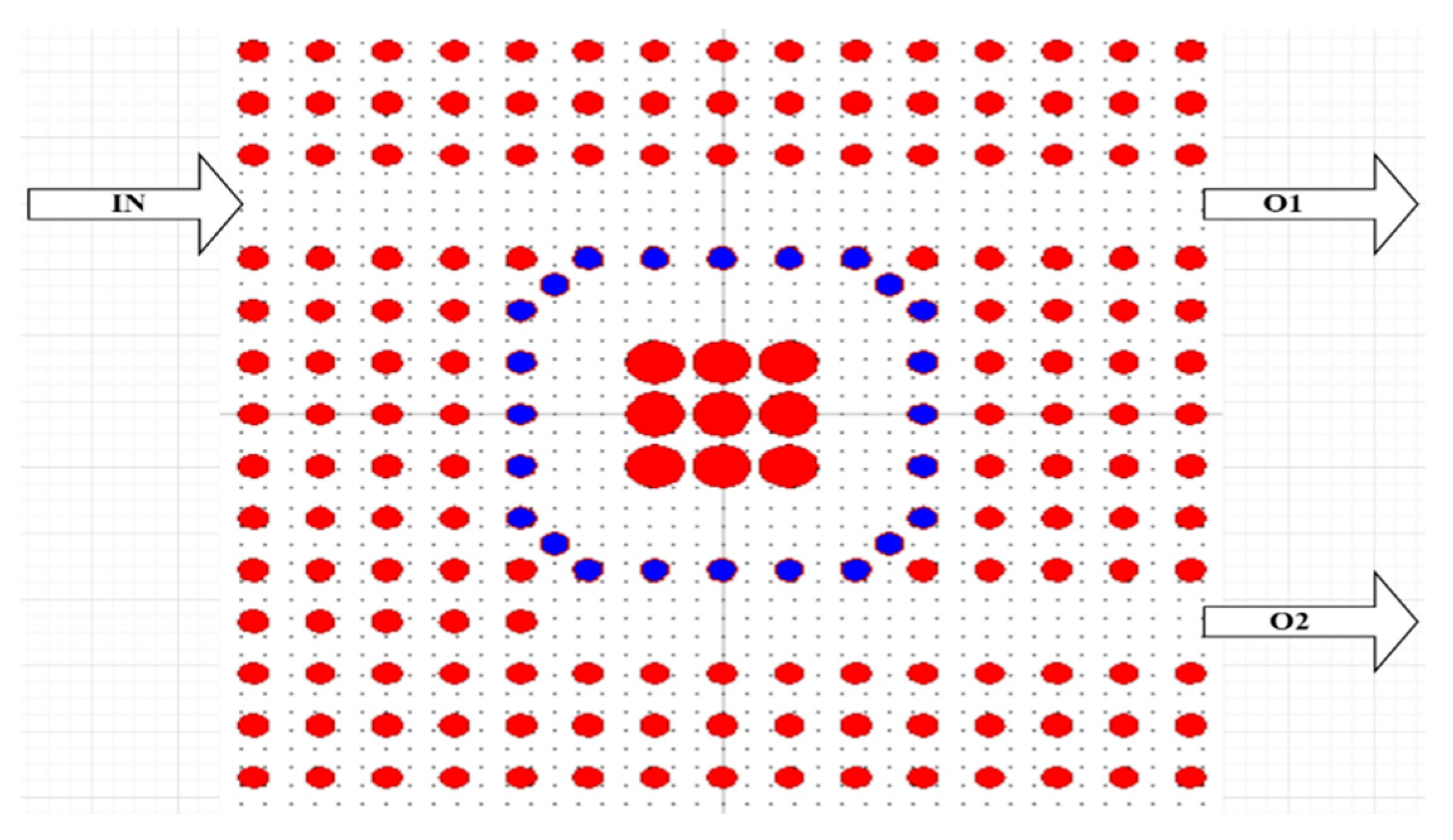
2. Materials and Methods
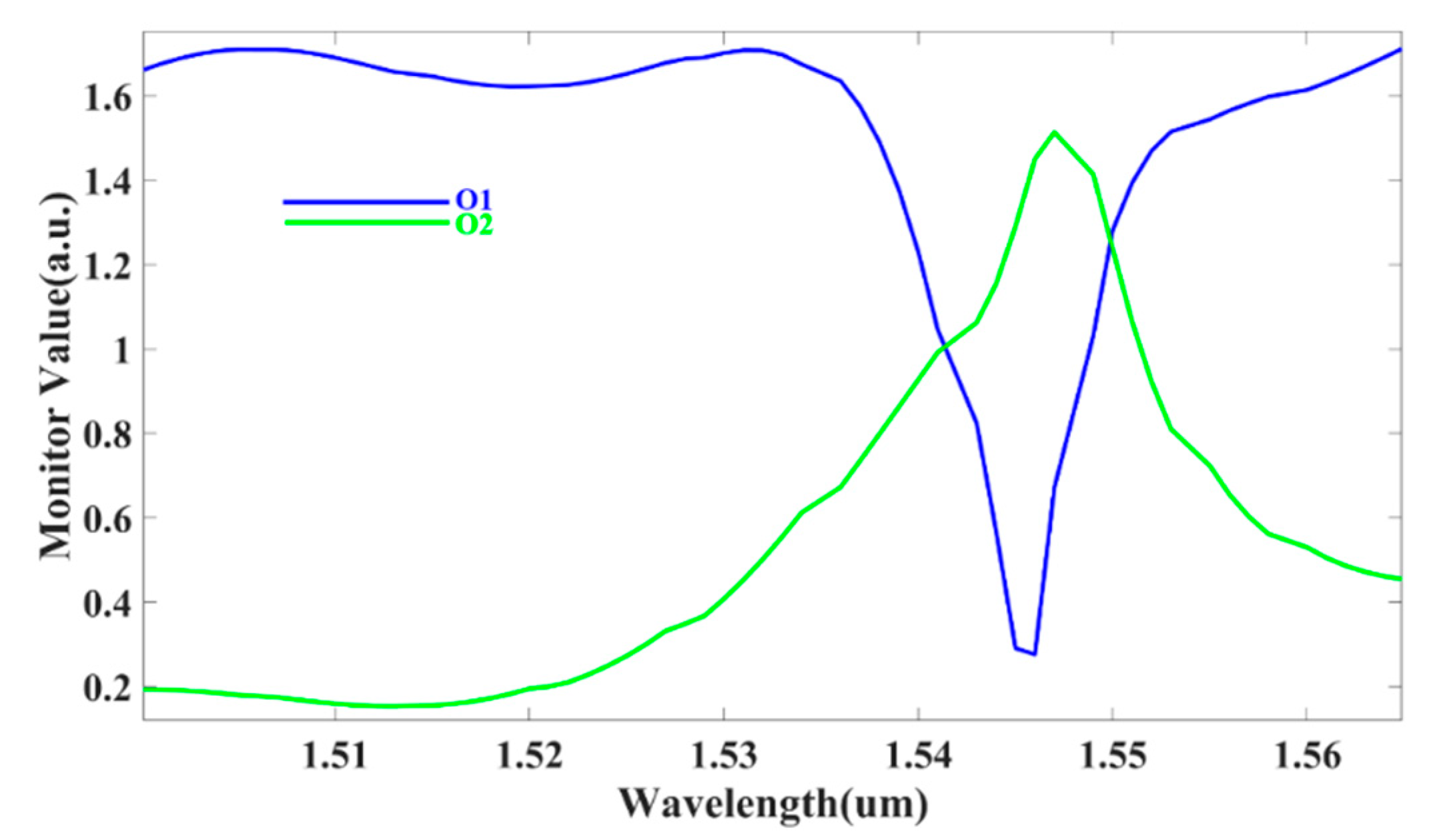
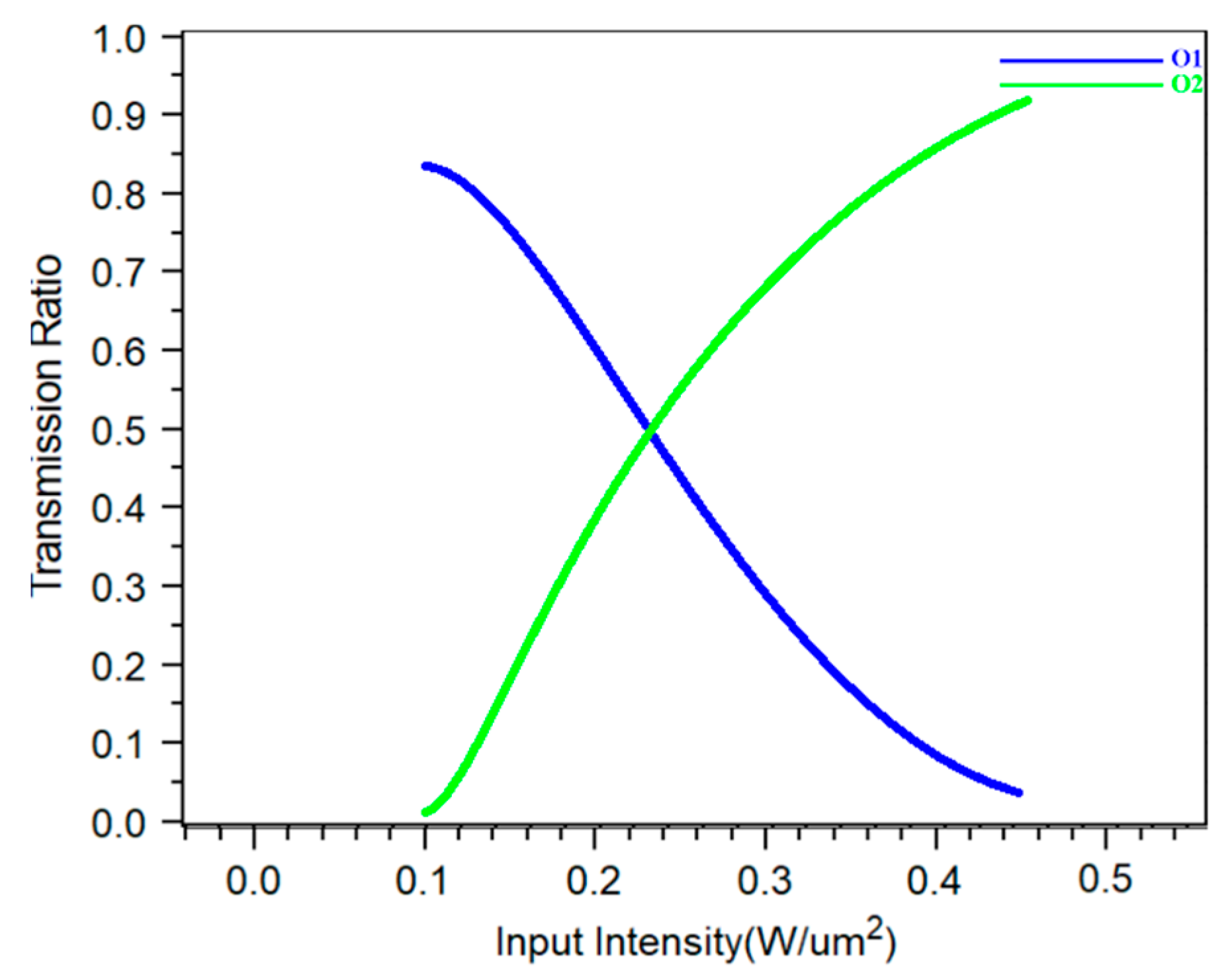
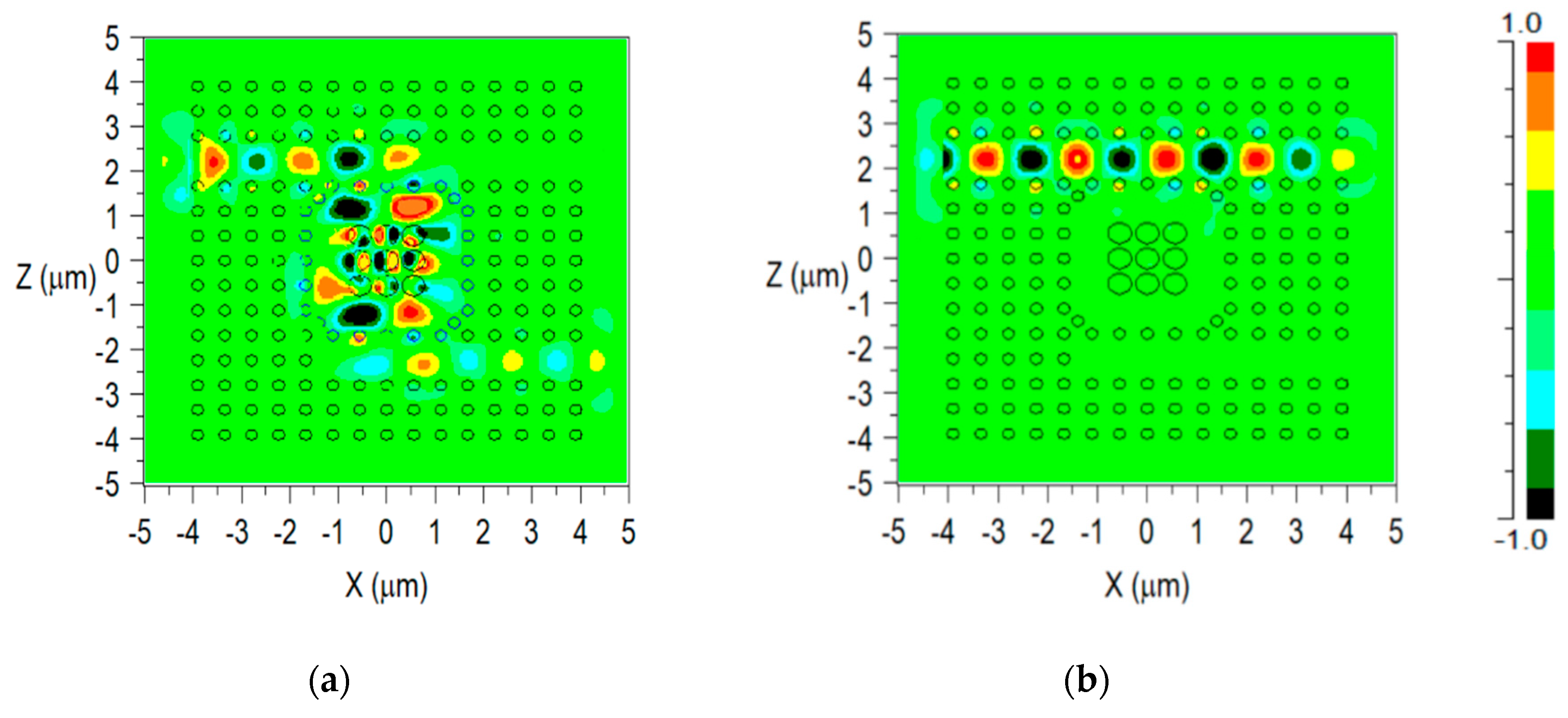
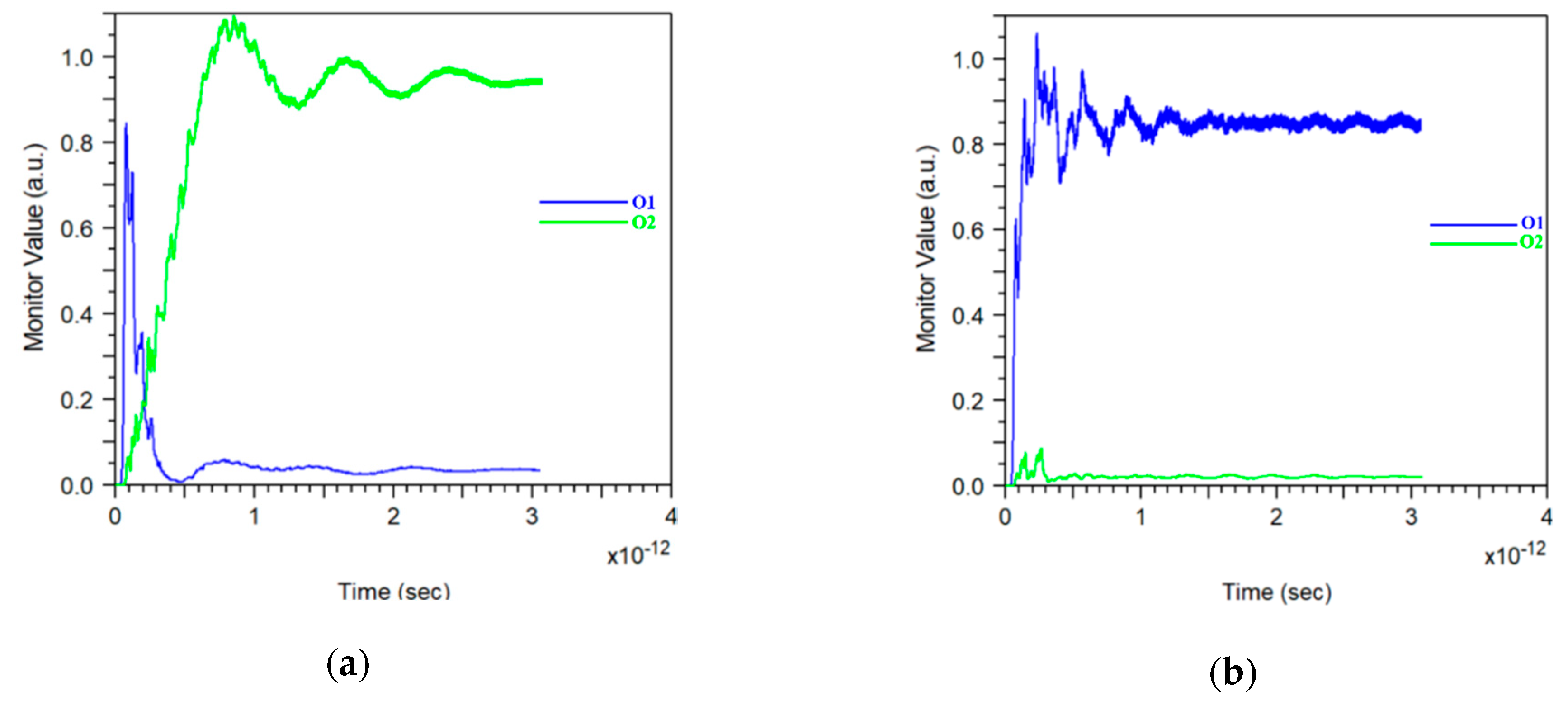
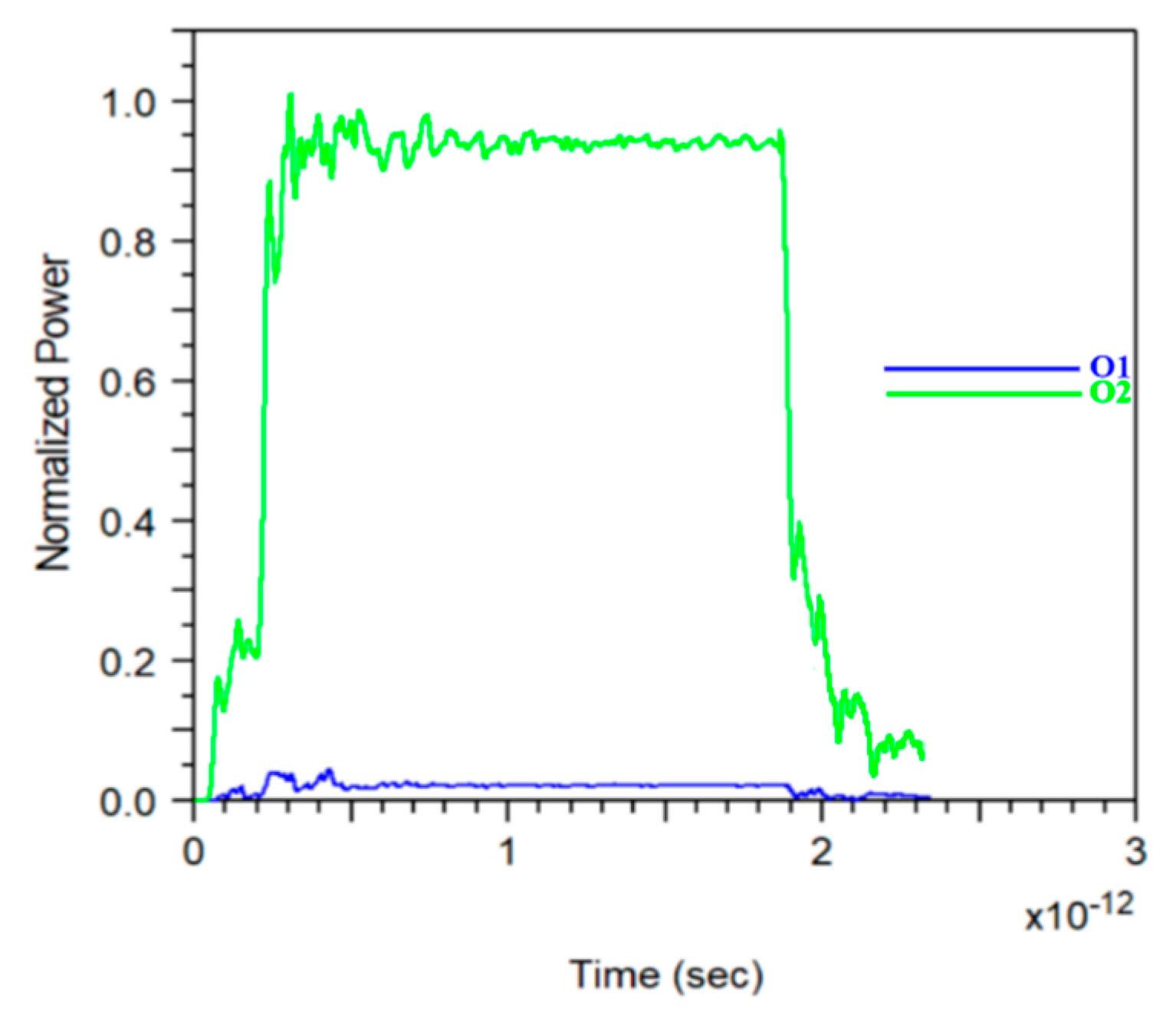
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nagarajan, R.; Joyner, C.H.; Schneider, R.P.; Bostak, J.S.; Butrie, T.; Dentai, A.G.; Dominic, V.G.; Evans, P.W.; Kato, M.; Kauffman, M. Large-scale photonic integrated circuits. IEEE J. Sel. Top. Quantum 2005, 11, 50–65. [Google Scholar] [CrossRef]
- Bogaerts, W.; Chrostowski, L. Silicon photonics circuit design: Methods, tools and challenges. Laser Photonics Rev. 2018, 12, 1700237. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486. [Google Scholar] [CrossRef] [PubMed]
- Pu, S.; Dong, S.; Huang, J. Tunable slow light based on magnetic-fluid-infiltrated photonic crystal waveguides. J. Opt. 2014, 16, 045102. [Google Scholar] [CrossRef]
- Soljačić, M.; Johnson, S.G.; Fan, S.; Ibanescu, M.; Ippen, E.; Joannopoulos, J. Photonic-crystal slow-light enhancement of nonlinear phase sensitivity. JOSA B 2002, 19, 2052–2059. [Google Scholar] [CrossRef] [Green Version]
- Vlasov, Y.A.; O’boyle, M.; Hamann, H.F.; McNab, S.J. Active control of slow light on a chip with photonic crystal waveguides. Nature 2005, 438, 65. [Google Scholar] [CrossRef]
- Noori, M.; Soroosh, M.; Baghban, H. Highly efficient self-collimation based waveguide for Mid-IR applications. Photonics Nanostruct. 2016, 19, 1–11. [Google Scholar] [CrossRef]
- Noori, M.; Soroosh, M.; Baghban, H. All-angle self-collimation in two-dimensional square array photonic crystals based on index contrast tailoring. Opt. Eng. 2015, 54, 037111. [Google Scholar] [CrossRef]
- Witzens, J.; Loncar, M.; Scherer, A. Self-collimation in planar photonic crystals. IEEE J. Sel. Top. Quantum 2002, 8, 1246–1257. [Google Scholar] [CrossRef] [Green Version]
- Kosaka, H.; Kawashima, T.; Tomita, A.; Notomi, M.; Tamamura, T.; Sato, T.; Kawakami, S. Self-collimating phenomena in photonic crystals. Appl. Phys. Lett. 1999, 74, 1212–1214. [Google Scholar] [CrossRef]
- Rani, P.; Kalra, Y.; Sinha, R. Realization of AND gate in Y shaped photonic crystal waveguide. Opt. Commun. 2013, 298, 227–231. [Google Scholar] [CrossRef]
- Mansouri-Birjandi, M.A.; Tavousi, A.; Ghadrdan, M. Full-optical tunable add/drop filter based on nonlinear photonic crystal ring resonators. Photonics Nanostruct. 2016, 21, 44–51. [Google Scholar] [CrossRef]
- Tavousi, A.; Mansouri-Birjandi, M.A.; Ghadrdan, M.; Ranjbar-Torkamani, M. Application of photonic crystal ring resonator nonlinear response for full-optical tunable add–drop filtering. Photonic Netw. Commun. 2017, 34, 131–139. [Google Scholar] [CrossRef]
- Musavizadeh, S.M.; Soroosh, M.; Mehdizadeh, F. Optical filter based on photonic crystal. Indian J. Pure Appl. Phys. 2015, 53, 736–739. [Google Scholar]
- Qiang, Z.; Zhou, W.; Soref, R.A. Optical add-drop filters based on photonic crystal ring resonators. Opt. Express 2007, 15, 1823–1831. [Google Scholar] [CrossRef] [PubMed]
- Ying, C.; Jing, D.; Jia, S.; Qiguang, Z.; Weihong, B. Study on tunable filtering performance of compound defect photonic crystal with magnetic control. Optik 2015, 126, 5353–5356. [Google Scholar] [CrossRef]
- Dideban, A.; Habibiyan, H.; Ghafoorifard, H. Photonic crystal channel drop filter based on ring-shaped defects for DWDM systems. Phys. E 2017, 87, 77–83. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Soroosh, M. A new proposal for eight-channel optical demultiplexer based on photonic crystal resonant cavities. Photonic Netw. Commun. 2016, 31, 65–70. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Soroosh, M.; Alipour-Banaei, H. An optical demultiplexer based on photonic crystal ring resonators. Optik 2016, 127, 8706–8709. [Google Scholar] [CrossRef]
- Talebzadeh, R.; Soroosh, M.; Mehdizadeh, F. Improved low channel spacing high quality factor four-channel demultiplexer based on photonic crystal ring resonators. Opt. Appl. 2016, 46, 553–564. [Google Scholar]
- Talebzadeh, R.; Soroosh, M.; Kavian, Y.S.; Mehdizadeh, F. Eight-channel all-optical demultiplexer based on photonic crystal resonant cavities. Optik 2017, 140, 331–337. [Google Scholar] [CrossRef]
- Zavvari, M. Design of photonic crystal-based demultiplexer with high-quality factor for DWDM applications. J. Opt. Commun. 2019, 40, 135–138. [Google Scholar] [CrossRef]
- Khorshidahmad, A.; Kirk, A.G. Composite superprism photonic crystal demultiplexer: Analysis and design. Opt. Express 2010, 18, 20518–20528. [Google Scholar] [CrossRef] [PubMed]
- Jiu-Sheng, L.; Han, L.; Le, Z. Compact four-channel terahertz demultiplexer based on directional coupling photonic crystal. Opt. Commun. 2015, 350, 248–251. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Soroosh, M.; Alipour-Banaei, H. A novel proposal for optical decoder switch based on photonic crystal ring resonators. Opt. Quantum Electron. 2016, 48, 20. [Google Scholar] [CrossRef]
- Nozhat, N.; Taher Rahmati, A.; Granpayeh, N. An all optical switch based on nonlinear photonic crystal microcavities. In Proceedings of the Progress in Electromagnetics Research Symposium, Moscow, Russia, 18–21 August 2009. [Google Scholar]
- Serajmohammadi, S.; Alipour-Banaei, H.; Mehdizadeh, F. All optical decoder switch based on photonic crystal ring resonators. Opt. Quantum Electron. 2015, 47, 1109–1115. [Google Scholar] [CrossRef]
- Ouahab, I.; Naoum, R. A novel all optical 4 × 2 encoder switch based on photonic crystal ring resonators. Optik 2016, 127, 7835–7841. [Google Scholar] [CrossRef]
- Teo, H.; Liu, A.; Singh, J.; Yu, M.; Bourouina, T. Design and simulation of MEMS optical switch using photonic bandgap crystal. Microsyst. Technol. 2004, 10, 400–406. [Google Scholar] [CrossRef]
- Bai, J.; Wang, J.; Jiang, J.; Chen, X.; Li, H.; Qiu, Y.; Qiang, Z. Photonic not and nor gates based on a single compact photonic crystal ring resonator. Appl. Opt. 2009, 48, 6923–6927. [Google Scholar] [CrossRef]
- Hussein, H.M.; Ali, T.A.; Rafat, N.H. A review on the techniques for building all-optical photonic crystal logic gates. Opt. Laser Technol. 2018, 106, 385–397. [Google Scholar] [CrossRef]
- Saidani, N.; Belhadj, W.; AbdelMalek, F. Novel all-optical logic gates based photonic crystal waveguide using self-imaging phenomena. Opt. Quantum Electron. 2015, 47, 1829–1846. [Google Scholar] [CrossRef]
- haq Shaik, E.; Rangaswamy, N. Improved design of all-optical photonic crystal logic gates using T-shaped waveguide. Opt. Quantum Electron. 2016, 48, 33. [Google Scholar] [CrossRef]
- Andalib, P.; Granpayeh, N. All-optical ultracompact photonic crystal AND gate based on nonlinear ring resonators. J. Opt. Soc. Am. Rev. B 2009, 26, 10–16. [Google Scholar] [CrossRef]
- Fasihi, K. Design and simulation of linear logic gates in the two-dimensional square-lattice photonic crystals. Optik 2016, 127, 4669–4674. [Google Scholar] [CrossRef]
- Moniem, T.A. All-optical digital 4 × 2 encoder based on 2D photonic crystal ring resonators. J. Mod. Opt. 2016, 63, 735–741. [Google Scholar] [CrossRef]
- Hassangholizadeh-Kashtiban, M.; Sabbaghi-Nadooshan, R.; Alipour-Banaei, H. A novel all optical reversible 4 × 2 encoder based on photonic crystals. Optik 2015, 126, 2368–2372. [Google Scholar] [CrossRef]
- Haddadan, F.; Soroosh, M. Low-power all-optical 8-to-3 encoder using photonic crystal-based waveguides. Photon. Net. Comm. 2019, 37, 83–89. [Google Scholar] [CrossRef]
- Alipour-Banaei, H.; Rabati, M.G.; Abdollahzadeh-Badelbou, P.; Mehdizadeh, F. Application of self-collimated beams to realization of all optical photonic crystal encoder. Phys. E 2016, 75, 77–85. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Soroosh, M.; Alipour-Banaei, H. Proposal for 4-to-2 optical encoder based on photonic crystals. IET Optoelectron. 2016, 11, 29–35. [Google Scholar] [CrossRef]
- Rajasekar, R.; Latha, R.; Robinson, S. Ultra-contrast ratio optical encoder using photonic crystal waveguides. Matt. Lett. 2019, 251, 144–147. [Google Scholar] [CrossRef]
- Alipour-Banaei, H.; Ghorbanzadeh Rabati, M.; Abdollahzadeh-Badelbou, P.; Mehdizadeh, F. Effect of self-collimated beams on the operation of photonic crystal decoders. J. Electromagn. Wave 2016, 30, 1440–1448. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Alipour-Banaei, H.; Serajmohammadi, S. Study the role of non-linear resonant cavities in photonic crystal-based decoder switches. J. Mod. Opt. 2017, 64, 1233–1239. [Google Scholar] [CrossRef]
- Daghooghi, T.; Soroosh, M.; Ansari-Asl, K. A novel proposal for all-optical decoder based on photonic crystals. Photonic Netw. Commun. 2018, 34, 335–341. [Google Scholar] [CrossRef]
- Chattopadhyay, T.; Roy, J.N. An all-optical technique for a binary-to-quaternary encoder and a quaternary-to-binary decoder. J. Opt. A Pure Appl. Opt. 2009, 11, 075501. [Google Scholar] [CrossRef]
- Alipour-Banaei, H.; Mehdizadeh, F.; Serajmohammadi, S.; Hassangholizadeh-Kashtiban, M. A 2*4 all optical decoder switch based on photonic crystal ring resonators. J. Mod. Opt. 2015, 62, 430–434. [Google Scholar] [CrossRef]
- Zhang, C.; Qiu, K. Design and analysis of coherent OCDM en/decoder based on photonic crystal. Opt. Lasers Eng. 2008, 46, 582–589. [Google Scholar] [CrossRef]
- Tavousi, A.; Mansouri-Birjandi, M.A.; Saffari, M. Successive approximation-like 4-bit full-optical analog-to-digital converter based on Kerr-like nonlinear photonic crystal ring resonators. Phys. E 2016, 83, 101–106. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Soroosh, M.; Alipour-Banaei, H.; Farshidi, E. Ultra-fast analog-to-digital converter based on a nonlinear triplexer and an optical coder with a photonic crystal structure. Appl. Opt. 2017, 56, 1799–1806. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Soroosh, M.; Alipour-Banaei, H.; Farshidi, E. All optical 2-bit analog to digital converter using photonic crystal based cavities. Opt. Quantum Electron. 2017, 49, 38. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Soroosh, M.; Alipour-Banaei, H.; Farshidi, E. A novel proposal for all optical analog-to-digital converter based on photonic crystal structures. IEEE Photonics J. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Xu, C.; Liu, X. Photonic analog-to-digital converter using soliton self-frequency shift and interleaving spectral filters. Opt. Lett. 2003, 28, 986–988. [Google Scholar] [CrossRef] [PubMed]
- Youssefi, B.; Moravvej-Farshi, M.K.; Granpayeh, N. Two-bit all-optical analog-to-digital converter based on nonlinear Kerr effect in 2D photonic crystals. Opt. Commun. 2012, 285, 3228–3233. [Google Scholar] [CrossRef]
- Tajaldini, M.; Jafri, M.Z. An optimum multimode interference coupler as an all-optical switch based on nonlinear modal propagation analysis. Optik 2015, 126, 436–441. [Google Scholar] [CrossRef]
- Haché, A.; Bourgeois, M. Ultrafast all-optical switching in a silicon-based photonic crystal. Appl. Phys. Lett. 2000, 77, 4089–4091. [Google Scholar] [CrossRef]
- Alipour-Banaei, H.; Serajmohammadi, S.; Mehdizadeh, F. All optical NOR and NAND gate based on nonlinear photonic crystal ring resonators. Optik 2014, 125, 5701–5704. [Google Scholar] [CrossRef]
- Serajmohammadi, S.; Absalan, H. All optical NAND gate based on nonlinear photonic crystal ring resonator. IPA 2016, 3, 119–123. [Google Scholar] [Green Version]
- Alipour-Banaei, H.; Serajmohammadi, S.; Mehdizadeh, F. All optical NAND gate based on nonlinear photonic crystal ring resonators. Optik 2017, 130, 1214–1221. [Google Scholar] [CrossRef]
- Daghooghi, T.; Soroosh, M.; Ansari-Asl, K. A low power all optical decoder based on photonic crystal nonlinear ring resonators. Optik 2018, 174, 400–408. [Google Scholar] [CrossRef]
- Ogusu, K.; Yamasaki, J.; Maeda, S.; Kitao, M.; Minakata, M. Linear and nonlinear optical properties of Ag–As–Se chalcogenide glasses for all-optical switching. Opt. Lett. 2004, 29, 265–267. [Google Scholar] [CrossRef]
- Soh, D.B.S.; Hamerly, R.; Mabuchi, H. Comprehensive analysis of the optical Kerr coefficient of graphene. Phys. Rev. A 2016, 94, 023845. [Google Scholar] [CrossRef] [Green Version]
- Soavi, G.; Wang, G.; Rostami, H.; Purdie, D.G.; Fazio, D.D.; Ma, T.; Luo, B.; Wang, J.; Ott, A.K.; Yoon, D.; et al. Broadband, electrically tunable third-harmonic generation in graphene. Nat. Nanotechnol. 2018, 13, 583–588. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, T.; Huang, D.; Cheng, J.; Fan, X.; Zhang, Z.; Shan, Y.; Yi, Y.; Dai, Y.; Shi, L.; Liu, K.; et al. Gate-tunable third-order nonlinear optical response of massless Dirac fermions in graphene. Nat. Nanotechnol. 2018, 12, 430–436. [Google Scholar] [Green Version]
- Hendry, E.; Hale, P.J.; Moger, J.; Savchenko, A.K. Coherent Nonlinear Optical Response of Graphene. Phys. Rev. Lett. 2010, 105, 091401. [Google Scholar] [CrossRef] [PubMed]
- Virga, A.; Ferrante, C.; Batingnani, G.; Fazio, D.D.; Nunn, A.D.G.; Ferrari, A.C.; Cerullo, G.; Scopigno, T. Coherent anti-Stokes Raman Spectroscopy of single and multi-layer graphene. Nat. Commun. 2019, 10, 3658. [Google Scholar] [CrossRef] [PubMed]
- Khurgin, J.B. Graphene—A rather ordinary nonlinear optical material. Appl. Phys. Lett. 2014, 104, 16116. [Google Scholar] [CrossRef]
- Zhang, H.; Virally, S.; Bao, Q.; Ping, L.K.; Massar, S.; Godbout, N.; Kockaert, P. Z-scan measurement of the nonlinear refractive index of graphene. Opt. Lett. 2012, 37, 1856–1858. [Google Scholar] [CrossRef]
- Cheng, J.L.; Vermeulen, N.; Sipe, J.E. Third order optical nonlinearity of graphene. New J. Phys. 2014, 16, 053014. [Google Scholar] [CrossRef]
- Gu, T.; Petrone, N.; McMillian, J.F.; Zande, A.V.D.; Yu, M.; Lo, G.Q.; Kwong, D.L.; Hone, J.; Wong, C.W. Regenerative oscillation and four-wave mixing in graphene optoelectronics. Nat. Photonics 2012, 6, 554–559. [Google Scholar] [CrossRef] [Green Version]
- Johnson, S.G.; Joannopoulos, J.D. Block-iterative frequency-domain methods for Maxwell’s equations in a planewave basis. Opt. Express 2001, 8, 173–190. [Google Scholar] [CrossRef]
- Berman, O.L.; Boyko, V.S.; Kezerashvili, R.Y.; Kolesnikov, A.A.; Lozovik, Y.E. Graphene-based photonic crystal. Phys. Lett. A 2010, 374, 4784–4786. [Google Scholar] [CrossRef] [Green Version]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: Hoboken, NJ, USA, 1991; Chapter 19. [Google Scholar]
- Sullivan, D.M. Electromagnetic Simulation Using the FDTD Method; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Daghooghi, T.; Soroosh, M.; Ansari-Asl, K. Ultra-fast all-optical decoder based on nonlinear photonic crystal ring resonators. Appl. Opt. 2018, 57, 2250–2257. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jalali Azizpour, M.R.; Soroosh, M.; Dalvand, N.; Seifi-Kavian, Y. All-Optical Ultra-Fast Graphene-Photonic Crystal Switch. Crystals 2019, 9, 461. https://doi.org/10.3390/cryst9090461
Jalali Azizpour MR, Soroosh M, Dalvand N, Seifi-Kavian Y. All-Optical Ultra-Fast Graphene-Photonic Crystal Switch. Crystals. 2019; 9(9):461. https://doi.org/10.3390/cryst9090461
Chicago/Turabian StyleJalali Azizpour, Mohammad Reza, Mohammad Soroosh, Narges Dalvand, and Yousef Seifi-Kavian. 2019. "All-Optical Ultra-Fast Graphene-Photonic Crystal Switch" Crystals 9, no. 9: 461. https://doi.org/10.3390/cryst9090461





