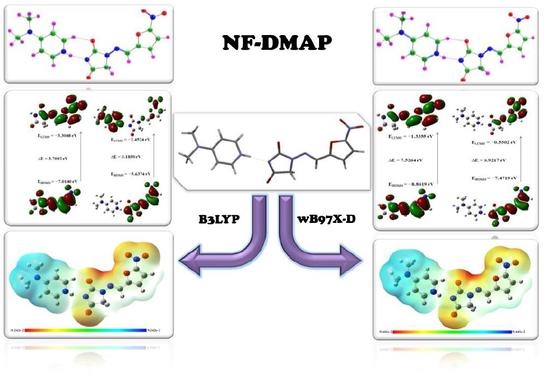
Structural and Reactivity Analyses of Nitrofurantoin–4-dimethylaminopyridine Salt Using Spectroscopic and Density Functional Theory Calculations
Abstract
1. Introduction
2. Experimental Details
3. Computational Details
4. Results and Discussion
4.1. Geometry Optimization and Energies
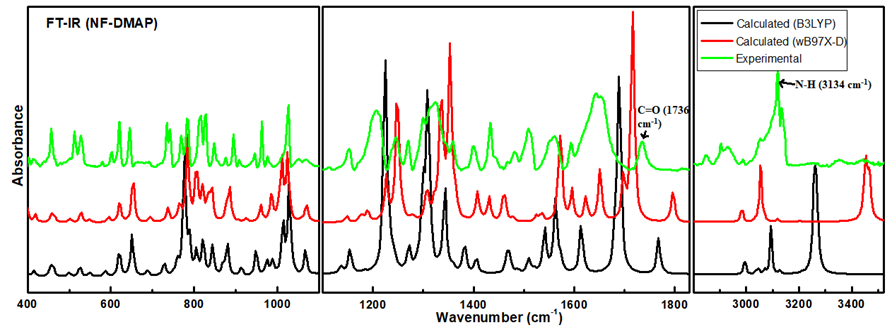
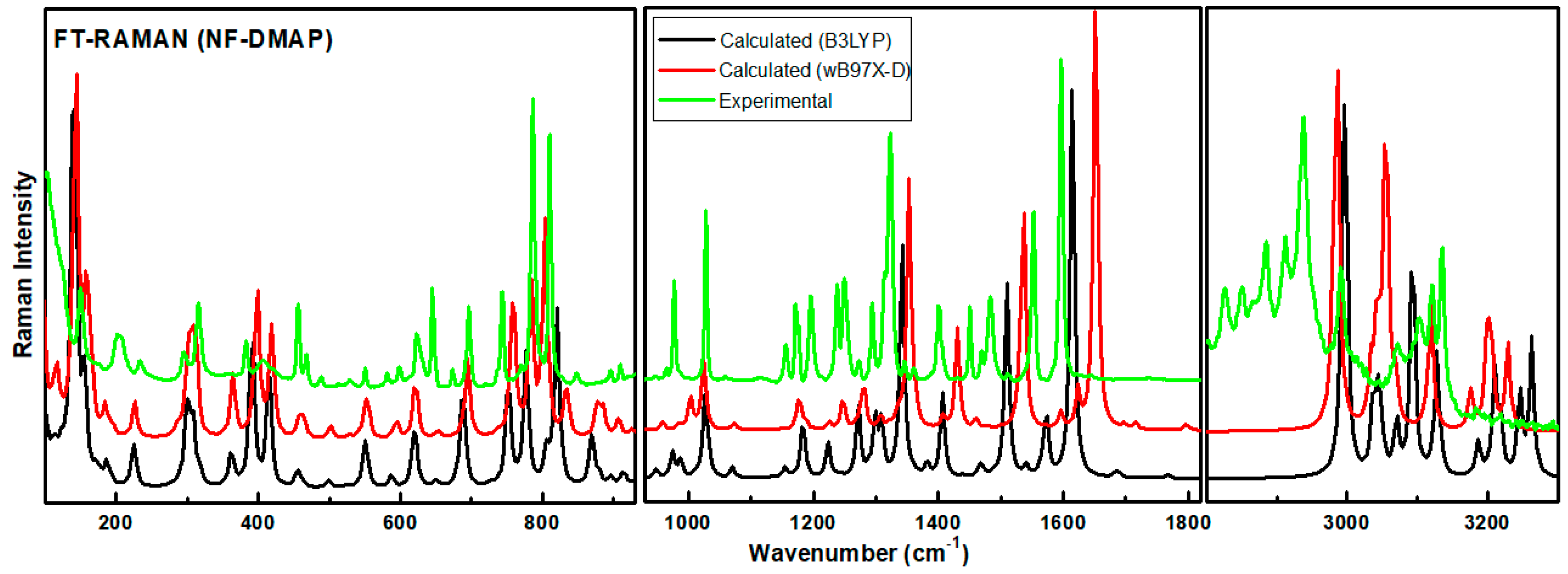
4.2. Vibrational Assignment
4.3. Vibrational Wavenumbers Involved in Hydrogen Bonding
4.4. Quantum Theory of Atoms in Molecules (QTAIM) Calculations for Hydrogen Bonding
4.5. Natural Bond Orbital (NBO) Analysis
4.6. Chemical Reactivity
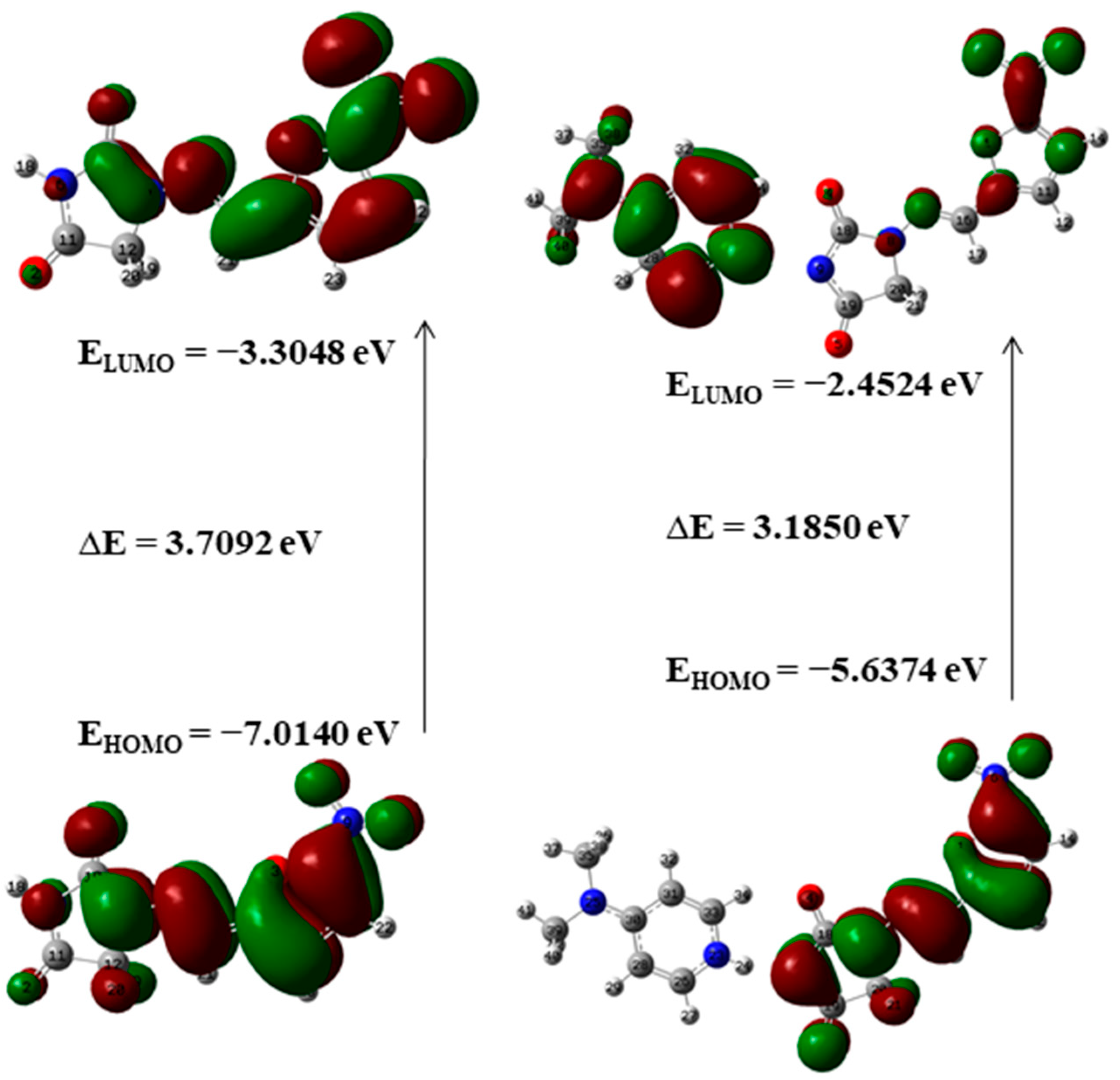
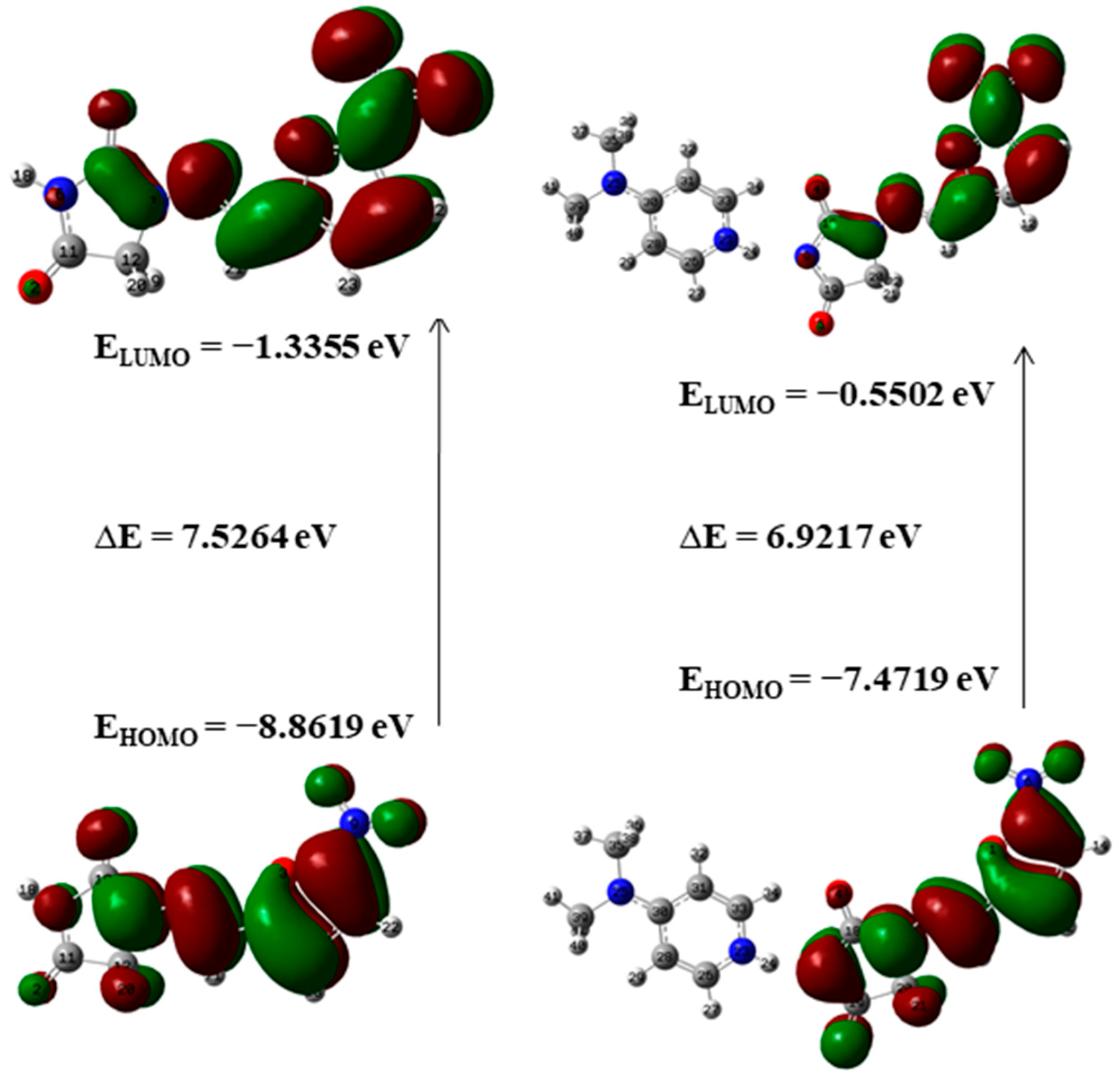
4.6.1. Frontier Molecular Orbitals (FMOs)
4.6.2. Molecular Electrostatic Potential (MEP) Analysis
4.6.3. Global Reactivity Descriptors
4.6.4. Local Reactivity Descriptors
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Duggirala, N.K.; Perry, M.L.; Almarsson, Ö.; Zaworotko, M.J. Pharmaceutical cocrystals: Along the path to improved medicines. Chem. Commun. 2016, 52, 640–655. [Google Scholar] [CrossRef] [PubMed]
- Grothe, E.; Meekes, H.; Vlieg, E.; ter Horst, J.H.; de Gelder, R. Solvates, salts, and cocrystals: A proposal for a feasible classification system. Cryst. Growth Des. 2016, 16, 3237–3243. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, J.R.; Zhang, Q.; Li, M.; Guo, C.; Ren, G.; Mei, X. Stable cocrystals and salts of the antineoplastic drug apatinib with improved solubility in aqueous solution. Cryst. Growth Des. 2018, 18, 4701–4714. [Google Scholar] [CrossRef]
- Skorepova, E.; Bím, D.; Husak, M.; Klimes, J.; Chatziadi, A.; Ridvan, L.; Boleslavska, T.; Beranek, J.; Sebek, P.; Rulísek, L. Increase in solubility of poorly-ionizable pharmaceuticals by salt formation: A case of agomelatine sulfonates. Cryst. Growth Des. 2017, 17, 5283–5294. [Google Scholar] [CrossRef]
- Brittain, H.G. Vibrational spectroscopic studies of cocrystals and salts. 1. The benzamide-benzoic acid system. Cryst. Growth Des. 2009, 9, 2492–2499. [Google Scholar] [CrossRef]
- Brittain, H.G. Vibrational spectroscopic studies of cocrystals and salts. 2. The benzylamine-benzoic acid system. Cryst. Growth Des. 2009, 9, 3497–3503. [Google Scholar] [CrossRef]
- Brittain, H.G. Vibrational spectroscopic studies of cocrystals and salts. 3. Cocrystal products formed by benzene carboxylic acids and their sodium salts. Cryst. Growth Des. 2010, 10, 1990–2003. [Google Scholar] [CrossRef]
- Brittain, H.G. Vibrational spectroscopic studies of cocrystals and salts. 4. Cocrystal products formed by benzylamine, α-methylbenzylamine, and their chloride salts. Cryst. Growth Des. 2011, 11, 2500–2509. [Google Scholar] [CrossRef]
- Aitipamula, S.; Vangala, V.R. X-ray crystallography and its role in understanding the physicochemical properties of pharmaceutical cocrystals. J. Ind. Inst. Sci. 2017, 97, 227–243. [Google Scholar] [CrossRef]
- Pienaar, E.W.; Caira, M.R.; Lotter, A.P. Polymorphs of nitro-furantoin 1. Preparation and X-ray crystal-structures of two monohydrated forms of nitrofurantoin. J. Crystallogr. Spectr. Res. 1993, 23, 739–744. [Google Scholar] [CrossRef]
- WHO Model List of Essential Medicines [WWW Document]. Available online: http://www.who.int/selectionmedicines/committees/expert/17/sixteenthadultlisten (accessed on 8 March 2017).
- Macrodantin Package Insert; Procter & Gamble—US: Pineville, LA, USA, 2009.
- Ebian, A.E.A.R.; Moustafa, R.M.A.; Abul-Enin, E.B. Nitrofurantoin. I. Effect of aging at different relative humidities and higher temperatures on the drug release and the physical properties of tablets. Egypt J. Pharm. Sci. 1985, 26, 287–300. [Google Scholar]
- Ebian, A.E.A.R.; Fikrat, H.T.; Moustafa, R.M.A.; Abul-Enin, E.B. Nitrofurantoin. II. Correlation of in vivo bioavailability to in vitro dissolution of nitrofurantoin tablets aged at different relative humidities and elevated temperatures. Egypt J. Pharm. Sci. 1986, 27, 347–358. [Google Scholar]
- Bertolasi, B.Y.V.; Gilli, P.; Ferretti, V.; Gilli, G. Structure and crystal packing of the antibacterial drug 1-{[(5-nitro-2-furanyl)methylene]amino}-2,4-imidazolidinedione (nitrofurantoin). Acta Crystallogr. Sect. C 1993, 49, 741–744. [Google Scholar] [CrossRef]
- Marshall, P.V.; York, P. Crystallisation solvent induced solid- state and particulate modifications of nitrofurantoin. Int. J. Pharm. 1989, 55, 257–263. [Google Scholar] [CrossRef]
- Otsuka, M.; Teraoka, R.; Matsuda, Y. Physicochemical stability of nitrofurantoin anhydrate and monohydrate under various temperature and humidity conditions. Pharm. Res. 1991, 8, 1066. [Google Scholar] [CrossRef]
- Vangala, V.R.; Chow, P.S.; Tan, R.B.H. The solvates and salt of antibiotic agent, nitrofurantoin: Structural, thermochemical and desolvation studies. CrystEngComm 2013, 15, 878–889. [Google Scholar] [CrossRef]
- Stephen Chan, H.C.; Kendrick, J.; Neumann, M.A.; Leusen, F.J.J. Towards abinitio screening of co-crystal formation through lattice energy calculations and crystalstructure prediction of nicotinamide, isonicotinamide, picolinamide and paracetamolmulti-component crystals. CrystEngComm 2013, 15, 3799. [Google Scholar] [CrossRef]
- Srivastava, K.; Shukla, A.; Karthick, T.; Velaga, S.P.; Tandon, P.; Sinha, K.; Shimpi, M.R. Molecular structure, spectroscopic signature and reactivity analyses of paracetamol hydrochloride monohydrate salt using density functional theory calculations. CrystEngComm 2019, 21, 857–865. [Google Scholar] [CrossRef]
- Sacchi, M.; Brewer, A.Y.; Jenkins, S.J.; Parker, J.E.; Friščić, T.; Clarke, S.M. Combined diffraction and density functional theory calculations of halogen-bonded cocrystal monolayers. Langmuir 2013, 29, 14903–14911. [Google Scholar] [CrossRef]
- Shukla, A.; Khan, E.; Alsirawan, M.B.; Mandal, R.; Tandon, P.; Vangala, V.R. Spectroscopic (FT-IR, FT-Raman, 13C SS-NMR) and quantum chemical investigations to explore the structural insights of nitrofurantoin-4-hydroxybenzoic acid cocrystal. New J. Chem. 2019, 43, 7136–7149. [Google Scholar] [CrossRef]
- Shukla, A.; Khan, E.; Srivastava, K.; Sinha, K.; Tandon, P.; Vangala, V.R. Study of molecular interactions and chemical reactivity of the nitrofurantoin–3-aminobenzoic acid cocrystal using quantum chemical and spectroscopic (IR, Raman, 13 C SS-NMR) approaches. CrystEngComm 2017, 19, 3921–3930. [Google Scholar] [CrossRef]
- Khan, E.; Shukla, A.; Jhariya, A.N.; Tandon, P.; Vangala, V.R. Nitrofurantoin-melamine monohydrate (cocrystal hydrate): Probing the role of H-bonding on the structure and properties using quantum chemical calculations and vibrational spectroscopy. Spectrochim. Acta Part. A Mol. Biomol. Spectrosc. 2019, 221, 117170. [Google Scholar] [CrossRef] [PubMed]
- Khan, E.; Shukla, A.; Jadav, N.; Telford, R.; Ayala, A.P.; Tandon, P.; Vangala, V.R. Study of molecular structure, chemical reactivity and H-bonding interactions in the cocrystal of nitrofurantoin with urea. New J. Chem. 2017, 41, 11069–11078. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Petersson, G.A.; Allaham, M.A. A complete basis set model chemistry. II. Open-shell systems and the total energies of the first-row atoms. J. Chem. Phys. 1991, 94, 6081–6091. [Google Scholar] [CrossRef]
- Petersson, G.A.; Bennett, A.; Tensfeldt, T.G.; Allaham, M.A.; Shirley, W.A.; Mantzaris, J. A complete basis set model chemistry. I. The total energies of closed-shell atoms and hydrides of the first-row elements. J. Chem. Phys. 1988, 89, 2193–2218. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.T.; Yang, W.T.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Pulay, P.; Fogarasi, G.; Pang, F.; Boggs, J.E. Systematic ab initio gradient calculation of molecular geometries, force constants, and dipole moment derivatives. J. Am. Chem. Soc. 1979, 101, 2550–2560. [Google Scholar] [CrossRef]
- Martin, J.M.L.; Alsenoy, C.V. Gar2ped; University of Antwerp: Antwerpen, Belgium, 1995. [Google Scholar]
- Frisch, A.; Nielson, A.B.; Holder, A.J. Gaussview User Manual; Gaussian, Inc.: Pittsburgh, PA, USA, 2000. [Google Scholar]
- Bader, R.F.W.; Cheeseman, J.R. AIMPAC: A Suite of Programs for the AIM Theory; McMaster University: Hamilton, ON, Canada, 2000. [Google Scholar]
- National Center for Biotechnology Information. Pubchem Compound Database [WWW Document]. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/14284 (accessed on 15 January 2017).
- Karasulu, B.; Götze, J.P.; Thiel, W. Assessment of Franck–Condon methods for computing vibrationally broadened UV–vis absorption spectra of flavin derivatives: Riboflavin, roseoflavin, and 5-thioflavin. J. Chem. Theory Comput. 2014, 10, 5549–5566. [Google Scholar] [CrossRef] [PubMed]
- Scott, A.P.; Radom, L. Harmonic vibrational frequencies: An evaluation of hartree−fock, møller−plesset, quadratic configuration interaction, density functional theory, and semiempirical scale factors. J. Phys. Chem. 1996, 100, 16502–16513. [Google Scholar] [CrossRef]
- Wong, M.W. Vibrational frequency prediction using density functional theory. Chem. Phys. Lett. 1996, 256, 391–399. [Google Scholar] [CrossRef]
- Banwell, C.N.; McCash, E.M. Fundamentals of Molecular Spectroscopy; Mcgraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Lambert, J.B. Introduction to Organic Spectroscopy; Macmillan: New York, NY, USA, 1987. [Google Scholar]
- Delgado, M.C.R.; Hernandez, V.; Navarrete, J.T.L.; Tanaka, S.; Yamashita, Y. Electronic, optical, and vibrational properties of bridged dithienylethylene-based NLO chromophores. J. Phys. Chem. B. 2004, 108, 2516–2526. [Google Scholar] [CrossRef]
- Socrates, G. Infrared and Raman Characteristic Group Frequencies: Tables and Charts; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Smith, B.C. Infrared Spectral Interpretation: A Systematic Approach; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Koch, U.; Popelier, P.L.A. Characterization of C-H∙∙∙O hydrogen bonds on the basis of the charge density. J. Phys. Chem. 1995, 99, 9747–9754. [Google Scholar] [CrossRef]
- Rozas, I.; Alkorta, I.; Elguero, J. Behavior of ylides containing N, O, and C atoms as hydrogen bond acceptors. J. Am. Chem. Soc. 2000, 122, 11154–11161. [Google Scholar] [CrossRef]
- Fukui, K. Role of frontier orbitals in chemical reactions. Science 1982, 218, 747. [Google Scholar] [CrossRef]
- Khan, E.; Shukla, A.; Srivastava, A.; Shweta, P.; Tandon, P. Molecular structure, spectral analysis and hydrogen bonding analysis of ampicillin trihydrate: A combined DFT and AIM approach. New J. Chem. 2015, 39, 9800–9812. [Google Scholar] [CrossRef]
- Chidangil, S.; Shukla, M.K.; Mishra, P.C. A molecular electrostatic potential mapping study of some fluoroquinolone anti-bacterial agents. J. Mol. Model. 1998, 4, 250–258. [Google Scholar] [CrossRef]
- Luque, F.J.; Lopez, J.M.; Orozco, M. Perspective on electrostatic interactions of a solute with a continuum. A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Theor. Chem. Acc. 2000, 103, 343–345. [Google Scholar] [CrossRef]
- Parr, R.G.; Szentpaly, L.; Liu, S. Electrophilicity index. J. Am. Chem. Soc. 1999, 121, 1922. [Google Scholar] [CrossRef]
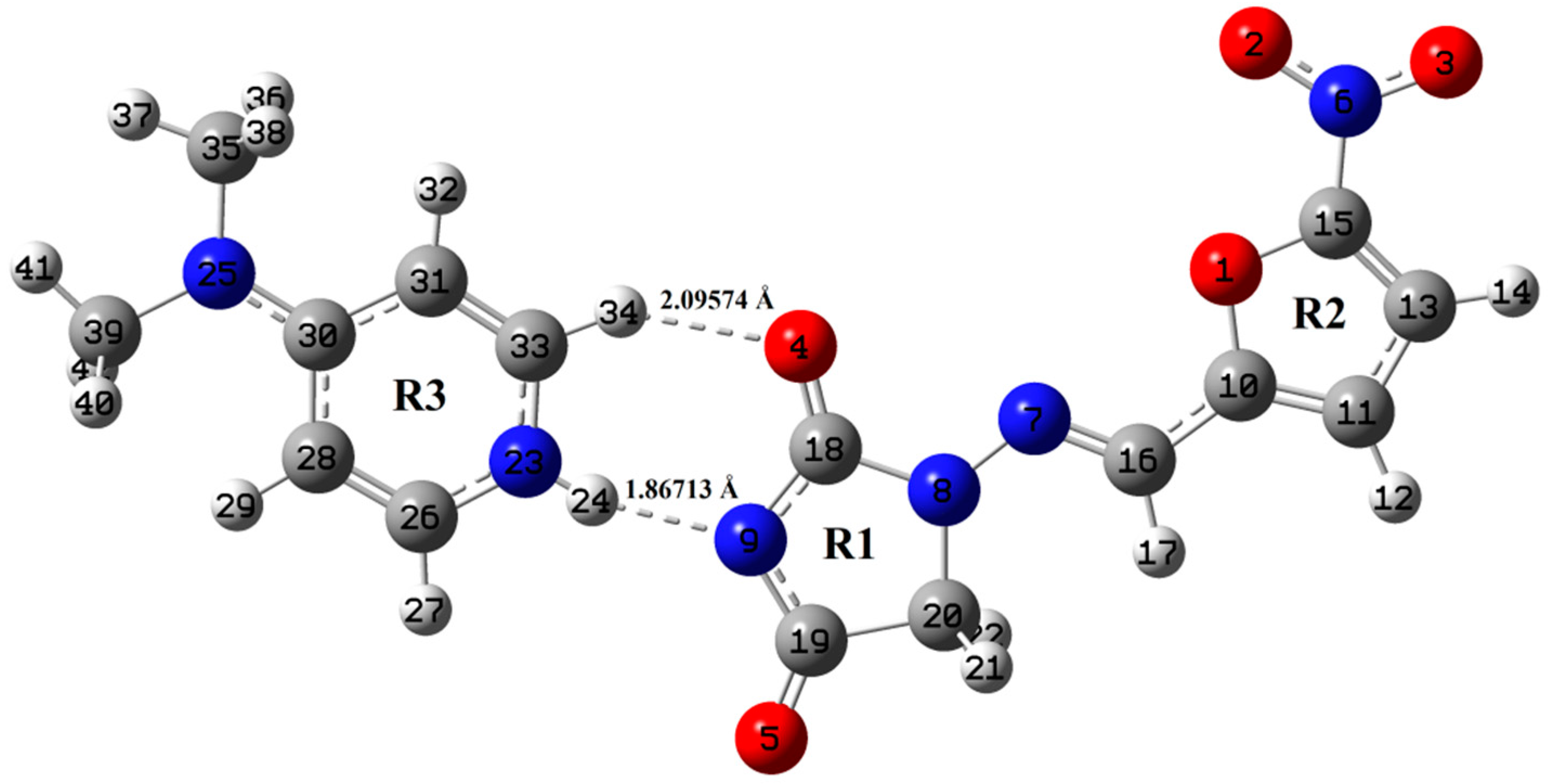

| Interactions | Bond Length (Å) | ρBCP (a.u.) | ∇2ρBCP (a.u.) | GBCP (a.u.) | VBCP (a.u.) | HBCP (a.u.) | EHB (kcal mol−1) |
|---|---|---|---|---|---|---|---|
| B3LYP | |||||||
| N23-H24⋅⋅⋅N9 | 1.86713 | 0.03701 | 0.11551 | 0.00107 | −0.03103 | −0.02996 | −9.7358 |
| C33-H34⋅⋅⋅O4 | 2.09574 | 0.02015 | 0.06811 | −0.00216 | −0.01270 | −0.01486 | −3.9847 |
| wB97X-D | |||||||
| N23-H24⋅⋅⋅N9 | 1.84679 | 0.03882 | 0.12267 | 0.00156 | −0.03378 | −0.03222 | −10.5986 |
| C33-H34⋅⋅⋅O4 | 2.05102 | 0.02196 | 0.07461 | −0.00216 | −0.01432 | −0.01648 | −4.4926 |
| Molecule | EH (eV) | EL (eV) | EL–EH (eV) | χ (eV) | μ (eV) | η (eV) | S (eV−1) | ω (eV) | ΔNmax | ECT |
|---|---|---|---|---|---|---|---|---|---|---|
| B3LYP | ||||||||||
| NF | −7.0140 | −3.3048 | 3.7092 | 5.1590 | −5.1594 | 1.8546 | 0.2696 | 7.1766 | 2.7819 | |
| DMAP | −5.9664 | −0.5276 | 5.4388 | 3.2470 | −3.2470 | 2.7194 | 0.1839 | 1.9385 | 1.1940 | 1.5879 |
| NF-DMAP | −5.6374 | −2.4524 | 3.1850 | 4.0449 | −4.0449 | 1.5925 | 0.3139 | 5.1369 | 2.5400 | |
| wB97X-D | ||||||||||
| NF | −8.8619 | −1.3355 | 7.5264 | 5.0990 | −5.0987 | 3.7632 | 0.1329 | 3.4541 | 1.3549 | |
| DMAP | −7.8984 | −0.8765 | 7.0219 | 4.3870 | −4.3875 | 3.5110 | 0.1424 | 2.7414 | 1.2496 | 0.1053 |
| NF-DMAP | −7.4719 | −0.5502 | 6.9217 | 4.0110 | −4.0110 | 3.4608 | 0.1445 | 2.3243 | 1.1590 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, E.; Shukla, A.; Srivastava, K.; Gangopadhyay, D.; Assi, K.H.; Tandon, P.; Vangala, V.R. Structural and Reactivity Analyses of Nitrofurantoin–4-dimethylaminopyridine Salt Using Spectroscopic and Density Functional Theory Calculations. Crystals 2019, 9, 413. https://doi.org/10.3390/cryst9080413
Khan E, Shukla A, Srivastava K, Gangopadhyay D, Assi KH, Tandon P, Vangala VR. Structural and Reactivity Analyses of Nitrofurantoin–4-dimethylaminopyridine Salt Using Spectroscopic and Density Functional Theory Calculations. Crystals. 2019; 9(8):413. https://doi.org/10.3390/cryst9080413
Chicago/Turabian StyleKhan, Eram, Anuradha Shukla, Karnica Srivastava, Debraj Gangopadhyay, Khaled H. Assi, Poonam Tandon, and Venu R. Vangala. 2019. "Structural and Reactivity Analyses of Nitrofurantoin–4-dimethylaminopyridine Salt Using Spectroscopic and Density Functional Theory Calculations" Crystals 9, no. 8: 413. https://doi.org/10.3390/cryst9080413
APA StyleKhan, E., Shukla, A., Srivastava, K., Gangopadhyay, D., Assi, K. H., Tandon, P., & Vangala, V. R. (2019). Structural and Reactivity Analyses of Nitrofurantoin–4-dimethylaminopyridine Salt Using Spectroscopic and Density Functional Theory Calculations. Crystals, 9(8), 413. https://doi.org/10.3390/cryst9080413