Coherent Magnetization Rotation of a Layered System Observed by Polarized Neutron Scattering under Grazing Incidence Geometry
Abstract
1. Introduction
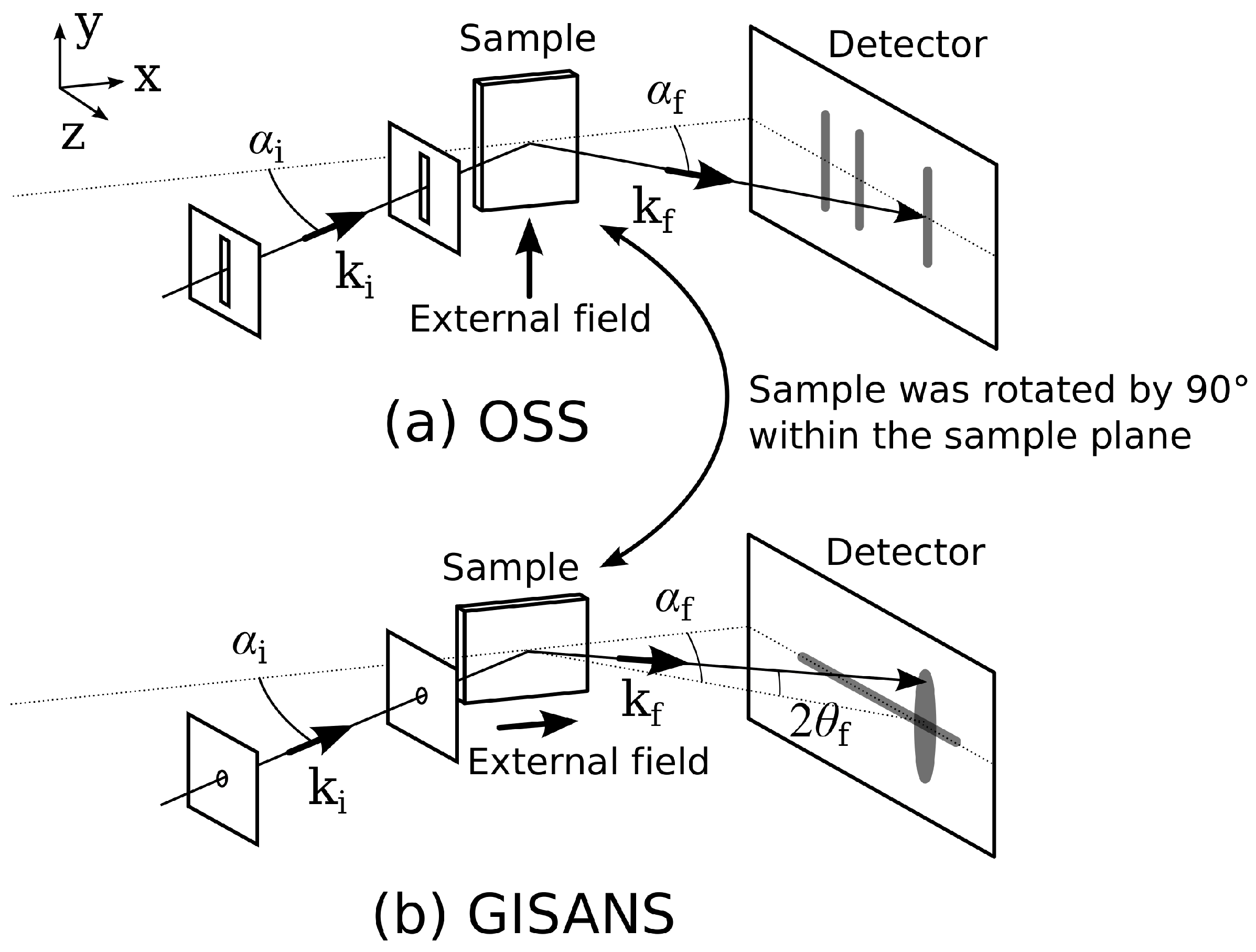
2. Materials and Methods
3. Results
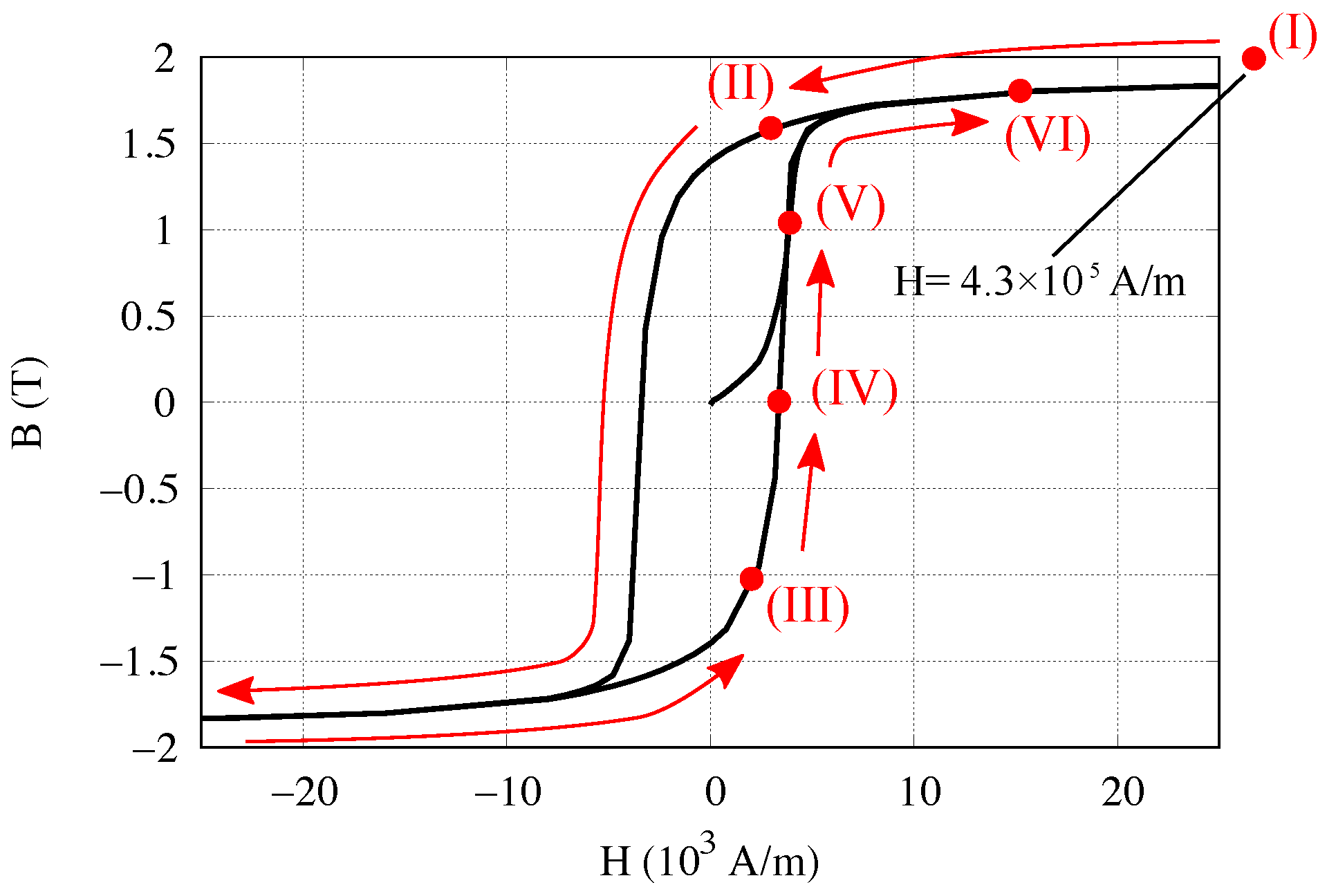
3.1. Magnetic Hysteresis Measurement
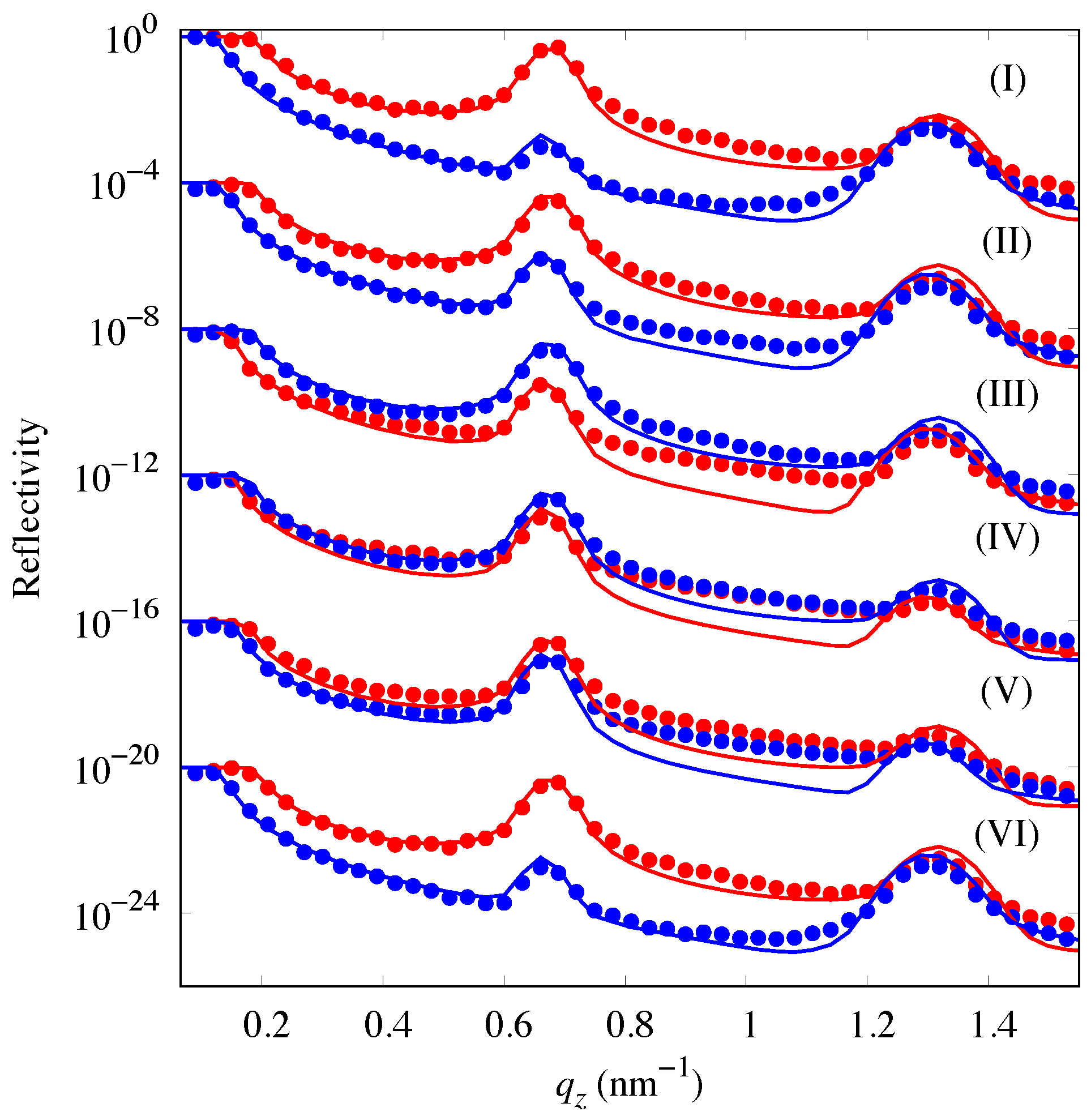
3.2. Polarized OSS Measurement
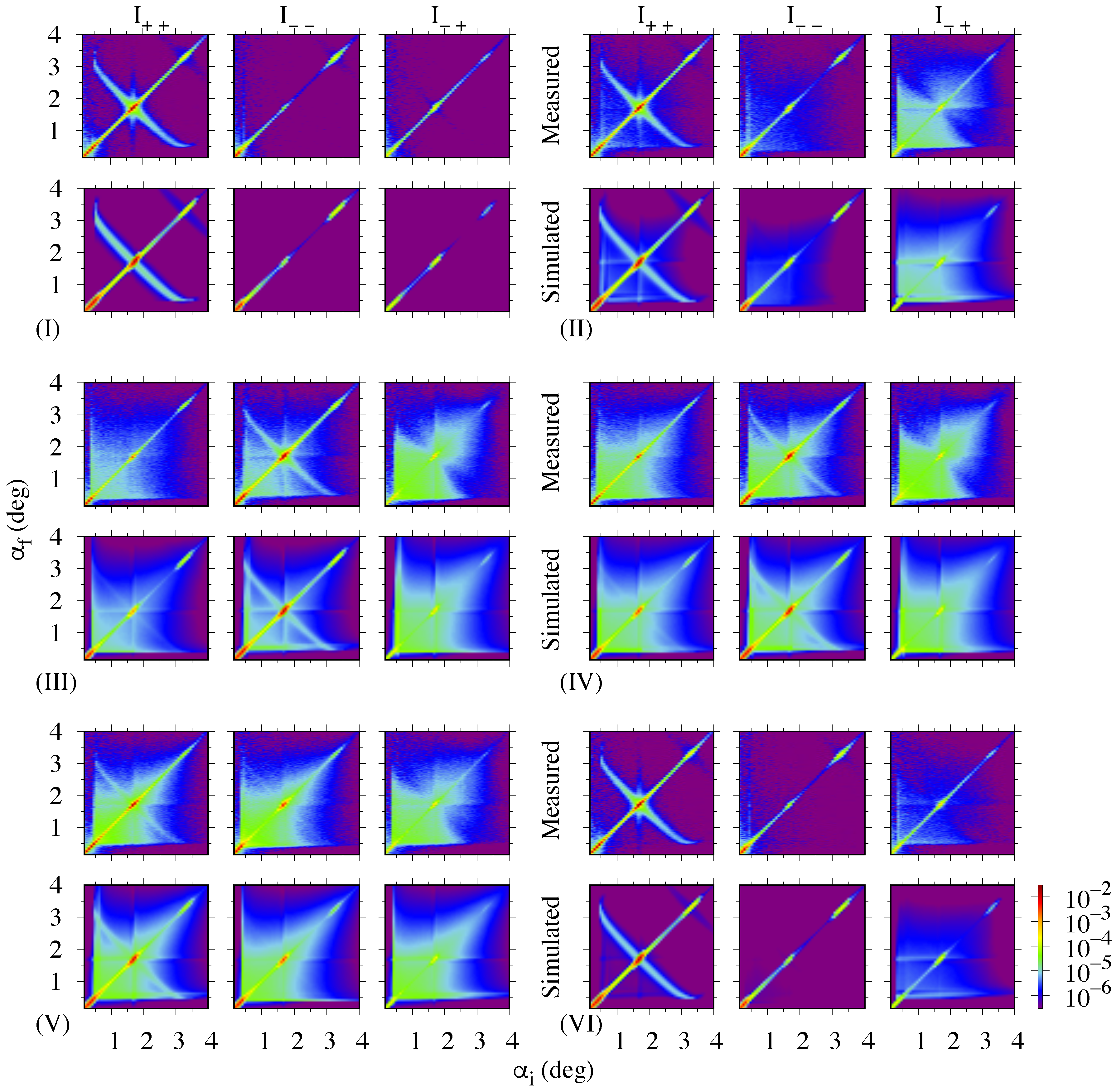
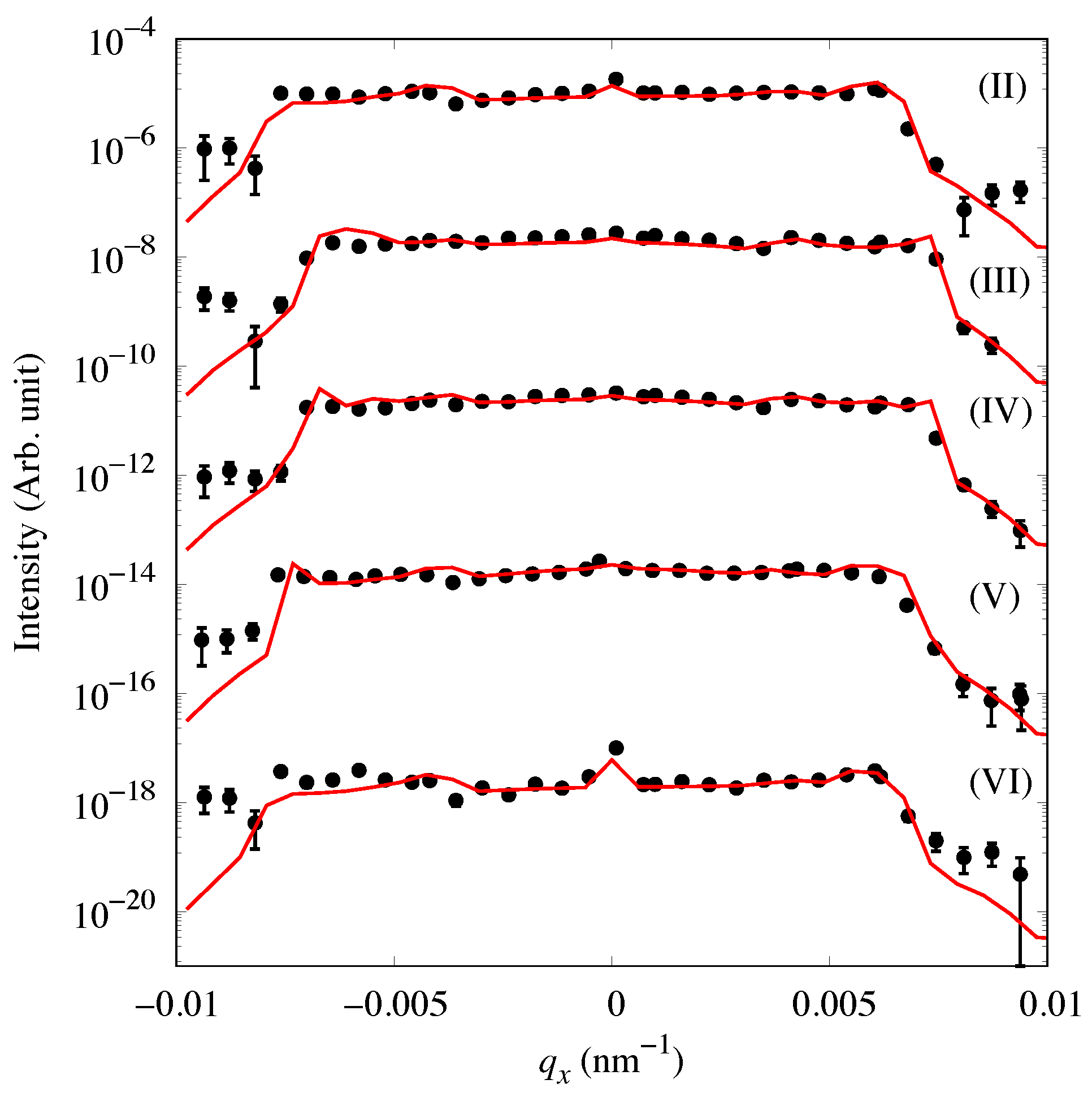
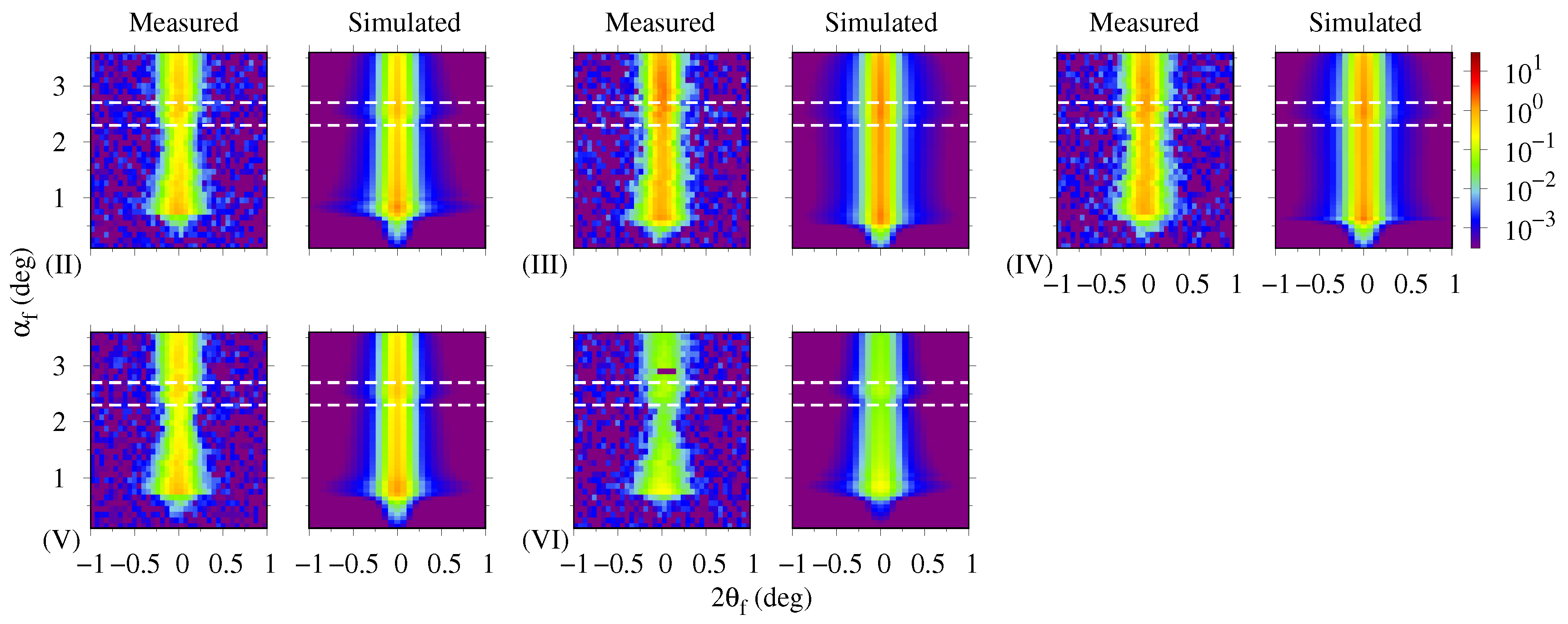
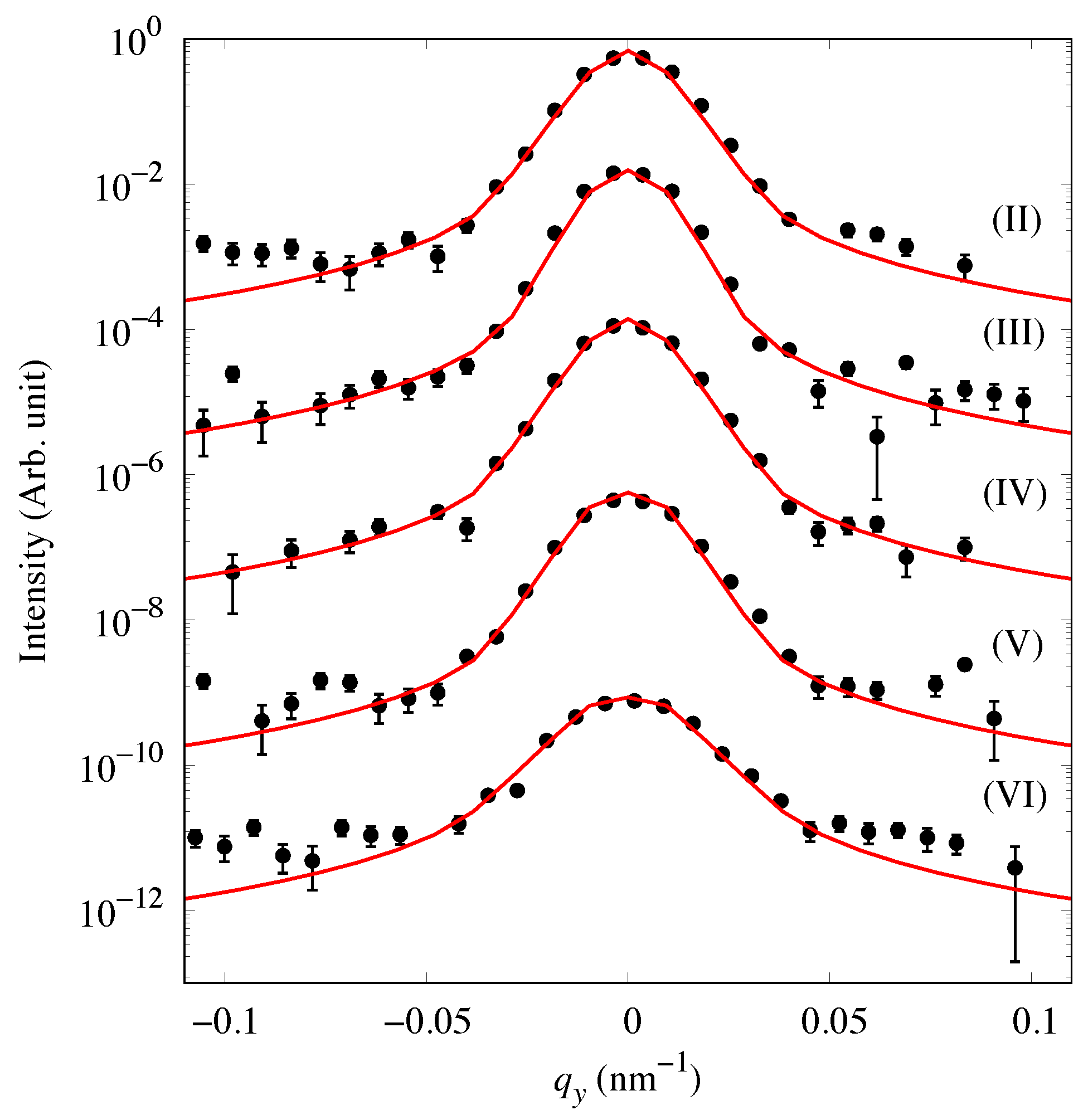
3.3. Polarized GISANS Measurement
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grünberg, P.; Schreiber, R.; Pang, Y. Layered magnetic structures: Evidence for antiferromagnetic coupling of Fe layers across Cr interlayers. Phys. Rev. Lett. 1986, 57, 2442–2445. [Google Scholar] [CrossRef] [PubMed]
- Baibich, M.N.; Broto, J.M.; Fert, A.; Nguyen Van Dau, F.; Pertroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant Magnetoresistance of (001)Fe/(001)Cr magnetic superlattices. Phys. Rev. Lett. 1988, 61, 2472–2475. [Google Scholar] [CrossRef] [PubMed]
- Binasch, G.; Grünberg, P.; Saurenbach, F.; Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 1989, 39, 4828–4830. [Google Scholar] [CrossRef] [PubMed]
- Alben, R.; Becker, J.J.; Chi, M.C. Random anisotropy in amorphous ferromagnets. J. Appl. Phys. 1978, 49, 1653–1658. [Google Scholar] [CrossRef]
- Herzer, G. Nanocrystalline soft magnetic materials. J. Magn. Magn. Mater. 1992, 112, 258–262. [Google Scholar] [CrossRef]
- Herzer, G. Anisotropies in soft magnetic nanocrystalline alloys. J. Magn. Magn. Mater. 2005, 294, 99–106. [Google Scholar] [CrossRef]
- Turchin, V.F. Diffraction of slow neutrons by stratified systems. At. Energy 1967, 22, 124–125. [Google Scholar] [CrossRef]
- Mezei, F. Novel polarized neutron devices: Supermirror ans spin component amplifier. Commun. Phys. 1976, 1, 81–85. [Google Scholar]
- Schärpf, O. Recent advances with supermirror polarizers. AIP Conf. Proc. 1982, 89, 182. [Google Scholar]
- Majkrzak, C.F.; Passell, L. Multilayer thin films as polarizing monochromators for neutrons. Acta Crystallogr. Sect. A 1985, 41, 41–48. [Google Scholar] [CrossRef]
- Mezei, F. Very high reflectivity supermirrors and their applications. Proc. SPIE 1988, 983, 10. [Google Scholar]
- Majkrzak, C.F.; Nunez, V.; Copley, J.R.D.; Ankner, J.F.; Greene, G.L. Supermirror transmission polarizers for neutrons. Proc. SPIE 1992, 1738, 90. [Google Scholar]
- Böni, P.; Clemens, D.; Senthil Kumar, M.; Pappas, C. Applications of remanent supermirror polarizers. Phys. B Condens. Matter 1999, 267–268, 320–327. [Google Scholar] [CrossRef]
- Høghøj, P.; Anderson, I.; Siebrecht, R.; Graff, W.; Ben-Saidane, K. Neutron polarizing Fe/Si mirrors at ILL. Phys. B Condens. Matter 1999, 267–268, 355–359. [Google Scholar] [CrossRef]
- Hino, M.; Hayashida, H.; Kitaguchi, M.; Kawabata, Y.; Takeda, M.; Maruyama, R.; Ebisawa, T.; Torikai, N.; Kume, T.; Tasaki, S. Development of large-m polarizing neutron supermirror fabricated by using ion beam sputtering instrument at KURRI. Phys. B Condens. Matter 2006, 385–386, 1187–1189. [Google Scholar] [CrossRef]
- Maruyama, R.; Yamazaki, D.; Okayasu, S.; Takeda, M.; Zettsu, N.; Nagano, M.; Yamamura, K.; Hayashida, H.; Soyama, K. Effect of Si interlayers on the magnetic and mechanical properties of Fe/Ge neutron-polarizing multilayer mirrors. J. Appl. Phys. 2012, 111, 063904. [Google Scholar] [CrossRef]
- Syromyatnikov, V.; Toperverg, B.; Deriglazov, V.; Schebetov, A.; Ebel, T.; Kampmann, R.; Wagner, R. Non-specular polarized neutron scattering from rough interfaces in periodic multilayered magnetic structures. Phys. B Condens. Matter 1997, 234–236, 475–476. [Google Scholar] [CrossRef]
- Syromyatnikov, V.G.; Menelle, A.; Toperverg, B.P.; Soroko, Z.N.; Schebetov, A.F. Off-specular polarised neutron scattering from rough interfaces in Co/Ti and Fe/Al multilayered structures. Phys. B Condens. Matter 1999, 267–268, 190–193. [Google Scholar] [CrossRef]
- Syromyatnikov, V.G.; Toperverg, B.P.; Siebrecht, R.; Menelle, A.; Pleshanov, N.K.; Pusenkov, V.M.; Schebetov, A.F.; Soroko, Z.N.; Ul’yanov, V.A. Observation of peculiarities in magnetic off-specular polarized neutron scattering from rough interfaces in Co/Ti periodic multilayer. Phys. B Condens. Matter 2000, 276–278, 700–701. [Google Scholar] [CrossRef]
- Kentzinger, E.; Rücker, U.; Toperverg, B.; Ott, F.; Brückel, T. Depth-resolved investigation of the lateral magnetic correlations in a gradient nanocrystalline multilayer. Phys. Rev. B 2008, 77, 104435. [Google Scholar] [CrossRef]
- Paul, A.; Teichert, A.; Krist, T.; Steitz, R. Substrate-stress-induced magnetic and nonmagnetic structural correlations in Fe/Si multilayers. J. Appl. Crystallogr. 2015, 48, 1023–1033. [Google Scholar] [CrossRef]
- Maruyama, R.; Bigault, T.; Wildes, A.R.; Dewhurst, C.D.; Soyama, K.; Courtois, P. Study of the in-plane magnetic structure of a layered system using polarized neutron scattering under grazing incidence geometry. Nucl. Instrum. Methods Phys. Res. A 2016, 819, 37–53. [Google Scholar] [CrossRef]
- Cubitt, R.; Fragneto, G. D17: The new reflectometer at the ILL. Appl. Phys. A 2002, 74 (Suppl. 1), S329–S331. [Google Scholar] [CrossRef]
- Saerbeck, T.; Cubitt, R.; Wildes, A.; Manzin, G.; Andersen, K.H.; Gutfreund, P. Recent upgrades of the neutron reflectometer D17 at ILL. J. Appl. Crystallogr. 2018, 51, 249–256. [Google Scholar] [CrossRef]
- Andersen, K.H.; Cubitt, R.; Humblot, H.; Jullien, D.; Petoukhov, A.; Tasset, F.; Schanzer, C.; Shah, V.R.; Wildes, A.R. The 3He polarizing filter on the neutron reflectometer D17. Phys. B Condens. Matter 2006, 385–386, 1134–1137. [Google Scholar] [CrossRef]
- Dewhurst, C.D. D33-a third small-angle neutron scattering instrument at the Institut Laue Langevin. Meas. Sci. Technol. 2008, 19, 034007. [Google Scholar] [CrossRef]
- Dewhurst, C.D. Modelling of wavelength cut-off filters and polarising mirrors in a neutron guide. Nucl. Instr. Meth. Phys. Res. A 2012, 683, 16–23. [Google Scholar] [CrossRef]
- Ankner, J.F.; Majkrzak, C.F.; Homma, H. Magnetic dead layer in Fe/Si multilayer: Profile refinement of polarized neutron reflectivity data. J. Appl. Phys. 1993, 73, 6436–6437. [Google Scholar] [CrossRef]
- Cubitt, R.; Saerbeck, T.; Campbell, R.A.; Barker, R.; Gutfreund, P. An improved algorithm for reducing reflectometry data involving divergent beams or non-flat samples. J. Appl. Crystallogr. 2015, 48, 2006–2011. [Google Scholar] [CrossRef]
- Björck, M.; Andersson, G. GenX: An extensible X-ray reflectivity refinement program utilizing differential evolution. J. Appl. Crystallogr. 2007, 40, 1174–1178. [Google Scholar] [CrossRef]
- Björck, M. Fitting with differential evolution: An introduction and evaluation. J. Appl. Crystallogr. 2011, 44, 1198–1204. [Google Scholar] [CrossRef]
- Parratt, L.G. Surface studies of solids by total reflection of X-rays. Phys. Rev. 1954, 95, 359–369. [Google Scholar] [CrossRef]
- Majkrzak, C.F.; Axe, J.D.; Böni, P. Magnetic structure of multiple bilayers of thin films of Fe and Ge. J. Appl. Phys. 1985, 57, 3657–3659. [Google Scholar] [CrossRef]
- Dufour, C.; Bruson, A.; George, B.; Marchal, G.; Mangin, P. Polarized neutron study of Fe/Si multilayers. Solid State Commun. 1989, 69, 963–968. [Google Scholar] [CrossRef]
- Boher, P.; Houdy, P.; Monkenbusch, M.; Penfold, J.; Eastoe, J.; Smith, D.J. RF-sputtered Fe/Ge multilayers for neutron polarizing monochromators. Proc. SPIE 1992, 1738, 176–189. [Google Scholar]
- Fullerton, E.E.; Mattson, J.E.; Lee, S.R.; Sowers, C.H.; Huang, Y.Y.; Felcher, G.; Bader, S.D. Non-oscillatory antiferromagnetic coupling in sputtered Fe/Si superlattices. J. Magn. Magn. Mater. 1992, 117, L301–L306. [Google Scholar] [CrossRef]
- Maruyama, R.; Yamazaki, D.; Akutsu, K.; Hanashima, T.; Miyata, N.; Aoki, H.; Takeda, M.; Soyama, K. Development of high-polarization Fe/Ge neutron-polarizing supermirror: Possibility of fine-tuning of scattering length density in ion beam sputtering. Nucl. Instrum. Methods Phys. Res. A 2018, 888, 70–78. [Google Scholar] [CrossRef]
- Zabel, H.; Theris-Bröhl, K.; Toperverg, B.P. Polarized neutron reflectivity and scattering from magnetic nanostructures and spintronic materials. In Handbook of Magnetism and Advanced Magnetic Materials; Kronmüller, H., Parkin, S., Eds.; John Wiely & Sons, Ltd.: Chichester, UK, 2007; pp. 1237–1307. [Google Scholar]
- Toperverg, B.P. Off-specular polarized neutron scattering from magnetic fluctuations in thin films and multilayers. Appl. Phys. A 2002, 74 (Suppl. 1), S1560–S1562. [Google Scholar] [CrossRef]
- Kentzinger, E.; Rücker, U.; Toperverg, B.; Brückel, T. Determination of the magnetic fluctuations in an Fe/Cr/Fe trilayer exhibiting a neutron resonance state. Phys. B Condens. Matter 2003, 335, 89–94. [Google Scholar] [CrossRef]
- Holý, V.; Baumbach, T. Nonspecular X-ray reflection from rough multilayers. Phys. Rev. B 1994, 49, 10668–10676. [Google Scholar] [CrossRef]
- Renaud, G.; Lazzari, R.; Leroy, F. Probing surface and interface morphology with grazing incidence small angle X-ray scattering. Surf. Sci. Rep. 2009, 64, 255–380. [Google Scholar] [CrossRef]
- Maruyama, R.; Bigault, T.; Wildes, A.R.; Dewhurst, C.D.; Saerbeck, T.; Honecker, D.; Yamazaki, D.; Soyama, K.; Courtois, P. Accessible length scale of the in-plane structure in polarized neutron off-specular and grazing-incidence small-angle scattering measurements. J. Phys. Conf. Ser. 2017, 862, 012017. [Google Scholar] [CrossRef]
- Herzer, G. Nanocrystalline soft magnetic alloys. In Handbook of Magnetic Materials; Buschow, K.H.J., Ed.; Elsevier: Amsterdam, The Netherlands, 1997; pp. 415–462. [Google Scholar]
- Herzer, G. Grain size dependence of coercivity and permeability in nanocrystalline ferromagnets. IEEE Trans. Magn. 1990, 26, 1397–1402. [Google Scholar] [CrossRef]
- Herzer, G. Magnetization process in nanocrystalline ferromagnetets. Mater. Sci. Eng. A 1991, 133, 1–5. [Google Scholar] [CrossRef]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Chikazumi, S. Physics of Magnetism; John Wiley & Sons: New York, NY, USA, 1964. [Google Scholar]
| Layers | Thickness | Roughness | Nuclear SLD | Magnetic SLD |
|---|---|---|---|---|
| (nm) | (nm) | ( fm/nm) | ( fm/nm) | |
| Si | ||||
| Fe | ||||
| Fe | (I) , (II) , (III) , | |||
| (IV) , (V) , (VI) | ||||
| Fe |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maruyama, R.; Bigault, T.; Saerbeck, T.; Honecker, D.; Soyama, K.; Courtois, P. Coherent Magnetization Rotation of a Layered System Observed by Polarized Neutron Scattering under Grazing Incidence Geometry. Crystals 2019, 9, 383. https://doi.org/10.3390/cryst9080383
Maruyama R, Bigault T, Saerbeck T, Honecker D, Soyama K, Courtois P. Coherent Magnetization Rotation of a Layered System Observed by Polarized Neutron Scattering under Grazing Incidence Geometry. Crystals. 2019; 9(8):383. https://doi.org/10.3390/cryst9080383
Chicago/Turabian StyleMaruyama, Ryuji, Thierry Bigault, Thomas Saerbeck, Dirk Honecker, Kazuhiko Soyama, and Pierre Courtois. 2019. "Coherent Magnetization Rotation of a Layered System Observed by Polarized Neutron Scattering under Grazing Incidence Geometry" Crystals 9, no. 8: 383. https://doi.org/10.3390/cryst9080383
APA StyleMaruyama, R., Bigault, T., Saerbeck, T., Honecker, D., Soyama, K., & Courtois, P. (2019). Coherent Magnetization Rotation of a Layered System Observed by Polarized Neutron Scattering under Grazing Incidence Geometry. Crystals, 9(8), 383. https://doi.org/10.3390/cryst9080383







