Field-Independent Features in the Magnetization and Specific Heat of Sm3Co4Ge13
Abstract
1. Introduction
2. Experimental Methods
3. Results
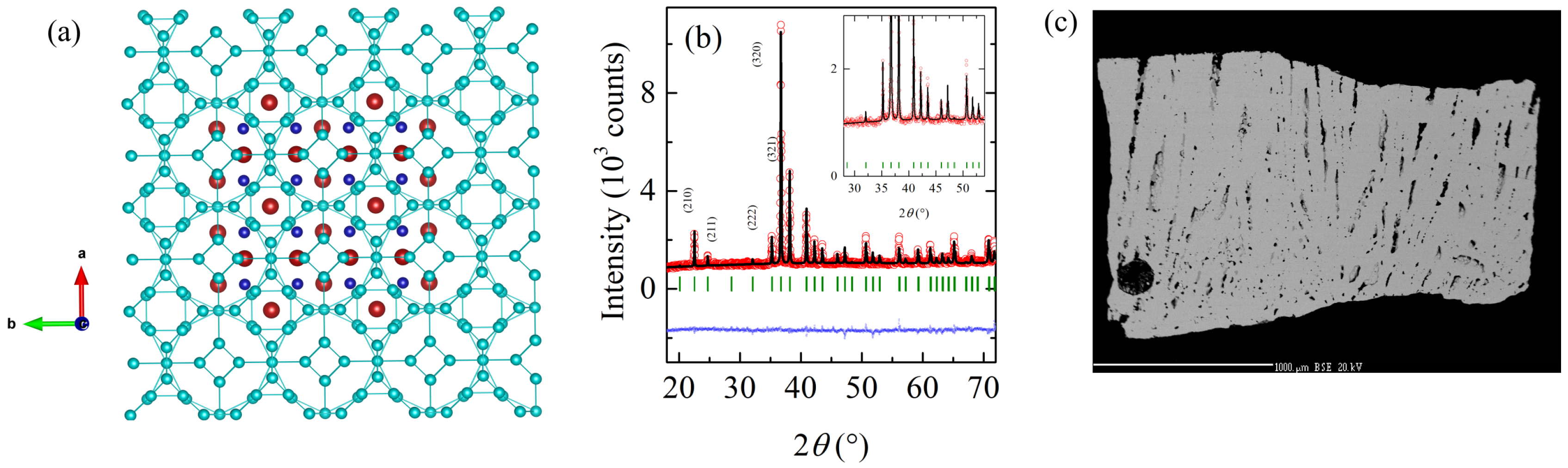
3.1. Crystal Structure
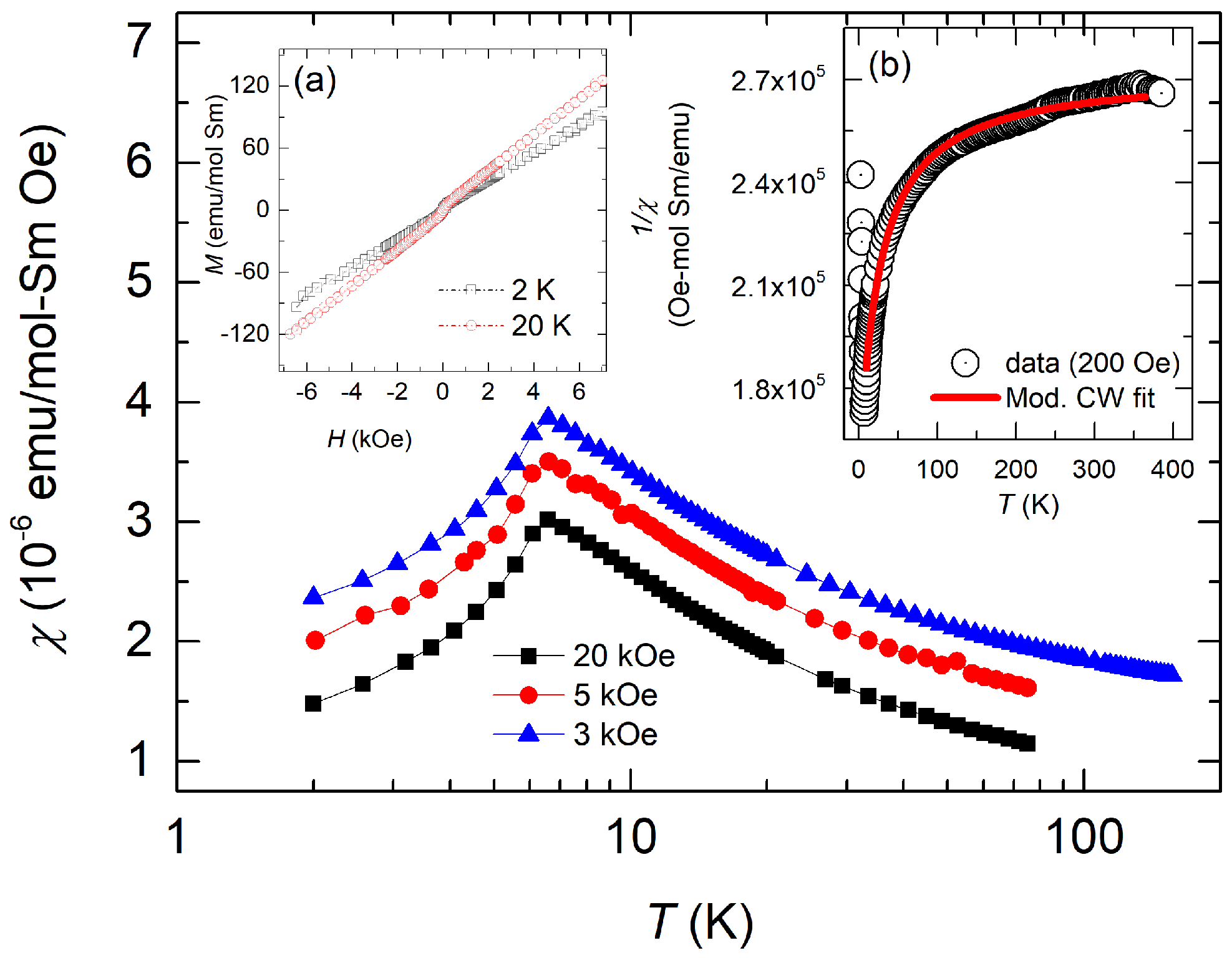
3.2. Magnetization
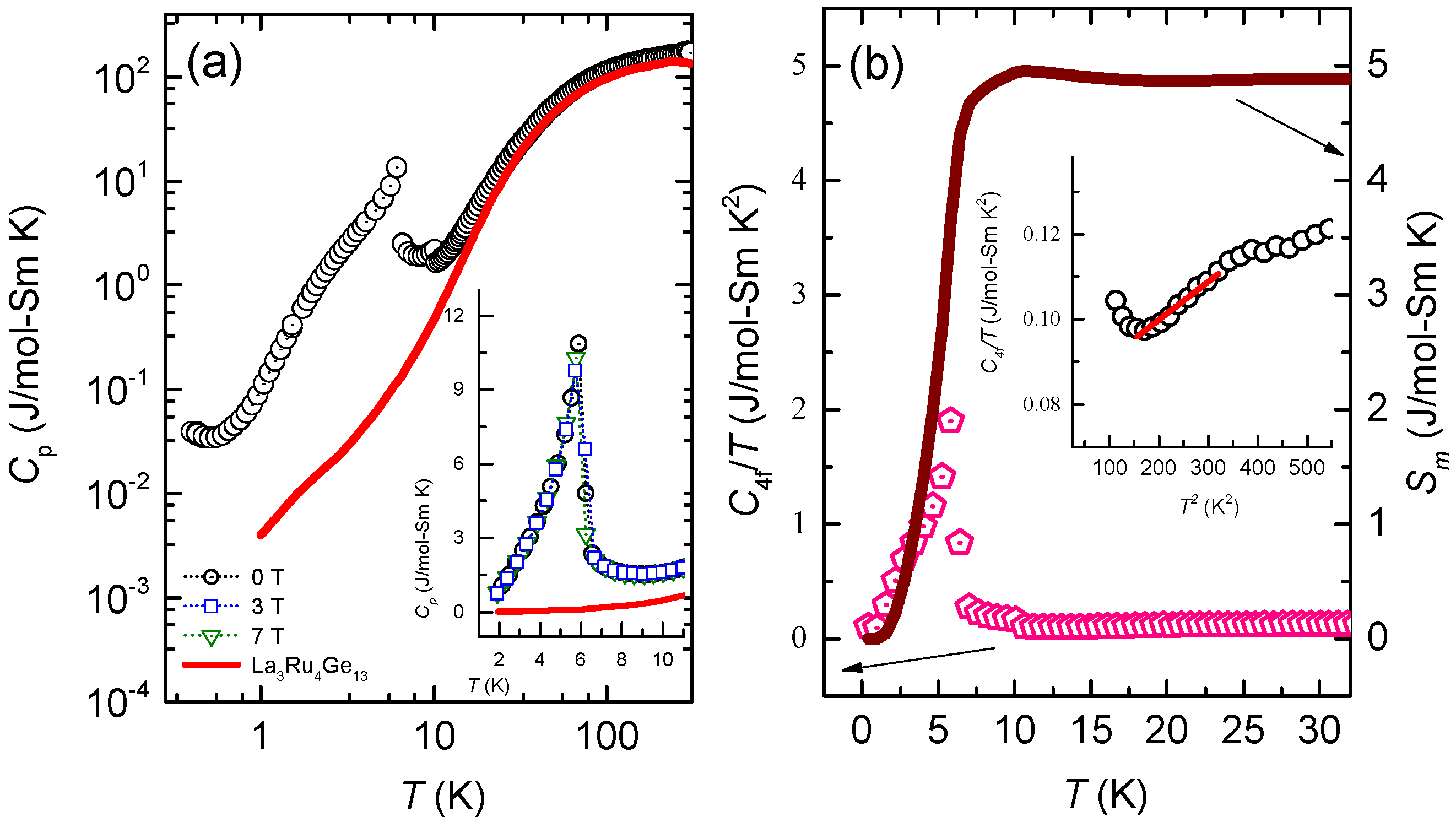
3.3. Specific Heat
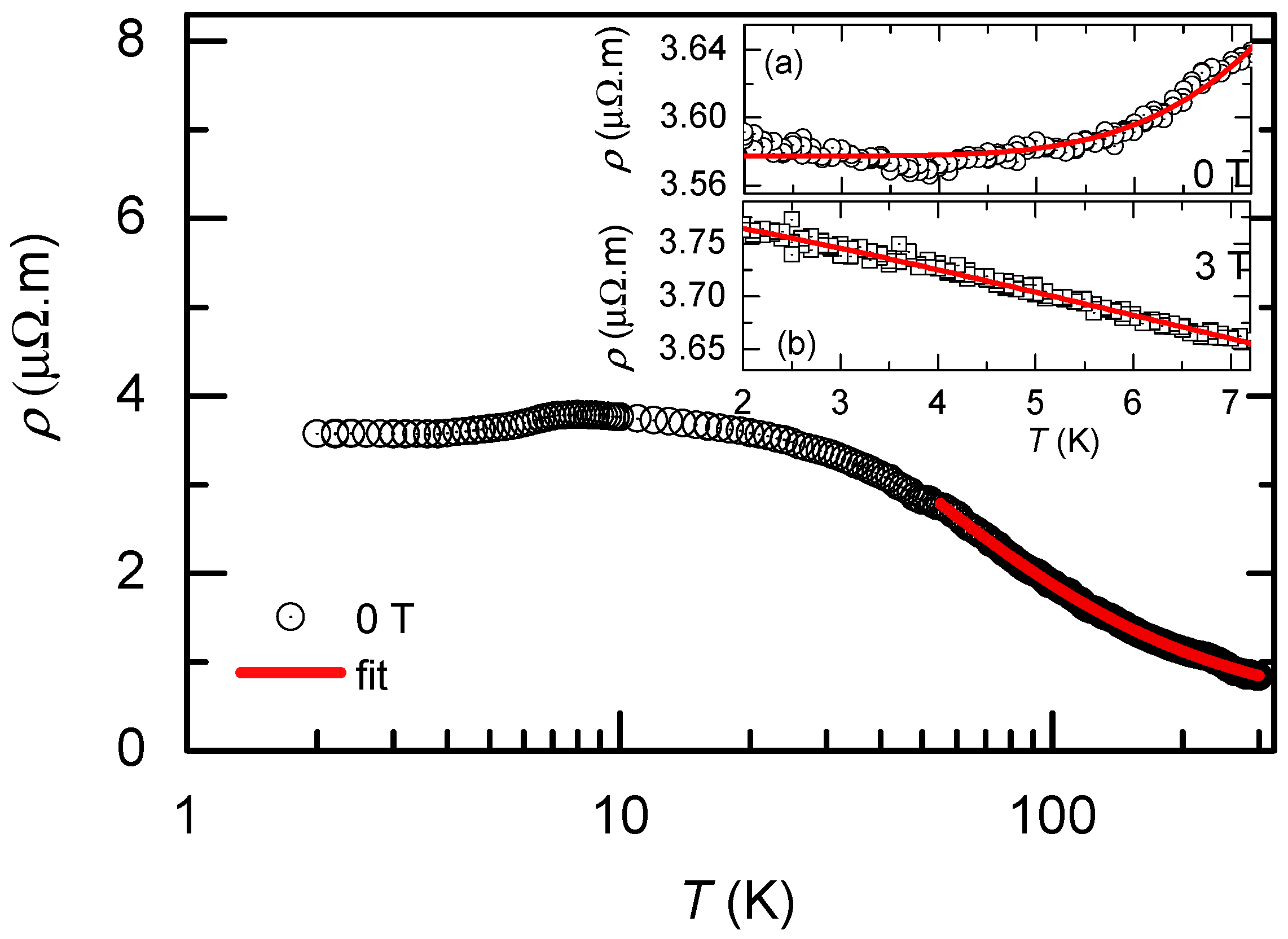
3.4. Electrical Transport
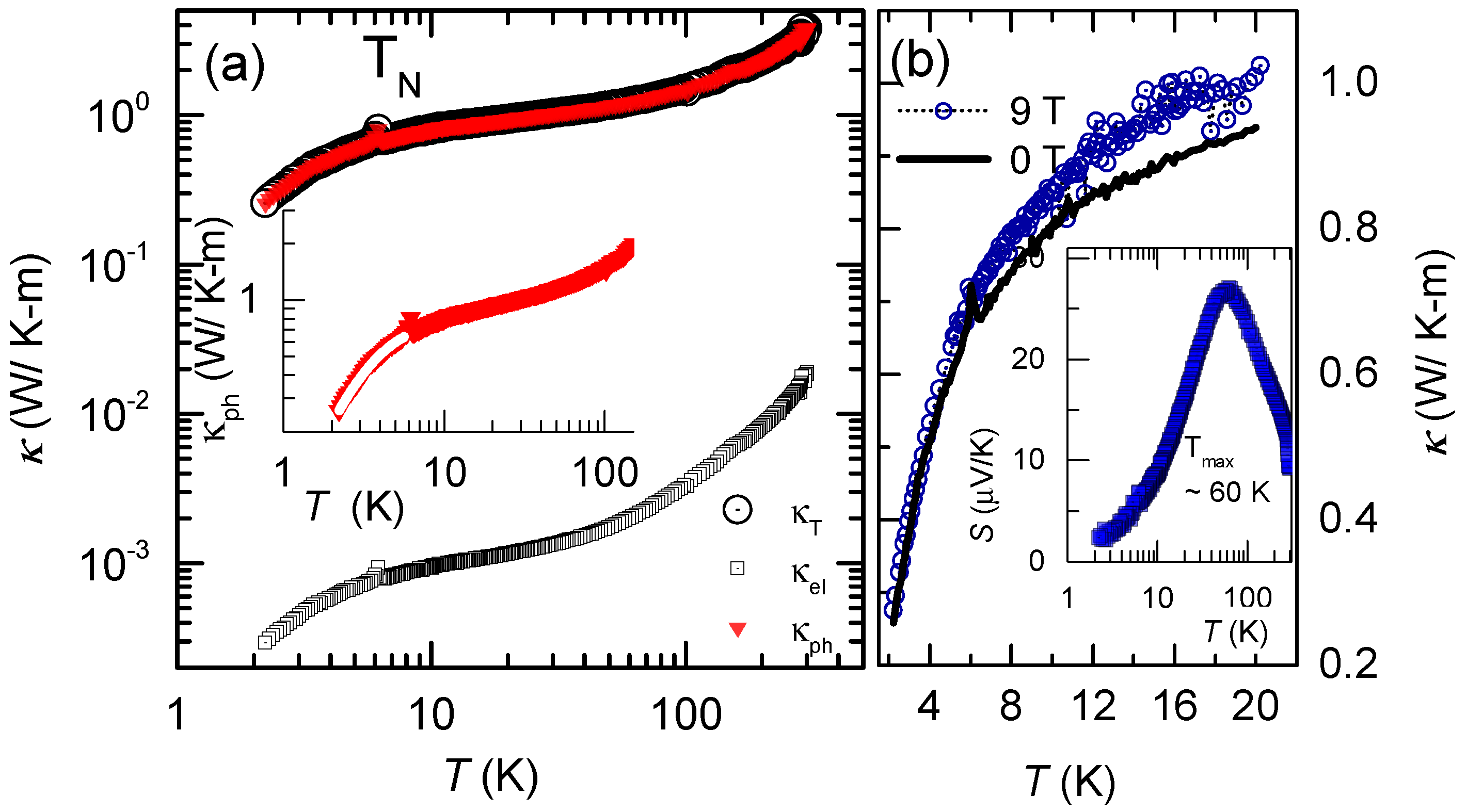
3.5. Thermal Transport
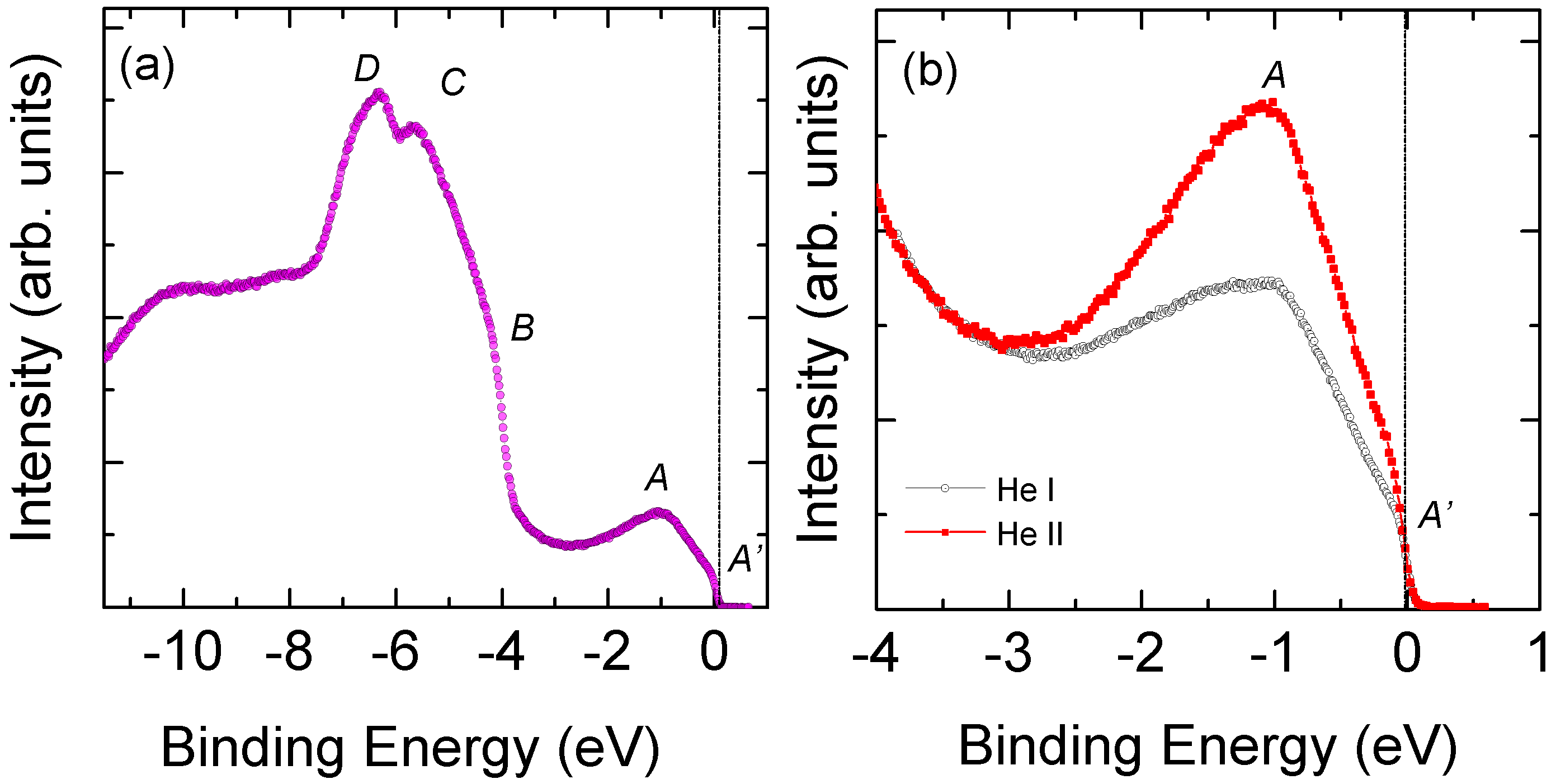
3.6. Photoemission
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| EPMA | Electron microprobe analysis |
| ZFC | Zero field-cooled |
| FC | Field-cooled |
| PPMS | Physical property measurement system |
| PXRD | Powder X ray diffraction |
| CEF | Crystalline electric field |
| DOS | Density of states |
References
- Collave, J.R.; Borges, H.A.; Ramos, S.M.; Hering, E.N.; Fontes, M.B.; Baggio-Saitovitch, E.; Mendonça-Ferreira, L.; Bittar, E.M.; Pagliuso, P.G. Heavy fermion Ce3Co4Sn13 compound under pressure. J. Appl. Phys. 2015, 117, 17E307. [Google Scholar] [CrossRef]
- Ghosh, K.; Ramakrishnan, S.; Dhar, S.K.; Malik, S.K.; Chandra, G.; Pecharsky, V.K.; Gschneidner, K.A., Jr.; Hu, Z.; Yelon, W.B. Crystal structures and low-temperature behaviors of the heavy-fermion compounds CeRuGe3 and Ce3Ru4Ge13 containing both trivalent and tetravalent cerium. Phys. Rev. B 1995, 52, 7267. [Google Scholar] [CrossRef]
- Gumeniuk, R.; Akselrud, L.; Kvashnina, K.O.; Schnelle, W.; Tsirlin, A.A.; Curfs, C.; Rosner, H.; Schöneich, M.; Burkhardt, U.; Schwarz, U.; et al. Ca3Pt4+xGe13−y and Yb3Pt4Ge13: New derivatives of the Pr3Rh4Sn13 structure type. Dalton Trans. 2012, 41, 6299–6309. [Google Scholar] [CrossRef] [PubMed]
- Gumeniuk, R.; Nicklas, M.; Akselrud, L.; Schnelle, W.; Schwarz, U.; Tsirlin, A.A.; Leithe-Jasper, A.; Grin, Y. Y3Pt4Ge13: A superconductor with a noncentrosymmetric crystal structure. Phys. Rev. B 2013, 87, 224502. [Google Scholar] [CrossRef]
- Remeika, J.P.; Espinosa, G.P.; Cooper, A.S.; Barz, H.; Rowell, J.M.; McWhan, D.B.; Vandenberg, J.M.; Moncton, D.E.; Fisk, Z.; Woolf, L.D.; et al. A new family of ternary intermetallic superconducting/magnetic stannides. Solid State Commun. 1980, 34, 923–926. [Google Scholar] [CrossRef]
- Hodeau, J.L.; Chenavas, J.; Marezio, M.; Remeika, J.P. The crystal structure of SnYb3Rh4Sn12, a new ternary superconducting stannide. Solid State Commun. 1980, 36, 839–845. [Google Scholar] [CrossRef]
- Hodeau, J.L.; Marezio, M.; Remeika, J.P.; Chen, C.H. Structural distortion in the primitive cubic phase of the superconducting/magnetic ternary rare-earth rhodium stannides. Solid State Commun. 1982, 42, 97–102. [Google Scholar] [CrossRef]
- Vandenberg, J.M. The crystallography of new ternary compounds in the system rare-earth-rhodium-tin. Mater. Res. Bull. 1980, 15, 835–847. [Google Scholar] [CrossRef]
- Venturini, G.; Meot-Meyer, M.; Malaman, B.; Roques, B. De nouvelles séries de germaniures, isotypes de Yb3Rh4Sn13] et BaNiSn3, dans les systémes ternaires TR3T4Ge13 oú TR est un élément des terres rares et T ≡ Co, Rh, Ir, Ru, Os. J. Less Common Met. 1985, 113, 197–204. [Google Scholar] [CrossRef]
- Venturini, G.; Meot-Meyer, M.; Mareche, J.F.; Malaman, B.; Roques, B. De nouveaux isotypes de U2Co3Si5 ou Lu2Co3Si5 dans les systems RT-Ge (R = elements des terres rares; T = Ru, Co, Rh, Ir). Supraconductivite de Y2Ir3Ge5. Mater. Res. Bull. 1986, 21, 33–39. [Google Scholar] [CrossRef]
- Niepmann, D.; Pöttgen, R.; Poduska, K.M.; DiSalvo, F.J.; Trill, H.; Mosel, B.D. Structure and properties of the stannides CeAuSn, Ce3Rh4Sn13, and Ce3Ir4Sn13. Z. Natur. 2001, 56b, 1–8. [Google Scholar] [CrossRef]
- Aoki, Y.; Sugawara, H.; Hisatomo, H.; Sato, H. Novel Kondo behaviors realized in the filled skutterudite structure. J. Phys. Soc. Jpn. 2005, 74, 209–221. [Google Scholar] [CrossRef]
- Nair, H.S.; RameshKumar, K.; Britz, D.; Ghosh, S.K.; Reinke, C.; Strydom, A.M. Field-insensitive heavy fermion features and phase transition in the caged-structure quasi-skutterudite Sm3Ru4Ge13. J. Alloy. Compd. 2016, 669, 254–261. [Google Scholar] [CrossRef]
- Higashinaka, R.; Maruyama, T.; Nakama, A.; Miyazaki, R.; Aoki, Y.; Sato, H. Unusual field-insensitive phase transition and Kondo behavior in SmTi2Al20. J. Phys. Soc. Jpn. 2011, 80, 093703. [Google Scholar] [CrossRef]
- Yamada, A.; Higashinaka, R.; Miyazaki, R.; Fushiya, K.; Matsuda, T.D.; Aoki, Y.; Fujita, W.; Harima, H.; Sato, H. Anomalously field-insensitive correlated electron behaviors in SmTa2Al20. J. Phys. Soc. Jpn. 2013, 82, 123710. [Google Scholar] [CrossRef]
- Sakai, A.; Nakatsuji, S. Strong valence fluctuation effects in SmTr2Al20 (Tr = Ti, V, Cr). Phys. Rev. B 2011, 84, 201106. [Google Scholar] [CrossRef]
- Otomo, Y.; Iwasa, K.; Suyama, K.; Tomiyasu, K.; Sagayama, H.; Sagayama, R.; Nakao, H.; Kumai, R.; Murakami, Y. Chiral crystal-structure transformation of R3Co4Sn13 (R = La and Ce). Phys. Rev. B 2016, 94, 075109. [Google Scholar] [CrossRef]
- Rodriguez-Carvajal, J. LLB, CEA-CNRS, France. 2010. Available online: http://www.ill.eu/sites/fullprof/ (accessed on 11 June 2019).
- Miraglia, S.; Hodeau, J.L.; Marezio, M.; Laviron, C.; Ghedira, M.; Espinosa, G.P. Nature of the structural distortion and of the chemical bonding in SnM3Rh4Sn12 (M = La, Gd, Yb, Ca, Sr, and Th). J. Solid State Chem. 1986, 63, 358–368. [Google Scholar] [CrossRef]
- Nair, H.S.; Ghosh, S.K.; Ramesh Kumar, K.; Strydom, A.M. Double-phase transition and giant positive magnetoresistance in the quasi-skutterudite Gd3Ir4Sn13. J. Appl. Phys. 2016, 119, 123901. [Google Scholar] [CrossRef]
- Zhong, G.; Lei, X.; Mao, J. Chemical bonding, electronic, and magnetic properties of R3Co4Sn13 intermetallics (R = La, Ce, Sm, Gd, and Tb): Density functional calculations. Phys. Rev. B 2009, 79, 094424. [Google Scholar] [CrossRef]
- Kaczorowski, D.; Gofryk, K.; Romaka, L.; Mudryk, Y.; Konyk, M.; Rogl, P. Magnetic and electrical transport properties of RE9Ni24Sn49 compounds (RE = Y, Ce, Pr, Sm and Tb). Intermetallics 2005, 13, 484–489. [Google Scholar] [CrossRef]
- Yuhasz, W.M.; Frederick, N.A.; Ho, P.C.; Butch, N.P.; Taylor, B.J.; Sayles, T.A.; Maple, M.B.; Betts, J.B.; Lacerda, A.H.; Rogl, P. Heavy-fermion behavior, crystalline electric field effects, and weak ferromagnetism in SmOs4Sb12. Phys. Rev. B 2005, 71, 104402. [Google Scholar] [CrossRef]
- Joshi, D.A.; Nagalakshmi, R.; Kulkarni, R.; Dhar, S.K.; Thamizhavel, A. Crystal growth and anisotropic magnetic properties of RAg2Ge2 (R = Pr, Nd and Sm) single crystals. Physica B 2009, 404, 2988–2991. [Google Scholar] [CrossRef]
- Bauer, E.; Paul, C.; Della Mea, M.; Hilscher, G.; Michor, H.; Reissner, M.; Steiner, W.; Grytsiv, A.; Rogl, P.; Scheidt, E.W. Crystal field effects and thermoelectric properties of PrFe4Sb12 skutterudite. Phys. Rev. B 2002, 66, 214421. [Google Scholar] [CrossRef]
- Sales, B.C.; Mandrus, D.; Williams, R.K. Filled skutterudite antimonides: a new class of thermoelectric materials. Science 1996, 272, 1325. [Google Scholar] [CrossRef] [PubMed]
- Avila, M.A.; Suekuni, K.; Umeo, K.; Fukuoka, H.; Yamanaka, S.; Takabatake, T. Ba8Ga16Sn30 with type-I clathrate structure: Drastic suppression of heat conduction. Appl. Phys. Lett. 2008, 92, 041901. [Google Scholar] [CrossRef]
- Young, D.; Mastronardi, K.; Khalifah, P.; Wang, C.C.; Cava, R.J.; Ramirez, A.P. Ln3Au3Sb4: Thermoelectrics with low thermal conductivity. Appl. Phys. Lett. 1999, 74, 3999–4001. [Google Scholar] [CrossRef]
- Schmitt, D.C.; Haldolaarachchige, N.; Xiong, Y.; Young, D.P.; Jin, R.; Chan, J.Y. Probing the lower limit of lattice thermal conductivity in an ordered extended solid: Gd117Co56Sn112, a phonon glass–electron crystal system. J. Am. Chem. Soc. 2012, 134, 5965–5973. [Google Scholar] [CrossRef] [PubMed]
- Paschen, S.; Carrillo-Cabrera, W.; Bentien, A.; Tran, V.H.; Baenitz, M.; Grin, Y.; Steglich, F. Structural, transport, magnetic, and thermal properties of Eu8Ga16Ge30. Phys. Rev. B 2001, 64, 214404. [Google Scholar] [CrossRef]
- Prokofiev, A.; Sidorenko, A.; Hradil, K.; Ikeda, M.; Svagera, R.; Waas, M.; Winkler, H.; Neumaier, K.; Paschen, S. Thermopower enhancement by encapsulating cerium in clathrate cages. Nat. Mater. 2013, 12, 1096–1101. [Google Scholar] [CrossRef] [PubMed]
- Nolas, G.S.; Cohn, J.L.; Slack, G.A. Effect of partial void filling on the lattice thermal conductivity of skutterudites. Phys. Rev. B 1998, 58, 164. [Google Scholar] [CrossRef]
- Ślebarski, A.; Goraus, J.; Witas, P.; Kalinowski, L.; Fijałkowski, M. Study of d-electron correlations in skutterudite-related Ce3M4Sn13 (M = Co, Ru, and Rh). Phys. Rev. B 2015, 91, 035101. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds SmCoGe and LaRhSn are available from the authors. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nair, H.S.; Kumar, K.R.; Sahu, B.; Xhakaza, S.P.; Mishra, P.; Samal, D.; Ghosh, S.K.; Sekhar, B.R.; Strydom, A.M. Field-Independent Features in the Magnetization and Specific Heat of Sm3Co4Ge13. Crystals 2019, 9, 322. https://doi.org/10.3390/cryst9060322
Nair HS, Kumar KR, Sahu B, Xhakaza SP, Mishra P, Samal D, Ghosh SK, Sekhar BR, Strydom AM. Field-Independent Features in the Magnetization and Specific Heat of Sm3Co4Ge13. Crystals. 2019; 9(6):322. https://doi.org/10.3390/cryst9060322
Chicago/Turabian StyleNair, Harikrishnan S., K. Ramesh Kumar, Baidyanath Sahu, Sindisiwe P. Xhakaza, Pramita Mishra, Debkanta Samal, Sarit K. Ghosh, Biju R. Sekhar, and André M. Strydom. 2019. "Field-Independent Features in the Magnetization and Specific Heat of Sm3Co4Ge13" Crystals 9, no. 6: 322. https://doi.org/10.3390/cryst9060322
APA StyleNair, H. S., Kumar, K. R., Sahu, B., Xhakaza, S. P., Mishra, P., Samal, D., Ghosh, S. K., Sekhar, B. R., & Strydom, A. M. (2019). Field-Independent Features in the Magnetization and Specific Heat of Sm3Co4Ge13. Crystals, 9(6), 322. https://doi.org/10.3390/cryst9060322



