Elasticity of Phases in Fe-Al-Ti Superalloys: Impact of Atomic Order and Anti-Phase Boundaries
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
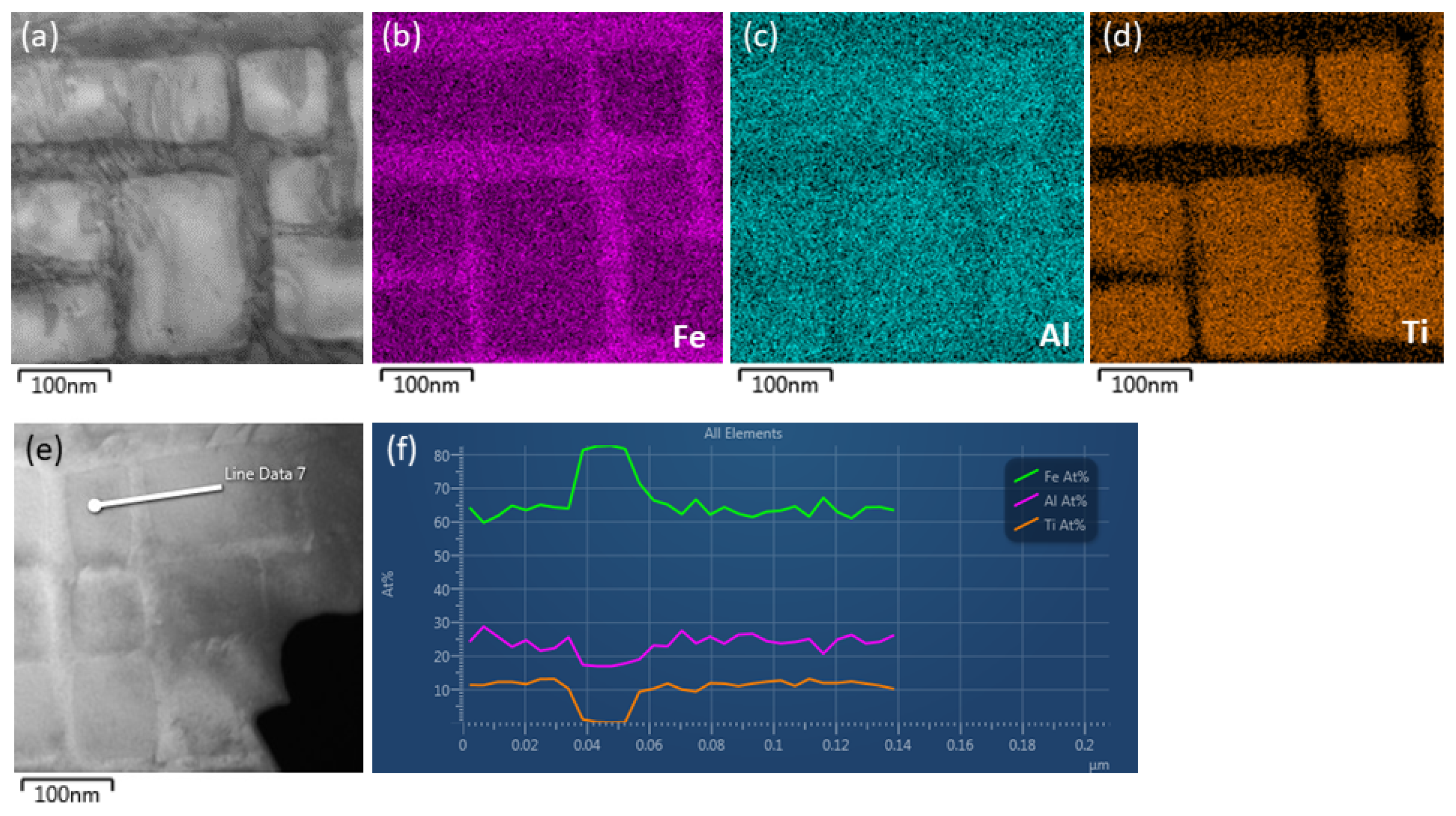
3.1. Transmission Electron Microscopy of Fe-Al-Ti Phases
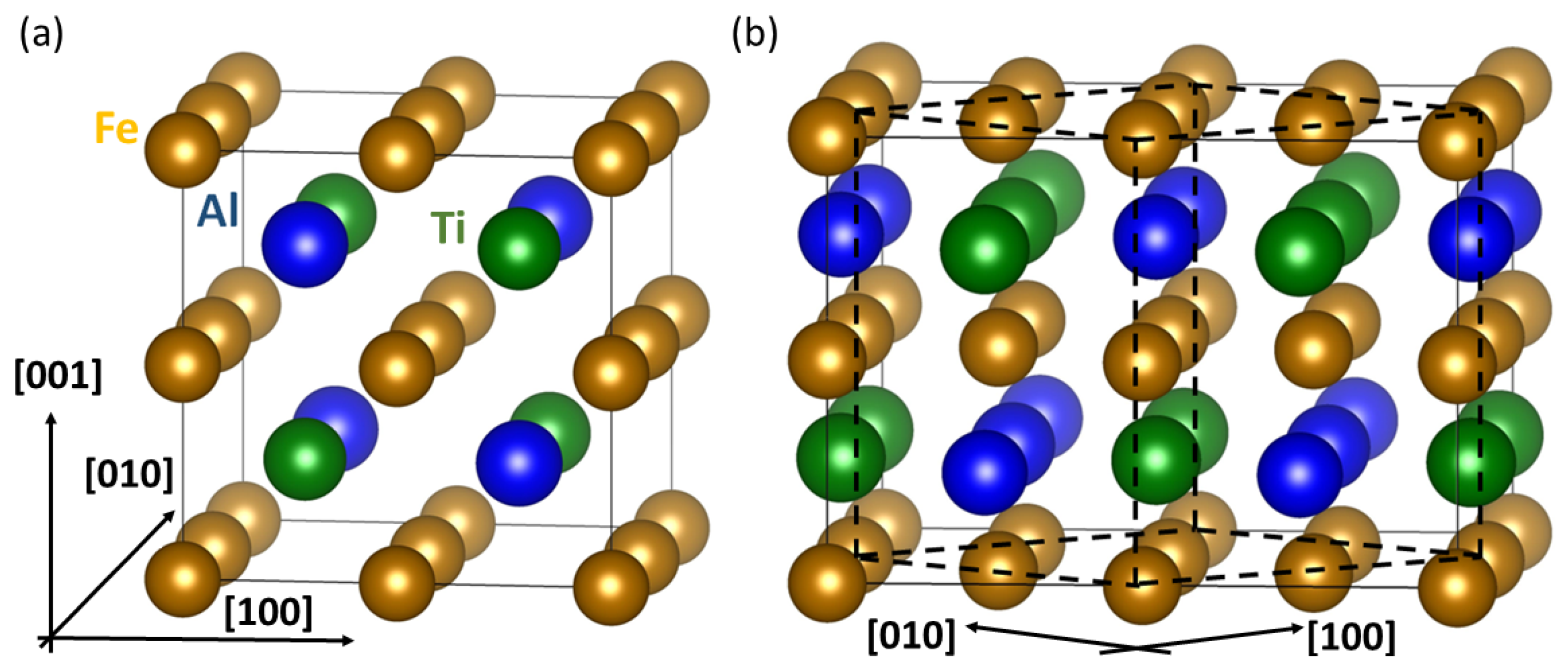
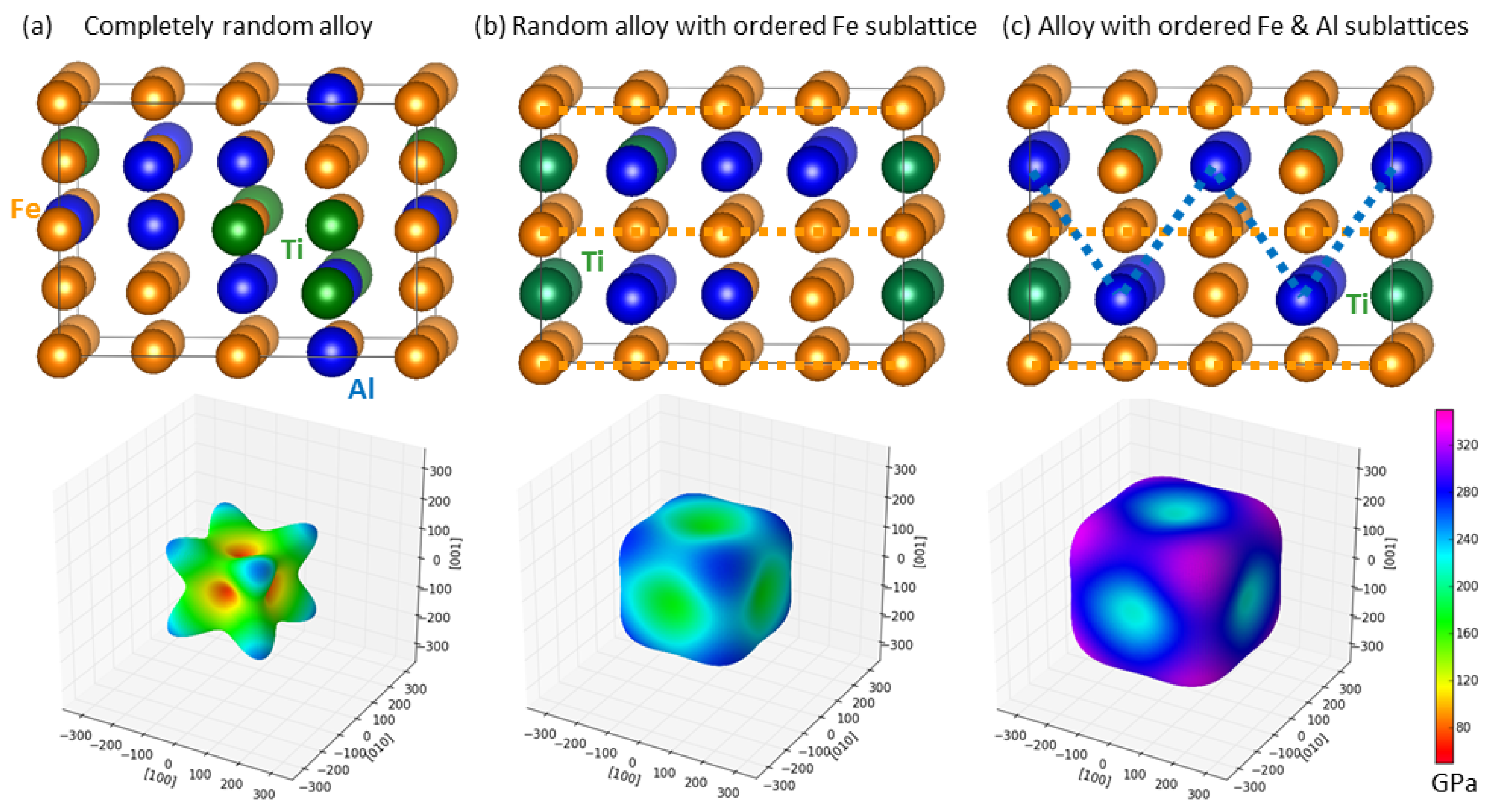
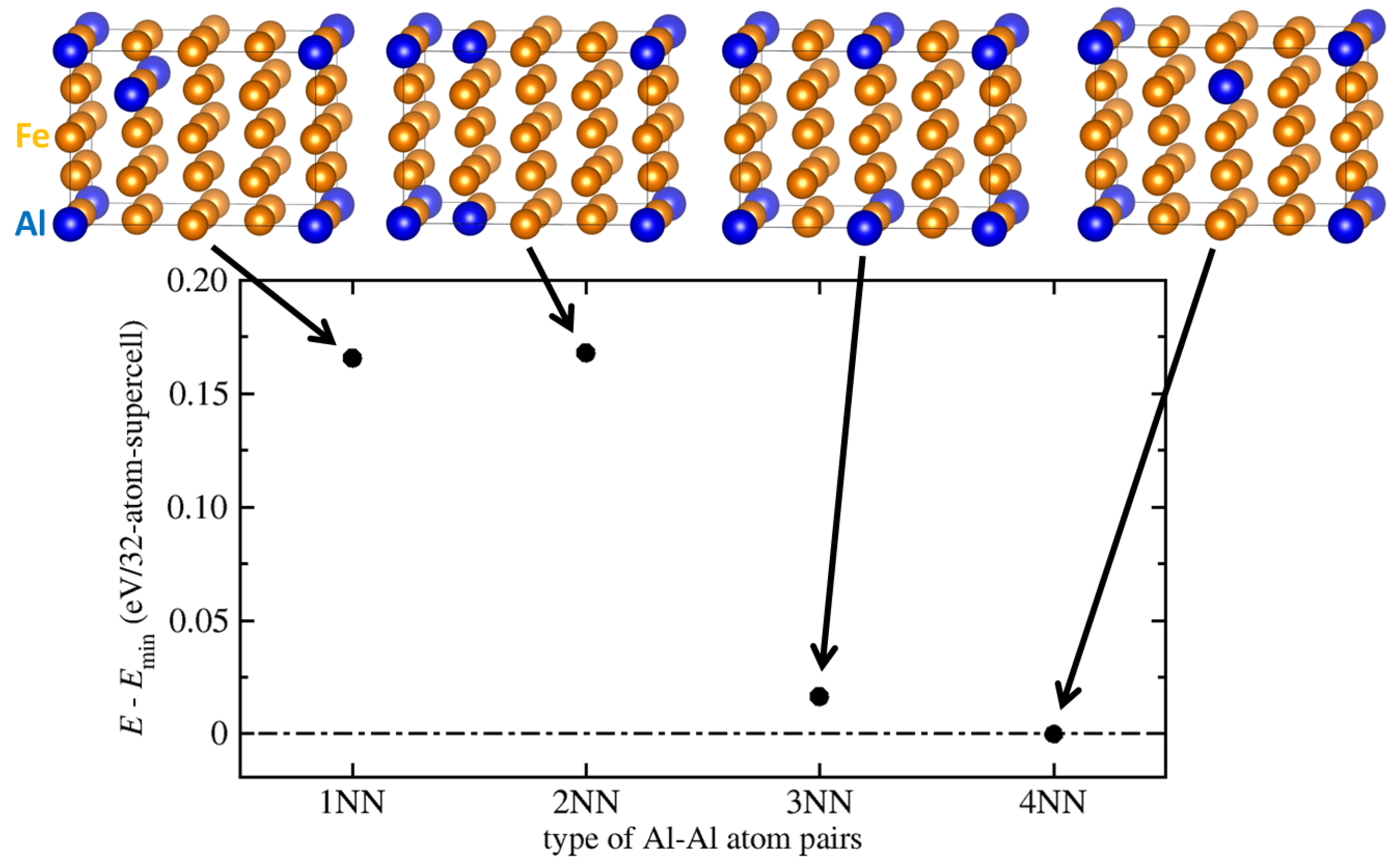
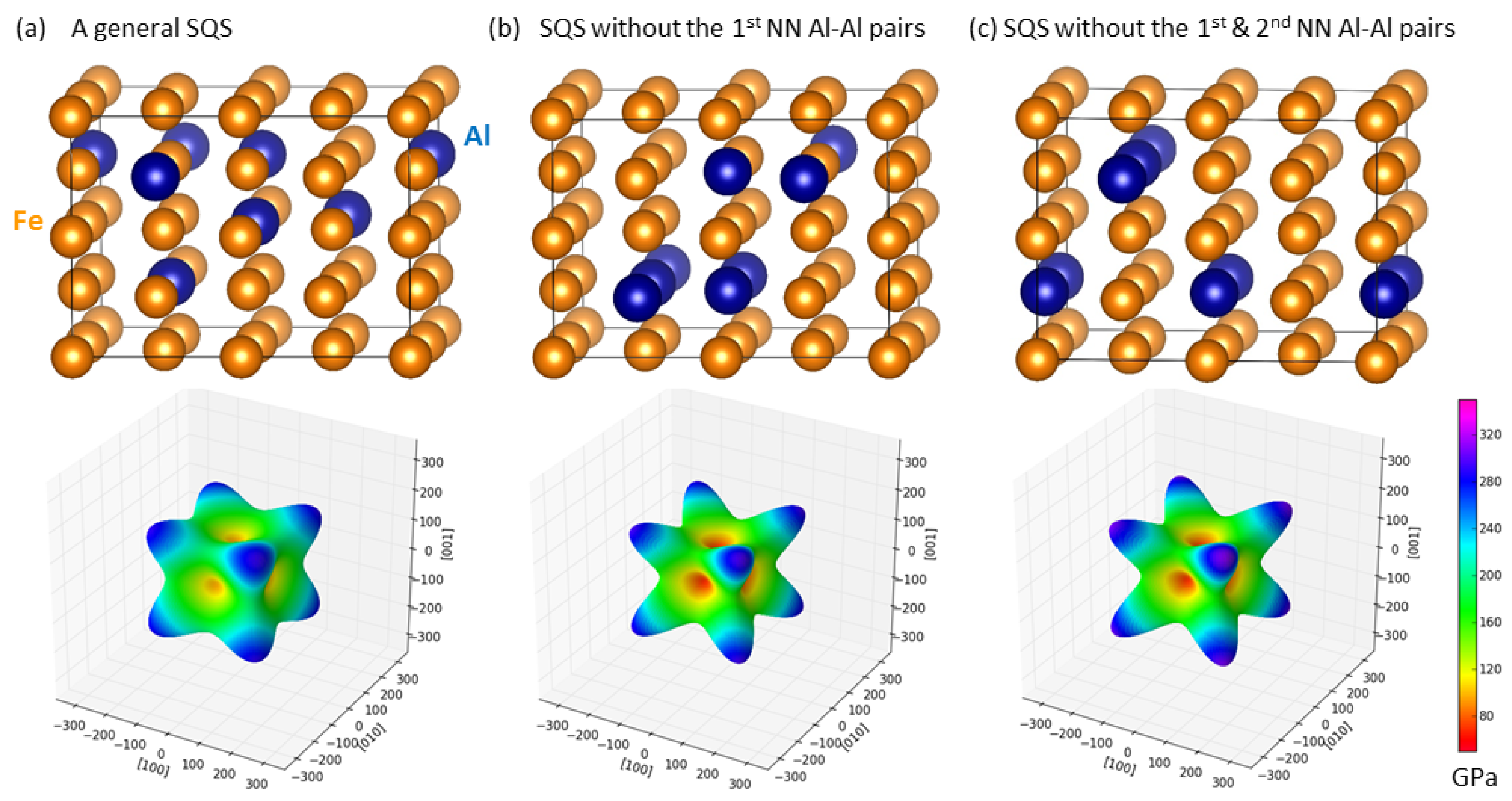
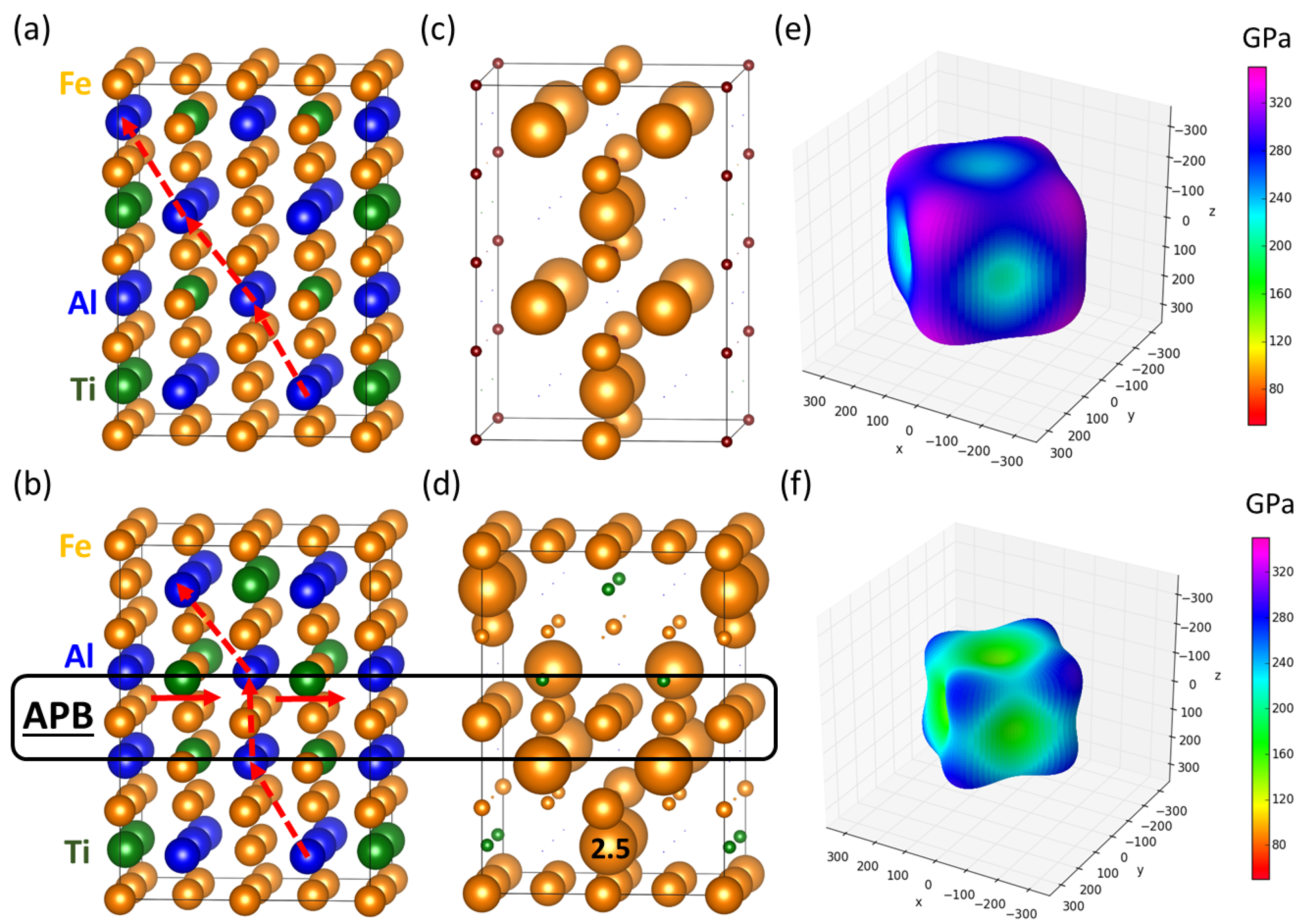
3.2. Theoretical Calculations of Thermodynamic and Elastic Properties
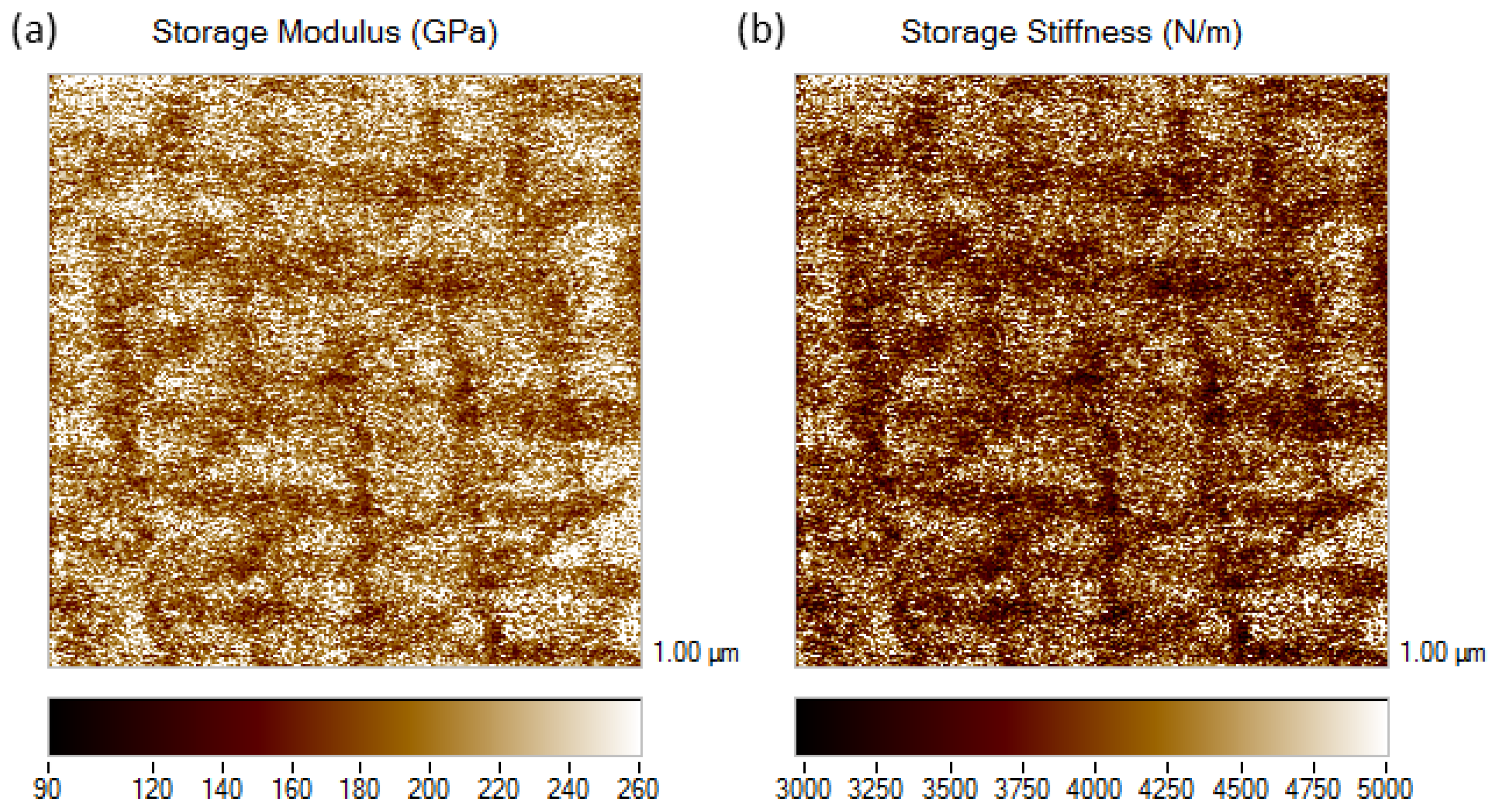
3.3. Nano-Scale Dynamical Mechanical Analysis of Fe-Al-Ti Phases
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Gorzel, A.; Palm, M.; Sauthoff, G. Constitution-based alloy selection for the screening of intermetallic Ti-Al-Fe alloys. Z. Metallkd. 1999, 90, 64–70. [Google Scholar]
- Palm, M. Concepts derived from phase diagram studies for the strengthening of Fe-Al-based alloys. Intermetallics 2005, 13, 1286–1295. [Google Scholar] [CrossRef]
- Brady, M.P.; Smialek, J.L.; Brindley, W.J. Oxidation-resistant Ti-Al-Fe alloy for diffusion barrier coatings. U.S. Patent No. 5,776,617, 7 July 1998. [Google Scholar]
- Dew-Hughes, D.; Kaufman, L. Ternary phase diagrams of the manganese-titanium-iron and the aluminum-titanium-iron systems: A comparison of computer calculations with experiment. Calphad 1979, 3, 175–203. [Google Scholar] [CrossRef]
- Raghavan, V. Al-Fe-Ti (aluminum-iron-titanium). J. Phase Equilib. 1993, 14, 617–618. [Google Scholar] [CrossRef]
- Raghavan, V. Al-Fe-Ti (Aluminum-Iron-Titanium). J. Phase Equilib. 2002, 23, 367–374. [Google Scholar] [CrossRef]
- Krein, R.; Palm, M.; Heilmaier, M. Characterization of microstructures, mechanical properties, and oxidation behavior of coherent A2+L21 Fe-Al-Ti. J. Mater. Res. 2009, 24, 3412–3421. [Google Scholar] [CrossRef]
- Capdevila, C.; Aranda, M.M.; Rementeria, R.; Chao, J.; Urones-Garrote, E.; Aldazabal, J.; Miller, M.K. Strengthening by intermetallic nanoprecipitation in Fe-Cr-Al-Ti alloy. Acta Mater. 2016, 107, 27–37. [Google Scholar] [CrossRef]
- Nakata, J.; Terada, Y.; Takizawa, S.; Ohkubo, K.; Mohri, T.; Suzuki, T. Thermal conductivity in X2YZ Heusler type intermetallic compounds. Mater. Trans. JIM 1996, 37, 442–447. [Google Scholar] [CrossRef]
- Kainuma, R.; Urushiyama, K.; Ishikawa, K.; Jia, C.; Ohnuma, I.; Ishida, K. Ordering and phase separation in bcc aluminides of the Ni-Fe-Al-Ti system. Mater. Sci. Eng. Struct. Mater. Prop. Microstruct. Process. 1997, 240, 235–244. [Google Scholar] [CrossRef]
- Fomina, K.A.; Marchenkov, V.V.; Shreder, E.I.; Weber, H.W. Electrical and optical properties of X2YZ (X = Co, Fe; Y = Cr, Mn, Ti; Z = Ga, Al, Si) Heusler alloys. Solid State Phenom. 2011, 168–169, 545–548. [Google Scholar] [CrossRef]
- Brzakalik, K. Nearest-neighbor configurations of Fe atoms in Fe3−xTixAl ordered alloys. Intermetallics 2008, 16, 1053–1060. [Google Scholar] [CrossRef]
- Suzuki, R.; Kyono, T. Thermoelectric properties of Fe2TiAl Heusler alloys. J. Alloys Compd. 2004, 377, 38–42. [Google Scholar] [CrossRef]
- Friák, M.; Deges, J.; Krein, R.; Frommeyer, G.; Neugebauer, J. Combined ab initio and experimental study of structural and elastic properties of Fe3Al-based ternaries. Intermetallics 2010, 18, 1310–1315. [Google Scholar] [CrossRef]
- Palm, M. Fe–Al materials for structural applications at high temperatures: Current research at MPIE. Int. J. Mater. Res. 2009, 100, 277–287. [Google Scholar] [CrossRef]
- Palm, M.; Lacaze, J. Assessment of the Al-Fe-Ti system. Intermetallics 2006, 14, 1291–1303. [Google Scholar] [CrossRef]
- Krein, R.; Friák, M.; Neugebauer, J.; Palm, M.; Heilmaier, M. L21-ordered Fe-Al-Ti alloys. Intermetallics 2010, 18, 1360–1364. [Google Scholar] [CrossRef]
- Palm, M.; Inden, G.; Thomas, N. The Fe-Al-Ti system. J. Phase Equilib. 1995, 16, 209–222. [Google Scholar] [CrossRef]
- Palm, M.; Sauthoff, G. Deformation behaviour and oxidation resistance of single-phase and two-phase L21-ordered Fe-Al-Ti alloys. Intermetallics 2004, 12, 1345–1359. [Google Scholar] [CrossRef]
- Michalcová, A.; Senčekova, L.; Rolink, G.; Weisheit, A.; Pešička, J.; Stobik, M.; Palm, M. Laser additive manufacturing of iron aluminides strengthened by ordering, borides or coherent Heusler phase. Mater. Des. 2017, 116, 481–494. [Google Scholar] [CrossRef]
- Jirásková, Y.; Pizúrová, N.; Titov, A.; Janickovic, D.; Friák, M. Phase separation in Fe-Ti-Al alloy—Structural, magnetic, and Mössbauer study. J. Magn. Magn. Mater. 2018, 468, 91–99. [Google Scholar] [CrossRef]
- Gilleßen, M.; Dronskowski, R. A combinatorial study of full Heusler alloys by first-principles computational methods. J. Comput. Chem. 2009, 30, 1290–1299. [Google Scholar] [CrossRef] [PubMed]
- Xian-Kun, L.; Cong, L.; Zhou, Z.; Xiao-Hua, L. First-principles investigation on the structural and elastic properties of cubic-Fe2TiAl under high pressures. Chin. Phys. B 2013, 22, 087102. [Google Scholar] [CrossRef]
- Shreder, E.; Streltsov, S.V.; Svyazhin, A.; Lukoyanov, A.; Anisimov, V. Electronic structure and physical properties of Fe2MAl (M = Ti, V, Cr) Heusler alloys. In Proceedings of the Third International Symposium on Magnetism, Moscow, Russia, 26–30 June 2005; p. 220. [Google Scholar]
- Shreder, E.; Streltsov, S.V.; Svyazhin, A.; Makhnev, A.; Marchenkov, V.V.; Lukoyanov, A.; Weber, H.W. Evolution of the electronic structure and physical properties of Fe(2)MeAl (Me = Ti, V, Cr) Heusler alloys. J. Phys. Condens. Matter 2008, 20, 045212. [Google Scholar] [CrossRef]
- Adebambo, P.O.; Adetunji, B.I.; Olowofela, J.A.; Oguntuase, J.A.; Adebayo, G.A. Prediction of metallic and half-metallic structure and elastic properties of Fe2Ti1−xMnxAl Heusler alloys. Phys. B Condens. Matter 2016, 485, 103–109. [Google Scholar] [CrossRef]
- Kourov, N.I.; Marchenkov, V.V.; Belozerova, K.A.; Weber, H.W. Specific features of the electrical resistivity of half-metallic ferromagnets Fe2MeAl (Me = Ti, V, Cr, Mn, Fe, Ni). J. Exp. Theor. Phys. 2014, 118, 426–431. [Google Scholar] [CrossRef]
- Slebarski, A.; Goraus, J.; Deniszczyk, J.; Skoczen, L. Electronic structure, magnetic properties and electrical resistivity of the Fe2V1−xTixAl Heusler alloys: Experiment and calculation. J. Phys. Condens. Matter 2006, 18, 10319–10334. [Google Scholar] [CrossRef]
- Buschow, K.H.J.; van Engen, P.G. Magnetic and magneto-optical properties of Heusler alloys based on aluminum and gallium. J. Magn. Magn. Mat. 1981, 25, 90–96. [Google Scholar] [CrossRef]
- Friák, M.; Slávik, A.; Miháliková, I.; Holec, D.; Všianská, M.; Šob, M.; Palm, M.; Neugebauer, J. Origin of the low magnetic moment in Fe2TiAl: An ab initio study. Materials 2018, 11, 1732. [Google Scholar] [CrossRef]
- Stein, F.; Palm, M. Re-determination of transition temperatures in the Fe–Al system by differential thermal analysis. Int. J. Mater. Res. 2007, 98, 580–588. [Google Scholar] [CrossRef]
- Amara, H.; Fu, C.C.; Soisson, F.; Maugis, P. Aluminum and vacancies in α-iron: Dissolution, diffusion, and clustering. Phys. Rev. B 2010, 81, 174101. [Google Scholar] [CrossRef]
- Liu, S.; Duan, S.; Ma, B. First-principles calculation of vibrational entropy for Fe-Al compounds. Phys. Rev. B 1998, 58, 9705–9709. [Google Scholar]
- Kulikov, N.I.; Postnikov, A.V.; Borstel, G.; Braun, J. Onset of magnetism in B2 transition-metal aluminides. Phys. Rev. B 1999, 59, 6824–6833. [Google Scholar] [CrossRef]
- Friák, M.; Neugebauer, J. Ab initio study of the anomalous volume-composition dependence in Fe-Al alloys. Intermetallics 2010, 18, 1316–1321. [Google Scholar] [CrossRef]
- Fähnle, M.; Drautz, R.; Lechermann, F.; Singer, R.; Diaz-Ortiz, A.; Dosch, H. Thermodynamic properties from ab-initio calculations: New theoretical developments, and applications to various materials systems. Phys. Status Solidi B Basic Solid State Phys. 2005, 242, 1159–1173. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys. 1980, 58, 1200. [Google Scholar] [CrossRef]
- Zlotnikov, I.; Zolotoyabko, E.; Fratzl, P. Nano-scale modulus mapping of biological composite materials: Theory and practice. Prog. Mater. Sci. 2017, 87, 292–320. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Zunger, A.; Wei, S.; Ferreira, L.; Bernard, J. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef]
- Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 184, 1172–1182. [Google Scholar] [CrossRef]
- Oganov, A.R.; Lyakhov, A.O.; Valle, M. How evolutionary crystal structure prediction works and why. Acc. Chem. Res. 2011, 44, 227–237. [Google Scholar] [CrossRef]
- Friák, M.; Counts, W.; Ma, D.; Sander, B.; Holec, D.; Raabe, D.; Neugebauer, J. Theory-Guided Materials Design of Multi-Phase Ti-Nb Alloys with Bone-Matching Elastic Properties. Materials 2012, 5, 1853–1872. [Google Scholar] [CrossRef]
- Zhu, L.-F.; Friák, M.; Lymperakis, L.; Titrian, H.; Aydin, U.; Janus, A.M.; Fabritius, H.-O.; Ziegler, A.; Nikolov, S.; Hemzalová, P.; et al. Ab initio study of single-crystalline and polycrystalline elastic properties of Mg-substituted calcite crystals. J. Mech. Behav. Biomed. Mat. 2013, 20, 296–304. [Google Scholar] [CrossRef]
- Miracle, D.; Senkov, O. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Hillert, M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Zhou, L.; Holec, D.; Mayrhofer, P.H. First-principles study of elastic properties of cubic Cr1−xAlxN alloys. J. Appl. Phys. 2013, 113, 043511. [Google Scholar] [CrossRef]
- Moakher, M.; Norris, A.N. The closest elastic tensor of arbitrary symmetry to an elasticity tensor of lower symmetry. J. Elast. 2006, 85, 215–263. [Google Scholar] [CrossRef]
- Tasnádi, F.; Abrikosov, I.A.; Rogström, L.; Almer, J.; Johansson, M.P.; Oden, M. Significant elastic anisotropy in Ti1−xAlxN alloys. Appl. Phys. Lett. 2010, 97, 3524502. [Google Scholar] [CrossRef]
- Tasnádi, F.; Odén, M.; Abrikosov, I.A. Ab initio elastic tensor of cubic Ti0.5Al0.5N alloys: Dependence of elastic constants on size and shape of the supercell model and their convergence. Phys. Rev. B 2012, 85, 144112. [Google Scholar] [CrossRef]
- Von Pezold, J.; Dick, A.; Friák, M.; Neugebauer, J. Generation and performance of special quasirandom structures for studying the elastic properties of random alloys: Application to Al-Ti. Phys. Rev. B 2010, 81, 094203. [Google Scholar] [CrossRef]
- Holec, D.; Tasnádi, F.; Wagner, P.; Friák, M.; Neugebauer, J.; Mayrhofer, P.H.; Keckes, J. Macroscopic elastic properties of textured ZrN-AlN polycrystalline aggregates: From ab initio calculations to grainscale interactions. Phys. Rev. B 2014, 90, 184106. [Google Scholar] [CrossRef]
- Šesták, P.; Friák, M.; Holec, D.; Všianská, M.; Šob, M. Strength and brittleness of interfaces in Fe-Al superalloy nanocomposites under multiaxial loading: An ab initio and atomistic study. Nanomaterials 2018, 8, 873. [Google Scholar] [CrossRef]
- Leamy, H.; Gibson, E.; Kayser, F. Elastic stiffness coefficients of iron-aluminum alloys. i. experimental results and thermodynamic analysis. Acta Metal. 1967, 15, 1827. [Google Scholar] [CrossRef]
- Gaillac, R.; Pullumbi, P.; Coudert, F.X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef]
- Mendiratta, M.; Ehlers, S.; Lipsitt, H. D03-B2-α phase-relations in Fe-Al-Ti alloys. Metal. Trans. A Phys. Metal. Mater. Sci. 1987, 18, 509–518. [Google Scholar] [CrossRef]
- Su, C.W.; Chao, C.G.; Liu, T.F. Formation of (B2+D03)phases at a/2〈100〉 anti-phase boundary in an Fe-23 at.%Al-8.5 at.%Ti alloy. Scr. Mater. 2007, 57, 917–920. [Google Scholar] [CrossRef]
- Su, C.W.; Jeng, S.C.; Chao, C.G.; Liu, T.F. Orientation relationship between C14 precipitate and (A2+D03) matrix in an Fe-20at.%Al-8at.%Ti alloy. Scr. Mater. 2007, 57, 125–128. [Google Scholar] [CrossRef]
- Su, C.W.; Chao, C.G.; Liu, T.F. Formation of (B2+D0(3)) two-phase microstructure in a Fe-23Al-7Ti alloy. Mater. Trans. 2007, 48, 2993–2996. [Google Scholar] [CrossRef]
- Marcinkowski, M.J.; Brown, N. Direct observation of antiphase boundaries in the Fe3Al superlattice. J. Appl. Phys. 1962, 33, 537–552. [Google Scholar] [CrossRef]
- Murakami, Y.; Niitsu, K.; Tanigaki, T.; Kainuma, R.; Park, H.S.; Shindo, D. Magnetization amplified by structural disorder within nanometre-scale interface region. Nat. Commun. 2014, 5, 4133. [Google Scholar] [CrossRef]
- Liebscher, C.H.; Radmilovic, V.R.; Dahmen, U.; Vo, N.Q.; Dunand, D.C.; Asta, M.; Ghosh, G. A hierarchical microstructure due to chemical ordering in the bcc lattice: Early stages of formation in a ferritic Fe-Al-Cr-Ni-Ti alloy. Acta Mater. 2015, 92, 220–232. [Google Scholar] [CrossRef]
- Fratzl, P.; Penrose, O.; Lebowitz, J.L. Modeling of phase separation in alloys with coherent elastic misfit. J. Stat. Phys. 1999, 95, 1429. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friák, M.; Buršíková, V.; Pizúrová, N.; Pavlů, J.; Jirásková, Y.; Homola, V.; Miháliková, I.; Slávik, A.; Holec, D.; Všianská, M.; et al. Elasticity of Phases in Fe-Al-Ti Superalloys: Impact of Atomic Order and Anti-Phase Boundaries. Crystals 2019, 9, 299. https://doi.org/10.3390/cryst9060299
Friák M, Buršíková V, Pizúrová N, Pavlů J, Jirásková Y, Homola V, Miháliková I, Slávik A, Holec D, Všianská M, et al. Elasticity of Phases in Fe-Al-Ti Superalloys: Impact of Atomic Order and Anti-Phase Boundaries. Crystals. 2019; 9(6):299. https://doi.org/10.3390/cryst9060299
Chicago/Turabian StyleFriák, Martin, Vilma Buršíková, Naděžda Pizúrová, Jana Pavlů, Yvonna Jirásková, Vojtěch Homola, Ivana Miháliková, Anton Slávik, David Holec, Monika Všianská, and et al. 2019. "Elasticity of Phases in Fe-Al-Ti Superalloys: Impact of Atomic Order and Anti-Phase Boundaries" Crystals 9, no. 6: 299. https://doi.org/10.3390/cryst9060299
APA StyleFriák, M., Buršíková, V., Pizúrová, N., Pavlů, J., Jirásková, Y., Homola, V., Miháliková, I., Slávik, A., Holec, D., Všianská, M., Koutná, N., Fikar, J., Janičkovič, D., Šob, M., & Neugebauer, J. (2019). Elasticity of Phases in Fe-Al-Ti Superalloys: Impact of Atomic Order and Anti-Phase Boundaries. Crystals, 9(6), 299. https://doi.org/10.3390/cryst9060299






