Field-Angle Dependence of Interlayer Magnetoresistance in Organic Dirac Electron System α-(BEDT-TTF)2I3
Abstract
:1. Introduction
2. Method
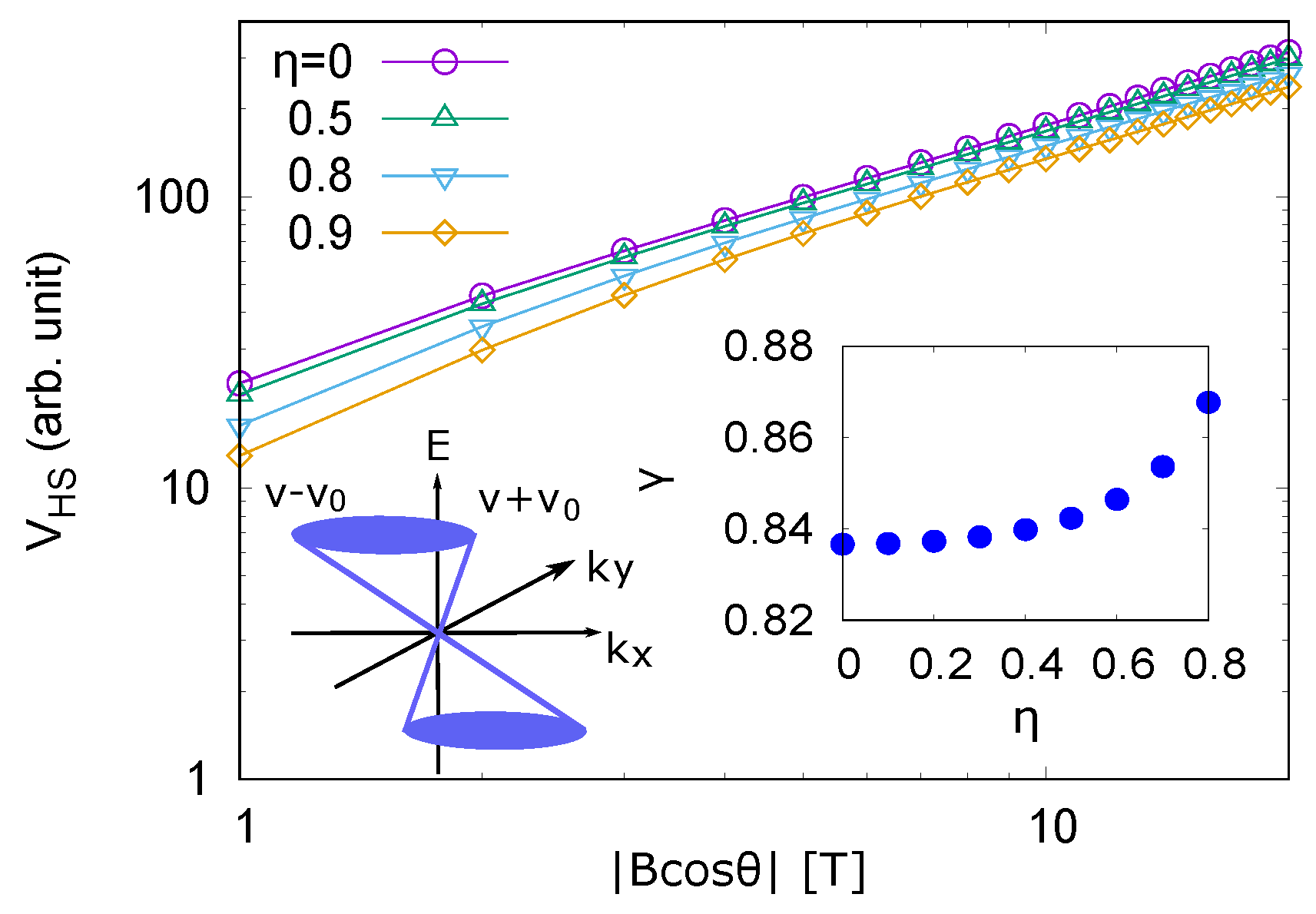
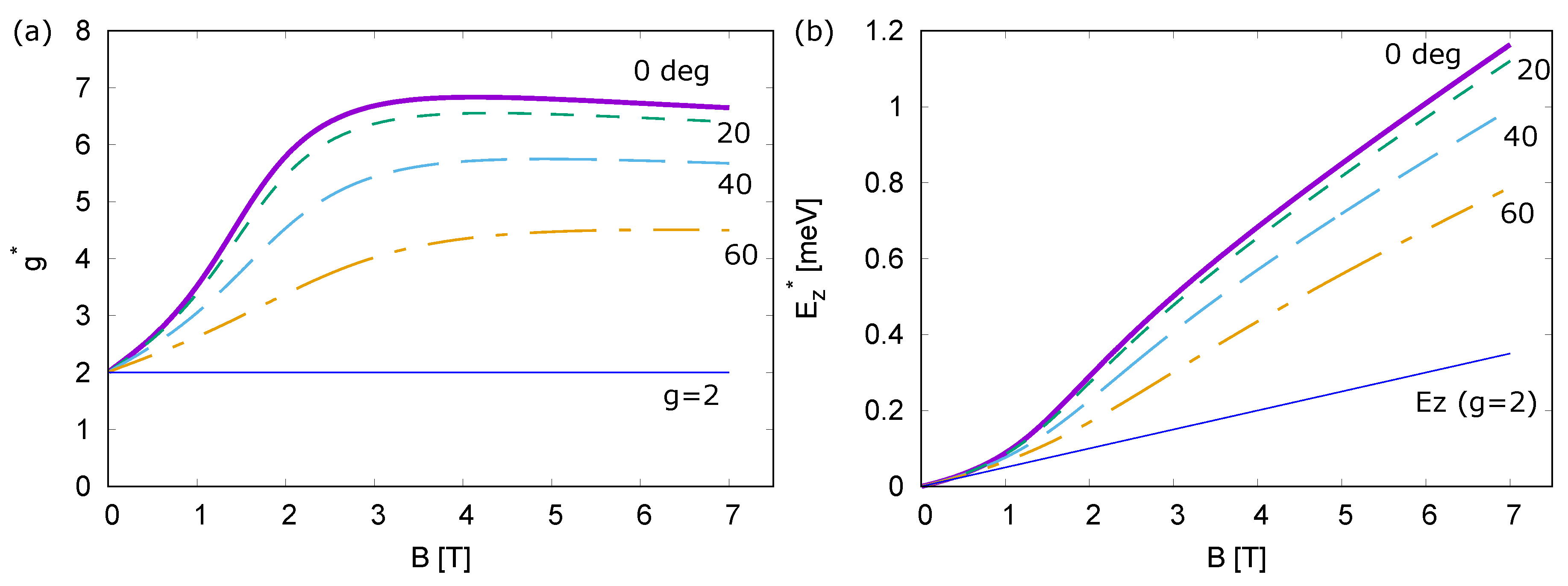
2.1. Formulation
2.2. Experimental Method
2.2.1. Crystal Growth
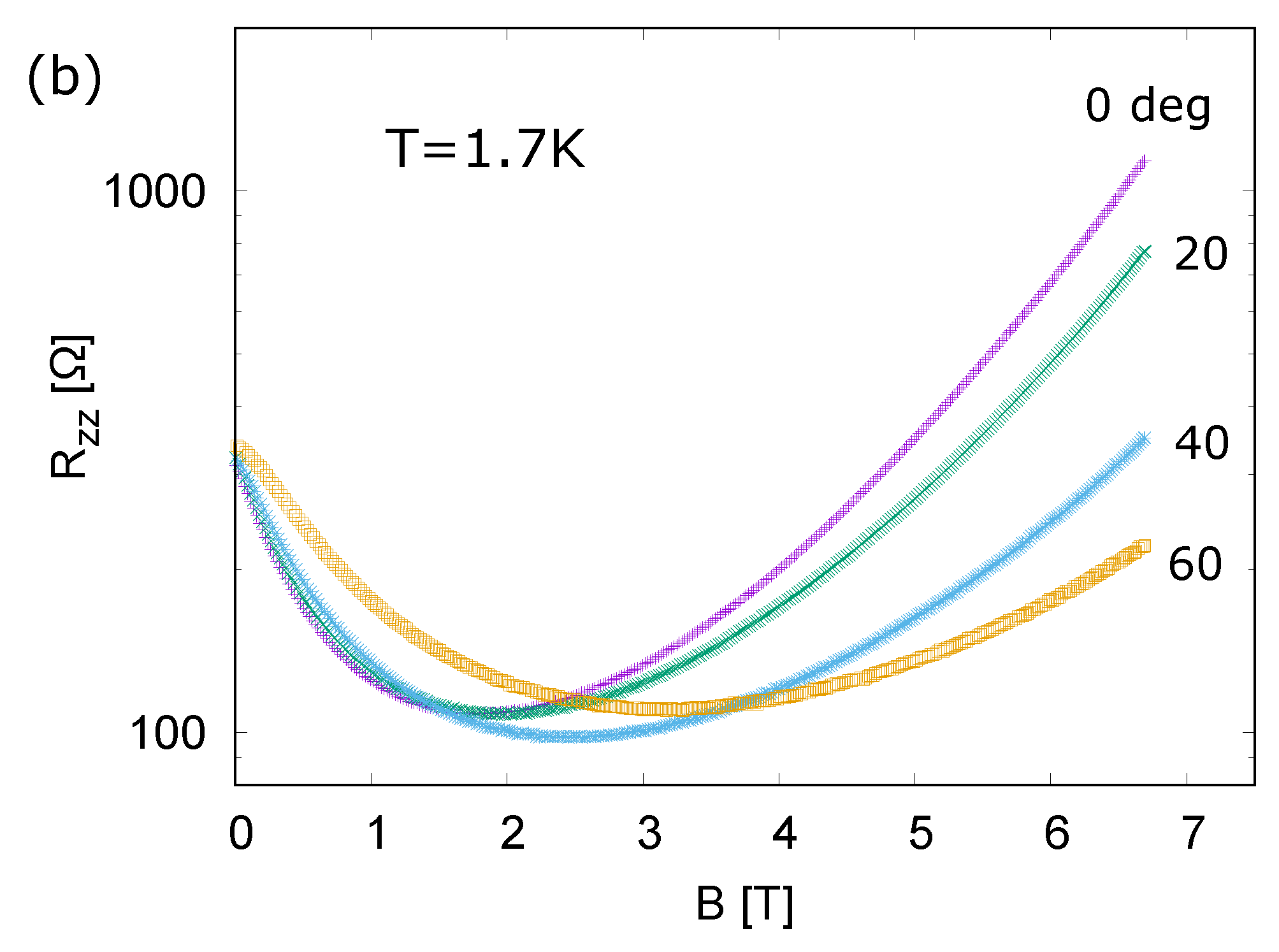
2.2.2. Experiments of Interlayer Magnetoresistance Under Pressure
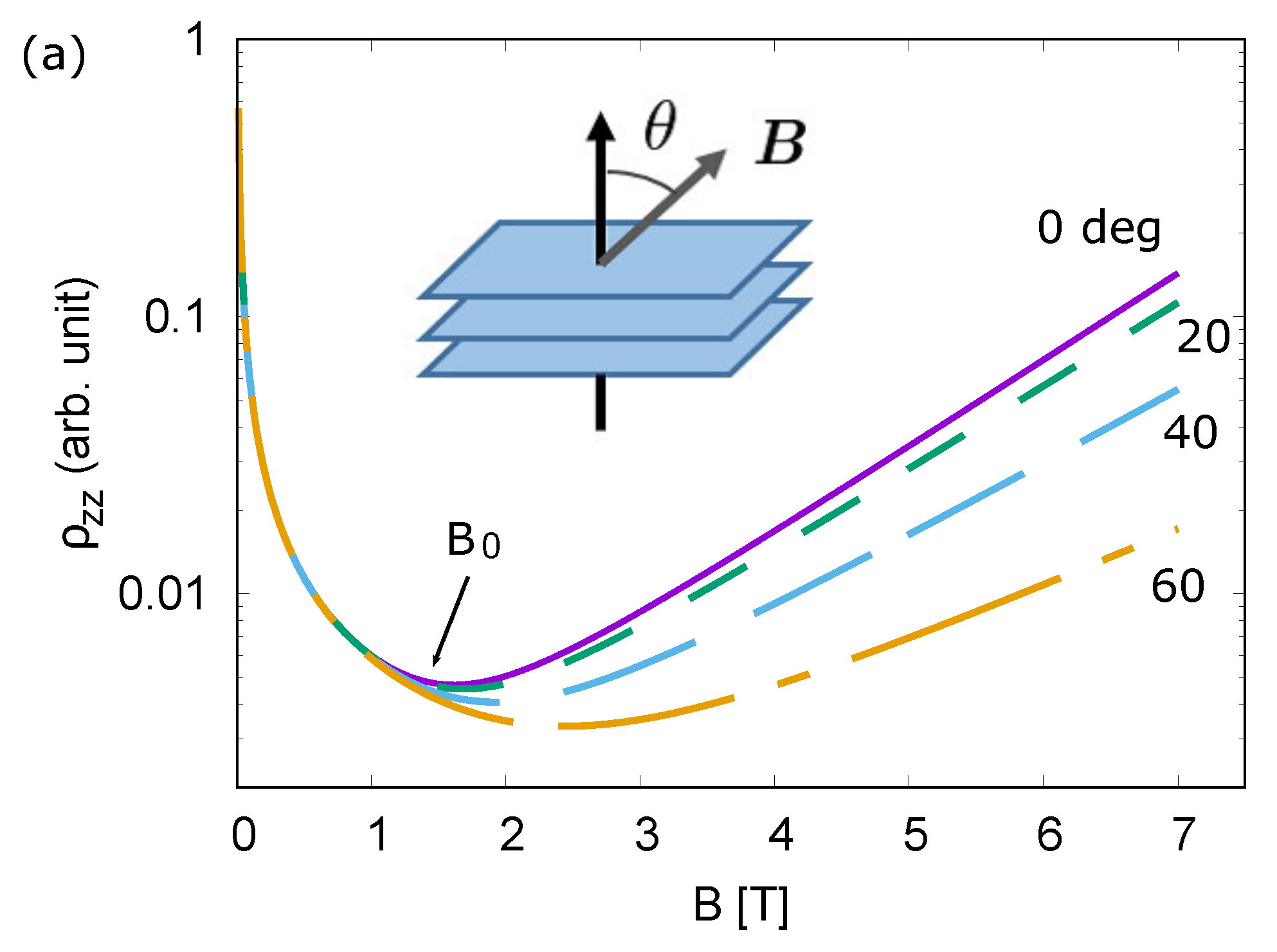
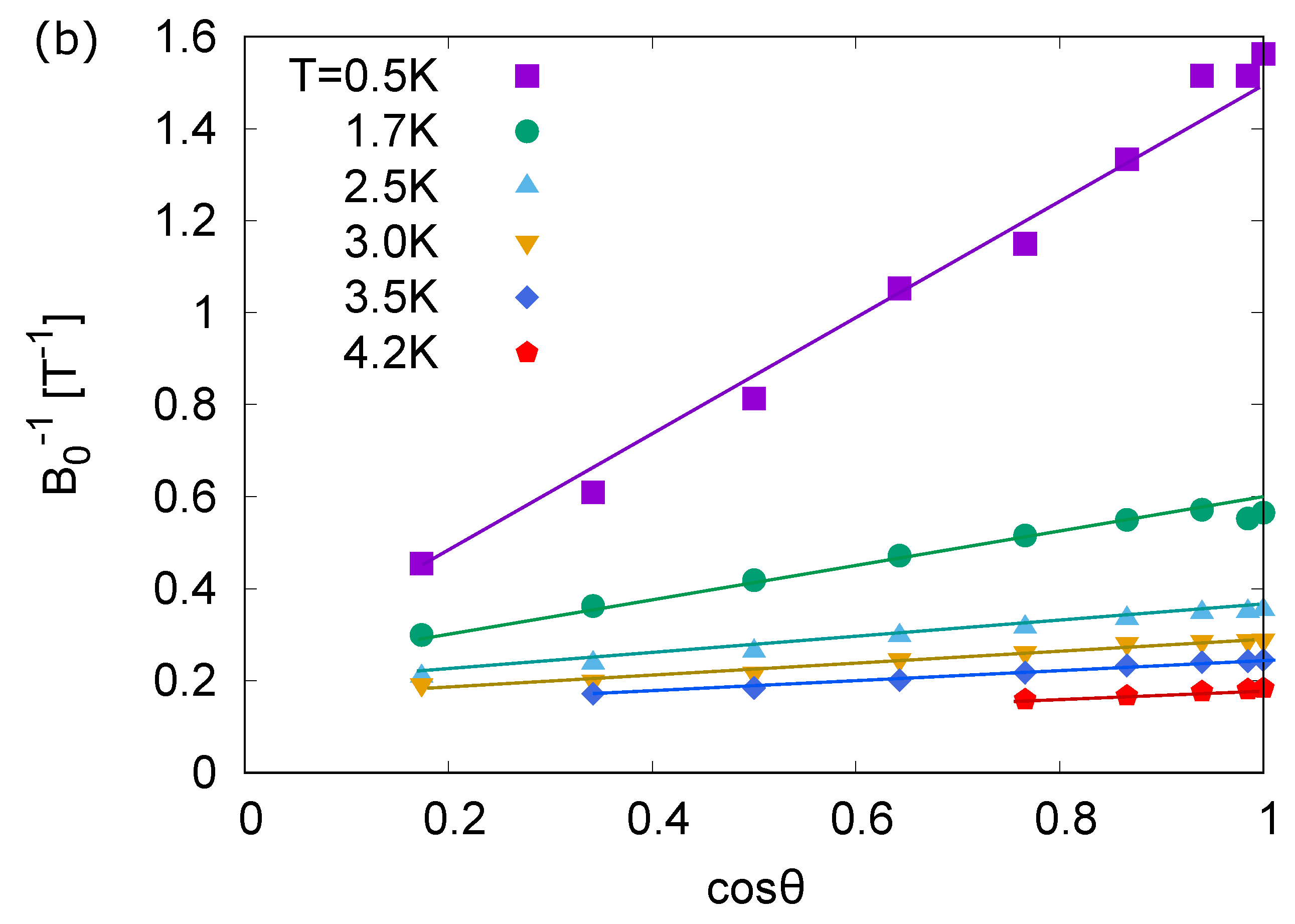
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| R | right |
| L | left |
References
- Goerbig, M.O. Electronic properties of graphene in a strong magnetic field. Rev. Mod. Phys. 2011, 83, 1193. [Google Scholar] [CrossRef]
- Suzumura, Y.; Kobayashi, A. Theory of Dirac Electrons in Organic Conductors. Crystals 2012, 2, 266. [Google Scholar] [CrossRef]
- Kotov, V.N.; Uchoa, B.; Pereira, V.M.; Guinea, F.; Castro Neto, A.H. Electron-Electron Interactions in Graphene: Current Status and Perspectives. Rev. Mod. Phys. 2012, 84, 1067. [Google Scholar] [CrossRef]
- Wehling, T.O.; Black-Schaffer, A.M.; Balatsky, A.V. Dirac materials. Adv. Phys. 2014, 63, 1. [Google Scholar] [CrossRef]
- Kajita, K.; Nishio, Y.; Tajima, N.; Suzumura, Y.; Kobayashi, A. Molecular Dirac Fermion Systems -Theoretical and Experimental Approaches-. J. Phys. Soc. Jpn. 2014, 83, 072002. [Google Scholar] [CrossRef]
- Kajita, K.; Ojiro, T.; Fujii, H.; Nishio, Y.; Kobayashi, H.; Kobayashi, A.; Kato, R. Magnetotransport Phenomena of α-Type (BEDT-TTF)2I3 under High Pressures. J. Phys. Soc. Jpn. 1992, 61, 23. [Google Scholar] [CrossRef]
- Tajima, N.; Tamura, M.; Nishio, Y.; Kajita, K.; Iye, Y. Transport Property of an Organic Conductor α-(BEDT-TTF)2I3 under High Pressure -Discovery of a Novel Type of Conductor-. J. Phys. Soc. Jpn. 2000, 69, 543. [Google Scholar] [CrossRef]
- Kobayashi, A.; Katayama, S.; Noguchi, K.; Suzumura, Y. Superconductivity in Charge Ordered Organic Conductor α-(ET)2I3 Salt. J. Phys. Soc. Jpn. 2004, 73, 3135. [Google Scholar] [CrossRef]
- Katayama, S.; Kobayashi, A.; Suzumura, Y. Pressure-Induced Zero-Gap Semiconducting State in Organic Conductor α-(BEDT-TTF)2I3 Salt. J. Phys. Soc. Jpn. 2006, 75, 054705. [Google Scholar] [CrossRef]
- Kobayashi, A.; Katayama, S.; Suzumura, Y.; Fukuyama, H. Massless Fermions in Organic Conductor. J. Phys. Soc. Jpn. 2007, 76, 034711. [Google Scholar] [CrossRef]
- Goerbig, M.O.; Fuchs, J.-N.; Montambaux, G.; Piechon, F. Tilted anisotropic Dirac cones in quinoid-type graphene and α-(BEDT-TTF)2I3. Phys. Rev. B 2008, 78, 045415. [Google Scholar] [CrossRef]
- Kobayashi, A.; Katayama, S.; Suzumura, Y. Theoretical study of the zero-gap organic conductor α-(BEDT-TTF)2I3. Sci. Technol. Adv. Mater. 2009, 10, 024309. [Google Scholar] [CrossRef]
- Tajima, N.; Kajita, K. Experimental study of organic zero-gap conductor α-(BEDT-TTF)2I3. Sci. Technol. Adv. Mater. 2009, 10, 024308. [Google Scholar] [CrossRef]
- Kino, H.; Fukuyama, H. Interrelationship among Electronic States of α-(ET)2I3, (ET)2MHg(SCN)4 and κ-(ET)2X. J. Phys. Soc. Jpn. 1995, 64, 4523. [Google Scholar] [CrossRef]
- Seo, H. Charge Ordering in Organic ET Compounds. J. Phys. Soc. Jpn. 2000, 69, 805. [Google Scholar] [CrossRef]
- Kobayashi, A.; Suzumura, Y.; Piechon, F.; Montambaux, G. Emergence of Dirac electron pair in the charge-ordered state of the organic conductor α-(BEDT-TTF)2I3. Phys. Rev. B 2011, 84, 075450. [Google Scholar] [CrossRef]
- Tanaka, Y.; Ogata, M. Correlation Effects on Charge Order and Zero-Gap State in the Organic Conductor α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2016, 85, 104706. [Google Scholar] [CrossRef]
- Hirata, M.; Ishikawa, K.; Miyagawa, K.; Tamura, M.; Berthier, C.; Basko, D.; Kobayashi, A.; Matsuno, G.; Kanoda, K. Observation of an anisotropic Dirac cone reshaping and ferrimagnetic spin polarization in an organic conductor. Nat. Commun. 2016, 7, 12666. [Google Scholar] [CrossRef]
- Matsuno, G.; Kobayashi, A. Effect of Interband Fluctuation on Spin Susceptibility in Molecular Dirac Fermion System α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2017, 86, 014705. [Google Scholar] [CrossRef]
- Hirata, M.; Ishikawa, K.; Matsuno, G.; Kobayashi, A.; Miyagawa, K.; Tamura, M.; Berthier, C.; Kanoda, K. Anomalous spin correlations and excitonic instability of interacting 2D Weyl fermions. Science 2017, 358, 1403. [Google Scholar] [CrossRef] [PubMed]
- Matsuno, G.; Kobayashi, A. Coexistence of Velocity Renormalization and Ferrimagnetic Fluctuation in the Organic Dirac Electron System α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2018, 87, 054706. [Google Scholar] [CrossRef]
- Ohki, D.; Matsuno, G.; Omori, Y.; Kobayashi, A. Optical Conductivity in a Two-Dimensional Extended Hubbard Model for an Organic Dirac Electron System α-(BEDT-TTF)2I3. Crystals 2018, 8, 137. [Google Scholar] [CrossRef]
- Kobayashi, A.; Suzumura, Y.; Fukuyama, H. Hall Effect and Orbital Diamagnetism in Zerogap State of Molecular Conductor α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2008, 77, 064718. [Google Scholar] [CrossRef]
- Tajima, N.; Kato, R.; Sugawara, S.; Nishio, Y.; Kajita, K. Interband effects of magnetic field on Hall conductivity in the multilayered massless Dirac fermion system α-(BEDT-TTF)2I3. Phys. Rev. B 2012, 85, 033401. [Google Scholar] [CrossRef]
- Osada, T. Negative Interlayer Magnetoresistance and Zero-Mode Landau Level in Multilayer Dirac Electron Systems. J. Phys. Soc. Jpn. 2008, 77, 084711. [Google Scholar] [CrossRef]
- Tajima, N.; Sugawara, S.; Kato, R.; Nishio, Y.; Kajita, K. Effect of the Zero-Mode Landau Level on Interlayer Magnetoresistance in Multilayer Massless Dirac Fermion Systems. Phys. Rev. Lett. 2013, 102, 176403. [Google Scholar] [CrossRef] [PubMed]
- Morinari, T.; Himura, T.; Tohyama, T. Possible Verification of Tilted Anisotropic Dirac Cone in α-(BEDT-TTF)2I3 Using Interlayer Magnetoresistance. J. Phys. Soc. Jpn. 2009, 78, 023704. [Google Scholar] [CrossRef]
- Morinari, T.; Tohyama, T. Crossover from Positive to Negative Interlayer Magnetoresistance in Multilayer Massless Dirac Fermion System with Non-Vertical Interlayer Tunneling. J. Phys. Soc. Jpn. 2010, 79, 044708. [Google Scholar] [CrossRef]
- Osada, T. Surface Transport in the ν = 0 Quantum Hall Ferromagnetic State in the Organic Dirac Fermion System. J. Phys. Soc. Jpn. 2015, 84, 053704. [Google Scholar] [CrossRef]
- Tajima, N.; Morinari, T. Tilted Dirac Cone Effect on Interlayer Magnetoresistance in α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2018, 87, 045002. [Google Scholar] [CrossRef]
- Kobayashi, A.; Suzumura, Y.; Fukuyama, H.; Goerbig, M.O. Tilted-Cone-Induced Easy-Plane Pseudo-Spin Ferromagnet and Kosterlitz Thouless Transition in Massless Dirac Fermions. J. Phys. Soc. Jpn. 2009, 78, 114711. [Google Scholar] [CrossRef]
- Tajima, N.; Sato, M.; Sugawara, S.; Kato, R.; Nishio, Y.; Kajita, K. Spin and valley splittings in multilayered massless Dirac fermion system. Phys. Rev. B 2010, 82, 121420(R). [Google Scholar] [CrossRef]
- Hirata, M. NMR Studies of Massless Dirac Fermions in the Quasi-Two-Dimensional Organic Conductor α-(BEDT-TTF)2I3. Ph.D. Thesis, The University of Tokyo, Tokyo, Japan, 2012. [Google Scholar]
- Kubo, K.; Morinari, T. Spin-Ordered States in Multilayer Massless Dirac Fermion Systems. J. Phys. Soc. Jpn. 2014, 83, 033702. [Google Scholar] [CrossRef]
- Kubo, K.; Morinari, T. Effect of Interlayer Spin-Flip Tunneling for Interlayer Magnetoresistance in Multilayer Massless Dirac Fermion Systems. J. Phys. Soc. Jpn. 2014, 83, 083701. [Google Scholar] [CrossRef]
- Tani, T.; Kobayashi, A. Spin-Lattice Relaxation Rate in Organic Dirac Electron System α-(BEDT-TTF)2I3 under Strong Magnetic Field. J. Phys. Soc. Jpn. 2019, 88. in press. [Google Scholar]
- Luttinger, J.M.; Kohn, W. Motion of Electrons and Holes in Perturbed Periodic Fields. Phys. Rev. 1955, 97, 869. [Google Scholar] [CrossRef]
- Sári, J.; Töke, C.; Goerbig, M.O. Magnetoplasmons of the tilted anisotropic Dirac cone material α-(BEDT-TTF)2I3. Phys. Rev. B 2014, 90, 155446. [Google Scholar] [CrossRef]
- Osada, T. Anomalous Interlayer Hall Effect in Multilayer Massless Dirac Fermion System at the Quantum Limit. J. Phys. Soc. Jpn. 2011, 80, 033708. [Google Scholar] [CrossRef]
- Osada, T. Magnetotransport in organic Diracfermion system at the quantum limit:Interlayer Hall effect and surfacetransport via helical edge states. Phys. Status Solidi 2012, 249, 962–966. [Google Scholar] [CrossRef]
- Sugawara, S.; Tamura, M.; Tajima, N.; Kato, R.; Sato, M.; Nishio, Y.; Kajita, K. Temperature Dependence of Inter-Layer Longitudinal Magnetoresistance in α-(BEDT-TTF)2I3: Positive versus Negative Contributions in a Tilted Dirac Cone System. J. Phys. Soc. Jpn. 2010, 79, 113704. [Google Scholar] [CrossRef]
- Proskurin, I.; Ogata, M. Thermoelectric Transport Coefficients for Massless Dirac Electrons in Quantum Limit. J. Phys. Soc. Jpn. 2013, 82, 063712. [Google Scholar] [CrossRef]
- Konoike, T.; Sato, M.; Uchida, K.; Osada, T. Anomalous Thermoelectric Transport and Giant Nernst Effect in Multilayered Massless Dirac Fermion System. J. Phys. Soc. Jpn. 2013, 82, 073601. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tani, T.; Tajima, N.; Kobayashi, A. Field-Angle Dependence of Interlayer Magnetoresistance in Organic Dirac Electron System α-(BEDT-TTF)2I3. Crystals 2019, 9, 212. https://doi.org/10.3390/cryst9040212
Tani T, Tajima N, Kobayashi A. Field-Angle Dependence of Interlayer Magnetoresistance in Organic Dirac Electron System α-(BEDT-TTF)2I3. Crystals. 2019; 9(4):212. https://doi.org/10.3390/cryst9040212
Chicago/Turabian StyleTani, Takehiro, Naoya Tajima, and Akito Kobayashi. 2019. "Field-Angle Dependence of Interlayer Magnetoresistance in Organic Dirac Electron System α-(BEDT-TTF)2I3" Crystals 9, no. 4: 212. https://doi.org/10.3390/cryst9040212
APA StyleTani, T., Tajima, N., & Kobayashi, A. (2019). Field-Angle Dependence of Interlayer Magnetoresistance in Organic Dirac Electron System α-(BEDT-TTF)2I3. Crystals, 9(4), 212. https://doi.org/10.3390/cryst9040212



