Modelling of the Polymorph Nucleation Based on Classical Nucleation Theory

Abstract

To elucidate the relative nucleation rates of different polymorphs, a competitive kinetic model is developed based on classical nucleation theory to describe the time evolution of two different polymorphic cluster size distributions controlled by the association and dissociation of the solute molecules during polymorph nucleation. Although there is only one type of the solute molecules, the agglomerated solute clusters are divided into two types–A form and B form, which resemble the structures and morphologies of the different mature polymorphs and eventually lead to the formation of two polymorphic crystals. A dissociation kernel is incorporated into the proposed model to account for gradual dissolution of the solute clusters smaller than a critical nucleus size due to the thermodynamic instability. By fitting the experimental induction period data and the final measured weight fractions of eflucimibe polymorphs with the proposed model, the association and dissociation rate constants for two polymorphs are determined. The developed model is satisfactory to explain the competitive mechanism of polymorph nucleation for eflucimibe that B form dominates at higher supersaturation while A form dominates at lower supersaturation. The results also indicate that A form is more stable than B form with a transition energy of 3.1 kJ/mole at 35 °C.

1. Introduction

A substance capable of crystallizing into different crystalline forms is said to exhibit polymorphism. Polymorphism plays an important role for pharmaceutical products. Different polymorphs of the same substance might lead to different biological activity due to the possibility of conversion among polymorphic forms affecting the dissolution rate [1,2].

Solute molecules in the supersaturated solution can aggregate and form clusters. Clusters can further aggregate to a bigger size or break into some smaller particles due to the thermodynamic instability. When the size of a cluster exceeds a critical size, it becomes stable and the subsequent growth leads to a new crystal [3,4,5]. The existence of solute clusters in the supersaturated solution for the single polymorphic system has been reported by many researchers [6,7,8,9,10]. For the multiple polymorphic system, a general hypothesis is accepted in the literature that the solute molecules in the supersaturated solution assemble to form different polymorphic clusters, which resemble the structures and morphologies of the various mature polymorphs and eventually lead to the formation of multiple polymorphic crystals [11,12]. Recently, Van Driessche et al. [13] observed polymorph nucleation events that are driven by oriented attachments between subcritical clusters of the protein glucose isomerase that already exhibit a degree of crystallinity. Consequently, the relative nucleation rates of different polymorphs should be closely related to the time evolution of multiple polymorphic clusters in nucleation.

Understanding the nucleation and growth mechanisms of polymorphism is crucial to better control of the desired forms during polymorph crystallization [14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Although various nucleation theories for the single polymorphic system have been developed based on either the thermodynamics of the process [4,5] or the kinetics of the process [28,29,30], nucleation theory for the multiple polymorphic system is comparatively less studied in the literature. Hammond et al. [31] used a molecular modeling approach to study the stability of different polymorphic forms of L-glutamic acid through building and optimizing molecular clusters of different sizes and shapes. ter Horst et al. [32] adopted a combination method of molecular simulations and process modeling to predict the polymorphic fraction and crystal size distribution during polymorph crystallization. Deij et al. [33] applied the growth probability method combined with a Monte Carlo routine to simulate polymorph formation for some dimorphic systems.

When multiple polymorphs of the same substance crystallize together out of a solution, the relative productivity of different polymorphs depends on supersaturation, temperature, cooling rate, solvent, agitation, PH, additive, impurity, seeding, etc. Among these factors, supersaturation is of utmost significance [34]. For example, Ni and Liao [35] and Qu et al. [36] indicated for L-glutamic acid that the metastable $\mathsf{\alpha }$ crystals are favored at lower supersaturations while the stable $\mathsf{\beta }$ crystals are favored at higher supersaturations. Sun et al. [37] reported that either spontaneously nucleating quiescent aqueous L-glycine solution or nonphotochemical laser-induced nucleation tends to produce the intermediate stable $\mathsf{\alpha }$ glycine at lower supersaturations and the most stable $\mathsf{\gamma }$ glycine at higher supersaturations. Gracin and Rasmuson [38] observed for the polymorph nucleation of p-aminobenzoic acid that cooling crystallization can be performed to produce the most stable pure $\mathsf{\beta }$ form in water and in ethyl acetate by careful control of supersaturation and temperature. Teychene and Biscans [39] investigated the nucleation kinetics of two eflucimibe polymorphs by induction time measurements and found that the stable A-form crystals are favored at lower supersaturations while the metastable stable B-form crystals are favored at higher supersaturations. Zhu et al. [40] indicated that the polymorph nucleation of gestodene in ethanol depends on both the supersaturation and crystallization temperature. Roelands et al. [41] and Wantha et al. [42] reported that the metastable polymorph increases with increasing supersaturation for the crystallization of L-histidine from aqueous solution with the antisolvent ethanol.

Stranki and Totomanov [43] attempted an explanation of the Ostwald rule of stages from the corresponding rates of crystal nucleation and argued that the first nucleated phase is the phase that has the lowest free-energy barrier of formation, i.e., the one which has the fastest nucleation rate, rather than the most stable phase; afterwards, the system may undergo a polymorphic form transition toward another metastable phase, or directly to the stable phase. Tahri et al. [44] evaluated the competition between the nucleation, the growth, and the Ostwald ripening of the different phases by means of the kinetic equation model and concluded that Ostwald ripening can induce the total dissolution of the slow growing stable polymorph nuclei, leading to a result in agreement with the Ostwald rule of stages.

As supersaturation plays an important role during polymorph crystallization, understanding the competition between nucleation rates of different polymorphs is crucial for polymorphism control in a supersaturated solution. In the current paper a competitive kinetic model for polymorph nucleation is proposed to elucidate the effects of supersaturation on polymorph selection.

2. Theory

A competitive kinetic model is developed to describe the time evolution of two different polymorphic cluster size distributions in a supersaturated solution, where the simultaneous nucleation of the two polymorphs is controlled by the association and dissociation mechanisms during the induction time period. Although the Ostwald rule of stages postulates that a crystallization system progresses from the supersaturated state to equilibrium in stages, each stage representing the smallest possible change in free energy [4]. In the dimorphic system this means the initial appearance of the metastable crystals, followed by their transformation to the stable crystals. However, in the actual crystallization system kinetics are often more important than thermodynamics. It is in fact, if more than one phase is thermodynamically possible, the resulting phase is not just the one that is thermodynamically most likely. Instead, the resulting crystals are determined by the relative rates of crystal nucleation and growth of the metastable and stable forms, which usually depends on the process conditions, e.g., supersaturation, crystallization temperature, and the solvent type [4,45,46,47].

In derivation of the competitive kinetic model for polymorph nucleation, it is assumed that: (1) Although there is only one type of the solute molecules $\left({\mathrm{n}}_1\right)$, the solute clusters are divided into two types—A form $\left({\mathrm{n}}_{\mathrm{i},\mathrm{A}}, \mathrm{i}\ge 2\right)$ and B form $\left({\mathrm{n}}_{\mathrm{i},\mathrm{B}}, \mathrm{i}\ge 2\right)$; (2) Depending on the steric colliding direction between two solute molecules, two solute molecules can collide to form either an A-type or B-type cluster; (3) Depending on the steric colliding direction, a solute molecule can collide with an A-type cluster to form a larger A-type cluster or collide with a B-type cluster to form a larger B-type cluster; (4) Only two solute clusters of the same type can collide to form a larger solute cluster of the same type, i.e., the collision between A-type clusters and B-type clusters results in no formation of a larger solute cluster due to the structure difference; (5) A solute cluster smaller than the critical nucleus size for ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$ or ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$ might dissociate to form one primary particle and one smaller solute cluster of the same type due to the thermodynamic instability; (6) As the size of a cluster exceeds the critical nucleus size for ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(\mathrm{i}\ge {\mathrm{g}}_{\mathrm{A}}\right)$ or ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(\mathrm{i}\ge {\mathrm{g}}_{\mathrm{B}}\right)$, it becomes stable and no dissociation occurs. The subsequent growth leads to a new crystal of the same type.

Various association and dissociation processes are depicted in simplified form in

Table 1. Various association and dissociation processes for polymorph nucleation.

Association and Dissociation Processes
${\mathrm{n}}_1+{\mathrm{n}}_1\stackrel{\hspace{1em}{\mathrm{k}}_{\mathrm{A}}\hspace{1em}}{\to }{\mathrm{n}}_{2,\mathrm{A}}$$\mathrm{or} {\mathrm{n}}_1+{\mathrm{n}}_1\stackrel{{\hspace{1em}\mathrm{k}}_{\mathrm{B}\hspace{1em}}}{\to }{\mathrm{n}}_{2,\mathrm{B}}$
${\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{i},\mathrm{A}}\stackrel{{\hspace{1em}\mathrm{k}}_{\mathrm{A}}\hspace{1em}}{\to }{\mathrm{n}}_{\mathrm{i}+1,\mathrm{A}} \left(\mathrm{i}\ge 2\right)$
${\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{i},\mathrm{B}}\stackrel{{\hspace{1em}\mathrm{k}}_{\mathrm{B}\hspace{1em}}}{\to }{\mathrm{n}}_{\mathrm{i}+1,\mathrm{B}} \left(\mathrm{i}\ge 2\right)$
${\mathrm{n}}_{\mathrm{i},\mathrm{A}}+{\mathrm{n}}_{\mathrm{j},\mathrm{A}}\stackrel{{\hspace{1em}\mathrm{k}}_{\mathrm{A}\hspace{1em}}}{\to }{\mathrm{n}}_{\mathrm{i}+\mathrm{j},\mathrm{A}} \left(\mathrm{i}\ge 2, \mathrm{j}\ge 2\right)$
${\mathrm{n}}_{\mathrm{i},\mathrm{B}}+{\mathrm{n}}_{\mathrm{j},\mathrm{B}}\stackrel{{\hspace{1em}\mathrm{k}}_{\mathrm{B}\hspace{1em}}}{\to }{\mathrm{n}}_{\mathrm{i}+\mathrm{j},\mathrm{B}}$$\left(\mathrm{i}\ge 2, \mathrm{j}\ge 2\right)$
${\mathrm{n}}_{\mathrm{i},\mathrm{A}}+{\mathrm{n}}_{\mathrm{j},\mathrm{B}}\to$$\mathrm{no} \mathrm{association} \left(\mathrm{i}\ge 2, \mathrm{j}\ge 2\right)$
${\mathrm{n}}_{2,\mathrm{A}}\stackrel{{\hspace{1em}\mathrm{k}}_{\mathrm{dA},2}\hspace{1em}}{\to }{\mathrm{n}}_1+{\mathrm{n}}_1$
${\mathrm{n}}_{2,\mathrm{B}}\stackrel{{\hspace{1em}\mathrm{k}}_{\mathrm{dB},2}\hspace{1em}}{\to }{\mathrm{n}}_1+{\mathrm{n}}_1$
${\mathrm{n}}_{\mathrm{i},\mathrm{A}}\stackrel{{\hspace{1em}\mathrm{k}}_{{\mathrm{dA}}_{\mathrm{i}}}\hspace{1em}}{\to }{\mathrm{n}}_{\mathrm{i}-1,\mathrm{A}}+{\mathrm{n}}_1 \left(3\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$
${\mathrm{n}}_{\mathrm{i},\mathrm{B}}\stackrel{{\hspace{1em}\mathrm{k}}_{{\mathrm{dB}}_{\mathrm{i}}\hspace{1em}}}{\to }{\mathrm{n}}_{\mathrm{i}-1,\mathrm{B}}+{\mathrm{n}}_1 \left(3\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$

. The time evolution of ${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(\mathrm{i}\ge 2\right)$ and ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(\mathrm{i}\ge 2\right)$ for polymorph nucleation in a super saturation solution can be derived as follows. Note that ${\mathrm{n}}_{1,\mathrm{A}}={\mathrm{n}}_{1,\mathrm{B}}={\mathrm{n}}_1$ due to only one type of the solute molecules. Based on Smoluchowski’s agglomeration theory [48,49], the net formation rate of ${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}} \left(\mathrm{i}\ge 2\right)$, and ${\mathrm{n}}_{\mathrm{i},\mathrm{B}} \left(\mathrm{i}\ge 2\right)$, by association can be described respectively as:

$${\mathrm{RA}}_1=-{\mathrm{k}}_{\mathrm{A}}{\mathrm{n}}_1\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)-{\mathrm{k}}_{\mathrm{B}}{\mathrm{n}}_1\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{B}}\right)$$

(1)

$${\mathrm{RA}}_{\mathrm{i},\mathrm{A}}=-{\mathrm{k}}_{\mathrm{A}}{\mathrm{n}}_{\mathrm{i},\mathrm{A}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)+\frac{1}{2}{\mathrm{k}}_{\mathrm{A}}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{A}}\hspace{1em}\left(\mathrm{i}\ge 2\right)$$

(2)

$${\mathrm{RA}}_{\mathrm{i},\mathrm{B}}=-{\mathrm{k}}_{\mathrm{B}}{\mathrm{n}}_{\mathrm{i},\mathrm{B}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{B}}\right)+\frac{1}{2}{\mathrm{k}}_{\mathrm{B}}{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{B}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{B}}\hspace{1em}\left(\mathrm{i}\ge 2\right)$$

(3)

where ${\mathrm{k}}_{\mathrm{A}}$ and ${\mathrm{k}}_{\mathrm{B}}$ represents the association rate constant of A-type clusters and B-type clusters, respectively. Note that ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}={{\displaystyle \sum }}_{\mathrm{i}=2}^{\infty }{\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ and ${\mathrm{n}}_{\mathrm{t},\mathrm{B}}={{\displaystyle \sum }}_{\mathrm{i}=2}^{\infty }{\mathrm{n}}_{\mathrm{i},\mathrm{B}}$.

According to classical nucleation theory (CNT) [4,5], a cluster becomes stable when its size reaches the critical nucleus size. Thus, dissociation only occurs for ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$ or ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$. As similar to the solute clustering process in a supersaturation solution [50], gradual dissociation kernel is proposed in this work. For gradual dissociation kernel, one large aggregate, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$, dissociates into one primary particle, ${\mathrm{n}}_1$, and one smaller aggregate, ${\mathrm{n}}_{\mathrm{i}-1,\mathrm{A}}$. Similar dissociation process is applied for ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$. Thus, gradual dissociation kernel corresponds to gradual dissolution of the solute clusters smaller than a critical nucleus size due to the thermodynamic instability.

The net formation rate of ${\mathrm{n}}_1$ by dissociation for gradual disruption kernel is given by

$${\mathrm{RD}}_1=2{\mathrm{k}}_{\mathrm{dA},2}{\mathrm{n}}_{2,\mathrm{A}}+2{\mathrm{k}}_{\mathrm{dB},2}{\mathrm{n}}_{2,\mathrm{B}}+{\displaystyle \sum }_{\mathrm{j}=3}^{{\mathrm{g}}_{\mathrm{A}}-1}{\mathrm{k}}_{\mathrm{dA},\mathrm{j}}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}+{\displaystyle \sum }_{\mathrm{j}=3}^{{\mathrm{g}}_{\mathrm{B}}-1}{\mathrm{k}}_{\mathrm{dB},\mathrm{j}}{\mathrm{n}}_{\mathrm{j},\mathrm{B}}$$

(4)

where the first and second terms on the right-hand side of Equation (4) represent the birth term due to dissociation of ${\mathrm{n}}_{2,\mathrm{A}}$ and ${\mathrm{n}}_{2,\mathrm{B}}$ while the third and fourth terms represent the birth term due to dissociation of ${\mathrm{n}}_{\mathrm{j},\mathrm{A}}$ $\left(3\le \mathrm{j}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$ and ${\mathrm{n}}_{\mathrm{j},\mathrm{B}}$ $\left(3\le \mathrm{j}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$. In this work, ${\mathrm{k}}_{\mathrm{dA},\mathrm{j}}={\mathrm{k}}_{\mathrm{dA}0}\left(\mathrm{j}-1\right)$ and ${\mathrm{k}}_{\mathrm{dB},\mathrm{j}}={\mathrm{k}}_{\mathrm{dB}0}(\mathrm{j}-1$) are assumed due to more molecules available for dissociation for larger clusters.

As dissociation occurs for ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$, the net formation rate of ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(\mathrm{i}\ge 2\right)$ by dissociation can be described as

$${\mathrm{RD}}_{\mathrm{i},\mathrm{A}}=-{\mathrm{k}}_{\mathrm{dA},\mathrm{i}}{\mathrm{n}}_{\mathrm{i},\mathrm{A}}+{\mathrm{k}}_{\mathrm{dA},\mathrm{i}+1}{\mathrm{n}}_{\mathrm{i}+1,\mathrm{A}}\hspace{1em}\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-2\right)$$

(5)

$${\mathrm{RD}}_{\mathrm{i},\mathrm{A}}=-{\mathrm{k}}_{\mathrm{dA},\mathrm{i}}{\mathrm{n}}_{\mathrm{i},\mathrm{A}}\hspace{1em}\left(\mathrm{i}={\mathrm{g}}_{\mathrm{A}}-1\right)$$

(6)

$${\mathrm{RD}}_{\mathrm{i},\mathrm{A}}=0\hspace{1em}\left(\mathrm{i}\ge {\mathrm{g}}_{\mathrm{A}}\right)$$

(7)

Note that no dissociation occurs for ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(\mathrm{i}\ge {\mathrm{g}}_{\mathrm{A}}\right)$. Similarly, as dissociation occurs for ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$, ${\mathrm{RD}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$ can be derived. Note that no dissociation occurs for ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(\mathrm{i}\ge {\mathrm{g}}_{\mathrm{B}}\right)$.

To determine the time evolution of ${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}\left(\mathrm{i}\ge 2\right)$, and ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}\left(\mathrm{i}\ge 2\right)$, the net formation rate by both association and dissociation should be considered. Thus, one obtains

$$\frac{{\mathrm{dn}}_1}{{\mathrm{d}}_{\mathrm{t}}}={\mathrm{RA}}_1+{\mathrm{RD}}_1$$

(8)

$$\frac{{\mathrm{dn}}_{\mathrm{i},\mathrm{A}}}{{\mathrm{d}}_{\mathrm{t}}}={\mathrm{RA}}_{\mathrm{i},\mathrm{A}}+{\mathrm{RD}}_{\mathrm{i},\mathrm{A}}\hspace{1em}\left(\mathrm{i}\ge 2\right)$$

(9)

$$\frac{{\mathrm{dn}}_{\mathrm{i},\mathrm{B}}}{{\mathrm{d}}_{\mathrm{t}}}={\mathrm{RA}}_{\mathrm{i},\mathrm{B}}+{\mathrm{RD}}_{\mathrm{i},\mathrm{B}}\hspace{1em}\left(\mathrm{i}\ge 2\right)$$

(10)

Substituting Equations (1,4) into Equation (8) yields

$$\frac{{\mathrm{dn}}_1}{{\mathrm{d}}_{\mathrm{t}}}=-{\mathrm{k}}_{\mathrm{A}}{\mathrm{n}}_1\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)-{\mathrm{k}}_{\mathrm{B}}{\mathrm{n}}_1\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{B}}\right)+2{\mathrm{k}}_{\mathrm{dA},2}{\mathrm{n}}_{2,\mathrm{A}}+2{\mathrm{k}}_{\mathrm{dB},2}{\mathrm{n}}_{2,\mathrm{B}}+{\displaystyle \sum }_{\mathrm{j}=3}^{{\mathrm{g}}_{\mathrm{A}}-1}{\mathrm{k}}_{\mathrm{dA},\mathrm{j}}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}+{\displaystyle \sum }_{\mathrm{j}=3}^{{\mathrm{g}}_{\mathrm{B}}-1}{\mathrm{k}}_{\mathrm{dB},\mathrm{j}}{\mathrm{n}}_{\mathrm{j},\mathrm{B}}$$

(11)

Substituting Equations (2,5–7) into Equation (9) yields

$$\frac{{\mathrm{dn}}_{\mathrm{i},\mathrm{A}}}{{\mathrm{d}}_{\mathrm{t}}}=-{\mathrm{k}}_{\mathrm{A}}{\mathrm{n}}_{\mathrm{i},\mathrm{A}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)+\frac{1}{2}{\mathrm{k}}_{\mathrm{A}}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{A}}-{\mathrm{k}}_{\mathrm{dA},\mathrm{i}}{\mathrm{n}}_{\mathrm{i},\mathrm{A}}+{\mathrm{k}}_{\mathrm{dA},\mathrm{i}+1}{\mathrm{n}}_{\mathrm{i}+1,\mathrm{A}}\hspace{1em}\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-2\right)$$

(12)

$$\frac{{\mathrm{dn}}_{\mathrm{i},\mathrm{A}}}{{\mathrm{d}}_{\mathrm{t}}}=-{\mathrm{k}}_{\mathrm{A}}{\mathrm{n}}_{\mathrm{i},\mathrm{A}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)+\frac{1}{2}{\mathrm{k}}_{\mathrm{A}}{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{A}}-{\mathrm{k}}_{\mathrm{dA},\mathrm{i}}{\mathrm{n}}_{\mathrm{i},\mathrm{A}}\hspace{1em}\left(\mathrm{i}={\mathrm{g}}_{\mathrm{A}}-1\right)$$

(13)

$$\frac{{\mathrm{dn}}_{\mathrm{i},\mathrm{A}}}{{\mathrm{d}}_{\mathrm{t}}}=-{\mathrm{k}}_{\mathrm{A}}{\mathrm{n}}_{\mathrm{i},\mathrm{A}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)+\frac{1}{2}{\mathrm{k}}_{\mathrm{A}}{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{A}}\hspace{1em}\left(\mathrm{i}\ge {\mathrm{g}}_{\mathrm{A}}\right)$$

(14)

Summing Equations (12–14) from $\mathrm{i}=2$ to $\infty$ yields

$$\begin{gathered} \frac{{\mathrm{dn}}_{\mathrm{t},\mathrm{A}}}{{\mathrm{d}}_{\mathrm{t}}}=-{\mathrm{k}}_{\mathrm{A}}{{\displaystyle \sum }}_{\mathrm{i}=2}^{\infty }{\mathrm{n}}_{\mathrm{i},\mathrm{A}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)+\frac{1}{2}{\mathrm{k}}_{\mathrm{A}}{{\displaystyle \sum }}_{\mathrm{i}=2}^{\infty }{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{A}}-{\mathrm{k}}_{\mathrm{dA},2}{\mathrm{n}}_{2,\mathrm{A}}=-{\mathrm{k}}_{\mathrm{A}}{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)+ \\ \frac{1}{2}{\mathrm{k}}_{\mathrm{A}}{\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)}^2-{\mathrm{k}}_{\mathrm{dA},2}{\mathrm{n}}_{2,\mathrm{A}}=\frac{1}{2}{\mathrm{k}}_{\mathrm{A}}\left({\mathrm{n}}_1{}^2-{\mathrm{n}}_{\mathrm{t},\mathrm{A}}{}^2\right)-{\mathrm{k}}_{\mathrm{dA},2}{\mathrm{n}}_{2,\mathrm{A}} \end{gathered}$$

(15)

where ${{\displaystyle \sum }}_{\mathrm{i}=2}^{\infty }{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{A}}={\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)}^2$ (see Equation (A1) in Appendix A). Multiplying Equations (14) by $\mathrm{i}$ and summing the resulting equation from $\mathrm{i}={\mathrm{g}}_{\mathrm{A}}$ to $\infty$ yields (see Equation (A2) in Appendix A)

$$\begin{array}{ll}\frac{{\mathrm{dM}}_{\mathrm{C},\mathrm{A}}}{\mathrm{dt}}& =-{\mathrm{k}}_{\mathrm{A}}({\displaystyle {\displaystyle \sum }_{\mathrm{i}={\mathrm{g}}_{\mathrm{A}}}^{\infty }}{\mathrm{in}}_{\mathrm{i},\mathrm{A}})\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)+\frac{1}{2}{\mathrm{k}}_{\mathrm{A}}{\displaystyle {\displaystyle \sum }_{\mathrm{i}={\mathrm{g}}_{\mathrm{A}}}^{\infty }}\mathrm{i}{\displaystyle {\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{i}-1}}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{A}}\\ & =-{\mathrm{k}}_{\mathrm{A}}{\mathrm{M}}_{\mathrm{C},\mathrm{A}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)\\ & +\frac{1}{2}{\mathrm{k}}_{\mathrm{A}}\left[2\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)\left({\mathrm{n}}_1+{\displaystyle {\displaystyle \sum }_{\mathrm{i}=2}^{{\mathrm{g}}_{\mathrm{A}}-1}}{\mathrm{in}}_{\mathrm{i},\mathrm{A}}+{\mathrm{M}}_{\mathrm{C},\mathrm{A}}\right)-{\displaystyle {\displaystyle \sum }_{\mathrm{i}=2}^{{\mathrm{g}}_{\mathrm{A}}-1}}\mathrm{i}{\displaystyle {\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{i}-1}}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{A}}\right]\\ & ={\mathrm{k}}_{\mathrm{A}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{A}}\right)\left({\mathrm{n}}_1+{\displaystyle {\displaystyle \sum }_{\mathrm{i}=2}^{{\mathrm{g}}_{\mathrm{A}}-1}}{\mathrm{in}}_{\mathrm{i},\mathrm{A}}\right)-\frac{1}{2}{\mathrm{k}}_{\mathrm{A}}{\displaystyle {\displaystyle \sum }_{\mathrm{i}=2}^{{\mathrm{g}}_{\mathrm{A}}-1}}\mathrm{i}{\displaystyle {\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{i}-1}}{\mathrm{n}}_{\mathrm{j},\mathrm{A}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{A}}\end{array}$$

(16)

where ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}={{\displaystyle \sum }}_{\mathrm{i}={\mathrm{g}}_{\mathrm{A}}}^{\infty }{\mathrm{in}}_{\mathrm{i},\mathrm{A}}$.

Similarly, one can derive

$$\frac{{\mathrm{dn}}_{\mathrm{i},\mathrm{B}}}{{\mathrm{d}}_{\mathrm{t}}}=-{\mathrm{k}}_{\mathrm{B}}{\mathrm{n}}_{\mathrm{i},\mathrm{B}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{B}}\right)+\frac{1}{2}{\mathrm{k}}_{\mathrm{B}}{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{B}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{B}}-{\mathrm{k}}_{\mathrm{dB},\mathrm{i}}{\mathrm{n}}_{\mathrm{i},\mathrm{B}}+{\mathrm{k}}_{\mathrm{dB},\mathrm{i}+1}{\mathrm{n}}_{\mathrm{i}+1,\mathrm{B}}\hspace{1em}\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-2\right)$$

(17)

$$\frac{{\mathrm{dn}}_{\mathrm{i},\mathrm{B}}}{{\mathrm{d}}_{\mathrm{t}}}=-{\mathrm{k}}_{\mathrm{B}}{\mathrm{n}}_{\mathrm{i},\mathrm{B}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{B}}\right)+\frac{1}{2}{\mathrm{k}}_{\mathrm{B}}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{B}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{B}}-{\mathrm{k}}_{\mathrm{dB},\mathrm{i}}{\mathrm{n}}_{\mathrm{i},\mathrm{B}}\hspace{1em}\left(\mathrm{i}={\mathrm{g}}_{\mathrm{B}}-1\right)$$

(18)

$$\frac{{\mathrm{dn}}_{\mathrm{i},\mathrm{B}}}{{\mathrm{d}}_{\mathrm{t}}}=-{\mathrm{k}}_{\mathrm{B}}{\mathrm{n}}_{\mathrm{i},\mathrm{B}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{B}}\right)+\frac{1}{2}{\mathrm{k}}_{\mathrm{B}}{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{B}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{B}}\hspace{1em}\left(\mathrm{i}\ge {\mathrm{g}}_{\mathrm{B}}\right)$$

(19)

Summing Equations (17–19) from $\mathrm{i}=2$ to $\infty$ yields

$$\frac{{\mathrm{dn}}_{\mathrm{t},\mathrm{B}}}{{\mathrm{d}}_{\mathrm{t}}}=\frac{1}{2}{\mathrm{k}}_{\mathrm{B}}\left({\mathrm{n}}_1{}^2-{\mathrm{n}}_{\mathrm{t},\mathrm{B}}{}^2\right)-{\mathrm{k}}_{\mathrm{dB},2}{\mathrm{n}}_{2,\mathrm{B}}$$

(20)

Multiplying Equations (19) by $\mathrm{i}$ and summing the resulting equation from $\mathrm{i}={\mathrm{g}}_{\mathrm{B}}$ to $\infty$ yields

$$\frac{{\mathrm{dM}}_{\mathrm{C},\mathrm{B}}}{\mathrm{dt}}={\mathrm{k}}_{\mathrm{B}}\left({\mathrm{n}}_1+{\mathrm{n}}_{\mathrm{t},\mathrm{B}}\right)\left({\mathrm{n}}_1+{\displaystyle \sum }_{\mathrm{i}=2}^{{\mathrm{g}}_{\mathrm{B}}-1}{\mathrm{in}}_{\mathrm{i},\mathrm{B}}\right)-\frac{1}{2}{\mathrm{k}}_{\mathrm{B}}{\displaystyle \sum }_{\mathrm{i}=2}^{{\mathrm{g}}_{\mathrm{B}}-1}\mathrm{i}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{i}-1}{\mathrm{n}}_{\mathrm{j},\mathrm{B}}{\mathrm{n}}_{\mathrm{i}-\mathrm{j},\mathrm{B}}$$

(21)

where ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}={{\displaystyle \sum }}_{\mathrm{i}={\mathrm{g}}_{\mathrm{B}}}^{\infty }{\mathrm{in}}_{\mathrm{i},\mathrm{B}}$.

When solutes exist as free molecules initially, ${\mathrm{n}}_1\left(0\right)={\mathrm{C}}_0$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}\left(0\right)={\mathrm{n}}_{\mathrm{i},\mathrm{B}}\left(0\right)=0$ ($\mathrm{i}\ge 2)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}\left(0\right)={\mathrm{n}}_{\mathrm{t},\mathrm{B}}\left(0\right)=0$, and ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}\left(0\right)={\mathrm{M}}_{\mathrm{C},\mathrm{B}}\left(0\right)=0$. Thus, Equations (11–13, 15–18, 20, 21) constitute of a set of ${\mathrm{g}}_{\mathrm{A}}+{\mathrm{g}}_{\mathrm{B}}+1$ differential equations that can be simultaneously solved for the time evolution of ${\mathrm{g}}_{\mathrm{A}}+{\mathrm{g}}_{\mathrm{B}}+1$ unknowns—${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}$, ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{B}}$, ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$.

The induction time is defined as the time at which the volume fraction of the newly formed solid phase in solutions becomes detectable [4]. For simplicity, the minimum detectable volume fraction of the newly formed solid phase, ${\mathrm{f}}_{\mathrm{V}}$, at the induction time is assumed corresponding to the total volume fraction of stable A-type and B-type clusters. As ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(\mathrm{i}\ge {\mathrm{g}}_{\mathrm{A}}\right)$ and ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(\mathrm{i}\ge {\mathrm{g}}_{\mathrm{B}}\right)$ represents the number concentration of stable A-type and B-type clusters, respectively, one obtains

At

$$\mathrm{t}={\mathrm{t}}_{\mathrm{ind}},\hspace{1em}{\mathrm{V}}_{\mathrm{m}}\left({\mathrm{M}}_{\mathrm{C},\mathrm{A}}+{\mathrm{M}}_{\mathrm{C},\mathrm{B}}\right)={\mathrm{f}}_{\mathrm{V}}$$

(22)

where ${\mathrm{V}}_{\mathrm{m}}$ denotes the volume of a solute molecule. As ${\mathrm{V}}_{\mathrm{m}}{\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{V}}_{\mathrm{m}}{\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ represents the volume fraction of stable A-type and B-type clusters in solutions, respectively, the weight fraction of the stable A-type crystals at the induction time is defined as

At

$$\mathrm{t}={\mathrm{t}}_{\mathrm{ind}},\hspace{1em}{\mathrm{w}}_{\mathrm{A}}=\frac{{\mathrm{M}}_{\mathrm{C},\mathrm{A}}}{{\mathrm{M}}_{\mathrm{C},\mathrm{A}}+{\mathrm{M}}_{\mathrm{C},\mathrm{B}}}$$

(23)

Note that ${\mathrm{f}}_{\mathrm{V}}$ depends on the measurement device and on the substance. Based on the study of 28 inorganic systems, Mersmann and Bartosch [51] estimated ${\mathrm{f}}_{\mathrm{V}}={10}^{-4}-{10}^{-3}$. As the intermediate value, ${\mathrm{f}}_{\mathrm{V}}=4\times {10}^{-4}$, was adopted at the detection of the nucleation point for the Lasentec focus beam reflectance measurements reported by Lindenberg and Mazzotti [52] and for the turbidity measurements reported by Shiau and his coworkers [53,54,55], this value is also adopted in this study.

The proposed model is applied to the polymorph nucleation based on CNT. However, for the two-step mechanism of nucleation, nucleation is thought to consist of two steps in series, i.e., the formation of the dense liquid clusters in solutions followed by the formation of the crystalline nucleus inside the dense liquid clusters [56]. Thus, the derivation above is not applicable to the two-step mechanism of nucleation.

3. Results and Discussion

The experimental results for eflucimibe polymorph nucleation reported by Teychene and Biscans [39] are illustrated to verify the developed model. Eflucimibe is a new drug inhibiting acyl-coenzyme A: cholesterol acyltransferase (ACAT), an enzyme which inhibition may lead to lower serum cholesterol concentration. Eflucimibe crystallizes from a mixture of ethanol and n-heptane into two polymorphic forms—A form and B form. A form is the stable form while B form is the metastable form. These two forms have different solubilities and interfacial energies. The experimental induction time data and the final measured weight fractions of eflucimibe polymorphs for various supersaturation at $35 {}^{°}\mathrm{C}$ are listed in

Table 2. The experimental induction time data and the final measured weight fractions of eflucimibe polymorphs for various supersaturation at $35 {}^{°}\mathrm{C}$ reported by Teychene and Biscans [39].

${\mathbf{S}}_{\mathbf{A}} (-)$	${\mathbf{S}}_{\mathbf{B}} (-)$	${\mathbf{C}}_0 (\mathbf{no}./{\mathbf{cm}}^3)$	${\mathbf{t}}_{\mathbf{ind},\mathbf{exp}} \left(\mathbf{s}\right)$	${\mathbf{g}}_{\mathbf{A}} (-)$	${\mathbf{g}}_{\mathbf{B}} (-)$	${\mathbf{w}}_{\mathbf{A},\mathbf{exp}} (-)$	Polymorphic Form
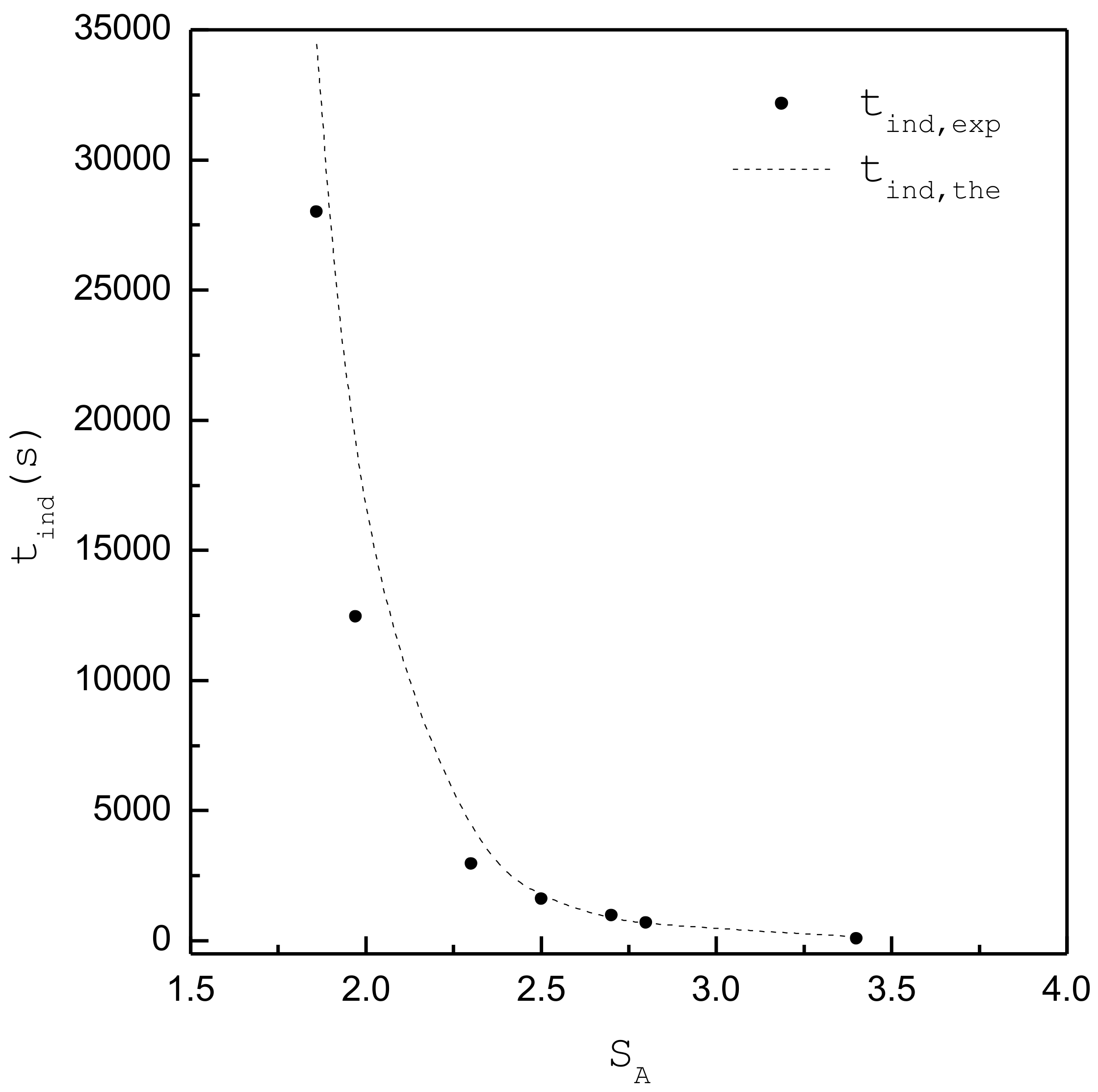
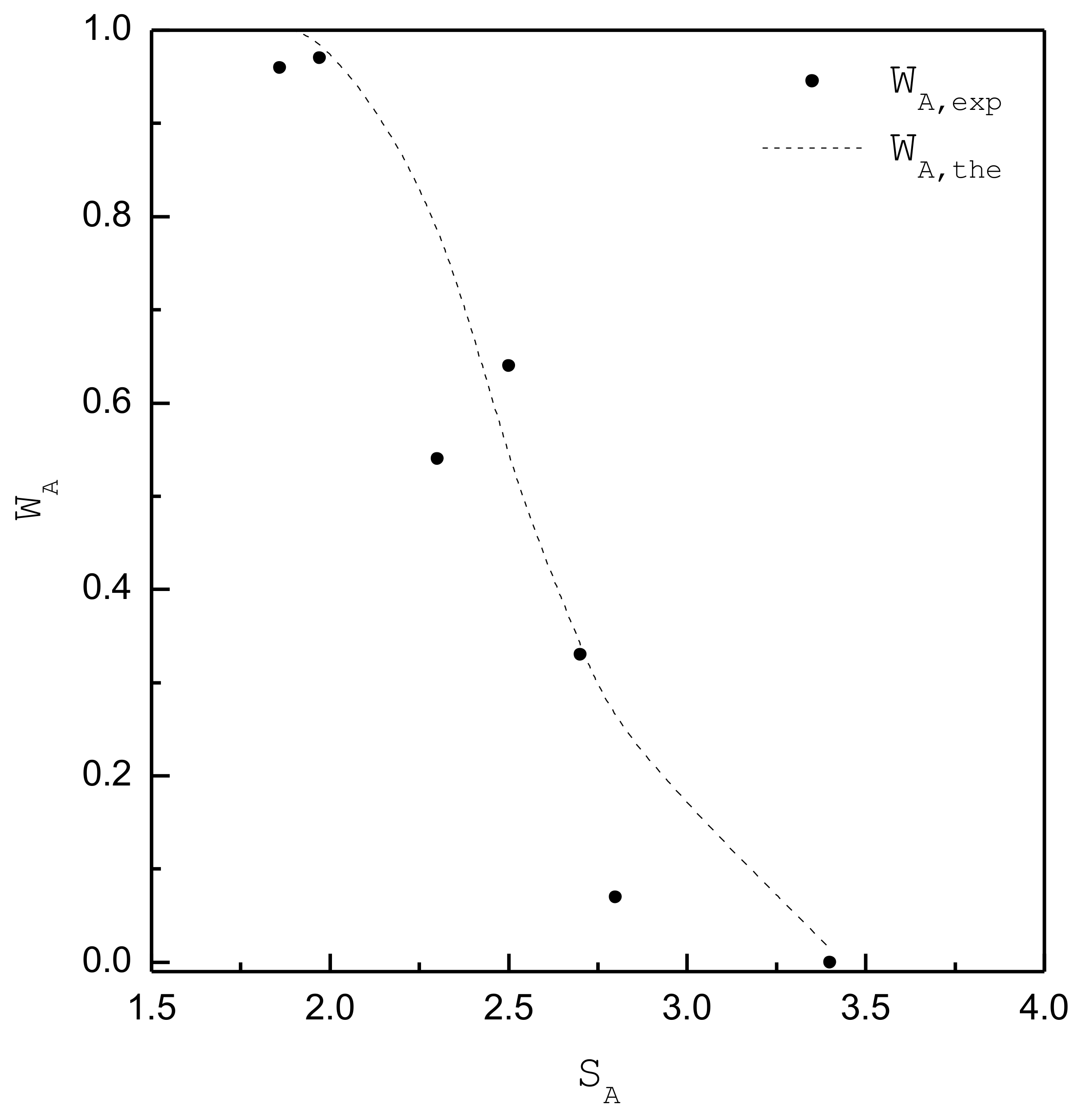
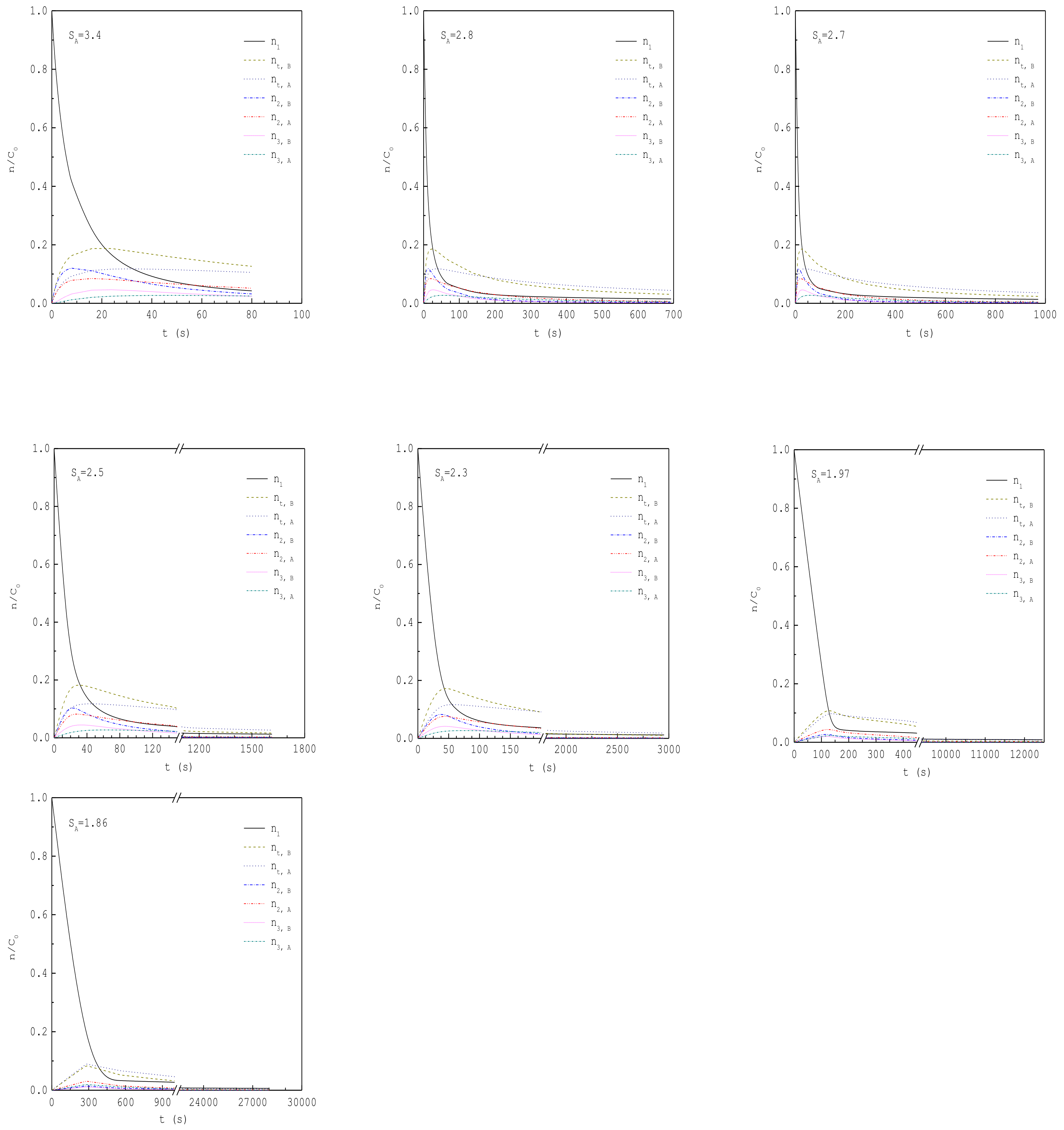
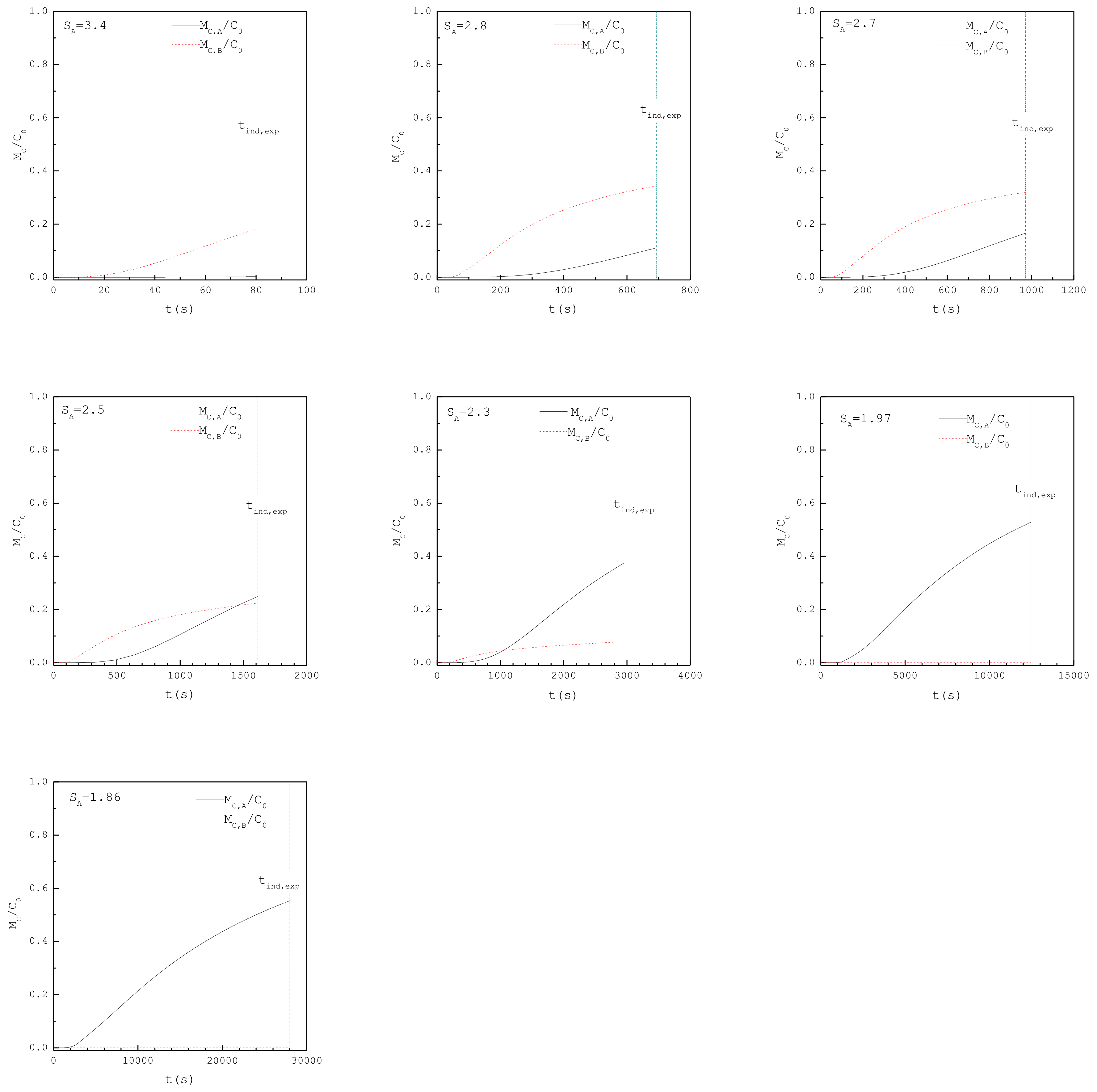
1.86	1.66	3.94 × 1019	28000	91	92	0.96	A
1.97	1.76	4.18 × 1019	12456	70	67	0.97	A
2.3	2.05	4.88 × 1019	2954	38	32	0.54	A+B
2.5	2.23	5.30 × 1019	1614	28	23	0.64	A+B
2.7	2.41	5.72 × 1019	971	22	18	0.33	A+B
2.8	2.50	5.94 × 1019	693	20	16	0.07	~B
3.4	3.03	7.21 × 1019	80	12	9	0	B

.

Based on CNT, critical nucleus sizes for A-type and B-type clusters can be respectively estimated as [4,5,57,58]

$${\mathrm{g}}_{\mathrm{A}}=\frac{32{\mathsf{\pi }\mathrm{V}}_{\mathrm{m}}{}^2{\mathsf{\gamma }}_{\mathrm{A}}{}^3}{3{\left({\mathrm{k}}_{\mathrm{B}}{\mathrm{T} \mathrm{lnS}}_{\mathrm{A}}\right)}^3}$$

(24)

$${\mathrm{g}}_{\mathrm{B}}=\frac{32{\mathsf{\pi }\mathrm{V}}_{\mathrm{m}}{}^2{\mathsf{\gamma }}_{\mathrm{B}}{}^3}{3{\left({\mathrm{k}}_{\mathrm{B}}{\mathrm{T} \mathrm{lnS}}_{\mathrm{B}}\right)}^3}$$

(25)

In Table 2, ${\mathrm{g}}_{\mathrm{A}}$ and ${\mathrm{g}}_{\mathrm{B}}$ are the closest integers calculated for each ${\mathrm{S}}_{\mathrm{A}}$ based on ${\mathsf{\gamma }}_{\mathrm{A}}=5.17\mathrm{erg}/{\mathrm{cm}}^2$ and ${\mathsf{\gamma }}_{\mathrm{B}}=4.23\mathrm{erg}/{\mathrm{cm}}^2$, respectively. Note that both ${\mathrm{g}}_{\mathrm{A}}$ and ${\mathrm{g}}_{\mathrm{B}}$ decrease with increasing ${\mathrm{S}}_{\mathrm{A}}$. The following values at $35 {}^{°}\mathrm{C}$ are used in the calculations: ${\mathsf{\rho }}_{\mathrm{c}}=1.3\mathrm{g}/{\mathrm{cm}}^3$, ${\mathrm{C}}_{\mathrm{eq},\mathrm{A}}=2.12\times {10}^{19}\mathrm{molecule}/{\mathrm{cm}}^3$, ${\mathrm{C}}_{\mathrm{eq},\mathrm{B}}=2.38\times {10}^{19}\mathrm{molecule}/{\mathrm{cm}}^3$, ${\mathrm{S}}_{\mathrm{B}}={\mathrm{S}}_{\mathrm{A}}/1.123$, ${\mathrm{M}}_{\mathrm{w}}=469.73$ and ${\mathrm{V}}_{\mathrm{m}}=1.59\times {10}^{-22}{\mathrm{cm}}^3/\mathrm{molecule}$. In Table 2 ${\mathrm{C}}_0$ represent the initial concentration of solutes for each ${\mathrm{S}}_{\mathrm{A}}$ calculated from ${\mathrm{S}}_{\mathrm{A}}={\mathrm{C}}_0/{\mathrm{C}}_{\mathrm{eq},\mathrm{A}}$.

By fitting the experimental induction time data and measured weight fractions of eflucimibe polymorphs with the proposed model, the following regression procedure is adopted to determine four parameters—${\mathrm{k}}_{\mathrm{A}}$, ${\mathrm{k}}_{\mathrm{B}}$, ${\mathrm{k}}_{\mathrm{dA}0}$ and ${\mathrm{k}}_{\mathrm{dB}0}$: (1) guess a set of ${\mathrm{k}}_{\mathrm{A}}$, ${\mathrm{k}}_{\mathrm{B}}$, ${\mathrm{k}}_{\mathrm{dA}0}$ and ${\mathrm{k}}_{\mathrm{dB}0}$; (2) determine the time evolution of ${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}$, ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{B}}$, ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ for each ${\mathrm{S}}_{\mathrm{A}}$ by solving Equations (11–13, 15–18, 20, 21) simultaneously; (3) calculate ${\mathrm{t}}_{\mathrm{ind},\mathrm{the}}$, at which it leads to ${\mathrm{V}}_{\mathrm{m}}\left({\mathrm{M}}_{\mathrm{C},\mathrm{A}}+{\mathrm{M}}_{\mathrm{C},\mathrm{B}}\right)={\mathrm{f}}_{\mathrm{V}}$, based on Equations (22) for each ${\mathrm{S}}_{\mathrm{A}}$; (4) calculate ${\mathrm{W}}_{\mathrm{A},\mathrm{the}}$ at ${\mathrm{t}}_{\mathrm{ind},\exp }$ based on Equation (23) for each ${\mathrm{S}}_{\mathrm{A}}$; (5) calculate ${\mathsf{\epsilon }}_{\mathrm{t}}$ from Equation (26); (6) calculate ${\mathsf{\epsilon }}_{\mathrm{w}}$ from Equation (27).

The average relative deviation between the experimental and theoretical induction time is defined as

$${\mathsf{\epsilon }}_{\mathrm{t}}=\frac{1}{\mathrm{H}}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{H}}\frac{|{\mathrm{t}}_{\mathrm{ind},\mathrm{the},\mathrm{j}}-{\mathrm{t}}_{\mathrm{ind},\exp ,\mathrm{j}}|}{{\mathrm{t}}_{\mathrm{ind},\exp ,\mathrm{j}}}$$

(26)

where $\mathrm{H}$ is the number of the experimental runs, ${\mathrm{t}}_{\mathrm{ind},\exp }$ is the induction time measured during the experiments, and ${\mathrm{t}}_{\mathrm{ind},\mathrm{the}}$ is the induction time calculated from Equation (22).

As shown in Table 2, pure A form is crystallized at low supersaturation and pure B form is crystallized at high supersaturation while a mixture of A form and B form is crystallized at intermediate supersaturation. For simplicity, the weight fractions of A-form eflucimibe measured at the end of the experiments are assumed close to the weight fractions of A-form eflucimibe nucleated at the induction time. The average relative deviation between the experimental and theoretical weight fraction of A-type crystals at the induction time is defined as

$${\mathsf{\epsilon }}_{\mathrm{w}}=\frac{1}{\mathrm{H}}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{H}}\frac{|{\mathrm{W}}_{\mathrm{A},\mathrm{the},\mathrm{j}}-{\mathrm{W}}_{\mathrm{A},\exp ,\mathrm{j}}|}{{\mathrm{W}}_{\mathrm{A},\exp ,\mathrm{j}}}$$

(27)

where ${\mathrm{w}}_{\mathrm{A},\exp }$ is the weight fractions of A-form eflucimibe measured at the end of the experiments, and ${\mathrm{w}}_{\mathrm{A},\mathrm{the}}$ is the weight fractions of A-form eflucimibe calculated from Equation (23).

It should be noted in the regression procedure that, for any guessed values of ${\mathrm{k}}_{\mathrm{A}}$, ${\mathrm{k}}_{\mathrm{B}}$, ${\mathrm{k}}_{\mathrm{dA}0}$ and ${\mathrm{k}}_{\mathrm{dB}0}$, a set of 184 differential equations for ${\mathrm{S}}_{\mathrm{A}}=1.86$ $\left({\mathrm{g}}_{\mathrm{A}}=91,{ \mathrm{g}}_{\mathrm{B}}=92\right)$ need to be simultaneously solved for the time evolution of ${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le 90\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}$, ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le 91\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{B}}$, ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$. However, as supersaturation is increased to ${\mathrm{S}}_{\mathrm{A}}=3.4$ $\left({\mathrm{g}}_{\mathrm{A}}=12,{ \mathrm{g}}_{\mathrm{B}}=9\right)$, only a set of 22 differential equations need to be simultaneously solved for the time evolution of ${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le 11\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}$, ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le 8\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{B}}$, ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$.

By repeating the regression procedure from (1) to (6), the optimal values of ${\mathrm{k}}_{\mathrm{A}}$, ${\mathrm{k}}_{\mathrm{B}}$, ${\mathrm{k}}_{\mathrm{dA}0}$ and ${\mathrm{k}}_{\mathrm{dB}0}$ with the smallest sum of ${\mathsf{\epsilon }}_{\mathrm{t}}$ and ${\mathsf{\epsilon }}_{\mathrm{w}}$ are determined based on ${\mathrm{f}}_{\mathrm{V}}=4\times {10}^{-4}$ in

Table 3. The optimal values of ${\mathrm{k}}_{\mathrm{A}}$, ${\mathrm{k}}_{\mathrm{B}}$, ${\mathrm{k}}_{\mathrm{dA}0}$ and ${\mathrm{k}}_{\mathrm{dB}0}$ with the smallest sum of ${\mathsf{\epsilon }}_{\mathrm{t}}$ and ${\mathsf{\epsilon }}_{\mathrm{w}}$ for $1.86\le {\mathrm{S}}_{\mathrm{A}}\le 3.4$ at 35 °C.

${\mathbf{k}}_{\mathbf{A}} ({\mathbf{cm}}^3/\mathbf{s})$	${\mathbf{k}}_{\mathbf{B}} ({\mathbf{cm}}^3/\mathbf{s})$	${\mathbf{k}}_{\mathbf{dA}0} (1/\mathbf{s})$	${\mathbf{k}}_{\mathbf{dB}0} (1/\mathbf{s})$	${\mathbf{\epsilon }}_{\mathbf{t}} (-)$	${\mathbf{\epsilon }}_{\mathbf{w}} (-)$
7.7 $\times$ 10−22	1.4 $\times$ 10−21	5.3 $\times$ 10−4	3.2 $\times$ 10−3	0.22	0.14

, which indicates ${\mathrm{k}}_{\mathrm{A}}=7.7\times {10}^{-22}{\mathrm{cm}}^3/\mathrm{s}$, ${\mathrm{k}}_{\mathrm{B}}=1.4\times {10}^{-21}{\mathrm{cm}}^3/\mathrm{s}$, ${\mathrm{k}}_{\mathrm{dA}0}=5.3\times {10}^{-4}{\mathrm{s}}^{-1}$ and ${\mathrm{k}}_{\mathrm{dB}0}=3.2\times {10}^{-3}{\mathrm{s}}^{-1}$, leading to $\frac{{\mathrm{k}}_{\mathrm{B}}}{{\mathrm{k}}_{\mathrm{A}}}=2$ and $\frac{{\mathrm{k}}_{\mathrm{dB}0}}{{\mathrm{k}}_{\mathrm{dA}0}}=6$. Thus, one obtains ${\mathrm{k}}_{\mathrm{B}}>{\mathrm{k}}_{\mathrm{A}}$ and ${\mathrm{k}}_{\mathrm{dB}0}>{\mathrm{k}}_{\mathrm{dA}0}$.

Due to the different activation energy for bonding between solute molecules, the association rate constants for A-type and B-type clusters can be expressed respectively as

$${\mathrm{k}}_{\mathrm{A}}={\mathrm{k}}_0\exp \left[-\frac{({\mathrm{E}}_{\mathrm{A}}^{*}-{\mathrm{E}}_0)}{\mathrm{RT}}\right]$$

(28)

$${\mathrm{k}}_{\mathrm{B}}={\mathrm{k}}_0\exp \left[-\frac{({\mathrm{E}}_{\mathrm{B}}^{*}-{\mathrm{E}}_0)}{\mathrm{RT}}\right]$$

(29)

where $\exp \left[-\frac{({\mathrm{E}}_{\mathrm{A}}^{*}-{\mathrm{E}}_0)}{\mathrm{RT}}\right]$ and $\exp \left[-\frac{({\mathrm{E}}_{\mathrm{B}}^{*}-{\mathrm{E}}_0)}{\mathrm{RT}}\right]$ represents the fraction of the successful collisions which overcomes the activation energy of association for A-type and B-type clusters, respectively. The collision rate constant, ${\mathrm{k}}_0$, is proportional to the diffusivity for solute clusters in a supersaturated solution [4]. Combining Equations (28–29) yields

$$\frac{{\mathrm{k}}_{\mathrm{B}}}{{\mathrm{k}}_{\mathrm{A}}}=\exp \left[\frac{({\mathrm{E}}_{\mathrm{A}}^{*}-{\mathrm{E}}_{\mathrm{B}}^{*})}{\mathrm{RT}}\right]$$

(30)

Substituting the optimal values of ${\mathrm{k}}_{\mathrm{A}}$ and ${\mathrm{k}}_{\mathrm{B}}$ at $35 {}^{°}\mathrm{C}$ into Equation (30) yields ${\mathrm{E}}_{\mathrm{A}}^{*}-{\mathrm{E}}_{\mathrm{B}}^{*}=1.5\mathrm{kJ}/\mathrm{mole}$. Thus, we conclude ${\mathrm{E}}_{\mathrm{A}}^{*}>{\mathrm{E}}_{\mathrm{B}}^{*}$ for association.

The dissociation rate constants for A-type and B-type clusters can be expressed respectively as

$${\mathrm{k}}_{\mathrm{dA}0}={\mathrm{k}}_{\mathrm{d}0}\exp \left[-\frac{({\mathrm{E}}_{\mathrm{A}}^{*}-{\mathrm{E}}_{\mathrm{A}})}{\mathrm{RT}}\right]$$

(31)

$${\mathrm{k}}_{\mathrm{dB}0}={\mathrm{k}}_{\mathrm{d}0}\exp \left[-\frac{({\mathrm{E}}_{\mathrm{B}}^{*}-{\mathrm{E}}_{\mathrm{B}})}{\mathrm{RT}}\right]$$

(32)

where the dissociation frequency factor, ${\mathrm{k}}_{\mathrm{d}0}$, mainly depends on the solution property. Combining Equations (32–33) yields

$$\frac{{\mathrm{k}}_{\mathrm{dB}0}}{{\mathrm{k}}_{\mathrm{dA}0}}=\exp \left[\frac{({\mathrm{E}}_{\mathrm{A}}^{*}-{\mathrm{E}}_{\mathrm{B}}^{*})+\left({\mathrm{E}}_{\mathrm{B}}-{\mathrm{E}}_{\mathrm{A}}\right)}{\mathrm{RT}}\right]$$

(33)

As ${\mathrm{E}}_{\mathrm{A}}^{*}-{\mathrm{E}}_{\mathrm{B}}^{*}=1.5\mathrm{kJ}/\mathrm{mole}$, substituting the optimal values of ${\mathrm{k}}_{\mathrm{dA}0}$ and ${\mathrm{k}}_{\mathrm{dB}0}$ at $35 {}^{°}\mathrm{C}$ into Equation (33) yields ${\mathrm{E}}_{\mathrm{B}}-{\mathrm{E}}_{\mathrm{A}}=3.1\mathrm{kJ}/\mathrm{mole}$. Thus, it yields ${\mathrm{E}}_{\mathrm{B}}>{\mathrm{E}}_{\mathrm{A}}$, which is consistent with the literature that form A is more stable than form B [39]. Based on the results using Equations (30,33), the change in potential energy during polymorph crystallization is plotted in Figure 1.

Based on the optimal values of ${\mathrm{k}}_{\mathrm{A}}$, ${\mathrm{k}}_{\mathrm{B}}$, ${\mathrm{k}}_{\mathrm{dA}0}$ and ${\mathrm{k}}_{\mathrm{dB}0}$ in Table 3, Figure 2 shows comparison of ${\mathrm{t}}_{\mathrm{ind},\mathrm{the}}$ and ${\mathrm{t}}_{\mathrm{ind},\exp }$ for various ${\mathrm{S}}_{\mathrm{A}}$, where ${\mathrm{t}}_{\mathrm{ind},\mathrm{the}}$ is calculated from Equation (22) using the time evolution ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$. The dashed line represents the calculated ${\mathrm{t}}_{\mathrm{ind},\mathrm{the}}$ while the solid circle represents the experimental ${\mathrm{t}}_{\mathrm{ind},\exp }$. It is found that ${\mathrm{t}}_{\mathrm{ind},\mathrm{the}}$ and ${\mathrm{t}}_{\mathrm{ind},\exp }$ decreases with increasing ${\mathrm{S}}_{\mathrm{A}}$ as both ${\mathrm{g}}_{\mathrm{A}}$ and ${\mathrm{g}}_{\mathrm{B}}$ decrease with increasing ${ \mathrm{S}}_{\mathrm{A}}$.

Figure 3 shows comparison of ${\mathrm{W}}_{\mathrm{A},\exp }$ and ${\mathrm{W}}_{\mathrm{A},\mathrm{the}}$ at the end of the experiments for various ${\mathrm{S}}_{\mathrm{A}}$, where ${\mathrm{W}}_{\mathrm{A},\mathrm{the}}$ is calculated from Equation (23) using the time evolution ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$. The dashed line represents the calculated ${\mathrm{W}}_{\mathrm{A},\mathrm{the}}$ while the solid circle represents the experimental ${\mathrm{W}}_{\mathrm{A},\exp }$. It is found that ${\mathrm{W}}_{\mathrm{A},\exp }$ and ${\mathrm{W}}_{\mathrm{A},\mathrm{the}}$ decreases with increasing ${\mathrm{S}}_{\mathrm{A}}$. These results can be attributed to ${\mathrm{k}}_{\mathrm{B}}>{\mathrm{k}}_{\mathrm{A}}$ and ${\mathrm{k}}_{\mathrm{dB}0}>{\mathrm{k}}_{\mathrm{dA}0}$. At higher ${\mathrm{S}}_{\mathrm{A}}$ due to smaller critical nucleus size and shorter induction time, association rate among ${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$, and ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$ plays a more important role than dissociation rate for ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$ and ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$ in nucleation. As ${\mathrm{k}}_{\mathrm{B}}>{\mathrm{k}}_{\mathrm{A}}$, it is easier for the metastable B-form to grow to smaller critical nucleus size at higher ${\mathrm{S}}_{\mathrm{A}}$. Thus, nucleation of the metastable B-form dominates at higher ${\mathrm{S}}_{\mathrm{A}}$, leading to ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}>{\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{w}}_{\mathrm{B}}>{\mathrm{w}}_{\mathrm{A}}$ at the end of the experiments. However, at lower ${\mathrm{S}}_{\mathrm{A}}$ due to greater critical nucleus size and longer induction time, dissociation rate becomes important for ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$ and ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$ in nucleation. As ${\mathrm{k}}_{\mathrm{dB}0}>{\mathrm{k}}_{\mathrm{dA}0}$, it becomes more difficult for the metastable B-form to grow to larger critical nucleus size at lower ${\mathrm{S}}_{\mathrm{A}}$. Subsequently, nucleation of the stable A-form dominates at lower ${\mathrm{S}}_{\mathrm{A}}$, leading to ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}>{\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ and ${\mathrm{w}}_{\mathrm{A}}>{\mathrm{w}}_{\mathrm{B}}$ at the end of the experiments. As displayed in Figure 2 and Figure 3, the fourteen experimental data points are fitted well to the corresponding calculated results by the developed model using the optimal values of ${\mathrm{k}}_{\mathrm{A}}$, ${\mathrm{k}}_{\mathrm{B}}$, ${\mathrm{k}}_{\mathrm{dA}0}$ and ${\mathrm{k}}_{\mathrm{dB}0}$.

The following time evolution of ${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{A}}-1\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}$, ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le {\mathrm{g}}_{\mathrm{B}}-1\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{B}}$, ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ are calculated based on the optimal values of ${\mathrm{k}}_{\mathrm{A}}$, ${\mathrm{k}}_{\mathrm{B}}$, ${\mathrm{k}}_{\mathrm{dA}0}$ and ${\mathrm{k}}_{\mathrm{dB}0}$ in Table 3. For example, a set of 184 differential equations for ${\mathrm{S}}_{\mathrm{A}}=1.86$ $\left({\mathrm{g}}_{\mathrm{A}}=91,{\mathrm{g}}_{\mathrm{B}}=92\right)$ are simultaneously solved for the time evolution of ${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le 90\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}$, ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le 91\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{B}}$, ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$. Similarly, a set of 22 differential equations for ${\mathrm{S}}_{\mathrm{A}}=3.4$ $\left({\mathrm{g}}_{\mathrm{A}}=12,{\mathrm{g}}_{\mathrm{B}}=9\right)$ are simultaneously solved for the time evolution of ${\mathrm{n}}_1$, ${\mathrm{n}}_{\mathrm{i},\mathrm{A}}$ $\left(2\le \mathrm{i}\le 11\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}$, ${\mathrm{n}}_{\mathrm{i},\mathrm{B}}$ $\left(2\le \mathrm{i}\le 8\right)$, ${\mathrm{n}}_{\mathrm{t},\mathrm{B}}$, ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$.

The variations of ${\mathrm{n}}_1$, ${\mathrm{n}}_{2,\mathrm{A}}$, ${\mathrm{n}}_{2,\mathrm{B}}$, ${\mathrm{n}}_{3,\mathrm{A}}$, ${\mathrm{n}}_{3,\mathrm{B}}$, ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}$ and ${\mathrm{n}}_{\mathrm{t},\mathrm{B}}$ with increasing time are displayed for various ${\mathrm{S}}_{\mathrm{A}}$ in Figure 4, where ${\mathrm{n}}_1$ decreases monotonically with increasing time; however, ${\mathrm{n}}_{2,\mathrm{A}}$, ${\mathrm{n}}_{2,\mathrm{B}}$, ${\mathrm{n}}_{3,\mathrm{A}}$, ${\mathrm{n}}_{3,\mathrm{B}}$, ${\mathrm{n}}_{\mathrm{t},\mathrm{A}}$ and ${\mathrm{n}}_{\mathrm{t},\mathrm{B}}$ passes through a maximum at certain time and then declines slowly for each ${\mathrm{S}}_{\mathrm{A}}$. A general trend is observed for various ${\mathrm{S}}_{\mathrm{A}}$ that, although ${\mathrm{n}}_1$ is significantly greater than ${\mathrm{n}}_{2,\mathrm{A}}$, ${\mathrm{n}}_{2,\mathrm{B}}$, ${\mathrm{n}}_{3,\mathrm{A}}$ and ${\mathrm{n}}_{3,\mathrm{B}}$ for $0<\mathrm{t}<0.1{ \mathrm{t}}_{\mathrm{ind}}$, ${\mathrm{n}}_{2,\mathrm{A}}$, ${\mathrm{n}}_{2,\mathrm{B}}$, ${\mathrm{n}}_{3,\mathrm{A}}$ and ${\mathrm{n}}_{3,\mathrm{B}}$ become not negligible compared to ${\mathrm{n}}_1$ for $\mathrm{t}>0.1{ \mathrm{t}}_{\mathrm{ind}}$. Thus, as ${\mathrm{n}}_1$ dominates in the earlier stage of nucleation, association between two solute clusters of the same type, ${\mathrm{n}}_{\mathrm{j},\mathrm{A}} \left(\mathrm{j}\ge 2\right)$ or ${\mathrm{n}}_{\mathrm{j},\mathrm{B}} \left(\mathrm{j}\ge 2\right)$, is nearly negligible for $0<\mathrm{t}<0.1{ \mathrm{t}}_{\mathrm{ind}}$. However, such association between two solute clusters of the same type becomes significant in the later stage of nucleation for $\mathrm{t}>0.1{ \mathrm{t}}_{\mathrm{ind}}$. In Figure 4, ${\mathrm{n}}_1/{\mathrm{C}}_0$ is decreased to 0.04 at ${\mathrm{t}}_{\mathrm{ind}}=80 \mathrm{s}$ for ${\mathrm{S}}_{\mathrm{A}}=3.4$; ${\mathrm{n}}_1/{\mathrm{C}}_0$ is decreased to 0.02 at ${\mathrm{t}}_{\mathrm{ind}}=1614\mathrm{s}$ for ${\mathrm{S}}_{\mathrm{A}}=2.5$; ${\mathrm{n}}_1/{\mathrm{C}}_0$ is decreased to 0.01 at ${\mathrm{t}}_{\mathrm{ind}}=28000 \mathrm{s}$ for ${\mathrm{S}}_{\mathrm{A}}=1.86$. Thus, ${\mathrm{n}}_1/{\mathrm{C}}_0$ at ${\mathrm{t}}_{\mathrm{ind}}$ becomes smaller for a lower ${\mathrm{S}}_{\mathrm{A}}$ due to longer induction time available for association.

The variations of ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ with increasing time are displayed for various ${\mathrm{S}}_{\mathrm{A}}$ in Figure 5, where ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ and ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ increases monotonically with increasing time for each ${\mathrm{S}}_{\mathrm{A}}$. For ${\mathrm{S}}_{\mathrm{A}}=1.86-1.97$, ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ is significantly greater than ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ at ${\mathrm{t}}_{\mathrm{ind}}$, leading to ${\mathrm{w}}_{\mathrm{A},\mathrm{the}}=1$ at ${\mathrm{t}}_{\mathrm{ind}}$ based on Equation (23), which is consistent with ${\mathrm{w}}_{\mathrm{A},\exp }=0.96-0.97$ in Table 2. Note that ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}/{\mathrm{C}}_0$ remains nearly zero in the range $0-{\mathrm{t}}_{\mathrm{ind}}$. Thus, nearly only form A is obtained at the end of experiments. For ${\mathrm{S}}_{\mathrm{A}}\ge 2.3$, ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ becomes significant compared to ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ at ${\mathrm{t}}_{\mathrm{ind}}$. For example, ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ is only slightly than ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ at ${\mathrm{t}}_{\mathrm{ind}}$ for ${\mathrm{S}}_{\mathrm{A}}=2.5$, leading to ${\mathrm{w}}_{\mathrm{A},\mathrm{the}}=0.55$ at ${\mathrm{t}}_{\mathrm{ind}}$ based on Equation (23), which is close to ${\mathrm{w}}_{\mathrm{A},\exp }=0.64$ in Table 2. Thus, form A is slightly more than form B at the end of experiments. For ${\mathrm{S}}_{\mathrm{A}}=2.7$, ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ becomes greater than ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ at ${\mathrm{t}}_{\mathrm{ind}}$, leading to ${\mathrm{w}}_{\mathrm{A},\mathrm{the}}=0.33$ at ${\mathrm{t}}_{\mathrm{ind}}$ based on Equation (23), which is consistent with ${\mathrm{w}}_{\mathrm{A},\exp }=0.33$ in Table 2. Thus, form B is more than form A at the end of experiments. For ${\mathrm{S}}_{\mathrm{A}}=3.4$, ${\mathrm{M}}_{\mathrm{C},\mathrm{B}}$ is significantly greater than ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}$ at ${\mathrm{t}}_{\mathrm{ind}}$, leading to ${\mathrm{w}}_{\mathrm{A},\mathrm{the}}=0$ at ${\mathrm{t}}_{\mathrm{ind}}$ based on Equation (23), which is consistent with ${\mathrm{w}}_{\mathrm{A},\exp }=0$ in Table 2. Note that ${\mathrm{M}}_{\mathrm{C},\mathrm{A}}/{\mathrm{C}}_0$ remains nearly zero in the range $0-{\mathrm{t}}_{\mathrm{ind}}$. Thus, nearly only form B is obtained at the end of experiments.

4. Conclusions

A competitive kinetic model for polymorph nucleation is developed in this work to describe the time evolution of two different polymorphic cluster size distributions in a supersaturated solution. By fitting the experimental induction time data and measured weight fractions of eflucimibe polymorphs with the proposed model, the association and dissociation rate constants for two polymorphs are determined, leading to ${\mathrm{k}}_{\mathrm{A}}=7.7\times {10}^{-22}{\mathrm{cm}}^3/\mathrm{s}$, ${\mathrm{k}}_{\mathrm{B}}=1.4\times {10}^{-21}{\mathrm{cm}}^3/\mathrm{s}$, ${\mathrm{k}}_{\mathrm{dA}0}=5.3\times {10}^{-4}{\mathrm{s}}^{-1}$ and ${\mathrm{k}}_{\mathrm{dB}0}=3.2\times {10}^{-3}{\mathrm{s}}^{-1}$. Thus, one obtains $\frac{{\mathrm{k}}_{\mathrm{B}}}{{\mathrm{k}}_{\mathrm{A}}}=2$ and $\frac{{\mathrm{k}}_{\mathrm{dB}0}}{{\mathrm{k}}_{\mathrm{dA}0}}=6$, leading to ${\mathrm{E}}_{\mathrm{A}}^{*}-{\mathrm{E}}_{\mathrm{B}}^{*}=1.5\mathrm{kJ}/\mathrm{mole}$ and ${\mathrm{E}}_{\mathrm{B}}-{\mathrm{E}}_{\mathrm{A}}=3.1\mathrm{kJ}/\mathrm{mole}$. This is consistent with Ostwald’s rule of stages that the metastable B-form tends to crystallize out more easily than the stable A-form due to ${\mathrm{E}}_{\mathrm{A}}^{*}>{\mathrm{E}}_{\mathrm{B}}^{*}$ while the stable A-form has a lower potential energy than the metastable B-form due to ${\mathrm{E}}_{\mathrm{B}}>{\mathrm{E}}_{\mathrm{A}}$.

Supersaturation is crucial in the polymorph selection for nucleation of eflucimibe. Association rate plays a more important role than dissociation rate at higher supersaturation due to smaller critical nucleus size and shorter induction period. As ${\mathrm{k}}_{\mathrm{B}}>{\mathrm{k}}_{\mathrm{A}}$, it is easier for the metastable B-form to grow to smaller critical nucleus size at higher supersaturation. Thus, nucleation of the metastable B-form dominates at higher supersaturation, leading to ${\mathrm{w}}_{\mathrm{B}}>{\mathrm{w}}_{\mathrm{A}}$ at the end of the experiments. However, dissociation rate becomes important at lower supersaturation due to larger critical nucleus size and longer induction period. As ${\mathrm{k}}_{\mathrm{dB}0}>{\mathrm{k}}_{\mathrm{dA}0}$, it becomes more difficult for the metastable B-form to grow to larger critical nucleus size at lower supersaturation. Subsequently, nucleation of the stable A-form dominates at lower supersaturation, leading to ${\mathrm{w}}_{\mathrm{A}}>{\mathrm{w}}_{\mathrm{B}}$ at the end of the experiments. These findings are consistent with the experimental results obtained by Teychene and Biscans [39], indicating that the metastable B-form dominates at higher supersaturation while the stable A-form dominates at lower supersaturation.