Improving the Performance of 2-To-4 Optical Decoders Based on Photonic Crystal Structures
Abstract
:1. Introduction
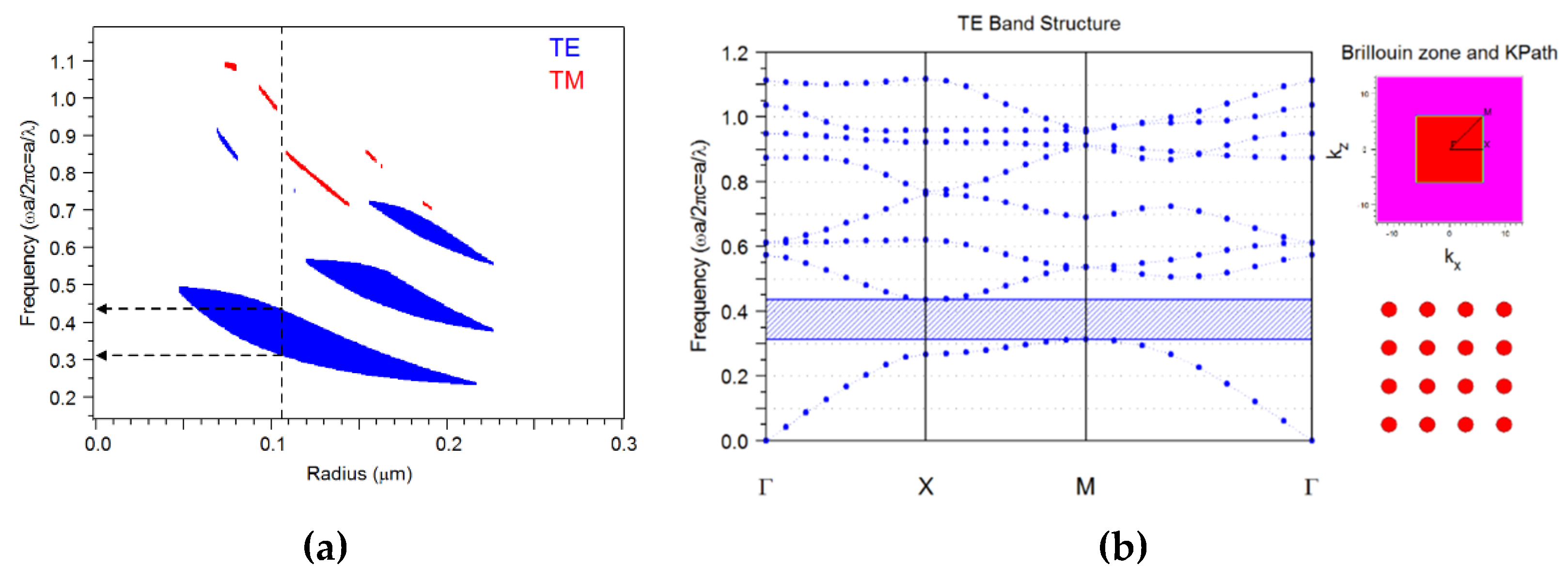
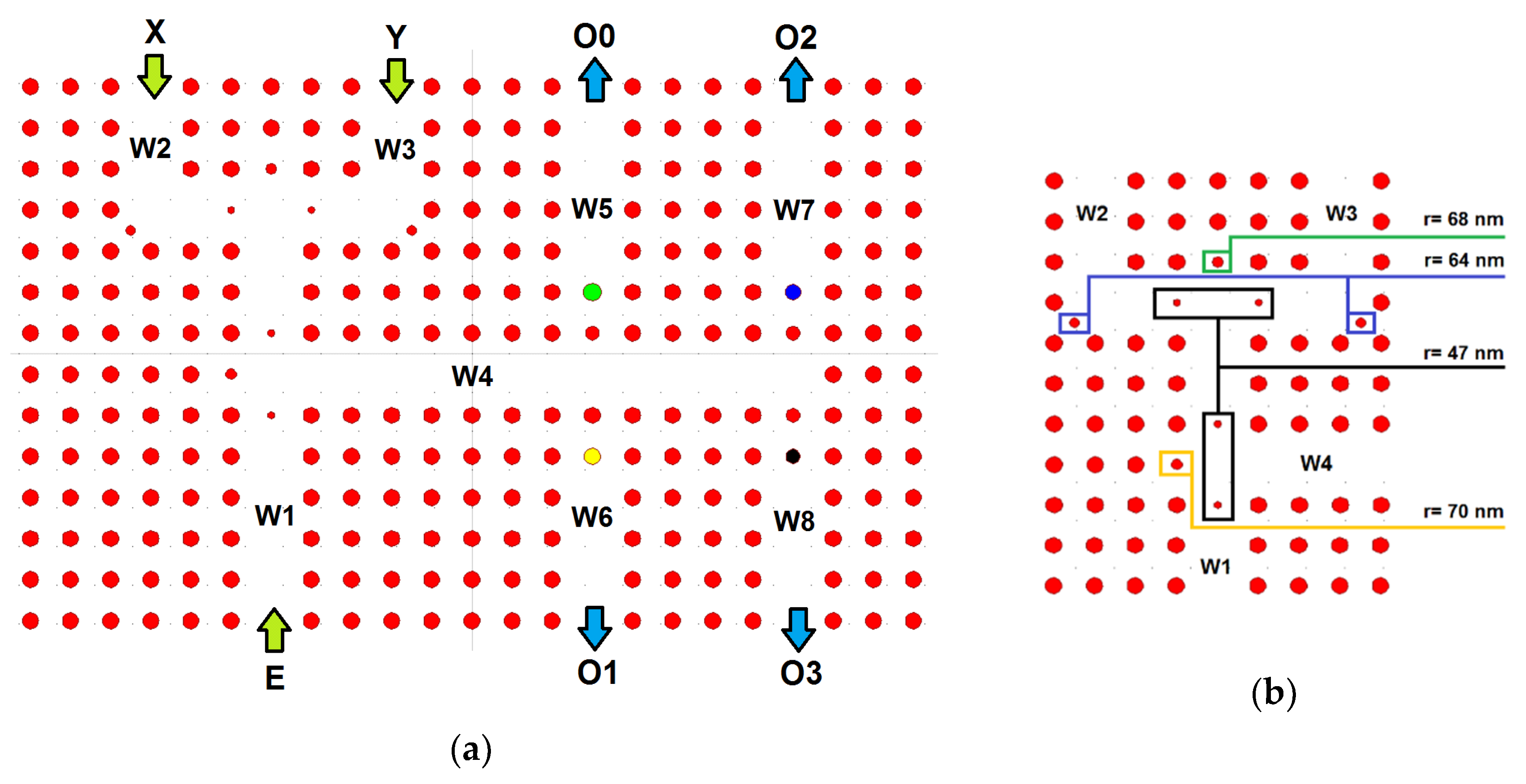
2. The Proposed Structure for the 2-To-4 Decoder
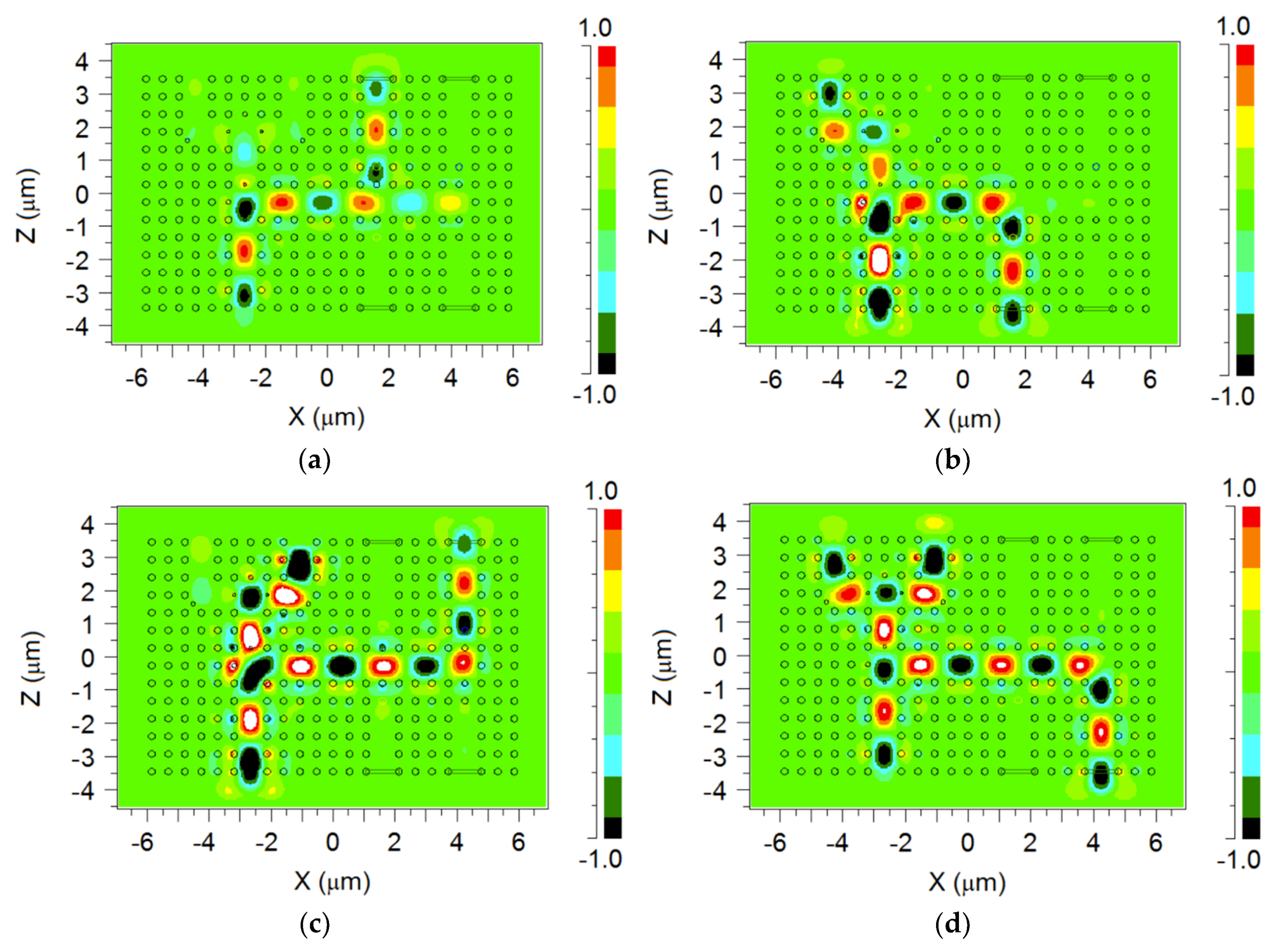
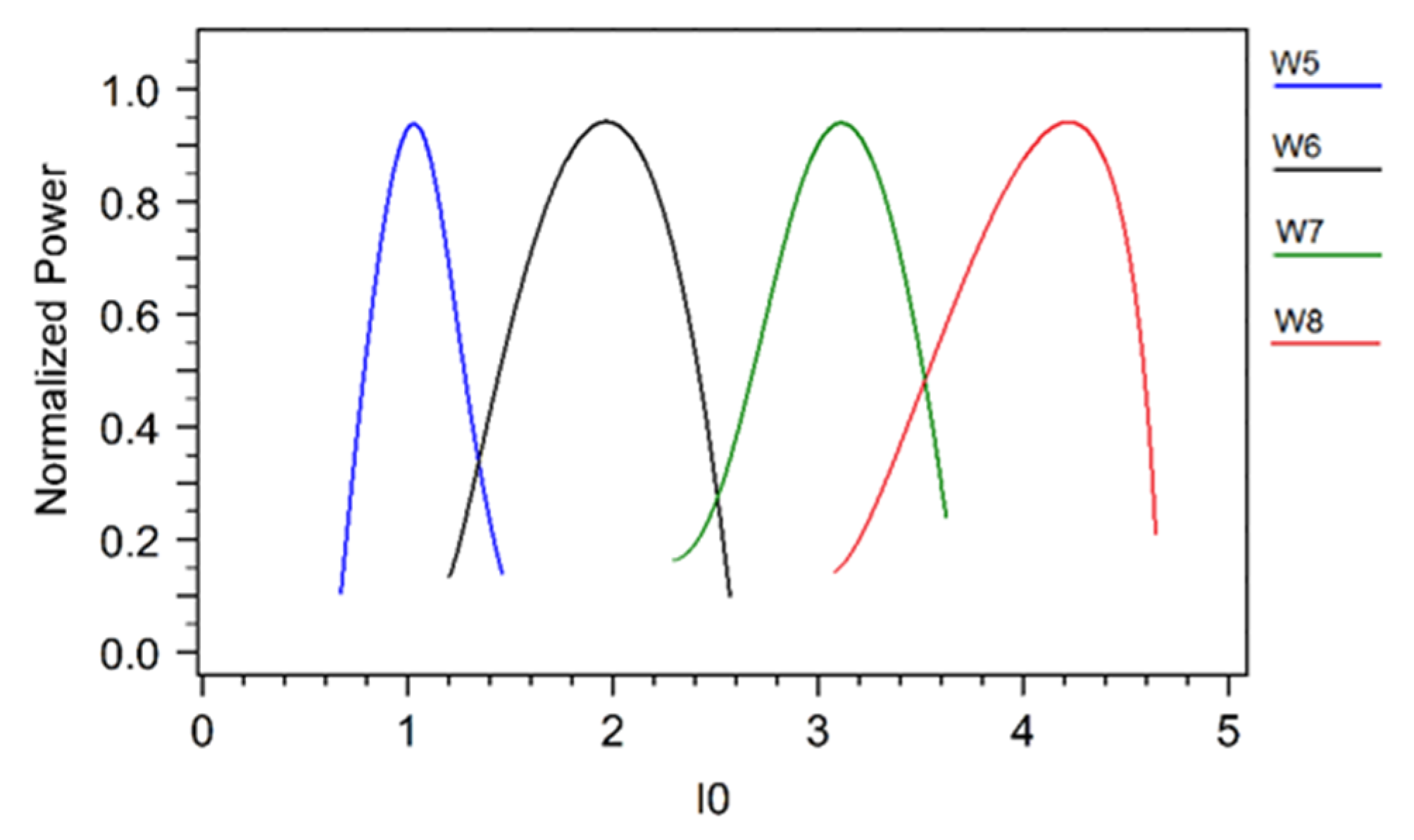
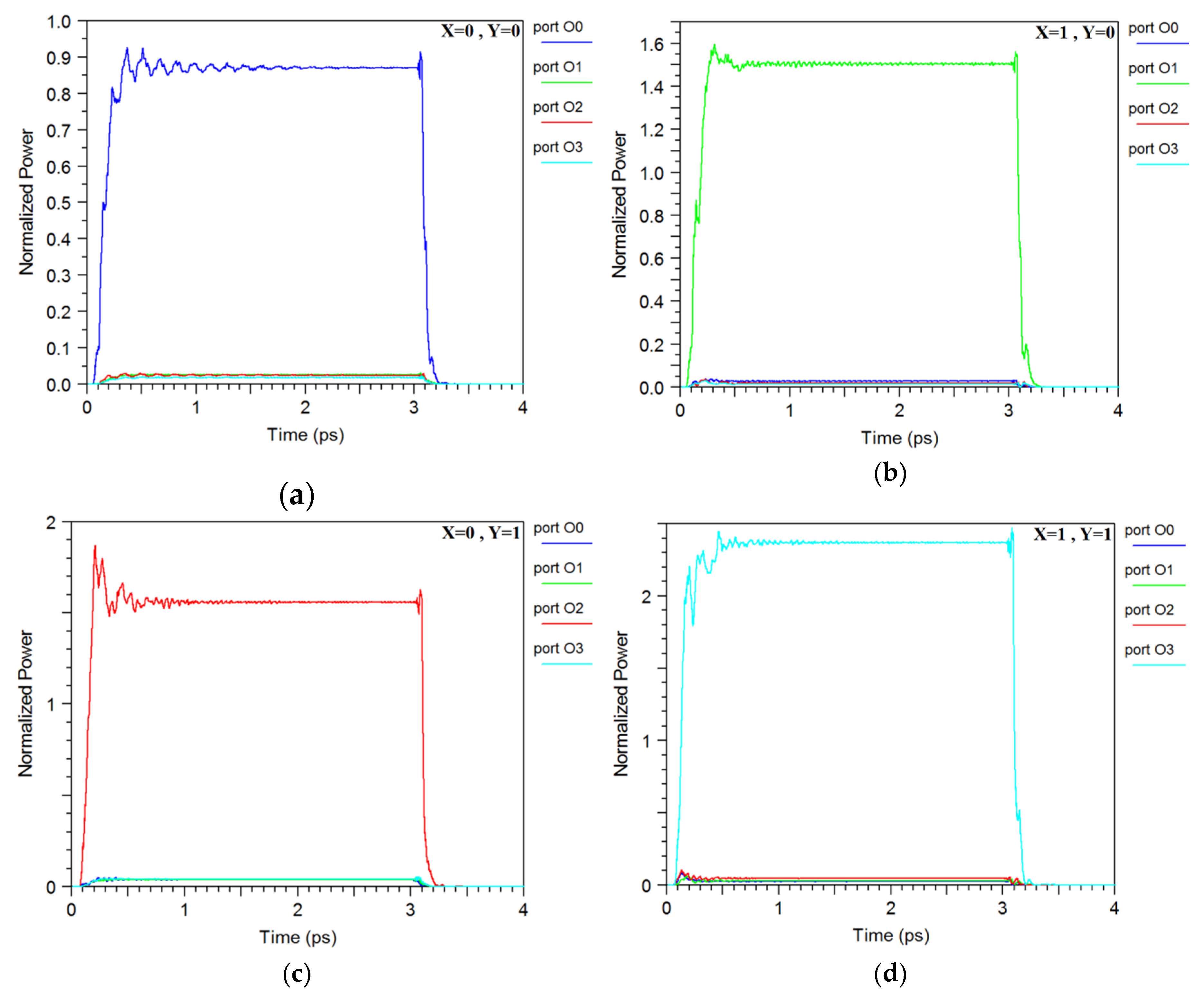
3. Simulations and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Binh, L.N. Digital Processing: Optical Transmission and Coherent Receiving Techniques; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Keiser, G. Optical Fiber Communications, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Alipour-Banaei, H. Bandgap management in two-dimensional photonic crystal thue-morse structures. J. Opt. Commun. 2013, 34, 61–65. [Google Scholar] [CrossRef]
- Scorobogati, M.; Yang, J. Fundamentals of Photonic Crystal Guiding, 1st ed.; Cambridge University Express: Cambridge, UK, 2009. [Google Scholar]
- Kraeh, C.; Martinez-Hurtado, J.L.; Popescu, H.; Hedler, A.; Finley, J.J. Slow light enhanced gas sensing in photonic crystals. Opt. Mater. 2018, 76, 106–110. [Google Scholar] [CrossRef]
- Myoung, N.; Park, H.C.; Ramachandran, A.; Lidorikis, E.; Ryu, J.W. Flat-band localization and self-collimation of light in photonic crystals. Sci. Rep. 2019, 9, 2862. [Google Scholar] [CrossRef] [PubMed]
- Alipour-Banaei, H.; Mehdizadeh, F.; Serajmohammadi, S.; Hassangholizadeh-Kashtiban, M. A 2*4 all optical decoder switch based on photonic crystal ring resonators. J. Mod. Opt. 2014, 62, 430–434. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Soroosh, M.; Alipour-Banaei, H. A novel proposal for optical decoder switch based on photonic crystal ring resonators. Opt. Quant. Electron. 2015, 48, 20. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Alipour-Banaei, H.; Serajmohammadi, S. Study the role of non-linear resonant cavities in photonic crystal-based decoder switches. J. Mod. Opt. 2017, 64, 1233–1239. [Google Scholar] [CrossRef]
- Daghooghi, T.; Soroosh, M.; Ansari-Asl, K. A novel proposal for all-optical decoder based on photonic crystals. Photonic Netw. Commun. 2017, 35, 335–341. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Alipour-Banaei, H.; Serajmohammadi, S. Design and Simulation of all optical Decoder based on nonlinear PhCRRs. Opt. Int. J. Light Electron Opt. 2018, 156, 701–706. [Google Scholar] [CrossRef]
- Daghooghi, T.; Soroosh, M.; Ansari-Asl, K. A Low-Power All Optical Decoder Based on Photonic Crystal Nonlinear Ring Resonators. Opt. Int. J. Light Electron Opt. 2018, 174, 400–408. [Google Scholar] [CrossRef]
- Daghooghi, T.; Soroosh, M.; Ansari-Asl, K. Ultra-fast all-optical decoder based on nonlinear photonic crystal ring resonators. Appl. Opt. 2018, 57, 2250–2258. [Google Scholar] [CrossRef] [PubMed]
- Daghooghi, T.; Soroosh, M.; Ansari-Asl, K. Slow light in ultracompact photonic crystal decoder. Appl. Opt. 2019, 58, 2050–2058. [Google Scholar] [CrossRef] [PubMed]
- Mehdizadeh, F.; Soroosh, M.; Alipour-Banaei, H. Proposal for 4-to-2 optical encoder based on photonic crystals. IET Optoelectron. 2017, 11, 29–35. [Google Scholar] [CrossRef]
- Moniem, T.A. All-optical digital 4 × 2 encoder based on 2D photonic crystal ring resonators. J. Mod. Opt. 2016, 63, 735–741. [Google Scholar] [CrossRef]
- Yang, Y.P.; Lin, K.C.; Yang, I.C.; Lee, K.Y.; Lee, W.Y.; Tsai, Y.T. All-optical photonic-crystal encoder capable of operating at multiple wavelengths. Opt. Int. J. Light Electron Opt. 2017, 142, 354–359. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Soroosh, M.; Alipour-Banaei, H.; Farshidi, E. A Novel Proposal for All Optical Analog-to-Digital Converter Based on Photonic Crystal Structures. IEEE Photonics J. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Mehdizadeh, F.; Soroosh, M.; Alipour-Banaei, H.; Farshidi, E. All optical 2-bit analog to digital converter using photonic crystal based cavities. Opt. Quant. Electron. 2017, 49, 38. [Google Scholar] [CrossRef]
- Youssefi, B.; Moravvej-Farshi, M.K.; Granpayeh, N. Two bit all-optical analog-to-digital converter based on nonlinear Kerr effect in 2D photonic crystals. Opt. Commun. 2012, 285, 3228–3233. [Google Scholar] [CrossRef]
- Alipour-Banaei, H.; Seif-Dargahi, H. Photonic crystal based 1-bit full-adder optical circuit by using ring resonators in a nonlinear structure. Photonics Nanostruct.-Fundam. Appl. 2017, 24, 29–34. [Google Scholar] [CrossRef]
- Cheraghi, F.; Soroosh, M.; Akbarizadeh, G. An ultra-compact all optical full adder based on nonlinear photonic crystal resonant cavities. Superlattices Microstruct. 2018, 28, 154–161. [Google Scholar] [CrossRef]
- Vali-Nasab, A.M.; Mir, A.; Talebzadeh, R. Design and simulation of an all optical full-adder based on photonic crystals. Opt. Quant. Electron. 2019, 51, 161. [Google Scholar] [CrossRef]
- Zamanian-Dehkordi, S.S.; Soroosh, M.; Akbarizadeh, G. An ultra-fast all-optical RS flip-flop based on nonlinear photonic crystal structures. Opt. Rev. 2018, 25, 523–531. [Google Scholar] [CrossRef]
- Abbasi, A.; Noshad, M.; Ranjbar, R.; Kheradmand, R. Ultra compact and fast All Optical Flip Flop design in photonic crystal platform. Opt. Commun. 2012, 285, 5073–5078. [Google Scholar] [CrossRef]
- Moniem, T.A. All-optical S-R flip flop using 2-D photonic crystal. Opt. Quant. Electron. 2015, 47, 2843–2851. [Google Scholar] [CrossRef]
- Mano, M.M. Digital Design, 6th ed.; Pearson: Bengaluru, India, 2018. [Google Scholar]
- Ogusu, K.; Yamasaki, J.; Maeda, S.H. Linear and nonlinear optical properties of Ag-As-Se chalcogenide glasses for all-optical switching. Opt. Lett. 2004, 29, 265–267. [Google Scholar] [CrossRef]
- Johnson, S.; Joannopoulos, J. Block-iterative frequency-domain methods for Maxwell’s equations in a planewave basis. Opt. Express 2001, 8, 173–190. [Google Scholar] [CrossRef]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics, 3rd ed.; Wiley: New Delhi, India, 2019. [Google Scholar]
- Petrenko, A.D. Nonlinear Kerr effect in magnetic crystals. Phys. Solid State 1999, 41, 591–594. [Google Scholar] [CrossRef]
- Li, C. Nonlinear Optics: Principles and Applications; Springer: Berlin, Germany, 2017. [Google Scholar]
- Werneck, M.M.M.; Allil, R.C.S.B.; De Nazaré, F.V.B. Fiber Bragg Gratings: Theory, Fabrication, and Applications; SPIE-The International Society for Optical Engineering: Bellingham, WA, USA, 2017. [Google Scholar]
- Sullivan, D.M. Electromagnetic Simulation Using the FDTD Method; IEEE Press: Piscataway, NJ, USA, 2000. [Google Scholar]
| Parameter | Value | Unit |
|---|---|---|
| Lattice constant | 530 | nm |
| Linear refractive index of the chalcogenide | 3.1 | - |
| Linear refractive index of the doped glass | 1.4 | - |
| Nonlinear refractive index of the chalcogenide | 1 × 10−20 | m2/W |
| Nonlinear refractive index of the doped glass | 1 × 10−14 | m2/W |
| Radius of fundamental rods | 106 | nm |
| Radius of the nonlinear rod in W5 | 118 | nm |
| Radius of the nonlinear rod in W6 | 111 | nm |
| Radius of the nonlinear rod in W7 | 104 | nm |
| Radius of the nonlinear rod in W8 | 97 | nm |
| Inputs | Output Ports | Delay Time (fs) | Fall Time (fs) | Steady-State Time (ps) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Logic | Normalized Power (%) | |||||||||||
| X | Y | O0 | O1 | O2 | O3 | O0 | O1 | O2 | O3 | |||
| 0 | 0 | 1 | 0 | 0 | 0 | 87 | 3 | 3 | 2 | 200 | 130 | 1.9 |
| 1 | 0 | 0 | 1 | 0 | 0 | 3 | 151 | 3 | 2 | 210 | 125 | 1.6 |
| 0 | 1 | 0 | 0 | 1 | 0 | 3 | 3 | 155 | 3 | 205 | 120 | 1.7 |
| 1 | 1 | 0 | 0 | 0 | 1 | 3 | 4 | 4 | 239 | 220 | 145 | 1.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maleki, M.J.; Soroosh, M.; Mir, A. Improving the Performance of 2-To-4 Optical Decoders Based on Photonic Crystal Structures. Crystals 2019, 9, 635. https://doi.org/10.3390/cryst9120635
Maleki MJ, Soroosh M, Mir A. Improving the Performance of 2-To-4 Optical Decoders Based on Photonic Crystal Structures. Crystals. 2019; 9(12):635. https://doi.org/10.3390/cryst9120635
Chicago/Turabian StyleMaleki, Mohammad Javad, Mohammad Soroosh, and Ali Mir. 2019. "Improving the Performance of 2-To-4 Optical Decoders Based on Photonic Crystal Structures" Crystals 9, no. 12: 635. https://doi.org/10.3390/cryst9120635
APA StyleMaleki, M. J., Soroosh, M., & Mir, A. (2019). Improving the Performance of 2-To-4 Optical Decoders Based on Photonic Crystal Structures. Crystals, 9(12), 635. https://doi.org/10.3390/cryst9120635





