1. Introduction
Time-differential perturbed angular correlation (TDPAC) [
1,
2] is a unique method for studying point defects in solids [
3]. Details of the TDPAC methodology and its formalism are well described in [
3,
4,
5,
6]. Ferroic materials can exhibit ferromagnetism, ferroelectricity, or ferroelasticity. Some ferroic materials, known as multiferroics, present multiple ferroic properties (e.g., ferromagnetism and ferroelectricity) in the same phase. For instance, CdCr
2S
4 is a very promising multiferroic material due to its strong electronic correlations along with strong coupling of its structural and electronic degrees of freedom. Bismuth ferrite is another multiferroic system. Studies of random point defects, dopants, and point-defect-induced in bismuth ferrite are valuable, and an understanding of its local properties allows this material to be tailored to various applications. TDPAC provides relevant information on the cooperative, solid-state properties of local centers, and can be an effective tool for studying such systems when used in combination with conventional characterization techniques and ab initio simulations. At ISOLDE-CERN [
7], several TDPAC probes are available that cannot be obtained elsewhere, enabling the laboratory to host experiments performed by several groups based around the world. However, in this paper, we discuss the TDPAC experiments performed in laboratories worldwide, not only at ISOLDE-CERN.
In all of the TDPAC experiments described in this work, the nuclear quadrupole interaction was studied in the nuclear spin state
I = 5/2. The electric field gradient (EFG) is represented by a symmetrical and traceless (3 × 3) tensor, which can be fully characterized by the magnitude
Vzz and the asymmetry parameter
η = (
Vxx −
Vyy)/
Vzz;
η varies from 0 to 1, where 1 signifies maximal asymmetry. The perturbation factor for polycrystalline samples and
is given by
where
is the transition frequency between the two
M states,
. This frequency is a function of the nuclear quadrupole frequency, defined as follows:
where Q is the nuclear quadrupole moment. The coefficient
skn, which indicates the amplitude of the transition frequency
ωn, is only slightly dependent on
η. Furthermore,
δ is the relative half-width of the field distribution, in this case EFG. The quantity
is the time spent in the intermediate state of gamma quantum emission.
We now briefly introduce the magnetic hyperfine field B
HF for the nuclear spin state
I = 5/2. This field can be expressed as the vector sum of three components:
where
BC is the Fermi contact term;
BD is a dipole term; and
BO is an orbital term. The Fermi contact term involves two contributions:
.
represents the field due to the polarization of the core (1
s, 2
s, and 3
s) electrons, and
BPB is assigned to the polarization of the band (4
s, 3
d, and 4
p conduction or valence) electrons. For the pure magnetic dipole interactions, two frequencies,
and
, are observed.
ωL is the Larmor frequency, which is
. Here,
, where
is the nuclear magneton and
. The perturbation function assumes the following form [
8]:
where
f is the amplitude of the modulation, which is related to the fraction of the TDPAC probes that occupy an environment that produces a nonzero B
HF, and
A22 is the anisotropy coefficient of the γ–γ cascade.
Below the Néel temperature, the study of multiferroic materials using TDPAC involves combined magnetic dipole and electric quadrupole interactions. The formalism for the influence of a combined interaction is well established and can be found in [
9].
Complementary conventional characterization techniques and simulations with ab initio codes [
10] are applied when interpreting data obtained using TDPAC.
In contrast to other hyperfine techniques like Moessbauer spectroscopy, the TDPAC experiment is not sensitive to the Coulomb interaction between the nucleus and the overlapping s-electrons. TDPAC is also insensitive to the Debye–Waller factor. The number of isotopes, which can be used as a probe in the TDPAC method, is also limited. Nevertheless, TDPAC experiments can be performed in a wide temperature range, even at temperatures up to and beyond the melting point of materials. Moreover, the TDPAC method can measure the hyperfine fields in matter (i.e., liquid, molecules, solids, and amorphous materials).
2. Chalcogenide Spinels
In particular, the TDPAC technique can deliver important information on off-center ions in crystals. Several TDPAC probes have been used to investigate the lattice site occupation of doping atoms and their behavior in chalcogenide spinels [
11]. The temperature dependence of the amplitude of Cr off-centering displacements were studied using pair distribution functions and the TDPAC method in CdCr
2S
4 [
12]. Surprisingly, the results obtained in both works with the probe
111In(
111Cd) showed that Cd occupies not only the Cd site, but also the Cr one. This allows for the investigation of Cr ions whose equilibrium positions have shifted away from the regular lattice site. The Cr ion plays the central key role in the dynamic off-centering displacement of the coordination sphere [
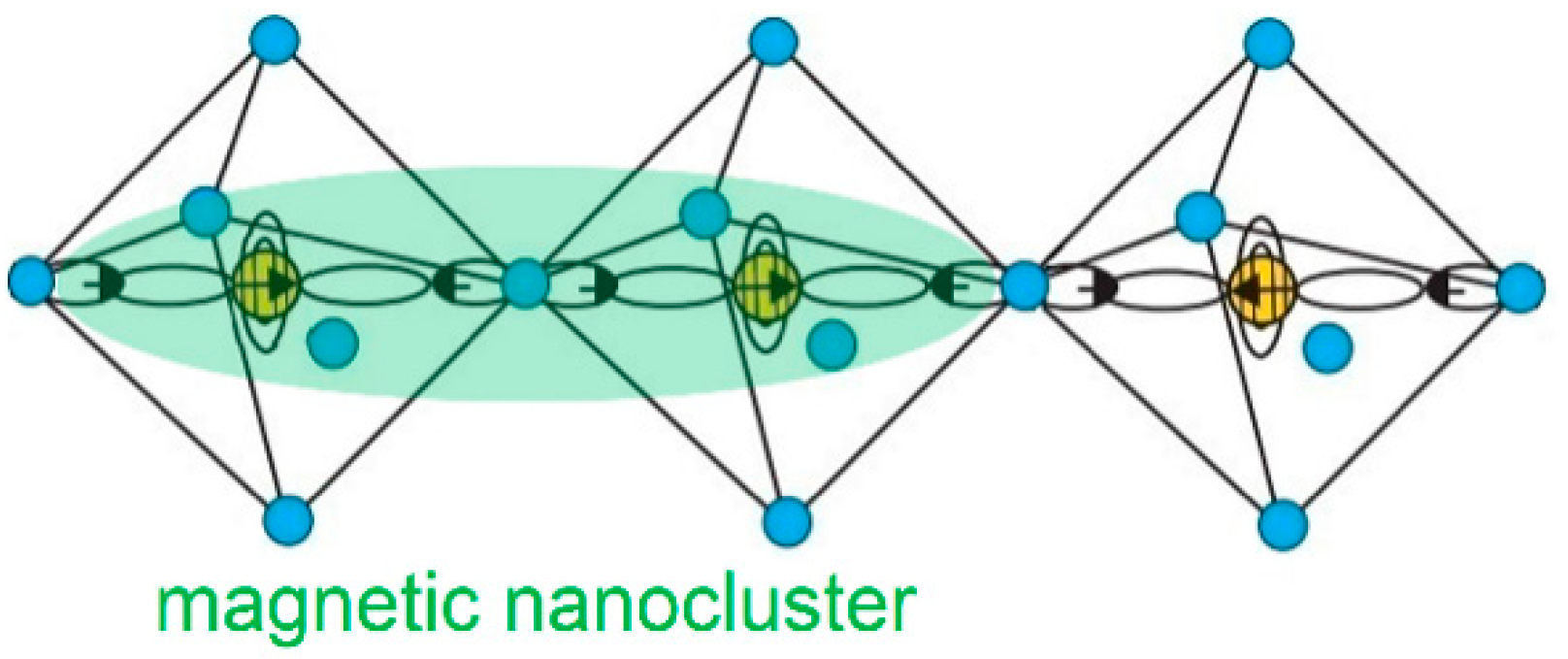
12]. The authors affirmed that the off-centering leads to an unusual entanglement between the polar and magnetic degrees of freedom. Remarkably, they refer to short-range magnetic nanoclusters in the paramagnetic phase, as seen in ultralow-field susceptibility experiments. The local environment for Cd substitution at the Cr site within tetrahedral sites is shown in
Figure 1.
The proposed nanocluster model is very consistent. In their bulk forms, such compounds display unusual magnetic properties due to exchange and superexchange interactions among the Cr
3+ ions [
13]. In addition, the nature of the cation A site plays a very important role because it can exhibit metallic, semiconducting, or insulating properties [
14]. These can occur due to strong electronic correlation along with strong coupling of the structural and electronic degrees of freedom [
14]. The TDPAC technique has proven to be an effective tool for the simultaneous investigation of both lattice sites.
Samokhvalov et al. [
11] carried out experiments with several ferromagnetic chalcogenide spinels including CdCr
2Se
4, CdCr
2S
4, HgCr
2Se
4, and CuCr
2Se
4 (metallic) single crystals. They observed that in semiconducting compounds, the probes
111mCd(
111Cd),
111Ag(
111Cd), and
199mHg(
199Hg) substituted at the A site, whereas
111In(
111Cd) occupied the A and B sites.
77Br(
77Se) substituted at the anion position. One goal of that study was to investigate, under different thermal conditions and treatments, the doping-induced local effects in the compounds that do not occur in the intrinsic materials. The information obtained using the TDPAC technique regarding the lattice site occupations of the dopant atoms is highly relevant to investigations of the strong influence of doping on the properties of ferromagnetic chalcogenide spinels or other functional materials. Moreover, the probes do not necessarily have to be implanted to be incorporated into the crystal lattice and can also be diffused [
15] or incorporated during the sample preparation process [
16]. A surface and interface study is also possible [
17,
18], and may be particularly interesting for the local investigation of 2D materials.
3. Width of the Field Distribution
The parameter
δ measures the width of the EFG or B
HF distribution and is related to the crystallinity of the sample. This is a crucial parameter for measuring the homogeneity of the crystal [
19]. Once incorporated into a crystal lattice with high crystallinity, the TDPAC probe nuclei interact with similar hyperfine fields. Measurement of the static interaction should then yield well-defined hyperfine frequencies, and the parameter
δ will assume very small values.
For each local environment, the software used for TDPAC analysis considers δ for only one field, EFG or BHF, even when the interaction is combined (EFG + BHF). This limitation forces the use of a fitting routine, where it is necessary to choose the field in which the δ value is to be determined. An inappropriate choice can hide defects in the physics of points for one field or the other. Moreover, when observing more than one local environment, the effects on the TDPAC spectrum originated by a highly distributed field can be particularly complex.
In some cases, fields that perturb the nucleus become time dependent [
20]. If this happens during the time window of the TDPAC experiment, the parameter
δ can be a measure of the onset of fluctuations in the fields over time. The relevant factors to be considered are the relative strength of the fields, the presence or absence of additional static interactions, the rate of fluctuation, and the spatial dependence of time-dependent interactions. For instance, the increased damping of the
R(
t) spectra obtained by measuring cadmium chromium sulfide with the probe
111In(
111Cd) is attributable to time-dependent interactions of Cd when it occupies cubic Cr sites [
12]. This effect becomes most visible in the spectra between 119 and 92 K and increases as the temperature decreases. This is associated with the probe at the cubic site of Cd and is considered a dynamic attenuation parameter (
λ) in the standard static fitting routine [
21]. In general, this approximation model can be used to study diffusive motions of atoms or ions in solids for TDPAC analysis. These results suggest that the Cr ions hop between equivalent potential energy minima according to the order–disorder model [
22], which was proposed for phase transitions occurring below the Curie temperature [
12]. Remarkably, the same hopping effect has been observed in lead titanate and is described below.
4. From Lead Titanate to Lead Zirconate
PbTiO
3 is a ferroelectric material with a high Curie temperature and strong tetragonal distortion, which is associated with high spontaneous polarization [
23].
Several studies have conducted TDPAC experiments in lead titanate. In [
24], a fluctuation in the EFG was clearly observed in measurements performed using the
181Hf(
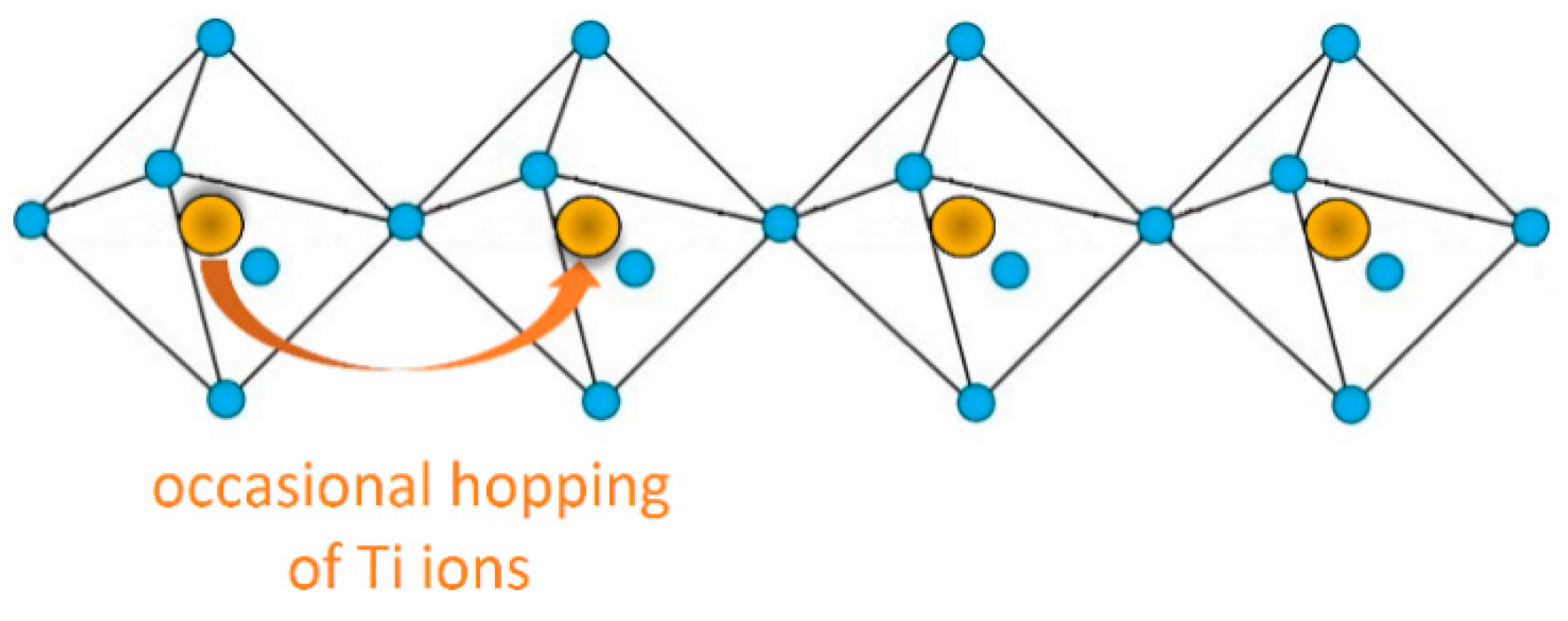
181Ta) probe near the Curie temperature. To interpret the data, the authors used the order–disorder model, in which the Ti ions were located at potential energy surface minima that were shifted away from the regular Ti site. They attributed the observed EFG fluctuations to the occasional hopping of probe ions from minimum location to minimum location (see
Figure 2), and associated them with a spin-relaxation mechanism for tetragonal ferroelectric PbTiO
3.
The hopping effect is clearly observed near the critical Curie temperature (i.e., as an approximation to the paraelectric phase), in agreement with the results for cadmium chromium sulfide.
TDPAC experiments using the probe
181Hf(
181Ta) in lead zirconate titanate were carried out as a function of temperature [
25] for PbZr
1−xTi
xO
3 with
x = 0.47 and
x = 0.48. As mentioned in the corresponding reports [
25], these compounds have various potentially very useful applications relating to radar, hydrophones, ultrasound, high-voltage sources, and micropositioners. The substitution of Zr
4+ with Ti
4+ in lead titanate can lead to the appearance of a ferroelectric phase with rhombohedral symmetry and decreased tetragonal distortion [
26]. If the Zr content is increased, an orthorhombic antiferroelectric phase can also appear [
26]. The TDPAC results found in [
25] indicate high-frequency distribution rates between room temperature and 900 K, and it was speculated that this effect was related to the coexistence of monoclinic and tetragonal phases. For the sample with
x = 0.48, the dynamic attenuation was also considered when fitting the spectra obtained at 973 K and room temperature. Interestingly, the spectra taken at room temperature before and after the measurements performed at high temperature were quite different. The results for the sample with
x = 0.47 indicate a unique site occupancy for the probe ion, and only the distribution of the nuclear electric quadrupole interaction frequency (
δ) was considered in the fitting routine.
Another report was also published with TDPAC measurements obtained using the
181Hf(
181Ta) probe, but at room temperature with different ratios of
x = 0.02,
x = 0.04,
x = 0.06, and
x = 0.08 [
27]. The authors referred to the observation of an antiferroelectric–ferroelectric phase transition. The fitting routine was performed considering two different local environments with static electric quadrupole interactions. Fascinatingly, one of them presented highly distributed frequencies over the whole concentration range of Ti, with a predominant site population. An increase in the quadrupole frequency was also observed when
x = 0.2 and
x = 0.4 [
28]. The potential atomic rearrangement observed here gradually decreased at higher Ti concentrations.
The temperature dependence of the hyperfine quadrupole interactions of polycrystalline samples of PbZr
0.9Ti
0.1O
3 and PbZr
0.8Ti
0.2O
3 was investigated in [
28]. In the ferroelectric and paraelectric phases, two different local environments were reported for the
181Hf(
181Ta) probe. The hyperfine parameters for both sites indicated a change in the Curie temperature, and the EFG in the cubic phase was nonzero. This effect was possibly associated with the presence of defects in the neighborhood of the probe nuclei.
Shifting our discussion to PbZrO
3, the TDPAC results obtained using
181Hf(
181Ta) were found to vary with temperature [
29]. Only one local environment was observed, which was assigned to the Zr site. At the Curie temperature of 235 °C, the spectra indicated damping of the angular correlation pattern. The frequency distribution effect observed for the other Pb compounds described here, especially close to the critical temperature, was apparently not as strong for PbZrO
3. In this case, the frequency distribution remained relatively narrow and constant up to temperatures close to the Curie point. In the antiferroelectric phase, the reported quadrupole frequency gradually decreased with increasing temperature. In the cubic phase, a very small quadrupole frequency was observed. This is due to lattice imperfections, which cause the local environment of the crystal to deviate from cubic symmetry. The same effect was recently observed in EuTiO
3 [
30].
Another interesting aspect was the interpretation of the slight decrease in the asymmetry parameter with increasing temperature. This effect indicates that, at the Zr site, the antiferroelectric distortion of the crystal lattice decreases as the temperature approaches the Curie point.
Recently, another work confirmed that only one lattice site was occupied by the TDPAC probe [
28], but only described a static nuclear quadrupole interaction below the Curie temperature. However, nuclear spin relaxation was observed above it.
Another effective probe for investigating these lead compounds would be
204mPb(
204Pb) [
31], which can be obtained at ISOLDE-CERN and is highly sensitive to deviations from axial symmetry.
5. Fractions of Local Environments
Since the TDPAC technique is based on hyperfine interactions, it often allows multiple crystalline structures to be characterized for the same sample. Moreover, the same TDPAC isotope can occupy different lattice sites. For instance,
111In(
111Cd) showed that Cd occupies not only the Cd site, but also the Cr one in CdCr
2S
4 [
12]. It is also possible to determine the temperature dependence of the probe fractions. By studying this dependence, it is possible to monitor the development of local distortions in AgCrO
2 [
32] and phase transitions at multiple lattice sites.
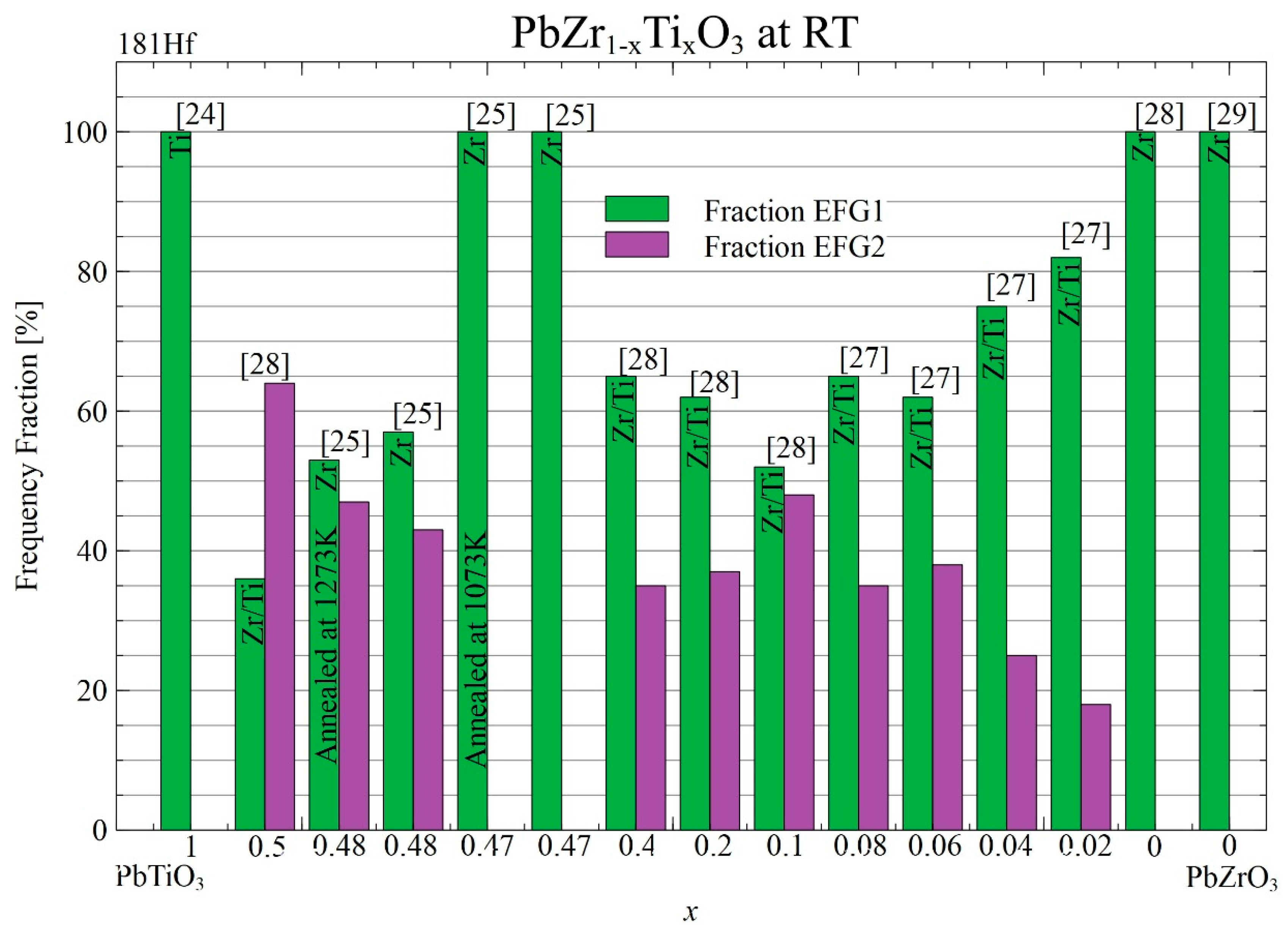
Figure 3 shows a bar graph comparing the fractions of local environments for compositions ranging from pure lead titanate to pure lead zirconate, as obtained via experiments using the
181Hf(
181Ta) probe at room temperature (RT). The reports above-mentioned noted that there were two different fractions for all measurements at room temperature when both Ti and Zr were present in the sample. Only one local environment was reported for pure PbTiO
3 or PbZrO
3, which was assigned to the
181Hf(
181Ta) probe at the Ti or Zr site, respectively. The same effect was observed when
x = 0.47. Different reports have proposed different origins for the second local environment, and it has not been assigned to the Ti or Zr site. Guarany et al. [
25] argued that the presence of two fractions may demonstrate the coexistence of monoclinic + tetragonal phases, which would occur at the morphotropic phase boundary when
x ≈ 0.50 and would separate tetragonal from rhombohedral phases [
25]. Other reports associate the fraction with the presence of defects in the neighborhood of TDPAC probes [
28] for the cubic phase, which occurs at high temperature.
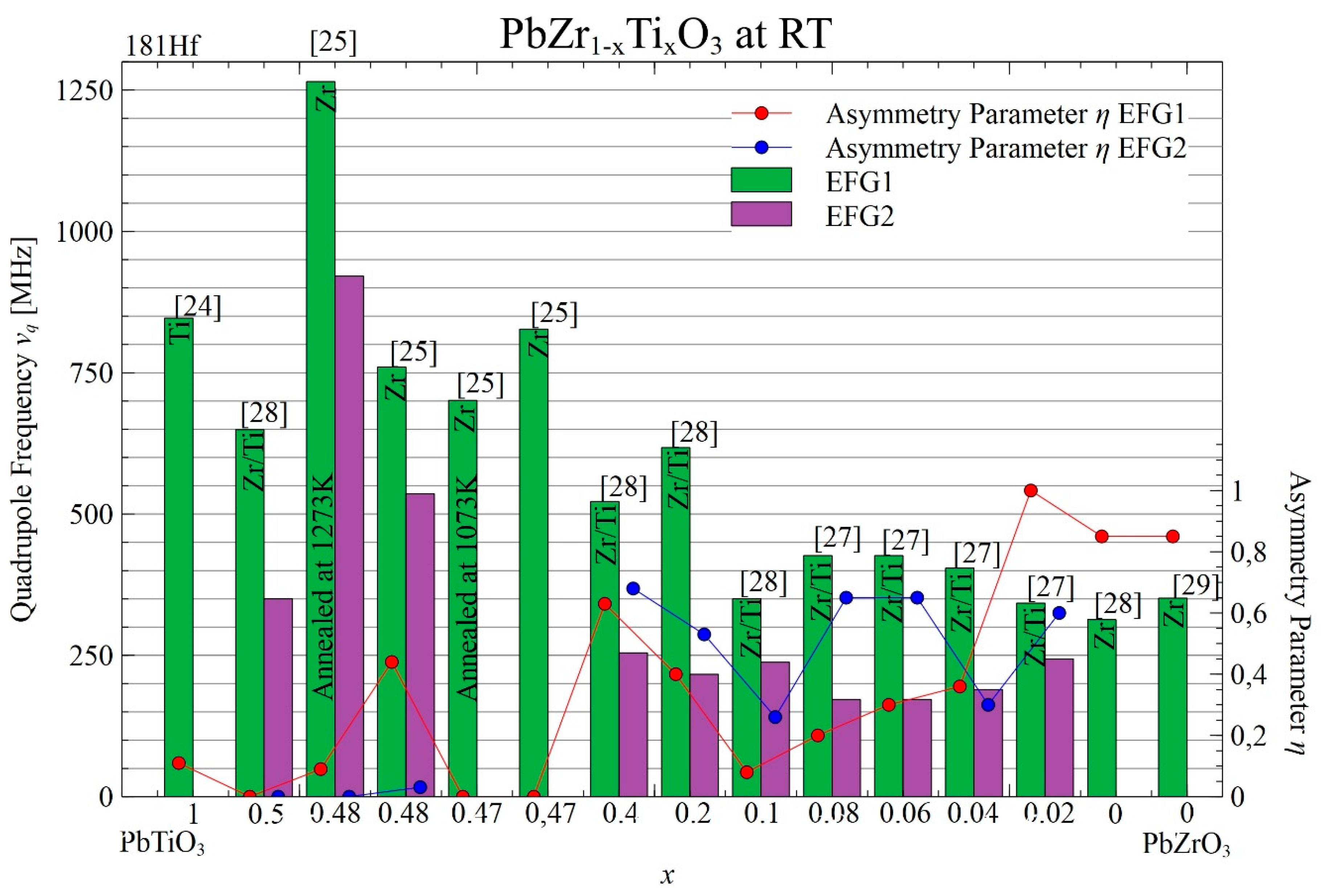
Figure 4 shows a vertical bar graph that compares the quadrupole frequencies of local environments in compositions ranging from pure lead titanate to pure lead zirconate, as discerned using the
181Hf(
181Ta) probe at room temperature (RT). It is apparent that the frequencies for both sites increase with rising Ti concentration. When
x = 0.48, EFG1 is much higher after annealing at 1273 K than at 1073 K.
6. Electric Field Gradient
The dependence of the EFG on the electric polarization (
P) depends on the material [
33]. This dependence can be proportional to
P2 in some cases, but the trend is not monotonic in others (e.g., in PbTiO
3). A theoretical study of EFG values as a function of polarization was performed for different lattice sites of BaTiO
3, KNbO
3, PbTiO
3, BaZrO
3, CaTiO
3, PbZrO
3, SrTiO
3, NaNbO
3, and LiNbO
3 without a TDPAC probe, with only the matrix ions themselves experiencing the respective EFGs [
33]. The incorporation of highly diluted TDPAC probes into the lattice would not be expected to affect the polarization of these systems, so EFG simulation with the pure systems is justified. However, temperature effects were not considered in these simulations. The simulations were performed for non-relaxed structures with intermediate displacements of the ferroelectric distortions.
The temperature dependence of the major component of the EFG tensor in metals was found to follow the three-halves power of temperature function
, whereas this dependency becomes
for ion-conducting ceramics [
24]. However, for ferroic and multiferroic materials, any predictable function is expected. Indeed, the temperature dependence is unique to each system and delivers information on the onset of charge and orbital ordering [
34]. Close to the ordering temperature, the temperature dependence of the EFG can present critical behavior, with abrupt changes observed within a short temperature interval. For instance, charge fluctuations in crystal lattices can cause dynamic interactions that are observable in TDPAC spectra when the interactions happen in the time window of the experiment. The effect of nonstatic hyperfine interactions results in a simple electric (sub)lattice susceptibility dependence of the EFG [
32].
7. Symmetry of the Electric Field Gradient
The EFG tensor is affected by lattice imperfections, ferroelectric distortions, the symmetry of the local charge distribution at different lattice sites, lattice vibrations, and lattice expansion. A non-axially symmetric EFG tensor (η ≠ 0) is frequently reported from TDPAC experiments on ferroic and multiferroic systems. However, it is important to emphasize that below the Néel temperature, the TDPAC spectra involve combined magnetic dipole and electric quadrupole interactions, and the determination of the asymmetry parameter is nontrivial or, in some cases, impossible.
For an axially symmetric EFG, the component
Vzz should vary in a monotonic manner as a function of the polarization if the sign of
Vzz is taken into account. However, in gamma–gamma TDPAC measurements, it is not possible to obtain the sign of
Vzz, only its absolute value. Therefore, the dependence of EFG on
Vzz(
P2) in TDPAC experiments may not be monotonic when the sign of
Vzz changes. For instance, in simulations of
Vzz at Pb in PbTiO
3, it varied from 6 × 10
21 V/m
2 to −7 × 10
21 V/m
2 with increasing polarization [
33]. However, in gamma–gamma TDPAC measurements, a decrease from 6 × 10
21 V/m
2 to zero would be observed, and then an increase from zero to 6 × 10
21 V/m
2 (which corresponds to the decrease from zero to −6 × 10
21 V/m
2 in the simulations). There can also be discontinuous changes in
Vzz at sites where the asymmetry parameter changes, and the largest component of the diagonal tensor
Vzz may then “interchange” with other diagonal components as the polarization changes, so it may not always correspond to the same EFG direction. However, when
η = 0, even in Pb (with a lone pair), which presents large lattice displacements, the variation has always been found to be monotonic if the sign of
Vzz is taken into account [
33].
Moreover, the dependence of the asymmetry parameter delivers information on the evolution of local distortions, which can be associated with the onset of short-range magnetic correlations. In some cases, magnetoelastic coupling seems to drive the system to a lower symmetry below
TN [
32,
34]. The ability of the TDPAC technique, following very rigorous and complex data analysis below
TN, to provide information on the lattice distortion behavior and crystallographic symmetry lowering is unique and important.
8. Silver Hypochromite
Investigations of silver hypochromite have been inspired by its potential applications in, for example, new nonvolatile memory for computers and cell phones [
35]. In the magnetic ground state below 21 K, the compound AgCrO
2 presents ferroelectric polarization (~5 μC/m
2) [
36]. In this phase, each triangular spin lattice of Cr
3+ ions separates into helical-spin chains of Cr
3+ ions [
36]. TDPAC experiments were performed in multiferroic AgCrO
2 using the probe
111In(
111Cd) as a function of the temperature [
35,
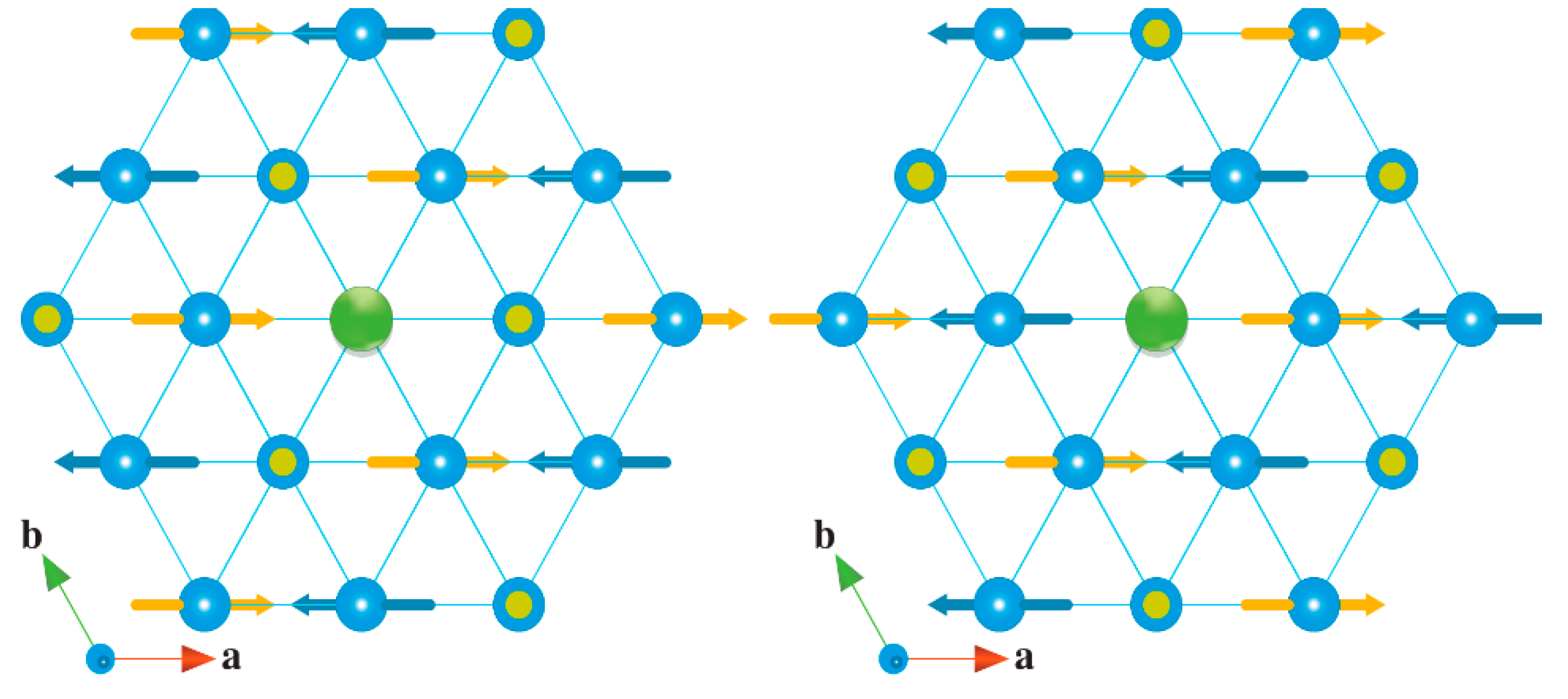
37] to investigate the origin of magnetoelectric coupling in this triangular lattice antiferromagnet with geometrically frustrated spin. The results near and below the Néel temperature were indicative of two nonequivalent substitutions with different spin arrangements, as shown in
Figure 5. One was associated with the probe, with the spin almost aligned with the
c-axis. The other configuration was assigned to the probe ion, and one of the spins was oriented 120° from the
c-axis. This 120° spin structure was obtained at the ground state due to geometric frustration of the antiferromagnetic interaction [
38]. Oohara et al. [
39] performed magnetic susceptibility and neutron diffraction measurements on a powder sample and verified that the magnetic structure is a modulated 120° structure caused by competition between the intraplane and interplane interactions. They also reported that this strong competition suppresses the development of long-range order [
39].
Data analysis of TDPAC measurements in the presence of magnetic frustration can be very complex, as the frustration results in complex spin orders for the probe nuclei. Up to four different local environments close to the Néel temperature were reviewed in the TDPAC experiments, with two presenting local symmetry in an undistorted lattice [
35]. The magnetic hyperfine fields associated with the other sites were stronger, and they had distorted local environments, referred to as f
d1 and f
d2. The temperature dependence of the site populations approximately respects the rule f
d1 = 2f
d2, which is predictable from the symmetry. Moreover, the results indicated that a minor fraction (around 10%) remain undistorted only at 12 K.
9. Future Perspectives and Measurements in Bismuth Ferrite
TDPAC measurements with bismuth ferrite were conducted as part of the ISOLDE-CERN project IS647 “Local Probing of Ferroic and Multiferroic Compounds” [
40]. Some of the results obtained have already been published [
41], while others are in the process of being reported [
42,
43].
Bismuth ferrite, also referred to as BFO, is an inorganic perovskite that is synthesized in a sintering process involving equal parts bismuth oxide (Bi
2O
3) and iron oxide (Fe
2O
3). As above-mentioned, the compound exhibits multiple ferroic properties, namely ferromagnetism and ferroelectricity, in the same phase. With a magnetic Néel temperature of 370 °C and an electric Curie temperature of about 822 °C [
42], BFO is a prominent multiferroic material because it retains its multiferroic character even at room temperature. Thus, among the multiferroic materials, bismuth ferrite is a promising candidate for widespread industrial use. The novel combination of ferroelectric and ferromagnetic properties leads to an entirely new approach to material and device design. The number of publications dealing with multiferroics, especially BFO, has risen steadily over the last 25 years, driven by the growing demand for materials that can facilitate enhanced storage management and computing power [
44,
45].
Before it disintegrates and melts, bismuth ferrite appears in three different phases: the rhombohedral alpha phase, the orthorhombic beta phase, and the cubic gamma phase. The alpha phase of BFO appears at room temperature in a rhombohedral perovskite structure with hexagonal lattice parameters of
a = 5.58 Å and
c = 13.87 Å in the R3c space group [
46] and continues to exist up to about 822 °C, where BFO undergoes its first phase transition to the beta phase. The appearance of the beta phase is the focus of considerable investigation and discussion. It has been observed to appear with a cubic, orthorhombic, trigonal, and even tetragonal order [
47]. One aspect in favor of the orthorhombic structure is its centrosymmetry, which eliminates its electrical polarizability, meaning that the phase change from alpha to beta also marks the Curie temperature [
48].
10. Ferroelectrically Induced In-Plane Contraction
Its small domain wall size and the ability to control their locations are attractive features of BFO in relation to its application in future electronic devices [
49]. The domain walls present a particular local symmetry [
46], and the TDPAC technique can provide local information. For example, local distortion of the Fe–O–Fe bond angle, as shown in
Figure 6, can be observed in the asymmetry parameter. This is caused by the dominance of ferroelectrically induced in-plane contraction. The straightening of the bond angle causes an expansion of the lattice perpendicular to the wall, which results in increased orbital overlap and higher conductivity [
46]. Moreover, the domain walls are found to be more conductive than the domains themselves [
49].
At ISOLDE-CERN, it is also possible to implant
111In and
111mCd probes [
50] simultaneously. In and Cd atoms have valences of 3 and 2, respectively, and Cd is subject to charge compensation when it replaces Bi
3+ or Fe
3+ at substitutional sites. Some effects of doping bismuth ferrite can be advantageous in applications of this material as they can allow limitations to be overcome (e.g., leakage currents can be reduced [
51]), although defects can also form. In addition, attractive defect–defect interactions may lead to the clustering of defects, even in diluted samples. TDPAC studies can play a key role in elucidating these effects in detail [
52] (including defects caused by implantation [
53,
54]), especially if they are performed in association with self-diffusion studies [
55,
56].