Molecular–Statistical Theory for the Description of Re-Entrant Ferroelectric Phase
Abstract
:1. Introduction
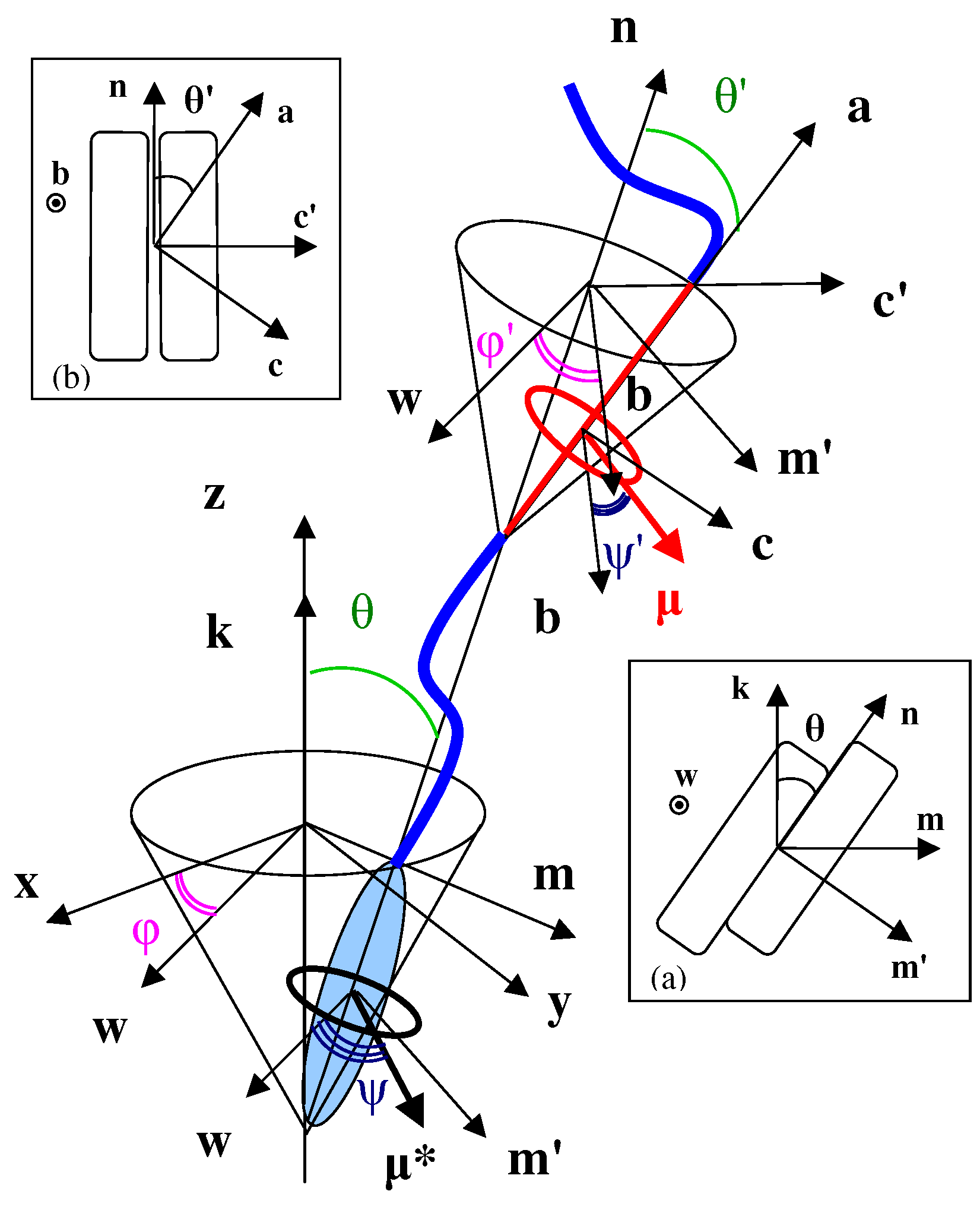
2. Molecular Model
3. Free Energy of Smectic Molecules with Transverse Dipoles in Rigid Cores and in Flexible Tails
4. Spontaneous Polarization in the Absence of Piezoelectricity and Flexoelectricity
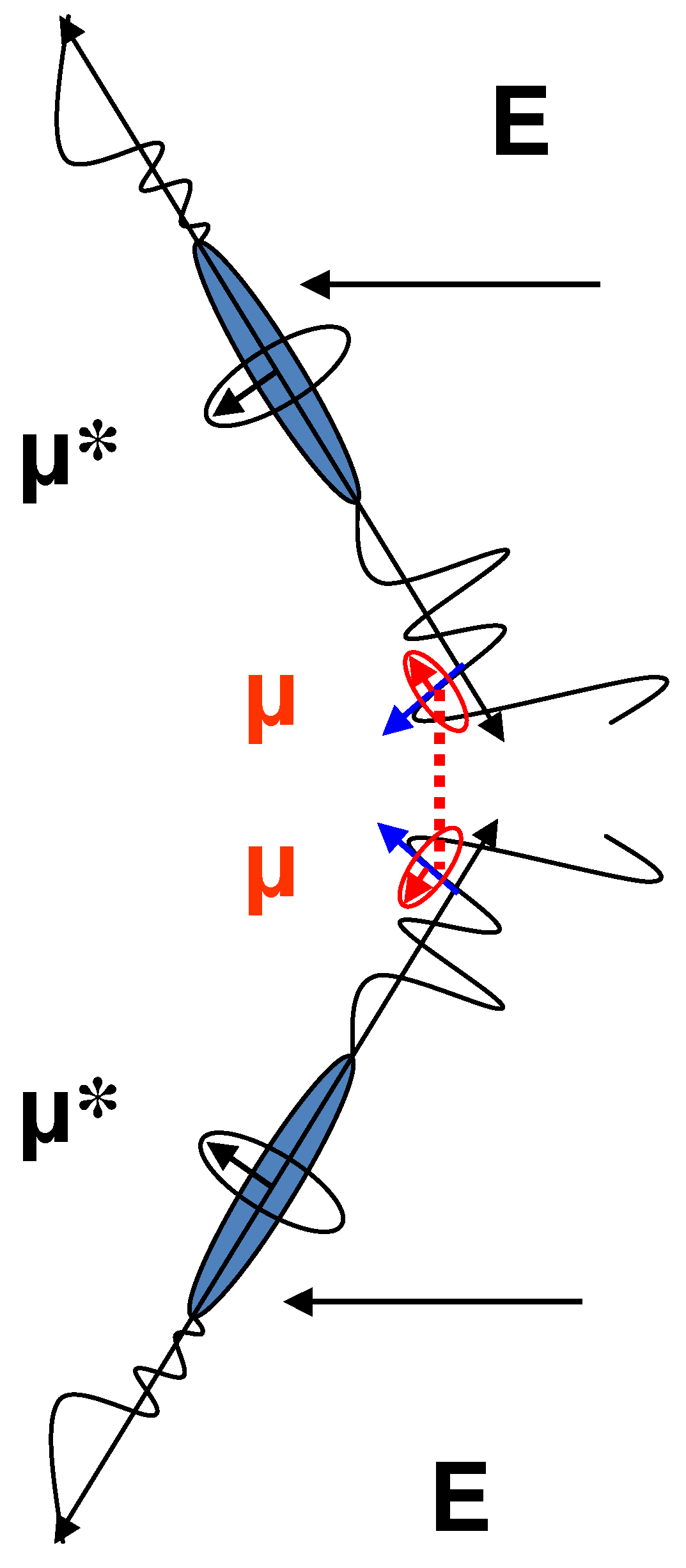
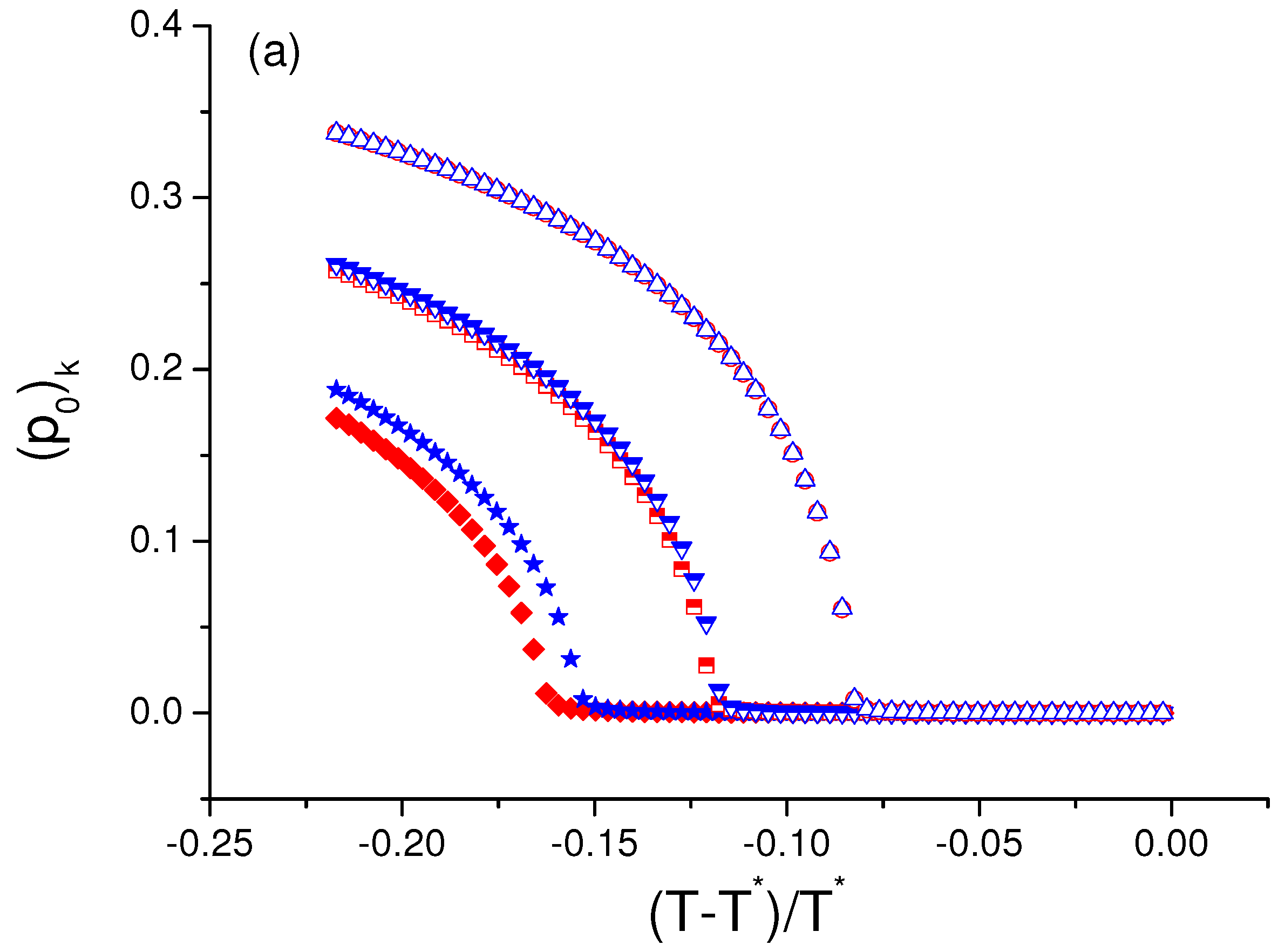
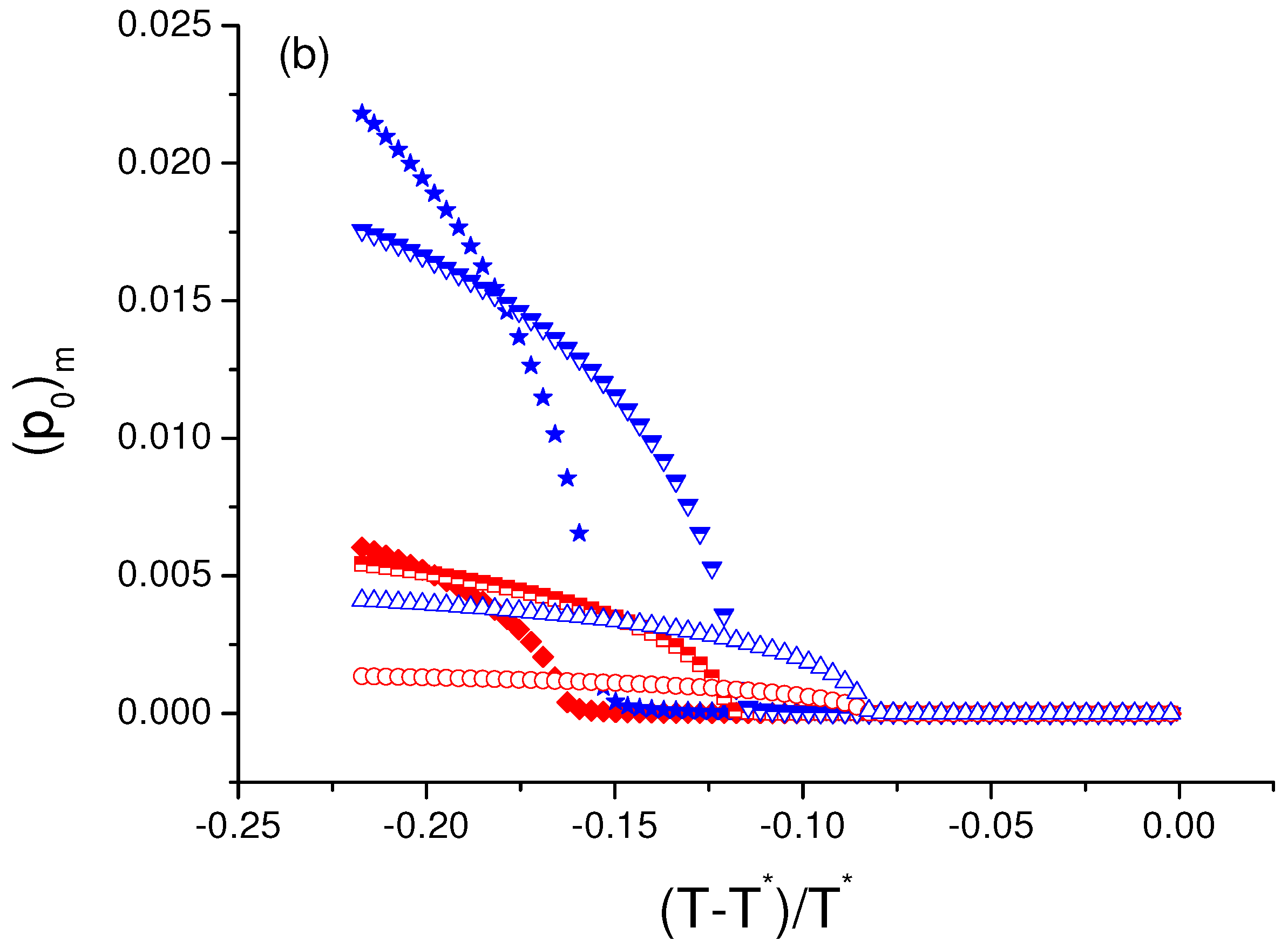
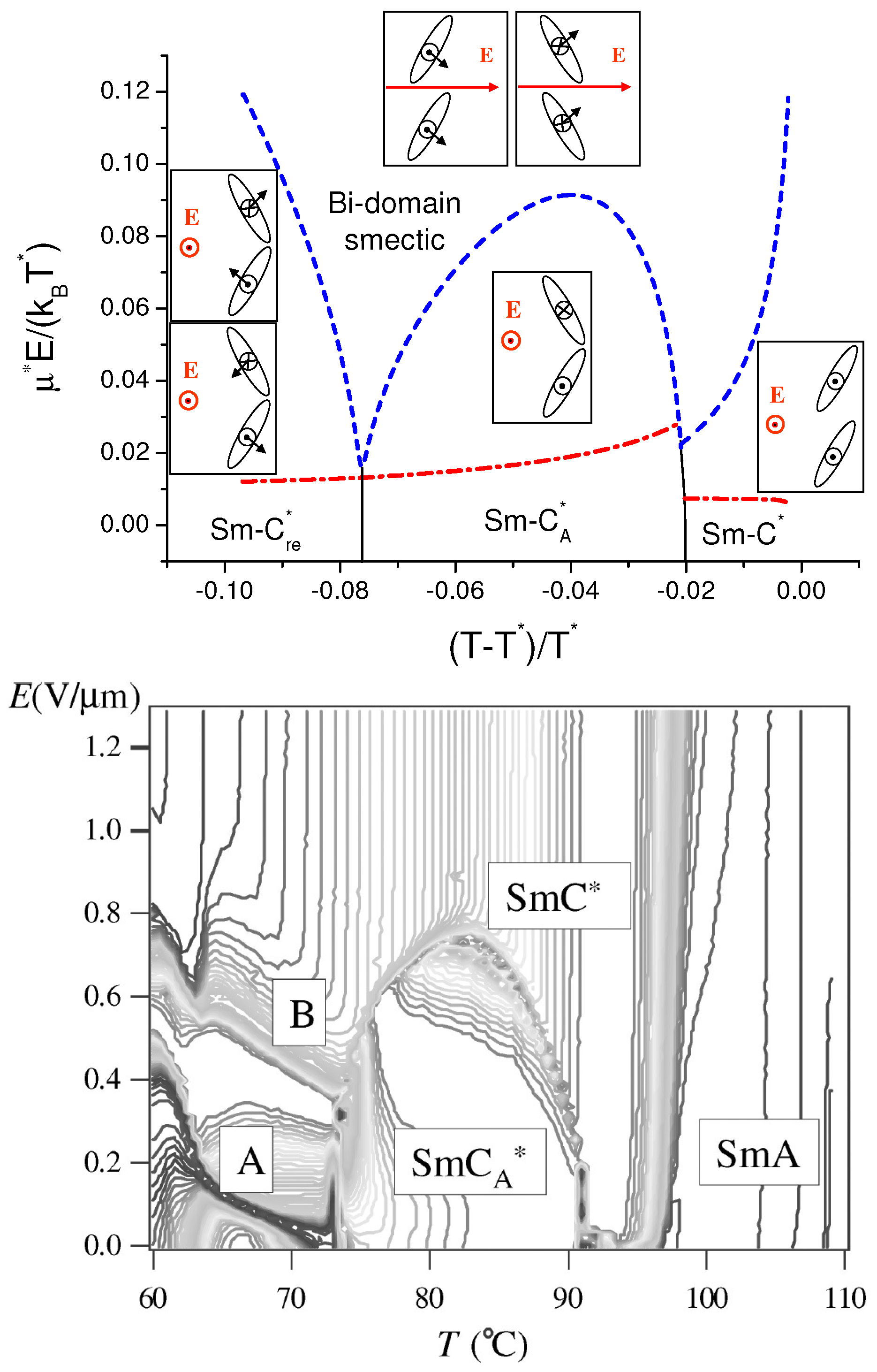
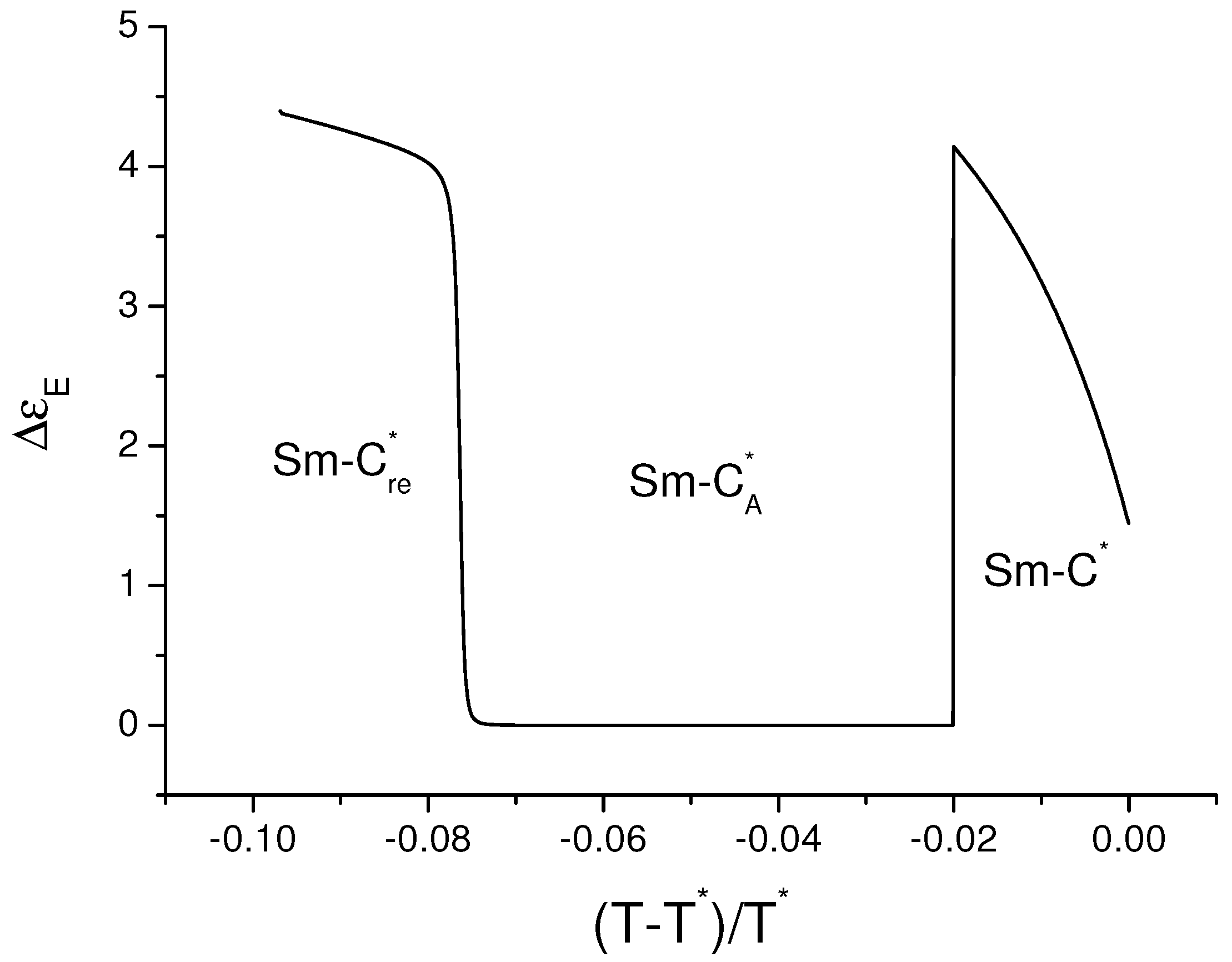
5. Polarization in the Presence of Electric Field: Re-Entrant Ferroelectric Phase
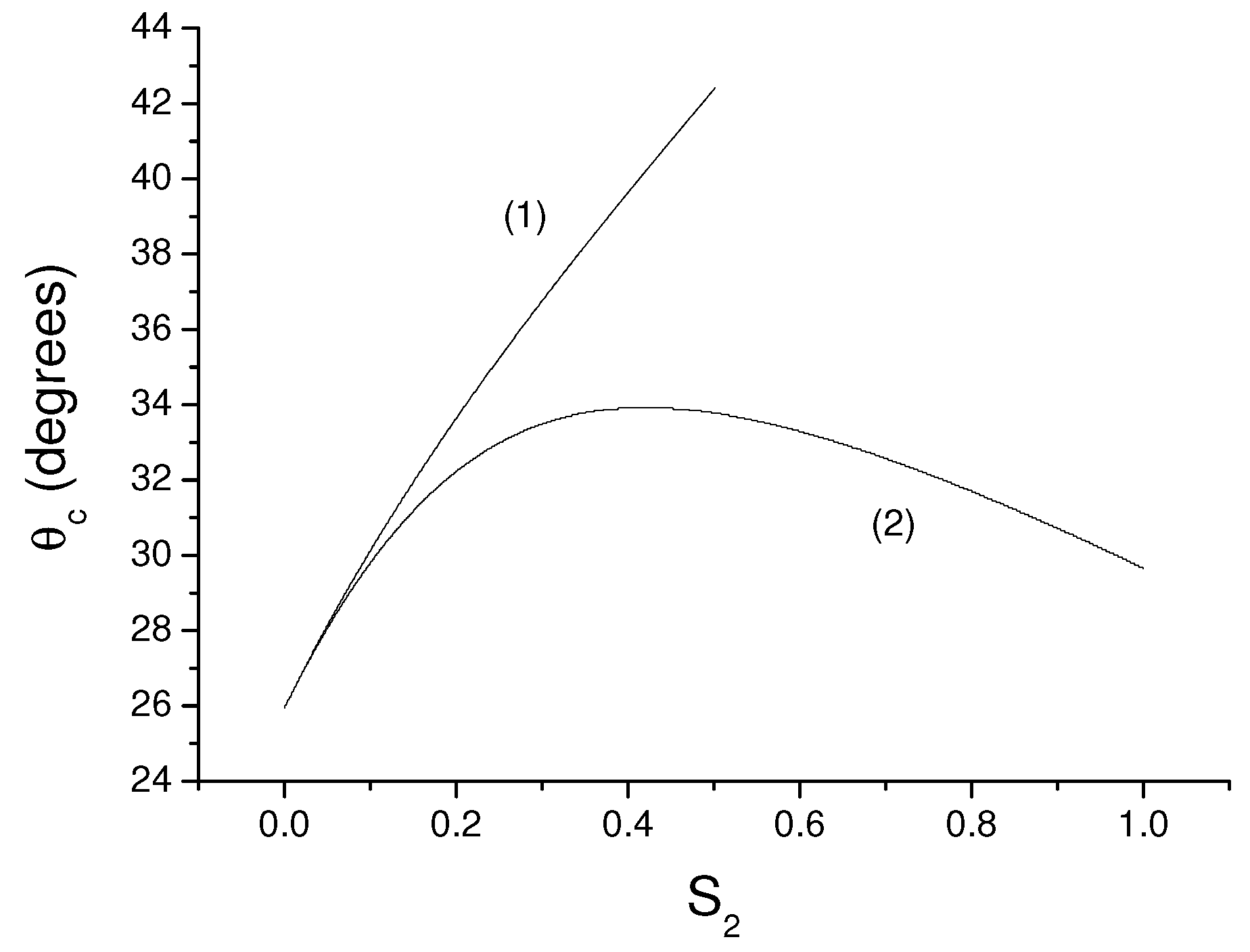
6. Temperature Induced Transition Between Synclinic And Anticlinic Smectic Phases
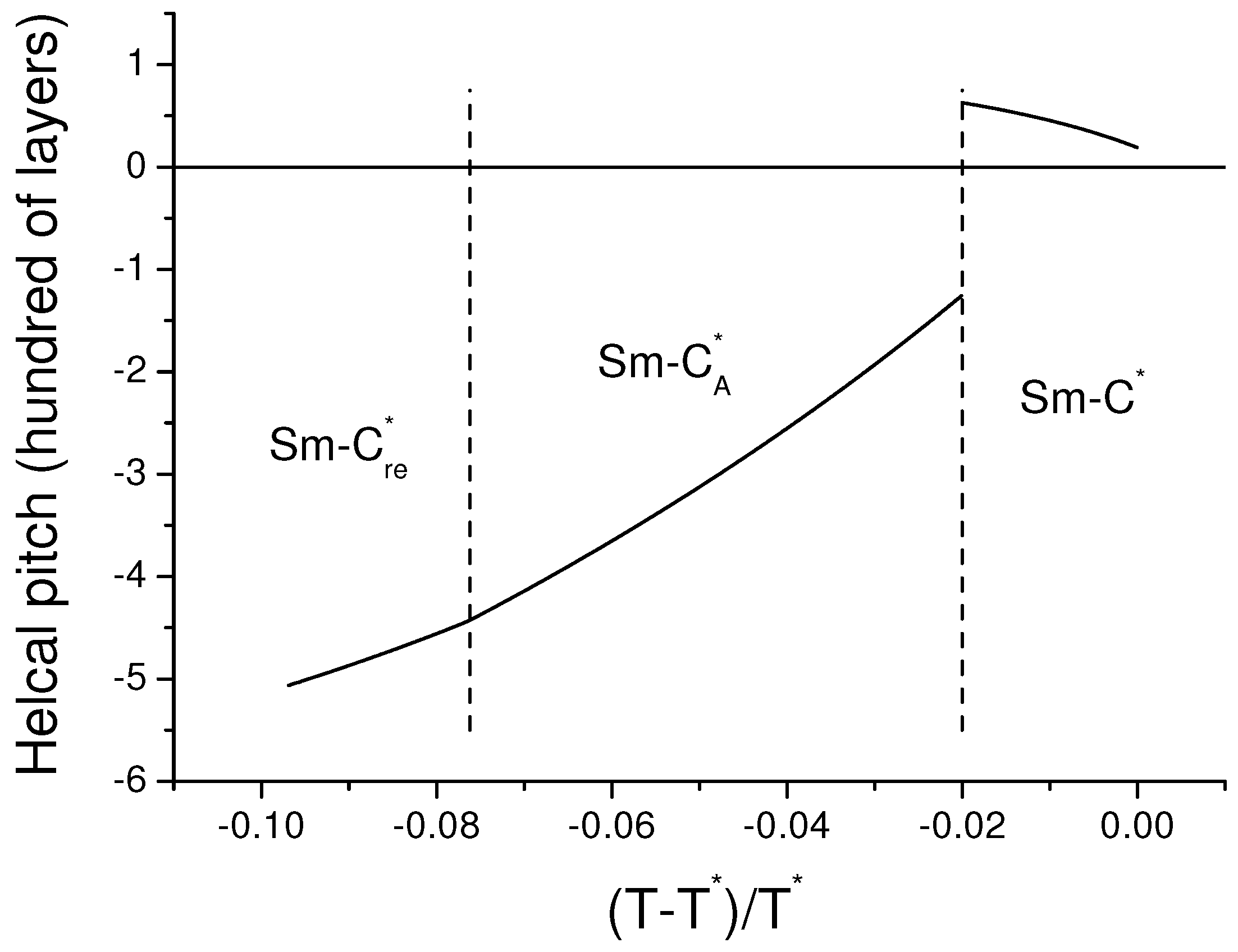
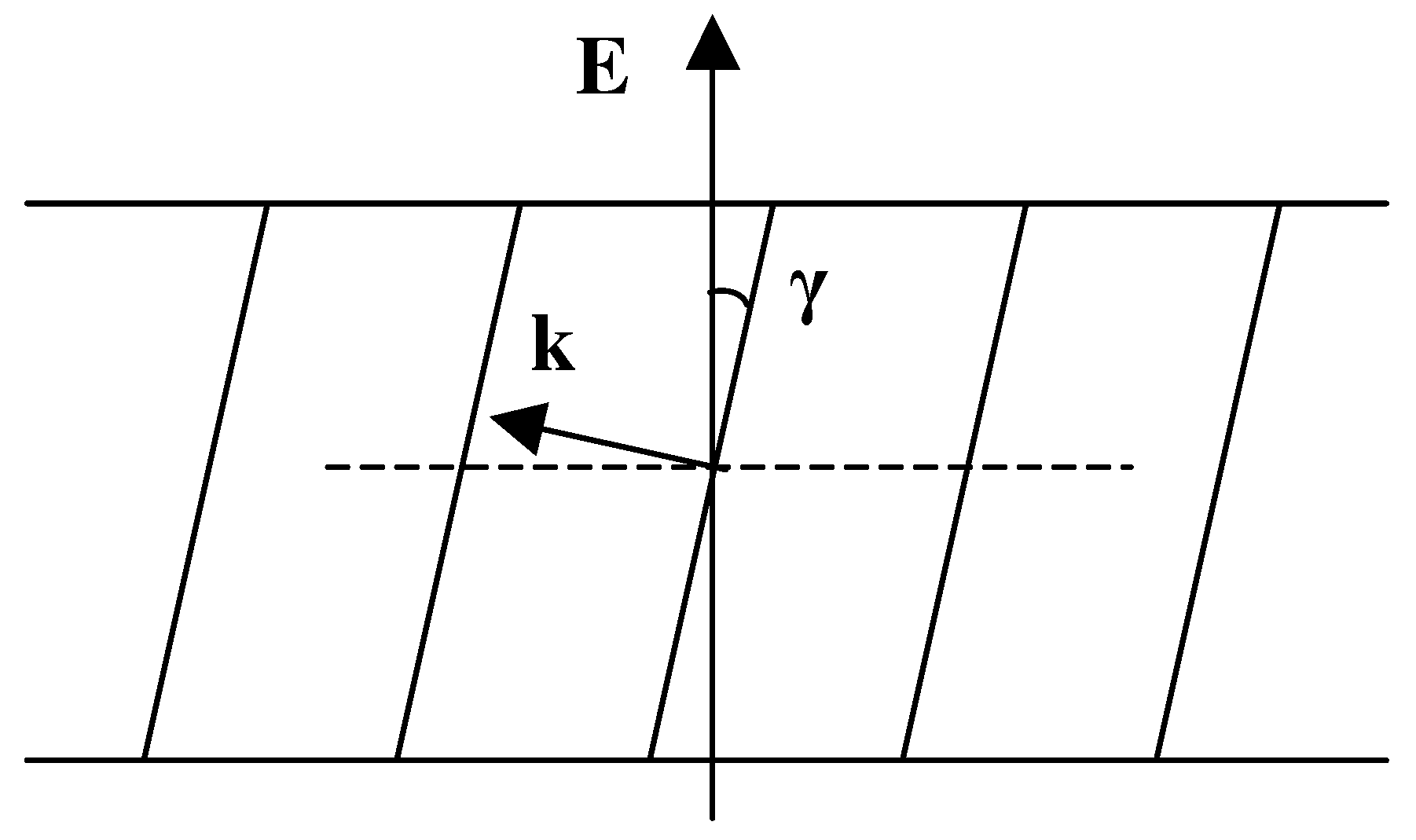
7. Helical Rotation, Elasticity and Deformation of Sm-, Sm- and Sm- in the Electric Field
8. Dielectric Response
9. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Average Multiple of Various Projections of Dipole Moments and
Appendix B. Free Energy Expansion in Taylor Series with Respect to the Local Field
References
- Meyer, R.B. Ferroelectric Liquid Crystals. Mol. Cryst. Liq. Cryst. 1977, 36, 69–71. [Google Scholar] [CrossRef]
- Chandani, A.D.L.; Gorecka, E.; Ouchi, Y.; Takezoe, H.; Fukuda, A. Antiferroelectric Chiral Smectic Phases Responsible for the Tristable Switching in MHPOBC. Jpn. J. Appl. Phys. 1989, 28, L1265. [Google Scholar] [CrossRef]
- Novotna, V.; Hamplova, V.; Kaspar, M.; Glogarova, M.; Bubnov, A.; Lhotakova, Y. Phase diagrams of binary mixtures of antiferroelectric and ferroelectric compounds with lactate units in the mesogenic core. Ferroelectrics 2004, 309, 103–109. [Google Scholar] [CrossRef]
- Bubnov, A.; Novotna, V.; Hamplova, V.; Kaspar, M.; Glogarova, M. Effect of multilactate chiral part of the liquid crystalline molecule on mesomorphic behaviour. J. Mol. Struct. 2008, 892, 151–157. [Google Scholar] [CrossRef]
- Novotna, V.; Glogarova, M.; Hamplova, V.; Kaspar, M. Re-entrant ferroelectric phases in binary mixtures of ferroelectric and antiferroelectric homologues of a series with three chiral centers. J. Chem. Phys. 2001, 115, 9036–9041. [Google Scholar] [CrossRef]
- Bubnov, A.; Kaspar, M.; Hamplova, V.; Glogarova, M.; Samaritani, S.; Galli, G.; Andersson, G.; Komitov, L. New polar liquid crystalline monomers with two and three lactate groups for preparation of side chain polysiloxanes. Liq. Cryst. 2006, 33, 559–566. [Google Scholar] [CrossRef]
- Kaspar, M.; Hamplova, V.; Novotna, V.; Glogarova, M.; Pociecha, D.; Vanek, P. New series of ferroelectric liquid crystals with two or three chiral centres exhibiting antiferroelectric and hexatic phases. Liq. Cryst. 2001, 28, 1203–1207. [Google Scholar]
- Na, Y.; Naruse, Y.; Fukuda, N.; Orihara, H.; Fajar, A.; Hamplova, V.; Kaspar, M.; Glogarova, M. E-T Phase Diagrams of an Antiferroelectric Liquid Crystal with Re-Entrant Smectic C* Phase. Ferroelectrics 2008, 364, 13–19. [Google Scholar] [CrossRef]
- Catalano, D.; Domenici, V.; Marini, A.; Veracini, C.A.; Bubnov, A.; Glogarova, M. Structural and orientational properties of the ferro, antiferroelectric, and re-entrant smectic C* phases of ZLL7* by Deuterium NMR and other experimental techniques. J. Phys. Chem. B 2006, 110, 16459–16470. [Google Scholar] [CrossRef] [PubMed]
- Domenici, V.; Marini, A.; Menicagli, R.; Veracini, C.A.; Bubnov, A.M.; Glogarova, M. Dynamic behaviour of a ferroelectric liquid crystal by means of Nuclear Magnetic Resonance and Dielectric Spectroscopy. In Proceedings of the SPIE 6587, Liquid Crystals and Applications in Optics, Prague, Czech Republic, 16–19 April 2007; Volume 6587, p. 65871F1. [Google Scholar]
- Domenici, V.; Bubnov, A.; Marini, A.; Hamplova, V.; Kaspar, M.; Glogarova, M.; Veracini, C.A. The ferroelectric SmC* phase studied by means of 2H and 13C NMR: structural and orientational features. In Proceedings of the 37th Topical Meeting of the German Liquid Crystal Society, Stuttgart, Germany, 1–3 April 2009; pp. 115–116. [Google Scholar]
- Emelyanenko, A.V. Molecular-ststistical approach to a behaviour of ferroelectric, antiferroelectric and ferrielectric smectic phases in the electric field. Eur. Phys. J. E 2009, 28, 441–455. [Google Scholar] [CrossRef] [PubMed]
- Emelyanenko, A.V. Theory for the evolution of ferroelectric, antiferroelectric, and ferrielectric smectic phases in the electric field. Phys. Rev. E 2010, 82, 031710. [Google Scholar] [CrossRef] [PubMed]
- Emelyanenko, A.V.; Ishikawa, K. Smooth transitions between biaxial intermediate smectic phases. Soft Matter 2013, 9, 3497–3508. [Google Scholar] [CrossRef]
- Emelyanenko, A.V. Induction of new ferrielectric smectic phases in the electric field. Ferroelectrics 2016, 495, 129–142. [Google Scholar] [CrossRef]
- Emelyanenko, A.V.; Osipov, M.A. Theoretical model for the discrete flexoelectric effect and a description for the sequence of intermediate smectic phases with increasing periodicity. Phys. Rev. E 2003, 68, 0517033. [Google Scholar] [CrossRef]
- Emelyanenko, A.V.; Fukuda, A.; Vij, J.K. Theory of the intermediate tilted smectic phases and their helical rotation. Phys. Rev. E 2006, 74, 011705. [Google Scholar] [CrossRef] [Green Version]
- Emelyanenko, A.V.; Filimonova, E.S. Molecular-statistical approach to the description of tilted smectic phases. Phase Transit. 2018, 91, 984–993. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emelyanenko, A.V. Molecular–Statistical Theory for the Description of Re-Entrant Ferroelectric Phase. Crystals 2019, 9, 583. https://doi.org/10.3390/cryst9110583
Emelyanenko AV. Molecular–Statistical Theory for the Description of Re-Entrant Ferroelectric Phase. Crystals. 2019; 9(11):583. https://doi.org/10.3390/cryst9110583
Chicago/Turabian StyleEmelyanenko, Alexander V. 2019. "Molecular–Statistical Theory for the Description of Re-Entrant Ferroelectric Phase" Crystals 9, no. 11: 583. https://doi.org/10.3390/cryst9110583
APA StyleEmelyanenko, A. V. (2019). Molecular–Statistical Theory for the Description of Re-Entrant Ferroelectric Phase. Crystals, 9(11), 583. https://doi.org/10.3390/cryst9110583




