Electronic Structure of Oxygen-Deficient SrTiO3 and Sr2TiO4
Abstract
1. Introduction
2. Results
2.1. Bulk and Surface of SrTiO
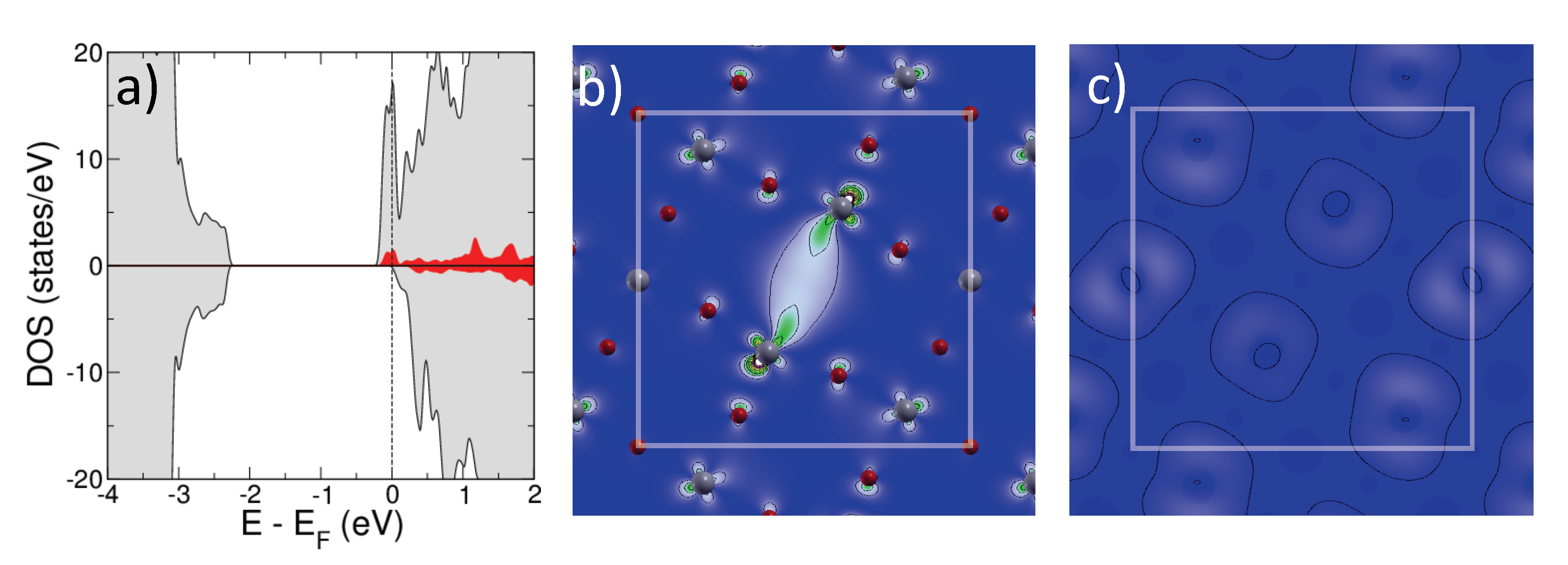
2.1.1. Isolated Defects
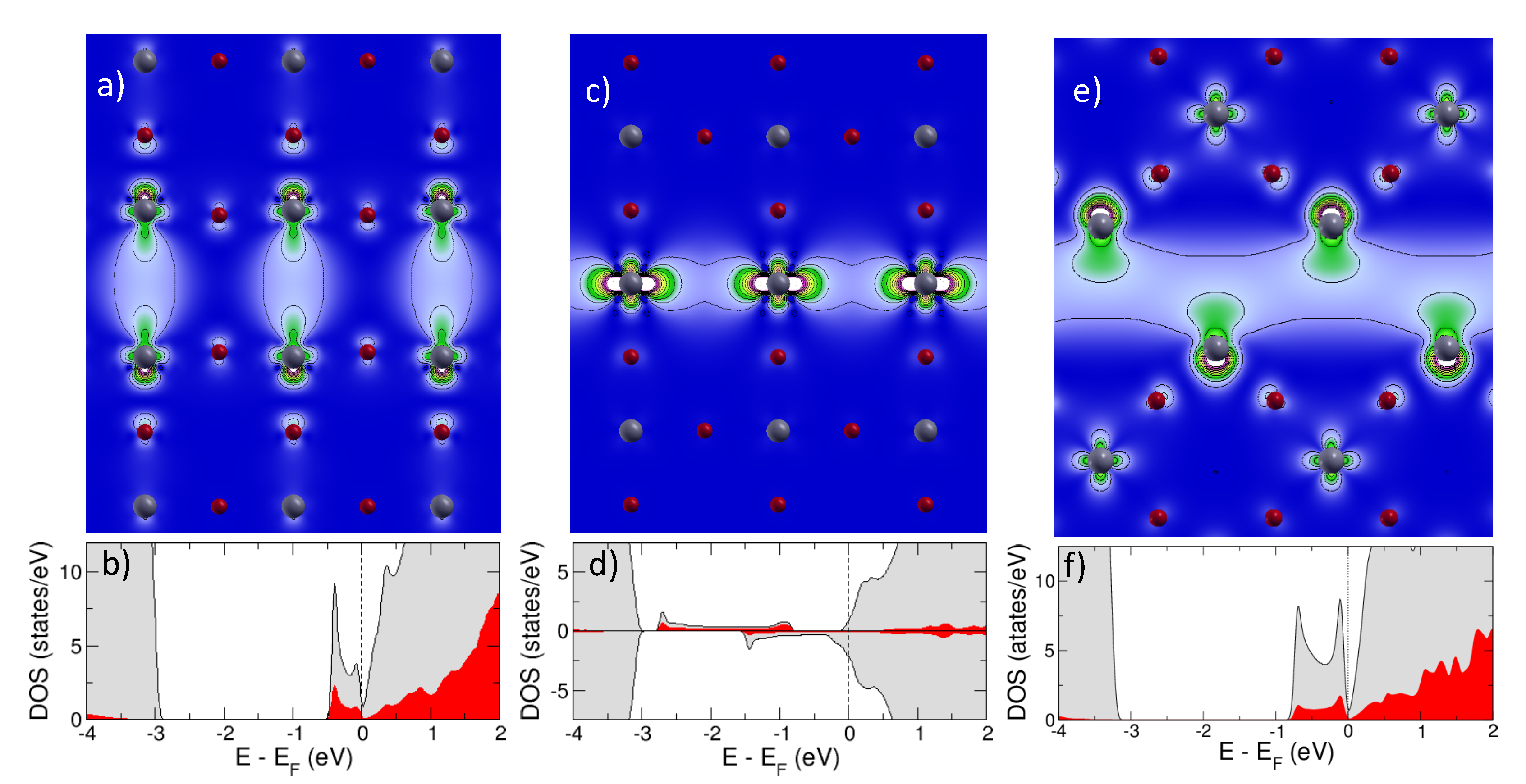
2.1.2. Extended Defects
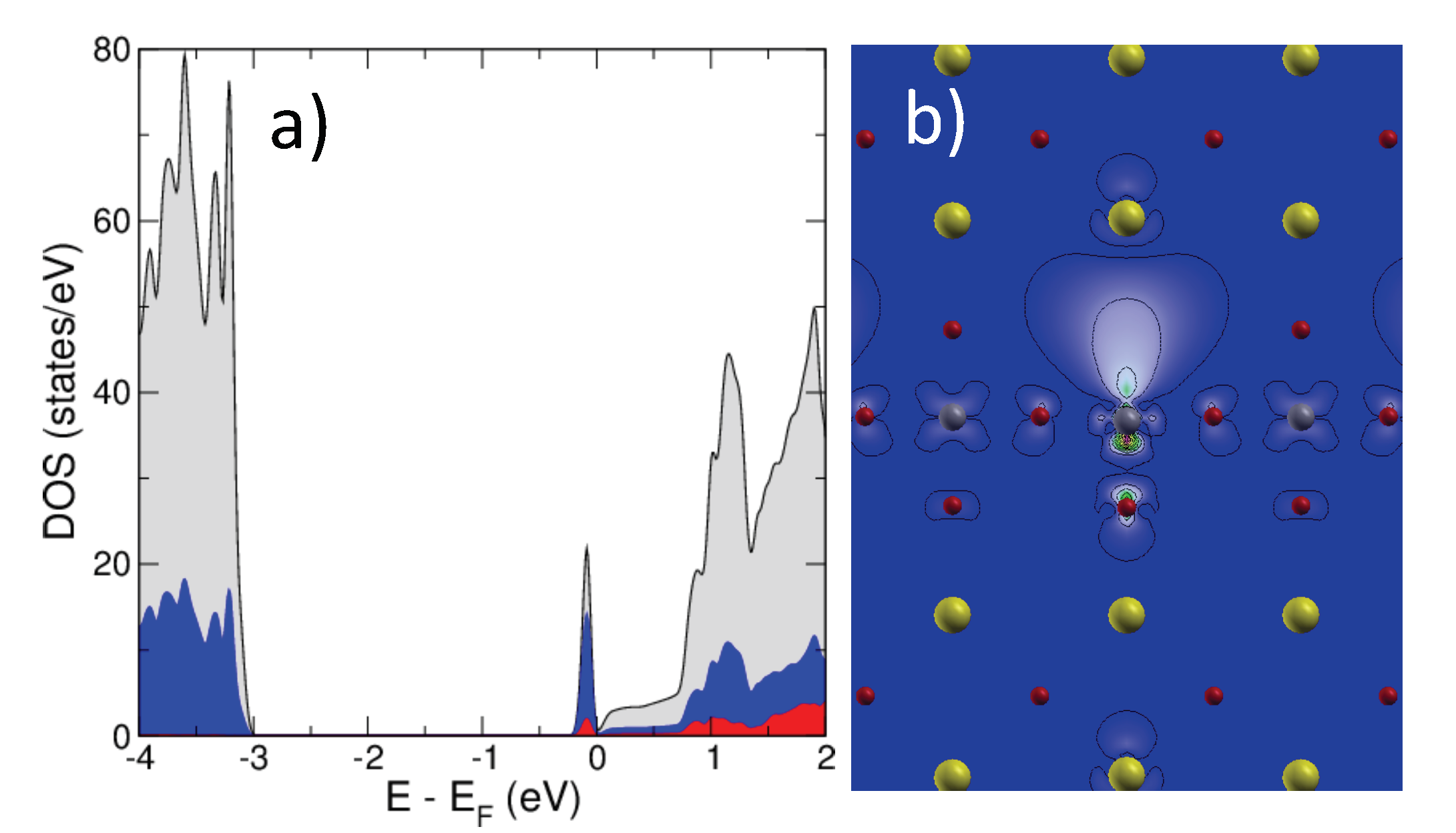
2.2. SrTiO
3. Discussion
4. Methods
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dearnaley, G.; Stoneham, A.M.; Morgan, D.V. Electrical phenomena in amorphous oxide films. Rep. Prog. Phys. 1970, 33, 1129. [Google Scholar] [CrossRef]
- Beck, A.; Bednorz, J.G.; Gerber, C.; Rossel, C.; Widmer, D. Reproducible switching effect in thin oxide films for memory applications. Appl. Phys. Lett. 2000, 77, 139–141. [Google Scholar] [CrossRef]
- Watanabe, Y.; Bednorz, J.G.; Bietsch, A.; Gerber, C.; Widmer, D.; Beck, A.; Wind, S.J. Current-driven insulator–conductor transition and nonvolatile memory in chromium-doped SrTiO3 single crystals. Appl. Phys. Lett. 2001, 78, 3738–3740. [Google Scholar] [CrossRef]
- Szot, K.; Speier, W.; Bihlmayer, G.; Waser, R. Switching the electrical resistance of individual dislocations in single crystalline SrTiO3. Nat. Mater. 2006, 5, 312–320. [Google Scholar] [CrossRef]
- Szot, K.; Bihlmayer, G.; Speier, W. Nature of the Resistive Switching Phenomena in TiO2 and SrTiO3: Origin of the Reversible Insulator-Metal Transition. Solid State Phys. 2014, 65, 353–559. [Google Scholar] [CrossRef]
- Marrocchelli, D.; Sun, L.X.; Yildiz, B. Dislocations in SrTiO3: Easy to reduce but not fast for oxygen transport. J. Am. Chem. Soc. 2015, 137, 4735–4748. [Google Scholar] [CrossRef]
- Kwon, D.H.; Lee, S.; Kang, C.S.; Choi, Y.S.; Kang, S.J.; Cho, H.L.; Sohn, W.; Jo, J.; Lee, S.Y.; Oh, K.H.; et al. Unraveling the Origin and Mechanism of Nanofilament Formation in Polycrystalline SrTiO3 Resistive Switching Memories. Adv. Mater. 2019, 31, 1901322. [Google Scholar] [CrossRef] [PubMed]
- Cuong, D.D.; Lee, B.; Choi, K.M.; Ahn, H.S.; Han, S.; Lee, J. Oxygen Vacancy Clustering and Electron Localization in Oxygen-Deficient SrTiO3: LDA + U Study. Phys. Rev. Lett. 2007, 98, 115503. [Google Scholar] [CrossRef] [PubMed]
- Jeschke, H.O.; Shen, J.; Valentí, R. Localized versus itinerant states created by multiple oxygen vacancies in SrTiO3. New J. Phys. 2015, 17, 023034. [Google Scholar] [CrossRef]
- Anderson, J.S.; Hyde, H.G. On the possible role of dislocations in generating ordered and disordered shear structures. J. Phys. Chem. Sol. 1967, 28, 1393–1408. [Google Scholar] [CrossRef]
- Bursill, L.A.; Hyde, H.G. Aggregation of Wadsley defrcts in slightly reduced rutile. Philos. Mag. 1971, 23, 3–15. [Google Scholar] [CrossRef]
- Park, S.G.; Magyari-Kope, B.; Nishi, Y. Impact of Oxygen Vacancy Ordering on the Formation of a Conductive Filament in TiO2 for Resistive Switching Memory. IEEE Electron Device Lett. 2011, 32, 197–199. [Google Scholar] [CrossRef]
- Gao, P.; Ishikawa, R.; Feng, B.; Kumamoto, A.; Shibata, N.; Ikuhara, Y. Atomic-scale structure relaxation, chemistry and charge distribution of dislocation cores in SrTiO3. Ultramicroscopy 2018, 184, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Rogala, M.; Bihlmayer, G.; Dabrowski, P.; Rodenbücher, C.; Wrana, D.; Krok, F.; Klusek, Z.; Szot, K. Self-reduction of the native TiO2 (110) surface during cooling after thermal annealing-in-operando investigation. Sci. Rep. 2019, 9, 12563. [Google Scholar] [CrossRef] [PubMed]
- Piskunov, S.; Heifets, E.; Eglitis, R.I.; Borstel, G. Bulk properties and electronic structure of SrTiO3, BaTiO3, PbTiO3 perovskites: An ab initio HF/DFT study. Comput. Mater. Sci. 2004, 29, 165–178. [Google Scholar] [CrossRef]
- Prosandeyev, S.A.; Fisenko, A.V.; Riabchinski, A.I.; Osipenko, I.A.; Raevski, I.P.; Safontseva, N. Study of intrinsic point defects in oxides of the perovskite family: I. Theory. J. Phys. Condens. Matter 1996, 8, 6705. [Google Scholar] [CrossRef]
- King-Smith, R.D.; Vanderbilt, D. First-principles investigation of ferroelectricity in perovskite compounds. Phys. Rev. B 1994, 49, 5828. [Google Scholar] [CrossRef]
- Ricci, D.; Bano, G.; Pacchioni, G. Electronic structure of a neutral oxygen vacancy in SrTiO3. Phys. Rev. B 2003, 68, 224105. [Google Scholar] [CrossRef]
- Evarestov, R.A.; Kotomin, E.A.; Zhukovskii, Y.F. DFT study of a single F center in cubic SrTiO3 perovskite. Int. J. Quantum Chem. 2005, 106, 2173–2183. [Google Scholar] [CrossRef]
- Carrasco, J.; Illas, F.; Lopez, N.; Kotomin, E.A.; Zhukovskii, Y.F.; Evarestov, R.A.; Mastrikov, Y.A.; Piskunov, S.; Maier, J. First-principles calculations of the atomic and electronic structure of F centers in the bulk and on the (001) surface of SrTiO3. Phys. Rev. B 2006, 73, 064106. [Google Scholar] [CrossRef]
- Kotomin, V.A.E.A.; Maier, J.; Evarestov, R.A. First-principles study of bulk and surface oxygen vacancies in SrTiO3 crystal. Eur. Phys. J. B 2009, 72, 53. [Google Scholar] [CrossRef]
- Astala, R.; Bristowe, P.D. Ab initio study of the oxygen vacancy in SrTiO3. Model. Simul. Mater. Sci. Eng. 2001, 9, 415. [Google Scholar] [CrossRef]
- Samanta, A.; Weinan, E.; Zhang, S.B. Method for defect stability diagram from ab initio calculations: A case study of SrTiO3. Phys. Rev. B 2012, 86, 195107. [Google Scholar] [CrossRef]
- Lin, C.; Mitra, C.; Demkov, A.A. Orbital ordering under reduced symmetry in transition metal perovskites: Oxygen vacancy in SrTiO3. Phys. Rev. B 2012, 86, 161102. [Google Scholar] [CrossRef]
- Lin, C.; Demkov, A.A. Electron Correlation in Oxygen Vacancy in SrTiO3. Phys. Rev. Lett. 2013, 111, 217601. [Google Scholar] [CrossRef]
- Hao, X.; Wang, Z.; Schmid, M.; Diebold, U.; Franchini, C. Coexistence of trapped and free excess electrons in SrTiO3. Phys. Rev. B 2015, 91, 085204. [Google Scholar] [CrossRef]
- Janotti, A.; Varley, J.B.; Choi, M.; Van de Walle, C.G. Vacancies and small polarons in SrTiO3. Phys. Rev. B 2014, 90, 085202. [Google Scholar] [CrossRef]
- Hou, Z.; Terakura, K. Defect States Induced by Oxygen Vacancies in Cubic SrTiO3: First-Principles Calculations. J. Phys. Soc. Jpn. 2010, 79, 114704. [Google Scholar] [CrossRef]
- Graetz, J.; Reilly, J.J.; Johnson, J.; Ignatov, A.Y.; Tyson, T.A. X-ray absorption study of Ti-activated sodium aluminum hydride. Appl. Phys. Lett. 2004, 85, 500–502. [Google Scholar] [CrossRef]
- Drera, G.; Salvinelli, G.; Brinkman, A.; Huijben, M.; Koster, G.; Hilgenkamp, H.; Rijnders, G.; Visentin, D.; Sangaletti, L. Band offsets and density of Ti3+ states probed by X-ray photoemission on LaAlO3/SrTiO3 heterointerfaces and their LaAlO3 and SrTiO3 bulk precursors. Phys. Rev. B 2013, 87, 075435. [Google Scholar] [CrossRef]
- Sitaputra, W.; Sivadas, N.; Skowronski, M.; Xiao, D.; Feenstra, R.M. Oxygen vacancies on SrO-terminated SrTiO3(001) surfaces studied by scanning tunneling spectroscopy. Phys. Rev. B 2015, 91, 205408. [Google Scholar] [CrossRef]
- Tanaka, H.; Matsumoto, T.; Kawai, T.; Kawai, S. Surface Structure and Electronic Property of Reduced SrTiO3 (100) Surface Observed by Scanning Tunneling Microscopy/Spectroscopy. Jpn. J. Appl. Phys. 1993, 32, 1405. [Google Scholar] [CrossRef]
- Fang, Z.; Terakura, K. Spin and orbital polarizations around oxygen vacancies on the (001) surfaces of SrTiO3. Surf. Sci. 2000, 470, L75. [Google Scholar] [CrossRef]
- Shen, J.; Lee, H.; Valentí, R.; Jeschke, H.O. Ab initio study of the two-dimensional metallic state at the surface of SrTiO3: Importance of oxygen vacancies. Phys. Rev. B 2012, 86, 195119. [Google Scholar] [CrossRef]
- Li, Z.Q.; Zhu, J.L.; Wu, C.Q.; Tang, Z.; Kawazoe, Y. Relaxations of TiO2- and SrO-terminated SrTiO3 (001) surfaces. Phys. Rev. B 1998, 58, 8075–8078. [Google Scholar] [CrossRef]
- Shiraki, I.; Miki, K. SrTiO3 (100) –R26.6 surface observed by high-resolution scanning tunneling microscopy. Surf. Sci. 2011, 605, 1304–1307. [Google Scholar] [CrossRef]
- Walker, S.M.; Bruno, F.Y.; Wang, Z.; de la Torre, A.; Riccó, S.; Tamai, A.; Kim, T.K.; Hoesch, M.; Shi, M.; Bahramy, M.S.; et al. Carrier-Density Control of the SrTiO3 (001) Surface 2D Electron Gas studied by ARPES. Adv. Mater. 2015, 27, 3894–3899. [Google Scholar] [CrossRef]
- Noguera, C. Theoretical investigation of the Ruddlesden-Popper compunds Srn+1TinO3n+1 (n = 1–3). Philos. Mag. Lett. 2000, 80, 173. [Google Scholar] [CrossRef]
- Szot, K.; Speier, W.; Herion, J.; Feiburg, C. Restructuring of the surface region in SrTiO3. Appl. Phys. A 1996, 64, 55. [Google Scholar] [CrossRef]
- Shibuya, K.; Dittmann, R.; Mi, S.; Waser, R. Impact of Defect Distribution on Resistive Switching Characteristics of Sr2TiO4 Thin Films. Adv. Mater. 2010, 22, 411–414. [Google Scholar] [CrossRef]
- Rodenbücher, C.; Speier, W.; Bihlmayer, G.; Breuer, U.; Waser, R.; Szot, K. Cluster-like resistive switching of SrTiO3:Nb surface layers. New J. Phys. 2013, 15, 103017. [Google Scholar] [CrossRef]
- Lee, C.; Yahia, J.; Brebner, J.L. Electronic Conduction in Slightly Reduced Strontium Titanate at Low Temperatures. Phys. Rev. B 1971, 3, 2525–2533. [Google Scholar] [CrossRef]
- Kolodiazhnyi, T. Insulator-metal transition and anomalous sign reversal of the dominant charge carriers in perovskite BaTiO3−δ. Phys. Rev. B 2008, 78, 045107. [Google Scholar] [CrossRef]
- Wimmer, E.; Krakauer, H.; Weinert, M.; Freeman, A.J. Full-potential self-consistent linearized-augmented-plane-wave method for calculating the electronic structure of molecules and surfaces: O2 molecule. Phys. Rev. B 1981, 24, 864. [Google Scholar] [CrossRef]
- The Jülich Full-Linearized Augmented Plane Waves (FLAPW) Code Family. Available online: http://www.flapw.de (accessed on 18 October 2019).
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Carrasco, J.; Illas, F.; Lopez, N.; Kotomin, E.A.; Zhukovskii, Y.F.; Piskunov, S.; Maier, J.; Hermansson, K. First principles simulations of F centers in cubic SrTiO3. Phys. Status Solidi C 2005, 2, 153–158. [Google Scholar] [CrossRef]
- Solovyev, I.V.; Dederichs, P.H.; Anisimov, V.I. Corrected atomic limit in the local-density approximation and the electronic structure of d impurities in Rb. Phys. Rev. B 1994, 50, 16861. [Google Scholar] [CrossRef]
- Park, S.G.; Magyari-Köpe, B.; Nishi, Y. Electronic correlation effects in reduced rutile TiO2 within the LDA + U method. Phys. Rev. B 2010, 82, 115109. [Google Scholar] [CrossRef]
- Shick, A.B.; Liechtenstein, A.I.; Pickett, W.E. Implementation of the LDA+U method using the full-potential linearized augmented plane-wave basis. Phys. Rev. B 1999, 60, 10763–10769. [Google Scholar] [CrossRef]
- Kokalj, A. Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale. Comput. Mater. Sci. 2003, 28, 155–168. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Zubi, A.; Bihlmayer, G.; Blügel, S. Electronic Structure of Oxygen-Deficient SrTiO3 and Sr2TiO4. Crystals 2019, 9, 580. https://doi.org/10.3390/cryst9110580
Al-Zubi A, Bihlmayer G, Blügel S. Electronic Structure of Oxygen-Deficient SrTiO3 and Sr2TiO4. Crystals. 2019; 9(11):580. https://doi.org/10.3390/cryst9110580
Chicago/Turabian StyleAl-Zubi, Ali, Gustav Bihlmayer, and Stefan Blügel. 2019. "Electronic Structure of Oxygen-Deficient SrTiO3 and Sr2TiO4" Crystals 9, no. 11: 580. https://doi.org/10.3390/cryst9110580
APA StyleAl-Zubi, A., Bihlmayer, G., & Blügel, S. (2019). Electronic Structure of Oxygen-Deficient SrTiO3 and Sr2TiO4. Crystals, 9(11), 580. https://doi.org/10.3390/cryst9110580




