Habit Change of Monoclinic Hydroxyapatite Crystals Growing from Aqueous Solution in the Presence of Citrate Ions: The Role of 2D Epitaxy
Abstract
1. Introduction
- The interaction between the adsorbed citrate ions and the different faces of the HAp crystal is ruled, at best, by the fit between the lattice parameters of a given face and the distance between the centres of the carboxylate groups in citrate; this means that each citrate ion acts alone, without cooperating with other ions to make aggregates adsorbed on the growing crystal surfaces.
- The adsorbed citrate ions are supposed to interact with a face of a HAp that is assumed to belong to a hexagonal space group. Accordingly, all the six symmetry-equivalent faces of the hexagonal prism could kinetically behave in the same way. Hence, the observed HAp habit change due to the action of citrate can be explained only by assuming that: (i) the space group of the HAp crystal growing in pure medium is originally monoclinic; and (ii) the action of citrate does not correspond to that of isolated entities (random adsorption) but to that of ordered 2D islands epitaxially adsorbed onto the different crystallographic surfaces of all the most important HAp forms.
2. Materials and Methods
3. Results and Discussion
- The Ca-HAp polymorph crystallizing in aqueous solutions at room temperature is monoclinic
- The citrate ions are adsorbed as ordered 2D-islands built by the sole stable phase of Ca-citrate-hydrate, at room temperature, that is, the Ca-Cit-TH (tri-Calcium di-Citrate tetra-Hydrate). This Ca-citrate phase has been recently pointed out as a new relevant biomaterial for bone formation [24].
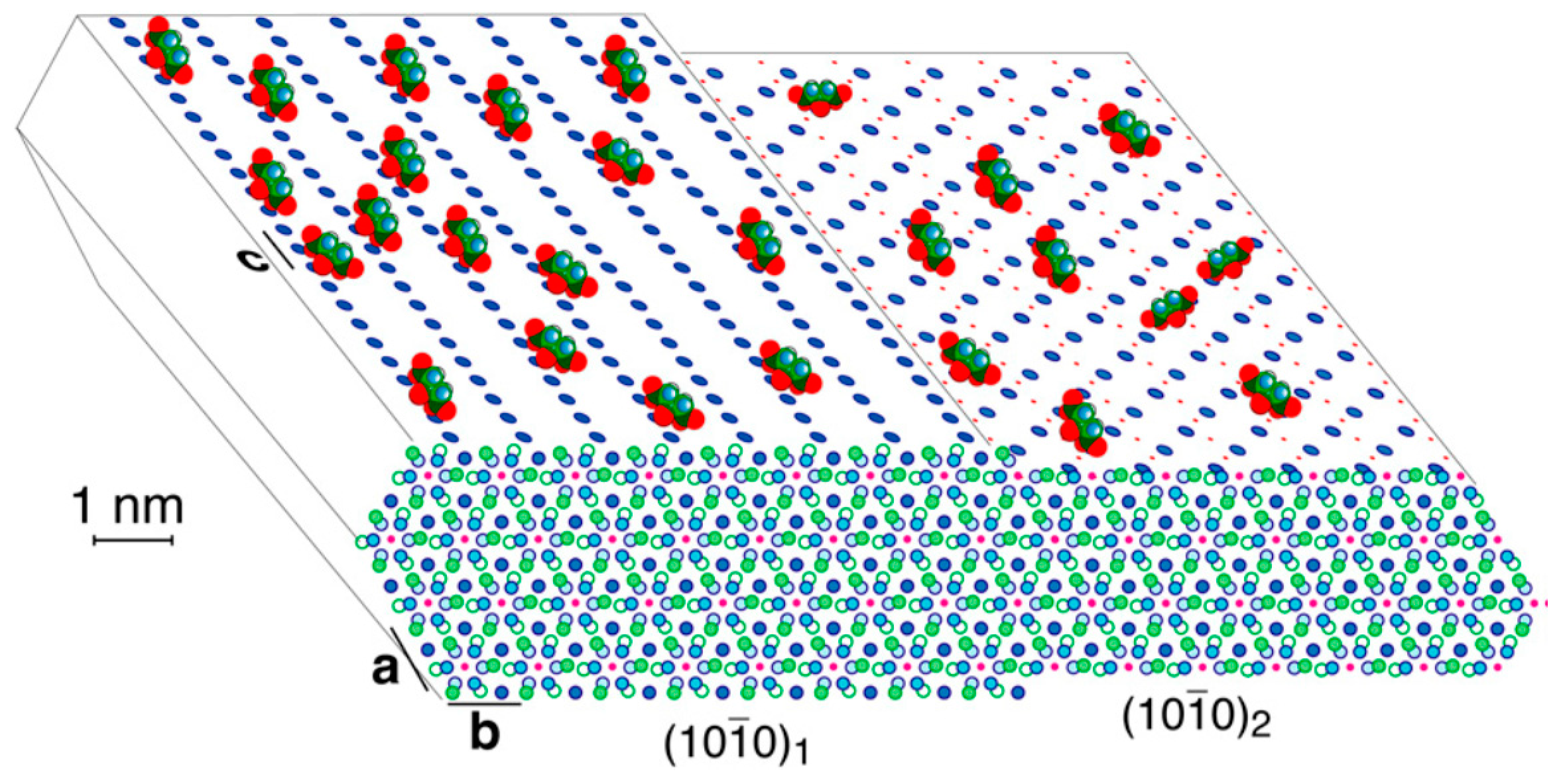
- the {001}HAp form shows 6 coincidence lattices, 5 of them having their multiplicity ranging between an absolute minimum (5×) and a moderate maximum (8×) with respect to the area of the {001}Ca-Cit-TH 2D-unit cell;
- for the HAp form, 6 coincidence lattices can be found as well, but only 2 of them do fulfil the just mentioned multiplicity criterion, their multiplicities being (7×);
- concerning the two pinacoids {100}HAp and HAp, 3 coincidence lattices are found, but only one of them shows a good multiplicity (6×), the other two being (10×) and (13×);
- the {010}HAp form, which is orthogonal to the OH− channels in HAp crystals, shows 10 coincidence lattices, only one of them having a reasonable multiplicity (7×) for a 2D epitaxy to occur.
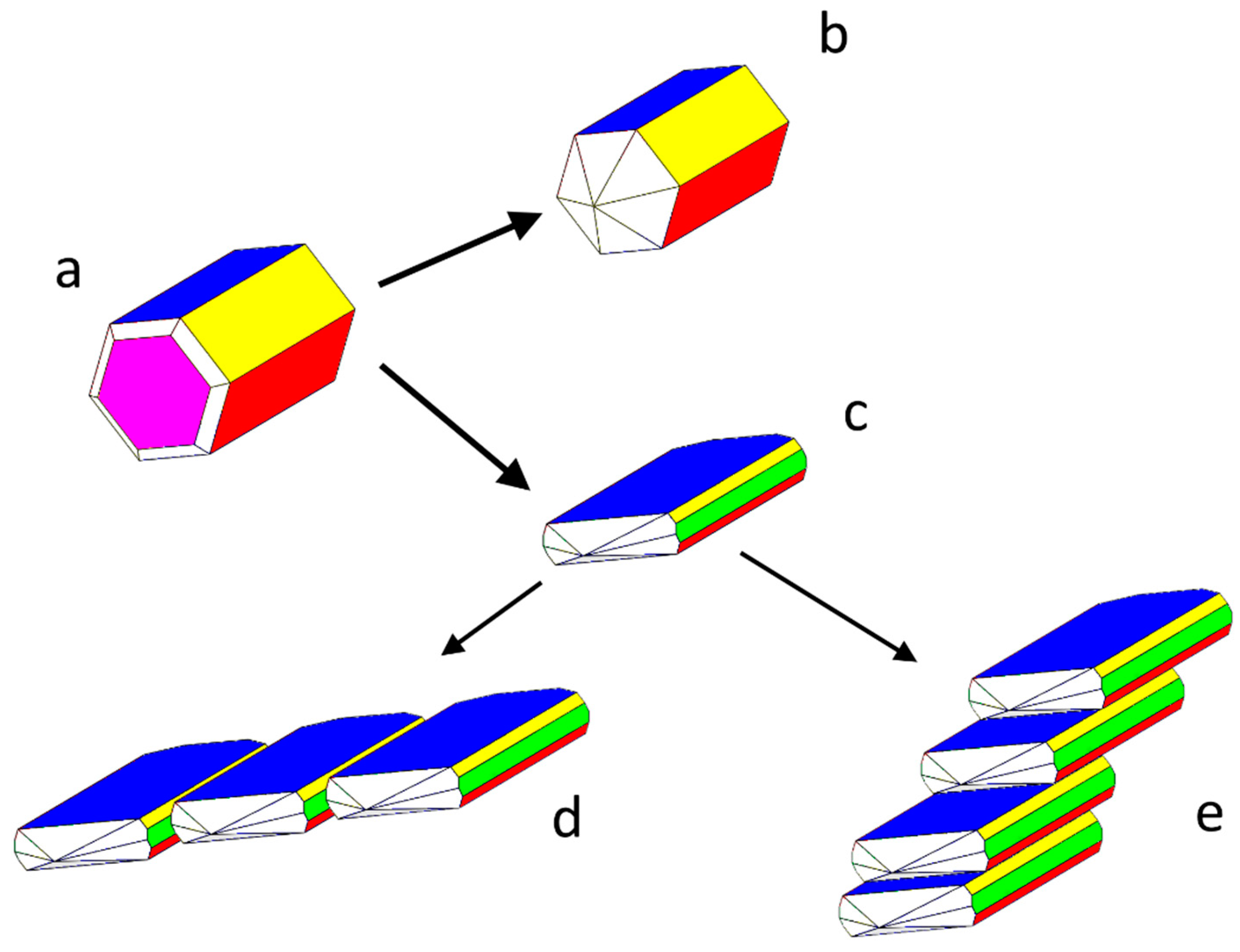
- The crystallographic allowance of the two involved 3D structures that originates the epitaxial relationships gives rise to the dramatic modifications of the HAp habit; it is worth outlining as well that the sandwiched Ca-citrate layers are centre-symmetric and, consequently, no constraints are imposed to the nucleation of a new HAp individual on a HAp crystal face which should work as a substrate. Moreover, when carefully looking at Figure 2b, it comes out that another kind of fence-like aggregate can form, made by stacked HAp single crystals all elongated along the [010] direction and “welded” together through their {001} faces. Having considered that {001}Ca-Cit-TH layers can be easily adsorbed onto the {001}HAp faces, one could accept also in this case the hypothesis that these layers can be sandwiched in between two successive adjacent single and iso-oriented HAp crystals.
- The few Ca-citrate layers favouring the formation of the flattened and fence-like HAp morphology assume the function of the “mortar” cementing the apatitic crystal, in the same way as the 2D-sericin ordered layers work in between aragonite and calcite crystals in assembling the mollusk shells [36].
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Dickens, F. The citric acid content of animal tissues, with reference to its occurrence in bone and tumour. Biochem. J. 1941, 35, 1011–1023. [Google Scholar] [CrossRef] [PubMed]
- Costello, L.C.; Chellaiah, M.; Zou, J.; Franklin, R.B.; Reynolds, M.A. The status of citrate in the hydroxyapatite/collagen complex of bone and its role in bone formation. J. Regener. Med. Tissue Eng. 2014, 3, 4. [Google Scholar] [CrossRef] [PubMed]
- Filgueiras, M.R.T.; Mkhonto, D.; de Leeuw, N.H. Computer simulations of the adsorption of citric acid at hydroxyapatite surfaces. J. Cryst. Growth 2006, 294, 60–68. [Google Scholar] [CrossRef]
- De Leeuw, N.H.; Rabone, J.A.L. Molecular dynamics simulations surfaces of the interaction of citric acid with the hydroxyapatite (00.1) and (01.0) surfaces in an aqueous environment. CrystEngComm 2007, 9, 1178–1186. [Google Scholar] [CrossRef]
- Jiang, W.G.; Chu, X.; Wang, B.; Pan, H.; Xu, X.; Tang, R. Biomimetically triggered inorganic crystal transformation by biomolecules: A new understanding of biomineralization. J. Phys. Chem. B 2009, 113, 10838–10844. [Google Scholar] [CrossRef] [PubMed]
- Rhee, S.H.; Tanaka, J. Effect of citric acid on the nucleation of hydroxyapatite in a simulated body fluid. Biomaterials 1999, 20, 2155–2160. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Rawal, A.; Schmidt-Rohr, K. Strongly bound citrate stabilizes the apatite nanocrystals in bone. Proc. Natl. Acad. Sci. USA 2010, 107, 22425–22429. [Google Scholar] [CrossRef] [PubMed]
- Terpstra, R.A.; Bennema, P.; Hartman, P.; Woensdregt, C.F.; Perdok, W.G.; Senechal, M.L. F-faces of apatite and its morphology: Theory and observation. J. Cryst. Growth 1986, 78, 468–478. [Google Scholar] [CrossRef]
- Delgado-López, J.M.; Iafisco, M.; Rodriguez, I.; Tampieri, A.; Prat, M.; Gómez-Morales, J. Crystallization of bioinspired citrate-functionalized nanoapatite with tailored carbonate content. Acta Biomater. 2012, 8, 3491–3499. [Google Scholar] [CrossRef] [PubMed]
- Delgado-López, J.M.; Frison, R.; Cervellino, A.; Gómez-Morales, J.; Guagliardi, A. Masciocchi, N. Crystal size, morphology, and growth mechanism in bio-inspired apatite nanocrystals. Adv. Funct. Mater. 2014, 24, 1090–1099. [Google Scholar] [CrossRef]
- Iafisco, M.; Ramirez-Rodriguez, G.B.; Sakhno, Y.; Tampieri, A.; Martra, G.; Gómez-Morales, J.; Delgado-López, J.M. The growth mechanism of apatite nanocrystals assisted by citrate: Relevance to bone mineralization. CrystEngComm 2015, 17, 507–511. [Google Scholar] [CrossRef]
- Martínez-Casado, F.J.; Iafisco, M.; Delgado-López, J.M.; Martínez-Benito, C.; Ruiz-Pérez, C.; Colangelo, D.; Oltolina, F.; Prat, M.; Gómez-Morales, J. Bioinspired citrate-apatite nanocrystals doped with divalent transition metal ions. Cryst. Growth Des. 2016, 16, 145–153. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Zhang, W.; Putnis, C.V.; Putnis, A. Direct observation of spiral growth, particle attachment, and morphology evolution of hydroxyapatite. Cryst. Growth Des. 2016, 16, 4509–4518. [Google Scholar] [CrossRef]
- Sato, K.; Kogure, T.; Kumagai, Y.; Tanaka, J. Crystal orientation of hydroxyapatite induced by ordered carboxyl groups. J. Colloid Interface Sci. 2001, 240, 133–138. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.Y.; Liu, X.P.; Ma, X.; Rawal, A.; Prozorov, T.; Akinc, M.; Mallapragada, S.K.; Schmidt-Rohr, K. Biomimetic self-assembling copolymer-hydroxyapatite nanocomposites with the nanocrystal size controlled by citrate. Chem. Mater. 2011, 23, 2481–2490. [Google Scholar] [CrossRef]
- Davies, E.; Müller, K.H.; Wong, W.C.; Pickard, C.J.; Reid, D.G.; Skepper, J.N.; Duer, M.J. Citrate bridges between mineral platelets in bone. Proc. Natl. Acad. Sci. USA 2014, 111, E1354–E1363. [Google Scholar] [CrossRef] [PubMed]
- Delgado-López, J.M.; Bertolotti, F.; Lyngsø, J.; Skov Pedersen, J.S.; Cervellino, A.; Masciocchi, N.; Guagliardi, A. The synergic role of collagen and citrate in stabilizing amorphous calcium phosphate precursors with platy morphology. Acta Biomater. 2017, 49, 555–562. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, L.; Liu, Z.; Zeng, Q.; Jiang, G.; Yang, M. Probing the surface structure of hydroxyapatite through its interaction with hydroxyl: A first principle study. RSC Adv. 2018, 8, 3716–3722. [Google Scholar] [CrossRef]
- Gómez-Morales, J. An overview of the role of the organic matrix in the formation of biogenic crystals. In Proceedings of the 6th International School of Crystallization, Granada, Spain, 21–25 May 2018. [Google Scholar]
- Aquilano, D.; Bruno, M.; Rubbo, M.; Pastero, L.; Massaro, F.R. Twin laws and energy in monoclinic hydroxyapatite, Ca5(PO4)3(OH). Cryst. Growth Des. 2015, 15, 411–418. [Google Scholar] [CrossRef]
- Pastero, L.; Aquilano, D. Monetite-assisted growth of micrometric Ca-hydroxyapatite crystals from mild hydrothermal conditions. Cryst. Growth Des. 2016, 16, 852–860. [Google Scholar] [CrossRef]
- Pastero, L.; Bruno, M.; Rubbo, M.; Cámara, F.; Aquilano, D. Growth of large ca-hydroxyapatite crystals from aqueous solution. In Proceedings of the IV Meeting of the Italian and Spanish Crystallographic Associations, IV MISCA, Puerto de la Cruz, Spain, 21–25 June 2016; p. 27. [Google Scholar]
- Barbooti, M.M.; Al-Sammerrai, D.A. Thermal decomposition of citric acid. Thermochim. Acta 1986, 98, 119–126. [Google Scholar] [CrossRef]
- Wang, L.M.; Wang, W.; Li, X.C.; Peng, L.; Lin, Z.Q.; Xu, H.Z. Calcium citrate: A new biomaterial that can enhance bone formation in situ. Asian Pac. J. Trop. Med. 2012, 15, 291–296. [Google Scholar]
- Pastero, L.; Costa, E.; Bruno, M.; Rubbo, M.; Sgualdino, G. Aquilano, D. Morphology of calcite (CaCO3) growing from aqueous solutions in the presence of Li+ ions. Surface behaviour of the {0001} form. Cryst. Growth Des. 2004, 4, 485–490. [Google Scholar] [CrossRef]
- Pastero, L.; Aquilano, D.; Costa, E.; Rubbo, M. 2D epitaxy of lithium carbonate inducing growth mechanism transitions on {0001}-K and {01 8}-S forms of calcite crystals. J. Cryst. Growth 2005, 275, e1625–e1630. [Google Scholar] [CrossRef]
- Pastero, L.; Aquilano, D. CaCO3 (calcite)/Li2CO3 (zabuyelite) anomalous mixed crystals. Sector zoning and growth mechanisms. Cryst. Growth Des. 2008, 8, 3451–3460. [Google Scholar] [CrossRef]
- Pastero, L.; Aquilano, D.; Moret, M. Selective adsorption/absorption of formamide in NaCl crystals growing from solution. Cryst. Growth Des. 2012, 12, 2306–2314. [Google Scholar] [CrossRef]
- Pastero, L.; Cossio, R.; Aquilano, D. {100} → {111} morphological change on KCl crystals grown from Pb2+ doped aqueous solutions. CrystEngComm 2015, 17, 7844–7855. [Google Scholar] [CrossRef]
- Pastero, L.; Aquilano, D. A three-modal epitaxial adsorption of formamide (HO-C-NH2) on the {111} surfaces of f.c.c. alkali halides crystals growing from aqueous solution. CrystEngComm 2016, 18, 9067–9076. [Google Scholar] [CrossRef]
- Aquilano, D.; Bruno, M.; Rubbo, M.; Massaro, F.R.; Pastero, L. Low symmetry polymorph of hydroxyapatite. Theoretical equilibrium morphology of the monoclinic Ca5(OH)(PO4)3. Cryst. Growth Des. 2014, 14, 2846–2852. [Google Scholar] [CrossRef]
- Herdtweck, E.; Kornprobst, T.; Sieber, R.; Straver, L.; Plank, J. Crystal structure, synthesis, and properties of tri-calcium di-citrate tetra-hydrate [Ca3(C6H5O7)2(H2O)2]·2H2O. Z. Anorg. Allg. Chem. 2011, 637, 655–659. [Google Scholar] [CrossRef]
- Bruno, M.; Massaro, F.R.; Rubbo, M.; Prencipe, M.; Aquilano, D. (10.4), (01.8), (01.2), and (00.1) twin laws of calcite (CaCO3): Equilibrium geometry of the twin boundary interfaces and twinning energy. Cryst. Growth Des. 2010, 10, 3102–3109. [Google Scholar] [CrossRef]
- Aquilano, D. Complex growth polytypism and periodic polysynthetic twins on octacosane crystals (n-C28H58). J. Cryst. Growth 1977, 37, 215–228. [Google Scholar] [CrossRef]
- Boistelle, R.; Aquilano, D. Interaction energy and growth mechanisms on twinned and polytypic crystals of long-chain even normal-alkanes. I. Interaction-energy calculations. Acta Crystallogr. A 1977, 33, 642–648. [Google Scholar] [CrossRef]
- Pastero, L.; Aquilano, D. Calcium carbonate polymorphs growing in the presence of sericin: A new composite mimicking the hierarchic structure of nacre. Crystals 2018, 8, 263. [Google Scholar] [CrossRef]
- Kern, R.; Le Lay, G.; Métois, J.J. Basic mechanisms in the early stages of epitaxy. In Current Topics in Materials Science; Kaldis, E., Ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1979; Volume 3, pp. 131–419. [Google Scholar]
- Hillier, A.C.; Ward, M.D. Epitaxial interactions between molecular over-layers and ordered substrates. Phys. Rev. B 1996, 54, 14037–14051. [Google Scholar] [CrossRef]
- Hooks, D.E.; Fritz, T.; Ward, M.D. Epitaxy and molecular organization on solid substrates. Adv. Mater. 2001, 13, 227–241. [Google Scholar] [CrossRef]

| Features of the 2D-Coincidence Cell | Ranking | HAp {001} Area 64.81 Å2 | Ca-Cit-TH {001} Area 60.80 Å2 | Misfit (%) | Rotation Angle (°) |
|---|---|---|---|---|---|
| 2D-lattice parameters (Å) | = 11.631 5 × [100] = 46.626 | = 11.848 = 46.397 | +1.86 −0.49 | 25 | |
| Area (Å2) and multiplicity of the 2D-coincidence cell | 1st | 324.068 (5×) | 304.011 (5×) | −6.6 | |
| 2 × [100] = 18.651 3 × [010] = 20.851 | 3 × [100] = 17.840 2 × [010] = 20.449 | −4.54 −1.74 | 0 | ||
| 2nd | 388.882 (6×) | 364.813 (6×) | −6.6 | ||
| [320] = 31.239 | [510] = 31.442 | +0.65 | 8 | ||
| = 19.903 | = 20.562 | +3.31 | |||
| 3rd (a) | 453.695 (7×) | 486.417 (8×) | +6.72 | ||
| = 33.477 | = 32.899 | −1.76 | 13 | ||
| = 31.239 | = 30.026 | −4.04 | |||
| 3rd (b) | 518.509 (8×) | 486.417 (8×) | −6.6 | ||
| = 19.903 | −[020] = 20.449 | +2.74 | 67 | ||
| [320] = 31.239 | = 30.026 | −4.04 | |||
| 3rd (c) | 453.695 (7×) | 486.417 (8×) | +6.72 | ||
| 4 × [100] =37.301 | = 37.122 | −0.48 | 16 | ||
| 3 × [010] =20.851 | [120] = 21.339 | +2.34 | |||
| 4th | 777.764 (12×) | 790.43 (13×) | +1.63 |
| Features of the 2D-Coincidence Cell | Ranking | HAp Å2 | Ca-Cit-TH {001} Area 60.80 Å2 | Misfit (%) | Rotation Angle (°) |
|---|---|---|---|---|---|
| 2D-lattice parameters (Å) | = 18.655 3 × [010] = 20.851 | 3 × [100] = 17.839 2 × [010] = 20.449 | −4.57 −1.745 | 0 | |
| Area (Å2) and multiplicity of the 2D-coincidence cell | 1st | 388.973 (3×) | 3.813 (6×) | −6.6 | |
| [412] = 38.542 −[21] = 23.264 | = 37.116 [20] = 23.656 | −3.82 +1.85 | 25 | ||
| 2nd | 648.289 (5×) | 608.022 (10×) | −6.62 | ||
| 2 × [201] = 37.310 3 × [010] = 20.851 | = 37.116 [120] = 21.339 | −0.506 +2.34 | 17 | ||
| 3rd | 777.946 (6×) | 790.43 (13×) | +1.60 |
| Features of the 2D-Coincidence Cell | Ranking | HAp {010} Area 150.60 Å2 | Ca-Cit-TH {001} Area 60.80 Å2 | Misfit (%) | Rotation Angle (°) |
|---|---|---|---|---|---|
| 2D-lattice parameters (Å) | −[101] = 16.150 3 × [100] = 27.975 | − = 15.648 [30] = 27.137 | −2.97 −3.09 | 47 | |
| Area (Å2) and multiplicity of the 2D-coincidence cell | 1st | 451.816 (3×) | 425.611 (7×) | −6.6 | |
| 2 × [100] = 18.650 −2× [101] = 32.301 | 3 × [100] = 17.84 3 × [010] = 30.673 | −4.54 −5.30 | 0 | ||
| 2nd | 602.422 (4×) | 547.215 (9×) | −10.09 | ||
| 4 × [100] = 37.301 3 × [301] =24.680 | = 37.122 − = 25.891 | −0.48 +4.90 | 17 | ||
| 3rd (a) | 602.4222 (4×) | 608.016 (10×) | −0.93 | ||
| 4 × [100] = 37.301 [101] = 16.1503 | [40] = 38.816 = 15.684 | +4.06 −2.97 | 53 | ||
| 3rd (b) | 602.4222 (4×) | 608.016 (10×) | −0.93 | ||
| 5 × [100] = 46.626 = 32.293 | [60] = 47.052 [20] = 32.898 | +0.91 +1.87 | 41 | ||
| 4th (a) | 753.025 (5×) | 729.619 (12×) | −3.21 | ||
| = 40.638 [201] = 18.655 | [10] = 41.328 3 × [100] = 17.84 | +1.70 −4.56 | 59 | ||
| 4th (b) | 753.025 (5×) | 729.619 (12×) | −3.21 | ||
| [401] = 32.313 [202] = 32.301 | [510] = 31.442 [130] = 31.244 | −2.77 −3.38 | 11 | ||
| 5th | 903.633 (6×) | 851.22 (14×) | −6.16 | ||
| = 40.638 [302] = 33.626 | [60] = 41.124 [230] = 32.898 | +1.19 −2.21 | 7 | ||
| 6th (a) | 1355.445 (9×) | 1337.63 (22×) | −1.33 | ||
| −[102] = 49.333 | −[230]= 32.898 [50] = 50.564 | −2.17 +2.49 | 35 | ||
| 6th (b) | 1355.445 (9×) | 1398.44 (23×) | +3.17 | ||
| = 42.716 2 × [201] = 37.310 | = 42.592 [520] = 36.086 | −0.25 −3.39 | 25 | ||
| 7th (a) | (10×) 1506.05 | (24×) 1459.24 | −3.21 | ||
| = 40.638 2 × [201] = 37.310 | −[140] = 41.328 = 37.122 | +1.70 −0.51 | 76 | ||
| 7th (b) | (10×) 1506.05 | (25×) 1520.04 | +0.93 |
| Features of the 2D-Coincidence Cell | Ranking | HAp Å2 | Ca-Cit-TH {001} Area 60.80 Å2 | Misfit (%) | Rotation Angle (°) |
|---|---|---|---|---|---|
| 2D-lattice parameters (Å) | = 16.322 4 × [010] = 27.801 | = 15.684 = 27.137 | −4.07 −2.44 | 41.5 | |
| Area (Å2) and multiplicity of the 2D-coincidence cell | 1st (a) | 453.782 (4×) | 425.615 (7×) | −6.61 | |
| = 32.645 = 21.44 | = 32.899 = 20.562 | +0.78 −4.27 | |||
| 1st (b) | 453.782 (4×) | 425.615 (7×) | −6.61 | 70 | |
| = 33.376 2 × [111] = 35.48 | = 32.899 = 36.086 | −1.45 +1.71 | |||
| 2nd (a) | 680.67 (6×) | 668.82 (11×) | −1.77 | 57 | |
| = 35.48 = 21.44 | = 36.086 = 20.562 | +1.71 −4.27 | |||
| 2nd (b) | 680.67 (6×) | 668.82 (11×) | −1.77 | 10 | |
| 2 × [101] = 32.645 3 × [010] = 20.851 | = 31.442 = 21.296 | −3.82 +2.137 | |||
| 2nd (c) | 680.67 (6×) | 668.82 (11×) | −1.77 | 20 | |
| [151] = 8.394 = 21.44 | = 37.116 2 × [010] = 20.45 | −3.44 −4.84 | |||
| 3rd | 793.25 (7×) | 729.622 (12×) | −8.72 | 50 | |
| =33.376 [151] =38.394 | = 32.899 = 37.116 | −1.45 −3.44 | |||
| 4th | 1019.90 (9×) | 972.83 (16×) | −4.83 | 82 | |
| = 42.88 [131] = 26.48 | = 42.767 = 27.137 | −0.076 +2.48 | |||
| 5th | 1134.45 (10×) | 1155.24 (19×) | +1.83 | 5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pastero, L.; Bruno, M.; Aquilano, D. Habit Change of Monoclinic Hydroxyapatite Crystals Growing from Aqueous Solution in the Presence of Citrate Ions: The Role of 2D Epitaxy. Crystals 2018, 8, 308. https://doi.org/10.3390/cryst8080308
Pastero L, Bruno M, Aquilano D. Habit Change of Monoclinic Hydroxyapatite Crystals Growing from Aqueous Solution in the Presence of Citrate Ions: The Role of 2D Epitaxy. Crystals. 2018; 8(8):308. https://doi.org/10.3390/cryst8080308
Chicago/Turabian StylePastero, Linda, Marco Bruno, and Dino Aquilano. 2018. "Habit Change of Monoclinic Hydroxyapatite Crystals Growing from Aqueous Solution in the Presence of Citrate Ions: The Role of 2D Epitaxy" Crystals 8, no. 8: 308. https://doi.org/10.3390/cryst8080308
APA StylePastero, L., Bruno, M., & Aquilano, D. (2018). Habit Change of Monoclinic Hydroxyapatite Crystals Growing from Aqueous Solution in the Presence of Citrate Ions: The Role of 2D Epitaxy. Crystals, 8(8), 308. https://doi.org/10.3390/cryst8080308






