1. Introduction
Stimulated polariton scattering (SPS) has proven to be an efficient scheme to generate terahertz (THz) waves [
1,
2,
3,
4,
5,
6,
7,
8]. A polariton is a coupled quantum between the pump laser and the infrared- and Raman-active transverse optical (TO) modes in a crystal, and it behaves like phonons near the resonant frequency associated with the TO mode and exhibits photon-like behavior for lower non-resonant frequencies [
1]. SPS consists of second-order and third-order nonlinear frequency conversion processes where a pump photon stimulates a Stokes photon at the difference frequency between the pump photon and the polariton. At the same time, a THz wave is generated by the parametric process due to the nonlinearity arising from both electronic and vibrational contributions of the crystal. The TO phonon resonances can contribute substantially to the magnitude of the second-and third-order nonlinearities, which are beneficial to the THz generation via SPS.
MgO:LiNbO
3 has been the most widely used crystal for THz wave generation via SPS [
1,
2,
3,
4,
5]. MgO:LiNbO
3 has strong second-order nonlinear response, as well as TO phonon resonances for efficient SPS [
9]. MgO:LiNbO
3 has five
A1 symmetric infrared- and Raman-active TO modes polarized parallel to the
c-axis with frequencies of 248 cm
−1, 274 cm
−1, 307 cm
−1, 628 cm
−1, and 692 cm
−1 [
10]. MgO:LiNbO
3 has eight
E symmetric infrared- and Raman-active TO modes polarized perpendicular to the
c-axis with frequencies of 152 cm
−1, 236 cm
−1, 265 cm
−1, 322 cm
−1, 363 cm
−1, 431 cm
−1, 586 cm
−1, and 670 cm
−1 [
10].
A1 symmetric TO modes have been the most widely used for THz wave generation via SPS [
1,
2,
3,
4,
5]. However,
E symmetric TO modes can be also employed to generate THz waves via SPS. In 1969, Yarborough reported the observation of tunable SPS from
A1 and
E symmetric TO modes with a pump wave in a LiNbO
3 crystal [
11]. If the SPS from
A1 and
E symmetric TO modes can be simultaneously excited, then two orthogonally polarized THz waves can be simultaneously generated. Orthogonally polarized THz waves are useful for imaging [
12]. Yu et al. [
12] showed that the addition or subtraction of two images, which were taken with a perpendicularly polarized THz wave and parallel polarized THz wave, was effective to enhance the contrast of terahertz images.
In this work, we theoretically study the simultaneous generation of two orthogonally polarized THz waves by SPS with a periodically poled LiNbO3 (PPLN) crystal. The two orthogonally polarized THz waves are generated from SPS with A1 and E symmetric TO modes in a MgO:LiNbO3 crystal, respectively. We calculate the photon flux density of the two orthogonally polarized THz waves by solving the coupled wave equations.
3. Phase-Matching Characteristics
Due to the different eigenfrequency, oscillator strength, and bandwidth of the TO modes, the two orthogonally polarized THz waves, THz
e and THz
o, have different dispersion and absorption characteristics.
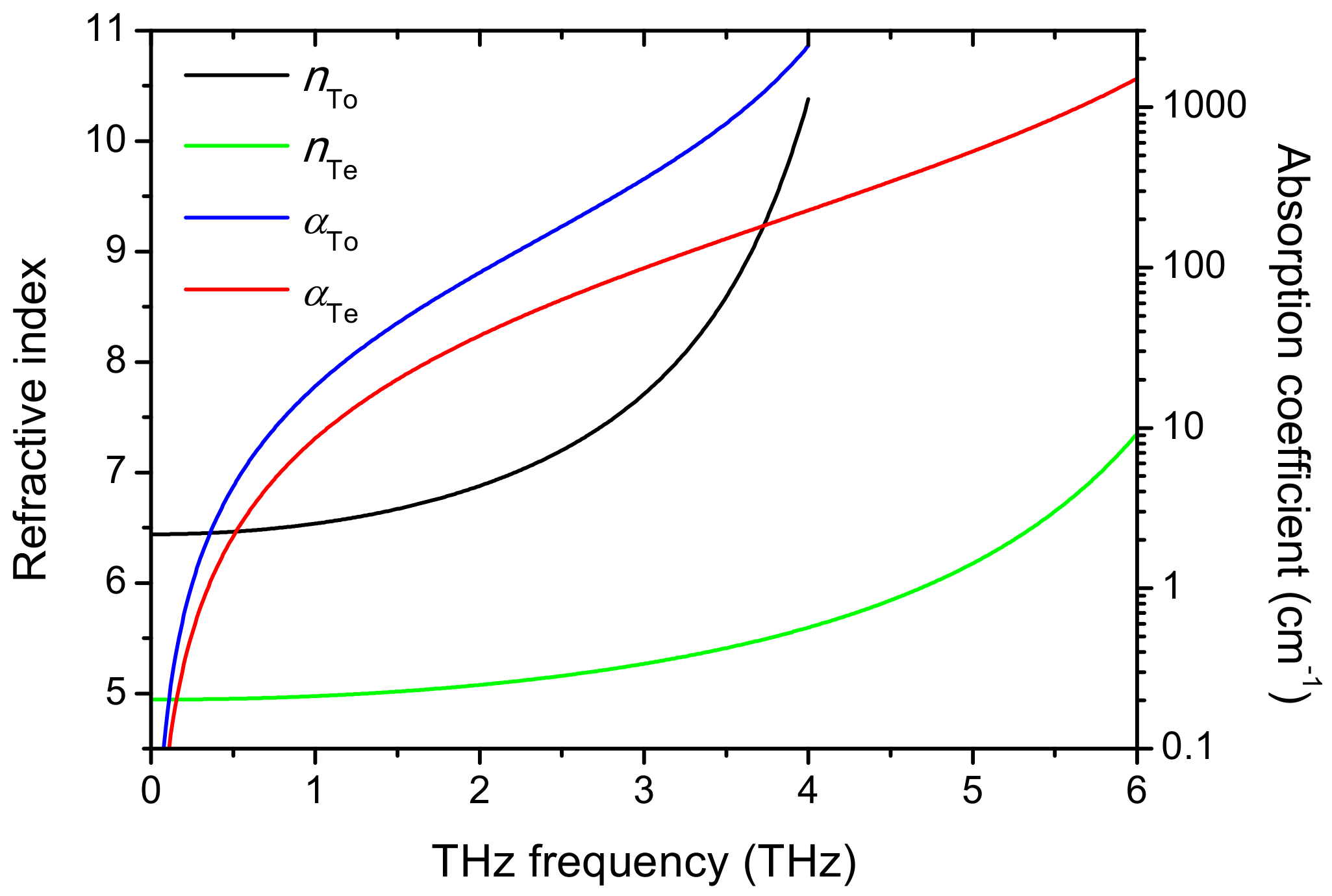
Figure 2 shows the dispersion and absorption characteristics of the THz
e and THz
o waves.
nTe and
nTo are the refractive indices of THz
e and THz
o, respectively, and
αTe and
αTo are the absorption coefficients of THz
e and THz
o, respectively. The curves of
nTe and
αTe are below the lowest
A1 symmetric TO mode, 248 cm
−1, and the curves of
nTo and
αTo are below the lowest
E symmetric TO mode, 152 cm
−1. The theoretical parameters of the refractive index and absorption coefficient for LiNbO
3 in the THz range are cited in [
9]. From the figure, we find that
nTe and
nTo are larger than 5. The value of the refractive index in the THz range is much larger than that in the optical range, so the collinear phase-matching is impossible to realize. The absorption coefficients
αTe and
αTo are very large, especially in the high THz frequency range.
In the optical SPS processes, the THz waves are generated, and the seed waves are amplified. The amplified seed waves are Stokes waves. In order to achieve efficient conversion of the SPS processes from the pump wave to the THz waves, a precise phase-matching condition must be satisfied. For the forward SPS processes, the pump, Seed
e, and THz
e waves satisfy the type-0 phase-matching of
e =
e +
e, and the phase mismatch
is as follows:
The pump, Seed
o, and THz
o waves satisfy the type-I phase-matching of
e =
o +
o, and the phase mismatch
is as follows:
where
is the wave vector of the pump wave,
and
are the wave vectors of the two Seed
e and Seed
o waves, respectively, and
are the wave vectors of the two THz
e and THz
o waves, respectively.
is the grating vector, and Λ is the poling period of the PPLN crystal.
For the backward SPS processes, the pump, Seed
e and THz
e waves satisfy the type-0 phase-matching of
e =
e +
e, and the phase mismatch
is as follows:
The pump, seed
o, and THz
o waves satisfy the type-I phase-matching of
e =
o +
o, and the phase mismatch
is as follows:
The energy conservation condition has to be fulfilled according to the following:
where
is the wavelength of pump wave,
and
are the wavelengths of the two Seed
e and Seed
o waves, respectively, and
are the wavelengths of the two THz
e and THz
o waves, respectively. If both the phase mismatches
and
are small enough, two perpendicular THz waves THz
e and THz
o can be generated simultaneously with a single pump wave.
For the SPS processes, we calculate the phase mismatches and according to Equations (1) and (2), respectively, at a fixed pump wavelength. The wavelengths of the two seed waves and the two THz waves are dependent on Equations (5) and (6). The sum phase mismatch . If the sum phase mismatch is small enough, the two phase mismatches and are small enough to realize the two phase-matching conditions of e = e + e and e = o + o.
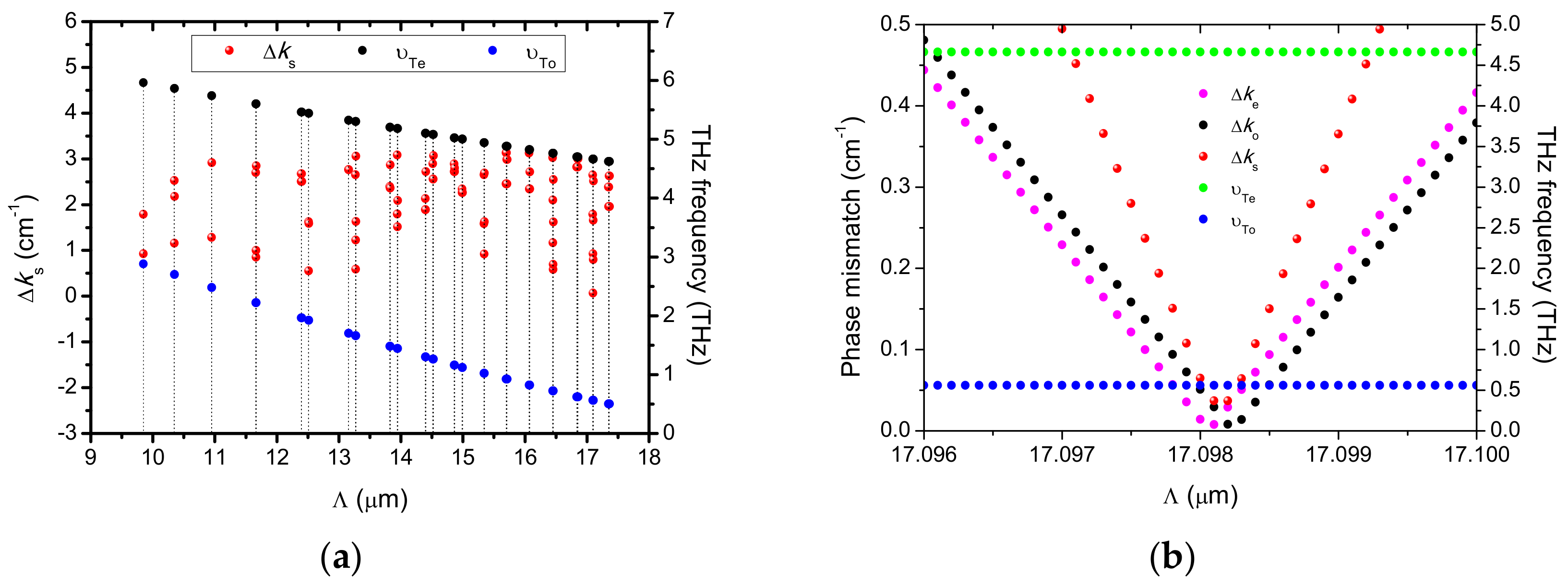
Figure 3 shows the phase-matching characteristics for the forward SPS processes with a pump wavelength of 1550 nm.
and
are the frequencies of the THz
e and THz
o waves, respectively. The theoretical values of the refractive indices are calculated using a Sellmeier equation for LiNbO
3 in the infrared range [
13]. From
Figure 3a, we find that as Λ varies from 9 to 18 μm, there are many points of
with values below π cm
−1, which indicates that the two SPS processes generating the THz
e and THz
o waves can be efficiently realized. Most frequencies from 4.6 to 6 THz of THz
e and most frequencies from 0.4 to 2.8 THz of THz
o can be efficiently generated. The minimum value of
is 0.064 cm
−1 with Λ of 17.1 μm, corresponding to
of 4.66 THz and
of 0.56 THz.
Figure 3b shows the detailed phase-matching characteristics with Λ from 17.096 to 17.100 μm. As Λ varies from 17.0981 to 17.0983 μm,
with a value of 0.0369 cm
−1 is small enough to stimulate the two SPS processes. In particular, as Λ is 17.0982 μm,
equals
, which indicates that the two SPS processes can be realized to equal degrees.
Figure 4 shows the phase-matching characteristics for the backward SPS processes with a pump wavelength of 1550 nm. From
Figure 4a, we find that as Λ varies from 20 to 100 μm, there are also many points of
with values below π cm
−1, particularly below 1 cm
−1. Most frequencies from 0.45 to 2.03 THz of THz
e and most frequencies from 2.01 to 3 THz of THz
o can be efficiently generated. The minimum value of
is 0.344 cm
−1 with Λ of 80.98 μm, corresponding to
of 0.52 THz and
of 2.06 THz.
Figure 4b shows the detailed phase-matching characteristics with Λ around 80.98 μm. As Λ varies from 80.960 to 80.995 μm,
with a value of 0.344 cm
−1 is small enough to stimulate the two SPS processes. In particular, as Λ is 80.978 μm,
equals
, which indicates that the two SPS processes can be realized to equal degrees.
4. THz Photon Flux Density
The coupled wave equations for the SPS processes can be found in [
9,
14]. The coupled wave equations describe the field envelope variation of the pump, Stokes, and THz waves. The analytical expression of THz parametric gain coefficient
gT under the QPM condition in the international system of units can be written as follows:
where
,
, and
denote the eigenfrequency, the oscillator strength of the polariton modes, and the bandwidth of the
jth TO mode in the LiNbO
3 crystal, respectively.
Ip is the power density of the pump wave, and
g0 is the low-loss parametric gain.
,
, and
are the refractive indices of the pump, Stokes, and THz waves, respectively.
is the angle between the wavevectors of the pump wave and THz wave.
is material absorption coefficient in THz region.
and
are nonlinear coefficients related to pure parametric (second-order) and Raman (third-order) scattering processes, respectively.
When THz frequencies are far below the lowest
A1 symmetry TO mode of 248 cm
−1 and the lowest
E symmetry TO mode of 152 cm
−1, Equation (8) can be rewritten as follows [
9]:
For SPS with type-0 phase-matching of
e =
e +
e, the relationship between
and
is given by [
9,
15,
16] the following:
For SPS with type-I phase-matching of
e =
o +
o, the relationship between
and
is as follows:
where
and
are the linear electro-optic coefficients of LiNbO
3.
With strong THz wave absorption and phase mismatch and without pump depletion, the coupled wave equations can be solved to give the THz photon flux density
with a general solution [
17], given by the following:
where
is the phase mismatching and
L is the crystal length. The initial THz photon flux density
is assumed to be zero, and
is the initial seed wave photon flux density. The initial photon flux densities of Seed
e and seed
o are
and
, respectively. The THz photon flux densities of THz
e and THz
o are
and
, respectively. The ratio
R of
to
is as follows:
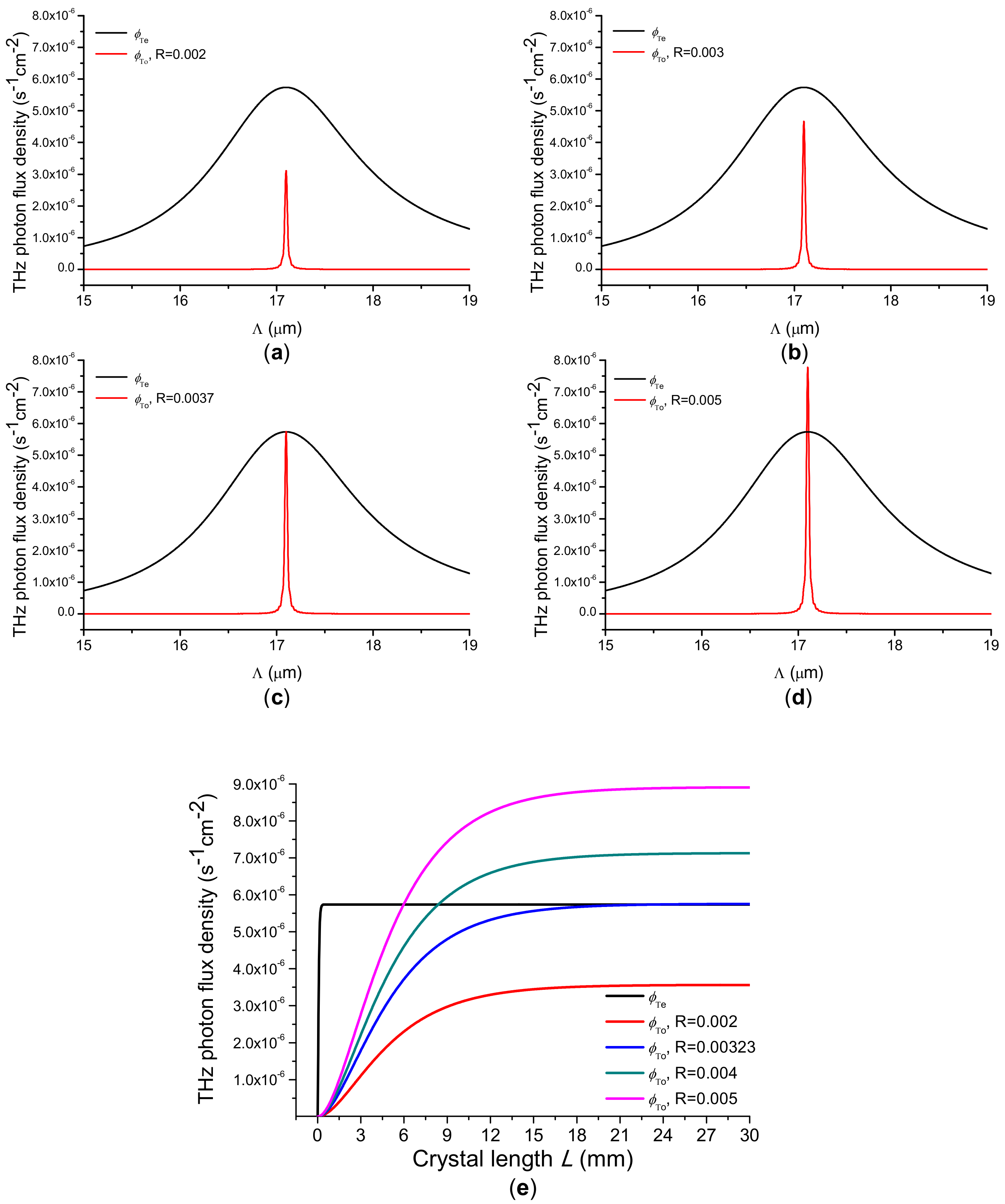
Figure 5 shows the THz wave photon flux densities
and
for the forward SPS processes. From
Figure 5a–d , we find that when Λ varies from 15 to 19 μm,
and
increase first and then decrease. When Λ is equal to 17.0982 μm,
and
reach their maximum values as the phase mismatches
and
reach their minimum values. The maximum value of
is 5.74 × 10
−6 s
−1cm
−2. The value of
is so small, because the THz absorption coefficient of 4.66 THz is very large.
increases with the increase of
R. The relative photon flux densities between
and
can be tuned by varying
R. When
R is 0.0037, the maximum values of
and
are approximately equal. From
Figure 5e, we find that when crystal length
L varies from 0 to 30 mm,
and
increase rapidly and smoothly. When
R is 0.00323, the values of
and
are approximately equal, as
L is larger than 20 mm.
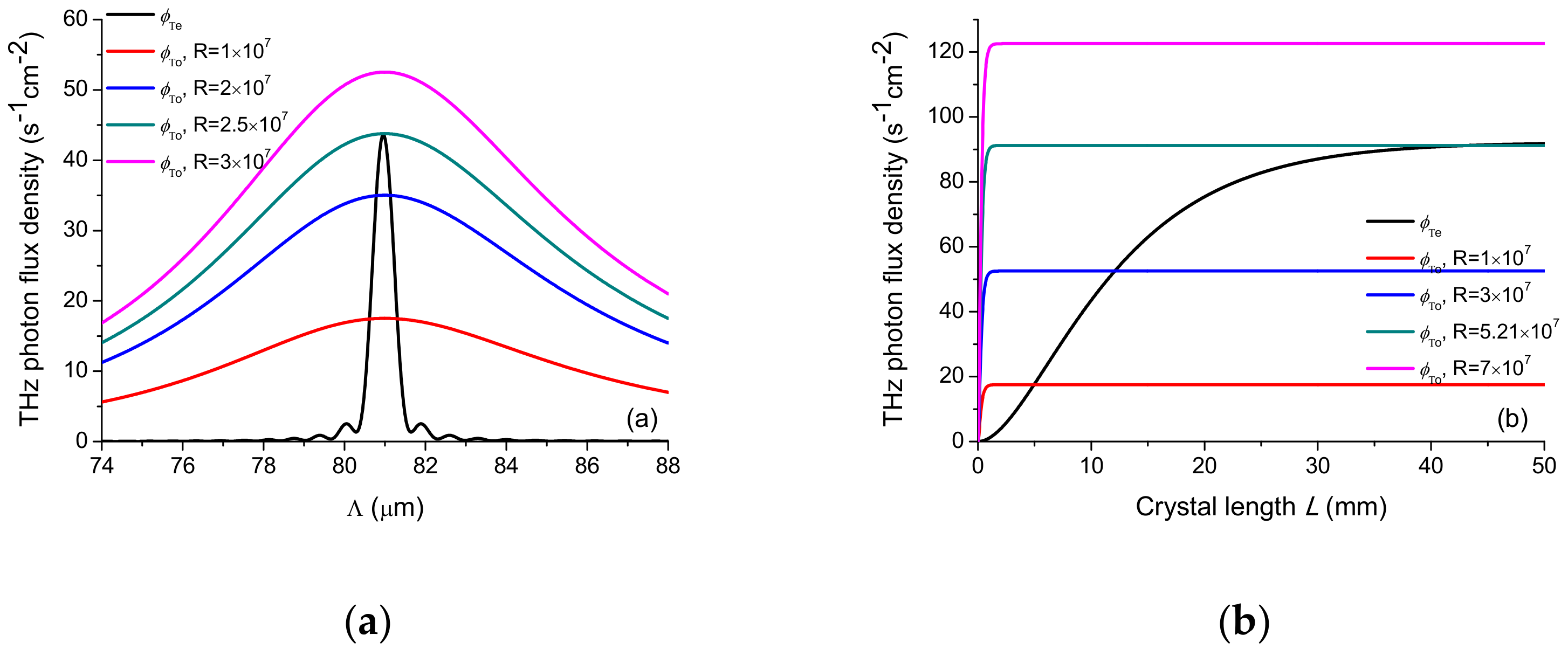
Figure 6 shows the THz wave photon flux densities
and
for the backward SPS processes. From
Figure 6a, we find that when Λ varies from 74 to 88 μm,
and
increase first and then decrease. When Λ is equal to 80.978 μm,
and
reach their maximum values as the phase mismatches
and
reach their minimum values. The maximum value of
is 43.62 s
−1cm
−2. The maximum value of
in the backward SPS processes is larger than that in the forward SPS processes, because the THz absorption coefficient of 0.52 THz in the backward SPS processes is smaller than that of 4.66 THz in the forward SPS processes. The relative photon flux densities between
and
can be tuned by varying
R. When
R is 2.5 × 10
7, the maximum values of
and
are approximately equal. From
Figure 6b, we find that when crystal length
L varies from 0 to 50 mm,
and
increase rapidly and smoothly. When
R is 5.21 × 10
7 and
L is larger than 40 mm, the values of
and
are approximately equal.
The intensities of generated THz waves are very low, because the THz waves are heavily absorbed by the PPLN crystal. However, the intensities of the THz waves can be enhanced by injection intense seed waves, as shown in Equation (13). Moreover, one can use organic crystals with QPM, because organic crystals have larger nonlinear optical coefficients and lower absorption coefficients in the THz region [
18]. Furthermore, the enhancement of the THz intensities can be realized by cryogenic cooling. At liquid nitrogen temperature, the gain coefficients of the THz waves in the SPS processes are enhanced. At the same time, the absorption coefficients of the THz waves decrease.
The scheme in this work of generating two orthogonally polarized THz waves by SPS processes has certain advantages. First of all, the two orthogonally polarized THz waves are simultaneously generated by a pump wave, which means that the two THz waves are phase-conjugate. Second, the two orthogonally polarized THz waves are generated only by a PPLN crystal. Third, the intensities of the two orthogonally polarized THz waves can be tuned by varying the intensities of the input seed waves.