Small Polaron Hopping in Fe:LiNbO3 as a Function of Temperature and Composition
Abstract
1. Introduction
2. Experiment
2.1. Samples
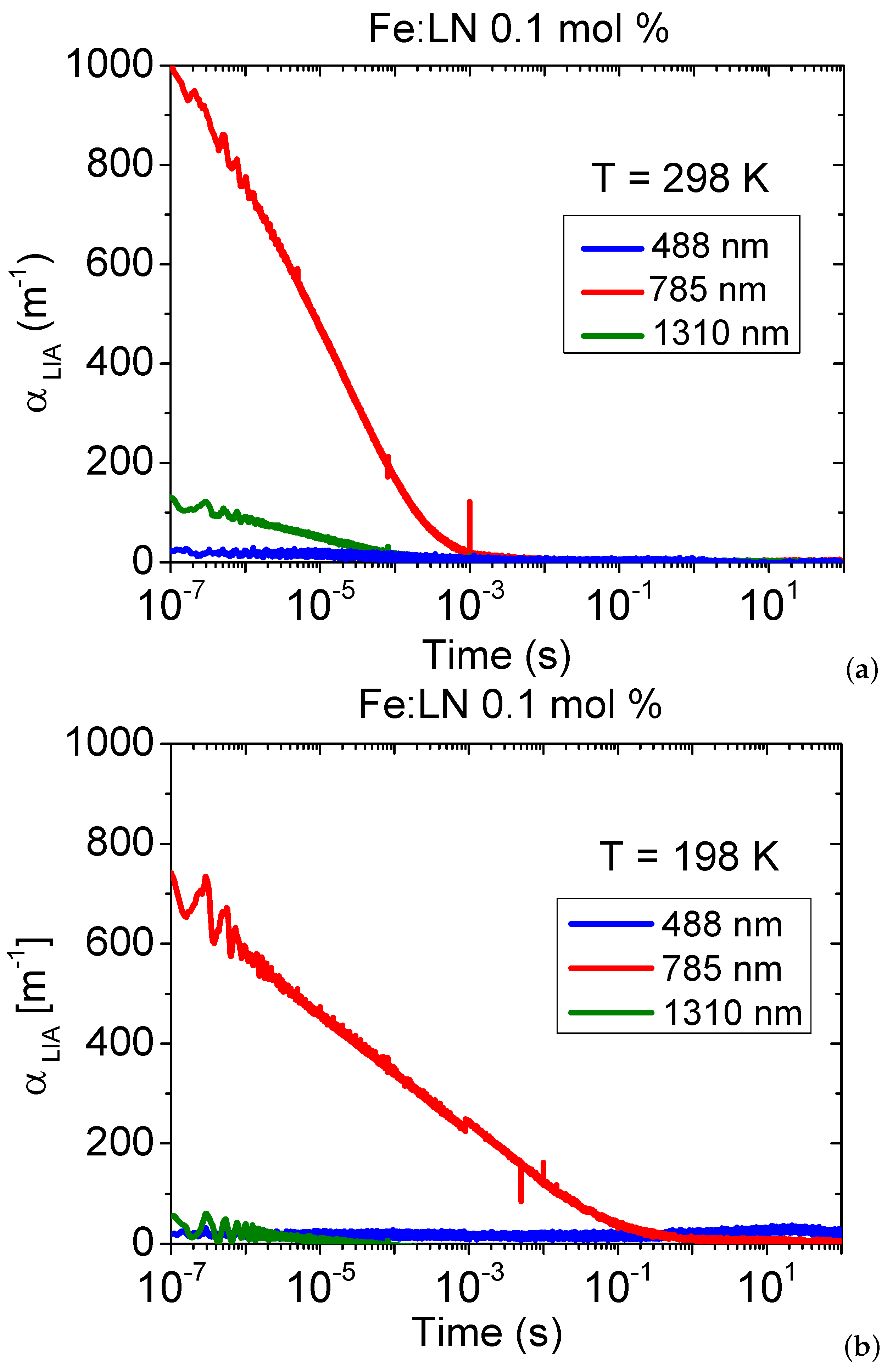
2.2. Transient Absorption
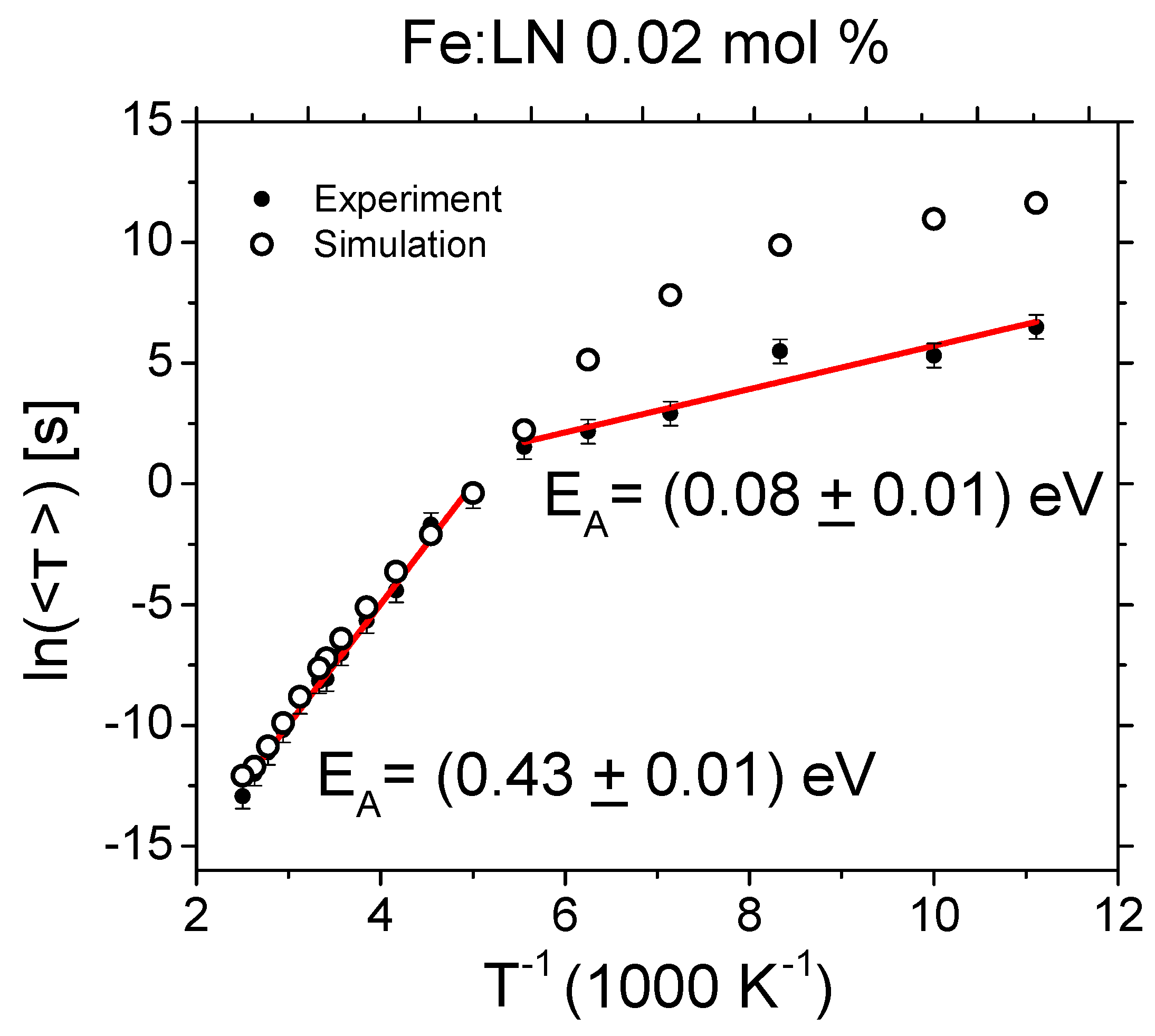
3. Monte Carlo Simulations
3.1. Decay Model
3.2. Simulation Code
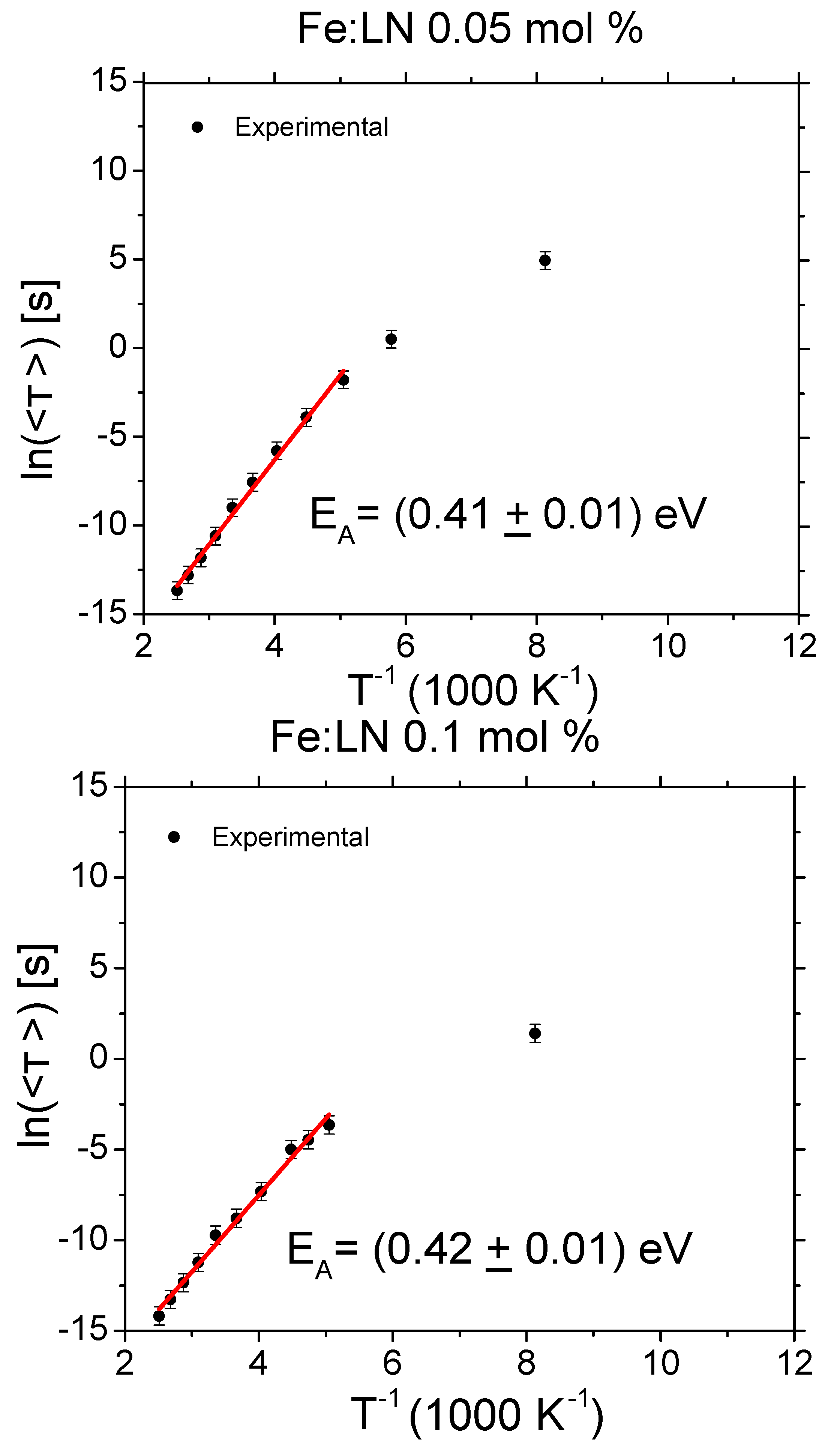
4. Results and Discussion
4.1. Activation Energies Deduced via TAS
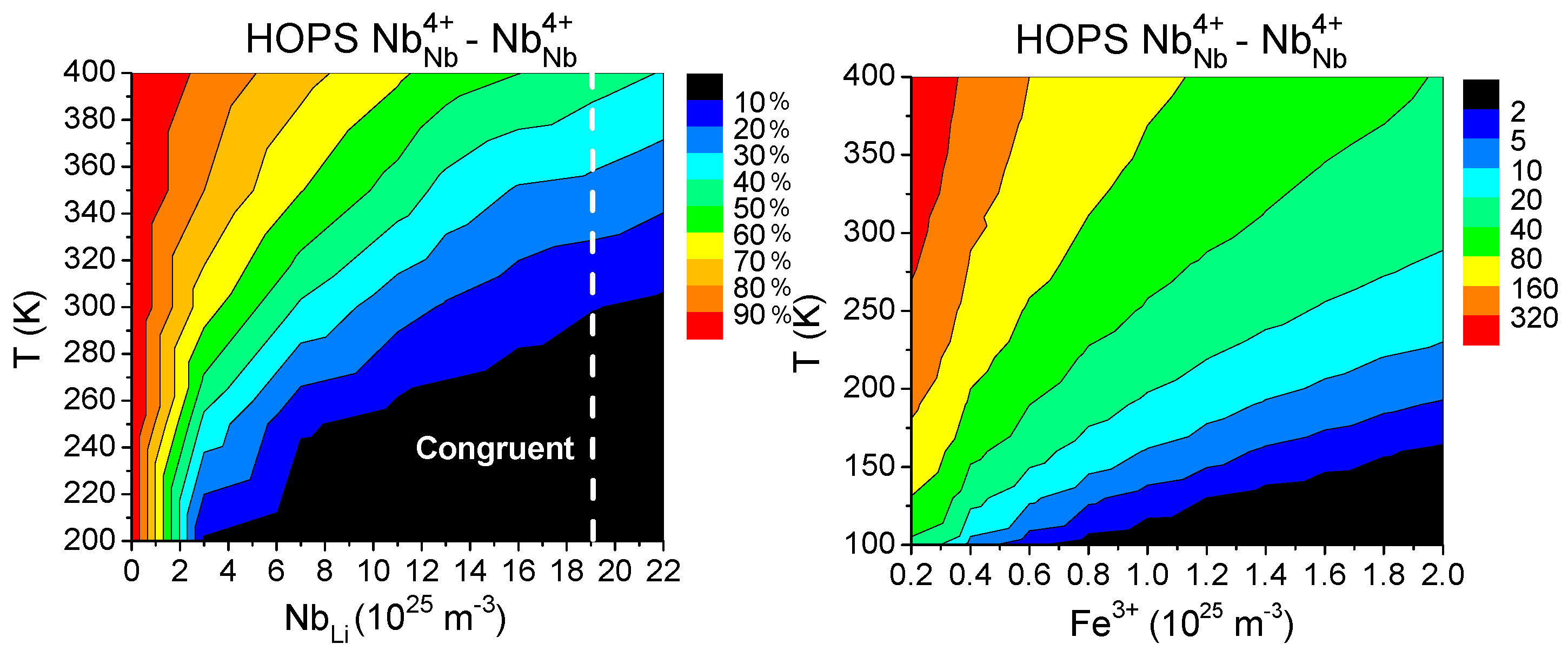
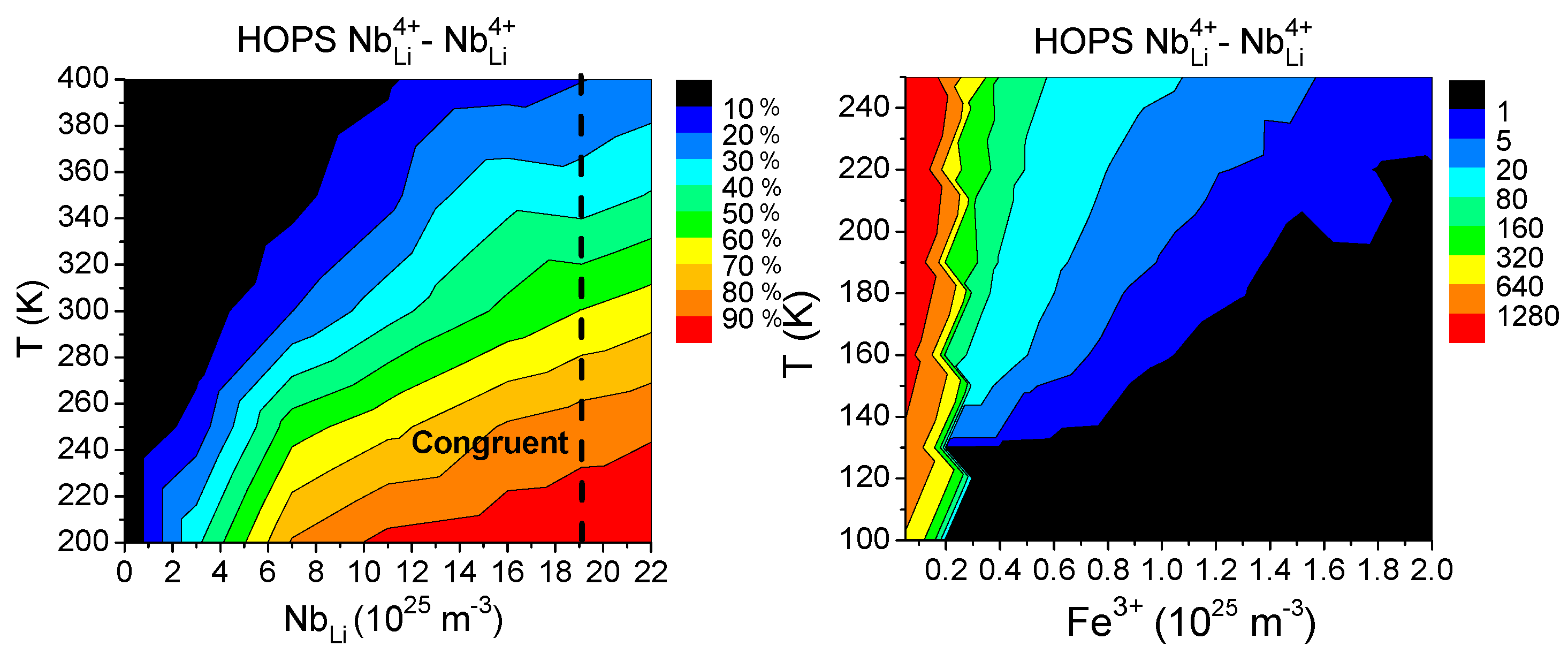
4.2. Hopping Regimes’ Landscapes Inspected by Monte Carlo Simulations
4.2.1. Free Polaron Transport
4.2.2. Bound Polaron Transport
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Imlau, M.; Badorreck, H.; Merschjann, C. Optical nonlinearities of small polarons in lithium niobate. Appl. Phys. Rev. 2015, 2, 040606. [Google Scholar] [CrossRef]
- Bazzan, M.; Sada, C. Optical waveguides in lithium niobate: Recent developments and applications. Appl. Phys. Rev. 2015, 2, 040603. [Google Scholar] [CrossRef]
- Günter, P.; Huignard, J.-P. Photorefractive Materials and Their Applications 1; Springer: New York, NY, USA, 2006; Volume 113. [Google Scholar]
- He, J.; Franchini, C.; Rondinelli, J.M. Lithium niobate-type oxides as visible light photovoltaic materials. Chem. Mater. 2016, 28, 25–29. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Imlau, M.; Merschjann, C. Bulk photovoltaic effect of LiNbO3: Fe and its small-polaron-based microscopic interpretation. Phys. Rev. B 2011, 83, 165106. [Google Scholar] [CrossRef]
- Tisdale, W.A.; Williams, K.J.; Timp, B.A.; Norris, D.J.; Aydil, E.S.; Zhu, X.-Y. Hot-electron transfer from semiconductor nanocrystals. Science 2010, 328, 1543–1547. [Google Scholar] [CrossRef] [PubMed]
- Nolan, M. First-principles prediction of new photocatalyst materials with visible-light absorption and improved charge separation: Surface modification of rutile TiO2 with nanoclusters of MgO and Ga2O3. ACS Appl. Mater. Interfaces 2012, 4, 5863–5871. [Google Scholar] [CrossRef] [PubMed]
- Migani, A.; Blancafort, L. Excitonic interfacial proton-coupled electron transfer mechanism in the photocatalytic oxidation of methanol to formaldehyde on TiO2(110). J. Am. Chem. Soc. 2016, 138, 16165–16173. [Google Scholar] [CrossRef] [PubMed]
- Sezen, H.; Shang, H.; Bebensee, F.; Yang, C.; Buchholz, M.; Nefedov, A.; Heissler, S.; Carbogno, C.; Scheffler, M.; Rinke, P.; et al. Evidence for photogenerated intermediate hole polarons in ZnO. Nat. Commun. 2015, 6, 6901. [Google Scholar] [CrossRef] [PubMed]
- Volk, T.; Wöhlecke, M. Lithium Niobate: Defects, Photorefraction and Ferroelectric Switching; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 115. [Google Scholar]
- Marcus, R.A. On the theory of oxidation-reduction reactions involving electron transfer. I. J. Chem. Phys. 1956, 24, 966–978. [Google Scholar] [CrossRef]
- Holstein, T. Studies of polaron motion: Part II. The “small” polaron. Ann. Phys. 1959, 8, 343–389. [Google Scholar] [CrossRef]
- Emin, D. Polarons; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Austin, I.G.; Mott, N.F. Polarons in crystalline and non-crystalline materials. Adv. Phys. 2001, 50, 757–812. [Google Scholar] [CrossRef]
- Schirmer, O.F.; Imlau, M.; Merschjann, C.; Schoke, B. Electron small polarons and bipolarons in LiNbO3. J. Phys. Condens. Matter 2009, 21, 123201. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Mhaouech, I.; Guilbert, L. Temperature dependence of small polaron population decays in iron-doped lithium niobate by monte carlo simulations. Solid State Sci. 2016, 60, 28–36. [Google Scholar] [CrossRef]
- Guilbert, L.; Vittadello, L.; Bazzan, M.; Mhaouech, I.; Messerschmidt, S.; Imlau, M. The elusive role of NbLi bound polaron energy in hopping charge transport in Fe:LiNbO3. J. Phys. Condens. Matter 2018, 30, 125701. [Google Scholar] [CrossRef] [PubMed]
- Herth, P.; Granzow, T.; Schaniel, D.; Woike, T.; Imlau, M.; Krätzig, E. Evidence for light-induced hole polarons in LiNbO3. Phys. Rev. Lett. 2005, 95, 067404. [Google Scholar] [CrossRef] [PubMed]
- Ciampolillo, M.V.; Zaltron, A.; Bazzan, M.; Argiolas, N.; Sada, C. Quantification of iron (Fe) in lithium niobate by optical absorption. Appl. Spectrosc. 2011, 65, 216–220. [Google Scholar] [CrossRef]
- Kurz, H.; Krätzig, E.; Keune, W.; Engelmann, H.; Gonser, U.; Dischler, B.; Räuber, A. Photorefractive centers in LiNbO3, studied by optical-, mössbauer-and epr-methods. Appl. Phys. A Mater. Sci. Process. 1977, 12, 355–368. [Google Scholar] [CrossRef]
- Merschjann, C.; Schoke, B.; Imlau, M. Influence of chemical reduction on the particular number densities of light-induced small electron and hole polarons in nominally pure LiNbO3. Phys. Rev. B 2007, 76, 085114. [Google Scholar] [CrossRef]
- Merschjann, C.; Schoke, B.; Conradi, D.; Imlau, M.; Corradi, G.; Polgar, K. Absorption cross sections and number densities of electron and hole polarons in congruently melting LiNbO3. J. Phys. Condens. Matter 2008, 21, 015906. [Google Scholar] [CrossRef] [PubMed]
- Kohlrausch, R. Ueber das dellmann’sche elektrometer. Annalen der Physik 1847, 148, 353–405. [Google Scholar] [CrossRef]
- Berben, D.; Buse, K.; Wevering, S.; Herth, P.; Imlau, M.; Woike, T. Lifetime of small polarons in iron-doped lithium-niobate crystals. J. Appl. Phys. 2000, 87, 1034–1041. [Google Scholar] [CrossRef]
- Carnicero, J.; Carrascosa, M.; García, G.; Agulló-López, F. Site correlation effects in the dynamics of iron impurities Fe2+/Fe3+ and antisite defects after a short-pulse excitation in LiNbO3. Phys. Rev. B 2005, 72, 245108. [Google Scholar] [CrossRef]
- Zylbersztejn, A. Thermally activated trapping in Fe-doped LiNbO3. Appl. Phys. Lett. 1976, 29, 778–780. [Google Scholar] [CrossRef]
- Sheri, L.; Shamblin, B.C.; Hancock, Y.D.; Michael, J.P. Interpretation of relaxation time constants for amorphous pharmaceutical systems. J. Pharm. Sci. 2000, 89, 417–427. [Google Scholar]
- Wöhlecke, M.; Volk, T. Lithium Niobate; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]

| Final site | ||||
| Energy in eV | Free (FP) | Antisite (GP) | Fe | |
| Free (FP) | 0.273 | 0.156 | 0.003 | |
| Initial site | Antisite (GP) | 0.551 | 0.375 | 0.038 |
| Fe | 1.378 | 1.018 | 0.350 | |
| [Fe] | [] | [] | []/[] | [] | |
|---|---|---|---|---|---|
| Fe:LN 0.02 mol % | 3.8 | 0.1 | 3.7 | 0.04 | 190.9 |
| Fe:LN 0.05 mol % | 9.5 | 0.8 | 7.9 | 0.1 | 190.9 |
| Fe:LN 0.1 mol % | 18.90 | 13.7 | 5.2 | 2.62 | 190.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vittadello, L.; Bazzan, M.; Messerschmidt, S.; Imlau, M. Small Polaron Hopping in Fe:LiNbO3 as a Function of Temperature and Composition. Crystals 2018, 8, 294. https://doi.org/10.3390/cryst8070294
Vittadello L, Bazzan M, Messerschmidt S, Imlau M. Small Polaron Hopping in Fe:LiNbO3 as a Function of Temperature and Composition. Crystals. 2018; 8(7):294. https://doi.org/10.3390/cryst8070294
Chicago/Turabian StyleVittadello, Laura, Marco Bazzan, Simon Messerschmidt, and Mirco Imlau. 2018. "Small Polaron Hopping in Fe:LiNbO3 as a Function of Temperature and Composition" Crystals 8, no. 7: 294. https://doi.org/10.3390/cryst8070294
APA StyleVittadello, L., Bazzan, M., Messerschmidt, S., & Imlau, M. (2018). Small Polaron Hopping in Fe:LiNbO3 as a Function of Temperature and Composition. Crystals, 8(7), 294. https://doi.org/10.3390/cryst8070294






