Radiation Damage in Macromolecular Crystallography—An Experimentalist’s View
Abstract
1. Introduction
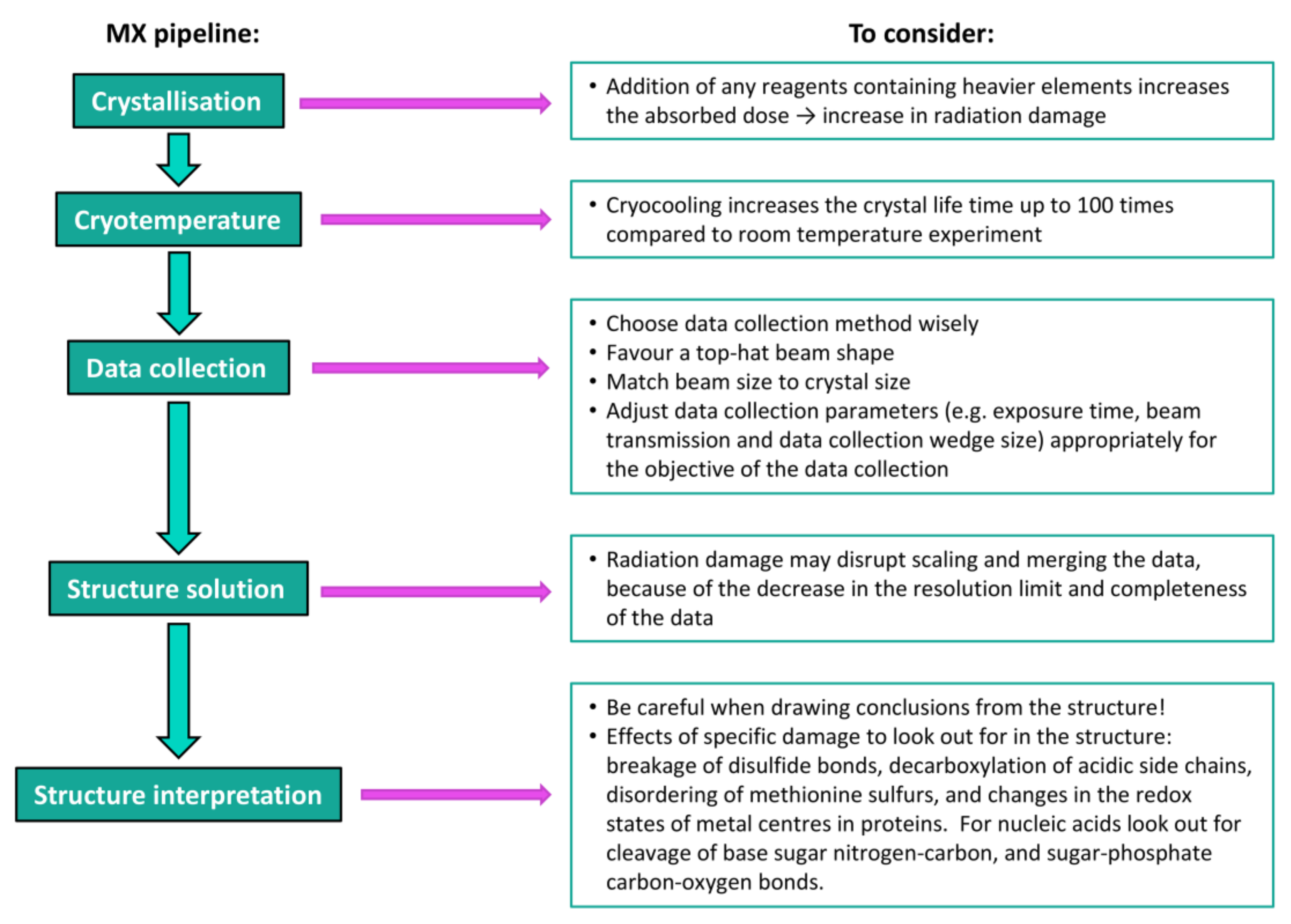
2. Crystallisation
3. Cryocrystallography
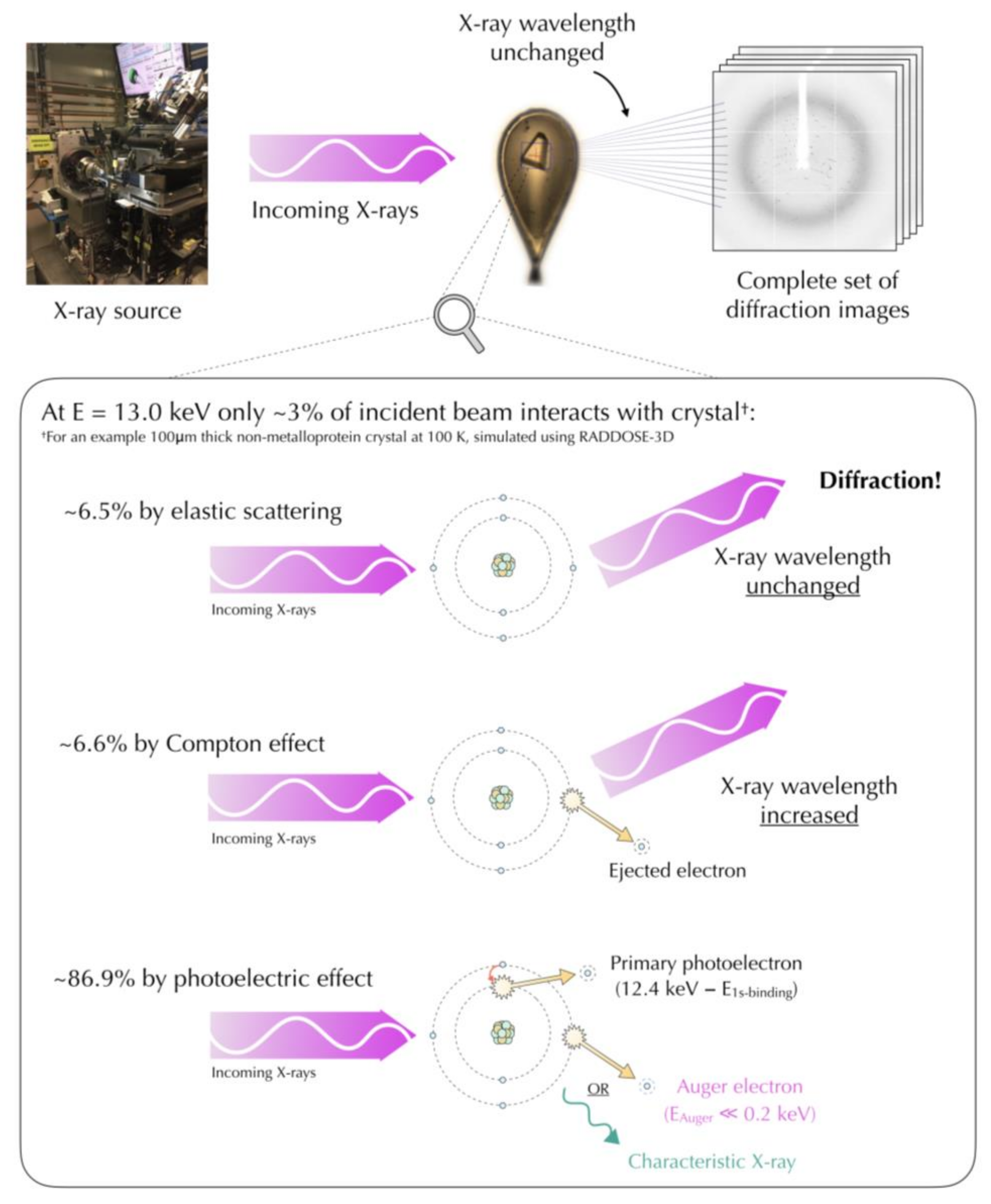
4. Diffraction Data Collection
4.1. Mechanisms of Radiation Damage
4.2. Data Collection Methods
4.3. Data Collection Parameters
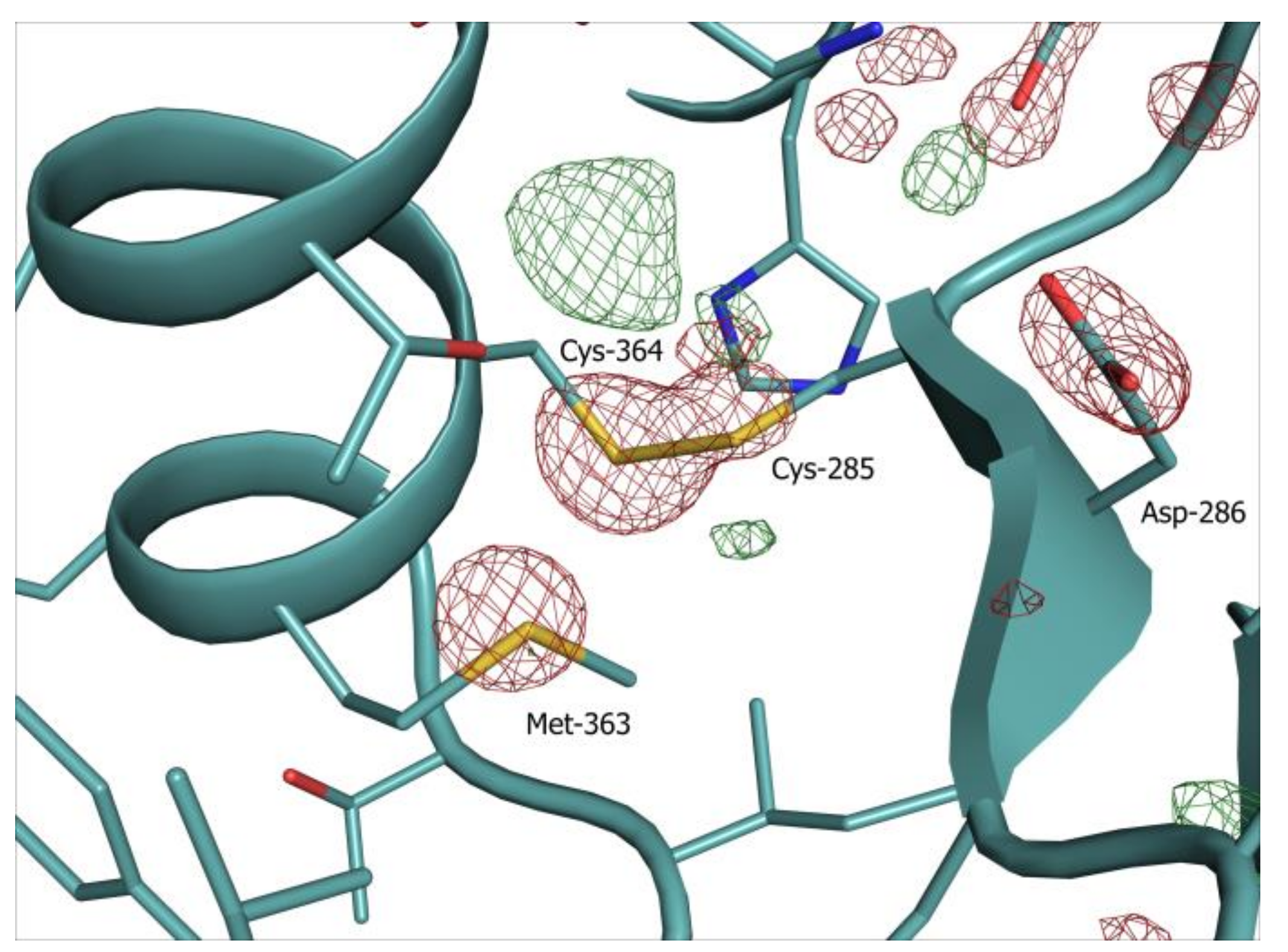
5. Structure Solution and Interpretation
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Blake, C.C.F.; Phillips, D.C. Effects of X-irradiation on single crystals of myoglobin. In Biological Effects of Ionizing Radiation at the Molecular Level; International Atomic Energy Agency: Vienna, Austria, 1962; pp. 183–191. [Google Scholar]
- Ravelli, R.B.; McSweeney, S.M. The ‘fingerprint’ that X-rays can leave on structures. Structure 2000, 8, 315–328. [Google Scholar] [CrossRef]
- Weik, M.; Ravelli, R.B.; Kryger, G.; McSweeney, S.; Raves, M.L.; Harel, M.; Gros, P.; Silman, I.; Kroon, J.; Sussman, J.L. Specific chemical and structural damage to proteins produced by synchrotron radiation. Proc. Natl. Acad. Sci. USA 2000, 97, 623–628. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.; Garman, E. Investigation of possible free-radical scavengers and metrics for radiation damage in protein cryocrystallography. J. Synchrotron Radiat. 2002, 9, 347–354. [Google Scholar] [CrossRef] [PubMed]
- Burmeister, W.P. Structural changes in a cryo-cooled protein crystal owing to radiation damage. Acta Crystallogr. Sect. D Biol. Crystallogr. 2000, 56, 328–341. [Google Scholar] [CrossRef]
- Carugo, O.; Carugo, K.D. When X-rays modify the protein structure: Radiation damage at work. Trends Biochem. Sci. 2005, 30, 213–219. [Google Scholar] [CrossRef] [PubMed]
- Weiss, M.S.; Panjikar, S.; Mueller-Dieckmann, C.; Tucker, P.A. On the influence of the incident photon energy on the radiation damage in crystalline biological samples. J. Synchrotron Radiat. 2005, 12, 304–309. [Google Scholar] [CrossRef] [PubMed]
- Corbett, M.C.; Latimer, M.J.; Poulos, T.L.; Sevrioukova, I.F.; Hodgson, K.O.; Hedman, B. Photoreduction of the active site of the metalloprotein putidaredoxin by synchrotron radiation. Acta Crystallogr. Sect. D Biol. Crystallogr. 2007, 63, 951–960. [Google Scholar] [CrossRef] [PubMed]
- Garman, E.F. Radiation damage in macromolecular crystallography: What is it and why should we care? Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, 66, 339–351. [Google Scholar] [CrossRef] [PubMed]
- Dubnovitsky, A.P.; Ravelli, R.B.; Popov, A.N.; Papageorgiou, A.C. Strain relief at the active site of phosphoserine aminotransferase induced by radiation damage. Protein Sci. 2005, 14, 1498–1507. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.W.; Rudino-Pinera, E.; Owen, R.L.; Grininger, M.; Ravelli, R.B.; Garman, E.F. Parameters affecting the X-ray dose absorbed by macromolecular crystals. J. Synchrotron Radiat. 2005, 12, 268–275. [Google Scholar] [CrossRef] [PubMed]
- Fioravanti, E.; Vellieux, F.M.; Amara, P.; Madern, D.; Weik, M. Specific radiation damage to acidic residues and its relation to their chemical and structural environment. J. Synchrotron Radiat. 2007, 14, 84–91. [Google Scholar] [CrossRef] [PubMed]
- McCoy, A.J.; Read, R.J. Experimental phasing: Best practice and pitfalls. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, 66, 458–469. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Šrajer, V.; Purwar, N.; Tripathi, S. The kinetic dose limit in room-temperature time-resolved macromolecular crystallography. J. Synchrotron Radiat. 2012, 19, 264–273. [Google Scholar] [CrossRef] [PubMed]
- Matsui, Y.; Sakai, K.; Murakami, M.; Shiro, Y.; Adachi, S.; Okumura, H.; Kouyama, T. Specific damage induced by X-ray radiation and structural changes in the primary photoreaction of bacteriorhodopsin. J. Mol. Biol. 2002, 324, 469–481. [Google Scholar] [CrossRef]
- Hope, H. Cryocrystallography of biological macromolecules: A generally applicable method. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 1988, 44, 22–26. [Google Scholar] [CrossRef]
- Teng, T. Mounting of crystals for macromolecular crystallography in a free-standing thin film. J. Appl. Crystallogr. 1990, 23, 387–391. [Google Scholar] [CrossRef]
- Garman, E.F.; Schneider, T.R. Macromolecular cryocrystallography. J. Appl. Crystallogr. 1997, 30, 211–237. [Google Scholar] [CrossRef]
- Garman, E. Cool data: Quantity AND quality. Acta Crystallogr. Sect. D Biol. Crystallogr. 1999, 55, 1641–1653. [Google Scholar] [CrossRef]
- Nave, C.; Garman, E.F. Towards an understanding of radiation damage in cryocooled macromolecular crystals. J. Synchrotron Radiat. 2005, 12, 257–260. [Google Scholar] [CrossRef] [PubMed]
- Allan, E.G.; Kander, M.C.; Carmichael, I.; Garman, E.F. To scavenge or not to scavenge, that is STILL the question. J. Synchrotron Radiat. 2013, 20, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Ravelli, R.B.; Garman, E.F. Radiation damage in macromolecular cryocrystallography. Curr. Opin. Struct. Biol. 2006, 16, 624–629. [Google Scholar] [CrossRef] [PubMed]
- Bourenkov, G.P.; Popov, A.N. Optimization of data collection taking radiation damage into account. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, 66, 409–419. [Google Scholar] [CrossRef] [PubMed]
- Kmetko, J.; Husseini, N.S.; Naides, M.; Kalinin, Y.; Thorne, R.E. Quantifying X-ray radiation damage in protein crystals at cryogenic temperatures. Acta Crystallogr. Sect. D Biol. Crystallogr. 2006, 62, 1030–1038. [Google Scholar] [CrossRef] [PubMed]
- Owen, R.L.; Rudino-Pinera, E.; Garman, E.F. Experimental determination of the radiation dose limit for cryocooled protein crystals. Proc. Natl. Acad. Sci. USA 2006, 103, 4912–4917. [Google Scholar] [CrossRef] [PubMed]
- Sliz, P.; Harrison, S.C.; Rosenbaum, G. How does radiation damage in protein crystals depend on X-ray dose? Structure 2003, 11, 13–19. [Google Scholar] [CrossRef]
- Leiros, H.; Timmins, J.; Ravelli, R.B.; Mcsweeney, S.M. Is radiation damage dependent on the dose rate used during macromolecular crystallography data collection? Acta Crystallogr. Sect. D Biol. Crystallogr. 2006, 62, 125–132. [Google Scholar] [CrossRef] [PubMed]
- Paithankar, K.S.; Garman, E.F. Know your dose: RADDOSE. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, 66, 381–388. [Google Scholar] [CrossRef] [PubMed]
- Garman, E.F.; Owen, R.L. Cryocooling and radiation damage in macromolecular crystallography. Acta Crystallogr. Sect. D Biol. Crystallogr. 2006, 62, 32–47. [Google Scholar] [CrossRef] [PubMed]
- Southworth-Davies, R.J.; Garman, E.F. Radioprotectant screening for cryocrystallography. J. Synchrotron Radiat. 2007, 14, 73–83. [Google Scholar] [CrossRef] [PubMed]
- Nowak, E.; Brzuszkiewicz, A.; Dauter, M.; Dauter, Z.; Rosenbaum, G. To scavenge or not to scavenge: That is the question. Acta Crystallogr. Sect. D Biol. Crystallogr. 2009, 65, 1004–1006. [Google Scholar] [CrossRef] [PubMed]
- Kmetko, J.; Warkentin, M.; Englich, U.; Thorne, R.E. Can radiation damage to protein crystals be reduced using small-molecule compounds? Acta Crystallogr. Sect. D Biol. Crystallogr. 2011, 67, 881–893. [Google Scholar] [CrossRef] [PubMed]
- De la Mora, E.; Carmichael, I.; Garman, E.F. Effective scavenging at cryotemperatures: Further increasing the dose tolerance of protein crystals. J. Synchrotron Radiat. 2011, 18, 346–357. [Google Scholar] [CrossRef] [PubMed]
- Barker, A.I.; Southworth-Davies, R.J.; Paithankar, K.S.; Carmichael, I.; Garman, E.F. Room-temperature scavengers for macromolecular crystallography: Increased lifetimes and modified dose dependence of the intensity decay. J. Synchrotron Radiat. 2009, 16, 205–216. [Google Scholar] [CrossRef] [PubMed]
- Holton, J.M. A beginner’s guide to radiation damage. J. Synchrotron Radiat. 2009, 16, 133–142. [Google Scholar] [CrossRef] [PubMed]
- Holton, J.M.; Frankel, K.A. The minimum crystal size needed for a complete diffraction data set. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, 66, 393–408. [Google Scholar] [CrossRef] [PubMed]
- Garman, E.F.; Weik, M. Radiation Damage in Macromolecular Crystallography. In Protein Crystallography: Methods and Protocols; Wlodawer, A., Dauter, Z., Jaskolski, M., Eds.; Springer Nature: New York, NY, USA, 2017; pp. 467–489. [Google Scholar]
- Fraser, J.S.; van den Bedem, H.; Samelson, A.J.; Lang, P.T.; Holton, J.M.; Echols, N.; Alber, T. Accessing protein conformational ensembles using room-temperature X-ray crystallography. Proc. Natl. Acad. Sci. USA 2011, 108, 16247–16252. [Google Scholar] [CrossRef] [PubMed]
- Owen, R.L.; Axford, D.; Nettleship, J.E.; Owens, R.J.; Robinson, J.I.; Morgan, A.W.; Doré, A.S.; Lebon, G.; Tate, C.G.; Fry, E.E. Outrunning free radicals in room-temperature macromolecular crystallography. Acta Crystallogr. Sect. D Biol. Crystallogr. 2012, 68, 810–818. [Google Scholar] [CrossRef] [PubMed]
- Gati, C.; Bourenkov, G.; Klinge, M.; Rehders, D.; Stellato, F.; Oberthür, D.; Yefanov, O.; Sommer, B.P.; Mogk, S.; Duszenko, M. Serial crystallography on in vivo grown microcrystals using synchrotron radiation. IUCrJ 2014, 1, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Standfuss, J.; Spence, J. Serial crystallography at synchrotrons and X-ray lasers. IUCrJ 2017, 4, 100–101. [Google Scholar] [CrossRef] [PubMed]
- Warkentin, M.; Hopkins, J.B.; Badeau, R.; Mulichak, A.M.; Keefe, L.J.; Thorne, R.E. Global radiation damage: Temperature dependence, time dependence and how to outrun it. J. Synchrotron Radiat. 2013, 20, 7–13. [Google Scholar] [CrossRef] [PubMed]
- Pflugrath, J. Macromolecular cryocrystallography—Methods for cooling and mounting protein crystals at cryogenic temperatures. Methods 2004, 34, 415–423. [Google Scholar] [CrossRef] [PubMed]
- Zeldin, O.B.; Gerstel, M.; Garman, E.F. RADDOSE-3D: Time-and space-resolved modelling of dose in macromolecular crystallography. J. Appl. Crystallogr. 2013, 46, 1225–1230. [Google Scholar] [CrossRef]
- Bury, C.S.; Brooks-Bartlett, J.C.; Walsh, S.P.; Garman, E.F. Estimate your dose: RADDOSE-3D. Protein Sci. 2018, 27, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Nave, C. Radiation damage in protein crystallography. Radiat. Phys. Chem. 1995, 45, 483–490. [Google Scholar] [CrossRef]
- Sanishvili, R.; Yoder, D.W.; Pothineni, S.B.; Rosenbaum, G.; Xu, S.; Vogt, S.; Stepanov, S.; Makarov, O.A.; Corcoran, S.; Benn, R.; et al. Radiation damage in protein crystals is reduced with a micron-sized X-ray beam. Proc. Natl. Acad. Sci. USA 2011, 108, 6127–6132. [Google Scholar] [CrossRef] [PubMed]
- Krause, M.O. Atomic radiative and radiationless yields for K and L shells. J. Phys. Chem. Ref. Data 1979, 8, 307–327. [Google Scholar] [CrossRef]
- O’Neill, P.; Stevens, D.L.; Garman, E.F. Physical and chemical considerations of damage induced in protein crystals by synchrotron radiation: A radiation chemical perspective. J. Synchrotron Radiat. 2002, 9, 329–332. [Google Scholar] [CrossRef] [PubMed]
- Nave, C.; Hill, M.A. Will reduced radiation damage occur with very small crystals? J. Synchrotron Radiat. 2005, 12, 299–303. [Google Scholar] [CrossRef] [PubMed]
- Jones, G.D.; Lea, J.S.; Symons, M.C.; Taiwo, F.A. Structure and mobility of electron gain and loss centres in proteins. Nature 1987, 330, 772–773. [Google Scholar] [CrossRef] [PubMed]
- Taylor, G.L. Introduction to phasing. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, 66, 325–338. [Google Scholar] [CrossRef] [PubMed]
- Dodson, E. The befores and afters of molecular replacement. Acta Crystallogr. Sect. D Biol. Crystallogr. 2008, 64, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Vijayan, M.; Ramaseshan, S. Isomorphous replacement and anomalous scattering. In International Tables for Crystallography Volume B; Shmueli, U., Ed.; Springer: Dordrecht, The Netherlands, 1993; pp. 264–275. [Google Scholar]
- Schneider, T.R.; Sheldrick, G.M. Substructure solution with SHELXD. Acta Crystallogr. Sect. D Biol. Crystallogr. 2002, 58, 1772–1779. [Google Scholar] [CrossRef]
- Sheldrick, G.M. A short history of SHELX. Acta Crystalloger. Sect. A Found. Crystallogr. 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Pike, A.C.; Garman, E.F.; Krojer, T.; von Delft, F.; Carpenter, E.P. An overview of heavy-atom derivatization of protein crystals. Acta Crystallogr. Sect. D Biol. Crystallogr. 2016, 72, 303–318. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, A. Optimizing data collection for structure determination. Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, 59, 1935–1942. [Google Scholar] [CrossRef]
- Schmidt, A.; Gonzalez, A.; Morris, R.J.; Costabel, M.; Alzari, P.M.; Lamzin, V.S. Advantages of high-resolution phasing: MAD to atomic resolution. Acta Crystallogr. Sect. D Biol. Crystallogr. 2002, 58, 1433–1441. [Google Scholar] [CrossRef] [PubMed]
- González, A.; Delft, F.V.; Liddington, R.C.; Bakolitsa, C. Two-wavelength MAD phasing and radiation damage: A case study. J. Synchrotron Radiat. 2005, 12, 285–291. [Google Scholar] [CrossRef] [PubMed]
- Rice, L.M.; Earnest, T.; Brunger, A.T. Single-wavelength anomalous diffraction phasing revisited. Acta Crystallogr. Sect. D Biol. Crystallogr. 2000, 56, 1413–1420. [Google Scholar] [CrossRef]
- González, A. A comparison of SAD and two-wavelength MAD phasing for radiation-damaged Se-MET crystals. J. Synchrotron Radiat. 2007, 14, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Ravelli, R.B.; Leiros, H.S.; Pan, B.; Caffrey, M.; McSweeney, S. Specific radiation damage can be used to solve macromolecular crystal structures. Structure 2003, 11, 217–224. [Google Scholar] [CrossRef]
- Weiss, M.S.; Mander, G.; Hedderich, R.; Diederichs, K.; Ermler, U.; Warkentin, E. Determination of a novel structure by a combination of long-wavelength sulfur phasing and radiation-damage-induced phasing. Acta Crystallogr. Sect. D Biol. Crystallogr. 2004, 60, 686–695. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, N.; Hirata, K.; Hasegawa, K.; Ueno, G.; Yamamoto, M. Dose dependence of radiation damage for protein crystals studied at various X-ray energies. J. Synchrotron Radiat. 2007, 14, 4–10. [Google Scholar] [CrossRef] [PubMed]
- Homer, C.; Cooper, L.; Gonzalez, A. Energy dependence of site-specific radiation damage in protein crystals. J. Synchrotron Radiat. 2011, 18, 338–345. [Google Scholar] [CrossRef] [PubMed]
- Fourme, R.; Honkimäki, V.; Girard, E.; Medjoubi, K.; Dhaussy, A.; Kahn, R. Reduction of radiation damage and other benefits of short wavelengths for macromolecular crystallography data collection. J. Appl. Crystallogr. 2012, 45, 652–661. [Google Scholar] [CrossRef]
- Liebschner, D.; Rosenbaum, G.; Dauter, M.; Dauter, Z. Radiation decay of thaumatin crystals at three X-ray energies. Acta Crystallogr. Sect. D Biol. Crystallogr. 2015, 71, 772–778. [Google Scholar] [CrossRef] [PubMed]
- Schulze-Briese, C.; Wagner, A.; Tomizaki, T.; Oetiker, M. Beam-size effects in radiation damage in insulin and thaumatin crystals. J. Synchrotron Radiat. 2005, 12, 261–267. [Google Scholar] [CrossRef] [PubMed]
- Bourenkov, G.P.; Popov, A.N. A quantitative approach to data-collection strategies. Acta Crystallogr. Sect. D Biol. Crystallogr. 2006, 62, 58–64. [Google Scholar] [CrossRef] [PubMed]
- Schneider, T.R. Synchrotron radiation: Micrometer-sized X-ray beams as fine tools for macromolecular crystallography. HFSP J. 2008, 2, 302–306. [Google Scholar] [CrossRef] [PubMed]
- Krojer, T.; von Delft, F. Assessment of radiation damage behaviour in a large collection of empirically optimized datasets highlights the importance of unmeasured complicating effects. J. Synchrotron Radiat. 2011, 18, 387–397. [Google Scholar] [CrossRef] [PubMed]
- Berglund, G.I.; Carlsson, G.H.; Smith, A.T.; Szöke, H.; Henriksen, A.; Hajdu, J. The catalytic pathway of horseradish peroxidase at high resolution. Nature 2002, 417, 463. [Google Scholar] [CrossRef] [PubMed]
- Polsinelli, I.; Savko, M.; Rouanet-Mehouas, C.; Ciccone, L.; Nencetti, S.; Orlandini, E.; Stura, E.A.; Shepard, W. Comparison of helical scan and standard rotation methods in single-crystal X-ray data collection strategies. J. Synchrotron Radiat. 2017, 24, 42–52. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W. XDS. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, D66, 125–132. [Google Scholar] [CrossRef] [PubMed]
- Waterman, D.G.; Winter, G.; Gildea, R.J.; Parkhurst, J.M.; Brewster, A.S.; Sauter, N.K.; Evans, G. Diffraction-geometry refinement in the DIALS framework. Acta Crystallogr. Sect. D Biol. Crystallogr. 2016, 72, 558–575. [Google Scholar] [CrossRef] [PubMed]
- Teng, T.Y.; Moffat, K. Primary radiation damage of protein crystals by an intense synchrotron X-ray beam. J. Synchrotron Radiat. 2000, 7, 313–317. [Google Scholar] [CrossRef] [PubMed]
- Sutton, K.A.; Black, P.J.; Mercer, K.R.; Garman, E.F.; Owen, R.L.; Snell, E.H.; Bernhard, W.A. Insights into the mechanism of X-ray-induced disulfide-bond cleavage in lysozyme crystals based on EPR, optical absorption and X-ray diffraction studies. Acta Crystallogr. Sect. D Biol. Crystallogr. 2013, 69, 2381–2394. [Google Scholar] [CrossRef] [PubMed]
- Bury, C.S.; Carmichael, I.; Garman, E.F. OH cleavage from tyrosine: Debunking a myth. J. Synchrotron Radiat. 2017, 24, 7–18. [Google Scholar] [CrossRef] [PubMed]
- Kort, R.; Hellingwerf, K.J.; Ravelli, R.B. Initial events in the photocycle of photoactive yellow protein. J. Biol. Chem. 2004, 279, 26417–26424. [Google Scholar] [CrossRef] [PubMed]
- Aoyama, H.; Muramoto, K.; Shinzawa-Itoh, K.; Hirata, K.; Yamashita, E.; Tsukihara, T.; Ogura, T.; Yoshikawa, S. A peroxide bridge between Fe and Cu ions in the O2 reduction site of fully oxidized cytochrome c oxidase could suppress the proton pump. Proc. Natl. Acad. Sci. USA 2009, 106, 2165–2169. [Google Scholar] [CrossRef] [PubMed]
- Bury, C.; Garman, E.F.; Ginn, H.M.; Ravelli, R.B.; Carmichael, I.; Kneale, G.; McGeehan, J.E. Radiation damage to nucleoprotein complexes in macromolecular crystallography. J. Synchrotron Radiat. 2015, 22, 213–224. [Google Scholar] [CrossRef] [PubMed]
- Bury, C.S.; McGeehan, J.E.; Antson, A.A.; Carmichael, I.; Gerstel, M.; Shevtsov, M.B.; Garman, E.F. RNA protects a nucleoprotein complex against radiation damage. Acta Crystallogr. Sect. D Biol. Crystallogr. 2016, 72, 648–657. [Google Scholar] [CrossRef] [PubMed]
- Ten Eyck, L.F. Crystallographic fast Fourier transforms. Acta Crystallogr. Sect A Cryst. Phys. Diffr. Theor. Gen. Crystallogr. 1973, 29, 183–191. [Google Scholar] [CrossRef]
- Bury, C.S.; Garman, E.F. RIDL: A tool to investigate Radiation-Induced Density Loss. J. Appl. Crystallogr. 2018, in press. [Google Scholar]
- Gerstel, M.; Deane, C.M.; Garman, E.F. Identifying and quantifying radiation damage at the atomic level. J. Synchrotron Radiat. 2015, 22, 201–212. [Google Scholar] [CrossRef] [PubMed]
- Shelley, K.L.; Dixon, T.P.E.; Brooks-Bartlett, J.C.; Garman, E.F. RABDAM: Quantifying specific radiation damage in individual protein crystal structures. J. Appl. Crystallogr. 2018, 51, 552–559. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taberman, H. Radiation Damage in Macromolecular Crystallography—An Experimentalist’s View. Crystals 2018, 8, 157. https://doi.org/10.3390/cryst8040157
Taberman H. Radiation Damage in Macromolecular Crystallography—An Experimentalist’s View. Crystals. 2018; 8(4):157. https://doi.org/10.3390/cryst8040157
Chicago/Turabian StyleTaberman, Helena. 2018. "Radiation Damage in Macromolecular Crystallography—An Experimentalist’s View" Crystals 8, no. 4: 157. https://doi.org/10.3390/cryst8040157
APA StyleTaberman, H. (2018). Radiation Damage in Macromolecular Crystallography—An Experimentalist’s View. Crystals, 8(4), 157. https://doi.org/10.3390/cryst8040157



