Information Capacity of Positron Emission Tomography Scanners

Abstract

Background: The aim of the present study was to assess the upper information content bound of positron emission tomography (PET) images, by means of the information capacity (IC). Methods: The Geant4 Application for the Tomographic Emission (GATE) Monte Carlo (MC) package was used, and reconstructed images were obtained by using the software for tomographic image reconstruction (STIR). The case study for the assessment of the information content was the General Electric (GE) Discovery-ST PET scanner. A thin-film plane source aluminum (Al) foil, coated with a thin layer of silica and with a 18F-fludeoxyglucose (FDG) bath distribution of 1 MBq was used. The influence of the (a) maximum likelihood estimation-ordered subsets-maximum a posteriori probability-one step late (MLE-OS-MAP-OSL) algorithm, using various subsets (1 to 21) and iterations (1 to 20) and (b) different scintillating crystals on PET scanner’s performance, was examined. The study was focused on the noise equivalent quanta (NEQ) and on the single index IC. Images of configurations by using different crystals were obtained after the commonly used 2-dimensional filtered back projection (FBP2D), 3-dimensional filtered back projection re-projection (FPB3DRP) and the (MLE)-OS-MAP-OSL algorithms. Results: Results shown that the images obtained with one subset and various iterations provided maximum NEQ values, however with a steep drop-off after 0.045 cycles/mm. The single index IC data were maximized for the range of 8–20 iterations and three subsets. The PET scanner configuration incorporating lutetium orthoaluminate perovskite (LuAP) crystals provided the highest NEQ values in 2D FBP for spatial frequencies higher than 0.028 cycles/mm. Bismuth germanium oxide (BGO) shows clear dominance against all other examined crystals across the spatial frequency range, in both 3D FBP and OS-MAP-OSL. The particular PET scanner provided optimum IC values using FBP3DRP and BGO crystals (2.4829 bits/mm²). Conclusions: The upper bound of the image information content of PET scanners can be fully characterized and further improved by investigating the imaging chain components through MC methods.

1. Introduction

Physical signals acquired, quantized, and processed in imaging systems (especially in nuclear medicine) are prone to various noise sources, imposing a fundamental limit on the overall performance of the system [1,2]. It is well known that there is a compromise between sensitivity and resolution in collimated nuclear medicine systems [3,4]. The detectability of the radiopharmaceutical concentration in abnormalities depends on the interplay between various parameters, such as the positron emission tomography (PET) scanner’s sensitivity, the amount of activity, the ratio of the target-to-background activity, the size of the target, and the irradiation time, among others [5,6,7,8,9].

Quantitative measures of the lesion’s (or target region) size and shape, and relative or absolute activity will depend upon the ability to correct for spatial resolution degradations, detector efficiency, scattered radiation, photon attenuation, collimator penetration, etc. [10].

Thus, knowledge of their impact on the overall imaging information recorded in the final image, by using a single imaging performance index, would be of interest. The final nuclear medicine image tends to be noisy and of poor resolution, due to practical limitations arising from the allowable radiation dosage to the patient, and the inherent characteristics of the imaging system [3,11]. The interrelation between sensitivity and resolution has been thoroughly examined in the past, towards the quest for the optimum lesion detection [3].

Upon designing a digital medical imaging system the recorded signal and noise statistics can be quantified in an information theory context to obtain an optimal bit-efficient quantization state [1]. Information capacity (IC) has been used in the past for the quantitative estimation of the encoded scintillation event information, transferred to image, in order to improve the imaging capabilities of the gamma camera [12].

Information capacity is the maximum rate (upper bound of information content) at which information can be transmitted through a channel (or system) with an average power limitation and random noise [13,14,15]. Shannon introduced information capacity, within the context of information theory in electrical communication channels [15,16].

The adaptation of this work to medical imaging information has been addressed in the past by various groups [13,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Dolazza and Poulo have shown that the uniform linear quantizer provides maximum information capacity for a fixed number of bits [1]. Information capacity has been also used to quantify the sharpness information that is lost during the spatial averaging process when smoothing filters are applied in tomography scanners [30]. The validity for the use of an objective metric, such as the information capacity in nuclear medicine, has been examined, by investigating IC as a function of collimator diameter, showing that the maximum IC values, for various collimators, are also those that are generally accepted as being optimum by clinical experience [12,31]. In this way, the optimum detector spatial resolution can be determined when the information capacity of the detector system is maximized, or in turn, when the signal-to-noise ratio (SNR) in the image is maximized [12,32]. Essential information regarding the maximum available signal-to-noise ratio, as a function of frequency, can be obtained through the noise-equivalent quanta (NEQ), which is the ratio of the modulation transfer function (MTF), describing the signal response of a system at a given frequency, and the noise power spectrum (NPS), describing the amplitude variance at a given frequency [33,34]. This information can be further utilized to optimize the examination procedure in terms of examination time and administered 18F-fludeoxyglucose (FDG) activity.

The iterative algorithm parameters determine the reconstruction time, as well as, the final image quality. In addition, parameter combinations that yield superior performance may lead to a reduction in the administered radioactivity (18F-FDG) to the patient. Thus, an optimum set of crystal materials, number of subsets, and number of iterations, as well as reconstruction type, could benefit the patient, optimize the acquisition time, or reduce the radiation burden of the procedure.

The aim of this study is to extend a previous validated Monte Carlo model for the assessment of the maximum information content that can be attributed to PET images by investigating the influence of the iterative algorithm parameters (iterations, subsets), as well as, the possibility for the further improvement of the image quality in PET scanners by replacing the current crystal material with various new materials, not available in the detector modules of the commercial scanner [35,36].

To this aim, NEQ was estimated by a simulation with the GATE (Geant4 application for tomographic emission) Monte Carlo package of a thin layer chromatography (TLC) plane source covered with 18F-FDG [37,38,39,40]. GATE was used in combination with the software for tomographic image reconstruction (STIR) [41] to obtain reconstructed images of the plane TLC source. GATE is a very popular tool in nuclear medicine, since it can realistically simulate the dynamic processes, such as respiratory and cardiac motions, tracer kinetics, time-of-flight (TOF) PET, radioactive decay, and dead-time effects. GATE can be employed to study the biodistribution of radiotracers, to predict the dose-distribution of a therapeutic agent, or modeling the radiotracer heterogeneity within tumors [42]. The simulation of the plane source phantom also provides an accurate model that is useful to fully characterize, beyond performance, the information content of nuclear medicine imaging systems.

2. Materials and Methods

2.1. Modeled PET System Geometry

For the purposes of the present study, a previously validated Monte Carlo code simulating the GE Discovery ST positron emission tomography/Computed tomography (PET/CT) scanner was used. The system, in its factory setup, incorporates Bismuth germanium oxide (BGO) [43,44] crystals with dimensions of 6.3 × 6.3 × 30 mm in the tangential, axial, and radial directions, respectively. Blocks of 6 × 6 crystals were assembled, and each block was coupled to a four square channels photomultiplier tube (PMT). Modules of eight blocks (2 × 4 each) were assembled. The integrated detector ring consists of 35 modules (280 crystal blocks), or 24 rings of 420 crystals (for a total of 10080 BGO crystals). The dimensions of the rings are 88.6 cm diameter with a 15.7 cm axial and 70 cm transaxial fields of view (FOV) [35].

In order to examine the influence of the crystal material on the information content of the final PET image, the system was also simulated by replacing the BGO crystal arrays with crystals of various quantum detection efficiency (QDE) [45] values, i.e., yttrium orthoaluminate perovskite (YAlO₃:Ce or YAP, QDE = 0.75) [36,43,44], lutetium orthoaluminate perovskite LuAlO₃:Ce or LuAP:Ce, lutetium yttrium orthoaluminate perovskite ((LuY)AlO₃:Ce or LuYAP:Ce, QDE = 0.90) with 70% lutetium (Lu) atomic fraction, LuYAP:Ce with 80% Lu atomic fraction (QDE = 0.91) [44,46], lutetium oxyorthosilicate (Lu₂SiO₅:Ce or LSO, QDE = 0.93) [46,47,48,49,50], and gadolinium oxyorthosilicate (Gd₂SiO₅:Ce or GSO, QDE = 0.88) [43,44,51] crystals with dimensions equal to those of BGO (QDE = 0.94) (6.3 × 6.3 × 30 mm) in the tangential, axial, and radial directions, respectively.

2.2. Software Customization and Plane Source Test Object

The radiation transfer and interaction parameters were settled by thresholds similar with Geant4 [37,39]. The standard and low-energy Geant-4 packages were used from GATE in order to simulate the electromagnetic processes [37]. In this study, the standard energy package was used to model the photoelectric and Compton interactions, and the low-energy package, to simulate the Rayleigh interactions.

The sinogram output file (.ima), which is a raw data file (unsigned short integer), obtained from the emission computerized axial tomography (ECAT) system, were used by STIR as an input file for the reconstruction of the simulated plane source image [52]. All simulations were performed using a computer cluster with 12 dual core Intel(R) Xeon(TM) CPU 3.00 GHz processors (Supermicro SuperServer 6015B-UR/NTR, San Jose, CA, USA). GATE simulation is extended beyond physics processes, upon the scanner’s detectors and the signal processing chain. A series of signal processors were used, known as the Gate Digitizer object, or Digitizer. The Digitizer was composed of different modules that may be inserted into the linear signal processing chain to process photon interactions that produce single events, from which the coincidence events are formed. Every Digitizer’s signal processed mimics a separate segment of the simulated PET scanner’s signal processing chain [8]. Then, the particles interact within an individual crystal and an Adder module sums the deposited energy to yield a pulse. Following this, a Readout module regroups pulses for every block of crystals, in order to create a final pulse per detected photon. Afterwards, a Gaussian energy blur, with an average energy resolution is applied for each crystal of the detector block by a Crystal Blurring module, applying Quantum Detection Efficiency values [36,45]. Next, dead-time values are applied on the single events for crystal by a paralyzable Deadtime module. Then, at the same level, an Energy Window discriminator is applied via the Thresholder and Upholder modules, both incorporated within the energy window. The chain describing single events as above can result in the creation of different types of files (e.g., ASCII, root, interfile, sonogram, ECAT7, etc. [52]), in order to be used for various applications that require the specific file types. These file types contain the detected single events, and they can be enabled or disabled, when needed. For each single event, they contain data about the energy that deposited in the crystal, and the coordinates of detection within the modeled scanner geometry.

The plane source, that is simulated in this study, is based on an initial idea of Boone [53] for computed tomography, Fountos et al. [54] for single photon emission computed tomography (SPECT) systems, and appropriately implemented for PET by Michail et al. and Karpetas et al. [36,40]. It is based on the excellent binding of 18F-FDG onto TLC plates [40]. The TLC plate simulated was an Al foil coated with a thin layer of Silica (Al density 2.7 g/cm³) [40]. The dimensions of the TLC plate were 5 × 10 cm and it was simulated to be immersed in 18F-FDG bath solution (1 MBq), corresponding to radioactivity of 200 Bq/mm². The plane test object (plane source, i.e., the radioactive plate) was simulated within a phantom, consisting of two semi-cylindrical polyethylene blocks with 20 cm diameter and 70 cm length, in the horizontal and vertical directions for both 2D and 3D data acquisitions [40]. Plane source images were acquired from STIR, after the reconstruction of the arc-corrected sinogram data, with commonly used 2D-filtered back projections (FBP2D) (Ramp filter 0.5) [55], the Kinahan and Rogers [55,56] 3-dimensional filtered back projection re-projection (FPB3DRP) [55] (Colsher filter 0.5) [57] and the maximum likelihood estimation (MLE)-OS-MAP-OSL [55] algorithms.

2.3. Noise Equivalent Quanta

The ratio of the signal and noise (SPS(f)/NPS(f)) [58,59,60,61] properly normalized, provides information about the maximum available signal-to-noise ratio, as a function of frequency and can be expressed by the noise equivalent quanta [28,33,62]. This concept relates the detective quantum efficiency (DQE) (the ratio of the detector output to the input signal-to-noise ratio as a function of spatial frequency, DQE = SNR²_out/SNR²_in) [20] with the input signal (SNR²_in), defined as the plane source phantom activity (counts/mm²) incident on the detectors, and can be given as [36,40]:

NEQ(u) = DQE(u)∙SNR²_in

(1)

The latter provides an index of the signal-to-noise ratio associated with the diagnostic value of a medical image [2,58,63].

2.4. Information Capacity

Beyond the spatial frequency dependent NEQ, image quality can be expressed by single index parameters, expressed through integration over the useful spatial frequency range. Such a parameter is the information capacity (IC) [64]. The concept of information capacity has been introduced within the context of Shannon’s information theory, in order to assess image information content [65]. However, little work relevant to nuclear medicine imaging has been published up to now [1,3,11,20]. The research on IC has been spread in various disciplines, spanning from radiographic screen-film combinations, CT and SPECT in the past, up to neural networks, magnetic resonance imaging (MRI), and digital imaging systems today [66,67,68,69,70,71].

Information capacity is the maximum rate (upper bound of information content) at which information can be sent through a channel (or system), with average signal power and random noise [12,13,14]. The transition from the time-rates in communication theory to two-dimensional medical imaging can be made feasible by the replacement of time with area [12]. Thus, the transmitted ‘message’ becomes the recorded average density of events (counts per unit area), and the power/noise-limited channel (or system) becomes the actual detected stream of randomly varying particles from the radiopharmaceutical’s source [12]. The assumption of the Gaussian signal’s distribution, in order for the capacity to be maximum, also stands for the distribution of the source over the plane of view. This interpretation of information capacity can be shown to be equivalent to the statistical mean information that is gained (or content) per unit area from one measurement of the signal and noise, both with Gaussian distribution [12,72]. Therefore, IC does not determine the information content of a totally viewed field, but the maximum amount of information (per unit area) that can be gained when using a particular system [12]. Thus, IC can quantify any changes in the system or various systems [12].

According to Shannon’s theory, the IC, per unit of image area, is given by the product n_plog₂N_s, where n_p is the number of image elements (pixels) per unit of area, and N_S is the number of distinguishable signal intensity levels that can be registered in an image element [73]. However, since IC can be expressed as a function of the output SNR squared [14,40], it can written as [19,40]:

$$\mathrm{IC}=\mathsf{\pi }{\int }_0^{\infty }{\log }_2\left[1+{\mathrm{SNR}}_0^2\left(\mathrm{v}\right)\right]\mathrm{vdv}=\mathsf{\pi }{\int }_0^{\infty }{\log }_2\left[1+\mathrm{NEQ}\left(\mathrm{v}\right)\right]\mathrm{vdv}$$

(2)

It is important to note that, apart from the detector properties, information capacity depends on the level of the incident activity (input signal). The practical value of IC is that it defines an imaging performance index that evaluates the image information quantity by a single numerical value. IC is not expressed for specific frequency values, since it is the outcome of integrating over the spatial frequency bandwidth. It may be considered as being roughly proportional to the area under the curve of the frequency-dependent image SNR. Thus, it mainly reflects the quantity, and not the quality of image information. Image quality is better described via frequency-dependent signal parameters [36,40].

3. Results

3.1. NEQ

Figure 1a–d shows NEQ curves (Equation (1)), calculated from the combined resolution and noise properties, as depicted by DQE and the input plane source phantom activity (200 counts/mm²), incident on the detectors. Results are shown for various combinations of subsets and iterations of the maximum likelihood estimation (MLE)-OS-MAP-OSL algorithm, covering the commonly used range in clinical practice [40]. The shapes of the NEQ curves are affected by both resolution and noise, whereas the amplitude of NEQ is affected by the input plane source phantom activity incident on the detectors. As has been pointed out in a previous study of our group, as the number of iterations increase, the resolution in terms of the MTF is improved, however, with a simultaneous increase of magnitude in image noise (NNPS). However, due to the non-linear nature of the iterative reconstruction algorithms, noise levels tend to fluctuate locally, yielding to peak in different spatial frequencies [40]. Since the improvement of the resolution is restricted up to the 12th iteration and remains almost constant thereafter, whereas noise increases constantly [40], their ratio results in a reduction of the image SNR. In the quest for the maximum available signal-to-noise ratio, per frequency, Figure 1a shows that with one subset and various iterations, higher NEQ values can be preserved in the spatial frequency range up to 0.045 cycles/mm. Afterwards, all NEQ curves show a steep drop-off, due to the excessive increase of noise. In particular, NEQ values of Figure 1a saturate in the range from eight to 14 iterations, with a maximum value (101.92 at 0.038 cycles/mm) for eight iterations, showing that low-contrast objects of large dimensions may be better visualized with this subset and iterations combination. This finding is in close agreement with the IC results that are shown in

Table 1. Information capacity values for different subsets/iterations.

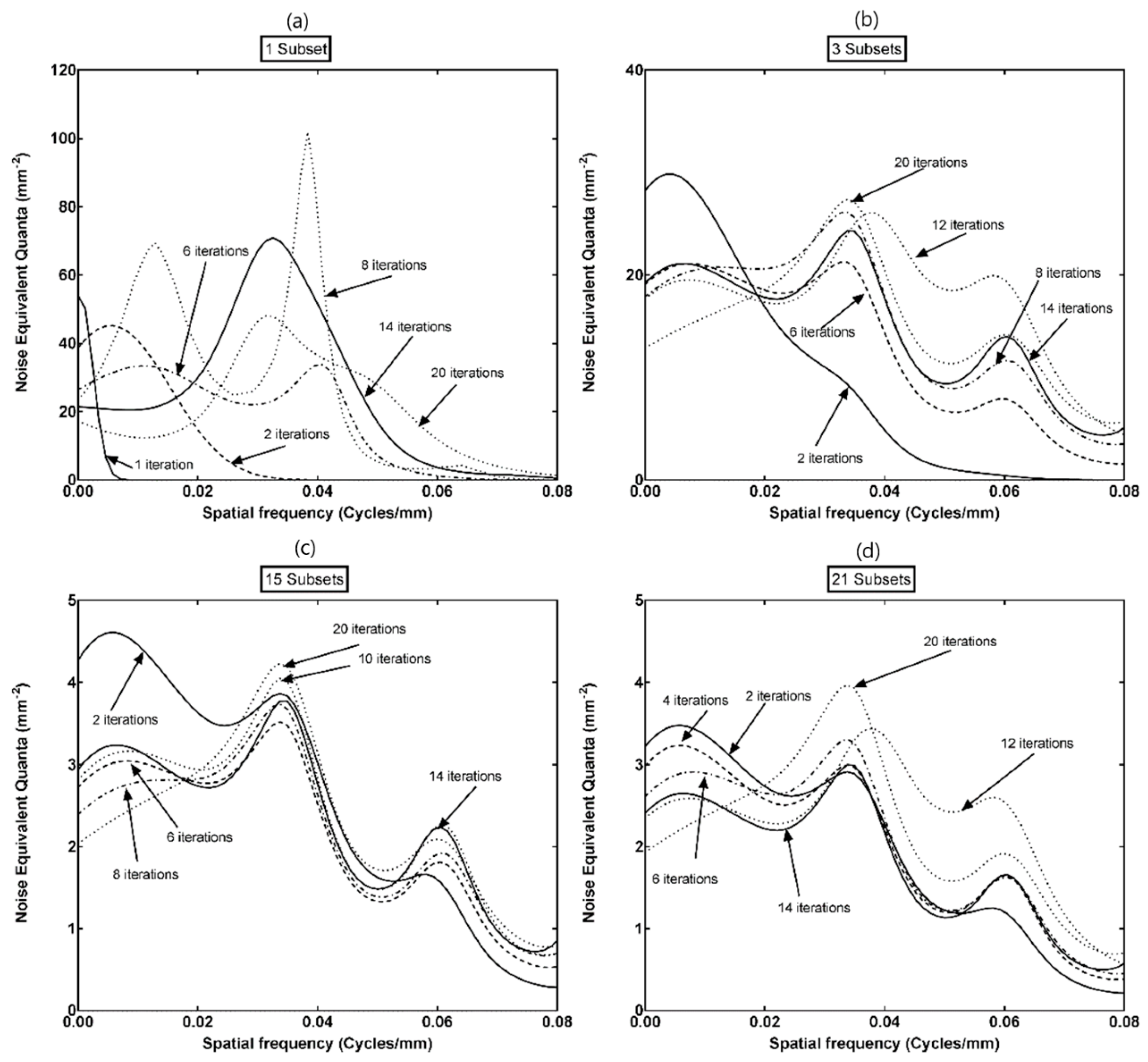
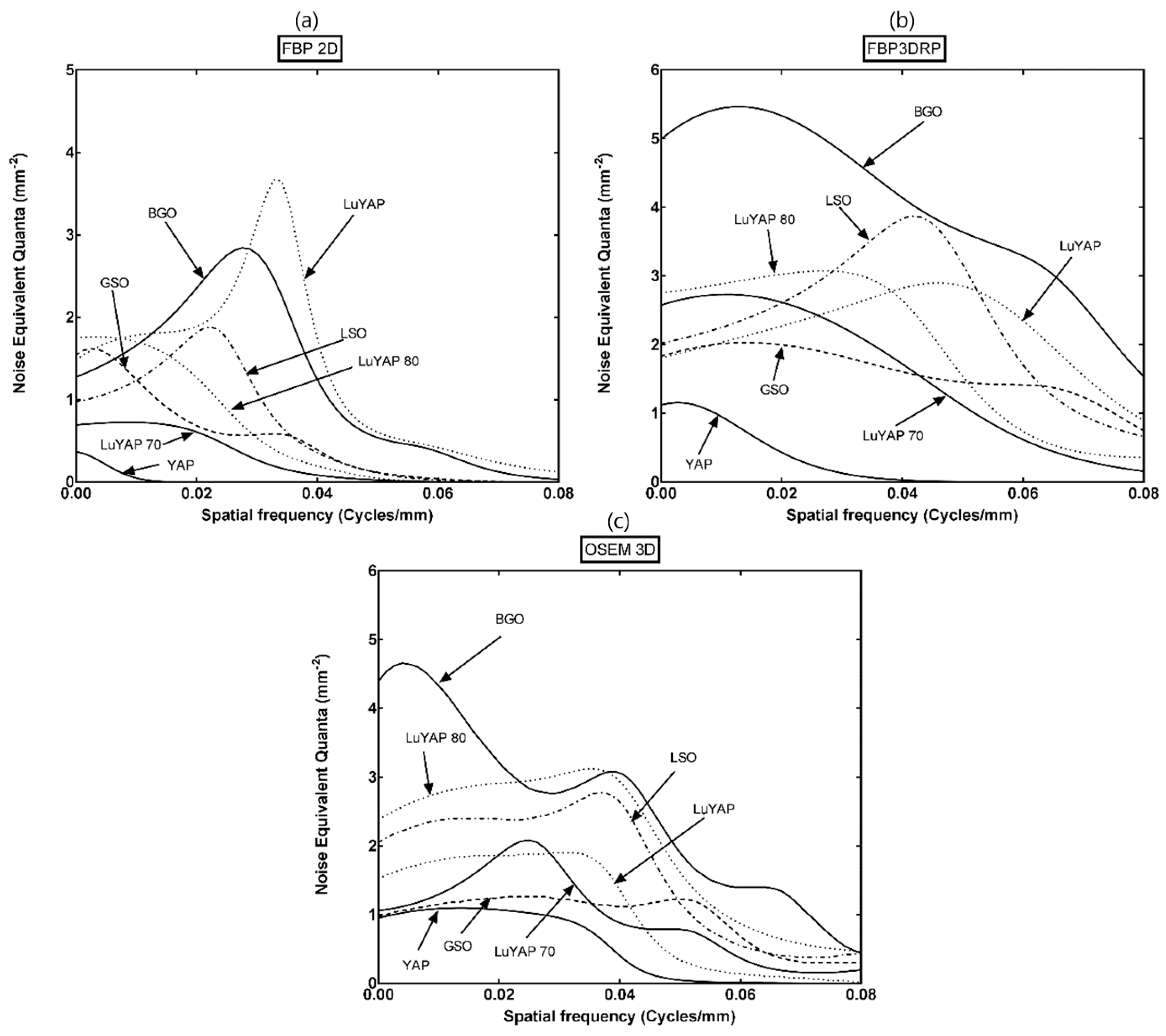
Iterations	Subsets
	1	3	15	21
	Information Capacity (bits/mm2)
1	0.0217	-	-	-
2	0.5577	1.3774	1.6869	1.4100
4	-	-	-	1.6770
6	2.2899	3.8744	1.9202	1.7926
8	2.8716	4.5902	1.9510	-
12	-	4.7432	2.2109	1.7690
14	3.5305	4.7080	1.9586	1.6097
20	4.0222	5.1947	2.1936	2.0781

. However, NEQ values obtained with one subset practically demonstrate higher values compared to 3, 15, and 21 subsets, as shown in Figure 1b–d, respectively, in the frequency range under investigation. This effect is due to the resolution saturation, which occurs at 12 iterations in combination with the progressive increase in image noise, resulting in a constant reduction in the output signal-to-noise ratio, for higher subsets.

In particular, from Figure 1c, it can be shown that the higher NEQ value is 4.61 at 0.08 cycles/mm, obtained from the combination of 15 subsets and two iterations, which is almost 22 times lower than the higher value of Figure 1a. The results are even worse in Figure 1d, in which the higher NEQ value is 3.97 at 0.033 cycles/mm, obtained from a time-consuming combination of 21 subsets and 20 iterations. Thus, higher values of iterations and subsets were not considered, since their contribution could be the further increase of the computation time and image noise.

Figure 2a–c shows a comparison between the NEQ values obtained from the FBP2D, FBP3DRP, and OS-MAP-OSL algorithms, for the PET scanner configurations successively incorporating BGO, YAP, LuAP, LuYAP-70, LuYAP-80, LSO, and GSO crystals [36]. The NEQ values of the 2D FBP images (Figure 2a) are considerably lower than that of the corresponding FBP3DRP (Figure 2b) and OS-MAP-OSL (Figure 2c), across the spatial frequency range, due to the inferior resolution and noise performance, as was depicted in a previous study of our group [36]. NEQ values of the FBP3DRP were found to be higher compared to the FBP2D, due to the absence of collimation between image slices in 3D mode [36]. The low noise values of the FBP2D image preserve high NEQ values in the low-frequency range (up to 0.03 cycles/mm) but thereafter, the restriction of the gamma rays entering the crystals with retractable tungsten septa leads to reduced output SNR values.

The PET scanner configuration incorporating LuYAP crystals provided the highest NEQ values in 2D FBP (Figure 2a) for spatial frequencies that are higher than 0.028 cycles/mm. BGO shows clear dominance against all other examined crystals across the spatial frequency range, in both 3D FBP image reconstruction (Figure 2b) and OS-MAP-OSL (Figure 2c). This configuration has the lowest noise levels, thus justifying the commercial use of BGO crystals in the assembly of the particular PET system.

3.2. Information Capacity

The interpretation of the output signal-to-noise ratio results shown in Figure 1 and Figure 2 cannot be straightforwardly translated into predictions about the clinical usefulness of images that are produced by the system for a human observer. When the quantum noise is a limiting factor for the observer, the performance is dependent on the task, and hence, the clinical relevance of NEQ may be accordingly affected, by the influence of the different spatial frequencies. For example, Figure 1a (1 subset various iterations) shows higher maximum NEQ values compared to Figure 1b (3 subsets various iterations); however, the overall output signal-to-noise ratio values shown in Figure 1b are higher in a wider spatial frequency range, compared to the noise-limited values of Figure 1a. Due to this, cumulative image quality results, in the sense of information capacity, should be also examined by appropriately integrating NEQ values, using Equation (2), for spatial frequencies up to the Nyquist frequency. Table 1 and

Table 2. Information capacity values for different crystal materials.

PET Module/Scintillating Crystal Combination	Algorithm
	FBP2D	FBP3DRP	OS-MAP-OSL
	Information Capacity (bits/mm2)
BGO	0.7197	2.4829	1.6042
Gd2SiO5:Ce	0.2481	1.4735	0.8864
Lu2SiO5:Ce	0.3215	1.7611	1.1651
LuAP:Ce	0.8648	1.8757	0.5875
LuYAP:Ce—70%	0.1242	0.9860	0.7620
LuYAP:Ce—80%	0.2265	1.2798	1.4028

show IC values for different subsets and iterations combinations using iterative algorithm (Table 1), as well as, for different crystal materials and algorithm combinations (Table 2). From Table 1 can be shown that from the spatial frequency range up to the Nyquist frequency the optimum information capacity values are attributed to the combination of three subsets with a range of eight to 20 iterations. The latter suggests that higher subset numbers do not necessarily yield higher IC and NEQ values, as shown in Figure 1a,b, since the resolution has already saturated, and afterwards, only noise increases, leading to a progressive decrease in signal-to-noise ratio [40]. It is also clear from Table 1 that for lower or higher combinations of subsets/iterations, this single index value is lower. With a maximum information capacity value of IC = 5.19 bits/mm² obtained in this study (Table 1), it is derived, for example, that in a 30 cm × 30 cm PET image, there would be roughly 4.67 × 10⁵ bits.

Table 2 shows the IC results for all the crystals and different algorithms (the 2D-filtered back projection, the 3D-filtered back projection, and the maximum likelihood estimation) in the spatial frequency range under investigation. As can be depicted from this Table, the Discovery ST PET scanner provided the optimum information capacity values using FBP3DRP reconstruction and BGO scintillating crystals in the PET camera modules.

4. Discussion

Image quality in PET scanners is affected by a variety of parameters, including the crystal’s properties, size and arrangement, the mode of operation (2D or 3D), photon noncollinearity and positron range, oblique detector penetration, photon scatter, the measured standardized uptake values (SUVs), patient motion, the position of the source within the FOV, sensitivity, and noise, all of which contribute to PET system’s performance [8,40,46,74,75,76,77]. Among the other factors affecting resolution, the most dominant is positron range, which can degrade resolution up to a few millimeters, depending the system settings, from the ideal resolution, which is defined as twice the pixel size, due to the Nyquist theorem [76,78]. Furthermore, image quality is dependent on the number of iterations and subsets in ordered subset-type algorithms, filters in FBP, and post-filtering [75]. When using iterative reconstruction algorithms, the number of iterations should be carefully selected, in order to compromise between resolution and noise, in order to maximize the SNR.

The available information contained in medical images is evaluated by human observers. Thus, the information content that is of diagnostic relevance is limited to what is visibly detected by the nuclear medicine physicians’ eye and translated to information by the brain [13]. From the viewpoint of information theory, the criterion for the detectability of a signal is that it exceeds the root mean square (rms) noise [13]. Following the basic hypothesis of the Rose model, the eye approaches the model of an ideal photon detection device, and if a human observer could integrate noise over the whole area of a specific object in the image, then their perceptual SNR would be insuperable [13,30,79]. However, there is a difference between visibility and detectability. Motz and Danos [80] showed that there exist density differences in conventional radiographs that meet the detectability criterion, but they may be obscured to the human being, and therefore lost for diagnosis. Thus, testing by visual inspection of test pictures is not always a sufficient criterion for evaluating different system configurations.

In a previous study by our group, the image quality of PET scanners was also examined through a single index figure of merit (FOM) that is related to the performance of the ideal observer in the task of detecting a point source [36]. However, for any other task, a different weighting of the frequencies could be useful, and consequently, the optimal system setting for obtaining the maximal FOM will change [80]. This issue is addressed by the information capacity, which is an objective single index evaluation metric, based on the estimation of objective quantitative measures (i.e., input and output SNR, resolution and noise) and integrating information across the spatial frequencies, independently of the experience of a human observer. Signal-to-noise ratio, among other objective image quality metrics such as the noise equivalent counts (NEC), are in good agreement with physician’s subjective assessment, and have been used to examine the relationship between image quality and administered activity, in regions such as the liver and aortic arch [81].

In this study, the information content of PET images was assessed using GATE Monte Carlo. PET images were obtained from STIR reconstruction software through the simulation of the specific radiopharmaceutical distribution of a previously validated 18F-FDG plane source. The results showed that IC can be an efficient tool that can be used in the assessment of the information contained in PET images, obtained with various algorithms (FBP, iterative), clinical protocols, etc., through a single index.

The influence of the detector material on the image information content of a PET scanner was also investigated. Results showed that lutetium orthoaluminate perovskite crystal provided the optimum NEQ in 2D FBP for spatial frequencies higher than 0.028 cycles/mm whereas bismuth germanium oxide shows clear dominance against all other examined crystals across the spatial frequency range, in both 3D FBP image reconstruction and OS-MAP-OSL. These findings show that the BGO crystal provided the optimum overall image information content for the specific PET scanner implementation; however, the rather slow decay time of this material is a drawback for time-of-flight applications.

Since NEQ combines resolution and noise in the signal-to-noise ratio, it could be useful for comparing the effects of different scan and reconstruction parameters (FBP, OS-MAP-OSL, etc.) and for determining the appropriate number of iterations, in order for the SNR to saturate, without the addition of excessive noise in PET images, when iterative algorithms are used. Finally, IC can be useful for evaluating the accuracy of size and density measurements of fine details in nuclear imaging.

5. Conclusions

The method presented in this study can be used for image information content assessment and optimization, but it can be also useful for the further development of PET and SPECT scanners though GATE simulations.