1. Introduction
First introduced by Conway [
1], the ‘game of life’, a cellular automaton algorithm proposed to simulate real life patterns with simple rules, quickly drew the attention of scientists in various fields [
2,
3,
4,
5]. The ‘game of life’ variations explored so far have employed a periodic grid [
6] or have used only local rules [
7,
8]. For the first time, we simulate a game of life following non-local rules on an aperiodic grid, the Penrose tiling [
9], a two-dimensional quasicrystal (QC). The existence of quasicrystals was first considered ruled out because of their forbidden symmetry, before Kleinert in 1981 [
10] and Levine and Steinhardt in 1984 [
11] predicted and theorized them. Shechtman discovered them in 1982 and published his results two years later [
12]. The special properties of quasicrystals, their aperiodic order and their non-local nature dictated from higher dimensions [
13], make them an interesting research subject not just in the field of material science, but in many other fields, including more recently quantum computing. They are thus an interesting candidate for modeling game of life algorithms. The distribution and frequency of the vertex configurations or local patches are strictly governed by the higher dimensional ‘mother lattice’ and the manner in which the quasicrystal is generated from it. Each vertex configuration or local patch has an empire [
14,
15,
16,
17], a feature unique to quasicrystals representing the totality of all the tiles whose existence and positions are forced by the local patch. Therefore, the local patches propagate under the influence of the empire fields.
Respecting the inherent aperiodic order of quasicrystals and their non-local nature, we construct a non-local game of life simulation on Penrose tiling, a well-known 2D quasicrystal. In this paper we study one of the eight possible vertex configurations of the Penrose tiling, the K vertex type (VT). For a certain vertex of this type, we consider the vertex patch formed by the tiles surrounding the vertex. We treat the configuration formed by the vertex patch together with the tiles belonging to its local empire as a quasiparticle. We then simulate and track the evolution of this configuration, dynamically, in several scenarios, finding patterns like rotations, quasi-translations and oscillations. These patterns are dictated by the interaction of the quasiparticle with its own empire field, a self-interaction. Furthermore, we explore the behavior of two such configurations as interactions between two quasiparticles and their non-local fields. Our results are discussed in the context of higher dimensional symmetries, which could prove to be crucial in describing by first principles the particles observed in nature.
We review the important properties of quasicrystals and the methods to generate them in
Section 2. In
Section 3 we describe the method used to simulate a non-local game of life on Penrose tiling. The results for both a quasiparticle’s self-interaction and a two-particle interaction are shown in
Section 4. Finally, we discuss in a broader context the implications of our results and we present our conclusions in
Section 5.
2. Properties of Quasicrystals
The forbidden symmetry of quasicrystals comes from the symmetry breaking from a higher dimensional lattice, through projection. For example, five-fold symmetry is forbidden in 2D crystals, but it exists in projection of the
lattice. Penrose tiling can be obtained through projecting a layer of the
lattice along the five-fold axis, to two dimensions [
18,
19]. Although Penrose tiling does not have the perfect periodic order that crystals possess, it has aperiodic order that is non-local and repetitive, in other words, given any local patch of the tiling of any size, one could find an infinite number of identical patches in a full (infinite) Penrose tiling. The following properties of quasicrystals make them extremely interesting candidates for a game of life simulation:
Each local configuration type is distributed uniformly throughout the whole quasicrystal. This matches the fact that particles tend to be distributed uniformly in a ground state or at very low temperature when there is a lack of interactive forces.
The ratio of the frequencies of any two vertex types is a constant.
The empire of each local configuration is non-local. This property could prove important in explaining the non-local interaction between particles.
For a better understanding of the aforementioned properties of quasicrystals, we will briefly review a few important concepts.
The Cut-and-Project Method
There are several methods to generate a quasicrystal: the cut-and-project method [
18,
19,
20], the multigrid method [
20] and the inflation/deflation or substitution rule method [
20]. Here we will focus only on the cut-and-project method not just because it is conceptually simple and computationally efficient, but also because it provides better clarity on the concepts of empire and possibility space, concepts crucial for our non-local game of life model.
The cut-and-project method for generating quasiperiodic tilings from a higher dimensional lattice—the mother lattice—expanded to generating empires in quasicrystals is a well-developed method [
17]. We will review here some notions related to the non-local properties of quasicrystals, namely the acceptance domain/QC window and the empire and possibility space windows using the
lattice and its 1D quasicrystal, the Fibonacci chain, as an example. Even though in this paper we have performed the game of life on Penrose tiling projected from the
lattice, for illustration purposes we will show here the one-dimensional crystal projected from the two-dimensional lattice in order to simplify the representation of the cut-and-project method and concepts. We review below some key concepts used by the cut-and-project method and we give a graphic example in
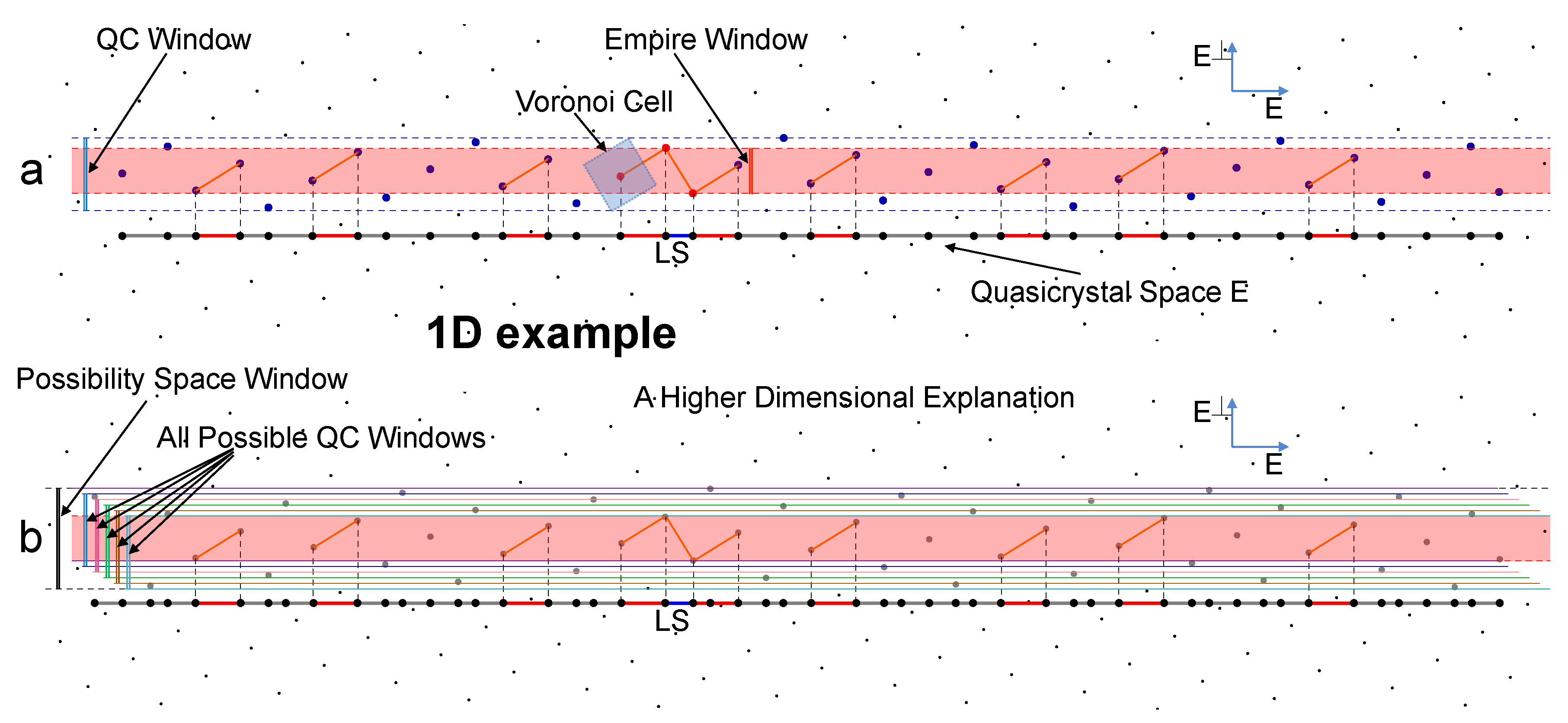
Figure 1 for a simple case, the LS configuration, a vertex type in the Fibonacci chain.
The QC Window/Acceptance Domain
A one-dimensional quasicrystal can be obtained by projection from a two-dimensional lattice. To avoid a dense set, the QC window or acceptance domain is defined in order to select a subset from the two-dimensional lattice. Taking the
lattice as an example, we denote the quasicrystal space as
E and the perpendicular space as
. To select a subset that has uniform distribution, the acceptance domain,
W, is often defined as the projection of the Voronoi cell in
. The blue vertical line shown in
Figure 1a is the QC window. This QC window captures all the
points and edges between the two dashed blue lines and they are projected to the quasicrystal’s space
E as the points and tiles of the 1D quasicrystal, respectively.
The Empire Window
The empire window is defined in relation to a vertex type that covers the mother lattice representation of all the tiles forced by the given vertex type; it is the convex hull of the whole vertex configuration in the mother lattice.
Figure 1a shows the empire window of the labeled LS vertex type, as the red vertical line. This empire window covers all the edges that when projected to
E give the forced tiles of the LS VT. These forced tiles represent the empire of the LS VT.
The Possibility Space Window
For a given vertex type, from the empire window we get the forced tiles. The tiles that are not forced, but are allowed to coexist with a given vertex configuration are covered by the possibility space window. By definition, the possibility space window is the union of all possible QC windows that cover the empire window. For the LS vertex type, this is shown as the black vertical line in
Figure 1b. Each tile covered by this window is just one possible way to tile that part of
E, and therefore it overlaps with other possibilities. These tiles form (shape) the possibility space of the LS vertex type.
Thus, both the empire (forced tiles) and the possibility space (possible tiles) are non-locally determined by the chosen vertex patch, or the chosen local patch, making them perfect tools in modeling the non-local interactions between quasiparticles.
3. Rules of Life
To develop a non-local game of life movement in Penrose tiling, a 2D quasicrystal that can be cut-and-projected from a
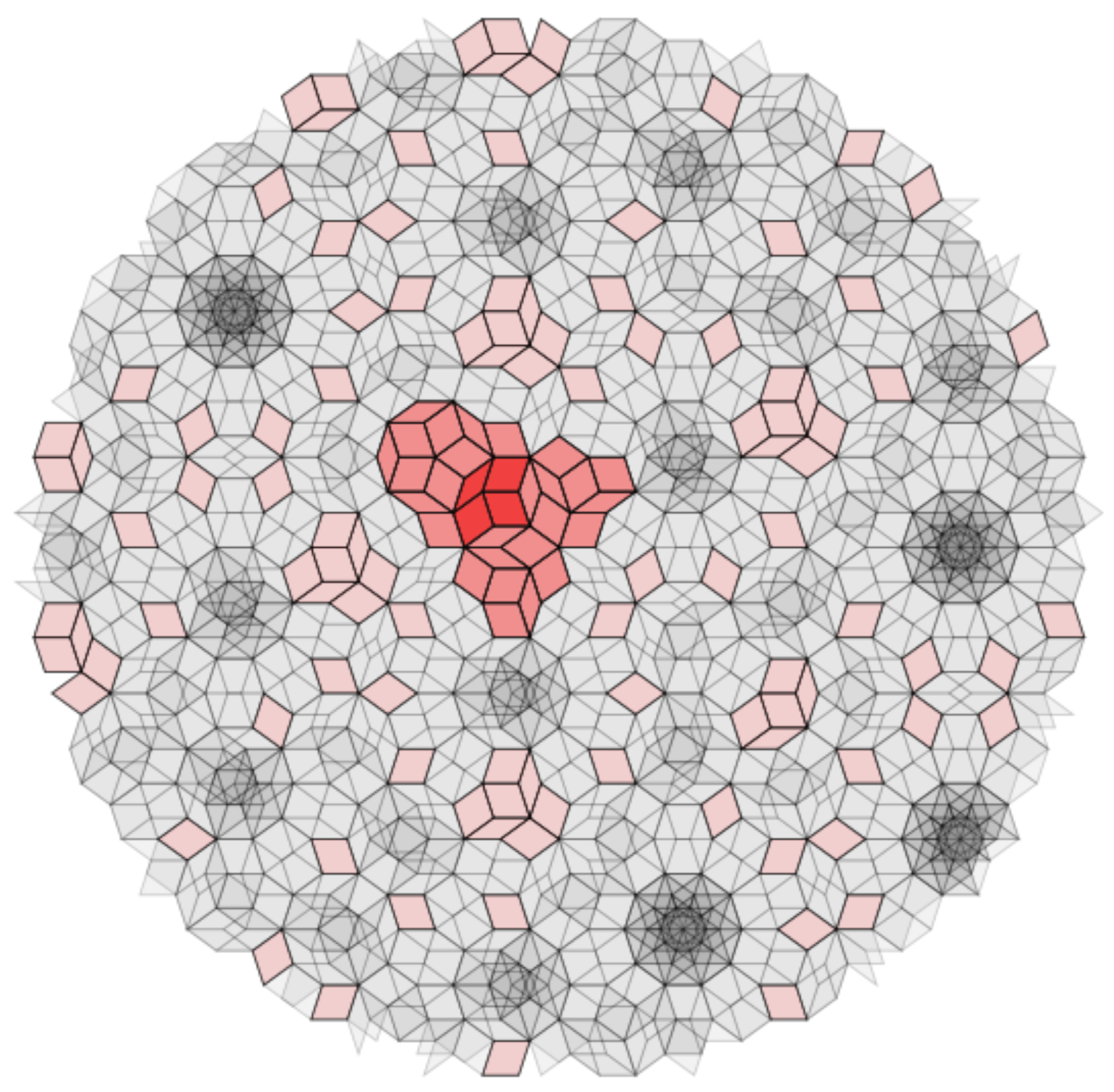
lattice, we consider the movement of the smallest local patches, which consist of all the tiles sharing one vertex. Each quasicrystal has a finite number of possible vertex types. In Penrose tiling there is a total of eight VTs, each of them having its own forced tiles—its own empire field—a disconnected large space (
Figure 2) that can be used to interact with other vertices non-locally.
A vertex patch has a local empire and a non-local empire, as one can see in
Figure 2 for one K vertex [
21,
22]. In Penrose tiling, there are two decagon shaped configurations, one with a five-fold symmetry and one without, the Cartwheel decagon. This decagon configuration has the same local and non-local empire as the K vertex patch shown in
Figure 2. For this first simulation, we have chosen the vertex type isomorphic to the decagon that does not have five-fold symmetry because it allows a larger variety of movement patterns and it has an interesting configuration, being bordered by a star configuration on one side and a sun on the other. The analysis of other vertex types, however, is the subject of our ongoing work. In this study, we select a K vertex/vertex patch as the ‘living’ or dominant vertex/patch. All tiles in the local empire live also inside the empire window, and therefore any local patch that includes K and is included in the local empire would have the same empire field. Hence, the local empire of the chosen K type vertex patch can be treated as part of its quasiparticle, its ‘supporting’ tiles. The rest of the empire, the non-local part, will be considered as the field of the quasiparticle and will be used to calculate its interaction with the environment. The gray tiles shown in
Figure 2 are the tiles that can possibly coexist with the K vertex configuration, forming thus the possibility space.
A vertex patch can only walk to its designated neighboring locations. Since a vertex tends to maintain its identity during its movement, the neighbors of the vertex should be of the same VT. For a living vertex patch we consider two types of movement: translation and rotation. When there is no translational momentum, a vertex patch should rotate as though it has an internal clock. When there is translational momentum, however, the movement is a sequence of rotations of different centers. Due to the discreteness of quasicrystals and the lack of translational periodicity, a vertex patch cannot perform a ‘straight’ walk, tile-by-tile.
While previous studies of cellular automata on nonperiodic grids have considered the classic von Neumann and Moore neighborhoods [
7,
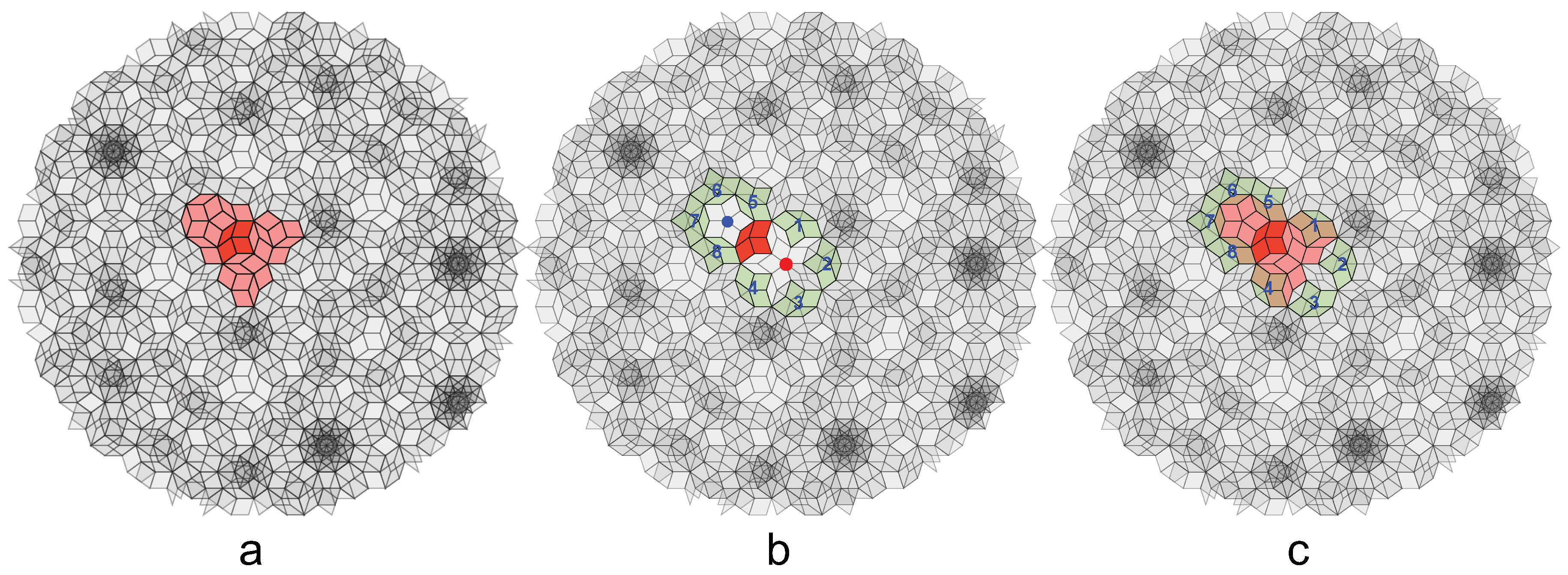
8], we consider the neighborhood to be dictated by the higher dimensional representation, namely the position in the perpendicular space. From the vertex patch’s nearest neighbors in the 2D tiling, we consider only those which are also in the same plane in the perpendicular space. All Penrose tiling vertices are on four planes in the perpendicular space, each plane distribution forming a pentagonal area [
23]. Using this method, the neighbors of the K vertex patch are the eight neighbors shown in
Figure 3b, labeled 1–8. The neighbors around the five-fold star vertex (red point) are labeled from 1 to 4 and the neighbors around the five-fold sun vertex (blue point) are labeled from 5 to 8. Even though it appears the neighbors 2 and 3 are not the closest ones in the 2D tiling, if we look at the nearest neighbors in the perpendicular space, neighbors 2 and 3 are actually closer to the vertex (
Figure 3c). Indeed, all of the eight chosen neighbors are on the same pentagonal area in the perpendicular space, forming two pentagons with the K vertex, as shown in
Figure 4. As a first step, the living vertex patch can walk only to one of the neighbors of the same VT in
Figure 3; the chosen neighbor will become a living vertex patch once that step is taken.
For the dynamic advancement of the quasiparticle in our game of life model, we employ the following general rules:
Intrinsic rotation: A living vertex patch never stays in a fixed location for two consecutive outputs—frames. Depending on its intrinsic properties, it will perform either a clockwise (to neighbors 1, 2, 3 or 4) or a counterclockwise rotation (to neighbors 5, 6, 7, 8), rotation that we refer to as an intrinsic clock.
Least change principle: In our game of life algorithm, the chosen general rule by which the quasiparticle moves is based on the least change principle, which states that the preferred path is the path where the number of tiles in the empire field that are required to change as a result of that move, is minimal. According to the least change principle, gliders move forward following a maximum trits-saving path, where trits, or bits in the 2D case, refer to the number of tiles changed during the motion. That is, each timestep the particle will take the path that causes the least ‘amount’ of change in the empire field, while it cannot stay in the same position for two consecutive timesteps. In the higher dimensional approach, in which the shift of the cut window is guided by the empire window and the possibility space window in the higher dimensional mother lattice, the ‘trits’ correspond to the number of shifts of the cut window. For example, let us define to be the union of the empire of all existing dominant vertices, to be the empire of the neighboring vertex, and . If is the maximum of the list of , then the neighbor will be the preferred dominant vertex in the next frame. If there is more than one maximum of the list, then a random choice will be made between the two maxima for the next step of the dominant vertex.
With these two rules, our game of life ensures first a continuous motion of our quasiparticles as well as a syntactical freedom present in the code, for the case in which the particle is guided by a random choice, resulting in a non-deterministic path for the quasiparticle.
For the self-interaction case, however, besides modeling the ‘least change’ walk, we have also modeled several scenarios in which we force the particle’s first step to be in the direction of one of the neighbors or a sequence of two of the neighbors, in order to explore different moving patterns and trajectories. In this case, choosing a vertex without five-fold symmetry allows for various moving patterns.
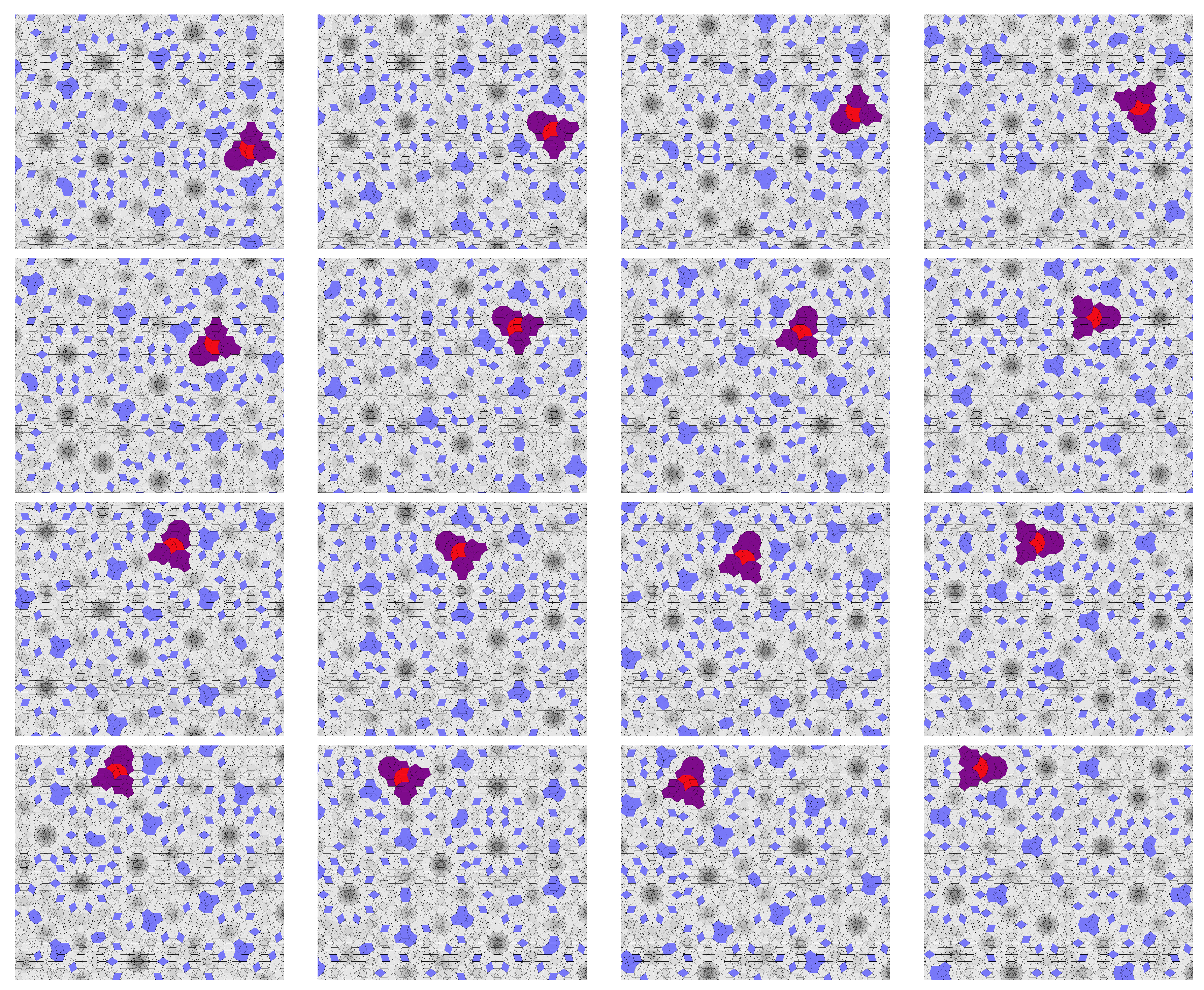
4. Walks of Life
In this Section we present the results, first for one quasiparticle, corresponding to the K VT, in several possible dynamic scenarios of self-interactions, followed by the case of two quasiparticles with their interacting empire fields. As previously mentioned, the quasiparticle moves under the influence of its non-local empire and possibility space, following the least change principle, if not instructed otherwise. For the two-particle interactions, there is one extra factor that influences the movement: the initial configuration, the distance between the particles and the initial positions-orientation with respect to each other (see
Supplementary Materials section).
4.1. Solo Walk
First we applied the algorithm to a single living vertex patch, which can only interact with its own empire field, such that when computing the
, we use only the empire of that vertex patch as the
. The vertex patch is shown in
Figure 3 and several scenarios are analyzed, depending on the choices made between the neighbors. The most ‘efficient’ walk, with respect to the principle of least change, implies two equal choices between the
and the
neighbors and it is shown in
Figure 5. The pattern of the walk will then be determined by the choices made between these two neighbors. Other moving patterns are described below:
Rotations: Several initial conditions, determined by the choice of the first steps between the neighbors, give a rotation pattern. Choosing the neighbors 1–2 results in the quasiparticle having a clockwise rotation around a configuration of tiles (situated between 2 and 3), as can be seen in the movie at
https://youtu.be/HjvJEs_kUxU. Choosing the neighbors 3–4 gives the same rotation, but counterclockwise. Choosing the 3–8 neighbors, the quasiparticle rotates around a circular configuration of tiles, tangent to one of the particle’s tiles. The minimum area covered by rotation is achieved when only the neighbor 8 is chosen, while the maximum area covered by rotation is achieved for 3–6.
Quasi-translation: When choosing the sequence 4–8, the quasiparticle has the closest path to straight gliding, a quasi-translation movement (
https://youtu.be/fJT40Ec3ejE, e.g.).
Oscillations: When the steps are chosen to alternate between 5 and 8 or an equal sequence of 5s and 8s, an oscillation pattern results, as shown in the movie at
https://youtu.be/tq3pkKI4-3Y.
Random Walks: We have also performed simulations where the steps are chosen between the neighbors by a random number generator for each step. A special case of random walk, where between two neighbors, 5 and 8, for example, the choice was randomly made each step, was also performed.
Combined Motion: Most of the other choices of neighbors result in a combination of translation and rotation, like in the example displayed in the movie at
https://youtu.be/_LvJudfJq7s.
It is important to point out that as the living vertex patch walks to its neighbor in the possibility space, both the empire and the entire possibility space will change and update their positions from frame to frame. Therefore, the tiling background space does not remain fixed, but is in dynamic mode, showing that any self-interaction of the quasiparticles instantly changes the environment at infinite distance, step-by-step.
4.2. Two to Tango
When two or more living vertices are present, each dominant vertex patch can walk to one of its eight neighbors, following the least change principle. In this case, the
is the union of the empires of all dominant vertices. As a separate rule, we also restrict the movement of the quasiparticles by not allowing their local empires to overlap. For the case of two vertex patches, depending on the initial conditions, meaning the position and orientation of the particles with respect to each other, the two quasiparticles will eventually evolve into a stable oscillation or rotation pattern, as shown in
Figure 6. For one of the stable patterns (
Figure 6a), the dynamical evolution is shown in the movie at
https://youtu.be/L1KPckojco4. For a different initial configuration, where the local empires briefly overlap in the first timesteps, the particles still get locked in a quasi-stable motion (
Figure 6c), as can be seen in the movie at
https://youtu.be/5FCJWayzDfY from which several detailed steps are shown in
Figure 7.
5. The End Game—Discussions and Outlook
In this paper we present the results of the first non-local game of life in 2D quasicrystals. Using the Penrose tiling, we model and track the dynamical behavior of a vertex configuration belonging to the K VT based on its non-local empire field, following a newly developed algorithm.
Considering a quasiparticle composed by the emperor (vertex patch) and its local empire, for a K vertex type, which is projected from a higher dimensional lattice and which does not present five-fold symmetry, we analyze the quasiparticle’s self-interaction with its non-local empire field in various scenarios. We choose the neighbors of the quasiparticle to be the ones that are the closest to the vertex patch in 2D and also on the same plane in the perpendicular space. These are the K type vertex patches where the living vertex patch can move, the ones that can become alive once the movement is made. Depending on which one of these neighbors is chosen for the first steps movements, we find that a particle can rotate, oscillate or move in a quasi-translation pattern in the possibility space. The most ‘efficient’ walk, subjected to the least change principle rule, engages both rotation and forward movement. The choice between two equally efficient steps is made by a random hinge variable, resulting in an unpredictable path for the particle. Since the non-local empire changes with the change in the particle’s position each step, so does the possibility space, creating a mutual influence between the particle and its field on one hand and the possibility space, the environment, on the other. This influence propagates instantly and at all distances. Indeed, after one step, the possibility space changes because of the change in the empire field. As a consequence, for the next step, the movement is restricted depending on the new spatial configuration, creating a feedback loop of influence.
Furthermore, we explore the interactions between two quasiparticles of the same vertex type, considering a scenario in which the overlapping of their local empires is forbidden. We find that depending again on the choice of the initial conditions, the particles eventually end up bound in a ‘dance’, either in oscillation-like patterns or coupled rotations.
While this is purely a game of life algorithm applied to one vertex type on a 2D quasicrystal, these explorations can prove of extreme importance to the field of particles physics, having as the end game the first principles explanation of the observed particle physics rich phenomenology. Indeed, gauge theory and group theory have been used extensively in describing algebraically the standard model of particle physics. Several attempts of connecting the geometry with the algebra have also been made [
24,
25,
26,
27]. Symmetries corresponding to higher dimensional lattices, like
, have been studied in the context of grand unified theories [
28,
29]. From our preliminary results, we can draw some general parallels with results from the particle physics and quantum field theories, but these connections remain open to further exploration and constitute the subject of future planned research.
Firstly, in the quantum field theory, a particle and its field are considered ‘interchangeable’, in the sense in which the interaction of particles with the spacetime itself creates a field. In a similar manner, for a discretized space configuration, a vertex configuration projected from a higher lattice has a large empire, which acts as a field. Any change in the position of a quasiparticle exerts an influence at all distances, not only on the particle’s own field, but also on the aperiodic grid itself. Because of the forbidden symmetries of quasicrystals, only certain configurations can be found in projection, constraining perhaps the symmetries allowed in nature.
Our next goal is performing similar studies for several vertex types, analyzing also the interactions between quasiparticles with different vertex configurations in both 2D and 3D quasicrystals, while also varying the rules assumed. For example, when allowing the local empires to overlap, depending on the initial conditions, two quasiparticles can collide and the interacting vertex patches are expected to merge into configurations corresponding to other vertex types. Furthermore, the overlaps of empires correspond to local deflations in the tiling space or local curvatures in the QC window. As a next step, we intend to model many particle interactions, using this uneven distribution as a source of interaction forces between particles and to simulate the game of life based on the least action principle.
This study bridges several fields of physics, from high dimensional representations to quasicrystal math, phason dynamics and particle phenomenology, and opens a new avenue of research with multiple ramifications.