Evolution of Spin-Crossover Transition in Hybrid Crystals Involving Cationic Iron Complexes [Fe(III)(3-OMesal2-trien)]+ and Anionic Gold Bis(dithiolene) Complexes Au(dmit)2 and Au(dddt)2
Abstract
:1. Introduction
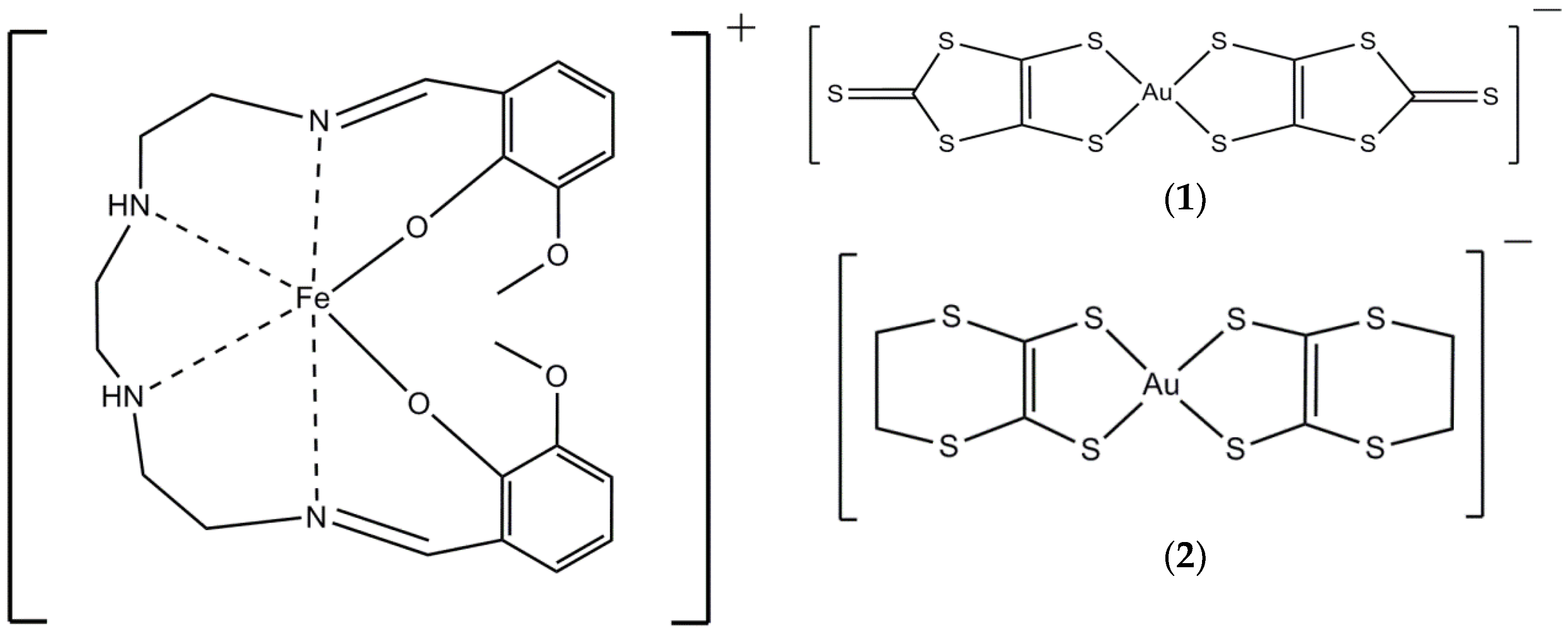
2. Results and Discussion
2.1. Synthesis
2.1.1. [Fe(3-OMesal2-trien)][Au(dmit)2] (1)
2.1.2. [Fe(3-OMesal2-trien)][Au(dddt)2]·CH3CN (2)
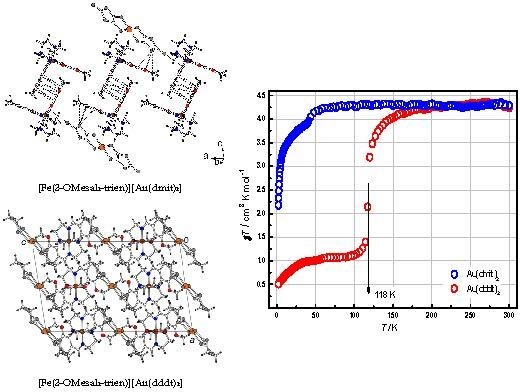
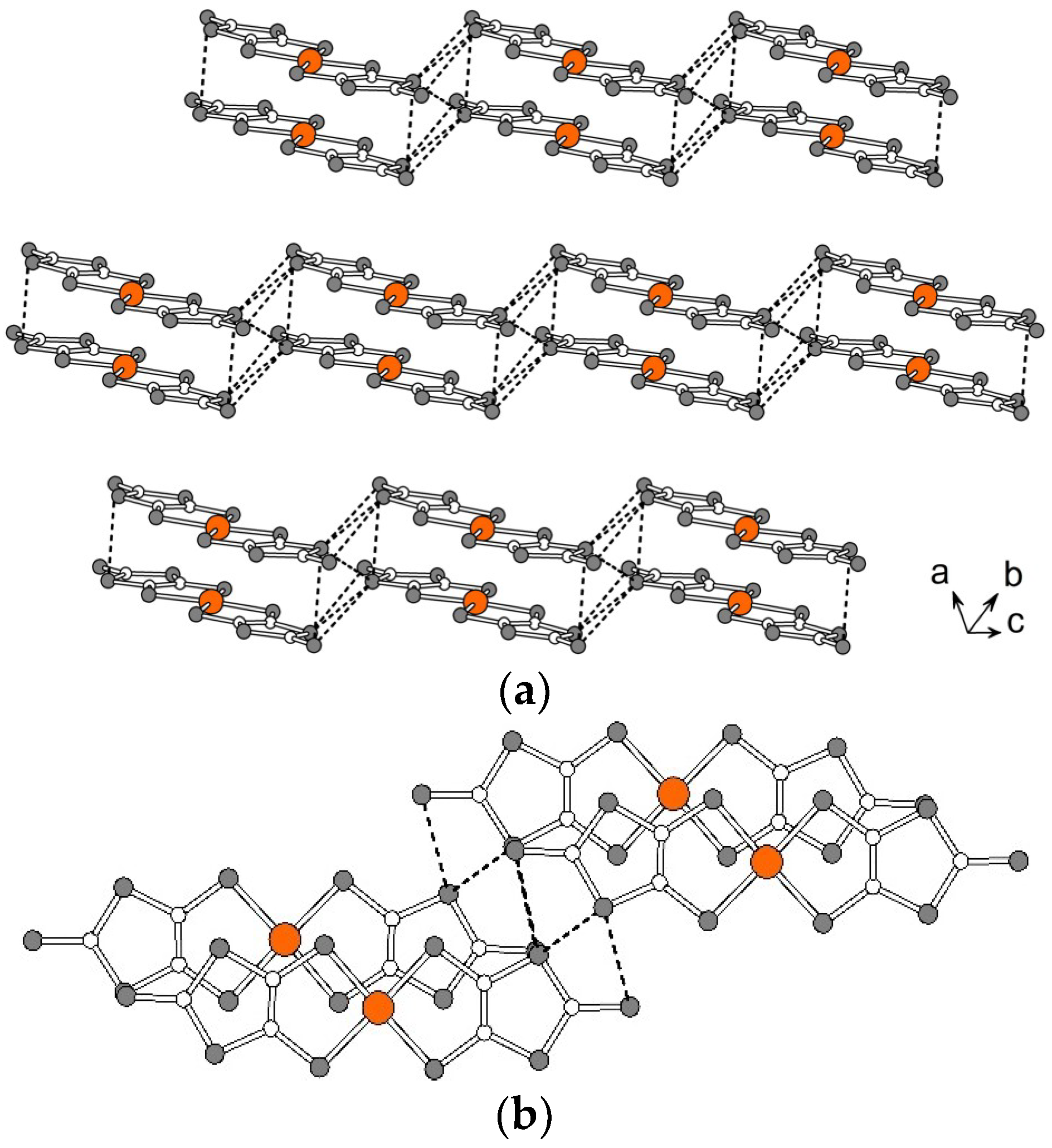
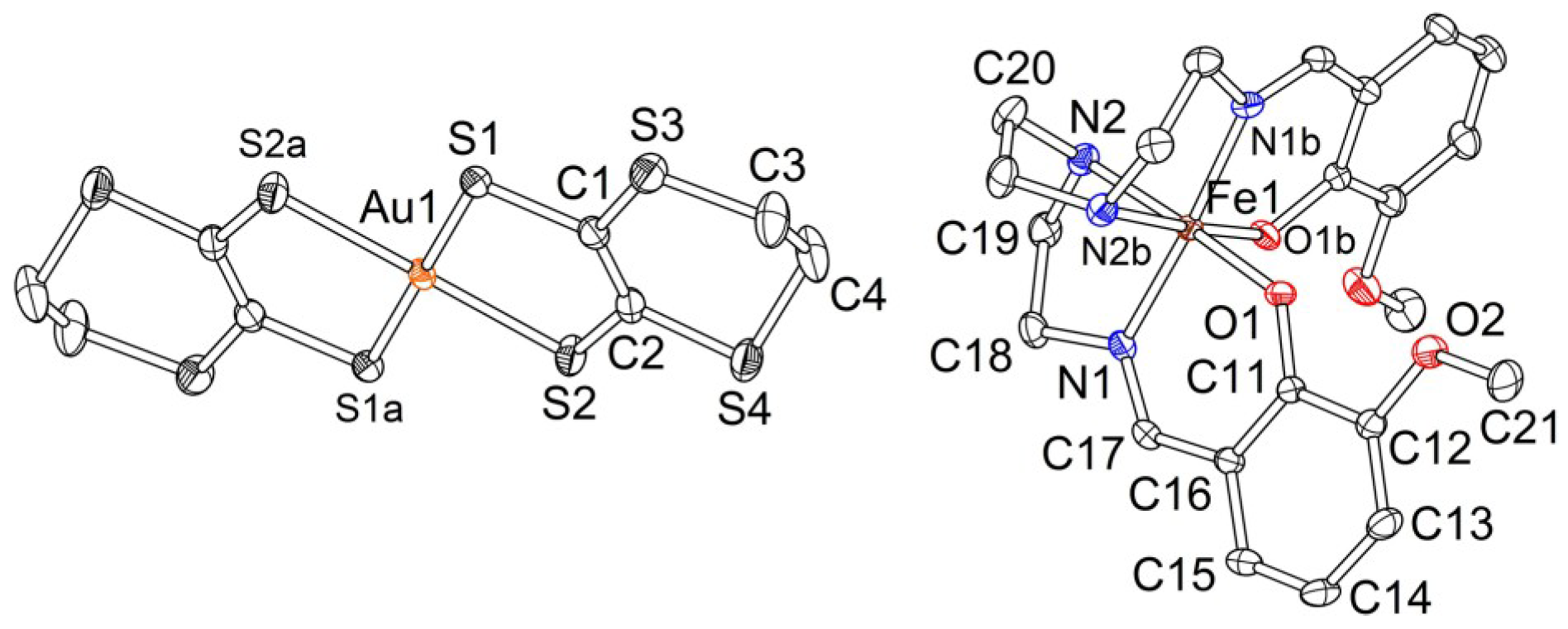
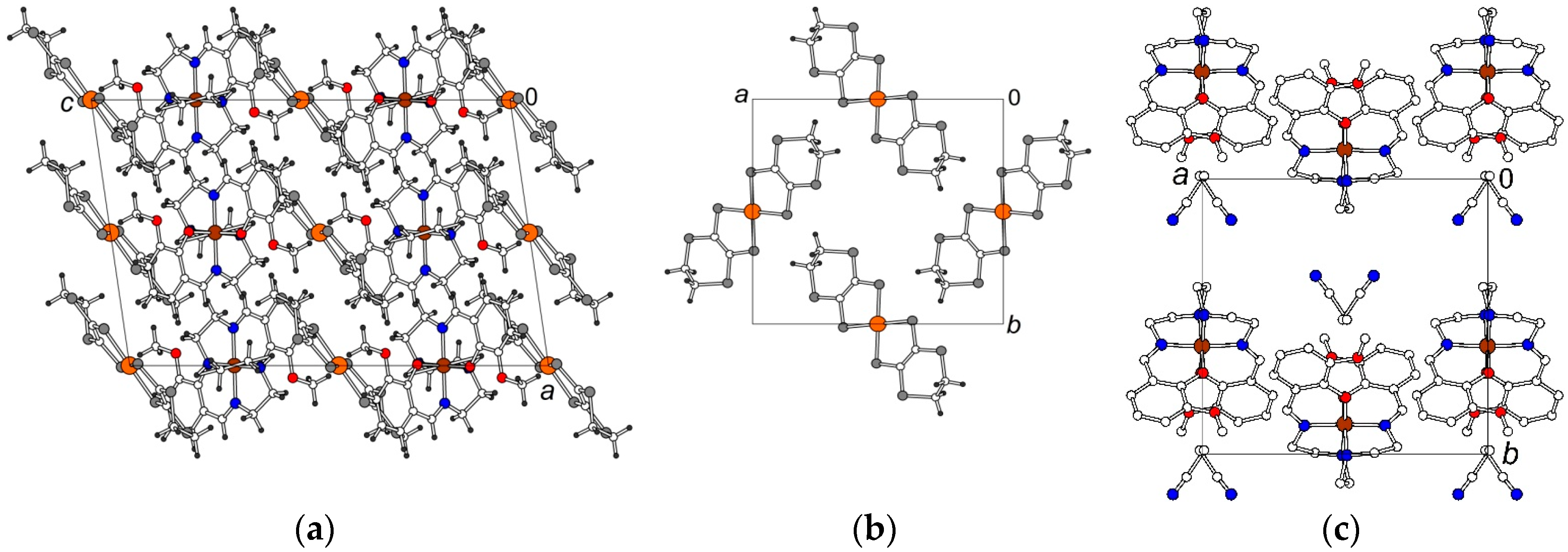
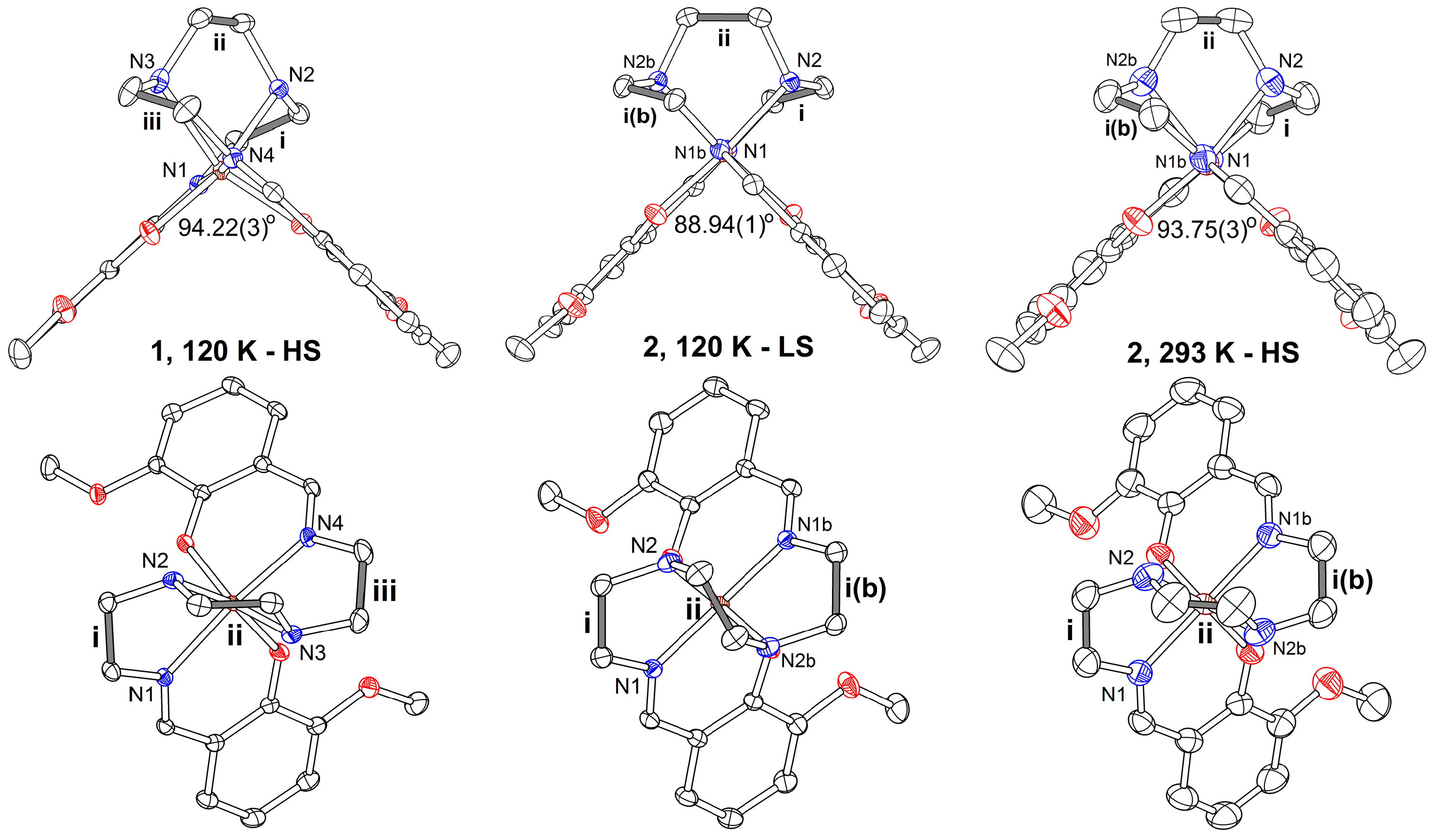
2.2. Crystal Structures
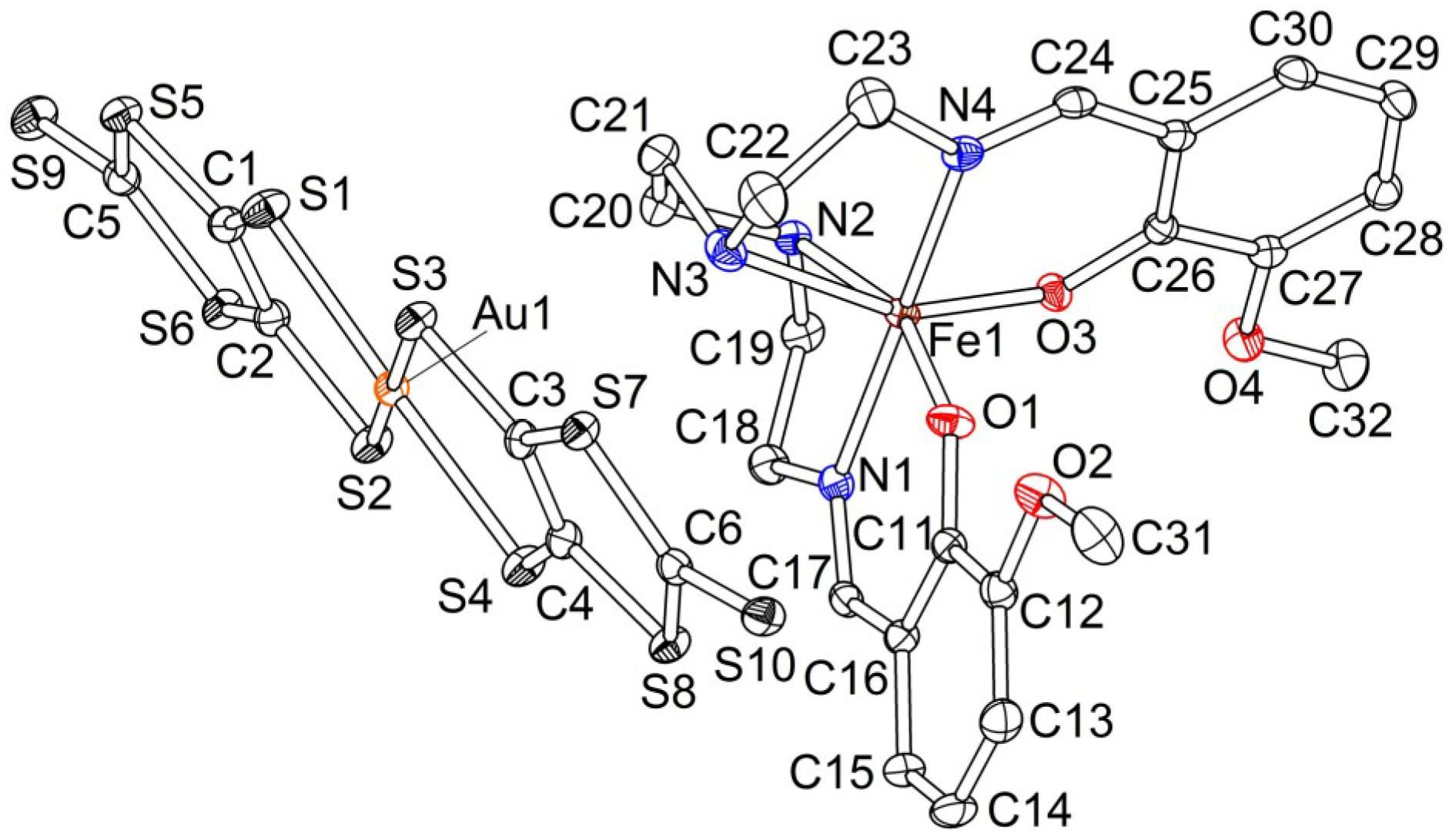
2.2.1. [Fe(III)(3-OMesal2-trien)] [Au(dmit)2] (1)
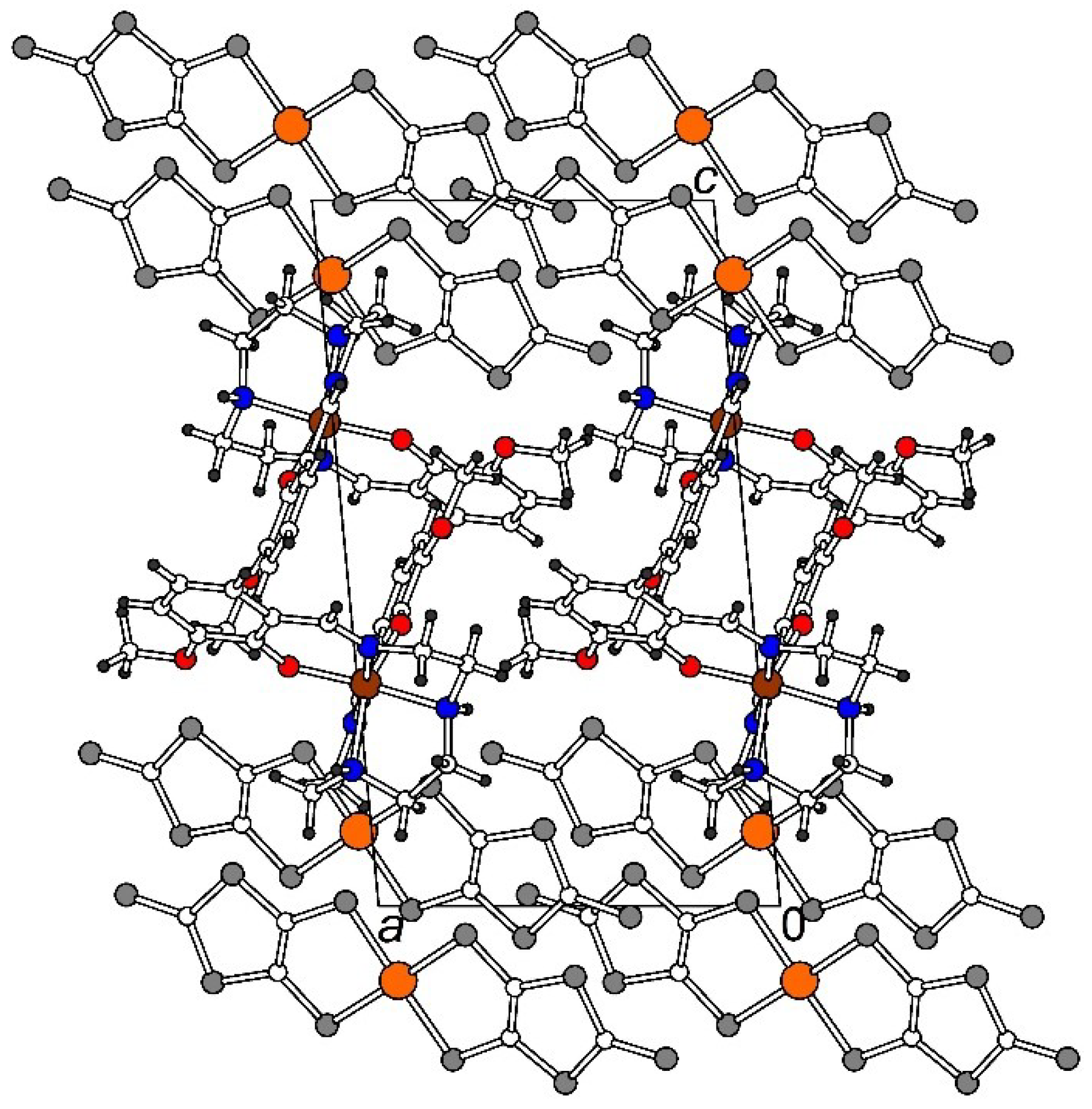
2.2.2. [Fe(3-OMesal2-trien)][Au(dddt)2]·CH3CN (2)
2.3. Conductivity.
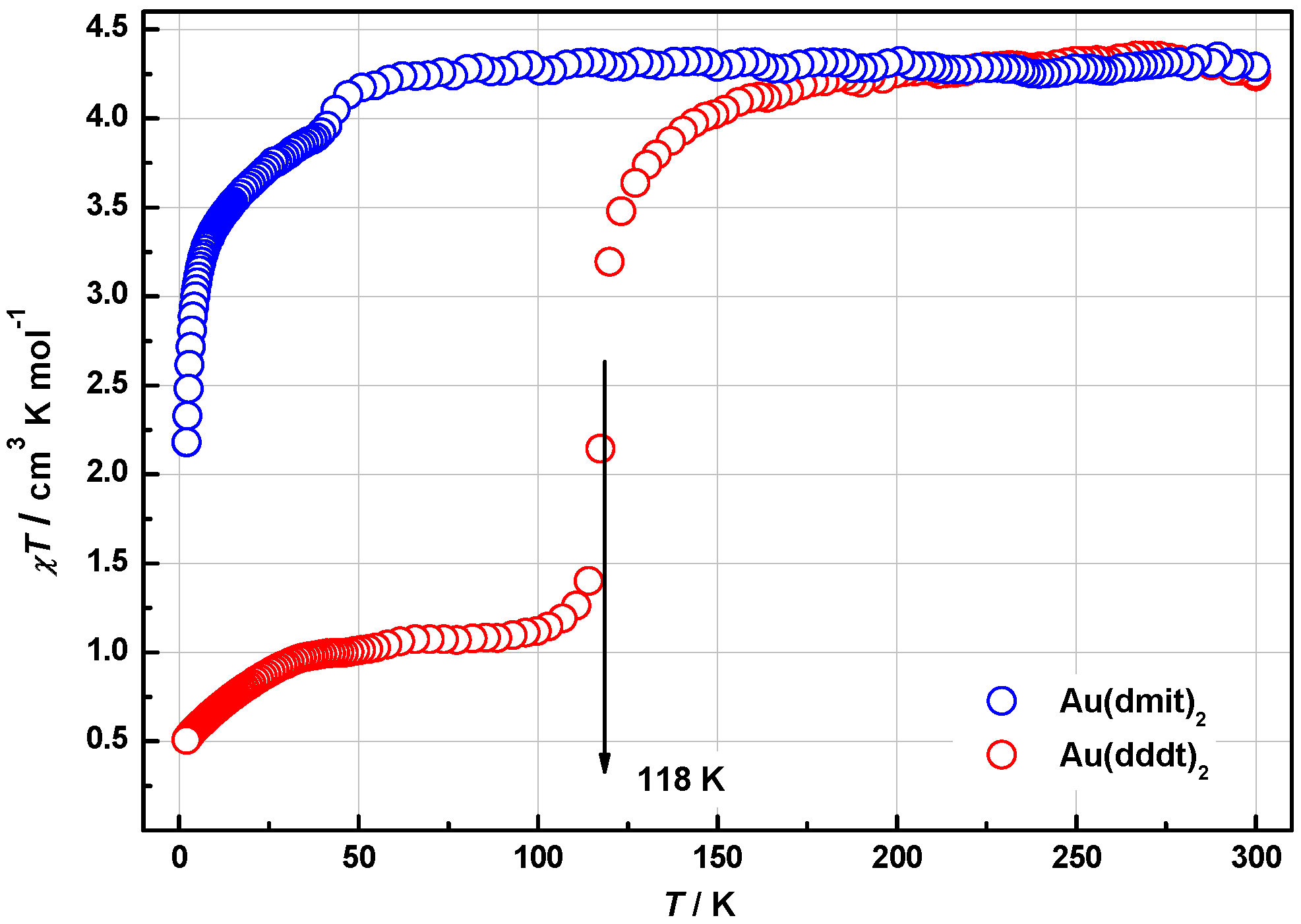
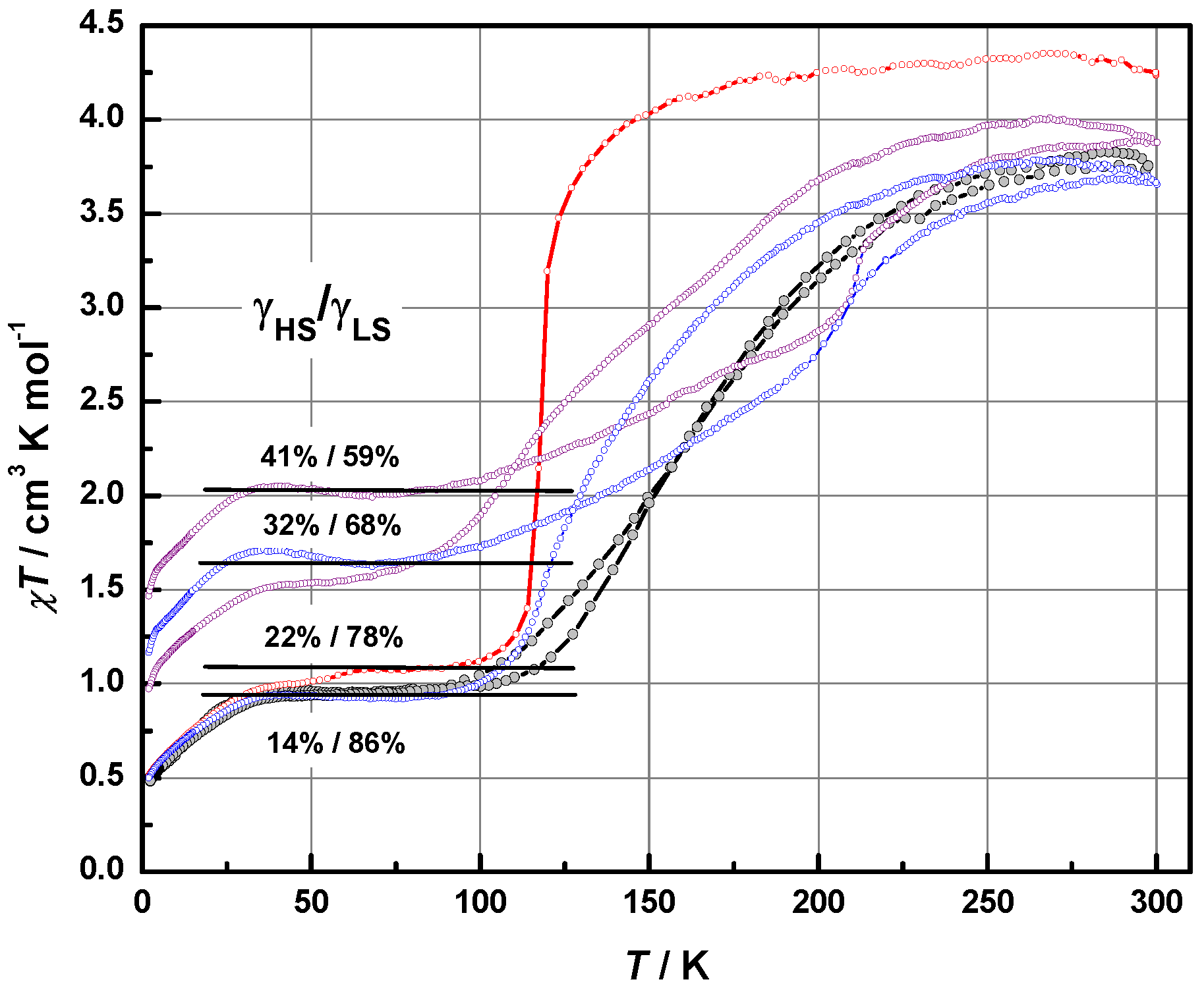
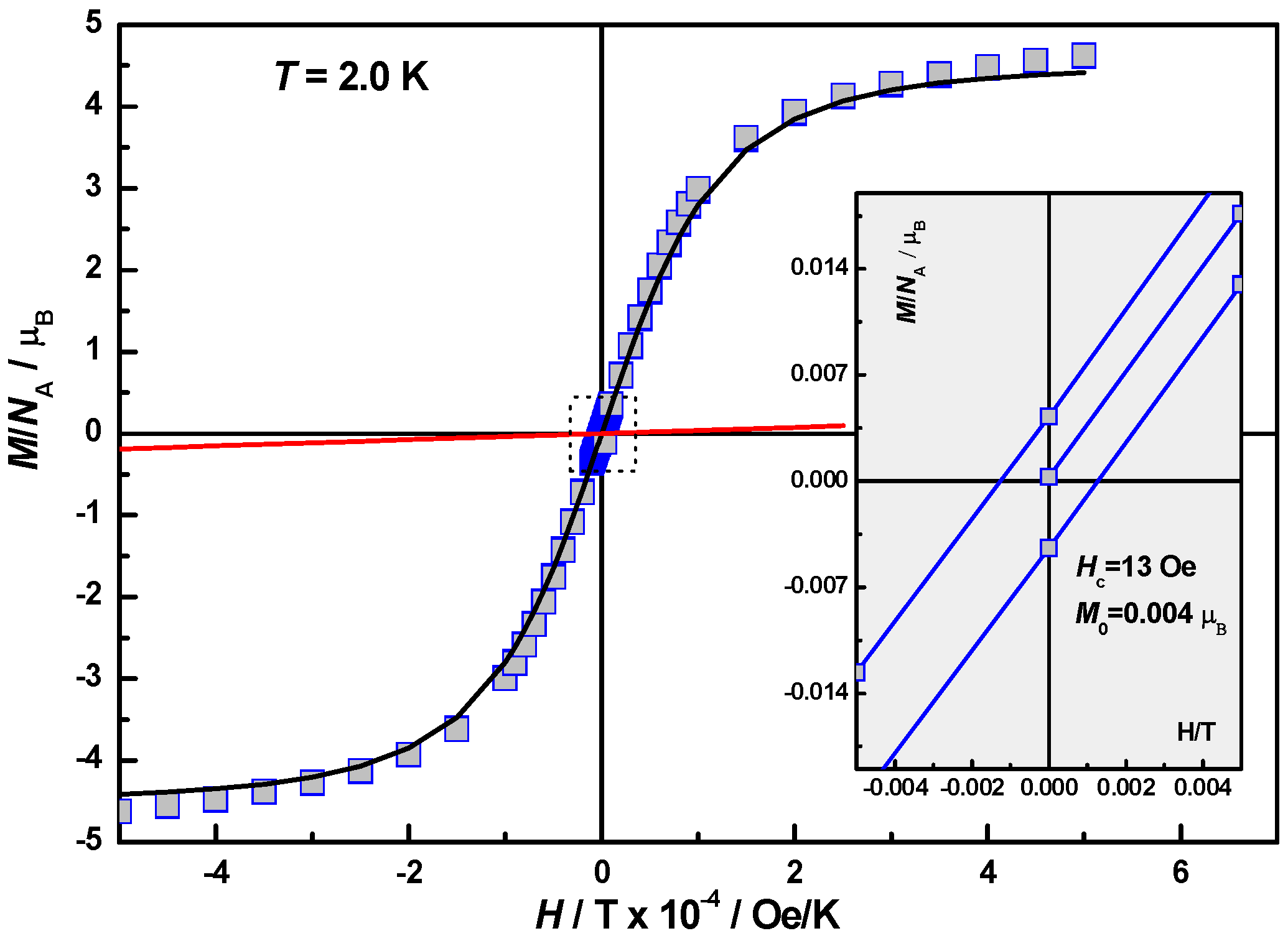
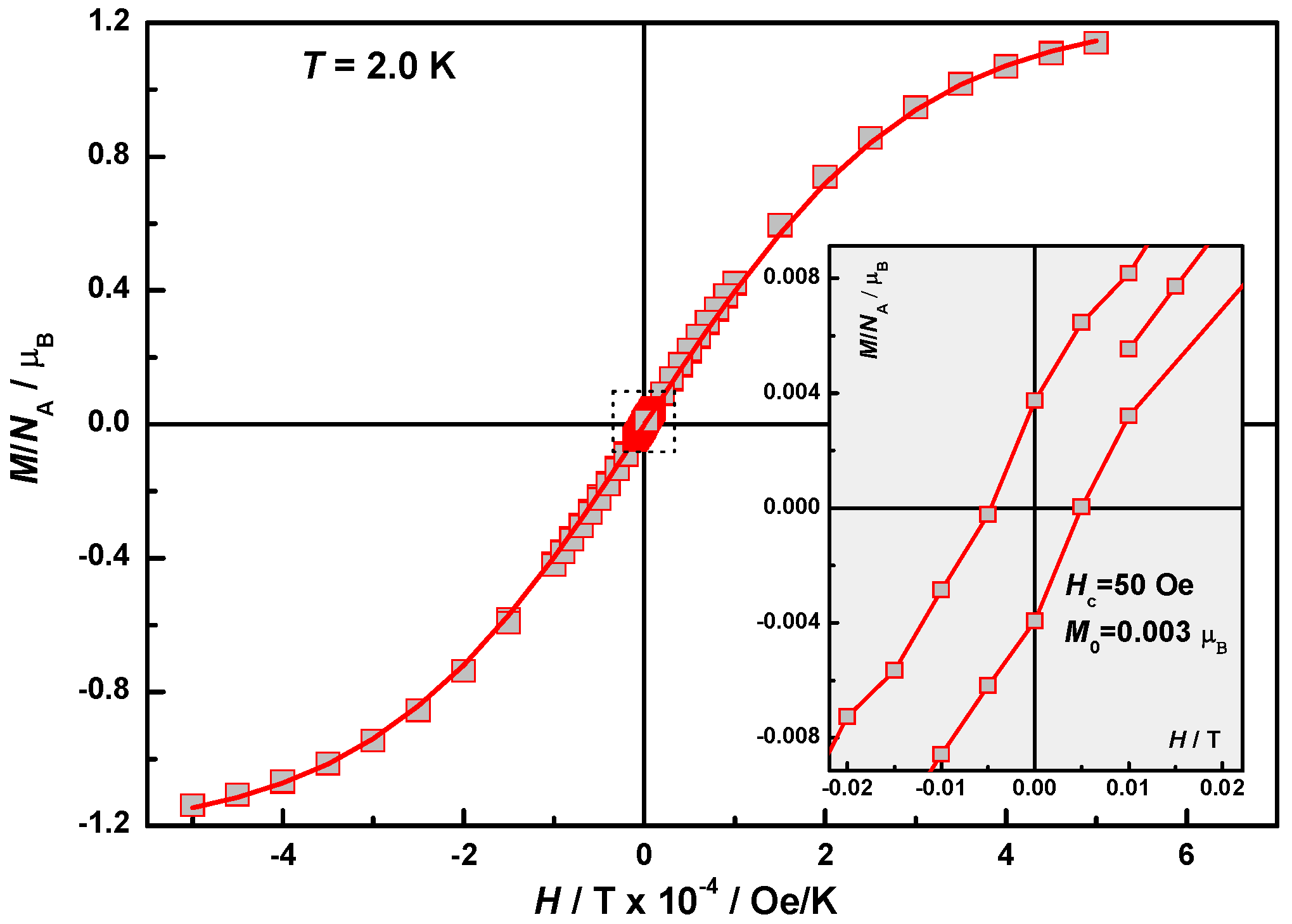
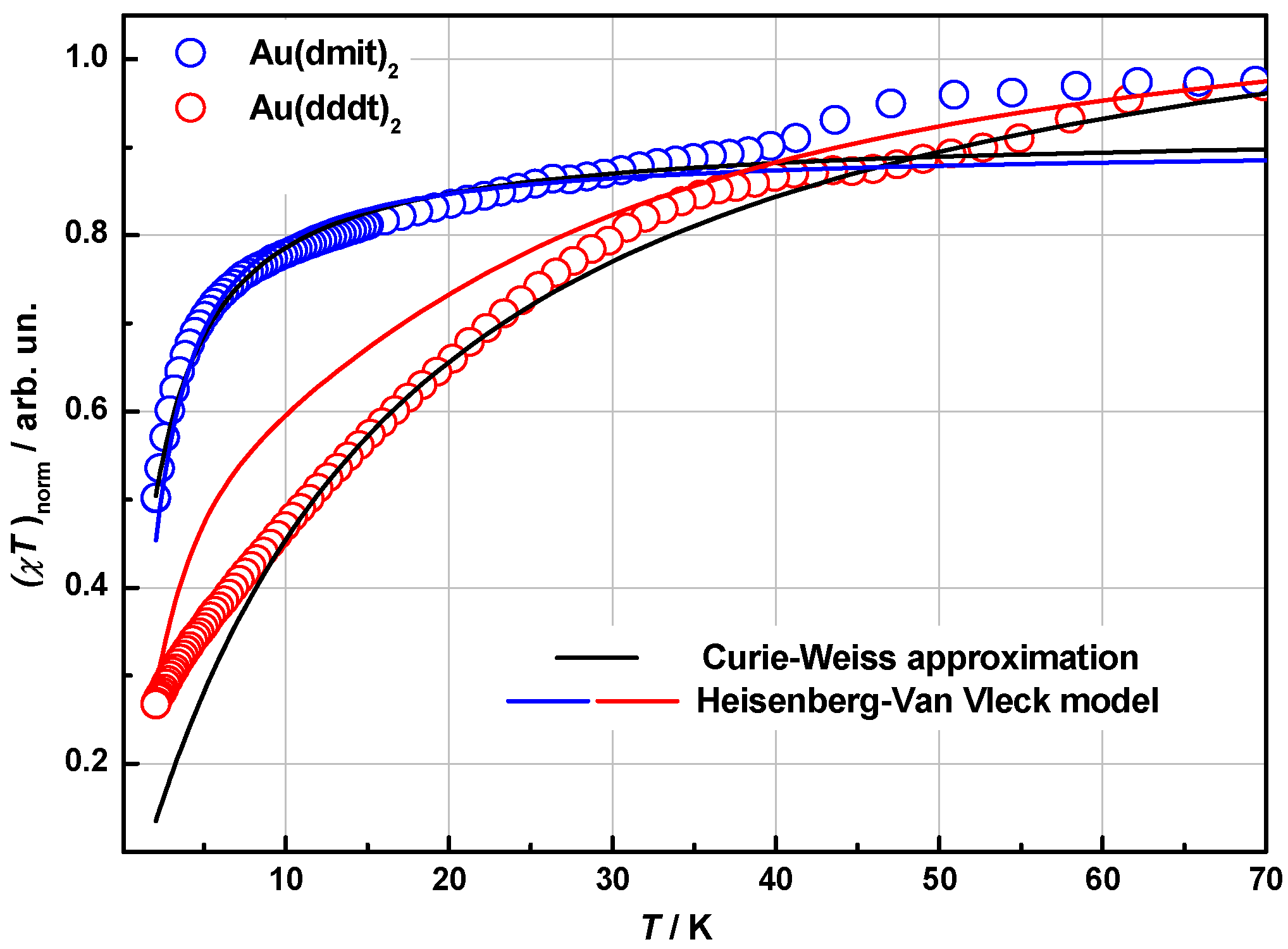
2.4. Magnetic Properties
3. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gutlich, P.; Goodwin, A.H. Spin Crossover in Transition Metal Compounds III; Springerlink: Berlin, Germany, 2004; Volume 235, p. 1. [Google Scholar]
- Brooker, S. Spin-crossover with thermal hysteresis: Practicalities and lessons learnt. Chem. Soc. Rev. 2015, 44, 2880–2892. [Google Scholar] [CrossRef] [PubMed]
- Gutlich, P. Spin Crossover—Quo Vadis? Eur. J. Inorg. Chem. 2013, 5–6, 581–591. [Google Scholar] [CrossRef]
- Okai, M.; Takahashi, K.; Sakurai, T.; Ohta, H.; Yamamoto, T.; Einagad, Y. Novel Fe(II) spin crossover complexes involving a chalcogen-bond and π-stacking interactions with a paramagnetic and nonmagnetic M(dmit)2 anion (M = Ni, Au; dmit = 4,5-dithiolato-1,3-dithiole-2-thione). J. Mater. Chem. C 2015, 3, 7858–7864. [Google Scholar] [CrossRef]
- Bousseksou, A.; Molnár, G.; Salmon, L.; Nicolazzi, W. Molecular spin crossover phenomenon: Recent achievements and prospects. Chem. Soc. Rev. 2011, 40, 3313–3335. [Google Scholar] [CrossRef] [PubMed]
- Gentili, D.; Demitri, N.; Schäfer, B.; Liscio, F.; Bergenti, I.; Ruani, G.; Ruben, M.; Cavallini, M. Multi-modal sensing in spin crossover compounds. J. Mater. Chem. C 2015, 3, 7836–7844. [Google Scholar] [CrossRef]
- Sato, O.; Li, Z.-Y.; Yao, Z.-S.; Kang, S.; Kanegawa, S. Multifunctional materials combining spin-crossover with conductivity and magnetic ordering. In Spin-Crossover Materials: Properties and Applications; Halcrow, M., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 303–319. [Google Scholar]
- Valade, L.; Malfant, I.; Faulmann, C. Toward bifunctional materials with conducting, photochromic, and spin crossover properties. In Multifunctional Molecular Materials; Ouahab, L., Ed.; Pan Stanford Publishing: Singapore, 2013; p. 149. [Google Scholar]
- Huang, J.; Xie, R.; Wang, W.; Li, Q.; Yang, J. Coherent transport through spin-crossover magnet Fe2 complexes. Nanoscale 2016, 8, 609–616. [Google Scholar] [CrossRef] [PubMed]
- Kato, R. Conducting metal dithiolene complexes: Structural and electronic properties. Chem. Rev. 2004, 104, 5319–5346. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.H.; Fox, S.B.; Yagubskii, E.B.; Kushch, L.A.; Kotov, A.I.; Whangbo, M.-H. Direct observation of the electron-donating property of the 5,6-dihydro-1,4-dithiin-2,3-dithiolate (dddt) ligands in square planar M(dddt)2 complexes (M = Ni, Pd, Pt, and Au). J. Am. Chem. Soc. 1997, 119, 7601–7602. [Google Scholar] [CrossRef]
- Yagubski, E.B. Molecular conductors based on M(dddt)2 bisdithiolene cation complexes. J. Solid State Chem. 2002, 168, 464–469. [Google Scholar] [CrossRef]
- Fujiyama, S.; Kato, R. Algebraic charge dynamics of the quantum spin liquid β-EtMe3Sb[Pd(dmit)2]2. Phys. Rev. B 2018, 97, 035131. [Google Scholar] [CrossRef]
- Shvachko, Y.N.; Starichenko, D.V.; Korolyov, A.V.; Kotov, A.I.; Buravov, L.I.; Zverev, V.N.; Simonov, S.V.; Zorina, L.V.; Yagubskii, E.B. The highly conducting spin-crossover compound combining Fe(III) cation complex with TCNQ in a fractional reduction state. Synthesis, structure, electric and magnetic properties. Magnetochemistry 2017, 3, 9. [Google Scholar] [CrossRef]
- Shvachko, Y.N.; Starichenko, D.V.; Korolyov, A.V.; Yagubskii, E.B.; Kotov, A.I.; Buravov, L.I.; Lyssenko, K.A.; Zverev, V.N.; Simonov, S.V.; Zorina, L.V.; et al. The conducting spin-crossover compound combining Fe(II) cation complex with TCNQ in a fractional reduction state. Inorg. Chem. 2016, 55, 9121–9130. [Google Scholar] [CrossRef] [PubMed]
- Phan, H.; Benjamin, S.M.; Steven, E.; Brooks, J.S.; Shatruk, M. Photomagnetic response in highly conductive iron(II) spin-crossover complexes with TCNQ radicals. Angew. Chem. Int. Ed. 2015, 127, 837–841. [Google Scholar] [CrossRef]
- Takahashi, K.; Cui, H.-B.; Okano, Y.; Kobayashi, H.; Einaga, Y.; Sato, O. Electrical conductivity modulation coupled to a high-spin–low-spin conversion in the molecular system [FeIII(qsal)2][Ni(dmit)2]3 CH3CN H2O. Inorg. Chem. 2006, 45, 5739–5741. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Cui, H.-B.; Okano, Y.; Kobayashi, H.; Mori, H.; Tajima, H.; Einaga, Y.; Sato, O. Evidence of the chemical uniaxial strain effect on electrical conductivity in the spin-crossover conducting molecular system: [FeIII(qnal)2][Pd(dmit)2]5 acetone. J. Amer. Chem. Soc. 2008, 130, 6688–6689. [Google Scholar] [CrossRef] [PubMed]
- Dorbes, S.; Valade, L.; Real, J.A.; Faulmann, C. [Fe(sal2-trien)][Ni(dmit)2]: Towards switchable spin crossover molecular conductors. Chem. Commun. 2005, 1, 69–71. [Google Scholar] [CrossRef] [PubMed]
- Coronado, E.; Gimenez-Lopez, M.C.; Gimenez-Saiz, C.; Romero, F.M. Spin crossover complexes as building units of hydrogen-bonded nanoporous structures. CrystEngComm 2009, 11, 2198–2203. [Google Scholar] [CrossRef]
- Steimecke, G.; Sieler, H.-J.; Kirmse, R.; Houer, E. 1.3-dithiol-2-thion-4.5 ditholat aus schwefelkohlenstoff und alkalimetall. Phosphorus Sulfur Silicon Relat. Elem. 1979, 7, 49–55. [Google Scholar] [CrossRef]
- Kirmse, R.; Stach, J.; Dietzsch, W.; Steimecke, G.; Hoyer, E. Single-crystal EPR studies on nickel(III), palladium(III), and platinum(III) dithiolene chelates containing the ligands isotrithionedithiolate, o-xylenedithiolate, and maleonitriledithiolate. Inorg. Chem. 1980, 19, 2679–2685. [Google Scholar] [CrossRef]
- Nweedle, M.F.; Wilson, L.J. Variable spin iron(III) chelates with hexadentate ligands derived from triethylenetetramine and various salicylaldehydes. Synthesis, characterization, and solution state studies of a new 2T-6A spin equilibrium system. J. Am. Chem. Soc. 1976, 98, 4824–4834. [Google Scholar]
- Halcrow, M.A. Structure: Functional relationship in molecular spin-crossover complexes. Chem. Soc. Rev. 2011, 40, 4119–4142. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, R.; Barrett, S.A.; Kilner, C.A.; Halcrow, M.A. The influence of ligand conformation on the thermal spin transitions in iron(III) saltrien complexes. Dalton Trans. 2008, 3159–3168. [Google Scholar] [CrossRef] [PubMed]
- Blagov, M.A.; Krapivin, V.B.; Simonov, S.V.; Spitsyna, N.G. Insights into the influence of ethylene groups orientation on iron (III) spin state in the spin crossover complex [FeIII(Sal2-trien)]+. Dalton Trans. 2018. submitted. [Google Scholar]
- Benelli, C.; Gatteschi, D. Introduction to Molecular Magnetism: From Transition Metals to Lanthanides; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2015. [Google Scholar]
- Faulmann, C.; Szilágyi, P.; Jacob, K.; Shahene, J.; Valade, L. Polymorphism and its effects on the magnetic behaviour of the [Fe(sal2-trien)][Ni(dmit)2] spin-crossover complex. New J. Chem. 2009, 33, 1268–1276. [Google Scholar] [CrossRef]
- Faulmann, C.; Dorbes, S.; Real, J.; Valade, L. Electrical conductivity and spin crossover: Towards the first achievement with a metal bis dithiolene complex. J. Low Temp. Phys. 2006, 142, 265–270. [Google Scholar]
- Faulmann, C.; Jacob, K.; Dorbes, S.; Lampert, S.; Malfant, I.; Doublet, M.-L.; Valade, L.; Real, J. Electrical conductivity and spin crossover: A new achievement with a metal bis dithiolene complex. Inorg. Chem. 2007, 46, 8548–8559. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Liu, M.-J.; Liu, C.-M.; Kou, H.-Z. Iron(III) complexes of 2-methyl-6-(pyrimidin-2-yl-hydrazonomethyl)-phenol as spin-crossover molecular materials. Dalton Trans. 2017, 46, 16562–16569. [Google Scholar] [CrossRef] [PubMed]
- Milin, E.; Benaicha, B.; El Hajj, F.; Patinec, V.; Triki, S.; Marchivie, M.; Gómez-García, C.J.; Pillet, S. Magnetic bistability in macrocycle-based FeII spin-crossover complexes: Counter ion and solvent effects. Eur. J. Inorg. Chem. 2016, 34, 5305–5314. [Google Scholar] [CrossRef]
- Vieira, B.J.C.; Dias, J.C.; Santos, I.C.; Pereira, L.C.J.; Vasco, D.G.; Waerenborgh, J.C. Thermal hysteresis in a spin-crossover FeIII quinolylsalicylaldimine complex, FeIII(5-Br-qsal)2Ni(dmit)2·solv: Solvent effects. Inorg. Chem. 2014, 54, 1354–1362. [Google Scholar] [CrossRef] [PubMed]
- Bill, E. JULX 1.4.1 Simulation of Molecular Magnetic Data Software; Matrix Diagonalization Was Realized with the Routine ‘zheev’ from the LAPACK Numerical Package; Max-Planck Institute for Bioinorganic Chemistry: Mulheim/Ruhr, Germany, May 2008. [Google Scholar]
- Nemec, I.; Herchel, R.; Ruben, I.M.; Linert, W. Anion driven modulation of magnetic intermolecular interactions and spin crossover properties in an isomorphous series of mononuclear iron(III) complexes with a hexadentate Schiff baseligand. CrystEngComm 2012, 14, 7015–7024. [Google Scholar] [CrossRef]


| 1 | 1 | 2 | 2 | |
|---|---|---|---|---|
| Chemical formula | C28H28AuFeN4O4S10 | C28H28AuFeN4O4S10 | C32H39AuFeN5O4S8 | C32H39AuFeN5O4S8 |
| Formula weight | 1057.96 | 1057.96 | 1066.98 | 1066.98 |
| Temperature (K) | 120 | 293 | 120 | 293 |
| Cell setting | triclinic | triclinic | monoclinic | monoclinic |
| Space group, Z | P, 2 | P, 2 | I2/c, 4 | I2/c, 4 |
| a (Å) | 10.3711(1) | 10.4935(3) | 13.7776(2) | 13.9679(4) |
| b (Å) | 10.9107(1) | 10.9970(3) | 12.9564(1) | 13.0757(4) |
| c (Å) | 17.7081(2) | 17.7948(6) | 21.9490(2) | 22.1473(6) |
| α (o) | 75.5043(8) | 75.649(3) | 90 | 90 |
| β (o) | 79.9758(8) | 79.768(3) | 98.4284(10) | 98.068(2) |
| γ (o) | 68.9996(9) | 68.289(3) | 90 | 90 |
| Cell volume (Å3) | 1803.23(3) | 1839.82(11) | 3875.77(7) | 4004.9(2) |
| Crystal size (mm) | 0.41 × 0.09 × 0.08 | 0.41 × 0.09 × 0.08 | 0.33 × 0.25 × 0.18 | 0.33 × 0.25 × 0.18 |
| ρ (Mg/m3) | 1.948 | 1.910 | 1.829 | 1.770 |
| μ, cm−1 | 50.86 | 49.85 | 46.30 | 44.81 |
| Refls collected/unique/observed with I > 2σ(I) | 35,223/10,301/9875 | 19,892/10,236/8987 | 44,538/5889/5523 | 11,307/5471/4459 |
| Rint | 0.0187 | 0.0223 | 0.0149 | 0.0305 |
| θmax (o) | 31.06 | 31.07 | 31.17 | 30.84 |
| Parameters refined | 441 | 441 | 251 | 269 |
| Final R1(obs), wR2 (all) | 0.0148, 0.0338 | 0.0262, 0.0540 | 0.0140, 0.0333 | 0.0307, 0.0697 |
| Goodness-of-fit | 1.004 | 1.007 | 1.000 | 1.002 |
| Residual el. density (e Å−3) | 0.606/−0.633 | 0.774/−0.756 | 0.807/−0.689 | 0.648/−0.561 |
| CCDC reference | 1868121 | 1868120 | 1868123 | 1868122 |
| 1, 120 K (HS) | 1, 293 K (HS) | 2, 120 K * (LS) | 2, 293 K (HS) |
|---|---|---|---|
| Fe1 O1 1.9103(11) | 1.9056(17) | Fe1 O1 1.8714(9) | 1.8904(16) |
| Fe1 O3 1.9090(10) | 1.9090(17) | ||
| Fe1 N1 2.1233(13) | 2.123(2) | Fe1 N1 1.9358(10) | 2.082(2) |
| Fe1 N2 2.1761(14) | 2.178(2) | Fe1 N2 1.9987(11) | 2.152(2) |
| Fe1 N3 2.1797(14) | 2.182(3) | ||
| Fe1 N4 2.1055(13) | 2.103(2) | ||
| O1 Fe1 O3 105.34(5) | 105.52(8) | O1 Fe1 O1b 95.02(6) | 99.39(11) |
| O1 Fe1 N1 86.24(5) | 86.08(8) | O1 Fe1 N1 94.13(4) | 88.47(8) |
| O1 Fe1 N2 160.07(5) | 159.41(9) | O1 Fe1 N2 174.82(5) | 162.63(10) |
| O1 Fe1 N3 93.52(5) | 93.26(9) | O1 Fe1 N1b 88.71(4) | 93.94(7) |
| O1 Fe1 N4 88.72(5) | 89.55(8) | O1 Fe1 N2b 89.87(4) | 92.50(9) |
| O3 Fe1 N1 96.91(5) | 97.02(8) | ||
| O3 Fe1 N2 88.47(5) | 88.82(8) | ||
| O3 Fe1 N3 155.30(5) | 155.27(9) | ||
| O3 Fe1 N4 87.32(5) | 87.17(8) | ||
| N1 Fe1 N2 77.74(5) | 77.41(8) | N1 Fe1 N2 84.27(5) | 78.06(11) |
| N1 Fe1 N3 100.16(5) | 100.23(9) | N1 Fe1 N2b 92.64(5) | 99.02(11) |
| N1 Fe1 N4 174.14(5) | 174.62(8) | N1 Fe1 N1b 175.81(6) | 176.28(12) |
| N2 Fe1 N3 77.94(5) | 77.89(9) | N2 Fe1 N2b 85.30(7) | 79.04(15) |
| N2 Fe1 N4 106.52(5) | 106.15(9) | ||
| N3 Fe1 N4 77.14(5) | 76.87(9) | ||
| α 94.22(3) | 95.29(4) | 88.94(1) | 93.75(3) |
| ∠(i–ii)88.1(1) | 88.5(2) | ∠(i–ii)31.1(1) | 85.7(2) |
| ∠(ii–iii)84.3(1) | 83.7(2) | ||
| ∠(i–iii))35.4(1) | 35.7(2) | ∠(i–i(b))21.3(1) | 29.4(2) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spitsyna, N.G.; Shvachko, Y.N.; Starichenko, D.V.; Lahderanta, E.; Komlev, A.A.; Zorina, L.V.; Simonov, S.V.; Blagov, M.A.; Yagubskii, E.B. Evolution of Spin-Crossover Transition in Hybrid Crystals Involving Cationic Iron Complexes [Fe(III)(3-OMesal2-trien)]+ and Anionic Gold Bis(dithiolene) Complexes Au(dmit)2 and Au(dddt)2. Crystals 2018, 8, 382. https://doi.org/10.3390/cryst8100382
Spitsyna NG, Shvachko YN, Starichenko DV, Lahderanta E, Komlev AA, Zorina LV, Simonov SV, Blagov MA, Yagubskii EB. Evolution of Spin-Crossover Transition in Hybrid Crystals Involving Cationic Iron Complexes [Fe(III)(3-OMesal2-trien)]+ and Anionic Gold Bis(dithiolene) Complexes Au(dmit)2 and Au(dddt)2. Crystals. 2018; 8(10):382. https://doi.org/10.3390/cryst8100382
Chicago/Turabian StyleSpitsyna, Nataliya G., Yuri N. Shvachko, Denis V. Starichenko, Erkki Lahderanta, Anton A. Komlev, Leokadiya V. Zorina, Sergey V. Simonov, Maksim A. Blagov, and Eduard B. Yagubskii. 2018. "Evolution of Spin-Crossover Transition in Hybrid Crystals Involving Cationic Iron Complexes [Fe(III)(3-OMesal2-trien)]+ and Anionic Gold Bis(dithiolene) Complexes Au(dmit)2 and Au(dddt)2" Crystals 8, no. 10: 382. https://doi.org/10.3390/cryst8100382
APA StyleSpitsyna, N. G., Shvachko, Y. N., Starichenko, D. V., Lahderanta, E., Komlev, A. A., Zorina, L. V., Simonov, S. V., Blagov, M. A., & Yagubskii, E. B. (2018). Evolution of Spin-Crossover Transition in Hybrid Crystals Involving Cationic Iron Complexes [Fe(III)(3-OMesal2-trien)]+ and Anionic Gold Bis(dithiolene) Complexes Au(dmit)2 and Au(dddt)2. Crystals, 8(10), 382. https://doi.org/10.3390/cryst8100382