Abstract
Pioneering explorations of the two-dimensional (2D) inorganic layered crystals (ILCs) in electronics have boosted low-dimensional materials research beyond the prototypical but semi-metallic graphene. Thanks to species variety and compositional richness, ILCs are further activated as hosting matrices to reach intrinsic magnetism due to their semiconductive natures. Herein, we briefly review the latest progresses of manipulation strategies that introduce magnetism into the nonmagnetic 2D and quasi-2D ILCs from the first-principles computational perspectives. The matrices are concerned within naturally occurring species such as MoS2, MoSe2, WS2, BN, and synthetic monolayers such as ZnO and g-C2N. Greater attention is spent on nondestructive routes through magnetic dopant adsorption; defect engineering; and a combination of doping-absorbing methods. Along with structural stability and electric uniqueness from hosts, tailored magnetic properties are successfully introduced to low-dimensional ILCs. Different from the three-dimensional (3D) bulk or zero-dimensional (0D) cluster cases, origins of magnetism in the 2D space move past most conventional physical models. Besides magnetic interactions, geometric symmetry contributes a non-negligible impact on the magnetic properties of ILCs, and surprisingly leads to broken symmetry for magnetism. At the end of the review, we also propose possible combination routes to create 2D ILC magnetic semiconductors, tentative theoretical models based on topology for mechanical interpretations, and next-step first-principles research within the domain.
1. Introduction
The rediscovery of monolayer graphene has revolutionarily extended materials research by realizing a paradoxical concept, the “atomic crystal” [1,2]. Inlayer stability of the thin film is protected through a covalence bond between the carbon atoms, which allows the formation of the graphite as the layered crystal through the van der Waals (vdW) force.
Compared with three-dimensional (3D) bulk materials, the two-dimensional (2D) crystal is more complex in larger surface areas due to its hosting of unconventional quantum effects that lead to unique electrical, optical, chemical, and thermal properties [3]. The plane extension also offers easier experimental operability than zero-dimensional (0D) atoms or free clusters. However, from these advantages, the zero bandgap limits its practical application in semiconductors. The stable structures and rather small C atom further poses complications in materials manipulations. To benefit semiconductors, several atomically thin layers have also been developed and studied. Similar to the graphene composed of the single C element, these single layer crystals were discovered by using group IV and group V elements [4,5,6].
Indeed, the stability and host ability at 2D are not limited to carbon-based graphene nor synthetic mono-elemental layers. A large number of inorganic layered crystals (ILCs) also exists as a naturally occurring species [7]. Within such a category, layered transition-metal dichalcogenide (LTMD) is a typical group of minerals with fair abundance on earth. Early research studies show that these LTMDs could form similar low-dimensional structures found in carbon, such as fullerene-styled and nanotube-styled TMDs [8].
For electronic structures, most LTMDs have non-zero narrow or wide bandgaps more capable in semiconductor applications than their semi-metallic organic counterparts [9]. The bandgap types can also be switched from indirect to direct when the LTMD dimensions are decreased [10,11]. Emerging electron transitions helped develop the single-layer MoS2 field emission transistor [12], which further inspired the research of ILCs beyond the prototypical graphene [13].
Compared with mono-elemental alkenes, rich species and element compositions of the LTMDs supplement the library of 2D crystals capable of multifunctional abilities [9]. Despite the distinguished electric properties, most of the ILCs are intrinsically nonmagnetic, which limits their wider applications as magnetic materials. Thus, anchoring magnetism to the 2D semiconductive hosts may display simultaneous manipulations of the electron spin and electron transport for spintronic devices.
In this paper, we briefly review the latest first-principles progresses of forming magnetism into 2D and quasi-2D non-graphene crystals. The paper starts by comparing the computational algorithms and packages and continues with magnetic manipulation strategies in 2D ILCs. The paper then discusses the potential physical mechanisms leading to magnetism and ends with possible synthetic routes to realize these magnetic systems. This work mainly concerns naturally occurring LTMD hosts due to their pioneering and representative roles in ILC research, but also includes synthetic matrices such as the monolayer ZnO (m-ZnO), and graphene-like C2N (g-C2N).
To fully benefit the structural uniqueness and stability of the ILC hosts, material manipulation routes are discussed as non-destructive routes of magnetic dopant adsorption, defect engineering, and a combination of doping and adsorbing. The intrinsic 2D magnetic layers are also briefly reviewed due to their complementary nature to the magnetic ones subjected to manipulations. Physical mechanisms for magnetism are also discussed in order to inspire theoretical progress that may solve the puzzles given by the computational results.
2. Computational Algorithms
Density functional theory (DFT) has become the most popular and versatile method in 2D ILCs studies over the last few decades. With the aid of DFT and first-principles methods, material behaviors and properties can be properly predicted and described with solely the input of physical constants. In general, one of the most important steps in DFT computations is properly preparing the objective structures. It usually creates a supercell of the material for the simulation by defining its range in unit cells, which always has P1 symmetry.
After constructing the supercell, geometry optimization is performed on the structures based on density functional theory. Typically, several DFT packages, such as DMOL3, SIESTA, VASP, and CASTEP, can give information towards total energies, forces, and stresses on an atomic system, as well as perform geometry optimizations, band structure calculations, optical spectra drawing, and molecular dynamics simulations. Among them, DMOL3 [14] and SIESTA [15] are composed of atomic orbital basis sets. The Vienna ab initio simulation program (VASP) [16], ABINIT [17], Quantum Expresso [18], and CASTEP [19] are based on planewave basis sets for periodic systems.
Here, we briefly introduce the merits of several packages. VASP uses the projector-augmented wave method or ultra-soft pseudopotentials. Therefore, the size of the basis-set can be kept very small even for transition metals and first-row elements such as C and O. The Quantum Expresso is based on the planewave self-consistent field program where both DFT and density functional perturbation theory are included, using planewave basis sets and pseudopotentials. Owing to its unique approach to electrostatics, DMol3 has long been one of the fastest methods for molecular DFT calculations. It can quickly perform structure optimizations of molecular systems using delocalized internal coordinates. CASTEP employs the density functional theory plane-wave pseudopotential method, which can simulate a wide range of the properties of crystals and surfaces in materials such as semiconductors, ceramics, metals, minerals, and zeolites.
Several levels of approximations, including the local density approximation (LDA) and the generalized gradient approximation (GGA), are widely accepted in calculations involving 2D materials. Two of the most widely used GGA functionals in such calculations are the Perdew-Wang functional (PW91) [20] and the Perdew-Burke-Ernzerhof functional (PBE) [18]. However, GGA is not adequate for more complicated systems, which may include localized electronic states and magnetic properties including transition metal oxides and rare earth elements.
The LDA and GGA are also plagued by large band-gap errors in semiconductors and insulators. The DFT + U method extends the functional approach to manage self-interacting electron correlations. It combines the high efficiency of LDA/GGA and explicates the treatment of correlation with a Hubbard-like model for a subset of states in the system. Thus, it has been used for calculating transition metal oxides in recent years. The hybrid functional based on a screened Coulomb potential by Heyd, Scuseria, and Ernzerhof (HSE) [21] accurately describes band gaps and magnetic effects for ILCs. The vdW interaction can be introduced, e.g., through the empirical correction scheme, as proposed in Reference [22].
So far, the first-principles calculation has been widely employed in computational materials science. The computational route in magnetism was successfully demonstrated in predicting ZnO-based dilute magnetic semiconductors (DMSs) [23]. Following the predictions, several sequences of magnetic materials have been continuously explored, which strengthens the material basis for future spintronics [24,25]. Introduction of the usages of first-principles calculation in magnetism can be found in Reference [26].
To show the magnetic properties of 2D magnetic materials, spin-polarized DFT calculations are used in studies to indicate that the calculations will be performed using different orbitals for different spins. Each possible spin multiplicity ranging from 1 to 10 of the comprehensive magnetic systems was selected during the geometry optimization to find the most stable spin state. Spin density and partial density of states show the distributions and origins of the magnetism in ILCs. They can be used to display the contribution from both spin-up and spin-down eigenstates. Impacts of doping concentration on DMSs are also compared in many works, for example through the size of supercells.
3. Magnetic Properties
3.1. Magnetic Materials Designs on Low-Dimensional MoS2 Matrices
This subsection reviews magnetic materials manipulations on the prototypical ILC layer of MoS2. As a typical LTMD, bulk MoS2 is widely used as a conventional solid lubricant [27]. Such a functionality can be attributed to its layered nature, which involves reducing friction by sliding the layers. Through micromechanical cleavage, the free-standing MoS2 monolayer was obtained and its electrical conductivity was reported as early as 2005 [3]. Later investigation showed a difference regarding the indirect band nature of the bulk. Its monolayer possesses a semiconductive but direct band nature that leads to a growth in photoluminescence following the electron transitions [10,11]. Thanks to its electrical uniqueness and effective design of the circuit, the MoS2 monolayer field-effect transistor was discovered to have a large current on/off ratio [12]. Electronics and optoelectronics were further developed based on the MoS2 monolayer and its LTMD relatives [28]. Research also shows that low-dimensional MoS2 is a good candidate for the ultrasensitive photodetector [29], and even applicable in detecting a UV photon by converting to visible emissions [30].
Schematic illustrations of the single layer and double layers are depicted in Figure 1a,b for the 5 × 5 supercells. The TMD monolayer, indeed, is a quasi-2D crystal where the covalently bonded three hexagonal atomic layers (S-Mo-S) extend vertically. The most common phase of the sulfide is the semiconductive 2H phase, shown in Figure 1a. However, the metastable phases, such as the metallic 1T and 1T’, also turned out to easily form a 1T/2H stable heterojunction structure [31].
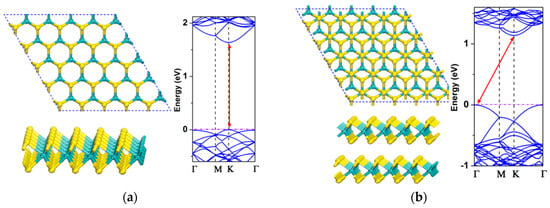
Figure 1.
A 5 × 5 supercell geometric structure and electron structure of the MoS2 monolayer (a) and bilayer (b) [32]. Copyright under CC BY license.
In this work, we mainly focus on the common 2H monolayer. When looking at the structure, the layers are arranged so that an offset enters between the upper layer S atoms and the lower ones. Consequently, the band type changes from direct to indirect, as shown in Figure 1 [32]. The pristine MoS2 crystal itself, in principle, is nonmagnetic. Weak ferromagnetism (FM) may also exist in the small m-MoS2 edges due to the magnetic ground states of the edges at the grain boundaries [33]. Nevertheless, the ‘infinitely’ large 2D plane is considered to be non-ferromagnetic in the computationally ideal models. Thus, external factors are needed to bring ferromagnetism into the systems.
Doping magnetic dopants has been considered a mature route. Benefiting from its technical readiness in the semiconductor industry, the doping strategy has been widely applied in materials research studies. In fact, before the emerging research of ILCs, this strategy was already widely applied in LTMD studies for other functionalities [34,35]. As for the DMS designs, spintronic materials were first predicted by doping the magnetic dopants into the ZnO matrix using a simple Zener model and features of the Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions [23].
The central Zn atom was substituted by different transition metal (TM) atoms, which provided tailored magnetic moments (MMs) in the DMSs. This route has been well-established theoretically and experimentally with the bulk ZnO matrix [36,37,38]. Following this, various works have been carried out by introducing proper magnetic dopants into the 2D MoS2. Typically, the dopants are selected from the 3d TM ions [39,40], to the 4d TMs [41,42]. In general, the structural stability can be kept in Mo substitution, while the MM in a doped unit cell is tunable from 0 µB to 5 µB. The final magnetic moments are also affected by the dopant concentrations and distances between the two central dopants [43].
Despite theoretical progress of the doping strategy, experimental realization of such a route is not an easy task due to the atomically thin 2D host. Ion substitution via bombardment into the chemically stable ILC slabs can barely circumvent radiation damages [44] before the incident ion substitutes the central atom. Precise control of charged particle bombardments suffers from severe heatloads [45] or uncertain depth distribution during implantations [46]. Additionally, incoming particles with low kinetic energies tend to nucleate on the ILC slabs before moving inside the layers. This forms a somewhat weak charge transfer on the substrate surface [47]. In wet synthesis, due to a large amount of defects at the edges of the ILCs, a chemical reaction tends to happen on the sides rather than within the layered slabs [48].
In fact, these unfavorable experimental results offer a synthesis route beyond the conventional ion substitution. Though rather chemically stable, ILCs have large in-plane surfaces which can also be employed as hosting sites for adatoms. When clusters or atoms contact the substrate, physical or chemical adsorptions occur due to the interaction schemes and kinetic energies of the 0D objects [49]. Along with tailored optic and electronic properties [50], the guest clusters are endowed with tunable magnetism and chemical reactivity [51,52], which allows them to act as essential building bricks for functional nanomaterials [53]. A previous doping strategy showed that replacing both the Mo and S atoms with FeX6 (X = S, C, N, O, F) clusters allowed for intrinsic ferromagnetism to be brought into the cluster-doped stable slabs [54]. Thus, when adsorbing the clusters onto the 2D surface, the very unique 0D clusters activate the 2D inorganic hosts to become stable but magnetic semiconductors.
To position the 0D cluster onto the 2D ILCs, both the guest and host materials should be well explored beforehand. Through DFT computations, it was shown that the Mnn (n = 1–4) clusters are good candidates for ferromagnetism carriers on the MoS2 hosts. Compared with the single atom, the Mnn clusters are rich in structure and magnetism. They can span from 0D to 3D structures, and can own MMs from 5 to 20 μB. Explorations of the mono- and bi-layer hosts were performed by using the DMOL3 package. Values for pristine layers were crosschecked with those given by the more precise and lengthy CASTEP package. It is worth mentioning that the validity of CASTEP was confirmed by experimental determination of the electronic structures and excitonic behaviors of the LTMD [30]. The chemically robust clusters can bond to the low-dimensional ILCs, and bolster the complex stabilities.
Geometries of the clusters were modified to minimize the system energies when adsorbing the clusters onto the monolayer slab, or inserting them into the bilayers. Large charge transfers are observed between the Mnn ad-clusters and the MoS2 hosts. The whole systems are also stable in ambient temperature according to thermodynamic simulations from the DMOL3 package. However, the MMs are reduced in the complexes due to pairing TM d-electrons to the S sites. A maximum MM of 9 μB is reached in Mnn@MoS2 monolayer systems (when n = 3), and 3 μB on the bilayer intercalations (when n = 1 or 3). It was discovered that the band of the semiconductive MoS2 bilayer can switch from indirect to direct after inserting the Mn1. Combined with its magnetism and stability, the Mn1@MoS2 bilayer is considered a promising direct band DMS for spintronics [32].
Indeed, the magnetic incident carriers are not only limited to the hereto-elemental clusters, but can also be found in the composites themselves. The “doping element into compound” route originates from the fact that most chemical reactions are accompanied with either redundant or deficient chemicals during synthesis, which results in a positive or negative influence on the final material properties. The synthetic route for MoS2 brings non-stoichiometric products globally or locally. These defective parts may also bring magnetism into the 2D system. For instance, the free Mo clusters are famous for their tunable magnetism [55,56], and the S clusters for their abundant geometric structures [57]. Thus, using clusters composed of compositional elements as the dopants is another strategy to find the ILC magnetism [58]. The schematic illustration of the route is shown in Figure 2, where the Mon or Sn (n = 1–3) clusters are added on or brought out from the MoS2 monolayer. Similar to Reference [32], theoretical modeling and computations were employed in first-principles predictions of magnetisms on the defective or redundant MoS2 monolayer. The results show that adsorbing the Mon (n = 1–3) clusters on the slab can also lead to the magnetism of the systems, but the substance only has a relatively low MM, up to 3 μB.
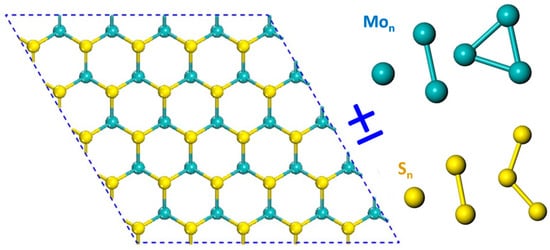
Figure 2.
The adsorption and desorption strategy uses the compositional elements as the dopants or deficits.
The removal of the Mo atom or clusters from the slab will deteriorate the substance’s stability. This is not surprising since Mo atoms are centered and bonded to the neighboring S atoms. When absorbing the Sn clusters, very weak charge transfers can be observed between the incoming clusters and the hosting slab, which denotes the preferences of physical adsorption. Subtracting the S atoms from the layer does not affect the stability of the system, which is in agreement with experimental results [59]. For this reason, engineering an S vacancy (Vs) can also be an effective route for magnetic manipulation.
In fact, the free-standing MoS2 is accompanied with large amount of Vs even in natural minerals. Precise control of the Vs is also achievable through many techniques, and the S-deficient monolayer can be activated for enhanced oxygen oxidization. The Vs can be filled by magnetic impurities with magnetism tunable from ferri- to ferromagnetism [60]. The combination of the central Mo doping and Vs engineering has also been noticed. For example, by both changing the central Mo to W, and the top S atom to Cr, a co-doping route was also suggested to change the electronic structure of the system [61]. However, the magnetic properties of such a system was not investigated in this suggestion.
The aforementioned routes mainly concern one side of the doping matrix. However, a plane has two opposite sides. Without any extrinsic manipulation, these two sides are symmetric and identical. The free-standing nature and stability under ambient strains further provide an experimental basis where each side can be activated under external materials engineering. Similar to casting coinage for special value and identification, patterning both sides of the 2D slab extends universal material functionality beyond the magnetism manipulation.
A very recent first-principles work has revealed such a double-sided doping strategy by utilizing the MoS2 matrix and 3d TM as the dopants [62]. In this case, calculations were performed on the PWscf code of the Quantum Espresso package [18] at the spin-polarized density functional (DFT) level. The correlation energy of the strongly localized 3d orbitals of the dopants was counted by using the Hubbard U-corrected PBE–GGA method based on the rotationally invariant DFT + U formalism [63]. Two 3d impurities were placed in the Vs of the same side and different sides of the slab. The single-sided doping, as expected, leads to the ferromagnetic state in the systems. The total magnetic moments can be viewed as the sum of the individually doped system. This trend can be accepted regardless of the placing order, distances between the dopants, or the MMs of the dopants.
However, in the Cr co-doped system, once two Cr ions were placed exactly mirror symmetric to each other on two sides of the slab, the whole system turned out to be antiferromagnetism (AFM). This is very different from the singly doped ferromagnetic Cr-MoS2 cases (4 μB), and doubly doped CrCr–MoS2 cases on the same side of the slab (8 μB). But if another Cr is not placed exactly beneath the primary Cr dopant, the systems’ magnetism retains FM with a total MM of 8 μB.
Furthermore, a more symmetric geometry of the dopant placement at the same side of the slab will lead to a smaller absolute value of the coupling energy, which leads to a higher likelihood of AFM states. It also shows that changing the lower dopant to a weaker magnetic impurity will yield FM states. The total magnetic moment is the sum of these of individually doped systems. However, if a change occurs between the dopants and the ions in which the same ferrimagnetic system can be achieved, the whole double-sided doped system again turns to be AFM.
3.2. Introducing Magnetism into Other Low-Dimensional Chalcogenides and Nitrides
Within the same LTMD family, MoSe2 and WS2 have similar inlayer and interlayer structures as MoS2. Following the growing research of prototypical MoS2, plenty of investigations have also been conducted on these two compounds. Here, we briefly review the first-principles predictions of possible magnetism by using them as the matrix. As noted before [33], the LTMDs may have very weak ferromagnetism due to boundary conditions. This feature was also found in MoSe2 and WS2 complexes [64], and confirmed through DFT calculations. However, these weak FM features are hardly applicable in DMS devices, where tailored MMs are normally needed.
The nonmetal adsorbed MoSe2 and WS2 matrices were found to have ferrimagnetism through first-principles computations in 2011 [65]. H, B, C, N, O, and F were chemically adsorbed on the LTMD monolayer, which resulted in rather stable structures. Later, the strains and vacancies were determined to be two beneficial impacts that tune the magnetism in the MoSe2 monolayer [66]. Placing the MoSe2 monolayer on proper substrates can also lead to FM states, as shown in Reference [67]. However, the main constrain of this route comes from magnetic substrates, e.g., Ni (111), which may also be magnetized by an external magnetic field. Other manipulation routes were also carried out through computational predictions. For instance, TM-doping was applied to enable FM states in the MoSe2 monolayer systems [68]. Though the route is not novel, detailed generalized gradient approximations (GGA) and GGA + U algorithms were further discussed.
Magnetism studies in the WS2 monolayer underwent similar progresses as those of MoS2 and MoSe2. In this case, FM was engineered through, e.g., strain [69], doping [70], and combinations of these two methods [71]. Dopants were also selected from nonmagnetic elements to 3d and 4d elements [72]. Interestingly, strong spin-orbit splittings were revealed in the point defective WS2 monolayer. The anti-sites exchanging between the S and W can lead to a magnetic moment of 2 μB localized at the anti-site W atom and the neighboring W atoms [73]. This is important because the intrinsic magnetism can be reached on the 2D semiconductor itself without introducing external dopants or adsorbents.
As a typical wide bandgap semiconductor, the hexagonal boron nitride (h-BN) owns isoelectronic and lattice constants similar to those of graphene systems. However, the hexagonal boron nitride also represents the group of layered nitrides. Also, similar to the organic counterpart, the h-BN is nonmagnetic. Introducing ferromagnetism into the system has been widely studied prior to the recent surge of ILC investigations using the MoS2.
For instance, 2D h-BN can be switched to ferromagnetism by vacancy engineering, where both B and N vacancies can induce spontaneous magnetization [74]. Adding the composite element, either B and N, can also lead to FM states, thanks to the non-paired p-electrons in these elements. The theoretically predicted result was verified through X-ray magnetic circular dichroism (XMCD) [75]. Later, weak FM was proven on a carbon-doped BN nanosheet in line with the theoretical prediction [76]. Doping with magnetic impurities can also lead to magnetic systems. For instance, h-BN monolayers were found to be FM after doping with Co or Ni ions [77]. Combining doping and adsorbing was also predicted as a possible route to induce ferromagnetism in the g-BN system. Besides the magnetism in the 2D nitride, electronic structures were substantially changed through the manipulation [78].
3.3. Other Synthetic Systems: m-ZnO and g-C2N
A synthetic ZnO (m-ZnO) monolayer was recently developed experimentally. The monolayer acts as a proper host for material manipulations due to its bulk form [79]. When a TM atom with the partially filled 3d orbital is adsorbed on the ZnO monolayer, results show that the magnetic property of the impurity TM atoms is not quenched by the nonmagnetic host ZnO substrate in most cases.
The calculated spin coupling of the TM@ZnO monolayer displays ferromagnetic properties. Optimizations show that the most stable adsorption sites of the TM atoms are right above the O atom for all TM@ZnO systems. Interestingly, the TM atoms maintain their atomic spins in the TM@ZnO system, as shown in Figure 3a. The axis labeled as a magnetic moment appears to be indicating that the moment is equal to the 3d unpaired electrons such as 5 μB for Mn, 4 μB for Fe, etc. However, the only exception is found in the Cr@ZnO system, where the 4s electron from Cr was excited to the 3d orbit, and turned the spin direction to minimize the total energy. As a result, the formed TM@ZnO generates diversiform MMs, varying from 1 to 5 μB per cell using different TM atoms. According to our DFT calculation, the spin density is almost entirely located on the TM atom site, resulting in the magnetic moment of TM@ZnO equaling the amount of the single TM atom. Introducing the TM dopants will maintain the semiconductive nature of the adsorbed system. As shown in Figure 3b, the TM@ZnO system owns non-zero but varied bandgaps. This indicates that TM@ZnO materials (TM = Sc, Ti, V, Cr, Mn, Fe, Co, Ni) could be used as new dilute magnetic semiconductors with tunable magnetic properties.
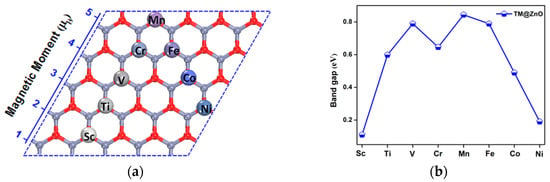
Figure 3.
Magnetic moments and bandgap of transition metal (TM) adsorbed on the ZnO monolayer complex. (a) The most stable adsorption sites and total magnetic moment of the TM-adsorbed complex; (b) Bandgap of the complex.
The original strategy to introduce magnetism into ZnO bulk hosts was designed through Zn substitutions but not through TM adsorptions [23]. On the TM-doped ZnO monolayer, intrinsic ferromagnetism was successfully introduced while the semiconductive structures were maintained [80]. A regionally excessive quantity of the dopants exceeded the solid solubility of the oxide thin films, which resulted in nodules on the films [81]. Such a phenomenon also exists when clusters interact with the ILC slabs [58]. Thus, a combination of TM adsorption-desorption may be another route for ZnO monolayer-based DMS designs. In a recent study, Zhang et al. showed that, after substituting the Zn to a 3d TM, the host monolayer was still able to adsorb another TM atom. The system magnetic moments follow the formula of |5 − x| μB, where x refers to the MM of the individual 3d atom [82].
Recent experimental advances in the graphene-like 2D layers have also inspired additional first-principles studies of magnetism manipulation in other man-made low-dimensional systems. The atomically thin g-C2N was developed through wet-chemical reactions [83], which expanded the 2D atomic crystal library. Strictly speaking, g-C2N cannot be classified as an ILC due to the carbon present in the composite. However, its semiconductive nature endows its potential in semiconductors and spintronics along with other functionalities, e.g., water desalination [84] and proton siege [85]. TM impurity doping was applied to enable the ferromagnetism in the system [86]. In spite of achieving this purpose, the intrinsic g-C2N network was deformed after the presence of the ions. This is not surprising since the atomic radius of the external dopants is much larger than those in the slab. More recently, by doping the C into the entirely nitrogenated graphene, the DFT results show that ferromagnetism can be reached in the planar metal free system [87,88]. This is an important finding since intrinsic magnetism was reached by an excessive amount of the composite element [58] but without introducing external magnetic atoms or defects.
3.4. Layered Transition Metal Dihalides and Trihalides
Designs of the previously mentioned DMS systems stem from introducing external factors into the intrinsically nonmagnetic ILC hosts to reach 2D. Many layered compounds hold intrinsic ferromagnetism and can be cleaved down to atomically thin layers. Among them, the TM metal di- and trihalides are some of the most promising candidates for 2D magnetic semiconductors with tunable ferromagnetism. The binary compounds consist of the transition metal M and halide element X. These compounds form the large combinations of MXn (n = 2, 3). Early studies showed that even the bulk forms are associated with very unique optical, electronic [89], and magnetic properties [90]. A recent work showed that the ferromagnetic order found in the bulk CrI3 may be present in the monolayer form [91]. Thanks to structural uniqueness and distinct properties, this group of materials is considered to be useful for studying magnetism in low dimensions and studying novel materials for different functionalities [92]. A very recent breakthrough demonstrated that magnetism is subject to the thickness of the CrI3, which highlights the potential physical properties of the vdW crystals in layer dependence [93]. Though the Curie temperature is not yet up to room temperature, it can be foreseen that with additional material manipulations, this group of vdW will eventually reach the required magnetic properties. One theoretical study also proved the energetic and dynamic stabilities of the MX2 monolayer complexes. Magnetic properties of this family of complexes can also be tailored by introducing strain or doping, and higher Curie temperature is predicted in a reasonable reach [94]. This topic, however, is out of the main scope of this brief review. However, the milestone of the CrI3 has already incited a new surge of research devoted to low-dimensional TM halides.
4. Magnetism Mechanisms: From Electronic Structural Analysis to Magnetic Interactions
4.1. Analysis from Electronic Structures
In general, electronic structures have been computed to find the physical origins of their magnetic states. When projecting the spin band structures, the spin-density helps in figuring out the net spins of the modified systems. In routes where 3d or 4d TM atoms are involved, the magnetic properties of the stable complexes are inherited from the magnetism of the incoming dopants.
After hybridizing with the ILC matrix, the lonely unpaired d electrons in the TM impurities contribute to a majority of the final MMs in the system. Charge transfers also occur between the TM ions and matrices, enabling system stability. Meanwhile, the local magnetic moments for impurity and host atoms will change slightly. The excessive spin density mainly resides next to the impurities, and control of the MMs can be achieved by changing the dopant types or doping density. However, when using clusters as dopants or adsorbents, the internal magnetic interaction between the cluster atoms also influences the final magnetism of the systems.
In the Mnn adsorbed or intercalated MoS2 systems, the incident clusters magnetically position the electron spins to reach the lowest-energy isomers, and then reorder them during the adsorbing process. Total magnetic moment of the clusters is mainly localized in the Mn atoms. The host slabs, which have small magnetic residues on S and Mo atoms, do not interfere with the main magnetic behavior of the doped complexes [32].
The trivial roles affecting the magnetism do not apply to the metal oxide ILC layer hosts. Competitive ion-matrix and ion-ion interactions start to dominate the final states of the modified systems. This is found in the m-ZnO doping-adsorbing case. The orbitals of the highest occupied valence band (HOVB) are depicted in Figure 4 to illustrate the mechanism. The 2p orbital of O atom not only overlaps with the 3d orbital of the adsorbed Mn in HOVB-1, but also with the 3d orbital of the doped Mn atom, which is shown in HOVB-2.
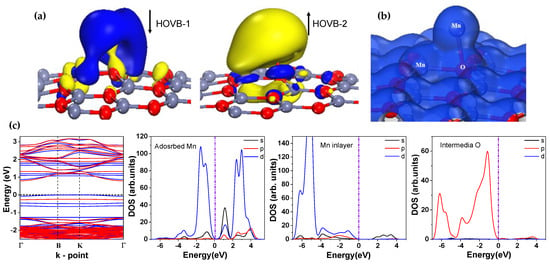
Figure 4.
Orbitals of the highest occupied valence band (HOVB) in the Mn adsorbed-doped ZnO monolayers (a); electronic charge density (b); and electronic structures (c) [82]. Copyright © (2017) American Chemical Society (ACS), http://pubs.acs.org/doi/full/10.1021/acsomega.7b00093. Reproduced with permission from ACS. Further permission related to the excerpted material should be directed to the ACS.
Geometrical allocations of the Mn–O–Mn tend to be perpendicular (see Figure 4b), which are similar to the MnO crystal and results in the magnetic superexchange. On the other hand, direct electron density overlap also exists between two Mn atoms, which leads to the direct exchange between the Mn dimer. This claim is verified in the spin-polarized band structure and the density of states (DOS) of the acting atoms of the Mn@Mn–ZnO system in Figure 4c. Both d orbitals from the adsorbed and doped Mn atoms coincide with the p orbital from the same O atom, which is visualized as the sharp peaks in Figure 4c. An interplay between magnetic superexchange (ion-matrix-ion) and direct exchange (ion-ion) is identified, which renders the complex AFM [82].
Dimensionality reduction, by reducing the spatial variables, introduces spatial symmetry effects into the doped ILC systems. As another basic concept, space symmetry is found to substantially influence the final magnetism. In the dually doped MoS2 complexes, a general trend illustrates that spatial symmetry leads the broken symmetries in magnetism. This is seen in the dually doped system when two Cr impurities are placed mirror symmetric to each other through the MoS2 monolayer (noted as TM0 and TM1 positions in Figure 5). The high symmetric configuration creates AFM in the double-sided doped system. Compared with the magnetic interactions between ions, such a geometric influence follows the symmetry of the systems. By extending the supercell to 10 × 10, as shown in Figure 5, the configuration of V(0)–MoS2–Co(5) is more symmetric compared with that of V(0)–MoS2–Co(4). Position (5) is almost in the middle of the four slabs of 5 × 5 dimensions. Such a symmetry of the V(0)–MoS2–Co(5) case resulted in a stronger AFM trend. This serves a bigger exchange energy value in the absolute scale [62].
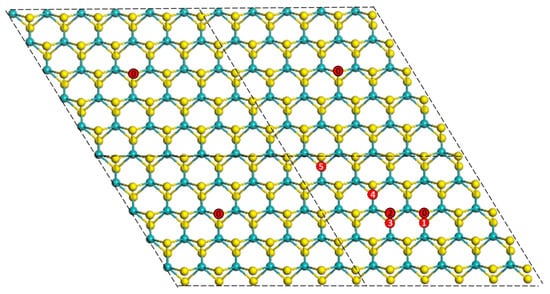
Figure 5.
Illustration of the symmetries of the double-sided TM (1 or 2)-doped MoS2 10 × 10 supercell. Defined by TM0, the symmetries of other TMs vary according to their displacement from the center of the 5 × 5 supercell.
Origins of the calculated magnetism in one-sided doped systems generally agree with the conventional physical models. Though most computational works were emphasized on materials designs, several distinct ones were dedicated in exploring physical levels. It is shown that the RKKY interactions were kept between magnetic impurities by substituting the metal atoms [95] and positioned on the edge of the LTMDs [96]. A similar oscillation trend from RKKY was also found between the distance of impurities and the interaction strength in the p-doped LTMD monolayer [97]. Therefore, the symmetry of the whole system also affects the final magnetism. In a recent work, the interaction decay exponent from the RKKY was labeled a “sub-2D” behavior for different band fillings. Yet, the dimensionality impact is considered as another crucial factor [98].
However, origins of the calculated magnetism in a two-sided doped system are beyond conventional physical models. While the Kondo effect and spin-orbital interaction [99] lose the metallic matrix playground, the RKKY interaction fails regarding the trends of interaction energies and magnetic moments in the double-sided doped systems. For those reasons, the interaction of single molecular magnet (SMM) is proposed. Let us suppose that each dopant constitutes an SMM locally, and the north/south poles are defined by the ILC plane. The SMM is able to magnetize other matter, or act as a ferromagnet, which makes it become magnetized itself. As shown in Figure 6a, when two ferromagnetic SMMs are placed on the same side of the slab, they act individually and the total MM is the sum of each SMM. However, the strong MMs will be cancelled once they are placed exactly mirror symmetric, as shown in Figure 6b. However, within the same arrangement, once an SMM is less magnetic than another, it will be magnetized by the stronger magnet. This process is illustrated in Figure 6c. In Figure 6d, a ferrimagnetic substrate was first composed by a single substitution of the Vs. When a ferromagnetic SMM was formed on this substrate, it antiferromagnetically interacted with the host, leading the whole system to become AFM [100].
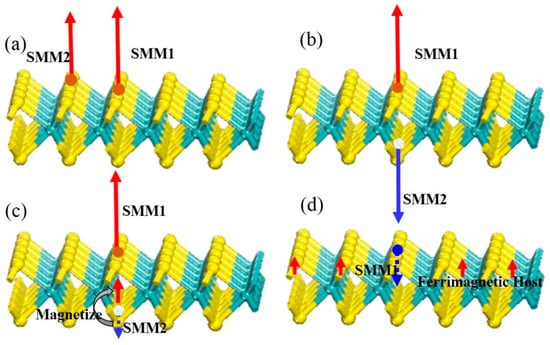
Figure 6.
Single molecular magnet (SMM) interaction schemes. (a) Two ferromagnetic SMMs are placed on the same side of the MoS2 host; and (b) placed exactly mirror symmetric to each other; (c) one ferrimagnetic SMM is magnetized by the top ferromagnetic SMM; and (d) denotes the antiferromagnetic interactions between a ferrimagnetic SMM and a ferrimagnetic substrate.
4.2. Magnetic Interactions
Despite the interpretation of computational aspects, the origins remain elusive for low-dimensional magnetic interactions. The well-known RKKY interaction between two spins includes an exchange integral that stands for the Fourier transform of the non-uniform susceptibility. Analogous to the Heisenberg model, this strength of the exchange coupling is related to the magnetic ordering temperature, but not rooted in the symmetry or topology effects. Additionally, the quantum dot style of the doped impurities can barely induce a magnetic vortex [101] in the singly doped or intrinsic 2D hosts. The solution may be explored in the mesoscale magnetism behaviors [102] where the spatial symmetry is introduced as another factor along with other short-long and static-dynamic interactions.
It is worth noting that magnetic interactions in the confined spaces are rather complicated and unable to be generalized under a one-theory umbrella. The 2D nature of the host limits the long-range magnetic coupling perpendicular to the plane. Additionally, understanding the spin of electrons in confined systems generally requires fundamental knowledge of the system including constrains and interaction schemes at operator levels [103]. Such a mechanism can even be traced down to the Planck scale [104]. Aside from the symmetry, the local magnetic interaction and long-range interaction should be considered specifically in order to understand the behavior of magnetism. These interactions are further affected by the dopant and host types, doping density, electronic structures, and mediation of the matrices. Nevertheless, we tentatively review the possible magnetic interactions at the low-dimensional systems post-treated by various materials manipulations.
We first review the ideal cases of introducing magnetisms into the nonmagnetic 2D ILCs. Using existing electronic materials as matrices is important for further engineering due to the industrial, technical, and application readiness. Incorporating this background, the first-principles predictions of novel DMSs utilize magnetic ordering subjected to impurity- and hole-mediated exchange interactions, while bringing subtle changes to the intrinsic electric properties of the host. In general, designs of 2D ILC DMSs also follow the route in manipulating group II-VI semiconductors, by using magnetic impurities as dopants [23,24,25]. The electron spins of the partially filled d and f orbits of the incident ions dominate the general magnetic behaviors of the doped systems, as shown in Figure 7a. The magnetic ions (Cr, Mn, Fe, Co, etc.), after substituting the central Mo atom in the MoS2 monolayer, still own uncoupled d electrons, leading to ferromagnetism in the TM-MoS2 systems [39]. The same mechanisms were observed in the single-layered MoS2 complexes where the S atom is replaced by TMs [58,60,62], and the TM-adsorbed ZnO monolayer. Partial magnetic moments can also be allocated to the host elements, but are limited in rather small contributions to the total magnetism. However, the MMs from single TM atoms are normally suppressed in doped monolayers due to bonding between the host and guest atoms. An exception is found in the TM-adsorbed ZnO monolayers, where most of the TM dopants keep the same MMs as those of their monomers (Figure 3a).
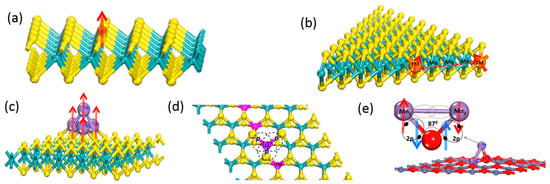
Figure 7.
Magnetic interaction schemes. (a) Localization of net spin from the dopant contributes to the ferromagnetism of the system; (b) Two magnetic impurities are connected to the edge of the flake MoS2, shown as orange arrows; (c) direct exchange in Mn4 cluster adsorbed on the MoS2 monolayer; (d) superexchange in 3d δ-type doped monolayer MoS2; and (e) superexchange and direct exchange competing in Mn atoms-doped-adsorbed ZnO monolayer.
In the reduced space of 2D, dopant concentrations can be interpreted as the distances between impurities. The 4f electrons from Gd are responsible for the magnetism in the doped MoS2 monolayers [42]. However, different from the 3d TM-doped cases, magnetic couplings also substantially changed the final magnetisms therein. When placed next to each other, the Gd ions can also become paramagnetically coupled through the matrix. However, the difference between AFM and FM energy is rather small. It is further noticed that the s- or p-type dopants can also contribute to the final ferromagnetism in ILCs. In the S substitution cases, the non-metallic light elements introduce ferrimagnetism up to 1 μB [60]. The MMs are mainly arisen from the unpaired Mo 4d electrons due to a lack of bonding electrons from the guests. The transition between magnetisms has been very recently reported following strain changes in the S-vacancy MoS2 monolayers [105]. The dangling bond turned out on the defect bonded Mo atom. It assists electron migrations to the defective parts [106], and induces net spins for ferromagnetism.
Magnetic interactions are also decisive in doped/adsorbed ILC systems. In a typical doped semiconductive system, the long-range interactions generally follow the RKKY scheme. As shown in Figure 7b, the magnetic impurity is locally bonded to the nonmagnetic host, leaving the unpaired electron to contribute to the net spin. The conduction electron is magnetized in the vicinity of the magnetic dopant. A magnetic dipole is formed, and the polarization decays in oscillations based on the distance from the dopant. Such a trend is well reproduced in the dually doped ILC systems [97,98]. On the other hand, in a dilute-doped system, the local magnet is strong enough, but the couplings from the neighboring supercells are general neglected. It was also found that the long-range magnetic interactions, though they may be not locally decisive, follow the RKKY interaction, and the magnets tend to align ferromagnetically [107].
Dopant-matrix interactions may also be subject to magnetization or different exchange interactions. An incremental MM of 0.3 μB was induced in the nonmagnetic graphene substrate after adsorbing the ferromagnetic Mn7 cluster [108]. In the cluster-doped or adsorbed ILC systems, inside the clusters, direct exchange was extremely strong among the atoms in the cluster compared to other magnetic interactions, as demonstrated in Figure 7c. The whole system follows the results of the direct exchange. This can be seen in the results of the Mn and Mo dimer-doped MoS2 layers [32,58]. Similar behavior has also been found in MXn systems [91]. Double exchange rarely occurs in the studied monolayer systems due to either the long distances or the isoelectronic states between the dopants.
On the other hand, superexchange occurs when the dopants are placed in certain orders, such as aligning the same line within the ILC (as seen in Figure 7d). For instance, in the Cr/Fe δ-doped MoS2 monolayers, the d electrons from the TM dopants strongly couple with the p electrons of the bonded S atom. Due to the difference in unpaired electrons from Cr and Fe, the whole system turns to ferrimagnetism due to the magnetic superexchange [109]. However, different magnetic interactions may also compete in multiple dopant-doped ILC systems. The interplay between superexchange and direct exchange is shown in Figure 7e. As seen in the Mn-doped-adsorbed m-ZnO, the interplay between the magnetic superexchange and direct exchange enables AFM in the system [82]. A similar observation was found in the Fe dually doped MoS2 mono- and multilayers. The layer-dependent magnetisms were produced as a result of the competition between the double exchange and superexchange. This arose from the couplings between magnetic impurities located in different sites of the layers, as well as within the impurities [110].
The magnetic schemes in the p orbital systems (d0 semiconductor) are also different in low-dimensional systems. The Stoner picture was reported in the carbon-doped ZnO bulk, where most of the net spin was localized to the C impurities. The theoretical prediction was further confirmed by the experiment [111]. Thanks to the hybridizations of the C and metal atoms, majority spins were fully occupied on the C site, while the spin-down states were partially filled. This scenario was also found in the carbon-doped holy g-C2N [88]. The product of local magnetic exchange strength and the DOS of the non-spin-polarized band is much larger than the magnetic equilibrium, and leads to robust intrinsic ferromagnetism. Due to the localized “magnetic interactions”, the spin coupling in the d0 semiconductors at low dimensions is further reduced to band coupling. Charge transfers between the up and down spins occur when defect bands introduced by the dopant are very close to each other [112].
5. Possible Synthesis Routes
Though our focus is computationally oriented, in this section, we briefly review and suggest possible synthetic routes to realize magnetic 2D inorganic materials. Compared to numerous devotions in the synthesis of large-scale 2D ILCs [113,114], experimental realizations of magnetic ILCs are rarely reported. Despite sophisticated synthetic routes to combine various metals with the ILCs, our key aim is not focused on 2D spintronic materials [115].
While experimental introduction of the magnetism into low-dimensional naturally occurring ILC matrices is complex, routes to realize magnetic synthetic slabs undergo even more stringent conditions. For instance, although chemical vapor deposition allows introducing other impurities during the host synthesis, doping with MoS2 can only be achieved by using graphene as the substrate [116]. The substitutional doping of ReS2 was achieved with Mo as the dopant, but the monolayer has not yet been magnetized due to the isoelectronic structures of Mo and Re [117]. Similarly, the magnetism is still lacking on the covalent N-doped MoS2 monolayer [118]. 3d TM dopants were also incorporated into MoS2 single crystals [119]. Therein, the energy of ion bombardment was controlled so as not to introduce radiation damage to the thin layer [44].
In fact, we noticed that large amounts of chemicals are prepared through wet methods. Among them, synthetic functional materials can be engineered to low-dimensional nanoparticles using facile wet routes [120,121,122], while various reaction parameters can effectively influence the final shape and functionality of the products [123,124]. Additionally, introducing impurities into low-dimensional matrices is much easier through ions in liquid form during synthesis [125,126], which may facilitate the results in the previous doping strategies. However, due to the stable nature of the ILCs, conventional wet methods can rarely be applied to stable monolayer synthesis. It was not until recently that the MoS2 monolayer was prepared via a hot-injection thermolytic decomposition method [127]. Following this method for the matrix synthesis, and combining with proper hybrid layers [54], hetero magnetic dopants may be introduced or anchored into/onto the atomically thin slabs for large quantity fabrications. Apart from facilitating the synthesis for nanometer-scaled particles or slabs, we noticed that the wet method has also been used to implant magnetic centers into semiconductor matrices [128,129]. 2D DMSs may be accessible by post-treatment of the bulk counterparts via chemical exfoliation [130] and liquid phase exfoliation [131].
6. Concluding Remarks and Outlooks
In this paper, we have briefly reviewed the status quo of introducing magnetism into nonmagnetic 2D inorganic semiconductive layers. Various doping, adsorbing, and substituting routes have been carried out to reach unique 2D spintronic materials. These first-principles results have generally reached the materials design aim. Following the invention of synthetic 2D ILCs, brewing magnetism into these low-dimensional systems will continue within popular research areas. It can be expected that many new DMS systems can be predicted via doping, adsorbing, vacancy engineering, strain, and more. Besides these routes for monolayers, strain manipulation has recently been combined with LTMD/g-C2N heterojunctions to enable tunable electronic structures in addition to achieving ferromagnetism [132]. In quasi-2D thin films, various materials manipulation strategies can be applied to reach the DMSs within such a category.
Apart from the large number of existing works regarding computational predictions of 2D DMSs, next-step research studies within the domain remain interesting but challenging. One step is to enlarge the supercells from 4 × 4 or 5 × 5 to, e.g., 10 × 10. By doing so, the long-range interactions of impurities may lead to different magnetic states of 2D systems. Another direction may come from introducing topological factors into 2D ILC planes, where a magnetic vortex [101] can lead to a general magnetic behavior apart from that of the individual dopant. The third route may involve introducing line defect or substitution into 2D systems, provided that they are kept stable after introducing large amounts of defects. Using the 2D ILC as a mediator/additive added into magnetic systems may also be useful for achieving DMSs. Similar to the catalytic roles of the LTMD [133], these nonmagnetic components may mediate or bolster the magnetic moments in ferromagnetic or ferrimagnetic systems. Incorporating the nonmagnetic ILC with the layered metal halides may also help the development of low-dimensional DMSs, provided that matching between these two species can take place as out-plane heterojunctions.
Despite the progress within materials science and engineering, physical insights of the reduced dimensions are still challenging. Magnetism remains one of the oldest and most fundamental problems for theoretical physics due to many theorem violations. The definition of dimensionality, another fundamental parameter for physical sciences, is always debated among various disciplines. Merging these two concepts into 2D ILC systems, while offering exciting phenomena, raises fundamentally important challenges to existing models. Each of the aforementioned aspects deserves a general review that concludes previous studies and inspires forthcoming investigations. While the present work is focused on first-principles computations, it touches domains from computational materials sciences and materials engineering to fundamental physics. It remains a brief review that combines concepts from various domains for the studied low-dimensional systems. Though a comprehensive topic review(s) will definitely be necessary for future research, the present brief review is hoped to be timely and inspiring in assisting 2D inorganic material researches, and in offering heuristics for theoretical progress, thus contributing to our scientific knowledge.
Acknowledgments
This work is financially supported by Oulu University Strategic Grant, and the National Natural Science Foundation of China (Grant Nos. 11204079, 21303054, 21601149), European Regional Development Grant and Oulu Council, and the Fundamental Research Funds for the Central Universities (Nos. 222201714050, 222201714018). X.S. acknowledges a scholarship sponsored by China Scholarship Council. With great thanks, the authors acknowledge S. Ulloa and A. Ávalos-Ovando from Ohio University for fruitful discussions on the magnetisms in doped systems, and J.-Z. Zhang from East China University of Science and Technology for his guidance in the theoretical physics.
Author Contributions
All authors contributed to the writing and production of this manuscript.
Conflicts of Interest
The authors declare no competing financial interests.
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.F.; Chen, W.J.; Xu, Y.; Gao, C.L.; Guan, D.D.; Liu, C.H.; Qian, D.; Zhang, S.C.; Jia, J.F. Epitaxial growth of two-dimensional stanene. Nat. Mater. 2015, 14, 1020–1025. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Fu, H.; Zhou, L.; Yao, K.; Zeng, X.C. Nine new phosphorene polymorphs with non-honeycomb structures: A much extended family. Nano Lett. 2015, 15, 3557–3562. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014, 9, 372–377. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Zhao, T. Recent advances in inorganic 2D materials and their applications in lithium and sodium batteries. J. Mater. Chem. A 2017, 5, 3735–3758. [Google Scholar] [CrossRef]
- Tenne, R. Inorganic nanotubes and fullerene-like nanoparticles. Nat. Nanotechnol. 2006, 21, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [PubMed]
- Tongay, S.; Zhou, J.; Ataca, C.; Lo, K.; Matthews, T.S.; Li, J.; Grossman, J.C.; Wu, J. Thermally driven crossover from indirect toward direct bandgap in 2D semiconductors: MoSe2 versus MoS2. Nano Lett. 2012, 12, 5576–5580. [Google Scholar] [CrossRef] [PubMed]
- Radenovic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 2011, 6, 147–150. [Google Scholar] [CrossRef]
- Manzeli, S.; Ovchinnikov, D.; Pasquier, D.; Yazyev, O.V.; Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. [Google Scholar] [CrossRef]
- Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Chem. Phys. 1990, 92, 508–517. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Gonze, X.; Beuken, J.M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-principles Computation of Material Properties: The ABINIT Software Project. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. Kristallogr. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Ortmann, F.; Bechstedt, F.; Schmidt, W.G. Semiempirical van der Waals correction to the density functional description of solids and molecular structures. Phys. Rev. B 2006, 73, 205101. [Google Scholar] [CrossRef]
- Dietl, T.; Ohno, H.; Matsukura, F.; Cibert, J.; Ferrand, D. Zener model description of ferromagnetism in zinc-blende magnetic semiconductors. Science 2000, 287, 1019–1022. [Google Scholar] [CrossRef] [PubMed]
- Dietl, T.; Ohno, H. Dilute ferromagnetic semiconductors: Physics and spintronic structures. Rev. Mod. Phys. 2014, 86, 187–251. [Google Scholar] [CrossRef]
- Dietl, T.; Sato, K.; Fukushima, T.; Bonanni, A.; Jamet, M.; Barski, A.; Kuroda, S.; Tanaka, M.; Hai, P.N.; Katayama-Yoshida, H. Spinodal nanodecomposition in semiconductors doped with transition metals. Rev. Mod. Phys. 2015, 87, 1311. [Google Scholar] [CrossRef]
- Rhim, S.H.; Hong, S.C. Introduction to First-principles Study in Magnetism: A Brief Guide to Nonexperts. J. Korean Magn. Soc. 2017, 57, 190–197. [Google Scholar] [CrossRef]
- Cohen, S.R.; Rapoport, L.; Ponomarev, E.A.; Cohen, H.; Tsirlina, T.; Tenne, R.; Lévy-Clément, C. The tribological behavior of type II textured MX2 (M = Mo, W, X = S, Se) films. Thin Solid Films 1998, 324, 190–197. [Google Scholar] [CrossRef]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Sanchez, O.; Lembke, D.; Kayci, M.; Radenovic, A.; Kis, A. Ultrasensitive photodetectors based on monolayer MoS2. Nat. Nanotechnol. 2013, 8, 497–501. [Google Scholar] [CrossRef] [PubMed]
- Pankratov, V.; Hoszowska, J.; Dousse, J.-C.; Huttula, M.; Kis, A.; Krasnozhon, D.; Zhang, M.; Cao, W. Vacuum Ultraviolet Excitation Luminescence Spectroscopy of Few-Layered MoS2. J. Phys. Condens. Matter 2016, 28, 015301. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Zhang, Q.; Yang, J.; Feng, S.; Lei, M.; Quhe, R. Computational study of phase engineered transition metal dichalcogenides heterostructures. Comput. Mater. Sci. 2018, 142, 129–134. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, Z.; Wang, X.; Zhang, H.; Li, T.; Wu, Z.; Luo, Y.; Cao, W. Magnetic MoS2 pizzas and sandwiches with Mnn (n = 1–4) cluster toppings and fillings: A first-principles investigation. Sci. Rep. 2016, 6, 19504. [Google Scholar] [CrossRef] [PubMed]
- Tongay, S.; Varnoosfaderani, S.S.; Appeleton, B.R.; Wu, J.; Hebard, A.F. Magnetic properties of MoS2: Existence of ferromagnetism. Appl. Phys. Lett. 2012, 101, 123105. [Google Scholar] [CrossRef]
- Park, K.T.; Kong, J.; Klier, K. Angle-Resolved X-ray Photoelectron Spectroscopy of in Situ Deposited Li on MoS2. J. Phys. Chem. B 2000, 104, 3145–3154. [Google Scholar] [CrossRef]
- Ding, X.Z.; Zeng, X.T.; He, X.Y.; Chen, Z. Tribological properties of Cr- and Ti-doped MoS2 composite coatings under different humidity atmosphere. Surf. Coat. Technol. 2010, 205, 224–231. [Google Scholar] [CrossRef]
- Wang, F.; Huang, W.-W.; Li, S.-Y.; Lian, A.-Q.; Zhang, X.-T.; Cao, W. The magnetic properties of FexZn1−xO synthesized via the solid-state reaction route: Experiment and theory. J. Magn. Magn. Mater. 2013, 340, 5–9. [Google Scholar] [CrossRef]
- Wang, F.; Lin, W.; Wang, L.-Z.; Ge, Y.-M.; Zhang, X.-T.; Lin, H.-R.; Huang, W.W.; Huang, J.-Q.; Cao, W. Magnetic properties of the Cu-doped ZnO: Experiments and theory. Acta. Phys. Sin. Chin. Ed. 2014, 63, 157502. [Google Scholar] [CrossRef]
- Chambers, S.A. Ferromagnetism in doped thin-film oxide and nitride semiconductors and dielectrics. Surf. Sci. Rep. 2006, 61, 345–381. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Zhu, Z.Y.; Mi, W.B.; Guo, Z.B.; Schwingenschlögl, U. Prediction of two-dimensional diluted magnetic semiconductors: Doped monolayer MoS2 systems. Phys. Rev. B 2013, 87, 100401. [Google Scholar] [CrossRef]
- Mishra, R.; Zhou, W.; Pennycook, S.J.; Pantelides, S.T.; Idrobo, J.-C. Long-range ferromagnetic ordering in manganese-doped two-dimensional dichalcogenides. Phys. Rev. B 2013, 88, 144409. [Google Scholar] [CrossRef]
- Dolui, K.; Rungger, I.; Pemmaraju, D.C.; Sanvito, S. Possible doping strtegies for MoS2 monolayers: An ab initio study. Phys. Rev. B 2013, 88, 075420. [Google Scholar] [CrossRef]
- Zhang, X.J.; Wang, X.C.; Mi, W.B. Density functional theory prediction on magnetism in Gd-doped monolayer MoS2. Solid State Commun. 2015, 212, 35–40. [Google Scholar] [CrossRef]
- Williamson, I.; Li, S.; Hernadez, A.C.; Lawson, M.; Chen, Y.; Li, L. Structural, electrical, phonon, and optical properties of Ti- and V-doped two-dimensional MoS2. Chem. Phys. Lett. 2017, 674, 157–163. [Google Scholar] [CrossRef]
- Ochedowski, O.; Marinov, K.; Wilbs, G.; Keller, G.; Scheuschner, N.; Severin, D.; Bender, M.; Maultzsch, J.; Tegude, F.J.; Schleberger, M. Radiation hardness of graphene and MoS2 field effect devices against swift heavy ion irradiation. J. Appl. Phys. 2016, 113, 214306. [Google Scholar] [CrossRef]
- Cao, W.; Dousse, J.-C.; Hoszowska, J.; Kavčič, M.; Kayser, Y.; Schenker, J.L.; Žitnik, M. Double L3M ionization of Pd induced by impact with medium-energy electrons. Phys. Rev. A 2011, 83, 022708. [Google Scholar] [CrossRef]
- Kayser, Y.; Banaś, D.; Cao, W.; Dousse, J.-C.; Hoszowska, J.; Jagodziński, P.; Kavčič, M.; Kubala-Kukuś, A.; Nowak, S.; Pajek, M.; et al. Depth profiling of dopants implanted in Si using the synchrotron radiation based high-resolution grazing emission technique. X-ray Spectrom. 2012, 41, 98–104. [Google Scholar] [CrossRef]
- Wang, F.; Xu, H.; Fang, J.; Wang, G.; Zhang, X. Probing the interfacial interaction between monolayer molybdenum disulfide and Au nanoclusters. Surf. Interface Anal. 2017, 49, 858–863. [Google Scholar] [CrossRef]
- Cao, W.; Panktratov, V.; Huttula, M.; Shi, X.; Saukko, S.; Huang, Z.; Zhang, M. Gold nanoparticles on MoS2 layered crystal flakes. Mater. Chem. Phys. 2017, 158, 89–95. [Google Scholar] [CrossRef]
- Popok, V.N.; Barke, I.; Campbell, E.E.B.; Meiwes-Broer, K.-H. Cluster-surface interaction: From soft landing to implantation. Surf. Sci. Rep. 2011, 66, 347–377. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, J.; Gu, T.; Zhang, H.; Luo, Y.; Cao, W. First-principles investigations of chirality in trimetallic alloy clusters: AlMnAun (n = 1–7). J. Phys. Chem. A 2015, 119, 3458–3470. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; He, L.M.; Zhao, L.X.; Feng, X.J.; Cao, W.; Luo, Y.H. A density functional theory study of the Au7Hn (n = 1–10) clusters. J. Mol. Struct. THEOCHEM 2009, 911, 65–69. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, J.; Feng, X.; Zhang, H.; Zhao, L.; Luo, Y.; Cao, W. Magnetic superatoms in VLin (n = 1–13) clusters: A first-principles prediction. J. Phys. Chem. A 2013, 117, 13025–13036. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Adeleke, A.A.; Cao, W.; Luo, Y.; Zhang, M.; Yao, Y. Structures of Nanoalloy Clusters AunAln (n = 1–10) and the Growth Patterns to the Bulk Phase. J. Phys. Chem. C 2016, 120, 25588–25595. [Google Scholar] [CrossRef]
- Feng, N.; Mi, W.; Cheng, Y.; Guo, Z.; Schwingenschlögl, U.; Bai, H. First principles prediction of the magnetic properties of Fe-X6 (X = S, C, N, O, F) doped monolayer MoS2. Sci. Rep. 2014, 4, 3987. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Ran, X.; Zhao, H.; Wang, L. The nonmetallicity of molybdenum clusters. J. Chem. Phys. 2004, 121, 7717–7724. [Google Scholar] [CrossRef] [PubMed]
- Pis Diez, R. Density Functional Study of Small Molybdenum Clusters. Int. J. Quant. Chem. 2000, 76, 105–112. [Google Scholar] [CrossRef]
- Raghavachari, K.; Rohlfing, C.M.; Binkley, J.S. Structures and stabilities of sulfur clusters. J. Chem. Phys. 1990, 93, 5862–5874. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Y.; Ye, Y.; Feng, J.; Zhang, M.; Luo, Y.; He, L.; Cao, W. First-principles study of monolayer MoS2 with deficient and excessive Mon and Sn (n = −3 → 3) clusters on 5 × 5 supercells. Comput. Mater. Sci. 2016, 121, 124–130. [Google Scholar] [CrossRef]
- Niu, Y.; Park, S.J.; Palmer, R.E. Modification of deposited, size-selected MoS2 nanoclusters by sulphur addition: An aberration-corrected STEM study. Inorganics 2017, 5, 1. [Google Scholar] [CrossRef]
- Yue, Q.; Chang, S.; Qin, S.; Li, J. Functionalization of monolayer MoS2 by substitutional doping: A first-principles study. Phys. Lett. A 2013, 377, 1362–1367. [Google Scholar] [CrossRef]
- Wu, M.; Xu, B.; Liu, G.; Ouyang, C. First-principles study on the electronic structures of Cr- and W-doped single-layer MoS2. Acta Phys. Sin. 2013, 62, 037103. [Google Scholar] [CrossRef]
- Vähäkangas, J.; Lantto, P.; Vaara, J.; Huttula, M.; Cao, W. Orienting spins in dually doped monolayer MoS2: From one-sided to double-sided doping. Chem. Commun. 2017, 53, 5428–5431. [Google Scholar] [CrossRef] [PubMed]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Zhang, Z.; Zou, X.; Crespi, V.H.; Yakobson, B.I. Intrinsic Magnetism of Grain Boundaries in Two-Dimensional Metal Dichalcogenides. ACS Nano 2013, 7, 10475–10481. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Dai, Y.; Guo, M.; Niu, C.; Lu, J.; Huang, B. Electronic and magnetic properties of perfect, vacancy-doped, and nonmetal adsorbed MoSe2, MoTe2 and WS2 monolayers. Phys. Chem. Chem. Phys. 2011, 13, 15546–15553. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Fan, X.; Yang, Y.; Xiao, P. Strain engineering the magnetic states of vacancy-doped monolayer MoSe2. J. Alloys Compd. 2015, 635, 307–313. [Google Scholar] [CrossRef]
- Wasey, A.H.M.A.; Chakrabarty, S.; Das, G.P. Substrate induced modulation of electronic, magnetic and chemical properties of MoSe2 monolayer. AIP Adv. 2014, 4, 047107. [Google Scholar] [CrossRef]
- Liu, P.; Qin, Z.; Yue, Y.; Zuo, X. Structural, electronic, and magnetic properties of vanadium atom-adsorbed MoSe2 monolayer. Chin. Phys. B 2017, 26, 027103. [Google Scholar] [CrossRef]
- Luo, M.; Yin, H.H.; Chu, J.H. Strain-Dependent Electronic and Magnetic of Mg-Doped Monolayer of WS2. J. Supercond. Nov. Magn. 2017, 1–6. [Google Scholar] [CrossRef]
- Luo, M.; Hao, S.Y.; Yang, Y.T. Ab initio study of electronic and magnetic properties in Ni-doped WS2 monolaye. AIP Adv. 2016, 6, 085112. [Google Scholar] [CrossRef]
- Luo, M.; Shen, Y.H. Effect of Strain on Magnetic Coupling in Ga-Doped WS2 Monolayer: Ab Initio Study. J. Supercond. Nov. Magn. 2017, 1–5. [Google Scholar] [CrossRef]
- Zhao, X.; Xia, C.; Wang, T.; Dai, X. Electronic and magnetic properties of X-doped (X = Ti, Zr, Hf) tungsten disulphide monolayer. J. Alloys Compd. 2016, 654, 574–579. [Google Scholar] [CrossRef]
- Li, W.; Fang, C.; van Huis, M.A. Strong spin-orbit splitting and magnetism of point defect states in monolayer WS2. Phys. Rev. B 2016, 94, 19542. [Google Scholar] [CrossRef]
- Si, S.M.; Xue, D.S. Magnetic properties of vacancies in a graphitic boron nitride sheet by first-principles pseudopotential calculations. Phys. Rev. B 2007, 75, 193409. [Google Scholar] [CrossRef]
- Yang, J.; Kim, D.; Hong, J.; Qian, X. Magnetism in boron nitride monolayer: Adatom and vacancy defect. Surf. Sci. 2010, 604, 1603–1607. [Google Scholar] [CrossRef]
- Zhao, C.; Xu, Z.; Wang, H.; Wei, J.; Wang, W.; Bai, X.; Wang, E. Carbon-Doped Boron Nitride Nanosheets with Ferromagnetism above Room Temperature. Adv. Funct. Mater. 2014, 24, 5985–5992. [Google Scholar] [CrossRef]
- Wang, M.; Tang, S.; Ren, J.; Wang, B.; Han, Y.; Dai, Y. Magnetism in Boron Nitride Monolayer Induced by Cobalt or Nickel Doping. J. Supercond. Nov. Magn. 2017. [Google Scholar] [CrossRef]
- Ning, Z.-R.; Chen, Z.; Du, X.-J.; Ran, R.-X. Mn adsorption on C substituted BN sheet: First-principle study. Superlat. Microstr. 2013, 62, 175–181. [Google Scholar] [CrossRef]
- Ta, H.Q.; Zhao, L.; Pohl, D.; Pang, J.; Trzebicka, B.; Rellinghaus, B.; Pribat, D.; Gemming, T.; Liu, Z.; Bachmatiuk, A.; et al. Graphene-like ZnO: A Mini Review. Crystals 2016, 6, 100. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, H.; Chen, X. Electronic and magnetic properties of all 3d transition-metal-doped ZnO monolayersm. Int. J. Quant. Chem. 2013, 113, 2243–2250. [Google Scholar] [CrossRef]
- Cao, W.; Pankratov, V.; Huttula, M.; Shirmane, L.; Niu, Y.R.; Wang, F. X-ray photoemission electron microscope determination of origins of room temperature ferromagnetism and photoluminescence in high co-content CoxZn1−xO films. Surf. Rev. Lett. 2014, 21, 1450058. [Google Scholar] [CrossRef]
- Zhang, M.; Shi, X.; Wang, X.; Li, T.; Huttula, M.; Luo, Y.; Cao, W. Transition Metal Adsorbed-Doped ZnO Monolayer: 2D Dilute Magnetic Semiconductor, Magnetic Mechanism, and Beyond 2D. ACS Omega 2017, 2, 1192–1197. [Google Scholar] [CrossRef]
- Mahmood, J.; Lee, E.K.; Jung, M.; Shin, D.; Jeon, I.Y.; Jung, S.M.; Choi, H.J.; Seo, J.M.; Bae, S.Y.; Sohn, S.D.; et al. Nitrogenated holey two-dimensional structures. Nat. Commun. 2015, 6, 6486. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Li, W.; Zhou, H.; Zhang, X.; Zhao, M. Tunable C2N Membrane for High Efficient Water Desalination. Sci. Rep. 2016, 6, 29218. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Li, F.; Zhao, M. Efficient hydrogen isotopologues separation through a tunable potential barrier: The case of a C2N membrane. Sci. Rep. 2017, 7, 1483. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Guo, M.; Zhang, G.; Li, W. Tuning the Electronic and Magnetic Properties of Porous Graphene-like Carbon Nitride through 3d Transition-Metal Doping. Carbon 2017, 117, 120–125. [Google Scholar] [CrossRef]
- Choudhuri, I.; Pathak, B. Ferromagnetism and Half-Metallicity in Atomically Thin Holey Nitrogenated Graphene Based Systems. Chem. Phys. Chem. 2017, 18. [Google Scholar] [CrossRef] [PubMed]
- Gong, S.; Wan, W.; Guan, S.; Tai, B.; Liu, C.; Fu, B.; Yang, S.A.; Yao, Y. Tunable Half-metallic Magnetism in Atom-thin Holey Two-dimensional C2N Monolayer. J. Mater. Chem. C 2017, 5, 8424–8430. [Google Scholar] [CrossRef]
- Grasso, V. Electronic Structure and Electronic Transitions in Layered Materials; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1986. [Google Scholar]
- De Jongh, L.J. Magnetic Properties of Layered Transition Metal Compounds; Kluwer Academic Press: Dordrecht, The Netherlands, 1990. [Google Scholar]
- McGuire, M.A.; Dixit, H.; Cooper, V.R.; Sales, B.C. Coupling of crystal structure and magnetism in the layered, ferromagnetic insulator CrI3. Chem. Mater. 2015, 27, 612–620. [Google Scholar] [CrossRef]
- McGuire, M.A. Crystal and Magnetic Structures in Layered, Transition Metal Dihalides and Trihalides. Crystals 2017, 7, 121. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef] [PubMed]
- Kulish, V.V.; Huang, W. Single-layer metal halides MX2 (X = Cl, Br, I): Stability and tunable magnetism from first principles and Monte Carlo simulations. J. Mater. Chem. C 2017, 5, 8734–8741. [Google Scholar] [CrossRef]
- Mastrogiuseppe, D.; Sandler, N.; Ulloa, S.E. RKKY interaction and intervalley processes in p-doped transition-metal dichalcogenides. Phys. Rev. B 2014, 90, 161403. [Google Scholar] [CrossRef]
- Ávalos-Ovando, O.; Mastrogiuseppe, D.; Ulloa, S.E. Noncollinear exchange interaction in transition metal dichalcogenide edges. Phys. Rev. B 2016, 93, 161404. [Google Scholar] [CrossRef]
- Ávalos-Ovando, O.; Mastrogiuseppe, D.; Ulloa, S.E. Symmetries and hybridization in the indirect interaction between magnetic moments in MoS2 nanoflakes. Phys. Rev. B 2016, 94, 245429. [Google Scholar] [CrossRef]
- Ávalos-Ovando, O.; Mastrogiuseppe, D.; Ulloa, S.E. Effective dimensionality of the indirect interaction on the edges of MoS2 triangular flakes. J. Phys. Condens. Matter 2017, in press. [Google Scholar] [CrossRef]
- Mastrogiuseppe, D.; Sandler, N.; Ulloa, S.E. Hybridization and anisotropy in the exchange interaction in three-dimensional Dirac semimetals. Phys. Rev. B 2016, 93, 094433. [Google Scholar] [CrossRef]
- Campbell, V.E.; Tonelli, M.; Cimatti, I.; Moussy, J.B.; Tortech, L.; Dappe, Y.J.; Rivière, E.; Guillot, R.; Delprat, S.; Mattana, R.; et al. Engineering the magnetic coupling and anisotropy at the molecule–magnetic surface interface in molecular spintronic devices. Nat. Commun. 2016, 7, 13646. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Yang, G.H.; Jiang, Y. Topological textures and their bifurcation processes in 2D ferromagnetic thin films. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 84, 37–45. [Google Scholar] [CrossRef]
- Hoffmann, A.; Schultheiß, H. Mesoscale magnetism. Curr. Opin. Solid State Mater. Sci. 2015, 19, 253–263. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Liu, H.P.; Cao, W.; Gao, K.-L. Testing spatial noncommutativity via magnetic hyperfine structure induced by fractional angular momentum of Rydberg system. EPL Europhys. Lett. 2012, 98, 40002. [Google Scholar] [CrossRef]
- Zhang, J.-Z. Testing Spatial Noncommutativity via Rydberg Atoms. Phys. Rev. Lett. 2004, 93, 043002. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Pan, J.; Yang, Z.; Zhou, L.; Xiong, X.; Ouyang, F. Charge and strain induced magnetism in monolayer MoS2 with S vacancy. J. Magn. Magn. Mater. 2018, 451, 520–525. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, C.; Li, F.; Li, T.; Zhang, M.; Cao, W. Improved photocatalytic Bi2WO6/BiOCl heterojunctions: One-step synthesis via an ionic-liquid assisted ultrasonic method and first-principles calculations. Mol. Catal. 2017, 435, 33–48. [Google Scholar] [CrossRef]
- Slobodskyy, A.H.; Dugaev, V.K.; Vieira, M. Ferromagnetic ordering in diluted magnetic semiconductors. Condens. Matter Phys. 2002, 5, 531–540. [Google Scholar] [CrossRef]
- Liu, X.; Wang, C.-Z.; Lin, H.-Q.; Ho, K.-M. Magnetic moment enhancement for Mn7 cluster on graphene. J. Phys. Chem. C 2014, 118, 19123–19128. [Google Scholar] [CrossRef]
- Xie, M.D.; Tan, C.G.; Zhou, P.; Lin, J.G.; Sun, L.Z. Ferrimagnetic half-metallic properties of Cr/Fe δ doped MoS2 monolayer. RSC Adv. 2017, 7, 20116–20122. [Google Scholar] [CrossRef]
- Shu, H.; Luo, P.; Liang, P.; Cao, D.; Chen, X. Layer-dependent dopant stability and magnetic exchange coupling of iron-doped MoS2 nanosheets. ACS Appl. Mater. Interfaces 2015, 7, 7534–7541. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Yi, J.B.; Shen, L.; Wu, R.Q.; Yang, J.H.; Lin, J.Y.; Feng, Y.P.; Ding, J.; Van, L.H.; Yin, J.H. Room-Temperature Ferromagnetism in Carbon-Doped ZnO. Phys. Rev. Lett. 2007, 99, 127201. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Xiang, H.J.; Wei, S.-H.; Li, S.-S.; Xia, J.-B.; Li, J. Origin and Enhancement of Hole-Induced Ferromagnetism in First-Row d0 Semiconductor. Phys. Rev. Lett. 2009, 102, 017201. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, G.; Li, L. Synthesis strategies about 2D materials. In Two-Dimensional Materials—Synthesis, Characterization and Potential Applications; Nayak, P.K., Ed.; InTechOpen: Vienna, Austria, 2016; pp. 1–20. ISBN 978-953-51-2555-6. [Google Scholar]
- Lin, Z.; McCreary, A.; Briggs, N.; Subramanian, S.; Zhang, K.; Sun, Y.; Li, X.; Borys, N.J.; Yuan, H.; Fullerton-Shirey, S.K.; et al. 2D materials advances: From large scale synthesis and controlled heterostructures to improved characterization techniques, defects and applications. 2D Mater. 2016, 3, 042001. [Google Scholar] [CrossRef]
- Tedstone, A.A.; Lewis, D.J.; O’Brien, P. Synthesis, Properties, and Applications of Transition Metal-Doped Layered Transition Metal Dichalcogenides. Chem. Mater. 2016, 28, 1965–1974. [Google Scholar] [CrossRef]
- Zhang, K.; Feng, S.; Wang, J.; Azcatl, A.; Lu, N.; Addou, R.; Wang, N.; Zhou, C.; Lerach, J.; Bojan, V.; et al. Manganese Doping of Monolayer MoS2: The Substrate Is Critical. Nano Lett. 2015, 15, 6586–6591. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.K.; Shao, W.Z.; Xu, C.Y.; Li, Y.; Ren, D.D.; Song, X.G.; Zhen, L. Chemical Vapor Deposition Growth of Degenerate p-Type Mo-Doped ReS2 Films and Their Homojunction. ACS Appl. Mater. Interfaces 2017, 9, 15583–15591. [Google Scholar] [CrossRef] [PubMed]
- Azcatl, A.; Qin, X.; Prakash, A.; Zhang, C.; Cheng, L.; Wang, Q.; Lu, N.; Kim, M.J.; Kim, J.; Cho, K.; et al. Covalent nitrogen doping and compressive strain in MoS2 by remote N2 plasma exposure. Nano Lett. 2016, 16, 5437–5443. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Tseng, L.-T.; Murmu, P.P.; Bao, N.; Kennedy, J.; Ionesc, M.; Ding, J.; Suzuki, K.; Li, S.; Yi, J. Defects engineering induced room temperature ferromagnetism in transition metal doped MoS2. Mater. Des. 2017, 121, 77–84. [Google Scholar] [CrossRef]
- Li, F.; Yang, C.; Li, Q.; Cao, W.; Li, T. The pH-controlled morphology transition of BiVO4 photocatalysts from microparticles to hollow microspheres. Mater. Lett. 2015, 145, 52–55. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, X.; Li, T.; Li, F.; Cao, W. Phase and morphology controllable synthesis of superhydrophobic Sb2O3 via a solvothermal method. J. Alloys Compd. 2017, 721, 149–156. [Google Scholar] [CrossRef]
- Yang, C.; Yang, X.; Li, F.; Li, T.; Cao, W. Controlled synthesis of hierarchical flower-like Sb2WO6 microspheres: Photocatalytic and superhydrophobic property. J. Ind. Eng. Chem. 2016, 39, 93–100. [Google Scholar] [CrossRef]
- Meng, W.; Bai, L.; Li, T.; Cao, W. Comparison of synthetic routes for large-scale synthesis of spherical BiVO4 with photocatalytic and superhydrophobic properties. Chem. Lett. 2018, 47, 148–151. [Google Scholar] [CrossRef]
- Yang, C.; Li, F.; Zhang, M.; Li, T.; Cao, W. Preparation and first-principles study for electronic structures of BiOI/BiOCl composites with highly improved photocatalytic and adsorption performances. J. Mol. Catal. A Chem. 2016, 423, 1–11. [Google Scholar] [CrossRef]
- Zhu, S.; Li, Q.; Li, F.; Cao, W.; Li, T. One-pot synthesis of Ag+ doped BiVO4 microspheres with enhanced photocatalytic activity via a facile hydrothermal method. J. Phys. Chem. Solids 2016, 92, 11–18. [Google Scholar] [CrossRef]
- Zhu, S.; Li, Q.; Huttula, M.; Li, T.; Cao, W. One-pot hydrothermal synthesis of BiVO4 microspheres with mixed crystal phase and Sm3+-doped BiVO4 for enhanced photocatalytic activity. J. Mater. Sci. 2017, 52, 1679–1693. [Google Scholar] [CrossRef]
- Savjani, N.; Lewis, E.A.; Bissett, M.A.; Brent, J.R.; Dryfe, R.A.W.; Haigh, S.J.; O’Brien, P. Synthesis of Lateral Size-Controlled Monolayer 1H-MoS2@Oleylamine as Supercapacitor Electrodes. Chem. Mater. 2016, 28, 657–664. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, B.; Wang, X.; Yao, N.; Gao, Z.; Ma, Y.; Zhang, L.; Ma, H. Nano-structure, magnetic and optical properties of Co-doped ZnO films prepared by a wet chemical method. J. Phys. D Appl. Phys. 2008, 41, 215308. [Google Scholar] [CrossRef]
- Narkiewicz, U.; Sibera, D.; Kuryliszyn-Kudelska, I.; Kilanski, L.; Dobrowolski, W.; Romcevic, N. Synthesis by Wet Chemical Method and Characterization of Nanocrystalline ZnO Doped with Fe2O3. Act. Phys. Pol. A 2008, 113, 1695–1700. [Google Scholar] [CrossRef]
- Ramakrishna Matte, H.S.S.; Gomathi, A.; Manna, A.K.; Late, D.J.; Datta, R.; Pati, S.K.; Rao, C.N.R. MoS2 and WS2 analogues of graphene. Angew. Chem. Inter. Ed. 2010, 49, 4059–4062. [Google Scholar] [CrossRef] [PubMed]
- Jawid, A.; Nepal, D.; Park, K.; Jespersen, M.; Qualley, A.; Mirau, P.; Drummy, L.F.; Vaia, R.A. Mechanism for Liquid Phase Exfoliation of MoS2. Chem. Mater. 2016, 28, 337–348. [Google Scholar] [CrossRef]
- Zheng, Z.D.; Wang, X.C.; Mi, W.B. Tunable electronic structure in stained two dimensional van der Waals g-C2N/XSe2 (X = Mo, W) heterostructures. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 94, 148–152. [Google Scholar] [CrossRef]
- Zong, X.; Yan, H.; Wu, G.; Ma, G.; Wen, F.; Wang, L.; Li, C. Enhancement of Photocatalytic H2 Evolution on CdS by Loading MoS2 as Cocatalyst under Visible Light Irradiation. J. Am. Chem. Soc. 2008, 130, 7176–7177. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).