Lempel-Ziv Complexity of Photonic Quasicrystals
Abstract
:1. Introduction
2. Generalized Fibonacci Quasicrystals
3. Spectral Measures of Generalized Fibonacci Quasicrystals
4. Lempel-Ziv Complexity
5. Complexity of Generalized Fibonacci Quasicrystals
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Joannopoulos, J.D.; Meade, R.D.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Buscha, K.; von Freymann, G.; Linden, S.; Mingaleev, S.; Tkeshelashvili, L.; Wegenerd, M. Periodic nanostructures for photonics. Phys. Rep. 2007, 444, 101–202. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Lekner, J. Theory of Reflection; Kluwer: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Fink, Y.; Winn, J.N.; Fan, S.; Chen, C.; Michel, J.; Joannopoulos, J.D.; Thomas, E.L. A dielectric omnidirectional reflector. Science 1998, 282, 1679–1682. [Google Scholar] [CrossRef] [PubMed]
- Dowling, J.P. Mirror on the wall: You’re omnidirectional after all? Science 1998, 282, 1841–1842. [Google Scholar] [CrossRef]
- Yablonovitch, E. Engineered omnidirectional external-reflectivity spectra from one-dimensional layered interference filters. Opt. Lett. 1998, 23, 1648–1649. [Google Scholar] [CrossRef] [PubMed]
- Chigrin, D.N.; Lavrinenko, A.V.; Yarotsky, D.A.; Gaponenko, S.V. All-dielectric one-dimensional periodic structures for total omnidirectional reflection and partial spontaneous emission control. J. Lightw. Technol. 1999, 17, 2018–2024. [Google Scholar] [CrossRef]
- Lekner, J. Omnidirectional reflection by multilayer dielectric mirrors. J. Opt. A 2000, 2, 349–352. [Google Scholar] [CrossRef]
- Kramer, B.; MacKinnon, A. Localization: Theory and experiment. Rep. Prog. Phys. 1993, 56, 1469–1564. [Google Scholar] [CrossRef]
- Segev, M.; Silberberg, Y.; Christodoulides, D.N. Anderson localization of light. Nat. Photonics 2013, 7, 197–204. [Google Scholar] [CrossRef]
- Lagendijk, A.; van Tiggelen, B.A. Resonant multiple scattering of light. Phys. Rep. 1996, 270, 143–215. [Google Scholar] [CrossRef]
- Van Tiggelen, B.A. Transverse Diffusion of Light in Faraday-Active Media. Phys. Rev. Lett. 1995, 75, 422–424. [Google Scholar] [CrossRef] [PubMed]
- Steurer, W.; Sutter-Widmer, D. Photonic and phononic quasicrystals. J. Phys. D 2007, 40, R229–R247. [Google Scholar] [CrossRef]
- Poddubny, A.; Ivchenko, E. Photonic quasicrystalline and aperiodic structures. Phys. E 2010, 42, 1871–1895. [Google Scholar] [CrossRef]
- Dal Negro, L.; Boriskina, S.V. Deterministic aperiodic nanostructures for photonics and plasmonics applications. Laser Photon. Rev. 2012, 6, 178–218. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Ostlund, S. The Physics of Quasicrystals; World Scientific: Singapore, 1987. [Google Scholar]
- Senechal, M. Quasicrystals and Geometry; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Janot, C. Quasicrystals: A Primer, 2nd ed.; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Vardeny, Z.V.; Nahata, A.; Agrawal, A. Optics of photonic quasicrystals. Nat. Photonics 2013, 7, 177–187. [Google Scholar] [CrossRef]
- Dal Negro, L.; Wang, R.; Pinheiro, F. Structural and Spectral Properties of Deterministic Aperiodic Optical Structures. Crystals 2016, 6, 161. [Google Scholar] [CrossRef]
- Albuquerque, E.L.; Cottam, M.G. Theory of elementary excitations in quasiperiodic structures. Phys. Rep. 2003, 376, 225–337. [Google Scholar] [CrossRef]
- Gumbs, G.; Ali, M.K. Dynamical maps, Cantor spectra, and localization for Fibonacci and related quasiperiodic lattices. Phys. Rev. Lett. 1988, 60, 1081–1084. [Google Scholar] [CrossRef] [PubMed]
- Nori, F.; Rodríguez, J.P. Acoustic and electronic properties of one-dimensional quasicrystals. Phys. Rev. B 1986, 34, 2207–2211. [Google Scholar] [CrossRef]
- Dulea, M.; Johansson, M.; Riklund, R. Localization of electrons and electromagnetic waves in a deterministic aperiodic system. Phys. Rev. B 1992, 45, 105–114. [Google Scholar] [CrossRef]
- Boriskina, S.V.; Gopinath, A.; Negro, L.D. Optical gap formation and localization properties of optical modes in deterministic aperiodic photonic structures. Opt. Express 2008, 16, 18813–18826. [Google Scholar] [CrossRef] [PubMed]
- Maciá, E.; Domínguez-Adame, F. Physical nature of critical wave functions in Fibonacci systems. Phys. Rev. Lett. 1996, 76, 2957–2960. [Google Scholar] [CrossRef] [PubMed]
- Thiem, S.; Schreiber, M.; Grimm, U. Wave packet dynamics, ergodicity, and localization in quasiperiodic chains. Phys. Rev. B 2009, 80, 214203. [Google Scholar] [CrossRef]
- Fujiwara, T.; Kohmoto, M.; Tokihiro, T. Multifractal wave functions on a Fibonacci lattice. Phys. Rev. B 1989, 40, 7413–7416. [Google Scholar] [CrossRef]
- Monsoriu, J.A.; Villatoro, F.R.; Marín, M.J.; Pérez, J.; Monreal, L. Quantum fractal superlattices. Am. J. Phys. 2006, 74, 831–836. [Google Scholar] [CrossRef]
- Esaki, K.; Sato, M.; Kohmoto, M. Wave propagation through Cantor-set media: Chaos, scaling, and fractal structures. Phys. Rev. E 2009, 79, 056226. [Google Scholar] [CrossRef] [PubMed]
- Maciá, E. The role of aperiodic order in science and technology. Rep. Prog. Phys. 2006, 69, 397–441. [Google Scholar] [CrossRef]
- Maciá, E. Aperiodic Structures in Condensed Matter: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Merlin, R.; Bajema, K.; Clarke, R.; Juang, F.Y.; Bhattacharya, P.K. Quasiperiodic GaAs-AlAs Heterostructures. Phys. Rev. Lett. 1985, 55, 1768–1770. [Google Scholar] [CrossRef] [PubMed]
- Kohmoto, M.; Kadanoff, L.P.; Tang, C. Localization problem in one dimension: Mapping and escape. Phys. Rev. Lett. 1983, 50, 1870–1872. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sutherland, B.; Iguchi, K. Localization in optics: Quasiperiodic media. Phys. Rev. Lett. 1987, 58, 2436–2438. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.H. Propagation of light waves in Thue-Morse dielectric multilayers. Phys. Rev. B 1997, 55, 3543–3547. [Google Scholar] [CrossRef]
- Tamura, S.; Nori, F. Transmission and frequency spectra of acoustic phonons in Thue-Morse superlattices. Phys. Rev. B 1989, 40, 9790–9801. [Google Scholar] [CrossRef]
- Kolář, M.; Ali, M.K.; Nori, F. Generalized Thue-Morse chains and their physical properties. Phys. Rev. B 1991, 43, 1034–1047. [Google Scholar] [CrossRef]
- Luck, J.M. Cantor spectra and scaling of gap widths in deterministic aperiodic systems. Phys. Rev. B 1989, 39, 5834–5849. [Google Scholar] [CrossRef]
- Cojocaru, E. Forbidden gaps in finite periodic and quasi-periodic Cantor-like dielectric multilayers at normal incidence. Appl. Opt. 2001, 40, 6319–6326. [Google Scholar] [CrossRef] [PubMed]
- Holzer, M. Three classes of one-dimensional, two-tile Penrose tilings and the Fibonacci Kronig-Penney model as a generic case. Phys. Rev. B 1988, 38, 1709–1720. [Google Scholar] [CrossRef]
- Severin, M.; Dulea, M.; Riklund, R. Periodic and quasiperiodic wavefunctions in a class of one-dimensional quasicrystals: An analytical treatment. J. Phys. Condens. Matter 1989, 1, 8851–8858. [Google Scholar] [CrossRef]
- Dulea, M.; Severin, M.; Riklund, R. Transmission of light through deterministic aperiodic non-Fibonaccian multilayers. Phys. Rev. B 1990, 42, 3680–3689. [Google Scholar] [CrossRef]
- Oh, G.Y.; Lee, M.H. Band-structural and Fourier-spectral properties of one-dimensional generalized Fibonacci lattices. Phys. Rev. B 1993, 48, 12465–12477. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Karmakar, S.N. Renormalization-group method for exact Green’s functions of self-similar lattices: Application to generalized Fibonacci chains. Phys. Rev. B 1991, 44, 896–899. [Google Scholar] [CrossRef]
- Fu, X.; Liu, Y.; Zhou, P.; Sritrakool, W. Perfect self-similarity of energy spectra and gap-labeling properties in one-dimensional Fibonacci-class quasilattices. Phys. Rev. B 1997, 55, 2882–2889. [Google Scholar] [CrossRef]
- Wang, X.; Grimm, U.; Schreiber, M. Trace and antitrace maps for aperiodic sequences: Extensions and applications. Phys. Rev. B 2000, 62, 14020–14031. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, X.; Guo, Q.; Lan, S. Second-harmonic generation in GF(m, 1) ferroelectric superlattices. J. Phys. Condens. Matter 2006, 18, 2587–2600. [Google Scholar] [CrossRef]
- Thiem, S.; Schreiber, M. Photonic properties of metallic-mean quasiperiodic chains. Eur. Phys. J. B 2010, 76, 339–345. [Google Scholar] [CrossRef]
- Zhang, Z.; Tong, P.; Gong, J.; Li, B. Wave packet dynamics in one-dimensional linear and nonlinear generalized Fibonacci lattices. Phys. Rev. E 2011, 83, 056205. [Google Scholar] [CrossRef] [PubMed]
- Thiem, S.; Schreiber, M.; Grimm, U. Light transmission through metallic-mean quasiperiodic stacks with oblique incidence. Philos. Mag. 2011, 91, 2801–2810. [Google Scholar] [CrossRef]
- Costa, C.H.O.; Vasconcelos, M.S. Band gaps and transmission spectra in generalized Fibonacci σ(p,q) one-dimensional magnonic quasicrystals. J. Phys. Condens. Matter 2013, 25, 286002. [Google Scholar] [CrossRef] [PubMed]
- Barriuso, A.G.; Monzón, J.J.; Yonte, T.; Felipe, A.; Sánchez-Soto, L.L. Omnidirectional reflection from generalized Fibonacci quasicrystals. Opt. Express 2013, 21, 30039–30053. [Google Scholar] [CrossRef] [PubMed]
- Brandão, E.R.; Costa, C.H.; Vasconcelos, M.S.; Anselmo, D.H.A.L.; Mello, V.D. Octonacci photonic quasicrystals. Opt. Mater. 2015, 46, 378–383. [Google Scholar] [CrossRef]
- Sánchez, F.; Sánchez, V.; Wang, C. Renormalization approach to the electronic localization and transport in macroscopic generalized Fibonacci lattices. J. Noncryst. Solids 2016, 450, 194–208. [Google Scholar] [CrossRef]
- Spinadel, V.W. The metallic means family and multifractal spectra. Nonlinear Anal. 1999, 36, 721–745. [Google Scholar] [CrossRef]
- Lloyd, S. Measures of Complexity: A Non-Exhaustive List. Available online: http://web.mit.edu/esd.83/www/notebook/Complexity.PDF (accessed on 20 April 2017).
- Aboy, M.; Hornero, R.; Abásolo, D.; Álvarez, D. Interpretation of the Lempel-Ziv Complexity Measure in the Context of Biomedical Signal Analysis. IEEE Trans. Biomed. Eng. 2006, 53, 2282–2288. [Google Scholar] [CrossRef] [PubMed]
- Lothaire, M. Combinatorics on Words, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Queffélec, M. Substitutional Dynamics Systems—Spectral Analysis; Lectures Notes in Mathematics; Springer: Berlin, Germany, 1987; Volume 1294. [Google Scholar]
- Dunlap, R.A. The Golden Ratio and Fibonacci Numbers; World Scientific: Singapore, 1997. [Google Scholar]
- Sánchez-Soto, L.L.; Monzón, J.J.; Barriuso, A.G.; Cariñena, J.F. The transfer matrix: A geometrical perspective. Phys. Rep. 2012, 513, 191–227. [Google Scholar] [CrossRef]
- Monzón, J.J.; Yonte, T.; Sánchez-Soto, L.L.; Cariñena, J.F. Geometrical setting for the classification of multilayers. J. Opt. Soc. Am. A 2002, 19, 985–991. [Google Scholar] [CrossRef]
- Yonte, T.; Monzón, J.J.; Sánchez-Soto, L.L.; Cariñena, J.F.; López-Lacasta, C. Understanding multilayers from a geometrical viewpoint. J. Opt. Soc. Am. A 2002, 19, 603–609. [Google Scholar] [CrossRef]
- Bombieri, E.; Taylor, J.E. Which distributions of matter diffract? An initial investigation. J. Phys. Colloq. 1986, 47, 19–28. [Google Scholar] [CrossRef]
- Bombieri, E.; Taylor, J. Quasicrystals, tilings, and algebraic number theory. Contemp. Math. 1987, 64, 241–264. [Google Scholar]
- Godrèche, C.; Luck, J.M. Indexing the diffraction spectrum of a non-Pisot self-similar structure. Phys. Rev. B 1992, 45, 176–185. [Google Scholar] [CrossRef]
- Meyer, C.D. Matrix Analysis and Applied Linear Algebra; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Severin, M.; Riklund, R. Using the Fourier spectrum to classify families of generalised extensions of the Fibonaccian lattice. J. Phys. Condens. Matter 1989, 1, 5607–5612. [Google Scholar] [CrossRef]
- Cheng, Z.; Savit, R. Structure factor of substitutional sequences. J. Stat. Phys. 1990, 60, 383–393. [Google Scholar] [CrossRef]
- Bellissard, J.; Bovier, A.; Ghez, J.M. Gap labelling theorems for one-dimensional discrete Schrödinger operators. Rev. Math. Phys. 1992, 4, 1–37. [Google Scholar] [CrossRef]
- Manson, S.M. Simplifying complexity: A review of complexity theory. Geoforum 2001, 32, 405–414. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, IT-22, 75–81. [Google Scholar] [CrossRef]
- Thai, Q. Available online: https://de.mathworks.com/matlabcentral/fileexchange/38211-calc-lz-complexity (accessed on 15 June 2012).
- Schürmann, T. Scaling behaviour of entropy estimates. J. Phys. A 2002, 35, 1589. [Google Scholar] [CrossRef]
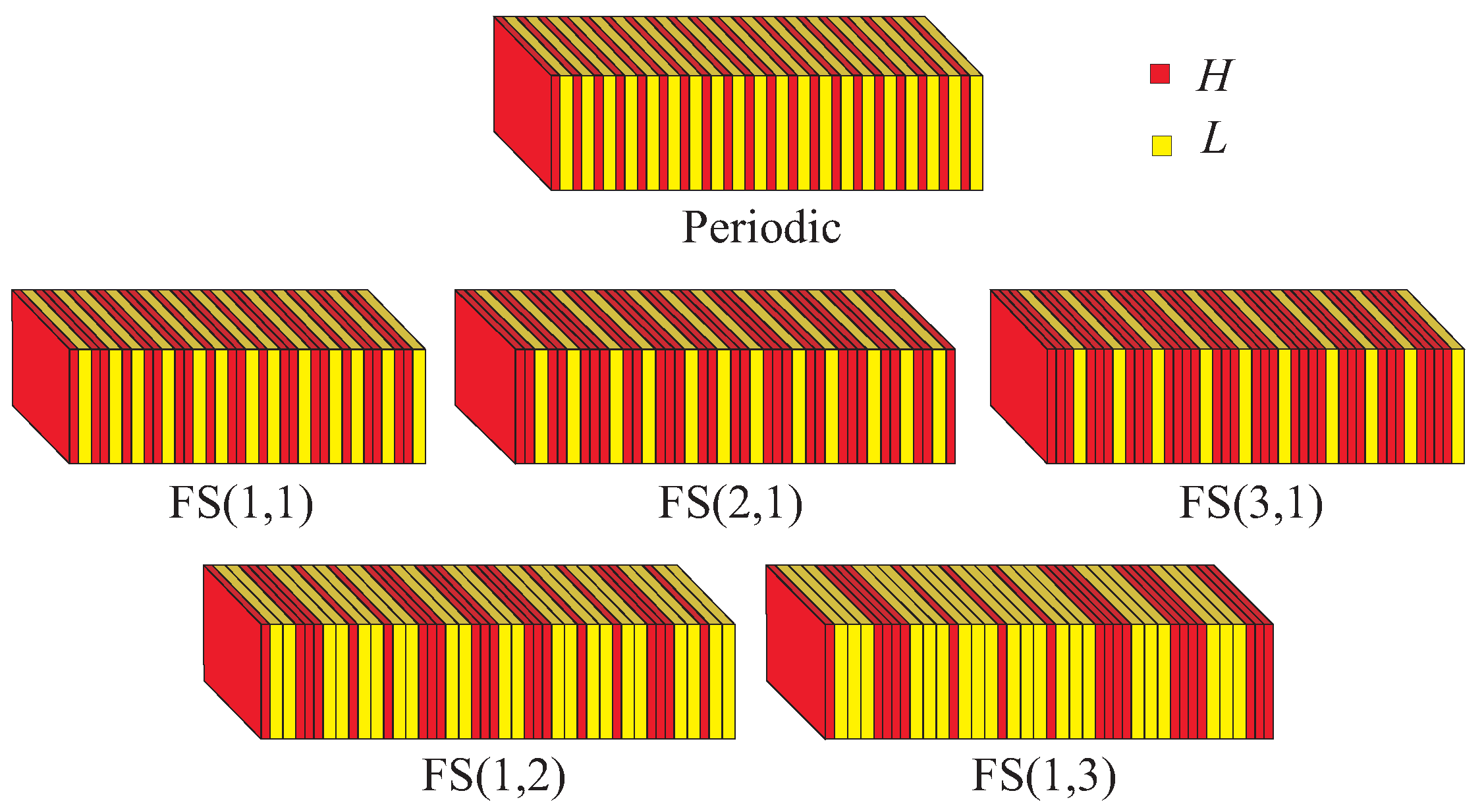

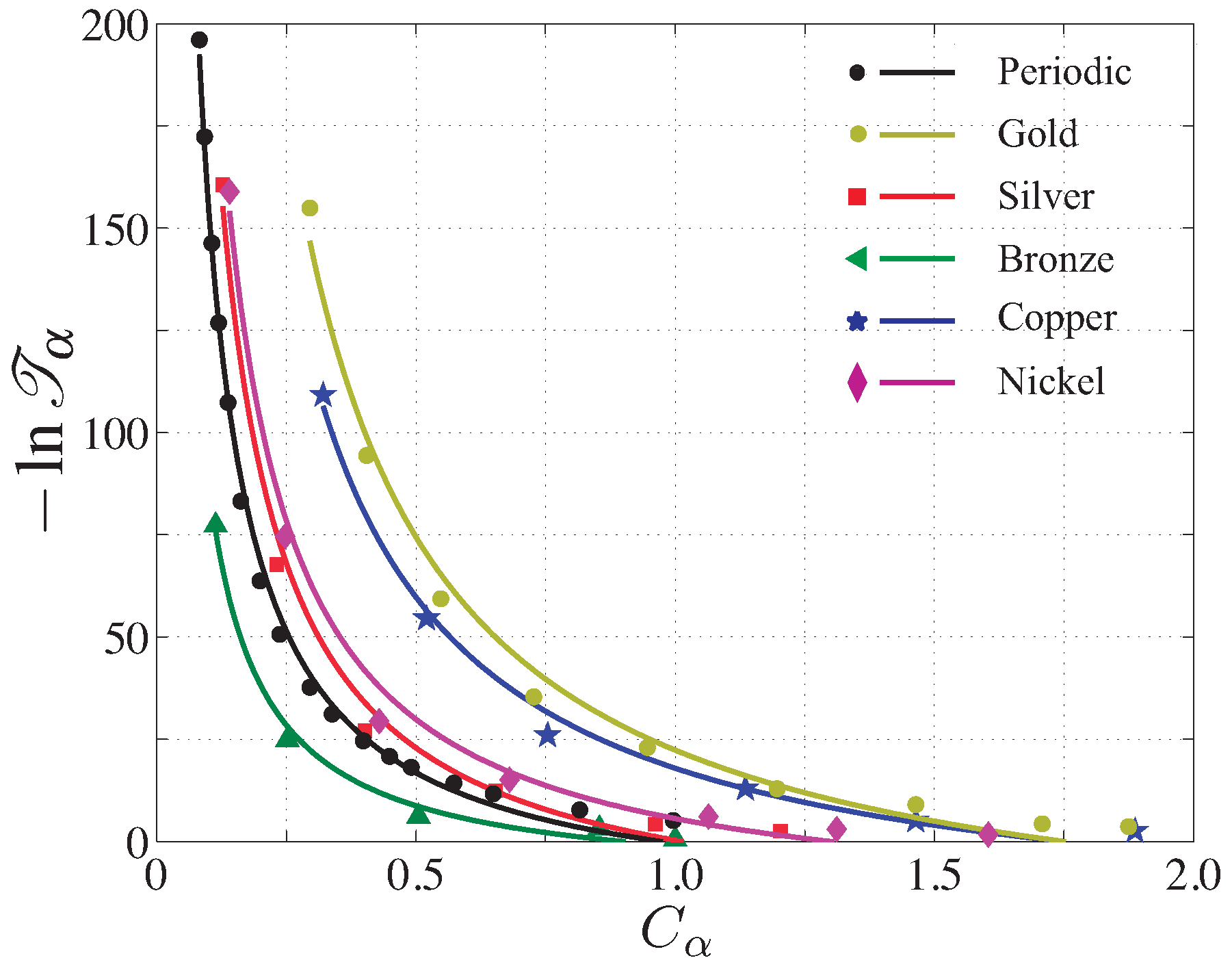
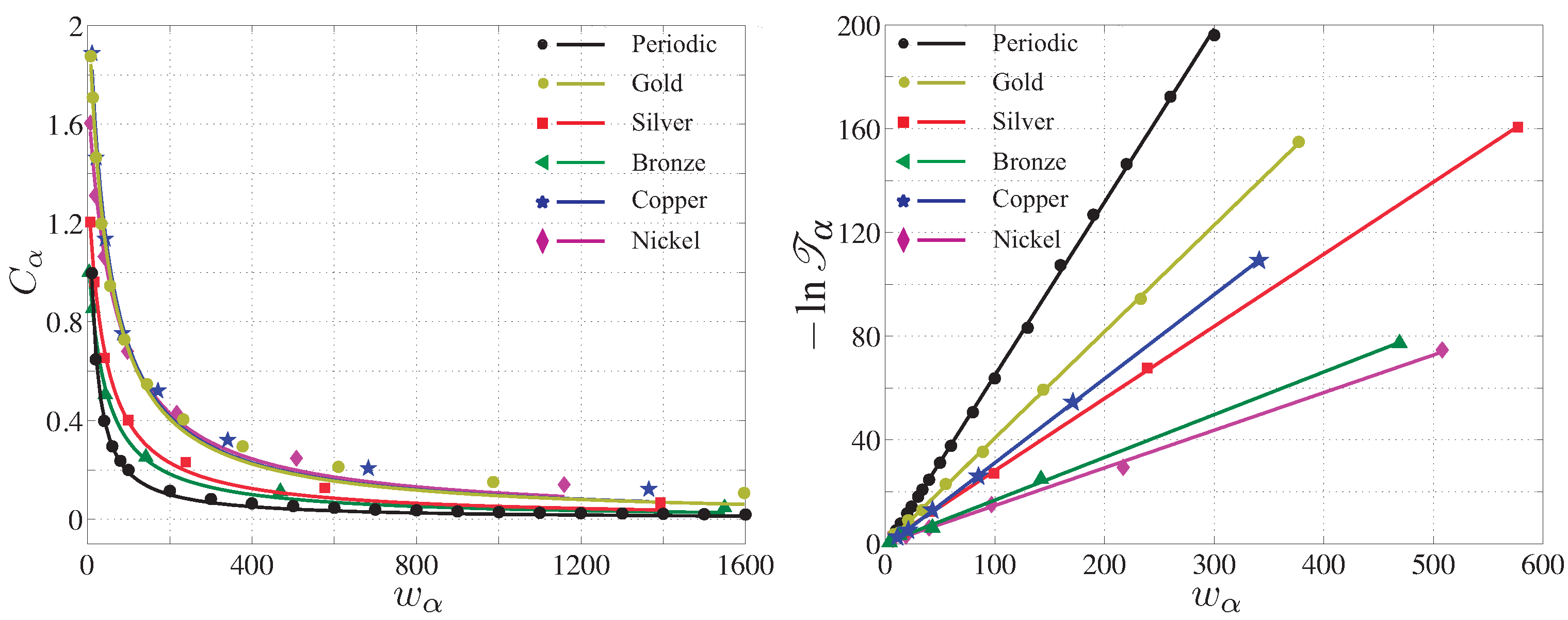
| System | Metal | ||
|---|---|---|---|
| Periodic | - | 0.2500 | 0.2500 |
| FS(1,1) | Gold | 0.2251 | 0.3417 |
| FS(2,1) | Silver | 0.2311 | 0.3809 |
| FS(3,1) | Bronze | 0.3416 | 0.2459 |
| FS(1,2) | Copper | 0.1249 | 0.2501 |
| FS(1,3) | Nickel | 0.2451 | 0.2277 |
| System | Metal | ||||||
|---|---|---|---|---|---|---|---|
| Periodic | - | −17.917 | 17.301 | 0.54422 | 0.04718 | −1.82860 | 0.66697 |
| FS(1,1) | Gold | −29.779 | 52.116 | 0.46257 | 0.00998 | −0.35174 | 0.41042 |
| FS(2,1) | Silver | −22.297 | 22.590 | 0.71580 | 0.01821 | 0.29576 | 0.27829 |
| FS(3,1) | Bronze | −10.953 | 9.847 | 0.90351 | 0.02264 | 0.28379 | 0.16478 |
| FS(1,2) | Copper | −23.922 | 41.833 | 0.44177 | 0.00980 | −1.27180 | 0.32427 |
| FS(1,3) | Nickel | −18.687 | 24.282 | 0.57597 | 0.00876 | 0.16579 | 0.14514 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monzón, J.J.; Felipe, A.; Sánchez-Soto, L.L. Lempel-Ziv Complexity of Photonic Quasicrystals. Crystals 2017, 7, 183. https://doi.org/10.3390/cryst7070183
Monzón JJ, Felipe A, Sánchez-Soto LL. Lempel-Ziv Complexity of Photonic Quasicrystals. Crystals. 2017; 7(7):183. https://doi.org/10.3390/cryst7070183
Chicago/Turabian StyleMonzón, Juan J., Angel Felipe, and Luis L. Sánchez-Soto. 2017. "Lempel-Ziv Complexity of Photonic Quasicrystals" Crystals 7, no. 7: 183. https://doi.org/10.3390/cryst7070183
APA StyleMonzón, J. J., Felipe, A., & Sánchez-Soto, L. L. (2017). Lempel-Ziv Complexity of Photonic Quasicrystals. Crystals, 7(7), 183. https://doi.org/10.3390/cryst7070183






