Combining Single- and Poly-Crystalline Measurements for Identification of Crystal Plasticity Parameters: Application to Austenitic Stainless Steel
Abstract
:1. Introduction
2. Constitutive Model
3. Two-Scale Calibration Strategy
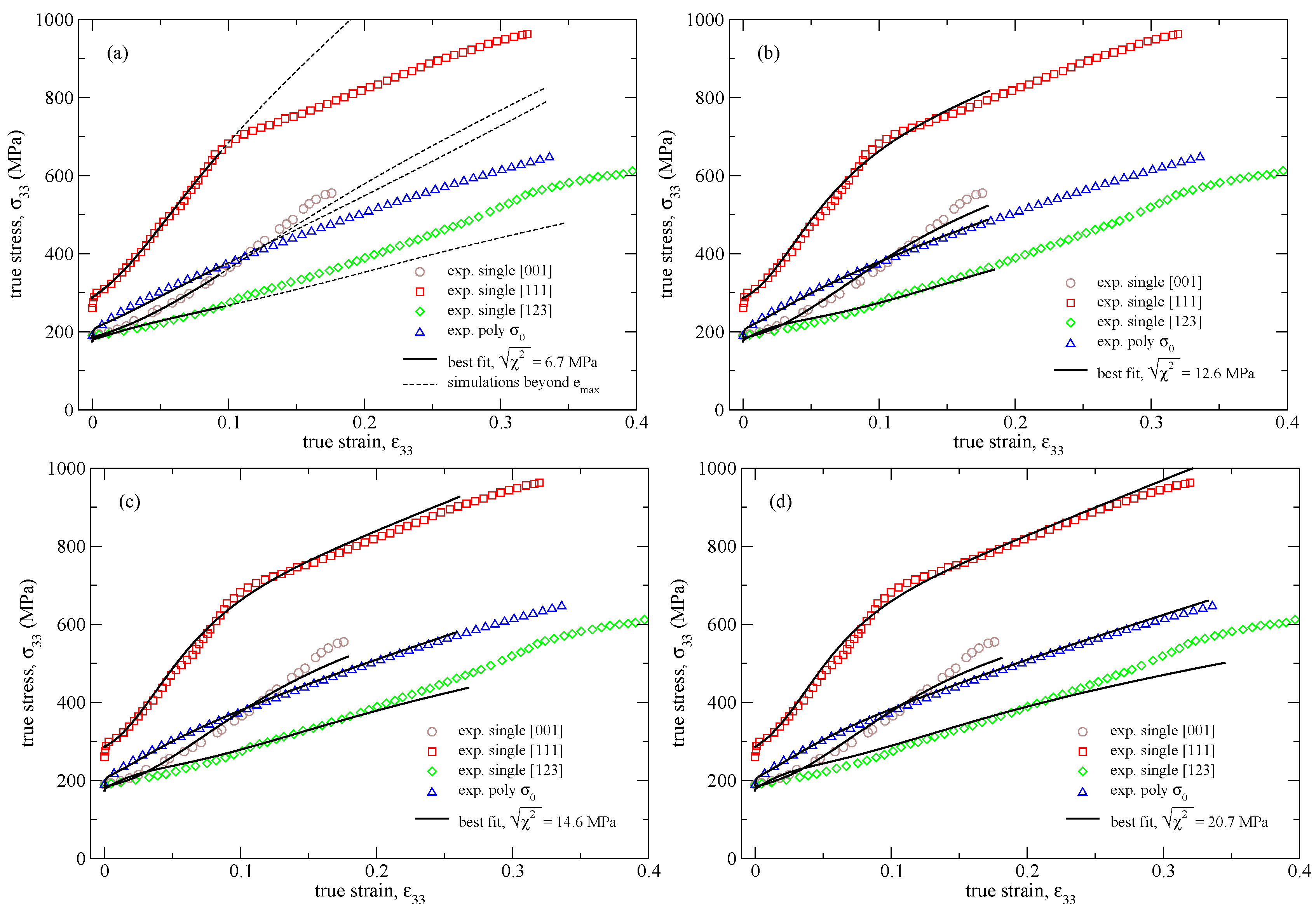
- The hardening parameters are identified on a grain scale by fitting the calculated tensile responses to corresponding experimental stress-strain curves. Simultaneous fitting is performed against single and polycrystalline tensile data.
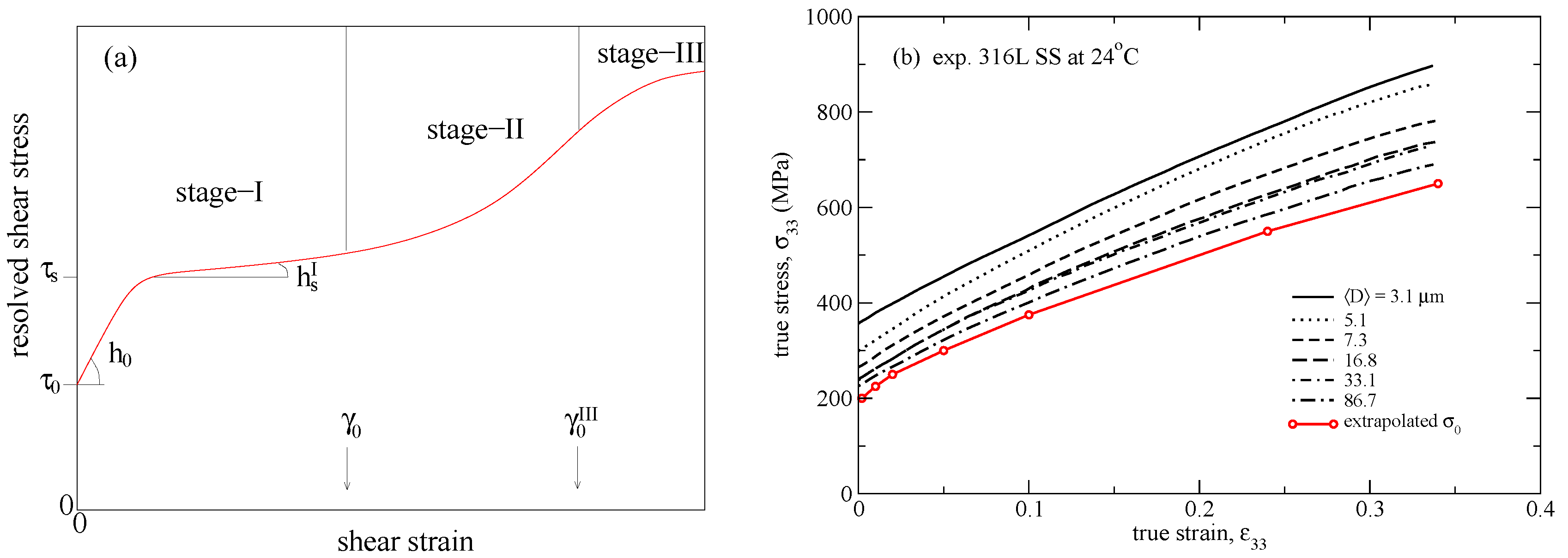
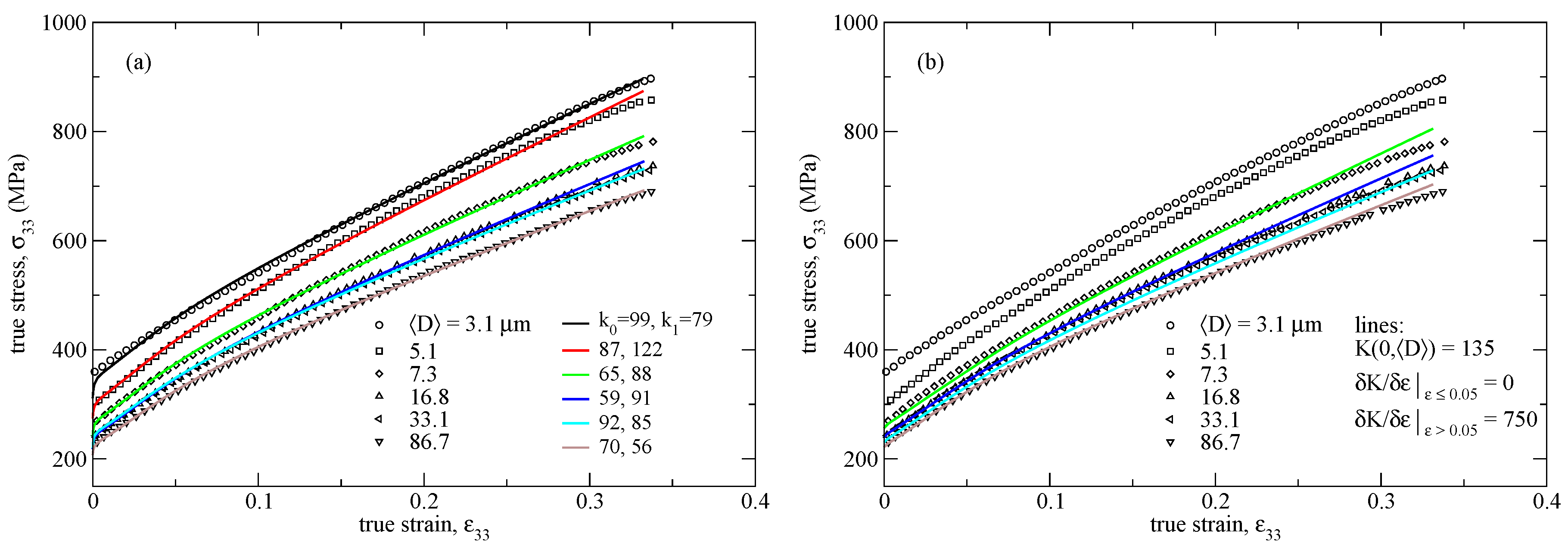
- Before being used in the calibration, the length scale effects due to grain boundary strengthening need to be subtracted from the measured polycrystalline data. The Hall–Petch relation is used to obtain the adjusted (infinite-grain-size) macroscopic tensile stress ( in Equation (1)).
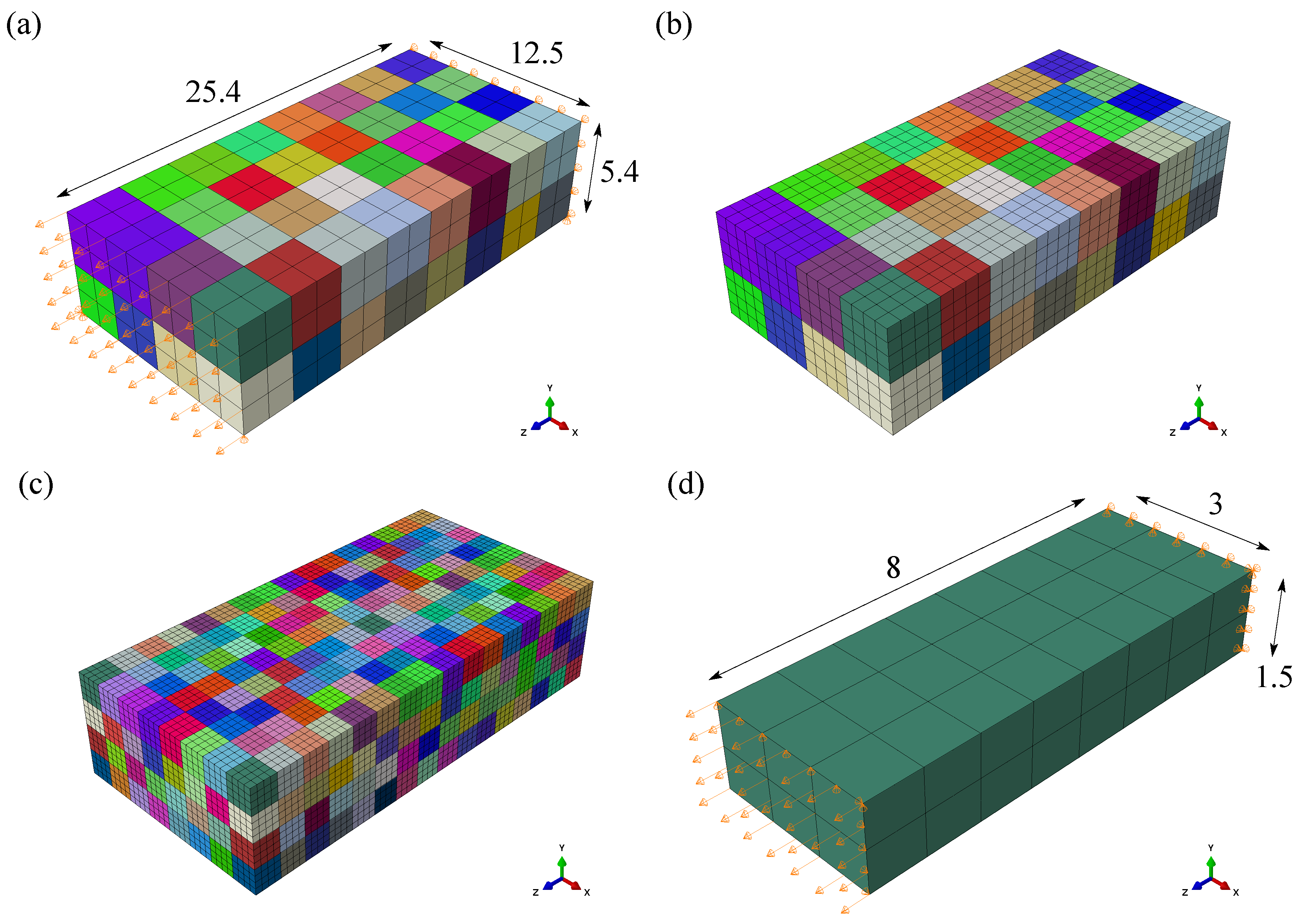
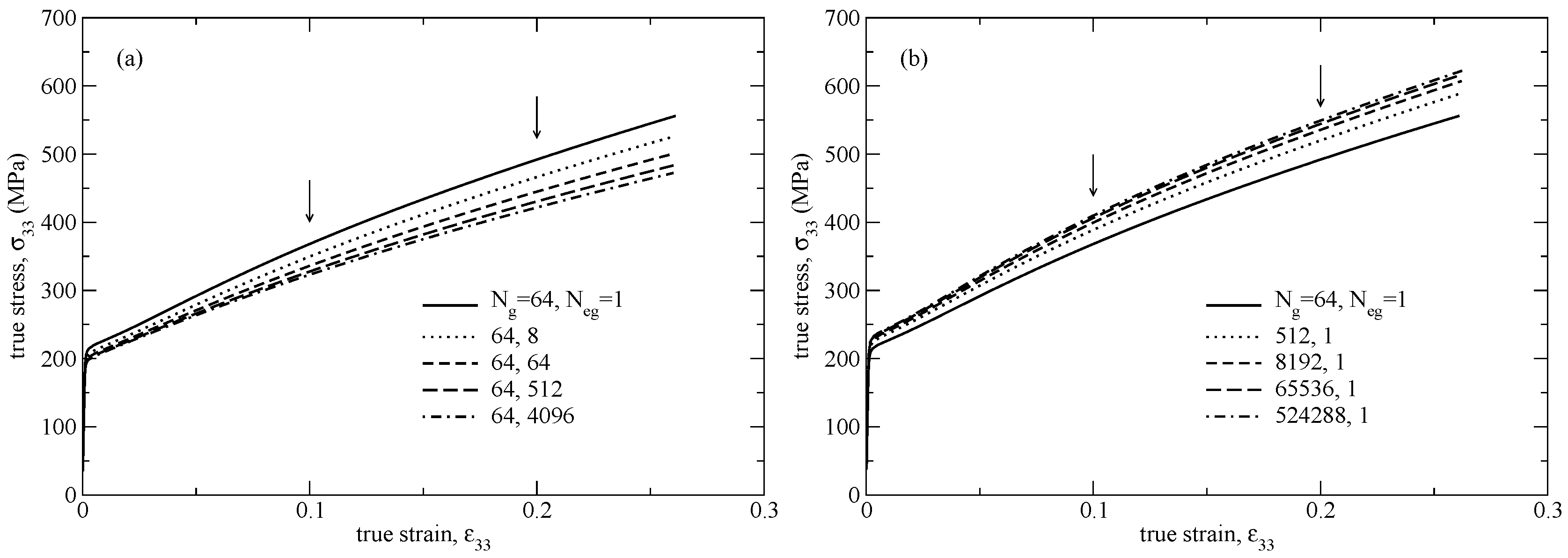
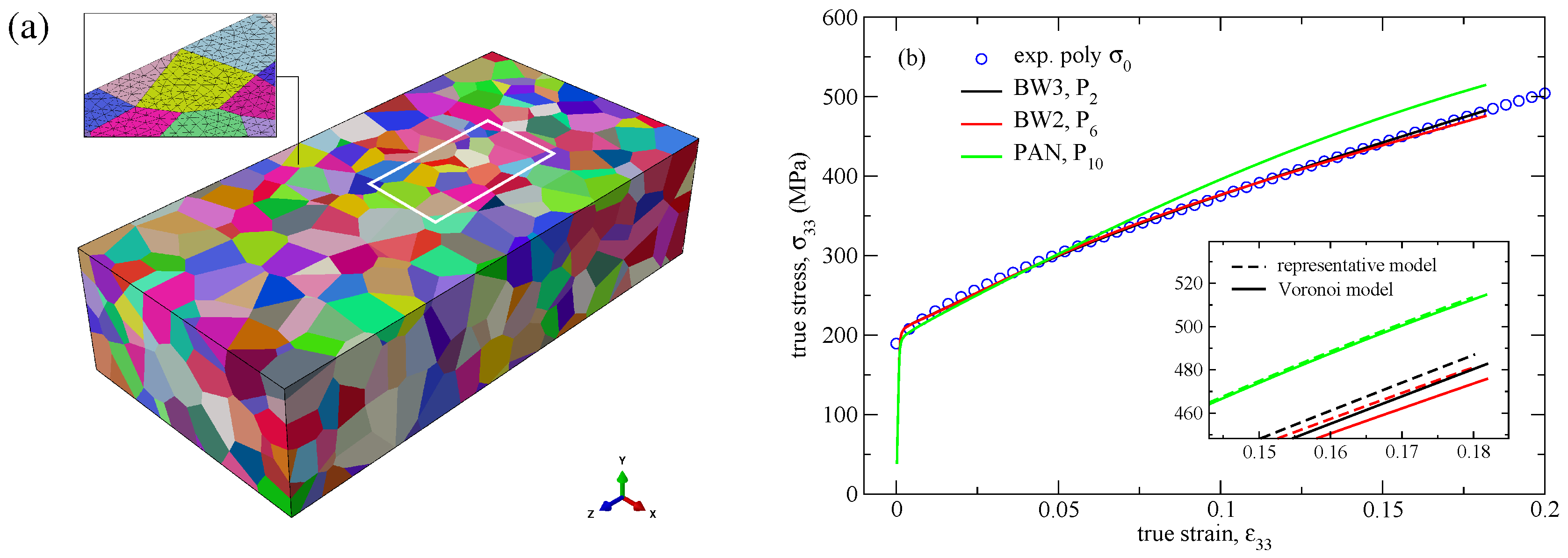
- The RVE model of the polycrystalline microstructure is identified and used in the identification procedure. To allow for fast simulations during calibration iterations, a small representative polycrystalline model is determined, containing a comparable number of finite elements as single crystalline FE models.
- The automated optimization procedure for hardening parameters is introduced where parameters are constrained to take only discrete values with a prescribed precision (step size).
3.1. Subtracting Grain Boundary Strengthening Effects from Raw Polycrystalline Data
3.2. Representative Volume Element
3.3. Single-Crystal Models
3.4. Automated Optimization of Model Parameters Defined on Discrete Range
4. Results of Model Calibration
4.1. Introduction of Length Scale into Crystal Plasticity
5. Discussion
5.1. Comparison with Simpler Hardening Models
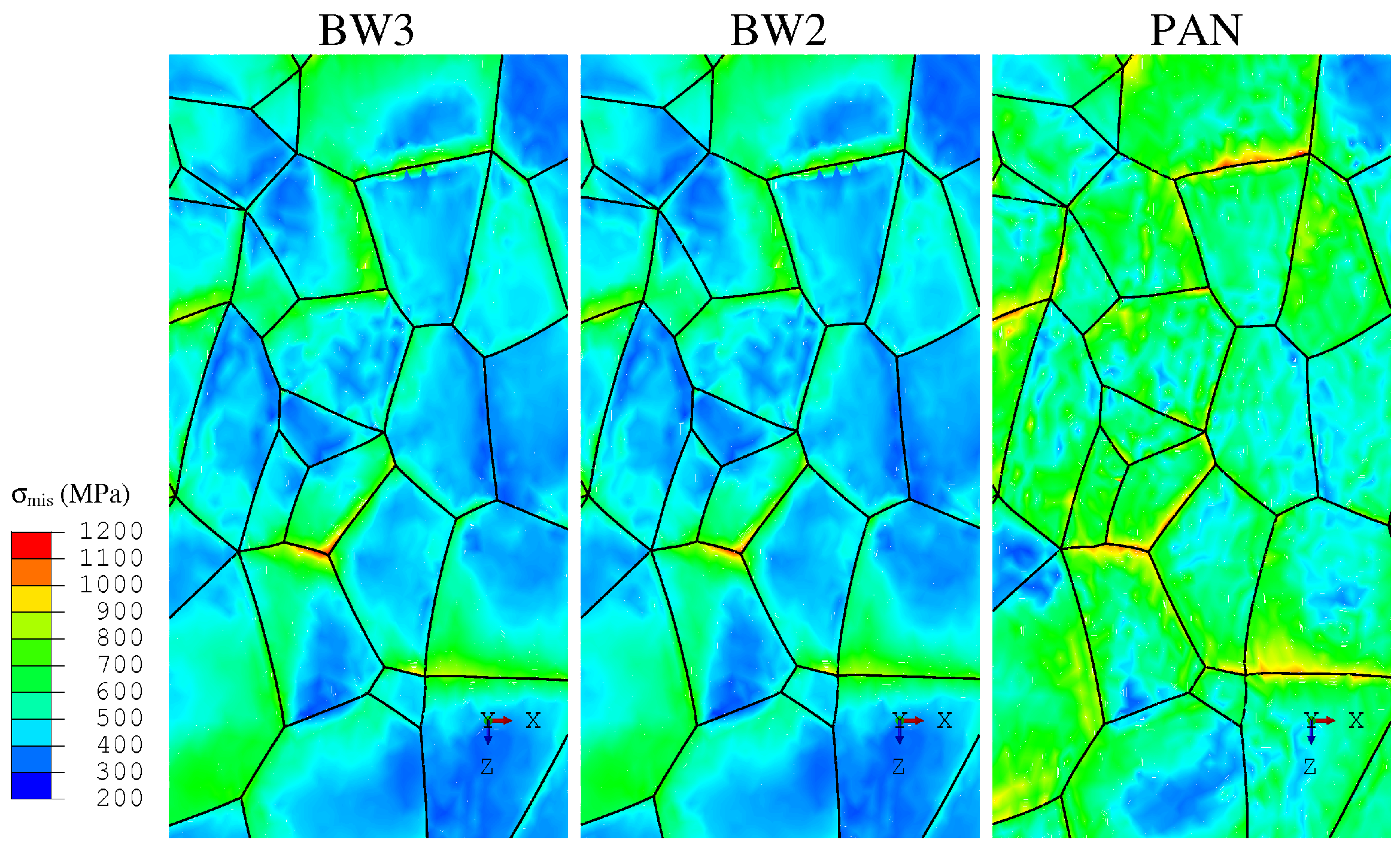
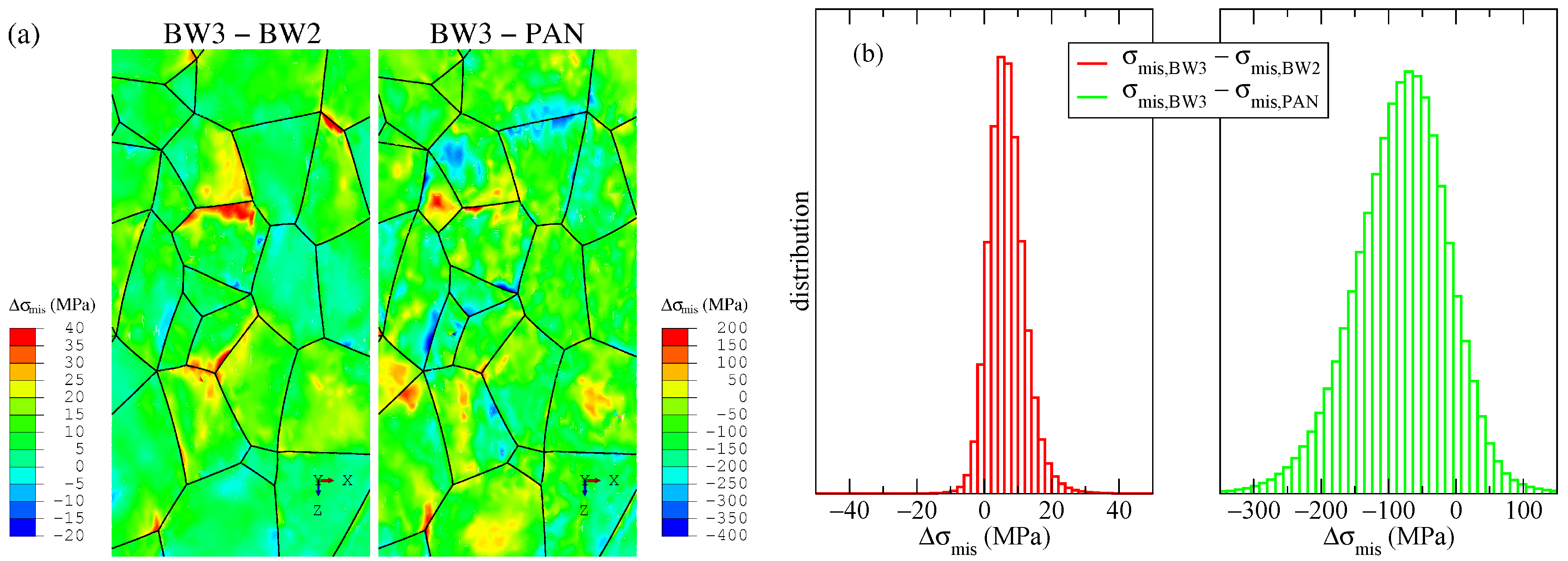
5.2. Local Fields
6. Conclusions
- A relatively small value of and a high value of in the Bassani and Wu hardening law indicate a short Stage I region and hard activation of cross slip during Stage II hardening. A low value of also suggests that self-hardening dominates over latent hardening.
- High similarities between two-stage and three-stage Bassani and Wu hardening models indicate a very slow Stage II to Stage III transition with slip.
- Grain boundary strengthening effects become relatively weak when average grain size m, thus providing negligible additional hardening in the tensile response.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I. Theoretical. In Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character; The Royal Society: London, UK, 1934; Volume 145, pp. 362–387. [Google Scholar]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part II. Comparison with observations. In Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character; The Royal Society: London, UK, 1934; Volume 145, pp. 388–404. [Google Scholar]
- Raabe, D.; Zhao, Z.; Park, S.J.; Roters, F. Theory of orientation gradients in plastically strained crystals. Acta Mater. 2002, 50, 421–440. [Google Scholar] [CrossRef]
- Zhao, Z.; Kuchnicki, S.; Radovitzky, R.; Cuitino, A. Influence of in-grain mesh resolution on the prediction of deformation textures in fcc polycrystals by crystal plasticity FEM. Acta Mater. 2007, 55, 2361–2373. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjanhjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Simonovski, I.; Cizelj, L. Towards modeling intergranular stress corrosion cracks on grain size scales. Nucl. Eng. Des. 2012, 246, 107–114. [Google Scholar] [CrossRef]
- Basseville, S.; Cailletaud, G.; Ghidossi, T.; Guilhem, Y.; Lacoste, E.; Proudhon, H.; Signor, L.; Villechaise, P. Numerical analysis on the local mechanical fields in polycrystalline 316LN stainless steel under cyclic fatigue loading: Comparison with experimental results. Mater. Sci. Eng. A 2017, 696, 122–136. [Google Scholar] [CrossRef]
- Asaro, R.J.; Needleman, A. Texture development and strain hardening in rate dependent polycrystals. Acta Mater. 1985, 33, 923–953. [Google Scholar] [CrossRef]
- Mathur, K.; Dawson, P. On modeling the development of crystallographic texture in bulk forming processes. Int. J. Plast. 1989, 5, 67–94. [Google Scholar] [CrossRef]
- Bronkhorst, C.A.; Kalidindi, S.R.; Anand, L. Polycrystalline plasticity and the evolution of crystallographic texture in FCC metals. Philos. Trans. R. Soc. A 1992, 341, 443–477. [Google Scholar] [CrossRef]
- Raabe, D. Simulation of rolling textures of b.c.c. metals considering grain interactions and crystallographic slip on {110}, {112} and {123} planes. Mater. Sci. Eng. A 1995, 197, 31–37. [Google Scholar] [CrossRef]
- Böhlke, T.; Risy, G.; Bertram, A. A texture component model for anisotropic polycrystal plasticity. Comput. Mater. Sci. 2005, 32, 284–293. [Google Scholar] [CrossRef]
- El Shawish, S.; Cizelj, L. Numerical investigation of grain misorientations at and close to the free surface of FCC polycrystalline metals. Comput. Mater. Sci. 2016, 113, 133–142. [Google Scholar] [CrossRef]
- Ahmadi, A.; Mirzaeifar, R.; Moghaddam, N.S.; Turabi, A.S.; Karaca, H.E.; Elahinia, M. Effect of manufacturing parameters on mechanical properties of 316L stainless steel parts fabricated by selective laser melting: A computational framework. Mater. Des. 2016, 112, 328–338. [Google Scholar] [CrossRef]
- Simonovski, I.; Cizelj, L. Automatic parallel generation of finite element meshes for complex spatial structures. Comput. Mater. Sci. 2011, 50, 1606–1618. [Google Scholar] [CrossRef]
- Diard, O.; Leclercq, S.; Rousselier, G.; Cailletaud, G. Evaluation of finite element based analysis of 3D multicrystalline aggregates plasticity: Application to crystal plasticity model identification and the study of stress and strain fields near grain boundaries. Int. J. Plast. 2005, 21, 691–722. [Google Scholar] [CrossRef]
- Zhang, C.; Li, H.; Eisenlohr, P.; Liu, W.; Boehlert, C.J.; Crimp, M.A.; Bieler, T.R. Effect of realistic 3D microstructure in crystal plasticity finite element analysis of polycrystalline Ti–5Al–2.5Sn. Int. J. Plast. 2015, 69, 21–35. [Google Scholar] [CrossRef]
- Hure, J.; El Shawish, S.; Cizelj, L.; Tanguy, B. Intergranular stress distributions in polycrystalline aggregates of irradiated stainless steel. J. Nuc. Mater. 2016, 476, 231–242. [Google Scholar] [CrossRef]
- Farukh, F.; Zhao, L.G.; Jiang, R.; Reed, P.; Proprentner, D.; Shollock, B.A. Realistic microstructure-based modelling of cyclic deformation and crack growth using crystal plasticity. Comput. Mater. Sci. 2016, 111, 395–405. [Google Scholar]
- Patra, A.; McDowell, D.L. Crystal plasticity investigation of the microstructural factors influencing dislocation channeling in a model irradiated bcc material. Acta Mater. 2016, 110, 364–376. [Google Scholar] [CrossRef]
- Signor, L.; Villechaise, P.; Ghidossi, T.; Lacoste, E.; Gueguen, M.; Courtin, S. Influence of local crystallographic configuration on microcrack initiation in fatigued 316LN stainless steel: Experiments and crystal plasticity finite elements simulations. Mater. Sci. Eng. A 2016, 649, 239–249. [Google Scholar] [CrossRef]
- Efstathiou, C.; Boyce, D.E.; Park, J.S.; Lienert, U.; Dawson, P.R.; Miller, M.P. A method for measuring single-crystal elastic moduli using high-energy X-ray diffraction and a crystal-based finite element model. Acta Mater. 2010, 58, 5806–5819. [Google Scholar] [CrossRef]
- Wielewski, E.; Boyce, D.E.; Park, J.S.; Miller, M.P.; Dawson, P.R. A methodology to determine the elastic moduli of crystals by matching experimental and simulated lattice strain pole figures using discrete harmonics. Acta Mater. 2017, 126, 46–480. [Google Scholar] [CrossRef]
- Pagan, D.C.; Shade, P.A.; Barton, N.R.; Park, J.S.; Kenesei, P.; Menasche, D.B.; Bernier, J.V. Modeling slip system strength evolution in Ti–7Al informed by in-situ grain stress measurements. Acta Mater. 2017, 128, 406–417. [Google Scholar] [CrossRef]
- Hall, E.O. The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. 1951, 64, 747–753. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Hill, R.; Rice, J.R. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Bassani, J.; Wu, T.Y. Latent hardening in single crystals. II. Analytical characterization and predictions. Proc. Math. Phys. Sci. 1991, 435, 21–41. [Google Scholar] [CrossRef]
- Bassani, J.L. Plastic flow of crystals. Adv. Appl. Mech. 1993, 30, 191–254. [Google Scholar]
- Karaman, I.; Sehitoglu, H.; Maier, H.J.; Chumlyakov, Y.I. Competing mechanisms and modeling of deformation in austenitic stainless steel single crystals with and without nitrogen. Acta Mater. 2001, 49, 3919–3933. [Google Scholar] [CrossRef]
- Kashyap, B.P.; Tangri, K. On the Hall–Petch relationship and substructural evolution in type 316L stainless steel. Acta Metall. Mater. 1995, 43, 3971–3981. [Google Scholar] [CrossRef]
- Gonzalez, D.; Kelleher, J.F.; da Fonseca, J.Q.; Withers, P.J. Macro and intergranular stress responses of austenitic stainless steel to 90∘ strain path changes. Mater. Sci. Eng. A 2012, 546, 263–271. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. Lond. A 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Needleman, A. Computational mechanics at the mesoscale. Acta Mater. 2000, 48, 105–124. [Google Scholar] [CrossRef]
- ABAQUS 6.14. Dassault Systèmes Simulia Corporation. Dassault Systèmes: Providence, RI, USA, 2014. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/ (accessed on 21 June 2017).
- Huang, Y. A User-Material Subroutine Incorporating Single Crystal Plasticity in the ABAQUS Finite Element Program; Division of Applied Sciences, Harvard University: Cambridge, MA, USA, 1991. [Google Scholar]
- El Shawish, S.; Bogataj, M.; Cizelj, L. Crystal plasticity model calibration for 316L stainless steel single crystals during deformation. In Proceedings of the XII International Conference on Computational Plasticity-Fundamentals and Applications, COMPLAS XII, Barcelona, Spain, 3–5 September 2013; pp. 811–821. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Karaman, I.; Sehitoglu, H.; Chumlyakov, Y.I.; Maier, H.J. The deformation of low-stacking-fault-energy austenitic steels. JOM J. Miner. Met. Mater. Soc. 2002, 54, 31–37. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 30, 1951–1976. [Google Scholar] [CrossRef]
- Weng, G.J. A micromechanical theory of grain-size dependence in metal plasticity. J. Mech. Phys. Solids 1983, 31, 193–203. [Google Scholar] [CrossRef]
- Verma, R.K.; Biswas, P. Crystal plasticity-based modelling of grain size effects in dual phase steel. Mater. Sci. Technol. 2016, 32, 1553–1558. [Google Scholar] [CrossRef]
- Ramtani, S.; Dirras, G.; Bui, H.Q. A bimodal bulk ultra-fine-grained nickel: Experimental and micromechanical investigations. Mech. Mater. 2010, 42, 522–536. [Google Scholar] [CrossRef]
- Bui, H.Q.; Pham, X.T.; Fafard, M. Modelling of microstructure effects on the mechanical behavior of aluminium tubes drawn with different reduction areas. Int. J. Plast. 2013, 50, 127–145. [Google Scholar] [CrossRef]
- Simonovski, I.; Nilsson, K.F.; Cizelj, L. Material properties calibration for 316L steel using polycrystalline model. In Proceedings of the 13th International Conference on Nuclear Engineering, Beijing, China, 16–20 May 2005; pp. 1–8. [Google Scholar]
- Herrera-Solaz, V.; LLorca, J.; Dogan, E.; Karaman, I.; Segurado, J. An inverse optimization strategy to determine single crystal mechanical behavior from polycrystal tests: Application to AZ31 Mg alloy. Int. J. Plast. 2014, 57, 1–15. [Google Scholar] [CrossRef]
- Quey, R.; Dawson, P.R.; Barbe, F. Large-scale 3D random polycrystals for the finite element method: Generation, meshing and remeshing. Comput. Methods Appl. Mech. Eng. 2011, 200, 1729–1745. [Google Scholar] [CrossRef]


| i | |||
|---|---|---|---|
| 1 | 64 | ||
| 2 | 64 | 512 | |
| 3 | 64 | 4096 | |
| 4 | 64 | 32,768 | |
| 5 | 64 | 262,144 | |
| 6 | 1 | 512 | |
| 7 | 512 | 8 | 4096 |
| 8 | 512 | 64 | 32,768 |
| 9 | 512 | 512 | 262,144 |
| 10 | 1 | 4096 | |
| 11 | 4096 | 8 | 32,768 |
| 12 | 4096 | 64 | 262,144 |
| 13 | = 32,768 | 1 | 32,768 |
| 14 | 32,768 | 8 | 262,144 |
| 15 | = 262,144 | 1 | 262,144 |
| 126 MPa | MPa | 359 MPa | |||
| 177 MPa | MPa | 461 MPa |
| 50 MPa | 300 MPa | |
| 50 MPa | 3000 MPa | |
| 0 MPa | 1000 MPa | |
| 0 MPa | 1000 MPa | |
| 0 MPa | 1000 MPa | |
| 0 | 1 | |
| 0 | 1 | |
| 0 | 1 | |
| q | 0 |
| Model | Set | q | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BW3 | 83.1 | 88.3 | 214 | 159 | 111 | 0.034 | 0.186 | 0.328 | 0.836 | 6.70 | ||
| 82.8 | 96.0 | 394 | 71 | 86 | 0.018 | 0.104 | 0.674 | 0.175 | 12.6 | |||
| 82.8 | 96.0 | 410 | 98 | 86 | 0.019 | 0.158 | 0.674 | 0.172 | 14.6 | |||
| 82.8 | 96.0 | 459 | 125 | 89 | 0.020 | 0.186 | 0.647 | 0.172 | 20.7 | |||
| BW2 | 83.1 | 84.9 | 210 | 150 | 0.026 | 0.321 | 0.836 | 7.20 | ||||
| 82.8 | 97.9 | 386 | 70 | 0.018 | 0.674 | 0.175 | 12.9 | |||||
| 84.5 | 96.0 | 418 | 98 | 0.019 | 0.674 | 0.172 | 16.3 | |||||
| 82.0 | 93.9 | 418 | 91 | 0.016 | 0.659 | 0.172 | 21.6 | |||||
| PAN | 78.6 | 2754 | 224 | 1.51 | 9.90 | |||||||
| 78.6 | 200 | 215 | 1.75 | 27.5 | ||||||||
| 78.6 | 200 | 215 | 1.75 | 29.7 | ||||||||
| 78.6 | 204 | 228 | 1.68 | 35.4 |
| Model | Set | q | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BW3 | 91.1 | 104 | 292 | 0 | 99 | 0.001 | 0.150 | 0.930 | 0.060 | 60.3 | ||
| 82.8 | 96.0 | 378 | 93 | 87 | 0.016 | 0.203 | 0.674 | 0.175 | 16.1 | |||
| ∞ | 82.8 | 96.0 | 394 | 71 | 86 | 0.018 | 0.104 | 0.674 | 0.175 | 12.6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Shawish, S.; Cizelj, L. Combining Single- and Poly-Crystalline Measurements for Identification of Crystal Plasticity Parameters: Application to Austenitic Stainless Steel. Crystals 2017, 7, 181. https://doi.org/10.3390/cryst7060181
El Shawish S, Cizelj L. Combining Single- and Poly-Crystalline Measurements for Identification of Crystal Plasticity Parameters: Application to Austenitic Stainless Steel. Crystals. 2017; 7(6):181. https://doi.org/10.3390/cryst7060181
Chicago/Turabian StyleEl Shawish, Samir, and Leon Cizelj. 2017. "Combining Single- and Poly-Crystalline Measurements for Identification of Crystal Plasticity Parameters: Application to Austenitic Stainless Steel" Crystals 7, no. 6: 181. https://doi.org/10.3390/cryst7060181
APA StyleEl Shawish, S., & Cizelj, L. (2017). Combining Single- and Poly-Crystalline Measurements for Identification of Crystal Plasticity Parameters: Application to Austenitic Stainless Steel. Crystals, 7(6), 181. https://doi.org/10.3390/cryst7060181





