Abstract
It is known that some of RMnO3 and RMn2O5 (R = rare earth) multiferroic crystals reveal a strong interplay between their magnetic and electric order parameters, paving the way for applications in spintronic technologies. Additionally, recent works have also pointed out their potential utilization as refrigerants in magnetocaloric cooling systems for cryogenic tasks. In this paper, recent advances regarding the magnetocaloric properties of both RMnO3 and RMn2O5 families of multiferroics are reviewed. With the aim of understanding the RMnO3 and RMn2O5 magnetocaloric features, their structural and magnetic properties are discussed. The physics behind the magnetocaloric effect as well as some of its key thermodynamic aspects are also considered.
Keywords:
RMnO3; RMn2O5; multiferroics; anisotropy; single crystals; magnetocaloric effect; magnetic cooling 1. Introduction
In recent years great attention has been paid to the development of new functional materials with potential applications in more efficient and clean technologies. In this context, magnetocaloric materials have generated a worldwide interest due to their potential utilization as solid-state refrigerants in magnetic cooling devices [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Based on the well-known magnetocaloric effect (MCE), the magnetic refrigeration technique would enable the harmful synthetic refrigerants usually present in the conventional refrigerators to be completely phased out while offering a high thermodynamic efficiency [15,16,17]. The search for optimum magnetocaloric materials is then a key parameter in the development of magnetic cooling systems. For room temperature tasks, rare-earth elements-based alloys [14] and particularly the gadolinium metal have been widely used as refrigerants and successfully implemented in functional devices [15,16,17]. However, their high cost and their poor resistance to corrosion and oxidation strictly limit their utilization in large scale applications of magnetocaloric refrigeration. For this purpose, worldwide intensive researches have been conducted leading to the discovery of new “cheaper and efficient” magnetocaloric materials including both transition elements and intermetallic-based compounds such as Fe2P type materials (MnFePAs) [6,7] and LaFe13-xSix compounds [8,9,10,11,12,13]. Most of these materials exhibit a first order magnetic phase transition close to room temperature which explains their large magnetocaloric effect, particularly in terms of the entropy change. On the other hand, much attention has also been paid to materials that present good magnetocaloric properties in the cryogenic temperature range due to their potential implementation in numerous applications such as scientific facilities, space technologies, and gas liquefaction.
It is worth noting that the rising cost of helium opens the way for the development of new alternatives to conventional liquid-helium refrigerators. In addition, as claimed by Barclay et al. [18], a large scale utilization of hydrogen as a source of energy will result in better energy security with major environmental, economic, and social benefits. In this context, several cryomagnetocaloric materials have been proposed [19,20,21,22,23,24,25,26,27,28]. Following this, Matsumoto et al. [29,30] unveiled a reciprocating magnetic refrigerator dedicated to hydrogen liquefaction that uses the Dy2.4Gd0.6Al5O12 garnet as refrigerant.
The multiferroic crystals RMn2O5 [31,32,33,34,35,36] and RMnO3 (R = rare earth) [37,38,39,40,41] have been extensively explored due to their fascinating physical properties as well as potential applications in spintronic devices. Especially, some of these systems show a strong coupling between magnetism and ferroelectricity which provides an additional degree of freedom regarding the design of magnetoelectric effect-based machines [30,31,32,33,34,35,36,37,38,39,40]. On the other hand, the investigation of their magnetocaloric properties has unveiled a great potential for application in magnetic refrigeration at low temperature regime [19,20,21,22,23,24,25,26,27,28]. This means that more than one task can be achieved by only using a single RMn2O5 or RMnO3 material which is of great interest from an economical point of view.
Although several intermetallic materials with excellent magnetocaloric properties such as RAl2 [42] have been proposed for low temperature application, the chemical and mechanical instabilities remain serious obstacles to their utilization. For example, one of the major problems with these materials is that they experience decomposition due to hydrogen absorption [30]. In addition, the implementation of intermetallics as refrigerants in functional devices, favors the creation of an eddy current during the magnetization-demagnetization process, leading to undesirable thermal losses [43]. These drawbacks could be avoided by using RMn2O5 or RMnO3 oxides which reveal an insulating character combined with high chemical and mechanical stabilities [12].
It is also worth noting that in addition to a large conventional MCE that can be generated by varying the magnitude of external magnetic field, some of the RMn2O5 and RMnO3 crystals exhibit a giant thermal effect when they are rotated around their intermediate axis in constant magnetic fields [19,20,21]. This rotating MCE resulting from the large magnetic anisotropy shown by these crystals would enable more efficient and compact cryomagnetocaloric refrigerators with simplified designs to be built [19,20]. In this paper, we particularly discuss the recent developments in relation with the magnetocaloric properties of RMn2O5 and RMnO3 crystals. In order to understand their magnetoelectric and magnetocaloric properties, some theoretical background is also given.
2. Magnetocaloric Effect: Theoretical Aspects
Nowadays, magnetic cooling systems are based on the conventional magnetocaloric effect, an intrinsic property that can be defined as the thermal response of certain magnetic materials when subjected to a variable external magnetic field. This effect manifests itself as a temperature change resulting from the magnetic entropy variation because of the magneto-thermal coupling between phonons and magnetic moment sublattices. In fact, the full entropy of a magnetic substance in the presence of an external magnetic field H (B = µ0H) can usually be expressed as follows:
where SLat, SEl, and Sm are the lattice, electronic and magnetic entropies, respectively. In a magnetic field, the magnetic moments change their ordering state, increasing (or decreasing) consequently the system’s magnetic entropy. In adiabatic conditions, the conservation of the full entropy involves the evolution of the lattice contribution in the opposite way, raising then (or lowering) the magnetic material’s temperature. For ferromagnets and paramagnets (Figure 1), the application of an external magnetic field tends to render the magnetic spins more ordered and correspondingly the magnetic entropy is decreased. The magnetic substance compensates for this loss by heating up (atoms vibrate more). When the magnetic field is reduced to zero, the magnetic moments randomize again, the magnetic entropy increases, the lattice part decreases and the magnetic material is cooled down. However, in the case of antiferromagnetic materials, the application of an external magnetic field usually transforms the magnetic phase from an ordered to a less-ordered state giving rise to a negative (or inverse) magnetocaloric effect [44].
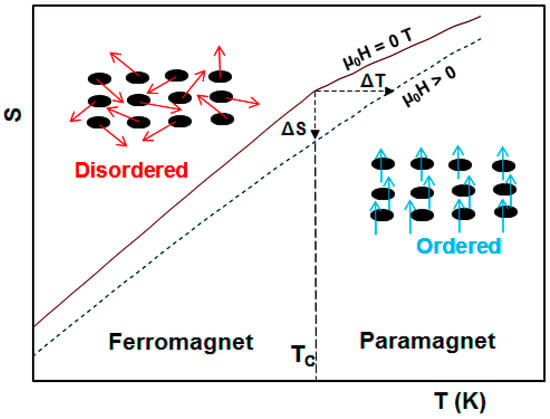
Figure 1.
Principle of the conventional magnetocaloric effect (MCE).
The MCE is mainly characterized by the adiabatic temperature change ΔTad and the isothermal entropy change ΔS. Both thermodynamic quantities are shown in Figure 1 for an initial temperature TC (Curie point) and a magnetic field changing from 0 to H. ΔTad can be directly measured by a system of thermocouples or indirectly deduced from specific heat measurements as a function of temperature and magnetic field using the following equation [42]:
ΔTad can then be determined from S(T,B) curves as shown in Figure 1. However, due to the complexity of calorimetric measurements, the MCE is usually reported in terms of ΔS that can be determined from isothermal magnetization curves with the help of the Maxwell equation. This latter is given by:
Since the magnetization data are usually collected at discrete values of magnetic field and temperature, ΔS can be approached by the following numerical form:
where Mi+1 and Mi are the magnetizations corresponding to Ti+1 and Ti, respectively, in a magnetic field B. However, this technique must be used carefully [45,46], particularly in the case of first order magnetic phase transition (FOMT) materials that show a large hysteresis effect (out of equilibrium). In some metamagnetic materials [45,46] the hysteresis effect results in phase-separated states. However, under the effect of an external magnetic field, the MCE is mainly contributed from only one magnetic phase which is not taken into account when directly integrating the Maxwell relation [45,46]. The MCE associated with metamagnetic regions can well be estimated from the Clausius-Clapeyron equation that directly links the entropy change to the magnetization jump [45,46]. It is given by
where BC and Tr are the critical magnetic field and the transition temperature, respectively.
As outlined in Section 1, thermal effects can also be induced by rotating some single crystals that show a large anisotropy between their easy and hard-axes (Figure 2) in constant magnetic fields [19,20]. As shown in Figure 2b, such an effect could open the way for the design of new types of magnetic refrigerators. Similarly to the standard MCE, the rotating MCE is also represented by adiabatic (ΔTad,R) and entropy (ΔSR) changes. Both parameters can be obtained from specific heat measurements by building full entropy curves along the hard and easy-axes (Figure 2a). Considering the magnetic field initially parallel to the hard-axis, the entropy change resulting from the rotation of a single crystal around its intermediate axis by an angle of 90 ° can be written as
where ΔS (H//e) and ΔS (H//h) are the entropy changes corresponding to the application of a magnetic field along the easy and hard-directions, respectively. This means that the rotating entropy change can also be evaluated from magnetization data using the Maxwell equation [19,20,21].
ΔSR,he = ΔS (H//e) − ΔS (H//h)
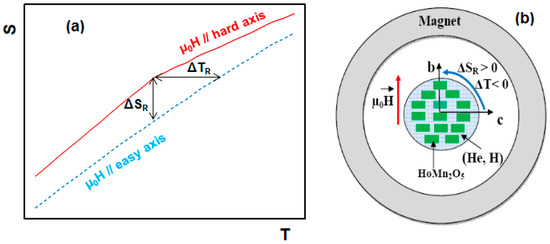
Figure 2.
(a) Principle of the rotating magnetocaloric effect. (b) Generation of the magnetocaloric effect by rotating HoMn2O5 single crystals between their easy (b-axis) and hard (c-axis) axes [19]. Helium and hydrogen gas can be then liquefied by using them as heat transfer fluids [19].
The refrigerant capacity is another figure of merit for the characterization of magnetocaloric materials [47]. This parameter, not only takes into account the magnitude of the MCE but also the operating temperature range. It is given by:
With TH and TC the cold and hot temperatures correspond to the half maximum of the ΔS as a function of temperature. More recently, RC was found to linearly scale with the exergetic cooling power of an AMR thermodynamic cycle [48].
3. Brief Description of the Magnetoelectric Interplay in RMnO3 and RMn2O5 Multiferroics
It is known that the ferroelectricity in hexagonal RMnO3 multiferroics mainly arises from structural distortions involving an asymmetric coordination of oxygen atoms around the rare earth ion [49]. In orthorhombic RMnO3 (R = Gd, Tb and Dy) and RMn2O5 systems, the ferroelectric order emerges from a frustrated magnetic order leading to a strong magnetoelectric coupling [50,51,52,53,54,55,56,57,58,59,60]. For these compounds the magnetic frustration originates from two different scenarios: the first one involves the competition between different magnetic exchange interactions while the second one arises from the incompatibility between the lattice geometry and the magnetic interaction ruling the spins configuration [33,37]. Due to the orbital ordering of Mn3+ ions in orthorhombic RMnO3, the exchange interactions favor a ferromagnetic (FM) configuration in the ab-planes and an antiferromagnetic arrangement (AFM) along the c-axis. Such order is observed in large R-radii RMnO3 (R = La, Pr, Nd, Sm, and Eu) [53,54]. However, the decrease of the R-radii (R = Dy, Tb, and Gd) increases both the GdFeO3-type lattice distortion and the octahedra tilting (see Figure 3). In these much-distorted systems, the competition between different magnetic exchange interactions is embedded and the spin structure becomes sinusoidally modulated in the ab-plane below 39–43 K and spirally modulated below 18–27 K [37]. On the contrary, all RMn2O5 (R = rare-earth, Y and Bi), except PrMn2O5, are multiferroic compounds [61]. For these systems, the ferroelectricity is induced by a collinear magnetic order. It is particularly observed when a commensurate magnetic (CM) phase appears. To explain the microscopic mechanism of the ferroelectricity in the non-collinear magnets RMnO3, Kastura et al. [55], suggested a pure electronic model. This latter suggests that the electronic polarization, induced by two adjacent magnetic moments and is given by where is the unit vector connecting the sites i and j. This model presumed that the ions are not displaced from their centrosymmetric positions. In contrast, Sergienko et al. [56] concluded that the oxygen ion displacements are essential for the ferroelectric polarization in these non-collinear magnets. This last model suggested that the ferroelectricity is rather induced by the antisymmetric Dzyaloshinskii-Moriya interaction . The system can stabilize its magnetic structure by pushing the oxygen further away from the two Mn3+ ions. Because of the spiral order symmetry, the exchange striction will move the oxygens along one direction perpendicular to the spiral direction breaking the inversion symmetry as shown in Figure 4 [56]. Other sophisticated mechanisms have suggested combined contributions [62]. The ferroelectricity in RMn2O5 is often connected to a symmetric Mn-Mn exchange interaction [33,63].
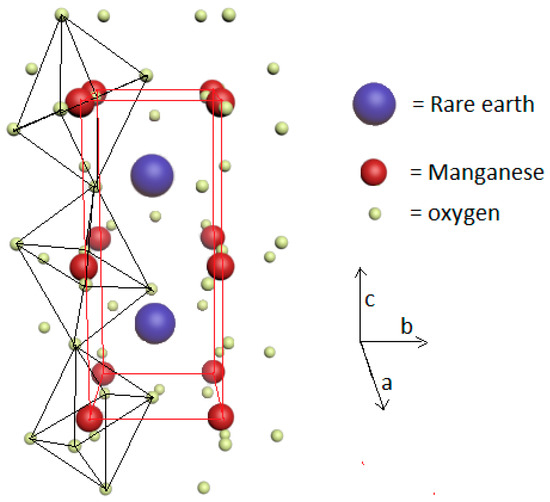
Figure 3.
Perovskite orthorhombic structure of RMnO3. Smaller R3+ radii will increase the oxygens’s octaedra tilting and ultimately will influence the super-exchange interaction mediating the ordering of Mn3+ spins.
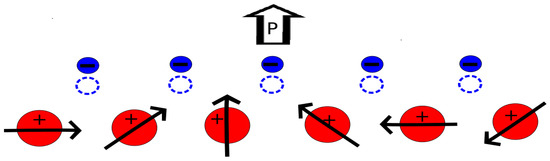
Figure 4.
Mn3+ (red) spiral spin order will induce with the exchange striction a uniform displacement of the O2− (blue) that breaks the space inversion symmetry and thus, induces a net electric polarization (P).
Phenomenologically, the coupling mechanism between the electric polarization P and the magnetization M can be explained in the framework of Landau theory. The order parameter P changes its sign under the inversion of all the coordinates, r → −r, but remains invariant on time reversal, t → −t. On the other hand, M transforms into the opposite way and changes its sign under time reversal while remaining invariant under spatial inversion. These symmetry considerations forbid any direct linear coupling mechanisms (P.M). For magnetic systems with non-collinear spin configurations, magnetoelectric coupling can be described with the spatial derivative term . For example, in a cubic crystal [50,51,52], such coupling could result in a net electric polarization moment . This expression confirms that only a spiral magnetic order can induce a ferroelectric order with a polarization P proportional to where Q is the wave vector propagation. For collinear magnets, Oh et al. [64] successfully explained the magnetoelectric phenomena in TbMn2O5 using a fourth order (P.M)² coupling term.
4. Magnetocaloric Properties of RMnO3 Multiferroic Crystals
The RMnO3 (R = rare earth) manganites have generated worldwide interest due to their rich physical properties and potential implementation in a wide range of applications going from spintronics such as four state memory systems [37] to magnetocaloric refrigeration [20,21,22,23,24,26,27]. In these highly frustrated multiferroics, the magnetic, electric and crystallographic structures are markedly coupled and strongly depend on the rare earth element size (rR) [22,27,65,66,67,68]. Usually, the RMnO3 systems with larger ionic radius of R (typically rR >rDy) crystallize in an orthorhombic structure illustrated in Figure 3 (Pbnm space group) [27,65,66,67,68]. This includes compounds such as TbMnO3 and GdMnO3 for example. When the ionic radius of R is smaller than that of Dy as in HoMnO3 and ErMnO3, the RMnO3 compounds form in a hexagonal structure with space group P63cm [27,65,66,67,68]. It is worth noting that the DyMnO3 compound is usually more stable in the orthorhombic structure at room temperature. However, the free energies of both of its crystallographic structures (hexagonal and orthorhombic) are closer to each other [66]. Consequently, the hexagonal phase of DyMnO3 can also be stabilized under some special conditions, as reported in Ivanov et al. [66].
On the other hand, the origin of the ferroelectricity in orthorhombic and hexagonal RMnO3 is different. In orthorhombic multiferroics RMnO3, the ferroelectricity is directly generated by the complex magnetic structure that breaks the inversion symmetry [49,65], which results in a strong coupling between magnetic and electric properties. For hexagonal phases, the spontaneous electric polarization arises from structural distortions that are induced by an asymmetric coordination of oxygen around the rare earth ions [65]. This usually gives rise to a weak magnetoelectric coupling and the ferroelectric order is retained up to TC = 900 K that is far above the AFM ordering point of the Mn-spins sublattice (around 80 K) [26]. The orthorhombic and hexagonal symmetries of DyMnO3 could be considered as representatives of RMnO3 (R = La to Ho) multiferroics. In fact, although they contain the same rare earth (Dy) element, their magnetic and magnetocaloric properties differ markedly and have been widely documented in the literature [39,40,41,65,66,67,68,69].
The orthorhombic structure (o-DyMnO3) exhibits successive magnetic phase transitions that can be clearly seen from specific heat data [70]. First, the Mn3+ magnetic moments antiferromagnetically order in an incommensurate state close to TN1 = 40 K. Upon decreasing the temperature below 40 K, the Mn3+ spins arrangement transforms into a longitudinal sinusoidal spin wave with a wave vector along the crystallographic axis b [67,68]. At around TL = 18 K, the ordered magnetic moments reveal a second component along the c-axis leading to a cycloidal (spiral) magnetic ordering. This breaks the inversion symmetry, leading to the appearance of a spontaneous electric polarization along the same crystallographic direction (c-axis). At temperatures below 15 K, the Dy3+ magnetic moments manifest a sinusoidal incommensurate ordering along the b-axis [40]. Below TN2 = 6.5 K [40], the formed phase transforms into a commensurate antiferromagnetic state. By using neutron diffraction and X-ray resonant magnetic scattering techniques, Prokhnenko et al. [40] also pointed out the contribution of Dy3+ moments in enhancing the electric polarization in o-DyMnO3.
The magnetic properties of the hexagonal form (h-DyMnO3) are not well understood. The Mn3+ moments order antiferromagnetically below TN1 = 60 K establishing triangular structures in the ab plane [65]. According to Nandi et al. [69], the Dy3+ magnetic moments are antiferromagnetically ordered along the c-axis at temperatures between 8 K and 68 K. The ordering of Dy3+ spins in this temperature range is linked to the exchange field of Mn3+ through the 4d–3f exchange interaction. However, by combining the optical second-harmonic generation and neutron diffraction, Wehrenfenning et al. [71] have revealed that 3d–4f coupling in the h-DyMnO3 compound is less rigid than suggested in previous studies. For temperatures below TN2,Dy = 10 K, the rare earth magnetic moments in the h-DyMnO3 crystal are ferrimagnetically aligned along the c-axis [65].
Isothermal magnetization curves of o-DyMnO3 and h-DyMnO3 single crystals as a function of magnetic field applied along their easy and hard-directions at 2 K are presented in Figure 5. As shown, the easy and hard-axes of the orthorhombic phase are clearly oriented along the b and c directions, respectively. The magnetization along the hard-orientation evolves almost linearly even under high magnetic fields, while a saturation tendency can be clearly seen following the b-axis for magnetic fields higher than 2 T. The magnetization saturation value obtained at 2 K from Figure 5 is 170 Am2/kg (about 8 µB) being closer to the free Dy3+ moment value (10 µB). This demonstrates the weak contribution of the Mn-sublattice to the full magnetization. On the other hand, the marked difference between magnetic isotherms along the crystallographic directions reveals a gigantic magneto-crystalline anisotropy in o-DyMnO3 crystals which is a common property of the orthorhombic RMnO3 manganites [39,40,41,65,67,72].
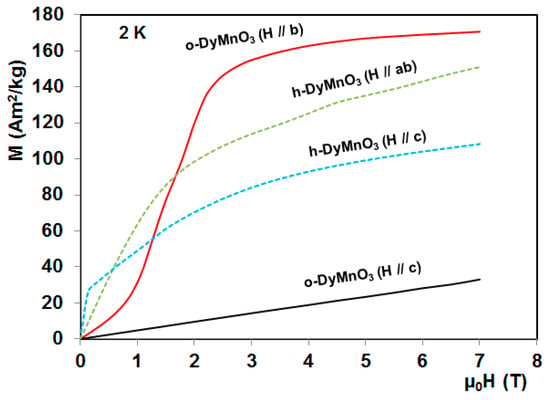
Figure 5.
Isothermal magnetization curves at 2 K for orthorhombic (o) and hexagonal (h) DyMnO3 single crystals along their easy and hard-orientations [22,24].
In contrast to the orthorhombic phase, the h-DyMnO3 crystal unveils its easy axis along the c-orientation, while the hard-direction is parallel to the ab-plane. At 2 K, the h-DyMnO3 magnetization under a magnetic field of 7 T applied along the c-axis is only 115 Am2/kg being much lower than its equivalent of the orthorhombic phase (170 Am2/kg) [22,24]. This can be mainly attributed to the ferrimagnetic ordering of Dy3+ moments that occupy non-equivalent crystallographic sites in the hexagonal form [65]. However, as shown in Figure 5 an enhancement of the h-DyMnO3 magnetization occurs when sufficiently high magnetic fields are applied within the ab-plane. Such behavior is not well understood, but the Mn lattice seems to contribute for this enhancement [22,65]. On the other hand, the o-DyMnO3 magnetization exhibits a metamagnetic transition along the b-axis at low temperatures with a tendency to saturate under high magnetic fields (Figure 5). Such behavior is absent in isotherm curves reported by Harikrishnan et al. [65] following the same axis where the magnetization varies slightly with magnetic field. As showed by Balli et al. [24], the observed difference can be explained by the fact that the magnetic isotherms reported in Ref. [65] correspond more probably to the hard-axis c.
The magnetocaloric effect associated with the order-disorder type-magnetic transitions were recently explored in DyMnO3 phases (Figure 6a,b) and reported in [22,24,26]. The magnetocaloric properties of o-DyMnO3 single crystals have been explored around the ordering point of Dy3+ cations [24]. Along the easy-axis b, o-DyMnO3 unveils a giant magnetocaloric effect (Figure 6a) on a large working temperature range being a favorable situation from a practical point of view. Under magnetic variations of 0–7, 0–5 and 0–3 T parallel to the easy axis b, the resulting isothermal entropy change (–ΔS) shows maximum values of about 17.25, 14.6 and 8.7 J/kg K [24], respectively, which are in good agreement with those reported by Midya et al. [26]. The adiabatic temperature change ΔTad was also estimated by Midya et al. according to isentropic curves using specific heat data [26]. It was found to be about 11.5 K under a magnetic field changing from 0 to 8 T along the b-axis [26]. For the hard-axis c, the induced entropy change is negligible and was found by Balli et al. [24] to be only 0.8 J/kg K in a magnetic field change of 0–7 T (Figure 6a). This value is 10 times lower than that reported in Ref. [26] following the hard-orientation (8 J/kg K). Looking at isothermal magnetization data reported in Ref. [26], it seems clearly that the large value of –ΔS along the hard-direction is rather related to the intermediate axis a [24]. On the other hand, the orthorhombic DyMnO3 shows a meaningful inverse (or negative) magnetocaloric effect at temperatures below 6 K. This was mainly attributed to the antiferromagnetic ordering of Dy3+ magnetic moments in this temperature range. In fact, under the effect of an external magnetic field, the AFM phase transforms into a less ordered “ferromagnetic” one increasing then the material’s magnetic entropy [24,26].
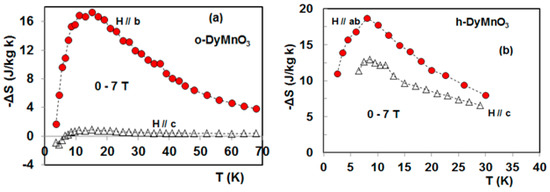
Figure 6.
Isothermal entropy change as a function of temperature under a magnetic field change of 7 T along the easy and hard-directions of orthorhombic (a) and hexagonal (b) DyMnO3 single crystals [22,24].
The rotating magnetocaloric effect was also investigated in the orthorhombic DyMnO3 single crystal [24]. In fact, the latter reveals a gigantic anisotropy of the magnetocaloric effect. As shown in Figure 6a, the maximum entropy change under 7 T applied parallel to the easy axis is more than 20 times larger than that along the hard-axis c. This means that thermal effects can also be induced by rotating o-DyMnO3 crystals between their hard and easy-axes in constant magnetic fields (Figure 7a,b). As reported in [24], the resulting entropy change from a 90° rotation in the bc-plane reaches maximum values of 8.4, 14.2, and 16.3 J/kg K in constant magnetic fields of 3, 5, and 7 T, respectively. The associated adiabatic temperature change was found to be 5, 9, and 11 K, respectively. It should be noticed that the reported rotating adiabatic temperature change in [24] is similar to the ΔTad obtained by Midya et al. [26] from the magnetization of o-DyMnO3 along the easy-axis b (10.5 K in 0–7 T). This can be explained by the fact that the full entropy along the hard-axis is practically equal to that shown in the absence of magnetic field since ΔS (H//c) is negligible [24].
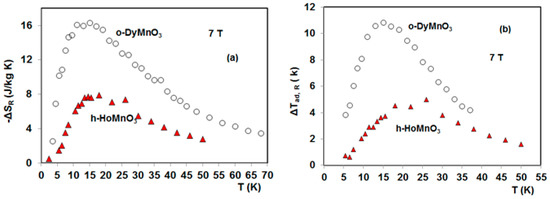
Figure 7.
(a) Rotating entropy change as a function of temperature under a constant magnetic field of 7 T for orthorhombic DyMnO3 and hexagonal HoMnO3. (b) Associated adiabatic temperature change [24,27].
In comparison with o-DyMnO3, the magnetic anisotropy is less pronounced in the hexagonal phase (Figure 5). The h-DyMnO3 magnetocaloric properties were more recently investigated by Balli et al. [22]. Along the ab plane, it was found that the position of ΔSmax varies from 3 to 8 K when the magnetic field strength is changed from 0–2 T to 0–7 T. For the easy-axis c, the h-DyMnO3 isothermal entropy change curves remain peaked (Figure 6b) on the Dy3+ transition temperature (8 K) even under high magnetic fields [22]. On the other hand, for sufficiently high magnetic fields, Balli et al. [22] showed that the entropy change associated within the ab-plane is much larger than that along the c-axis (Figure 6b). For field changes of 0–2, 0–5, and 0–7 T, the maximum entropy change (–ΔSmax) shown by the hexagonal DyMnO3 was found to be 8, 15, and 19 J/kg K for H//ab while it is 5, 10, and 13 J/kg K for H//c. The corresponding adiabatic temperature changes were found to be 2.86, 12.24, and 15 K for H//ab while those for H//c are 4.33, 8.6, and 11.2 K, respectively. As reported, the resulting –ΔS in h-DyMnO3 under a magnetic field changing from 0 to 5 T in the ab plane, exceeds that shown along the c-axis by nearly 50% [22]. This was mainly attributed to the enhancement of the magnetization under high magnetic fields applied within the ab-plane [22]. Additionally, a large MCE that can be obtained under very low magnetic fields was pointed out in h-DyMnO3 crystals by Balli et al. [22] along the c-axis. When varying the magnetic field along the easy axis c from 0 to 0.2, 0 to 0.3, and 0 to 0.5 T, –ΔSmax reaches values of 1, 1.5, and 2 J/kg K. This is of great importance from a practical point view since such low magnetic fields can be easily produced by using “cheaper” permanent magnets [16,73]. In contrast, –ΔS is negligible under low magnetic fields applied within the ab plane. This was attributed to the instability of the antiferromagnetic phase (along c-axis) near the ordering temperature of Dy3+ magnetic moments in h-DyMnO3 [22,66]. In the vicinity of 8 K, a metamagnetic transition from an antiferromagnetic to a ferrimagnetic state can be induced under very low magnetic fields applied along the c-axis, leading to interesting levels for MCE.
The magnetocaloric properties of HoMnO3 single crystals were investigated by Balli et al. [27] and Midya et al. [26]. Even though this compound shows some structural similarities with the hexagonal DyMnO3, their magnetic features are quite different [27]. For the HoMnO3 single crystal which forms in a hexagonal structure with space group P63cm, the “easy direction” is rather along the ab-plane while the hard-axis is oriented along the c-axis (Figure 8), which markedly contrast with the hexagonal DyMnO3 [22]. In h-HoMnO3, the Mn3+ magnetic moments usually order in an antiferromagnetic structure below TN1 = 75 K and rotate in ab-plane by an angle of 90° at around Tsr = 40 K. This spin reorientation initiates a partial ordering of Ho3+ magnetic moments because of the coupling between Mn3+ and Ho3+ spins [26,27,74,75,76,77,78,79]. A more ordered state of Ho3+ magnetic moments takes place bellow TN2 = 5 K [26,27,74,75,76,77,78,79].
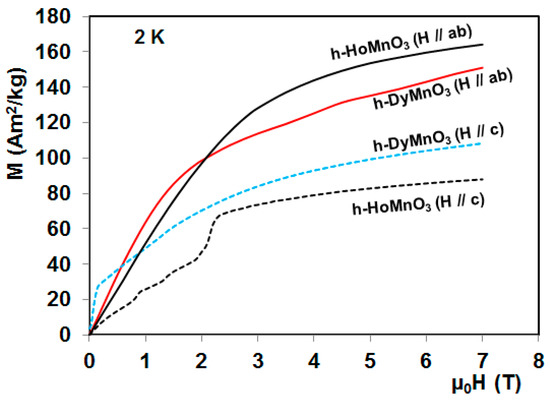
Figure 8.
Isothermal magnetization curves at 2 K for hexagonal DyMnO3 and HoMnO3 single crystals along their easy- and hard-directions [22,27].
It is worth noting that the magnetic structure of Ho3+ ions in the h-HoMnO3 compound is not yet well elucidated even though a large number of studies addressing this issue have been reported in the literature [74,75,76,77,78,79]. However, based on early works, Hur et al. [79] have established a more plausible magnetic structure in which the Ho3+ magnetic moments are strongly in plane coupled (antiferromagnetically) via the Ho(4b)-Ho(4b) exchange interaction leading to non-uncompensated in-plane moments. On the 2a site, the Ho3+ spins show a disordered feature [79]. Additionally, below Tsr the Ho3+ magnetic moments are ordered along the c-axis with a ferrimagnetic arrangement in the ab-plane [79]. On the other hand, the strong antiferromagnetic interplay between the Mn3+ magnetic moments through triangular sublattices in the ab-plane makes the Mn-lattice contribution to the full magnetization negligible [74].
As shown in Figure 8, the h-HoMnO3 magnetization shows an anisotropic behavior between the c-axis and the ab-plane. At 2 K, it was found that the magnetization under 7 T reaches about 7.872 µB/f.u for H//ab and only 4.22 µB/f.u for H//c, being about 80% and 42% of the Ho3+ individual magnetic moments (10 µB) [27,80], respectively. On the other hand, a first metamagnetic transition clearly occurs in h-HoMnO3 under magnetic fields higher than 2 T applied along the c-axis [27]. The corresponding critical magnetic field evolves linearly as a function of temperature with a rate of 0.1714 T/K.
A second field-induced phase transition was observed in some h-HoMnO3 crystals under a magnetic field of 6.5 T applied along the same axis [81]. This could originate from the ordering of 2a site moments that show a disordered feature. However such metamagnetic transformation is not visible in magnetization data reported in [27] up to 7 T (see also Figure 8).
The magnetocaloric properties of h-HoMnO3 single crystals have been carried out by Balli et al. [27] and Midya et al. [26,75]. The reported data demonstrate that the MCE shown by h-HoMnO3 is similar to that exhibited by the DyMnO3 hexagonal phase. As a consequence of the magnetic anisotropy, the obtained isothermal entropy change along the ab-plane largely exceeds that along the c-axis, particularly under sufficiently high applied magnetic fields (Figure 9a,b). Under field variations of 0–2, 0–5, and 0–7 T parallel to the ab-plane, the h-HoMnO3 compound produces a maximum entropy change of 3.86, 13.9, and 18.7 J/kg K, respectively. Along the c-axis, –ΔSmax was evaluated to be 2.86, 11.24, and 13.2 J/kg K, respectively [27]. These values are quite similar to those reported by Midya et al. [26]. The adiabatic temperature change was found to be 10.8 and 6 K under a magnetic field change of 7 T applied along the ab-plane and the c-axis, respectively [27]. According to Balli et al. [27], the MCE corresponding to the c-axis in h-HoMnO3 arises mainly from the field-induced metamagnetic transition zone, particularly under magnetic fields lower than 3.5 T. However, the entropy change associated with the metamagnetic region in h-HoMnO3 was found to be several times larger than its equivalent in the hexagonal DyMnO3 [22,27], as a consequence of their distinguished magnetic structures.
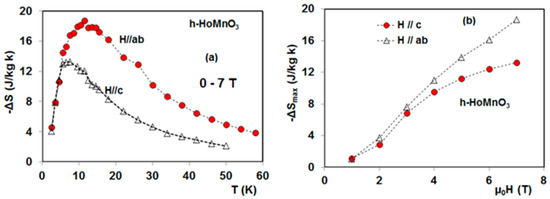
Figure 9.
(a) Isothermal entropy change as a function temperature of the hexagonal HoMnO3 for a magnetic field variation from 0 to 7 T along the easy and hard-directions. (b) Its maximum value as a function of magnetic field [27].
Taking advantage of the magnetic anisotropy, the rotating magnetocaloric effect has been investigated in the h-HoMnO3 single crystal and reported in Balli et al. [27]. The rotation of h-HoMnO3 around the a (or b) axis in a constant magnetic field of 7 T enables a maximum entropy change of 8 J/kg K to be generated and a maximum temperature change of about 5 K. As shown in Figure 7, the produced RMCE in terms of both ΔTad and ΔS is lower than that shown by the orthorhombic DyMnO3. This can mainly be explained by the gigantic magnetocrystalline anisotropy usually exhibited by orthorhombic RMnO3 manganites [24] as shown in Figure 6.
The magnetocaloric characteristics of the orthorhombic perovskite TbMnO3 single crystal were reported in Jin et al. [21] and Midya et al. [26]. According to early works [21,26,59,82,83], its Mn3+ magnetic moments order in an incommensurate phase below the Néel temperature TN1 = 42 K. A second magnetic phase transition to a commensurate state of Mn3+ moments takes place at TL = 27 K. Below TL the Mn3+ magnetic moments rotate in the bc-plane to form a spiral magnetic structure with the propagation vector along the b-axis. This results in a spontaneous electric polarization along the c-axis. The Tb3+ magnetic moments usually order below TN2 = 7 K [21,26,59,82,83]. However, in the work by Jin et al. [21], the ordering temperature of Tb3+ moments was evaluated to be about 9 K. In Ref. [21], the magnetization and MCE data were only reported along the a and b axes under magnetic fields up to 7 T. Along the a-axis, magnetization isotherms unveil a “metamagnetic” transition at low temperatures to reach a nearly saturation state (7.1 µB/f.u) after overpassing a critical magnetic field of about 1.4 T. This behavior originates from the switch of the spiral magnetic structure from the bc-plane to the ac-plane under the effect of an external magnetic field as a consequence of the strong coupling between Tb3+ and Mn3+ magnetic moments [21]. As for the a-axis, the change in the spiral magnetic structure leads to a sharp transition under a magnetic field of 4.8 T applied along the b-axis, while a change in the wave vector modulation induces a second magnetic transition under a low magnetic field of 0.8 T [21]. All these magnetic features lead to interesting levels for the magnetocaloric effect in TbMnO3 single crystals [21].
In the field change of 7 T applied along the easy-axis a, TbMnO3 exhibits a reversible maximum entropy change –ΔSmax = 18 J/kg K which compares well with that reported in HoMnO3 [27] and DyMnO3 [22,24] along their easy directions. The corresponding adiabatic temperature change was found by Midya et al. [26] to be about 10.5 K. For H//b, the maximum entropy change shown by TbMnO3 is only about 10 J/kg K (under 7 T) due to the magnetocrystalline anisotropy. It is also worth noting that below the ordering point of Tb3+ spins (9 K), the TbMnO3 single crystal shows a negative MCE under relatively low magnetic fields applied along its a-axis. This mainly originates from the suppression of the “more ordered” antiferromagnetic state, giving rise to a positive entropy change [21]. The MCE becomes conventional under sufficiently high magnetic fields since the magnetic phase is transferred to a more ordered ferromagnetic state [21]. However, along the b-axis the negative feature of the MCE is retained up to 7 T. This mainly arises from the strong antiferromagnetic interplay between the Mn3+ and Tb3+ moments in the bc-plane [21]. Additionally, the TbMnO3 single crystal unveils a maximum anisotropic entropy change of about 8 J/Kg K [21] in a magnetic field of 7 T, being much lower than that found in the orthorhombic DyMnO3 (16.3 J/kg K under 7 T) [24]. On the other hand, the rotation of theTbMnO3 single crystal in a constant magnetic field of 5 T between a and b axes enables a maximum adiabatic temperature change of about 6 K to be achieved [21].
In a following paper, Jin et al. [23] explored the magnetocaloric properties of TmMnO3 single crystals. This compound belongs to the family of hexagonal RMnO3 manganites such as h-HoMnO3 and h-DyMnO3 compounds discussed above. In this crystal, the Néel temperature associated with the ordering of Mn3+ magnetic moments was observed around 83 K [84]. Below this temperature, the Tm3+ ions unveil a magnetic moment at the 4b crystallographic site due to the Tm-Mn exchange interaction, while the 2a site shows a paramagnetic character down to 4.2 K [84]. This was particularly confirmed by Mossbauer data reported in Salama et al. [84]. The ordering temperature of Tm3+ was reported in the literature to be lower than 1.8 K [85]. As reported in [23], the hexagonal TmMnO3 shows large magnetic and magnetocaloric anisotropies between the c and a axes. For H//c, its magnetization reaches a value of 4.9 µB/f.u (under 7 T) at 2 K and only about 0.8 µB/f.u for H//a (under 7 T) [23]. The resulting maximum entropy change from the magnetization of TmMnO3 along the c-axis was reported to be 8.73 J/kg K in the field of 7 T, which is more than two times lower if compared with other RMnO3 compounds (R = Ho, Dy, Tb) [21,22,24,27]. This can be partly attributed to the partial ordering of the Tm3+ ions magnetic moment [84]. Along the a-axis, the entropy change in TmMnO3 was found to be negligible [23].
The magnetocaloric properties of the hexagonal YbMnO3 were briefly discussed in [26]. According to early neutron diffraction and Mossbauer spectroscopy data [86], the hexagonal form of YbMnO3 shows the antiferromagnetic ordering of Mn3+ magnetic moments at around TN1 = 85 K. This is accompanied by a partial ordering of Yb3+ magnetic moments at the 4b site through Yb-Mn exchange interactions. At temperatures below 3.5 K, the rest of the Yb3+ magnetic moments orders at the 2a site via Yb-Yb magnetic exchanges [86]. Midya et al. [26] found that the magnetic behavior of h-YbMnO3 is less anisotropic with strong antiferromagnetic interactions along the c and a axes. On the other hand, the h-YbMnO3 compound was found to present distinguished features depending on the a and c crystallographic axes. While the magnetization increases slightly with magnetic field applied along the a-axis, an abrupt change can be observed under magnetic fields higher than 3 T applied along the c-axis at low temperatures [26]. The maximum isothermal entropy change was evaluated to be about 7.24 J/kg K under a magnetic field change of 7 T, being much lower than that shown by the hexagonal HoMnO3, for example [27]. This can be mainly attributed to the smaller value of the Yb3+ magnetic moment which is about 4 µB [80]. However, despite the moderate value of ΔS, its adiabatic temperature change shows a maximum value that largely exceeds that exhibited by the RMnO3 compounds discussed above. Until now, the physics behind this enhancement has remained unclear.
The magnetocaloric properties of other RMnO3 compounds such as GdMnO3 [87,88], NdMnO3 [89], SmMnO3 [90], and EuMnO3 [91] were also investigated. In contrast with other o-RMnO3 manganites, the orthorhombic GdMnO3 ground state unveils a canted A-type antiferromagnetism [88]. According to magnetization measurements and specific heat data, three phase transitions can be clearly identified [87]. At around TN1 = 42 K, the Mn3+ magnetic moments order in an incommensurate antiferromagnetic state. This latter transforms into a canted A-type antiferromagnetic phase at 23 K. On decreasing temperature, the ordering of Gd3+ spins takes place at 5.2 K. Kimura et al. [67] reported that the GdMnO3 compound manifests a multiferroic feature when subjected to external magnetic fields. The application of magnetic fields along the b-axis generates an electric polarization along the a-axis [67]. This is in contradiction to Hemberger et al. [88] who claimed the absence of ferroelectricity in GdMnO3 as a result of non-spiral character of the magnetic ground state.
The magnetocaloric properties of the GdMnO3 single crystal were more recently reported by Wagh et al. [87] along its crystallographic axes. Under a magnetic field changing from 0 to 8 T along the c-axis around the ordering point of Dy3+ magnetic moments (7 K), a large isothermal entropy change of about 31.8 J/kg K can be reached. Along the a and b-axes the calculated −ΔS is slightly lower and found to be about 29.1 and 25.7 J/kg K, in a similar magnetic field, respectively. On the other hand, the GdMnO3 single crystal unveils a negative magnetocaloric effect following the a and c-axes. This was attributed by the authors [87] to the antiferromagnetic ordering of Gd3+ magnetic moments.
For NdMnO3, relatively low values of MCE were reported by Chandra et al. [89]. Under a magnetic field change of 5 T, the bulk polycrystalline NdMnO3 shows a maximum of about 4.4 J/kg K for –ΔS at 15 K. The entropy change of its nanocrystalline (40 nm) form exhibits two different maxima of about 2.3 and 3.7 J/kg K (under 5 T) at 70 and 15 K, respectively. For the polycrystalline SmMnO3, a maximum entropy change of about 9 J/kg K was reported for a magnetic field change of 7 T around TN = 57 K [90]. A similar value was also found at 9 K under the same magnetic field [90]. Regarding the EuMnO3 compound, a negligible MCE in terms of ΔS and ΔTad was reported by Sagar et al. [91].
The refrigerant capacity and the isothermal entropy change along the easy-axis of some relevant RMnO3 single crystals are reported in Figure 10 and Figure 11. As shown, the RC is particularly higher for compounds containing rare earth element with high magnetic moments such as Tb, Ho, and Dy. The largest RC is presented by the orthorhombic DyMnO3 (452 J/kg under 7 T) [24]. The exhibited RC largely exceeds that shown by some of the best intermetallics such as ErRu2Si2 (196.5 J/kg for 5 T) [92], but remain much lower when compared with the vanadate HoVO3 (620 J/kg under 7 T) [28]. For –ΔS, the largest value is shown by the GdMnO3 single crystal. This is probably attributed to a more pronounced first order phase transition associated with the ordering of Gd3+ spins. However, its adiabatic temperature change [87] remains comparable with that shown by other orthorhombic RMnO3 (R = Tb, Dy) [21,24].
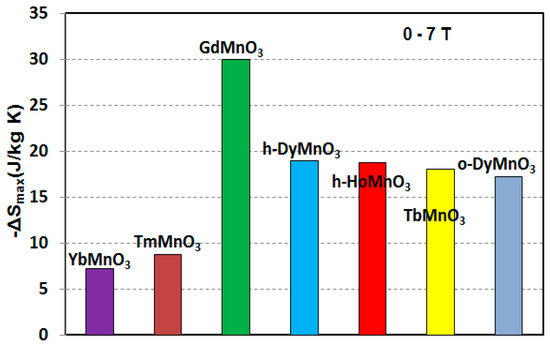
Figure 10.
Maximum entropy change of RMnO3 single crystals under a magnetic field of 7 T applied along their easy directions, with R = Yb [26], Tm [23], Gd [87], h-Dy [22], h-Ho [27], Tb [21], and o-Dy [24].
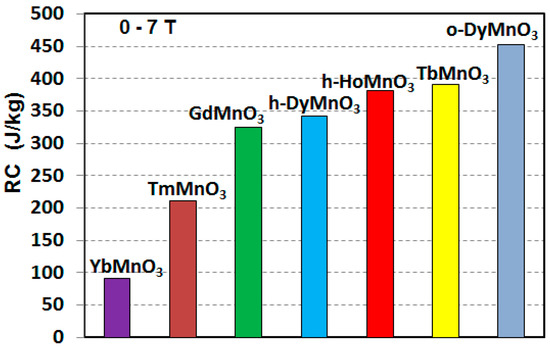
Figure 11.
Refrigerant capacity of RMnO3 single crystals under a magnetic field of 7 T applied along their easy directions, with R = Yb [26], Tm [23], Gd [87], h-Dy [22], h-Ho [27], Tb [21], and o-Dy [24].
In addition to RMnO3 manganites, the RTiO3 (titanates) [93,94,95] and RFeO3 [96] compounds emerge also as promising magnetocaloric materials for cryogenic applications. Particularly, a giant magnetocaloric effect was pointed out in EuTiO3 single crystals [93]. Around the antiferromagnetic ordering point of Eu2+ magnetic moments (TN = 5.8 K), a huge isothermal entropy change of 49 J/kg under 7 T was more recently reported by Midya et al. [93]. In a similar magnetic field, the associated adiabatic temperature change and the refrigerant capacity were found to be 21 K and 500 J/kg K, respectively. The reported ΔS and ΔTad in EuTiO3 [93] largely exceed those shown by the here reviewed RMnO3 manganites. However, its refrigerant capacity remains comparable with that presented by the orthorhombic DyMnO3 (Figure 11) but lower if compared with the HoVO3 vanadate [28]. On the other hand a large rotating entropy change that is comparable with that exhibited by o-DyMnO3 crystals [24] was more recently reported in TbFeO3 (–ΔSR = 17.42 J/kg K at 5 T) around 9 K [96]. These data underline the high potential of R(Ti, Fe)O3-based compounds in cryomagnetocaloric applications.
5. Magnetocaloric Properties of RMn2O5 Multiferroic Crystals
Several studies of RMn2O5 (R = rare earth) oxides have revealed a giant magnetoelectric effect (MEE), which is associated with an unusual commensurate–incommensurate magnetic phase transition. In the case of DyMn2O5, the dielectric constant was enhanced by more than 100% under the application of an external magnetic field leading to a colossal magnetodielectric effect (CMD) [34]. On the other hand, a highly reversible switching of electrical polarization in TbMn2O5 crystals can be achieved by using relatively low magnetic field of 2 T [33]. However, little interest has been paid to their magnetocaloric properties [19,20]. More recently, a large rotating MCE was reported in the HoMn2O5 single crystal at low temperatures [19], opening the way for the implementation of compact, simplified, and efficient magnetic refrigerators. On the basis of the rotating MCE observed in HoMn2O5, a new concept for the liquefaction of the helium and hydrogen was also proposed [19].
The multiferroics RMn2O5 (R = rare earth) are insulators displaying an orthorhombic structure (Pbam) composed of Mn4+O6 octahedral and Mn3+O5 pyramidal units (see Figure 12) [31,32,33,34,35,36]. The octahedra share edges to form chains along the c-axis. The formed chains are linked by pairs of pyramids within the ab-plane. The interaction between Mn4+, Mn3+, and rare earth R3+ ions magnetic moments lead to a pronounced magnetic frustration resulting in complex magnetic and electric responses [31,32,33,34,35,36]. Usually, the RMn2O5 compounds present various phase transitions at low temperatures below 50 K. Around TN1 = 45 K, an incommensurate antiferromagnetic ordering of the Mn3+/Mn4+ magnetic moments takes place. This transition coincides with the appearance of a spontaneous electric polarization that occurs slightly down to TN1 around TC = 38 K. The AFM ordering of Mn3+/Mn4+ spins transforms into a commensurate state at TL = 33 K (lock-in temperature) and becomes again incommensurate around TN2 = 20 K [31,32,33,34,35,36]. The R3+ spins usually order below 15 K [31,32,33,34,35,36].
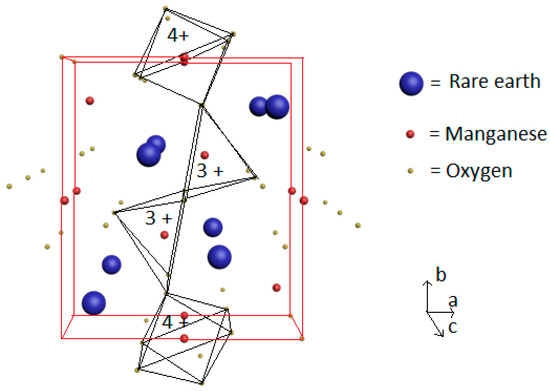
Figure 12.
RMn2O5 orthorhombic structure. Each Mn3+ (red) is encased in the oxygens’s (grey) pyramid while Mn4+ ions (red) are encased in the oxygens’s octaedra.
Until today, only the magnetocaloric properties of HoMn2O5 and TbMn2O5 single crystals (Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17) have been reported by Balli et al. [19,20]. The HoMn2O5 compound unveils a giant magnetic anisotropy (Figure 13) with the easy, intermediate, and hard crystallographic axes along the b-, a-, and c-orientations [19]. According to magnetization data, the Ho3+ magnetic moments were found to order around 10 K, whereas the phase transitions involving the Mn-sublattice are not clearly visible from thermomagnetic curves because of the large magnetic moment of Ho3+ that overshadows the weak magnetization resulting from the Mn moments [19]. As reported in Balli et al. [19], the inverse magnetic susceptibility at high temperatures indicates antiferromagnetic interactions along the c and a axes while a weak antiferromagnetic order or a paramagnetic disorder of Ho3+ moments is shown by HoMn2O5 along the easy-axis b. This is in good agreement with early reported neutron diffraction data by Blake et al. [32]. Magnetocaloric properties of the HoMn2O5 single crystal [19] have been reported in terms of entropy and adiabatic temperature changes (Figure 14, Figure 15a and Figure 17). Along the easy-axis b, the maximum isothermal entropy change was found to be 3.5 and 13.1 J/kg K in magnetic field changes of 2 and 7 T, respectively. For the intermediate a-axis, –ΔSmax reaches only 5 J/kg K under 7 T [19]. Following the hard-axis c, the resulting MCE is much lower even under high magnetic fields (Figure 15a). The associated refrigerant capacities were found to be 334, 157.5, and 44 J/Kg under a magnetic field of 7 T parallel to the b, a, and c axes, respectively [19]. This can be mainly explained by the gigantic magnetocrystalline anisotropy shown by HoMn2O5 single crystals as plotted in Figure 13. At 2 K, the magnetization under magnetic field of 7 T applied along the easy-axis is 124 Am2/kg and only 34 Am2/kg for H//c [19]. Taking advantage of the anisotropic MCE shown by HoMn2O5 (Figure 15a) a large rotating magnetocaloric effect was also reported by Balli et al. [19]. By rotating the HoMn2O5 single crystal in constant magnetic field of 7 T around its a-axis, the resulting entropy change reaches a maximum value of 12.43 J/kg K, being much larger that the rotating entropy change reported in TbMnO3 [21] and TmMnO3 [23], but lower if compared with the orthorhombic DyMnO3 single crystal [24] discussed above. On the other hand, the associated rotating adiabatic temperature change (6.5 K in 7 T) is about two times lower than that exhibited by o-DyMnO3 (11 K in 7 T). This is mainly due to the largest magnetocrystalline anisotropy of the orthorhombic DyMnO3 as well as the enhancement of its magnetization along the easy-axis (170 Am2/kg) [24].
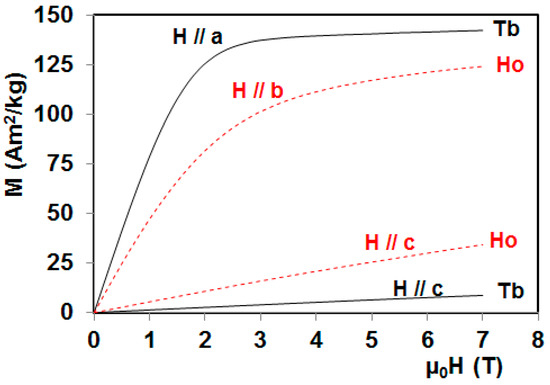
Figure 13.
Magnetic isotherms at 2 K of RMn2O5 (R = Ho and Tb) single crystals along their easy- and hard-axes [19,20].
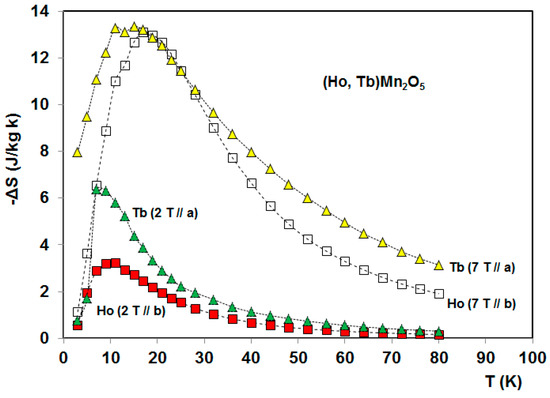
Figure 14.
A comparison between entropy changes of RMn2O5 (R = Ho and Tb) single crystals under relatively low (2 T) and high (7 T) magnetic fields applied along their easy-axes [19,20].
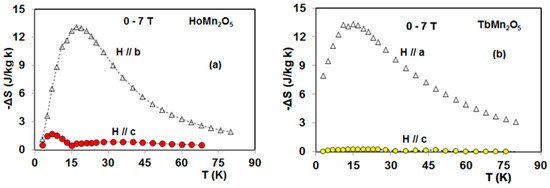
Figure 15.
Isothermal entropy change of HoMn2O5 (a) and TbMn2O5 (b) single crystals under a magnetic field change of 7 T applied along their easy- and hard-axes [19,20].
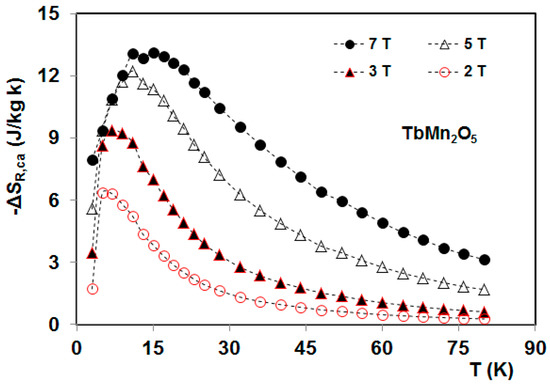
Figure 16.
Rotating entropy change as a function of temperature for the single crystal TbMn2O5 in several constant magnetic fields, initially parallel to the c-axis [20].
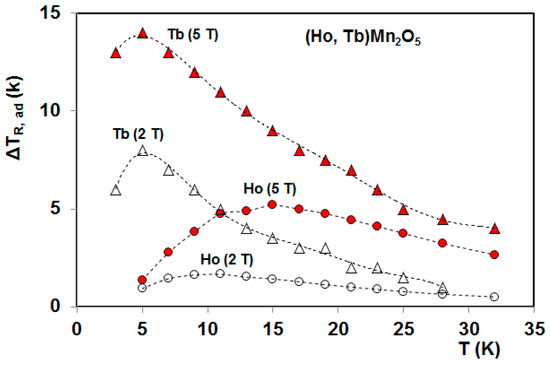
Figure 17.
Rotating adiabatic temperature change as a function of temperature for RMn2O5 (R = Ho and Tb) single crystals in constant magnetic fields of 2 and 5 T [19,20]. The crystals are rotated by an angle of 90° around their intermediate axes with magnetic fields initially parallel to the hard-axis.
In a following paper, the magnetocaloric properties of the TbMn2O5 single crystal were also reported by Balli et al. [20]. Thermomagnetic curves unveil clear features around 5 and 36 K corresponding to the ordering point of Tb3+ magnetic moment and the onset of ferroelectric order, respectively [33]. However, additional transitions which occur at 24 K and 40 K can be clearly seen in specific heat measurements [33,34] but are not visible in the thermomagnetic curves reported in Ref. [20]. The 24 K and 40 K transitions were attributed to the Mn3+/Mn4+ spins reorientation and to the long range antiferromagnetic order of the Mn3+/Mn4+ spins, respectively. The magnetization data also reveal strong antiferromagnetic interactions along the b and c axes, whereas ferromagnetic exchanges are further associated with the a-axis [20]. The isothermal magnetization curves M (µ0H) measured at 2 K (Figure 13), demonstrate the presence of a large magnetocrystalline anisotropy, where the easy and hard magnetization directions are parallel to the a and c axes, respectively. The gigantic magnetocrystalline anisotropy is mainly attributed to the large spin-orbit interplay of the Tb moments in TbMn2O5 single crystals [33,34]. Also, the magnetic exchange interactions between Tb3+, Mn3+, and Mn4+ moments in TbMn2O5 cannot all be satisfied simultaneously, leading to a geometrically frustrated magnetic system. The magnetization saturation can be clearly seen for a magnetic field above 2 T applied along the a-axis (Figure 13). The corresponding saturation magnetic moment is 140 Am2/kg (8.75 µB/f.u) which is about 52% of that calculated (268.8 Am2/kg) when considering a parallel configuration of all the magnetic moments of Tb3+ (9 µB), Mn4+ (3.8 µB) and Mn3+ (4 µB) [20]. Additionally, the resulting magnetization saturation is very close to the Tb3+ magnetic moment (9 µB). This means that the Tb3+ magnetic moments can be completely aligned under sufficiently high magnetic fields applied along the easy-axis, considering the weak contribution of Mn spins to the total magnetization [31,32,33,34,35,36]. Moreover, the magnetization at 7 T decreases by about 94% when the magnetic field direction is changed from the easy-axis to the hard-axis. This leads to a giant anisotropy of the MCE (Figure 15b) in TbMn2O5 single crystals [20]. For example, the maximum value of –ΔS along the easy axis in a field of 7 T is about 63 times larger than that along the hard-orientation.
The magnetic field variation from 0 to 2 and 0 to 7 T yields to a maximum entropy change of 6.4 and 13.35 J/kg K, for H//a (Figure 14) while it is only 0.33 and 3 J/kg K for H//b, respectively [20]. The resulting entropy change along the hard-axis c was found to be practically zero [20]. Considering the case in which the disordered magnetic phase of Tb3+ ions is changed to a completely ordered phase, the theoretical limit of the resulting entropy change is given by ΔSLimt = R*Ln(2J+1) = 61.18 J/kg K (here, R is the universal gas constant and J is the angular momentum quantum number). As for Tb3+, J was assumed to be 6 for the TbMn2O5 single crystal. For a magnetic field variation from 0 to 7 T along the ordering axis of Tb3+ moments (a-axis), only 22% of ΔSLimt can be obtained upon saturation of the magnetization, revealing that entropy changes larger than 13.35 J/kg K may be reached under intense external magnetic fields.
The TbMn2O5 refrigerant capacity was also reported by Balli et al. [20]. With increasing field, the RC was found to increase almost linearly with a rate of about 79 J/kg T, 8 J/kg T for H//a and H//b, respectively. Along the hard-direction, the RC is negligible. When changing the magnetic field from 0 to 7 T, the RC reaches values of 480 J/kg, 47 J/kg and only about 4 J/kg along the a, b, and c axes, respectively. Considering magnetocaloric oxides with similar working temperature range, the magnetocaloric properties of TbMnO3 were investigated and reported in [21]. Although the TbMnO3 and TbMn2O5 single crystals contain the same rare earth element (Tb3+) and present a similar magnetization saturation (about 140 Am2/kg), it was found that the maximum isothermal entropy change under 7 T along the easy-axis a for TbMnO3 is larger (18 J/kg K) than that exhibited by TbMn2O5 (13.35 J/kg K). However, the RC for TbMn2O5 is much larger than that for TbMnO3 (390 J/kg for 7 T//a). Theses observed deviations originate mainly from the significant difference in their magnetic structures. In fact, the antiferromagnetic ground state is not quite stable in TbMnO3 against applied magnetic field along the easy-axis a [21]. At low temperatures, the spiral magnetic structure of Tb3+ and Mn3+ ions in TbMnO3 enables a first-order magnetic transition of Tb3+ moments from the antiferromagnetic state to the ferromagnetic phase to be easily induced. Such metamagnetic-like transformation means that the magnetization can rapidly be changed with varying magnetic field leading to a large magnetic entropy change. In contrast to TbMnO3, the magnetic phase transition associated with the magnetic moments ordering of Tb3+ in the single crystal TbMn2O5 shows a second-order character, as determined from Arrott plots [97] (not shown here). This makes the magnetic transition broader, leading to a large RC in TbMn2O5 single crystals. On the other hand, the RC of the TbMn2O5 single crystal (314 J/kg for 5 T) along the easy-axis is much larger than that found in the HoMn2O5 oxide (334 J/kg for 7 T) [19] and even in some well-known intermetallics such as ErRu2Si2 (196.5 J/kg for 5 T) [92], DySb (144 J/kg for 5 T) [98], and ErMn2Si2 (273 J/kg for 5 T) [99].
In addition to a large standard MCE resulting from the magnetization-demagnetization process (Figure 14), the TbMn2O5 compound also exhibits a giant rotating MCE (Figure 16 and Figure 17) that can be obtained by spinning its single crystals in a constant magnetic field within the ac-plane (around its b-axis) [20,100]. For a constant magnetic field of 2 and 7 T applied in the ac-plane, the rotation of TbMn2O5 single crystals around the b-axis, enables maximum entropy changes of 6.4 and 13.14 J/kg K, respectively, to be induced, being much larger than the rotating entropy change reported in some known materials such as TbMnO3 (8.2 J/kg K) [21]. The corresponding RC was found to be 476 J/kg under 7 T instead of only 304 J/kg for TbMnO3 [21]. On the other hand, at low magnetic fields ΔSR shown by TbMn2O5 (6.4 J/kg K at 2 T) is two and three times larger than that exhibited by HoMn2O5 [19] and TbMnO3 [21] single crystals, respectively. This is mainly due to the giant magnetic anisotropy in TbMn2O5 as well as the possibility to reach the saturation state under relatively low magnetic fields giving rise to large magnetization along its easy-axis (Figure 13) [20]. Additionally, the RMCE was also investigated in TbMn2O5 in terms of the adiabatic temperature change (Figure 17). In a constant magnetic field of 2 T, the rotating ΔTad reaches a maximum value (8 K) that is six times higher than that presented by TbMnO3 [21]. The rotating adiabatic temperature change shown by TbMn2O5 also largely exceeds that presented by the HoMn2O5 single crystal (Figure 17). The enhancement of ΔTad in TbMn2O5 is partly caused by its low specific heat [34] that is about three times lower when compared with TbMnO3 [37] and HoMn2O5 [34] single crystals.
6. Conclusions
In this report we reviewed the magnetic and magnetocaloric properties of RMnO3 and RMn2O5 multiferroic single crystals. In both families of materials, the competition between different magnetic exchange interactions involving Mn3+, Mn4+ and R3+ sublattices results in several phase transitions usually occurring below 100 K. However, only the magnetic phase transition associated with the ordering of R3+ magnetic moments at temperatures usually below 20 K contributes to the magnetocaloric effect. The application of sufficiently high magnetic fields along the easy-axis enables large thermal effects to be generated around the ordering point of the rare earth elements (~10 K). In some compounds such as orthorhombic DyMnO3 and TbMn2O5 single crystals, relatively low magnetic fields are required to achieve a large MCE. This is of great importance from economical and practical points of view since the needed fields can be provided by permanent magnets. Additionally, most of RMnO3 and RMn2O5 single crystals unveil a gigantic anisotropy of the magnetocaloric effect which means that additional thermal effects can also be obtained by rotating them between the hard- and easy-directions in constant magnetic fields. This could open the way for the design of more compact, efficient, and simplified magnetocaloric devices. On the other hand, the strong magnetoelectric coupling usually observed in these compounds offers an additional degree of freedom since the MCE could, for example, be tailored by an electric field through the manipulation of the ferroelectric order.
All these features combined with the insulating character as well as the high chemical stability (in comparison with intermetallics) render RMnO3 and RMn2O5 multiferroics more attractive particularly in cryomagnetocaloric refrigerators.
Acknowledgments
The authors thank M. Castonguay, S. Pelletier and B. Rivard for technical support. We acknowledge the financial support from NSERC (Canada), FQRNT (Québec), CFI, CIFAR, Canada First Research Excellence Fund (Apogée Canada) and the Université de Sherbrooke. M. Balli would like to thank S. Mansouri for the fruitful discussion regarding the magnetoelectric interplay in multiferroic RMnO3 and RMn2O5 compounds.
Author Contributions
Mohamed Balli conceived the work prepared Figures and analyzed data, wrote the paper; Benoit Roberge prepared Figures and co-wrote the paper; Mohamed Balli, Benoit Reberge, Serge Jandl, and Patrick Fournier revised the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gschneidner, K.A., Jr.; Pecharsky, V.K.; Tsokol, A.O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 2005, 68, 1479. [Google Scholar] [CrossRef]
- Moya, X.; Kar-Narayan, S.; Mathur, N.D. Caloric materials near ferroic phase transitions. Nat. Mater. 2014, 13, 439–450. [Google Scholar] [CrossRef] [PubMed]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant Magnetocaloric Effect in Gd5Ge2Si2. Phys. Rev. Lett. 1997, 78, 4494. [Google Scholar] [CrossRef]
- Wada, H.; Tanabe, Y. Giant magnetocaloric effect of MnAs1-xSbx. Appl. Phys. Lett. 2001, 79, 3302. [Google Scholar] [CrossRef]
- Balli, M.; Fruchart, D.; Gignoux, D.; Dupuis, C.; Kedous-Lebouc, A.; Zach, R. Giant magnetocaloric effect in Mn1-x (Ti0. 5V0. 5) xAs: Experiments and calculations. J. Appl. Phys. 2008, 103, 103908. [Google Scholar] [CrossRef]
- Balli, M.; Fruchart, D.; Gignoux, D.; Tobola, J.; Hlil, E.K.; Wolfers, P.; Zach, R. Magnetocaloric effect in ternary metal phosphides (Fe 1-xNix)2 P. J. Magn. Magn. Mater. 2007, 316, 358–360. [Google Scholar] [CrossRef]
- Tegus, O.; Brück, E.; Buschow, K.H.J.; De Boer, F.R. Transition-metal-based magnetic refrigerants for room-temperature applications. Nature 2002, 415, 150–152. [Google Scholar] [CrossRef] [PubMed]
- Fujita, A.; Fujieda, S.; Hasegawa, Y.; Fukamichi, K. Itinerant-electron metamagnetic transition and large magnetocaloric effects in La(FexSi1-x)13 compounds and their hydrides. Phys. Rev. B 2003, 67, 104416. [Google Scholar] [CrossRef]
- Hu, F.X.; Shen, B.G.; Sun, J.R.; Wang, G.J.; Cheng, Z.H. Very large magnetic entropy change near room temperature in LaFe11.2Co0.7Si1.1. Appl. Phys. Lett. 2002, 80, 826–828. [Google Scholar] [CrossRef]
- Balli, M.; Fruchart, D.; Gignoux, D. The LaFe11.2Co0.7Si1.1Cx carbides for magnetic refrigeration close to room temperature. Appl. Phys. Lett. 2008, 92, 232505. [Google Scholar] [CrossRef]
- Balli, M.; Fruchart, D.; Gignoux, D. Optimization of La (Fe, Co)13-xSix based compounds for magnetic refrigeration. J. Phys. Condens. Matter 2007, 19, 236230. [Google Scholar] [CrossRef]
- Phan, M.H.; Yu, S.C. Review of the magnetocaloric effect in manganite materials. J. Magn. Magn. Mat 2007, 308, 325–340. [Google Scholar] [CrossRef]
- Balli, M.; Fruchart, D.; Gignoux, D. Effect of Ni substitution on the magnetic and magnetocaloric properties of the Dy (Co1-xNix)2 Laves phase. J. Phys. D Appl. Phys. 2007, 40, 7601. [Google Scholar] [CrossRef]
- Balli, M.; Fruchart, D.; Gignoux, D.; Hlil, E.K.; Miraglia, S.; Wolfers, P. Gd1-xTbx alloys for Ericsson-like magnetic refrigeration cycles. J. Alloys Compd. 2007, 442, 129–131. [Google Scholar] [CrossRef]
- Sari, O.; Balli, M. From conventional to magnetic refrigerator technology. Int. J. Refrig. 2014, 37, 8–15. [Google Scholar] [CrossRef]
- Balli, M.; Sari, O.; Mahmed, C.; Besson, C.; Bonhote, P.; Duc, D.; Forchelet, J. A pre-industrial magnetic cooling system for room temperature application. Appl. Energy 2012, 98, 556–561. [Google Scholar] [CrossRef]
- Zimm, C.; Jastrab, A.; Sternberg, A.; Pecharsky, V.; Gschneidner, K., Jr.; Osborne, M.; Anderson, I. Description and Performance of a Near-Room Temperature Magnetic Refrigerator. Adv. Cryog. Eng. 1998, 43, 1759–1766. [Google Scholar]
- Barclay, J.; Oseen-Senda, K.; Skrzypkowski, M. Unique feature of liquefaction of hydrogen and natural gas using magnetic refrigeration. In Proceedings of 6th IIF-IIR International Conference on Magnetic Refrigeration, Victoria, BC, Canada, 7–10 September 2014.
- Balli, M.; Jandl, S.; Fournier, P.; Gospodinov, M.M. Anisotropy-enhanced giant reversible rotating magnetocaloric effect in HoMn2O5 single crystals. Appl. Phys. Lett. 2014, 104, 232402. [Google Scholar] [CrossRef]
- Balli, M.; Jandl, S.; Fournier, P.; Dimitrov, D.Z. Giant rotating magnetocaloric effect at low magnetic fields in multiferroic TbMn2O5 single crystals. Appl. Phys. Lett. 2016, 108, 102401. [Google Scholar] [CrossRef]
- Jin, J.L.; Zhang, X.Q.; Li, G.K.; Cheng, Z.H.; Zheng, L.; Lu, Y. Giant anisotropy of magnetocaloric effect in TbMnO3 single crystals. Phys. Rev. B 2011, 83, 184431. [Google Scholar] [CrossRef]
- Balli, M.; Jandl, S.; Fournier, P.; Mansouri, S.; Mukhin, A.; Ivanov, Y.V.; Balbashov, A.M. On the magnetocaloric effect in the multiferroic hexagonal DyMnO3 single crystals. J. Magn. Magn. Mat. 2015, 374, 252–257. [Google Scholar] [CrossRef]
- Jin, J.L.; Zhang, X.Q.; Ge, H.; Cheng, Z.H. Rotating field entropy change in hexagonal TmMnO3 single crystal with anisotropic paramagnetic response. Phys. Rev. B 2012, 85, 214426. [Google Scholar] [CrossRef]
- Balli, M.; Mansouri, S.; Jandl, S.; Fournier, P.; Dimitrov, D.Z. Large rotating magnetocaloric effect in the orthorhombic DyMnO3 single crystal. Solid. Stat. Commun. 2016, 239, 9–13. [Google Scholar] [CrossRef]
- Li, L.; Namiki, T.; Huo, D.; Qian, Z.; Nishimura, K. Two successive magnetic transitions induced large refrigerant capacity in HoPdIn compound. Appl. Phys. Lett. 2013, 103, 222405. [Google Scholar]
- Midya, A.; Das, S.N.; Mandal, P.; Pandya, S.; Ganesan, V. Anisotropic magnetic properties and giant magnetocaloric effect in antiferromagnetic RMnO3 crystals (R = Dy, Tb, Ho, and Yb). Phys. Rev. B 2011, 84, 235127. [Google Scholar] [CrossRef]
- Balli, M.; Roberge, B.; Vermette, J.; Jandl, S.; Fournier, P.; Gospodinov, M.M. Magnetocaloric properties of the hexagonal HoMnO3 single crystal revisited. Physica B 2015, 478, 77–83. [Google Scholar] [CrossRef]
- Balli, M.; Roberge, B.; Jandl, S.; Fournier, P.; Palstra, T.T.M.; Nugroho, A.A. Observation of large refrigerant capacity in the HoVO3 vanadate single crystal. J. Appl. Phys. 2015, 118, 073903. [Google Scholar] [CrossRef]
- Matsumoto, K.; Kondo, T.; Yoshioka, S.; Kamiya, K.; Numazawa, T. Magnetic refrigerator for hydrogen liquefaction. J. Phys. Conf. Ser. 2009, 150, 012028. [Google Scholar] [CrossRef]
- Numazawa, T.; Kamiya, K.; Utaki, T.; Matsumoto, K. Magnetic refrigerator for hydrogen liquefaction. Cryogenics 2014, 62, 185–192. [Google Scholar] [CrossRef]
- Noda, Y.; Kimura, H.; Fukunaga, M.; Kobayashi, S.; Kagomiya, I.; Kohn, K. Magnetic and ferroelectric properties of multiferroic RMn2O5. J. Phys. Condens. Matter 2008, 20, 434206. [Google Scholar] [CrossRef]
- Blake, G.R.; Chapon, L.C.; Radaelli, P.G.; Park, S.; Hur, N.; Cheong, S.W.; Rodriguez-Carvajal, J. Spin structure and magnetic frustration in multiferroic RMn2O5 (R = Tb, Ho, Dy). Phys. Rev. B 2005, 71, 214402. [Google Scholar] [CrossRef]
- Hur, N.; Park, S.; Sharma, P.A.; Ahn, J.S.; Guha, S.; Cheong, S.W. Electric polarization reversal and memory in a multiferroic material induced by magnetic fields. Nature 2004, 429, 392–395. [Google Scholar] [CrossRef] [PubMed]
- Hur, N.; Park, S.; Sharma, P.A.; Guha, S.; Cheong, S.W. Colossal Magnetodielectric Effects in DyMn2O5. Phys. Rev. Lett. 2004, 93, 107207. [Google Scholar] [CrossRef] [PubMed]
- Mihailova, B.; Gospodinov, M.M.; Güttler, B.; Yen, F.; Litvinchuk, A.P.; Iliev, M.N. Temperature-dependent Raman spectra of HoMn2O5 and TbMn2O5. Phys. Rev. B 2005, 71, 172301. [Google Scholar] [CrossRef]
- Tzankov, D.; Skumryev, V.; Aroyo, M.; Puźniak, R.; Kuz’min, M.D.; Mikhov, M. Magnetic anisotropy of multiferroic HoMn2O5 single crystal. Solid. Stat. Commun. 2008, 147, 212–216. [Google Scholar] [CrossRef]
- Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.; Tokura, Y. Magnetic control of ferroelectric polarization. Nature 2003, 426, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Lottermoser, T.; Lonkai, T.; Amann, U.; Hohlwein, D.; Ihringer, J.; Fiebig, M. Magnetic phase control by an electric field. Nature 2004, 430, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Goto, T.; Kimura, T.; Lawes, G.; Ramirez, A.P.; Tokura, Y. Ferroelectricity and Giant Magnetocapacitance in Perovskite Rare-Earth Manganites. Phys. Rev. Lett. 2004, 92, 257201. [Google Scholar] [CrossRef] [PubMed]
- Prokhnenko, O.; Feyerherm, R.; Dudzik, E.; Landsgesell, S.; Aliouane, N.; Chapon, L.C.; Argyriou, D.N. Enhanced Ferroelectric Polarization by Induced Dy Spin Order in Multiferroic DyMnO3. Phys. Rev. Lett. 2007, 98, 057206. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Murugavel, P.; Lee, D.; Noh, T.W.; Jo, Y.; Jung, M.H.; Jang, K.H.; Park, J.G. Multiferroic properties of epitaxially stabilized hexagonal DyMnO3 thin films. Appl. Phys. Lett. 2007, 90, 012903. [Google Scholar] [CrossRef]
- Tishin, A.M.; Spichkin, Y.L. The Magnetocaloric Effect and Its Applications; IOP Publishing Ltd.: London, UK, 2003. [Google Scholar]
- Balli, M.; Mahmed, C.; Bonhote, P.; Sari, O. On the magnetic forces in magnetic cooling machines: Numerical calculations and experimental investigations. IEEE Trans. Magn. 2011, 47, 3383–3386. [Google Scholar] [CrossRef]
- Balli, M.; Fruchart, D.; Zach, R. Negative and conventional magnetocaloric effects of a MnRhAs single crystal. J. Appl. Phys. 2014, 115, 203909. [Google Scholar] [CrossRef]
- Balli, M.; Fruchart, D.; Gignoux, D.; Zach, R. The “colossal” magnetocaloric effect in Mn1-xFexAs: What are we really measuring? Appl. Phys. Lett. 2009, 95, 072509. [Google Scholar] [CrossRef]
- Balli, M.; Sari, O.; Fruchart, D.; Forchelet, J. Influence of the materials magnetic state on the accurate determination of the magnetocaloric effect. Eur. Phys. J. Web Conf. 2012, 29, 00005. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K. Magnetocaloric Materials. Annu. Rev. Mater. Sci. 2000, 30, 387–429. [Google Scholar] [CrossRef]
- Niknia, I.; Trevizoli, P.V.; Govindappa, P.; Campbell, O.; Christiaanse, T.V.; Teyber, R.; Rowe, A. A material screening technique for optimum performance of an AMR. In Proceedings of the Seventh IIF-IIR International Conference on Magnetic Refrigeration at Room Temperature, Thermag VII, Torino, Italy, 11–14 September 2016.
- Lee, S.; Pirogov, A.; Han, J.H.; Park, J.G.; Hoshikawa, A.; Kamiyama, T. Direct observation of a coupling between spin, lattice and electric dipole moment in multiferroic YMnO3. Phys. Rev. B 2005, 71, 180413. [Google Scholar] [CrossRef]
- Bary’achtar, V.G.; L’vov, V.A.; Jablonskii, D.A. Theory of inhomogeneous magnetoelectric effect. Sov. JETP Lett. 1983, 37, 565–567. [Google Scholar]
- Stefanovskii, E.P.; Jablonskii, D.A. Theory of electrical polarization of multisublattice orthorhombic antiferromagnets with a double-exchange superlattice. Sov. J. Low Temp. Phys. 1986, 12, 478–480. [Google Scholar]
- Mostovoy, M. Ferroelectricity in Spiral Magnets. Phys. Rev. Lett. 2006, 96, 067601. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, G. Study of (La1-xCax)MnO3. I. Magnetic Structure of LaMnO3. J. Phys. Soc. Jpn. 1970, 29, 606–615. [Google Scholar] [CrossRef]
- Wollan, E.O.; Koehler, W.C. Neutron Diffraction Study of the Magnetic Properties of the Series of Perovskite-Type Compounds [(1-x)La, xCa]MnO3. Phys. Rev. 1955, 100, 545. [Google Scholar] [CrossRef]
- Katsura, H.; Nagaosa, N.; Balatsky, V. Spin current and magnetoelectric effect in noncollinear magnets. Phys. Rev. Lett. 2005, 95, 057205. [Google Scholar] [CrossRef] [PubMed]
- Sergienko, I.A.; Dagotto, E. Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites. Phys. Rev. B 2006, 73, 094434. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I. Theory of Helicoidal Structures in Antiferromagnets. I. Nonmetals. Sov. Phys. JETP 1964, 19, 960–971. [Google Scholar]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Kenzelmann, M.; Harris, A.B.; Jonas, S.; Broholm, C.; Schefer, J.; Kim, S.B.; Zhang, C.L.; Cheong, S.-W.; Vajk, O.P.; Lynn, J.W. Magnetic Inversion Symmetry Breaking and Ferroelectricity in TbMnO3. Phys. Rev. Lett. 2005, 95, 087206. [Google Scholar] [CrossRef] [PubMed]
- Kimura, T.; Ishihara, S.; Shintani, H.; Arima, T.; Takahashi, K.T.; Ishizaka, K.; Tokura, Y. Distorted perovskite with e1g configuration as a frustrated spin system. Phys. Rev. B 2003, 68, 060403(R). [Google Scholar] [CrossRef]
- Fukunaga, M.; Noda, Y. Classification and interpretation of the polarization of multiferroic RMn2O5. J. Phys. Soc. Jpn. 2010, 79, 054705. [Google Scholar] [CrossRef]
- Xiang, H.J.; Wei, S.H.; Whangbo, M.H.; Da Silva, J.L. Spin-Orbit Coupling and Ion Displacements in Multiferroic TbMnO3. Phys. Rev. Lett. 2008, 101, 037209. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Jang, H.M. Modulated spin structure responsible for the magnetic-field-induced polarization switching in multiferroic TbMn2O5. Phys. Rev. B 2005, 91, 014403. [Google Scholar] [CrossRef]
- Oh, Y.S.; Jeon, B.G.; Haam, S.Y.; Park, S.; Correa, V.F.; Lacerda, A.H.; Cheong, S.-W.; Jeon, G.S.; Kim, K.H. Strong magnetoelastic effect on the magnetoelectric phenomena of TbMn2O5. Phys. Rev. B 2011, 83, 060405(R). [Google Scholar] [CrossRef]
- Harikrishnan, S.; Rößler, S.; Kumar, C.N.; Bhat, H.L.; Rößler, U.K.; Wirth, S.; Steglich, F.; Elizabeth, S. Phase transitions and rare-earth magnetism in hexagonal and orthorhombic DyMnO3 single crystals. J. Phys. Condens. Matter 2009, 21, 096002. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, V.Y.; Mukhin, A.A.; Prokhorov, A.S.; Balbashov, A.M.; Iskhakova, L.D. Magnetic properties and phase transitions in hexagonal DyMnO3 single crystals. Phys. Solid State 2006, 48, 1726–1729. [Google Scholar] [CrossRef]
- Kimura, T.; Lawes, G.; Goto, T.; Tokura, Y.; Ramirez, A.P. Magnetoelectric phase diagrams of orthorhombic RMnO3 (R = Gd, Tb, and Dy). Phys. Rev. B 2005, 71, 224425. [Google Scholar] [CrossRef]
- Feyerherm, R.; Dudzik, E.; Aliouane, N.; Argyriou, D.N. Commensurate Dy magnetic ordering associated with incommensurate lattice distortion in multiferroic DyMnO3. Phys. Rev. B 2006, 73, 180401(R). [Google Scholar] [CrossRef]
- Nandi, S.; Kreyssig, A.; Yan, J.Q.; Vannette, M.D.; Lang, J.C.; Tan, L.; Kim, J.W.; Prozorov, R.; Lagrasso, T.A.; McQueeney, R.J.; et al. Magnetic structure of Dy3+ in hexagonal multiferroic DyMnO3. Phys. Rev. B 2008, 78, 075118. [Google Scholar] [CrossRef]
- Kimura, T.; Tokura, Y. Magnetoelectric phase control in a magnetic system showing cycloidal/conical spin order. J. Phys. Condens. Matter 2008, 20, 434204. [Google Scholar] [CrossRef]
- Wehrenfennig, C.; Meier, D.; Lottermoser, T.; Lonkai, T.; Hoffmann, J.U.; Aliouane, N.; Argyriou, D.N.; Fiebig, M. Incompatible magnetic order in multiferroic hexagonal DyMnO3. Phys. Rev. B 2010, 82, 100414 (R). [Google Scholar] [CrossRef]
- Pękała, M.; Wolff-Fabris, F.; Fagnard, J.F.; Vanderbemden, P.; Mucha, J.; Gospodinov, M.M.; Lovchinov, V.; Ausloos, M. Magnetic properties and anisotropy of orthorhombic DyMnO3 single crystal. J. Magn. Magn. Mater. 2013, 335, 46–52. [Google Scholar] [CrossRef]
- Sari, O.; Balli, M.; Trottet, G.; Bonhote, P.; Egolf, P.W.; Muller, C.; Heitzler, J.C.; Bour, S. Initial results of a test-bed magnetic refrigeration machine with practical running conditions. In Proceedings of the 3rd International Conference on Magnetic Refrigeration at Room Temperature, Des Moines, IA, USA, 2009; pp. 371–380.
- Lorenz, B.; Yen, F.; Gospodinov, M.M.; Chu, C.W. Field-induced phases in HoMnO3 at low temperatures. Phys. Rev. B 2005, 71, 014438. [Google Scholar] [CrossRef]
- Midya, A.; Mandal, P.; Das, S.; Banerjee, S.; Chandra, L.S.; Ganesan, V.; Barman, S.R. Magnetocaloric effect in HoMnO3 crystal. Appl. Phys. Lett. 2010, 96, 142514. [Google Scholar] [CrossRef]
- Munoz, A.; Alonso, J.A.; Martínez-Lope, M.J.; Casáis, M.T.; Martínez, J.L.; Fernandez-Diaz, M.T. Evolution of the magnetic structure of hexagonal HoMnO3 from neutron powder diffraction data. Chem. Mater. 2001, 13, 1497–1505. [Google Scholar] [CrossRef]
- Fiebig, M.; Lottermoser, T.; Pisarev, R.V. Spin-rotation phenomena and magnetic phase diagrams of hexagonal RMnO3. J. Appl. Phys. 2003, 93, 8194–8196. [Google Scholar] [CrossRef]
- Lonkai, T.; Hohlwein, D.; Ihringer, J.; Prandl, W. The magnetic structures of YMnO3-δ and HoMnO3. Appl. Phys. A Mater. Sci. Process 2002, 74, s843–s845. [Google Scholar] [CrossRef]
- Hur, N.; Jeong, I.K.; Hundley, M.F.; Kim, S.B.; Cheong, S.W. Giant magnetoelectric effect in multiferroic HoMnO3 with a high ferroelectric transition temperature. Phys. Rev. B 2009, 79, 134120. [Google Scholar] [CrossRef]
- De Lacheisserie, E.D.T. Magnétisme: Fondements; EDP Sciences: Les Ulis, France, 2000. [Google Scholar]
- Kim, J.W.; Nenkov, K.; Schultz, L.; Dörr, K. Magnetic properties of thick multiferroic hexagonal HoMnO3 films. J. Magn. Magn. Mater. 2009, 321, 1727–1730. [Google Scholar] [CrossRef]
- Wilkins, S.B.; Forrest, T.R.; Beale, T.A.W.; Bland, S.R.; Walker, H.C.; Mannix, D.; Yakhou, F.; Prabhakaran, D.; Boothroyd, A.T.; Hill, J.P.; et al. Nature of the Magnetic Order and Origin of Induced Ferroelectricity in TbMnO3. Phys. Rev. Lett. 2009, 103, 207602. [Google Scholar] [CrossRef] [PubMed]
- Kajimoto, R.; Yoshizawa, H.; Shintani, H.; Kimura, T.; Tokura, Y. Magnetic structure of TbMnO3 by neutron diffraction. Phys. Rev. B 2004, 70, 012401. [Google Scholar] [CrossRef]
- Salama, H.A.; Stewart, G.A. Exchange-induced Tm magnetism in multiferroic h-TmMnO3. J. Phys. Condens. Matter 2009, 21, 386001. [Google Scholar] [CrossRef] [PubMed]
- Yen, F.; Dela Cruz, C.; Lorenz, B.; Galstyan, E.; Sun, Y.Y.; Gospodinov, M.; Chu, C.W. Magnetic phase diagrams of multiferroic hexagonal RMnO3 (R = Er, Yb, Tm, and Ho). J. Mater. Res. 2007, 22, 2163–2173. [Google Scholar] [CrossRef]
- Fabreges, X.; Mirebeau, I.; Bonville, P.; Petit, S.; Lebras-Jasmin, G.; Forget, A.; André, G.; Pailhes, S. Magnetic order in YbMnO3 studied by neutron diffraction and Mössbauer spectroscopy. Phys. Rev. B 2008, 78, 214422. [Google Scholar] [CrossRef]
- Wagh, A.A.; Suresh, K.G.; Kumar, P.A.; Elizabeth, S. Low temperature giant magnetocaloric effect in multiferroic GdMnO3 single crystals. J. Phys. D 2015, 48, 135001. [Google Scholar] [CrossRef]
- Hemberger, J.; Lobina, S.; Von Nidda, H.A.K.; Tristan, N.; Ivanov, V.Y.; Mukhin, A.A.; Balbashov, A.M.; Loidl, A. Complex interplay of 3d and 4f magnetism in La1-xGdxMnO3. Phys. Rev. B 2004, 70, 024414. [Google Scholar] [CrossRef]
- Chandra, S.; Biswas, A.; Phan, M.H.; Srikanth, H. Impacts of nanostructuring and magnetic ordering of Nd3+ on themagnetic and magnetocaloric response in NdMnO3. J. Magn. Magn. Mater. 2015, 384, 138–143. [Google Scholar] [CrossRef]
- Da Silva, C.A.; Silva, R.S.; Plaza, E.J.R.; Moreno, N.O. Magnetic State and Magnetocaloric Effect of SmMnO3. J. Supercond. Nov. Magn. 2013, 26, 2497–2499. [Google Scholar] [CrossRef]
- Sagar, E.; Pavan Kumar, N.; Esakkimuthuraju, M.; Reddy, P.V. Magnetocaloric effect in multiferroic EuMnO3. Phys. Express 2015, 5, 3. [Google Scholar]
- Samanta, T.; Das, I.; Banerjee, S. Giant magnetocaloric effect in antiferromagnetic ErRu2Si2 compound. Appl. Phys. Lett. 2007, 91, 152506. [Google Scholar] [CrossRef]
- Midya, A.; Mandal, P.; Rubi, K.; Chen, R.; Wang, J.S.; Mahendiran, R.; Lorusso, G.; Evangelisti, M. Large adiabatic temperature and magnetic entropy changes in EuTiO3. Phy. Rev. B 2016, 93, 094422. [Google Scholar] [CrossRef]
- Mo, Z.J.; Hao, Z.H.; Shen, J.; Li, L.; Wu, J.F.; Hu, F.X.; Sun, J.R.; Shen, B.G. Observation of giant magnetocaloric effect in EuTi1-xCrxO3. J. Alloys Compd. 2015, 649, 674–678. [Google Scholar] [CrossRef]
- Von Ranke, P.J.; Alho, B.P.; Nóbrega, E.P.; De Sousa, V.S.R.; Alvarenga, T.S.T.; Carvalho, A.M.G.; De Oliveira, N.A. The influence of magnetic and electric coupling properties on the magnetocaloric effect in quantum paraelectric EuTiO3. J. Magn. Magn. Mater. 2012, 324, 1290–1295. [Google Scholar] [CrossRef]
- Ke, Y.J.; Zhang, X.Q.; Ma, Y.; Cheng, Z.H. Anisotropic magnetic entropy change in RFeO3 single crystals (R = Tb, Tm, or Y). Sci. Rep. 2016, 6, 19775. [Google Scholar] [CrossRef] [PubMed]
- Arrott, A.; Noakes, J.E. Approximate equation of state for nickel near its critical temperature. Phys. Rev. Lett. 1967, 19, 786. [Google Scholar] [CrossRef]
- Hu, W.J.; Du, J.; Li, B.; Zhang, Q.; Zhang, Z.D. Giant magnetocaloric effect in the Ising antiferromagnet DySb. Appl. Phys. Lett. 2008, 92, 192505. [Google Scholar] [CrossRef]
- Li, L.; Nishimura, K.; Hutchison, W.D.; Qian, Z.; Huo, D.; NamiKi, T. Giant reversible magnetocaloric effect in ErMn2Si2 compound with a second order magnetic phase transition. Appl. Phys. Lett. 2012, 100, 152403. [Google Scholar] [CrossRef]
- Balli, M.; Jandl, S.; Fournier, P.; Dimitrov, D.Z. On the conventional and rotating magnetocaloric effects in multiferroic TbMn2O5 single crystals. arXiv 2016. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).