Influence of Alkali Metal Substitution on the Phase Transition Behavior of CsGaQ2 (Q = S, Se)
Abstract
:1. Introduction
2. Results
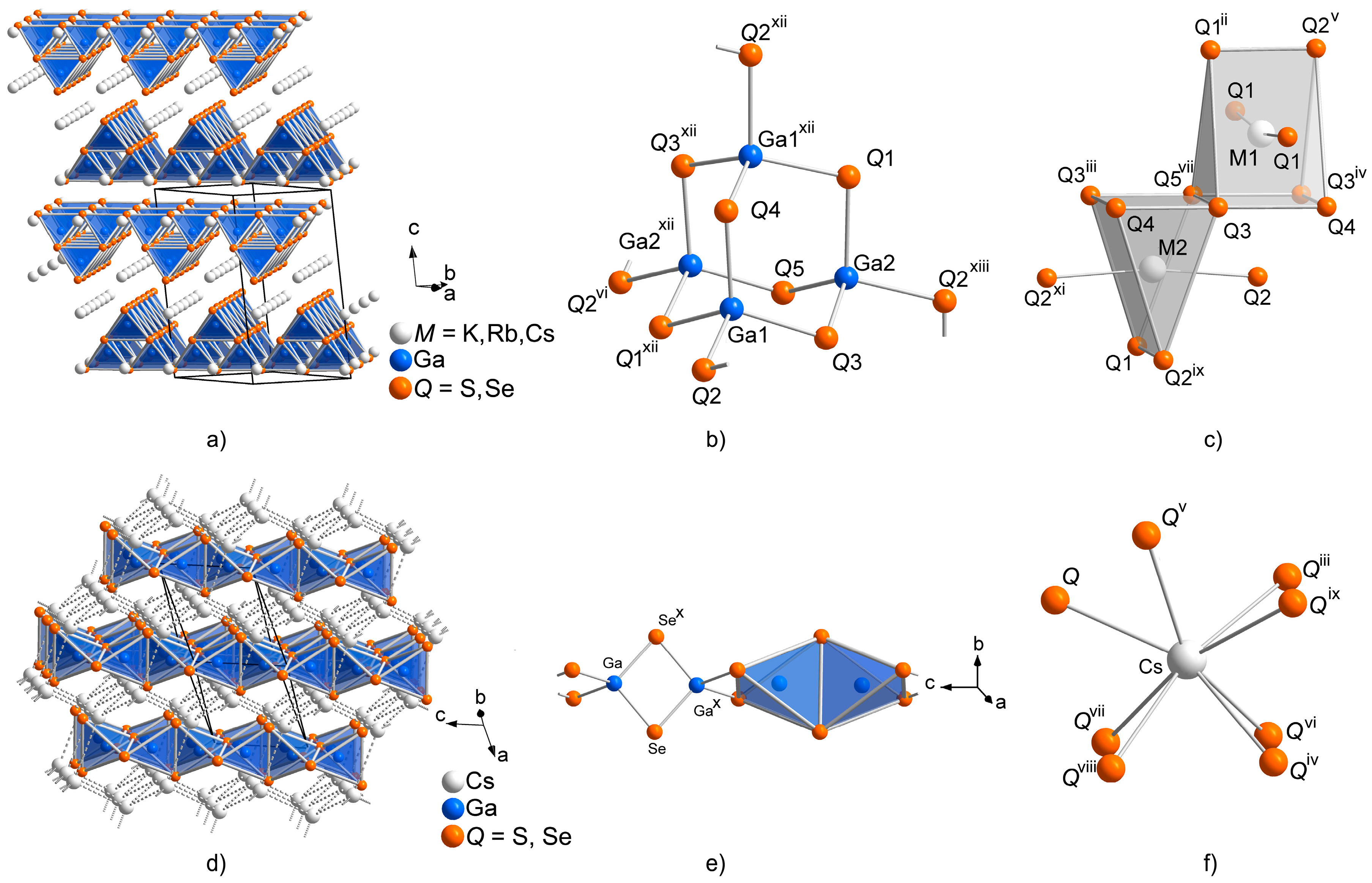
2.1. Crystal Structures of the CsGaQ2 Polymorphs
2.2. Formation of Solid Solutions Cs1−xMxGaQ2-mC64 (M = K, Rb; Q = S, Se; x = 0–1)
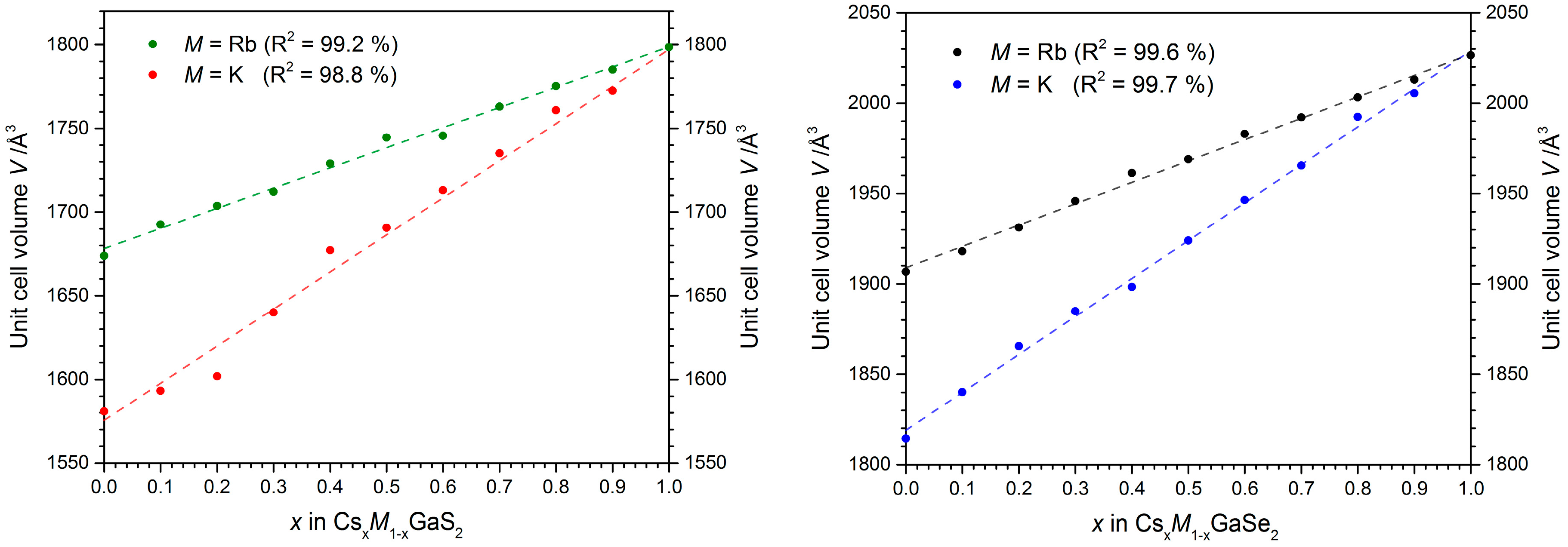
2.2.1. X-ray Diffraction Experiments
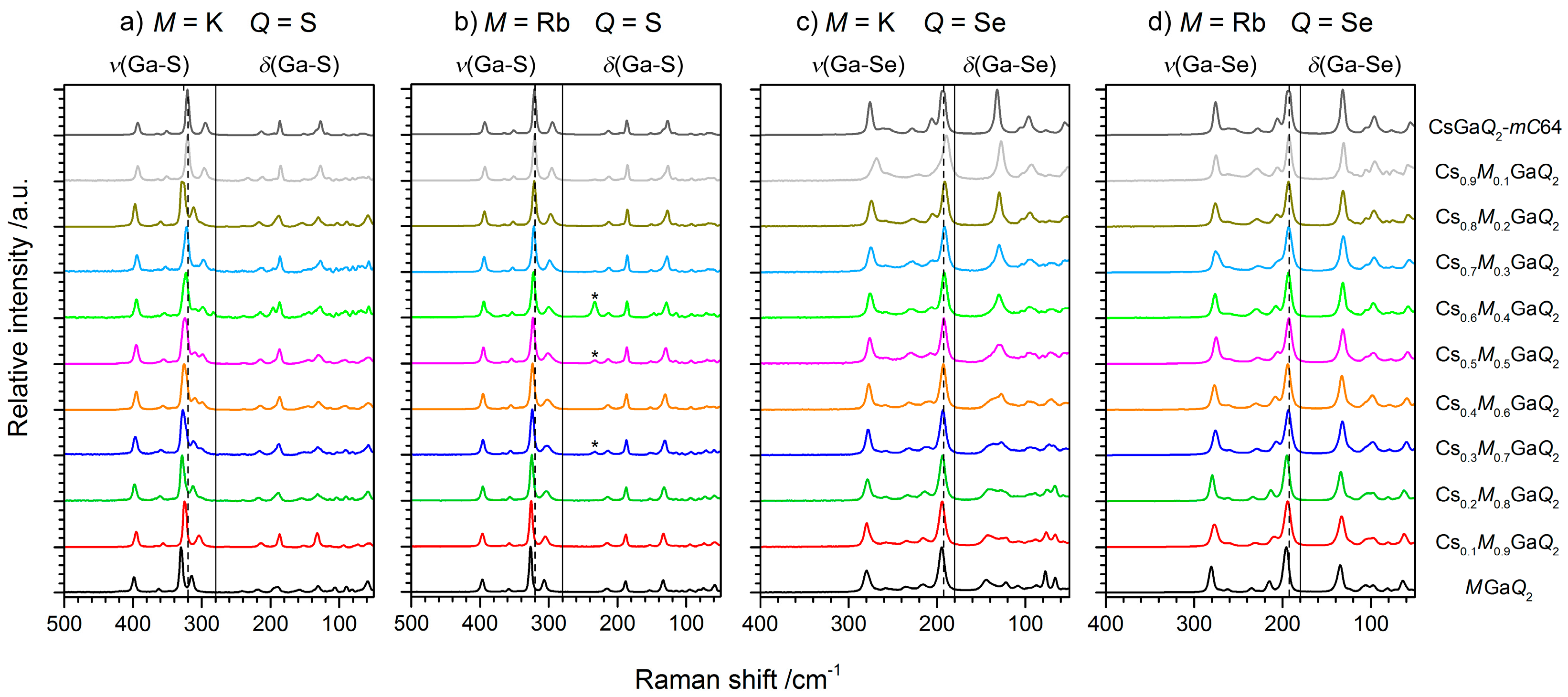
2.2.2. Raman Spectroscopy
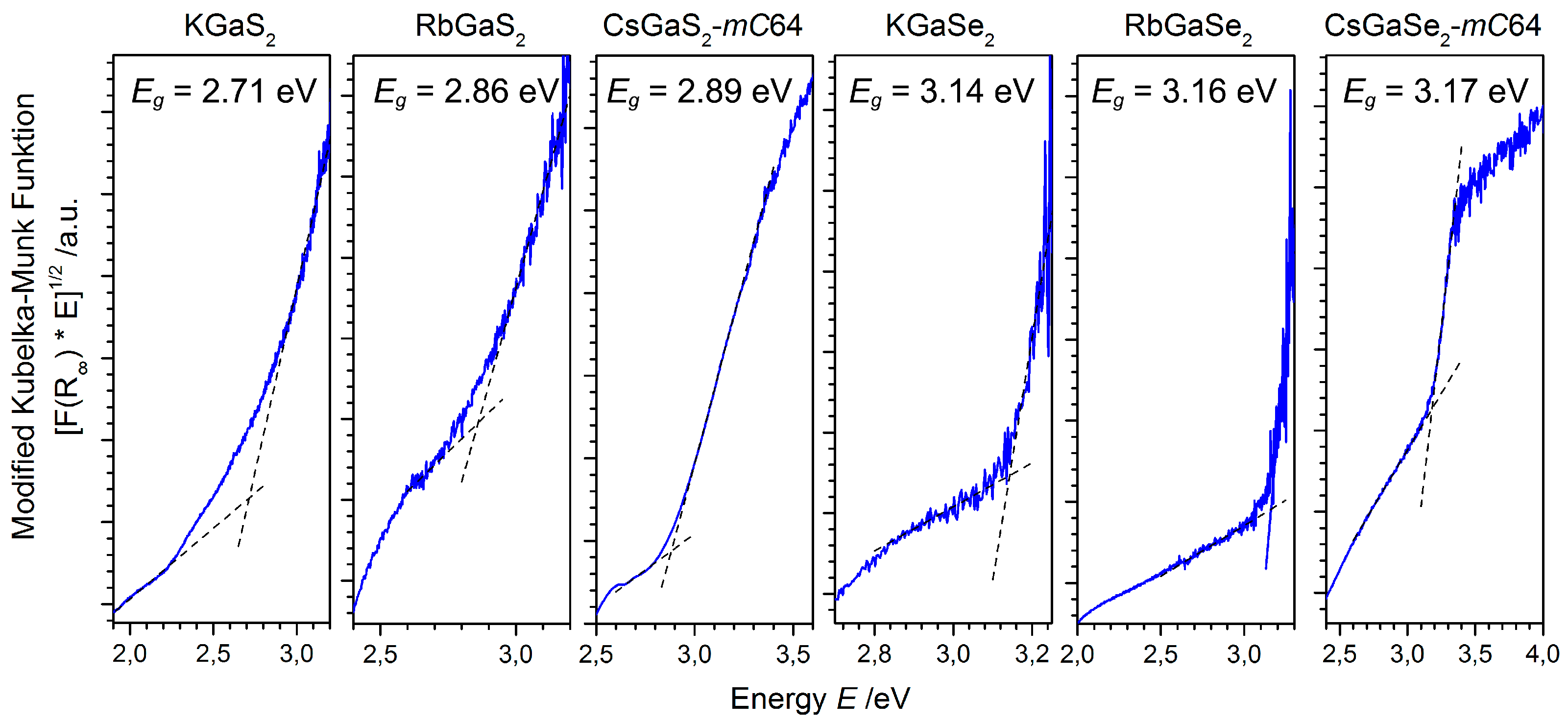
2.2.3. Optical Properties
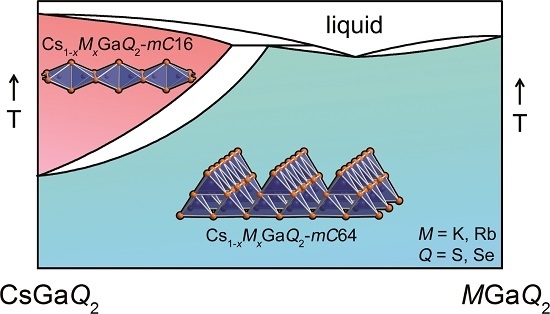
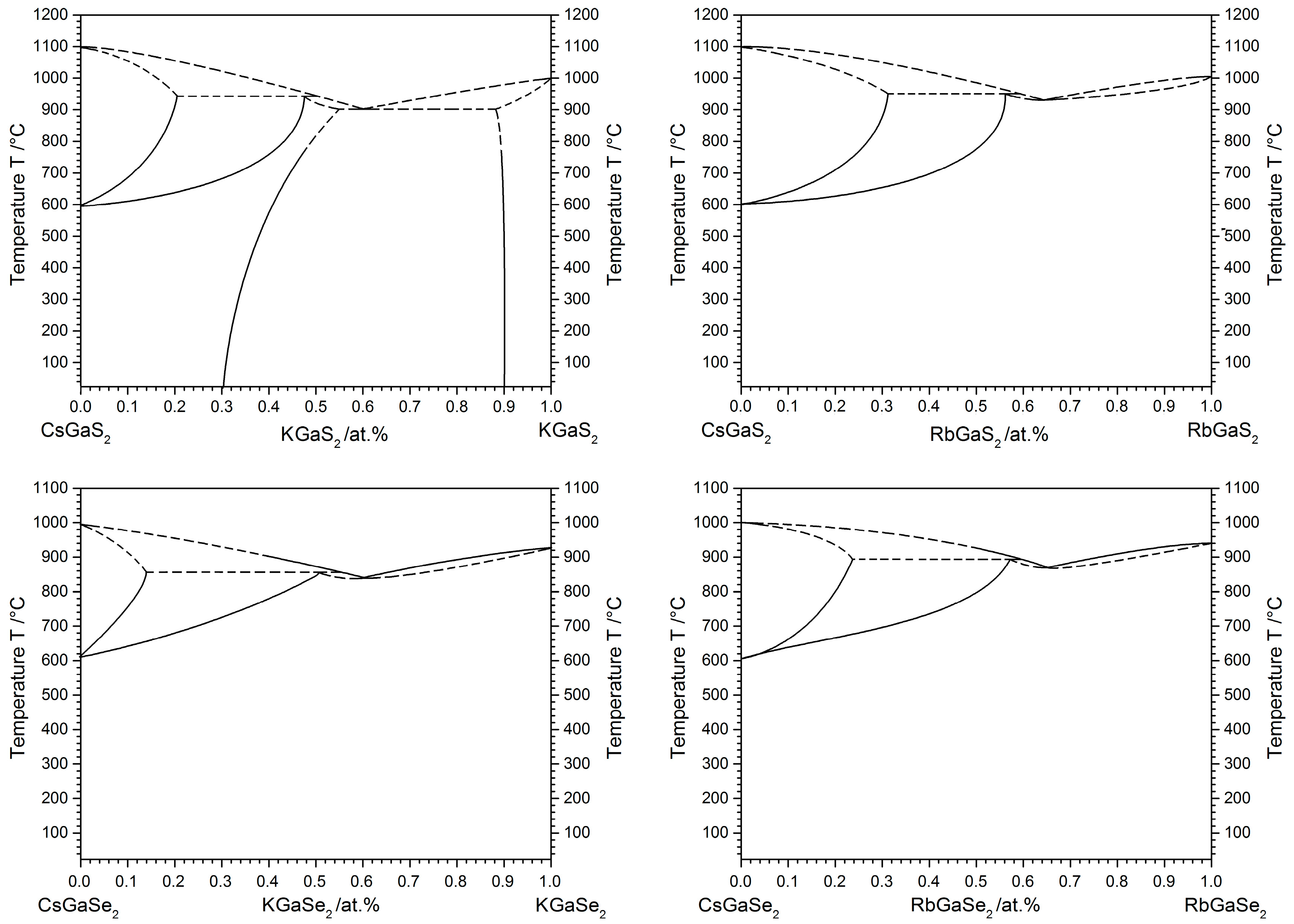
2.3. High-Temperature Phase Transition
2.3.1. Influence of the Alkali Metal Substitution on the Phase Transition Behavior
2.3.2. Structure Refinement of New Cs1-xMxGaQ2-mC16 (M = K, Rb; Q = S, Se) Phases
- (1)
- Using the least possible number of restrictions, we initially refined all atomic coordinates and displacement parameters independently with only the occupation factors of the alkali metals restrained to sum up to 1. While this procedure worked for all structures, reasonable refinements could only be obtained using isotropic displacement parameters. Furthermore, some refinements converged with unreasonably large or small displacement parameters of the minority alkali metal.
- (2)
- The best structural R values were obtained by separate refinement of the displacement parameters and atomic coordinates of two independent alkali metal positions. Due to the high cesium content in all solid solutions, only the Cs site could be refined with anisotropic displacement parameters, while isotropic displacement parameters were applied for Rb and K sites, respectively. Even though these refinements yielded the best values, the displacement parameters of the Rb and K sites, respectively, were unreasonably small (Uiso < 0.002 Å2).
- (3)
- As the anisotropic refinement using mixed Cs/M sites always yielded only slightly larger R values, but very reasonable displacement parameters, these results were chosen as the best refinements of these solid solutions.
3. Discussion and Summary
4. Materials and Methods
4.1. Synthesis of the Starting Materials
4.2. Synthesis of KGaQ2, RbGaQ2, and CsGaQ2-mC64 (Q = S, Se)
4.3. X-ray Powder Diffraction
4.4. Rietveld Refinement
4.5. Raman Spectroscopy
4.6. UV-VIS Diffuse Reflectance Spectroscopy
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Petrov, V.; Yelisseyev, A.; Isaenko, L.; Lobanov, S.; Titov, A.; Zondy, J.J. Second harmonic generation and optical parametric amplification in the mid-IR with orthorhombic biaxial crystals LiGaS2 and LiGaSe2. Appl. Phys. B Laser Opt. 2004, 78, 543–546. [Google Scholar] [CrossRef]
- Krebs, B. Thio- und Selenoverbindungen von Hauptgruppenelementen—Neue anorganische Oligomere und Polymere. Angew. Chem. 1983, 95, 113–134. [Google Scholar] [CrossRef]
- Müller, D.; Poltmann, F.E.; Hahn, H. Zur Struktur ternärer Chalkogenide des Thalliums mit Aluminium, Gallium und Indium, XXII. Zeitschrift für Naturforschung B 1974, 29B, 117–118. [Google Scholar]
- Ketelaar, J.A.A.; t’Hart, W.H.; Moerel, M.; Polder, D. The Crystal Structure of TlSe, Thallous Thallic or Thallosic Selenide. Zeitschrift für Kristallographie-Cryst. Mater. 1939, 101, 396–405. [Google Scholar] [CrossRef]
- Boon, J.W.; Mac Gillavry, C.H. The crystal structure of potassium thioferrite KFeS2 and sodium thiochromite NaCrS2. Recueil des Travaux Chimiques des Pays-Bas 1942, 61, 910–920. [Google Scholar] [CrossRef]
- Friedrich, D.; Schlosser, M.; Weihrich, R.; Pfitzner, A. Polymorphism of CsGaS2—Structural characterization of a new two-dimensional polymorph and study of the phase-transition kinetics. Inorg. Chem. Front. 2017, 4, 393–400. [Google Scholar] [CrossRef]
- Friedrich, D.; Schlosser, M.; Pfitzner, A. Synthesis, crystal structure, and physical properties of two polymorphs of CsGaSe2, and high-temperature X-ray diffraction study of the phase transition kinetics. Cryst. Growth. Des. 2016, 16, 3983–3992. [Google Scholar] [CrossRef]
- Feng, K.; Mei, D.; Bai, L.; Lin, Z.; Yao, J.; Wu, Y. Synthesis, structure, physical properties, and electronic structure of KGaSe2. Solid State Sci. 2012, 14, 1152–1156. [Google Scholar] [CrossRef]
- Lemoine, P.; Carre, D.; Guittard, M. Structure du sulfure de gallium et de potassium, KGaS2. Acta Cryst. C 1984, 40, 910–912. [Google Scholar] [CrossRef]
- Kumari, A.; Vidyasagar, K. Rubidium thiogallate. Acta Cryst. E 2005, 61, i193–i195. [Google Scholar] [CrossRef]
- Friedrich, D.; Schlosser, M.; Pfitzner, A. Synthesis and structural characterization of the layered selenogallate RbGaSe2. Zeitschrift für Anorganische und Allgemeine Chemie 2017, 643, 1589–1592. [Google Scholar] [CrossRef]
- Wu, E.J.; Pell, M.A.; Fuelberth, T.M.; Ibers, J.A. Crystal structure of cesium gallium ditelluride, CsGaTe2. Zeitschrift für Kristallographie-New Cryst. Struct. 1997, 212, 91. [Google Scholar]
- Friedrich, D.; Schlosser, M.; Pfitzner, A. Interconversion of one-dimensional thiogallates Cs2[Ga2(S2)2–xS2+x] (x = 0, 1, 2) by using high-temperature decomposition and polysulfide-flux reactions. Cryst. Growth Des. 2017, 17, 4887–4892. [Google Scholar] [CrossRef]
- Palatinus, L.; Chapuis, G. SUPERFLIP—A computer program for the solution of crystal structures by charge flipping in arbitrary dimensions. J. Appl. Cryst. 2007, 40, 786–790. [Google Scholar] [CrossRef]
- Petříček, V.; Dušek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Zeitschrift für Kristallographie-Cryst. Mater. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Tiwary, S.K.; Vasudevan, S. Regular versus alternating (FeS4)n chains: Magnetism in KFeS2 and CsFeS2. Phys. Rec. B 1997, 56, 7812–7814. [Google Scholar] [CrossRef]
- Guy, J.K.; Spann, R.E.; Martin, B.R. Solid state ion exchange chemistry of the solid solution KxRb1−xFeS2. Solid State Ionics 2008, 179, 409–414. [Google Scholar] [CrossRef]
- Stüble, P.; Röhr, C. Cs[FeSe2], Cs3[FeSe2]2, and Cs7[Fe4Se8]: Missing Links of Known Chalcogenido Ferrate Series. Zeitschrift für Anorganische und Allgemeine Chemie 2017, 643, 1462–1473. [Google Scholar]
- STOE WinXPOW, Version 3.10, STOE & Cie GmbH: Darmstadt, Germany, 2017.
- Hammersley, A.P.; Svensson, S.O.; Hanfland, M.; Fitch, A.N.; Hausermann, D. Two-dimensional detector software: From real detector to idealised image or two-theta scan. High Press. Res. 1996, 14, 235–248. [Google Scholar] [CrossRef]
- Kisch, H. Semiconductor photocatalysis—Mechanistic and synthetic aspects. Angew. Chem. Int. Ed. 2013, 52, 812–847. [Google Scholar] [CrossRef] [PubMed]
| KGaS2 | RbGaS2 | CsGaS2 | KGaSe2 | RbGaSe2 | CsGaSe2 | |||
|---|---|---|---|---|---|---|---|---|
| mC64 (LT) | mC16 (HT) | mC64 (LT) | mC16 (HT) | |||||
| Structure type | TlGaSe2 | TlGaSe2 | TlGaSe2 | KFeS2 | TlGaSe2 | TlGaSe2 | TlGaSe2 | KFeS2 |
| Space group | Monoclinic, C2/c (No. 15) | |||||||
| Z | 16 | 16 | 16 | 4 | 16 | 16 | 16 | 4 |
| a/Å | 10.421(2) | 10.495(3) | 10.622(2) | 7.432(1) | 10.909(2) | 10.974(3) | 11.046(1) | 7.659(2) |
| b/Å | 10.413(2) | 10.485(2) | 10.616(2) | 12.220(1) | 10.920(3) | 10.965(3) | 11.051(1) | 12.559(5) |
| c/Å | 14.799(3) | 15.432(5) | 16.170(2) | 5.911(1) | 15.470(4) | 16.084(4) | 16.827(1) | 6.177(1) |
| β/° | 100.13(2) | 99.71(2) | 99.46(2) | 113.10(1) | 100.12(2) | 99.87(3) | 99.40(1) | 113.66(2) |
| V/Å3 | 1580.9(6) | 1673.8(8) | 1798.5(6) | 493.8(1) | 1814.4(7) | 1906.7(9) | 2026.5(3) | 544.3(3) |
| Cs0.90K0.10GaS2 | Cs0.84Rb0.16GaS2 | Cs0.74Rb0.26GaS2 | Cs0.91Rb0.09GaSe2 | Cs0.79Rb0.21GaSe2 | |
|---|---|---|---|---|---|
| M/g·mol−1 | 257.38 | 259.17 | 254.43 | 356.28 | 350.59 |
| Space Group | monoclinic, C2/c (No. 15) | ||||
| a/Å | 7.431(2) | 7.426(1) | 7.427(1) | 7.653(1) | 7.655(1) |
| b/Å | 12.171(3) | 12.151(2) | 12.041(3) | 12.482(3) | 12.415(2) |
| c/Å | 5.906(1) | 5.907(1) | 5.908(1) | 6.166(1) | 6.161(1) |
| β/° | 113.15(2) | 113.11(1) | 113.24(1) | 113.75(2) | 113.88(1) |
| V/Å3 | 491.2(2) | 490.3(1) | 485.5(2) | 539.1(2) | 535.4(1) |
| Diffractometer | DESY P02.1 beamline; λ = 0.20717 Å; T = 20 °C | ||||
| 2θ range; increment | 0.7° < 2θ < 15°; Δθ = 0.004° | ||||
| Structure solution | Charge flipping, SUPERFLIP [14] | ||||
| Structure refinement | Full matrix against F2, Jana2006 [15] | ||||
| Background | Manual background combined with 8–10 Legendre polynomials | ||||
| Reflection profile | Pseudo-Voigt function; refined parameters GW, GU, LY | ||||
| No. of parameters | 39 | 38 | 39 | 37 | 39 |
| µ/mm−1 | 1.546 | 1.512 | 1.407 | 1.879 | 1.767 |
| GooF | 1.74 | 1.04 | 1.26 | 2.80 | 2.62 |
| Rp, wRp | 0.0069, 0.0097 | 0.0045, 0.0061 | 0.0060, 0.0075 | 0.0104, 0.0143 | 0.0093, 0.0131 |
| R1, wR2 (I > 3σ(I)) | 0.0173, 0.0244 | 0.0185, 0.0241 | 0.0197, 0.0256 | 0.0284, 0.0412 | 0.0114, 0.0158 |
| R1, wR2 (all data) | 0.0173, 0.0244 | 0.0185, 0.0241 | 0.0197, 0.0256 | 0.0284, 0.0412 | 0.0114, 0.0158 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friedrich, D.; Schlosser, M.; Etter, M.; Pfitzner, A. Influence of Alkali Metal Substitution on the Phase Transition Behavior of CsGaQ2 (Q = S, Se). Crystals 2017, 7, 379. https://doi.org/10.3390/cryst7120379
Friedrich D, Schlosser M, Etter M, Pfitzner A. Influence of Alkali Metal Substitution on the Phase Transition Behavior of CsGaQ2 (Q = S, Se). Crystals. 2017; 7(12):379. https://doi.org/10.3390/cryst7120379
Chicago/Turabian StyleFriedrich, Daniel, Marc Schlosser, Martin Etter, and Arno Pfitzner. 2017. "Influence of Alkali Metal Substitution on the Phase Transition Behavior of CsGaQ2 (Q = S, Se)" Crystals 7, no. 12: 379. https://doi.org/10.3390/cryst7120379
APA StyleFriedrich, D., Schlosser, M., Etter, M., & Pfitzner, A. (2017). Influence of Alkali Metal Substitution on the Phase Transition Behavior of CsGaQ2 (Q = S, Se). Crystals, 7(12), 379. https://doi.org/10.3390/cryst7120379