1. Introduction
Phononic crystals (PnC) comprise a periodic arrangement of acoustic scatterers in a one-, two-, or three-dimensional lattice. These scattering centers exhibit different acoustic properties, primarily density and speed of sound, than the surrounding matrix material. The characteristic feature of this regular arrangement is the formation of phononic band gaps, frequency ranges that prohibit the transmission of acoustic or elastic waves through the structure—see, e.g., [
1,
2] and references therein. In the past two decades, this field of research has grown considerably, with a focus on theoretical modeling and prediction, as well as experimental demonstration of 1D, 2D and simple 3D devices.
From early phononic crystal research onwards, several groups utilized clever assembly methods to build simple three-dimensional arrangements, typically consisting of solid spheres embedded in a soft or liquid matrix [
3,
4,
5,
6,
7,
8,
9]. While three-dimensional (3D) phononic structures of various complexity have also been investigated by a number of theoretical works using a variety of numerical methods (see, e.g., [
10,
11,
12,
13]), experimental fabrication and characterization of complex 3D elements are only now being reported due to rapid advances in additive manufacturing. As one of the first, we previously utilized 3D printing technology to fabricate cubic phononic crystals [
14] and demonstrate phononic behavior not attainable by corresponding 2D designs [
15]. The additional degree of freedom introduces considerable challenges for design, fabrication, and characterization. In particular, various limitations of additive manufacturing technologies must be taken into account when creating complex unit cell designs. These limitations include, but are not limited to, the choice of materials especially when considering multi-material structures, the minimum attainable feature size, reproducibility, surface roughness, feasible aspect ratios, and support requirements for overhanging or free-standing structures.
Furthermore, for practical applications, a finite crystal lattice and an acoustic wave of one polarization and propagation direction is typically employed. Numerical analysis usually focuses on the formation of a complete band gap between all types of propagation modes in an infinite lattice, or on a specific type of wave propagation through a semi-infinite lattice. Experimental acoustic transmission analysis is then often limited to only one primary propagation direction [
16,
17,
18,
19]. As early phononic crystal research has already shown, the band structure and transmission behavior will yield drastically different results for the complete, omnidirectional band gap and more application oriented directional band gaps for specific acoustic modes. As a primary application, we work on the development of phononic-fluidic sensor systems [
20]. To optimize the phononic building blocks, we require a comprehensive characterization of their transmission behavior to choose the most suitable designs.
In the following, we will first outline different additive technologies, practical fabrication challenges, and resulting design limitations derived from our recent research on complex, cubic phononic crystals. We will then demonstrate the differences between propagation directions as well as between longitudinal and shear waves, postulating a necessity for comprehensive experimental analysis, especially for a finite, three-dimensional lattice of complex unit cell geometries.
2. Choice of Fabrication Technology
The advent of additive manufacturing has made the realization of complex 3D unit cell designs feasible on smaller scales. Nowadays, a number of additive technologies are available, differing in the choice of materials, lateral and vertical resolution, processing complexity, and costs. Here, we will look at advantages and disadvantages of photopolymerization, powder bed fusion, material jetting, and filament extrusion. An overview of different additive microfabrication techniques can be found in [
21,
22]. Our own research focus is placed on the realization of millimeter and sub-millimeter devices for operation in the hundred kHz and MHz frequency range. Therefore, we specifically utilize the microstereolithography photopolymerization process [
23] for the fabrication of our 3D phononic crystal designs [
14].
All 3D technologies typically build a complex structure in a layer-by-layer process. The resulting minimum reproducible feature size is the primary factor limiting smaller lattice constants and thus higher operating frequencies of phononic devices. Short-range and long-range accuracy of the printing process are dominated by surface roughness and periodic positioning accuracy, respectively. The former is mainly influenced by the layer height (slicing thickness) and post-processing steps. In both cases, geometry deviations must be well below the acoustic wavelength in order to not negatively affect phononic behavior, e.g., formation of band gaps. The other important characteristic of the fabrication process is the choice of materials and the resulting elastic and acoustic properties such as density, speed of sound, and material losses. In
Table 1, we compare the four different technologies in terms of materials, option of printing different materials together, typical minimum feature sizes and slicing, as well as typical range of the characteristic acoustic impedance as a measure of material properties defining the phononic behavior.
In most processes, printing a stable layer requires contact with a previously printed layer. Overhanging and free-standing structures require connections to so-called support elements. These supports are typically a scaffold or pillar structure with minimal contact area to connect the build platform or lower solid layers to the supported geometry. Depending on technology, supports have to be mechanically removed or chemically dissolved during post-processing.
At the entry level, fused filament fabrication (FFF) is a low-cost and low-complexity printing method requiring supports. It allows processing of a wide range of thermoplastic and rubbery filaments, with the additional option of a considerable percentage of filler components such as metal powders, wood, or carbon particles. Therefore, it covers a wider range of elastic and acoustic material properties than other plastic printing techniques. Advanced equipment is also capable of multi-material extrusion, giving the option to build, e.g., phononic structures comprising stiff mass and elastic spring elements. However, the feature size is limited by the width of the nozzle through which the filament is extruded. This results in a typical line width of around half a millimeter. Positioning reproducibility and surface roughness on a similar scale lead to smallest reproducible geometry features around one millimeter to achieve structural stability and cohesion. With dual extrusion, supports can be made from an easily soluble material yielding less surface defects. Advanced techniques combine extrusion of special, filled filaments with sintering to fabricate ceramic prints [
24], which have been used to realize photonic crystals [
25] and recently also low frequency phononic crystals [
18].
Material jetting operates in a similar fashion to inkjet printers, with a more limited choice of materials, but higher resolution down to feature sizes of a few hundred micrometer. It is also capable of multi-material printing, with typically one material acting as soluble support for the primary object. However, a necessary washing cycle can severely degrade the surface quality, yielding a higher surface roughness than photopolymerization techniques. Utilizing different fillers and post-processing, ceramic and metal materials can also become feasible for jetting [
26,
27].
Powder bed processes such as selective laser sintering and especially laser melting (SLS, SLM) require a considerably larger investment. In return, metals, ceramics, and alloys can also be processed in addition to a range of plastic powders. This results in the widest range of possible material properties, from synthetic polymers such as nylon, over various ceramics and alloys, to steel and titanium. The powder bed allows a self-supporting printing process, the best choice for overhanging and free-standing structural elements. Feature sizes above a hundred micron can be reproduced. Further developments include substantial material research to optimize different metallic powders and minimize the grain size to improve resolution and surface roughness [
28]. SLS and SLM have recently been successfully employed to build 3D phononic crystals for lower frequency operation [
16,
19].
The smallest feature size and lowest surface roughness is offered by the stereolithography process, especially microstereolithography with UV-light exposure via laser scanning or a micromirror array (digital light processing, DLP). Similar to standard thin film lithography used in microfabrication, a liquid resin is locally polymerized by exposure to light. This limits the choice of materials to photopolymer resins, which can, however, contain various filler materials influencing, e.g., density, elasticity, and hardness. With commercially available microstereolithography machines, reproducible feature sizes as low as 50 micron are feasible, with a typical surface roughness below a few microns. The long-range and short-range accuracy is therefore well below the acoustic wavelength for frequencies up to a few MHz. Usually, only one resin material can be printed at a time, and free-hanging structures need supports. A special form of stereolithography using two-photon-polymerization can also yield sub-micron features, which has already been employed to build 3D photonic crystals and elastic metamaterials [
29,
30].
In our research, all phononic crystal samples have been additively manufactured with microstereolithography printing (
Perfactory Micro HiRes, EnvisionTEC Inc., Dearborn, MI, USA), using a batch of high-temperature resistant acrylic polymer resin (
HTM140 M, EnvisionTEC Inc.), as described previously [
14]. With this equipment, we can reliably realize the small feature sizes and low surface roughness necessary for lattice constants
a down to 1 mm. While limited to plastic resin materials, the acoustic contrast is high enough for air-filled phononic crystals. For larger test samples, we also use commercially available FFF and SLM printers, where reproducibility and surface roughness are still open challenges for reliably fabricating sub-millimeter feature sizes.
3. Design Considerations
For this discussion, we look at the following cubic unit cells. Our original 3D design was developed as an extension of the well established 2D design of circular (air) holes in a quadratic (solid) matrix. This 2D design can be extended to 3D by three circular cylindrical holes along the three Cartesian axes [
15]. For this work, the size of the hole (
) was maximized in regards to band gap width for a 1 mm unit cell taking fabrication accuracy and mechanical stability into account (giving 100 micron minimum feature size). The second design is a variation of the original with a different shape—in this case, a quadratic hole parallel to the sides of the cubic unit cell. Our third design was thought of as a representation of a simple cubic Bravais lattice, with solid spheres sitting in each corner of the cube connected by thin circular cylindrical beams along the sides. The diameter of the connecting beams (
) was again chosen to be minimal in regards to fabrication and stability for a 1 mm unit cell, while the size of the spheres (
) was optimized for maximum band gap width. To demonstrate certain fabrication challenges, we also look at a face centered cubic unit cell as introduced by D’Alessandro et al. [
16].
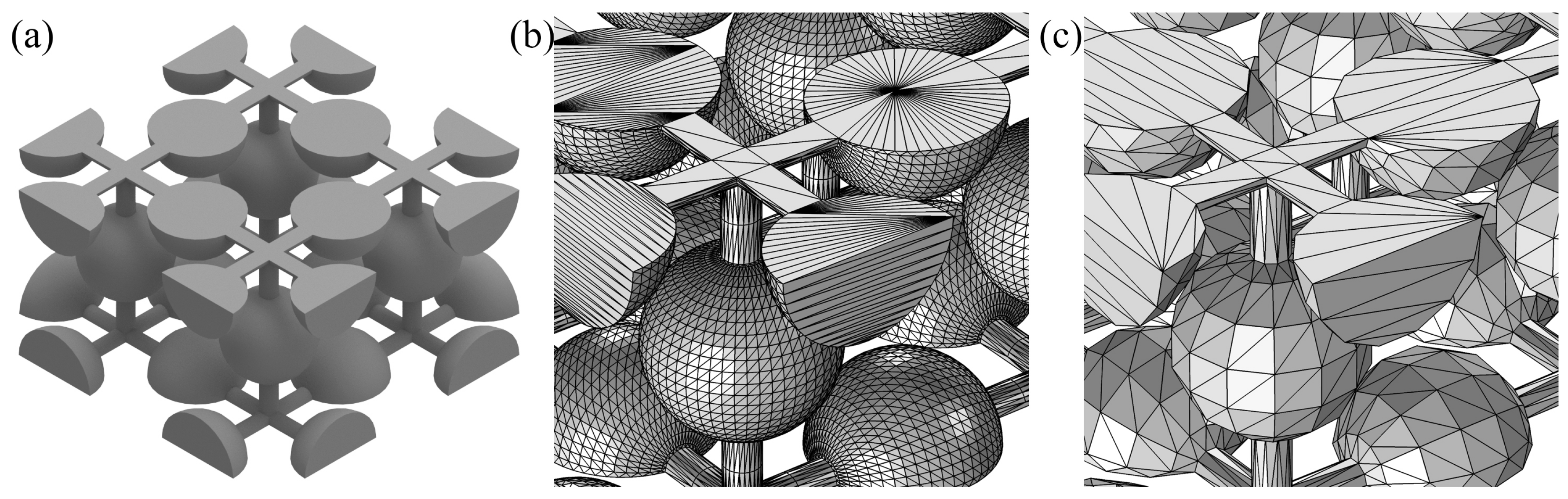
Figure 1 shows the unit cells of these four exemplary designs.
The minimum reproducible feature size of the selected fabrication technology effectively determines the lattice constant of a phononic unit cell, by limiting the minimum structural width of, e.g., a strut, beam, or contact point. Additionally, the mechanical stability of the resulting structure must be taken into account—for example, the length of thin beams connecting multiple larger masses. Any deformation of the beams due to gravity or intrinsic stress will invalidate any theoretical results for straight beams. When considering curved design elements, the varying surface deviation from the ideal shape due to slicing and lateral resolution requires larger geometrical limits than rectangular structures, but they are usually self-supporting as long as the lowest point is connected. On the other hand, rectangular elements inevitably lead to overhanging material within one slice as in
Figure 1b.
Constructing a phononic crystal out of such 3D unit cells requires spatial repetition into a lattice. After finalizing the model, the design is exported, typically using the STL (
Standard Tessellation Language, also
STereoLithography) file format. This format describes the surface of the 3D structure with triangles, and the surface normals of these triangles define the inner and outer part of a solid. Handling very large lattices is computationally challenging. In commercially available 3D CAD programs such as
Autocad, Inventor or Solidworks, the modeling of, e.g., a
lattice can already take several minutes up to an hour or more depending on complexity of the unit cell. Additionally, the STL export is also a critical step, as the triangle mesh must be fine enough to resolve complex, especially curved surfaces, but both too fine and too rough meshes may introduce unnecessary errors (
Figure 2). Errors in the STL may lead to faulty slicing data for printing. Therefore, a repair of the exported STL may be necessary to account for, e.g., noise shells, holes on the solid, overlapping or intersecting triangles.
As mentioned in the introduction, comprehensive experimental characterization of different acoustic wave modes and propagation directions is necessary for 3D phononic crystals to choose the most suitable configuration for a specific application. For transduction in water or other liquids, the geometric arrangement of acoustic transducers can be rotated accordingly; however, for measurements in air using contact transducers, the crystal lattice must be rotated in respect to the transducer arrangement instead. This requirement introduces additional design challenges. For the example of a cubic lattice, three main characteristic orientations are the body center normal propagation direction (ΓX), the center face diagonal (ΓM), and the body diagonal (ΓR)—see
Figure 3. To realize propagation in the diagonal directions, the lattice can be amended with diagonally oriented solid transducer contact faces or the lattice itself is rotated from the contact face normal. We found the latter solution to yield the best experimental results. When rotating a lattice that is self-supporting in ΓX, parts of it may become unsupported especially in ΓR. Cutting only the contact faces according to the propagation direction may also leave a face itself or elements of it unsupported. Successfully rotated and fabricated samples are shown in the following section.
4. Fabrication Results
Highly reproducible fabrication samples with sub-millimeter feature sizes and lattice constants down to one millimeter have been realized for all our simple cubic unit cell designs. In
Figure 4, we show samples of designs
Figure 1a–c with 3 mm lattice constant. Microscopic surface inspections using 3D laser profilometry indicate an average surface roughness with
values around 0.35 µm, well below the acoustic wavelength. All geometric design features, especially curved surfaces, are well reproduced. The chosen resin material exhibits negligible shrinking.
The rectangular scaffold example proves that lateral overhangs are still possible with stereolithography up to a certain distance, typically a few millimeters, without any support. Transducers are generally clamped to two opposite sides of the sample, with, or, as in these cases, without a solid wall boundary. We usually fabricate samples with supports connecting only the build platform and the bottom layer, for easier removal from the printer. However, as described in
Section 2, stereolithography requires support structures for larger overhanging or freestanding elements as the horizontally connected balls in design
Figure 1d. The results of omitting sufficient supports are demonstrated in
Figure 5. Vertically connected balls are properly supported and printed. The close-up photographs show that freestanding or insufficiently supported geometries are incompletely printed or not realized at all.
Fabrication samples oriented in ΓM and ΓR direction are shown in
Figure 6. By rotating and adjusting the crystal lattice, the transducer contact faces can be kept within a similar distance. This greatly helps for comparing different propagation directions as it reduces the influence of material losses over distance and features similar standing waves for transmission bands. However, depending on unit cell geometry, these rotations may lead to overhanging and freestanding structures, and, therefore, support issues.
5. Measurements and Discussion
In this final section, we present results for different propagation directions as well as acoustic wave modes to build a comprehensive picture of 3D phononic crystal behavior. An extensive discussion of the numerical methods used to calculate complete wave dispersion diagrams and semi-infinite transmission analysis through different crystal orientations, as well as our experimental parameter studies regarding geometric variations of unit cell elements, number of elements in propagation direction, or filling factor of scattering volume (amount of air to solid) are beyond the scope of this fabrication oriented paper—for more details, see, e.g., [
17,
31].
Measurement results presented here focus on designs
Figure 1a–c with 3 mm lattice constant. Transmission through the different samples is measured with a high-precision lock-in amplifier (
HF2LI, Zurich Instruments AG, Zurich, Switzerland) between two ultrasonic contact transducers. We employ two different sets of transducers, for longitudinal wave (
V103-RM, Olympus, Hamburg, Germany) and shear wave propagation (
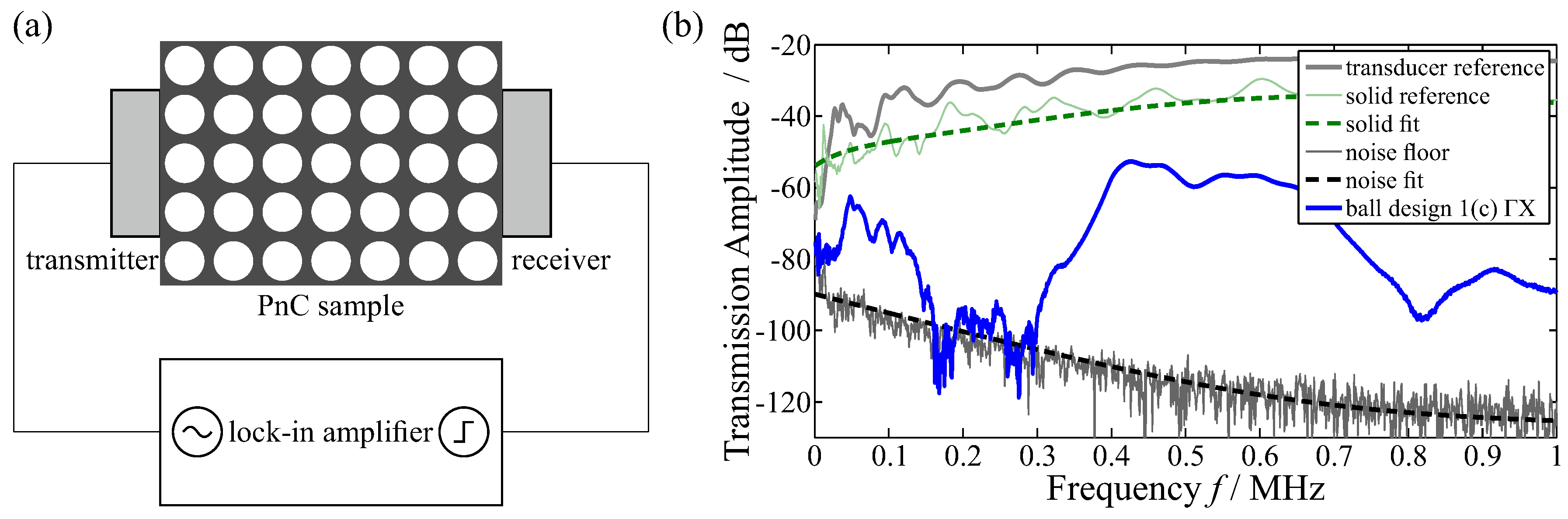
V153-RM, Olympus, Hamburg, Germany), using a suitable ultrasonic coupling gel. Maximum frequency range is 10 kHz to 2 MHz. The measurement setup is illustrated in
Figure 7a. Transducers, sample material, and experimental setup also exhibit a characteristic frequency dependence. In
Figure 7b, we plot the measured transmission spectra of longitudinal transducers in direct contact (solid gray), upper reference of longitudinal transmission through a solid sample of the same material and similar length and a corresponding fit (dashed green), lower reference of noise floor and fit (dashed black), and exemplary measurement curve of ball design
Figure 1c in direction ΓX. For direct transducer contact, the transmitted wave is around 30 dB lower than the incident wave, while material damping through the solid reference amounts to roughly 10 dB losses. Compared to the solid reference, longitudinal transmission in the band gap is suppressed down to the noise floor of our experimental setup by up to 50 dB and more depending on frequency, while transmission outside the band gap is typically around 10 dB lower than through the solid.
In the following, we plot transmission results normalized by their peak values over a non-dimensional frequency /c for optimal comparison independent of geometrical size (lattice constant a) and material property (longitudinal or shear mode speed of sound ). Regions of transmission minima correspond to phononic band gaps, characterized by the relative bandwidth as bandwidth divided by gap center frequency /. Measurement results (solid) lines are scaled and compared to simulation results (dashed lines). The latter are derived from the transmission analysis of an elastic wave through a semi-infinite PnC arrangement using the finite element method (COMSOL Multiphysics 5.3, COMSOL AB, Stockholm, Sweden). Here, the cubic unit cell is extended into the direction of wave propagation to a similar length as the fabrication samples, with periodic boundary conditions in the two perpendicular directions, a prescribed displacement in longitudinal or shear direction on the incident face, and a low-reflecting boundary condition given by the acoustic impedance of the transducers used in this work at the receiver face. Differences between measurements and simulation are primarily due to the finite nature of the fabrication samples compared to the semi-infinite model, the approximation of different frequency dependencies and material losses in a frequency dependent damping factor, and only approximate knowledge of the exact density and speed of sound through the 3D-printed material. In general, the most interesting features of band gaps and transmission bands are evident in both measurement and simulation and fit reasonably well.
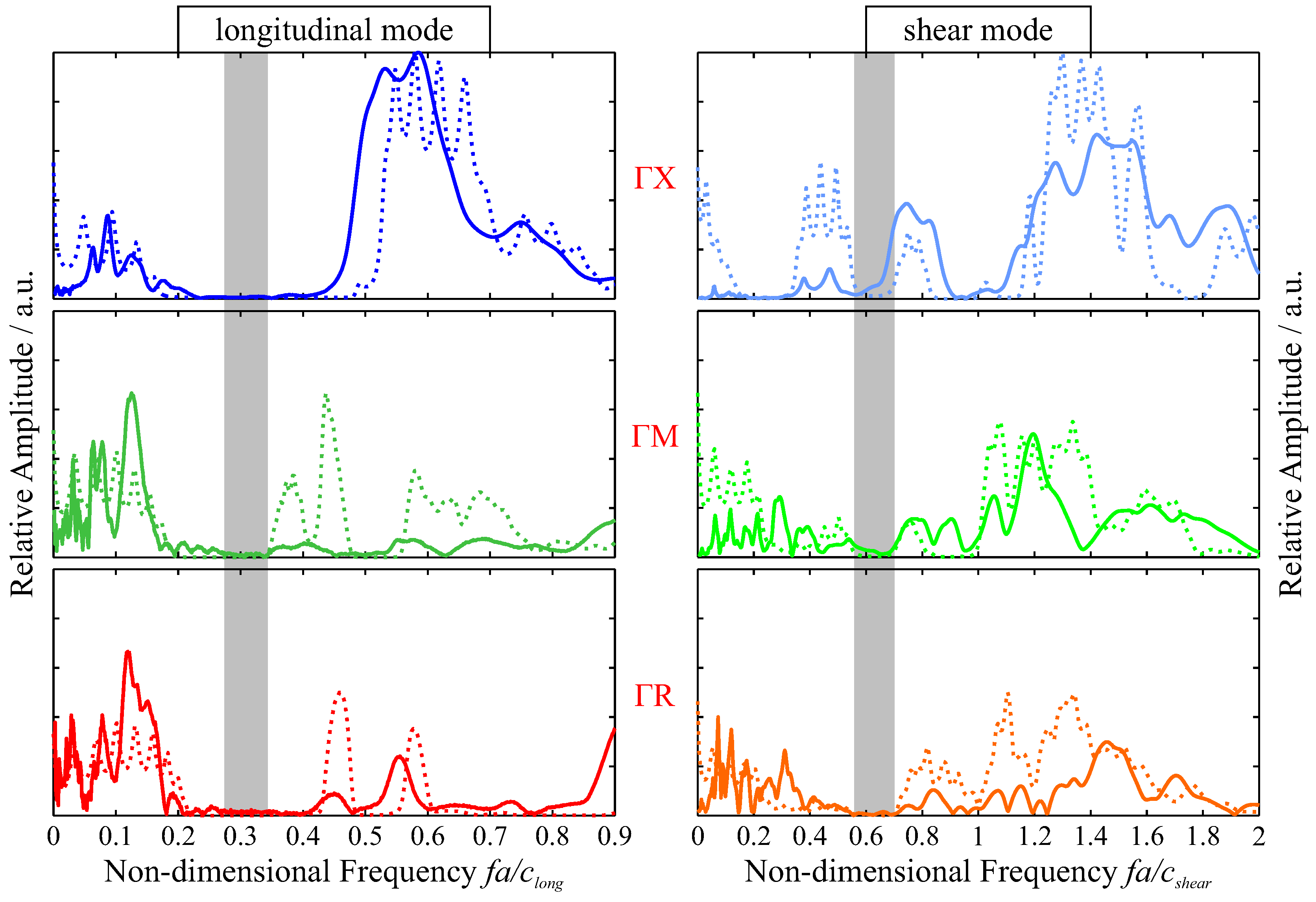
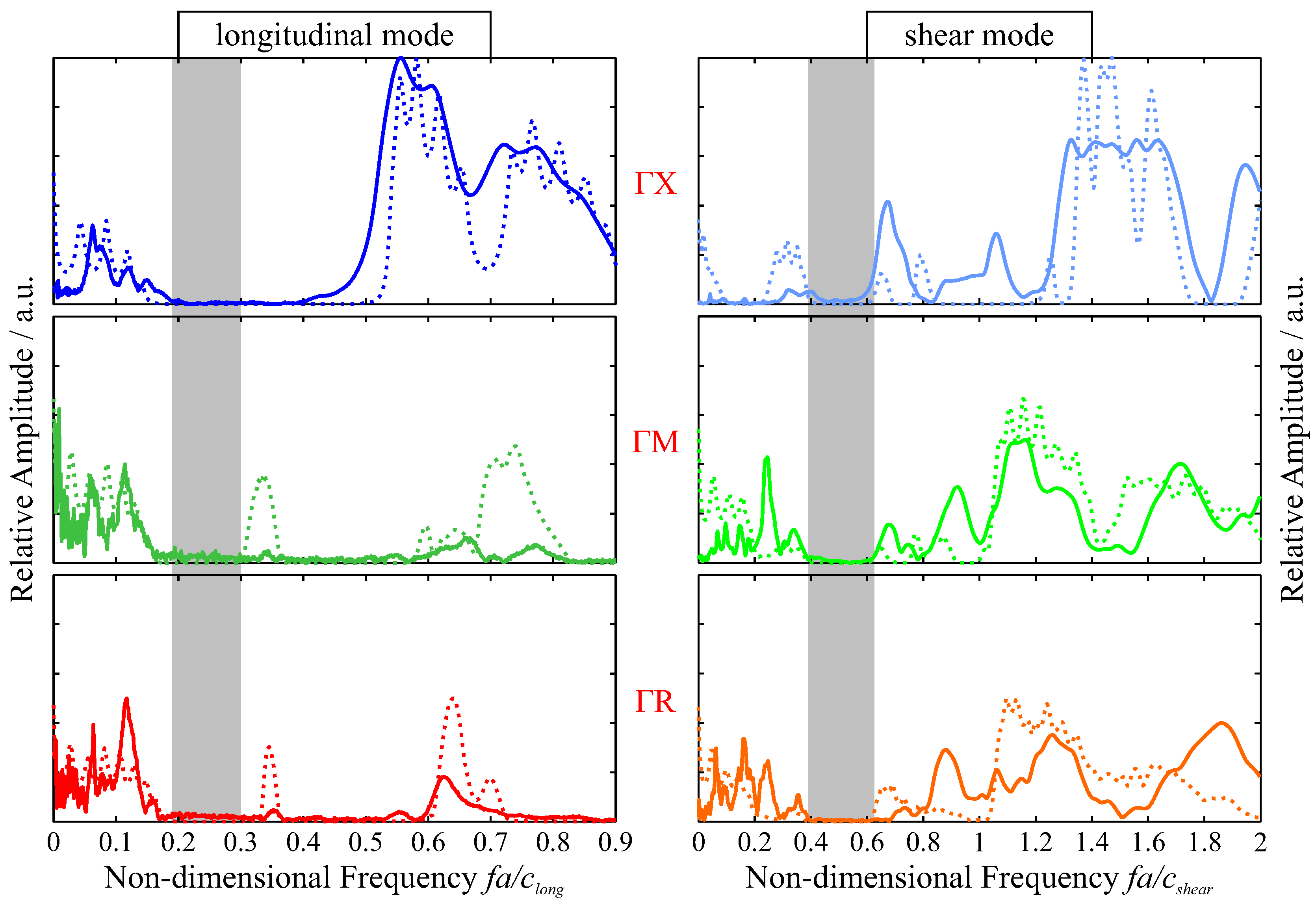
For our original design of cylindrical holes along the Cartesian axes through a cubic solid, the calculated dispersion diagram of an infinite lattice with
hole diameter features an omnidirectional, complete band gap with a relative width of 24.2%. In
Figure 8, we compare longitudinal and shear mode transmission in three characteristic directions ΓX, ΓM, and ΓR. These graphs show that, while the complete band gap is bound on the upper end by a longitudinal transmission band in ΓM direction, both primary bounds are only found for shear mode transmission. Corresponding to established phononic crystal theory, the directional band gaps for, e.g., longitudinal transmission in ΓX and ΓR far exceed the complete gap with measured relative widths up to 90% and strong band gap suppression more than 50 dB below transmission through a solid reference.
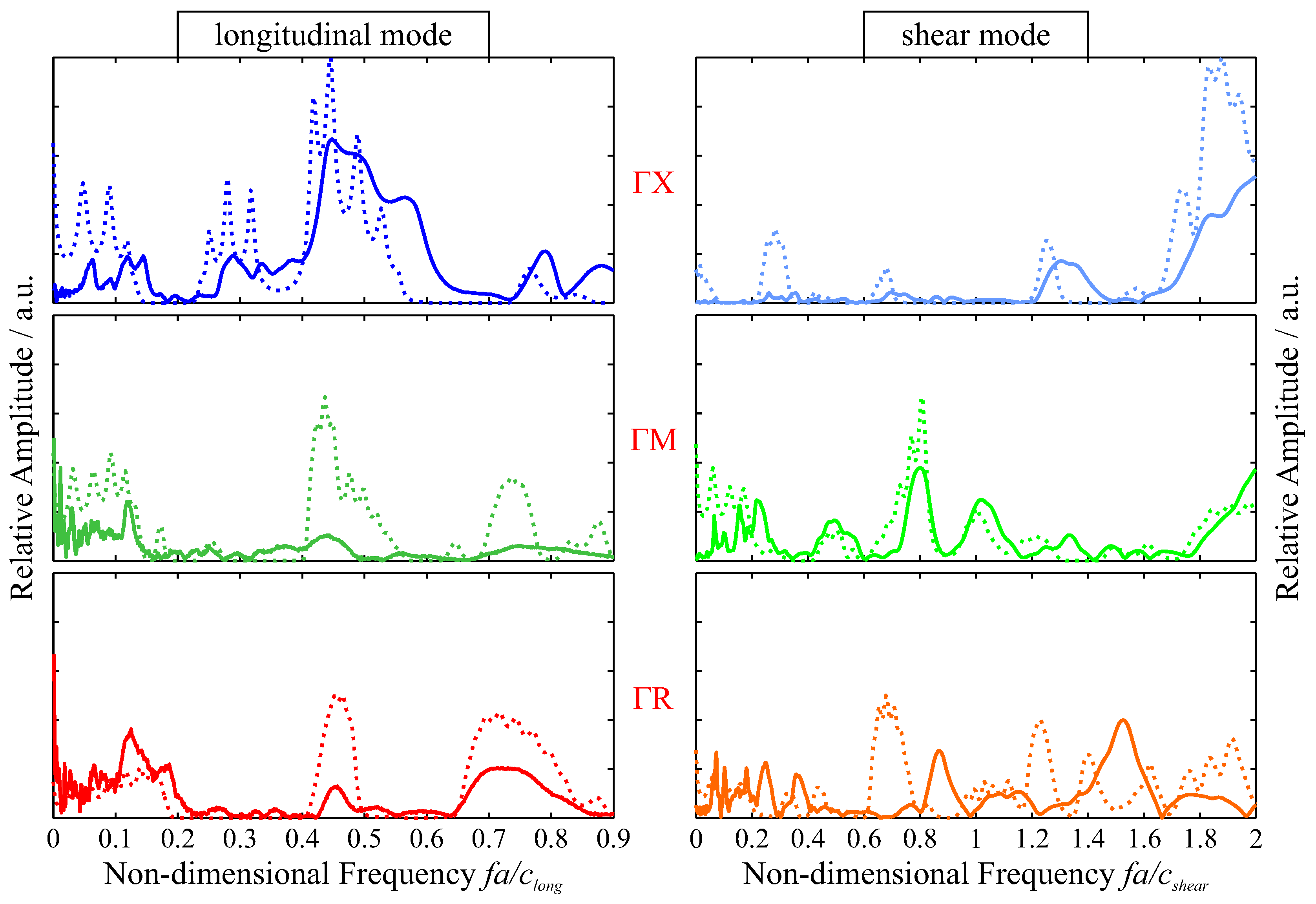
In contrast, the dispersion relation for the rectangular scaffold design
Figure 1b predicts no complete, omnidirectional band gap formation at all for quadratic holes of
side length. Experimental results shown in
Figure 9 validate that this design features strong directional band gaps with relative widths up to 75%, which, however, do not all overlap. Examples are gaps for longitudinal waves from reduced frequency 0.15 to 0.25 in ΓX or for shear waves from 0.4 to 0.8 in the ΓR direction.
This directionality can also be validated with the numerical transmission simulation of a semi-infinite lattice arrangement. For a longitudinal wave,
Figure 10 shows the wave deformation in the normal and rotated rectangular scaffolds at a single frequency. Here, wave transmission is suppressed in the ΓX direction, nearly unperturbed in ΓM, and only slightly damped in ΓR. For practical applications, the directional band gap, here in ΓX, can be completely sufficient.
Finally, for the corner ball design
Figure 1c with
ball diameter and
wide connecting beams, the dispersion relation gives a complete relative bandwidth of 46.2%. The measured directional bandwidths reach values up to 96% for longitudinal mode transmission in ΓX (
Figure 11). Shear mode transmission also exhibits band gaps above 60% width.
These examples demonstrate the often large differences between the complete, omnidirectional band gap for an infinite phononic crystal lattice and the directional band gaps for real, finite fabrication samples. Besides the gap bandwidth, the wave suppression efficiency inside the band gap and the overall transmission loss is also strongly dependent on propagation mode and direction. For the samples shown here, overall transmission loss compared to a solid reference is as low as 10 dB in ΓX but up to 50 dB in ΓM and ΓR. Band gap suppression typically reaches the noise floor of our experimental setup. In addition, for certain practical applications, low transmission loss outside the band gap and high suppression inside is required. To choose the unit cell geometry, lattice orientation, and incident wave polarization optimal for a specific system necessitates thorough experimental characterization with different acoustic modes and in different directions.
6. Conclusions
In this contribution, we have discussed the suitability of different additive manufacturing technologies to fabricate miniature, millimeter-sized three-dimensional phononic crystals. Fabrication characteristics lead to limitations in terms of minimum feature sizes and therefore operating frequencies, available materials and thus acoustic properties, and necessity of supporting overhanging and freestanding structural elements. The smallest crystal samples with feature sizes of 100 µm and below have been attained by microstereolithography printing, yielding operating frequencies in the hundred kHz to MHz range. However, this technology is not self-supporting and requires careful design considerations.
Additionally, we have presented comprehensive characterization of complex, finite, simple cubic phononic crystal lattices in terms of different propagation directions and acoustics modes. In contrast to the complete, omnidirectional band gap of a phononic unit cell calculated from its dispersion relation, the directional transmission behavior of a specific wave propagation mode can exhibit much wider gaps. The transmission loss inside and outside these gaps also differs between lattice orientations and wave modes. Experimental validation of directional band structures also introduces challenges of design and fabrication, especially for characterization in air. A comprehensive analysis is necessary to find a suitable fabrication technology, acoustic material properties, and unit cell design to realize operating frequency range, phononic band gap width, and transmission characteristic required by specific applications.