Band Structures Analysis Method of Two-Dimensional Phononic Crystals Using Wavelet-Based Elements

Abstract

A wavelet-based finite element method (WFEM) is developed to calculate the elastic band structures of two-dimensional phononic crystals (2DPCs), which are composed of square lattices of solid cuboids in a solid matrix. In a unit cell, a new model of band-gap calculation of 2DPCs is constructed using plane elastomechanical elements based on a B-spline wavelet on the interval (BSWI). Substituting the periodic boundary conditions (BCs) and interface conditions, a linear eigenvalue problem dependent on the Bloch wave vector is derived. Numerical examples show that the proposed method performs well for band structure problems when compared with those calculated by traditional FEM. This study also illustrates that filling fractions, material parameters, and incline angles of a 2DPC structure can cause band-gap width and location changes.

1. Introduction

On small scales, periodic compositions of structure with different material properties are termed phononic crystals (PCs) [1]. Since the 1990s, there has been a great deal of work devoted to studies of the PC band-gap and its mechanism [2,3]. The existence of a phononic band-gap where the propagation of acoustic or elastic waves is forbidden exhibits a lot of potential applications, such as noise reduction, acoustic filters, etc. [4]. The mechanism for tuning PC band-gap also possesses significant practical applications in the design of vibrationless environments for high-precision mechanical systems [5]. However, the calculation results had a great influence on the studies of PC band-gap mechanism and wave propagation characteristic. Therefore, a high-performance numerical method for studying the band-gap mechanism becomes a significant topic of future studies.

In the search for complete band-gaps, many mathematical models are constructed to calculate band-gaps (BGs) of two-dimensional phononic crystals (2DPCs), such as the plane-wave expansion method (PWE) [6,7,8], multiple scattering theory (MST) [9], finite difference time-domain method (FDTD) [10,11], lumped mass method (LM) [12], wavelet method [13,14], boundary element method (BEM) [15,16,17], etc. However, when materials are anisotropic, nonlinear, or have large acoustic mismatch, PWE requires a large number of plane waves to obtain a reliable band structure and results are non-convergent for PCs composed of different media. The MST method exhibits many advantages for BG calculation of PCs, such as possessing a faster convergence speed than PWE. However, the MST method can only calculate specific arrays of spheres or cylinders, and the eigenvalue equation, although it is of small size but it is nonlinear, and its solution is complex. LM adopts the lumped mass matrix into the discrete FEM stiffness matrix, which improves the calculation efficiency. However, this treatment also brings troubles in its further application when the multi-field coupling is considered. Furthermore, the simulation of a nonlinear medium using the frequency-domain method is faced with many difficulties because frequencies re no longer conserved.

Time-domain methods are used for dealing with these problems, such as FDTD. However, the accuracy of FDTD is reduced as the number of grids decrease. Some approaches to analyze phononic crystals using the finite element method (FEM), and, firstly, given a detailed review on theories and solution methods of plate/shell structures [18,19,20,21,22]. It should be pointed out that FEM performs well for band-gap calculations of 2DPCs as compared with many time-domain methods. FEM models of band-gap calculations give rise to an eigenvalue problem, which is usually solved for the unknown frequencies ω with a real wave number k, in what is called the ω (k) technique. Andreassen et al. [23] studied wave propagation in periodic materials with dissipation using ω (k) formulation. Collet et al. [24] proposed an alternative formulation that wave heading and frequency are adopted to scan the k-space and estimate the dispersion properties. Eatwell [25] derived the dispersion relation for free waves in the plate and developed a method for studying a structure, in which the exact positions of the stiffening ribs are subject to some degree of randomness. Hussein [26] proposed a reduced Bloch mode expansion for fast periodic media band structure calculations and maintained accuracy, while reducing the computation time. In [27], the solid-vacuum 2DPCs with circular holes were investigated using FEM and it proved to be successful in the band structure calculation. Rudykh et al. [28,29] studied wave propagation characteristics in deformed layered media and reported a mechanism that can be used for tuning and controlling wave propagation by deformation.

The wavelet finite element method (WFEM) [30,31,32] has already developed into a new numerical method in recent years. The WFEM, as a performance numerical approach using scale functions or the nesting wavelet functions to replace the traditional polynomial as approximating a function to analyze the dynamic problems. Since the BSWI scale functions have the analytical expression at all levels, the element stiffness and mass matrices can be calculated conveniently [33]. Any functions on the interval will be approximated completely due to the wavelets on a bounded interval have limited dimension at all levels and the wavelet space. Cubic B-spline interpolating functions have sufficient continuity when compared with the piecewise polynomial of traditional FEM. Thus, the wavelet-based FEM can obtain a higher precision of solution than traditional FEM. Xiang et al. successfully constructed classes of two-dimensional (2D) wavelet-based elements by using B-spline wavelets on the interval [34,35,36,37,38,39]. In this paper, we employ BSWI plane elastomechanical plate elements to construct a band-gap calculation model [34]. Zhang et al. developed the multivariable WFEM for structure dynamical simulation and vibration analysis [40,41]. Furthermore, WFEM has been successfully applied to damage detection field [42,43,44]. The wavelet Galerkin method has succeeded in being applied to solve band structures of 2D photonic crystal [45] and 2D phononic crystals [46]. The wavelet Galerkin method adopts the whole domain discretization with different type of partial differential equations (PDEs) that fail to accommodate the complex solving domains [47]. Liu proposed a WFEM model of 1DPC Euler beam and successfully computed the band structures [48]. Thus, developing a new band-gap calculation model of 2DPCs based on wavelet-based FEM is significant.

In this paper, a new numerical formulation is introduced for computing the band structures of 2DPCs. The paper is organized as follows. After a brief introduction, the band-gap calculation model of a unit cell is given based on periodic boundary conditions (BCs) and Bloch wave theorem, and then discretization was carried out by WFEM in Section 2. The band structures and parameter influence on wave propagation in 2DPCs are discussed in Section 3. Finally, some conclusions are presented in Section 4.

2. Theoretical Development

The band-gap of a periodic structure is usually calculated in the frequency domain by utilizing unit cells and periodic boundary conditions (BCs). The same approach is followed in this paper to investigate band structures of 2DPCs using wavelet-based FEM. A schematic of a 2DPC structure whose unit cell consists of two materials A and B with the same thickness lies in the xy-plane as shown in Figure 1a. The unit cell composed of a square B with length L_b embedded in square A with length Lx and width Ly. The lattice constant is Lx. As shown in Figure 1a, the internal square B of the unit cell forms section B and the rest of the unit cell is section A.

When PCs vibrate harmonically with angular frequency $\omega$, to analyze the dispersion in those structures, use of the wave equation of a unit cell is sufficient to obtain band structures of the whole structure. Since we study the free wave propagation, no external forces are applied to the structure. The spatially-discretized governing equation of 2DPC is obtained as:

$$\left(K-{\omega }^{2}M\right)v=Dv$$

(1)

where $D$ denotes the frequency-dependent dynamic stiffness matrix, $v$ is the vector of the nodal displacements, $\omega$ is the angular frequency, and $K$ and $M$ are the global stiffness and mass matrices of the unit cell, respectively.

Since a unit cell consists of nine BSWI4_j plane elastomechanical plate elements, $K$ and $M$ are formed by the superposition of $K^{A,j}$ (the superposition of BSWI4_j plate element stiffness matrices $K^{e_A,j}$ of section A) and $K^{B,j}$ (the superposition of BSWI4_j plate element stiffness matrices $K^{e_B,j}$ of section B), $M^{A,j}$ (the superposition of BSWI4_j element mass matrices $M^{e_A,j}$ of section A), and $M^{B,j}$ (the superposition of BSWI4_j plate element mass matrices $M^{e_B,j}$ of section B). The detailed expressions of BSWI plane elastomechanical plate elemental stiffness and mass matrices are shown in [34,35]. Expressions of The BSWI4_j plane elastomechanical plate element stiffness and mass matrices $K^{e_A,j}$, $K^{e_B,j}$, $M^{e_A,j}$, and $M^{e_B,j}$ are:

$$K^{e_i,j}=\left[\begin{array}{cc}{K}_1^{e,i}& K_2^{e,i}\\ K_3^{e,i}& K_4^{e,i}\end{array}\right]$$

(2)

$$M^{e_i,j}=l_{ex}^i{l}_{ey}^i{\rho }_{i}t{\Gamma }_1^{0,0}\otimes {\Gamma }_2^{0,0}$$

(3)

where:

$$K_1^{e,i}=E_i/(1-{{\mu }_i}^2)\left[{\Gamma }_1^{1,1}\otimes {\Gamma }_2^{0,0}+(1-{\mu }_i)/2{\Gamma }_1^{0,0}\otimes {\Gamma }_2^{1,1}\right]$$

(4)

$$K_2^{e,i}=E_i/(1-{{\mu }_i}^2)\left[{\mu }_i{\Gamma }_1^{1,0}\otimes {\Gamma }_2^{0,1}+(1-{\mu }_i)/2{\Gamma }_1^{0,1}\otimes {\Gamma }_2^{1,0}\right]$$

(5)

$$K_3^{e,i}={(K_2^{e,i})}^T$$

(6)

$$K_4^{e,i}=E_i/(1-{{\mu }_i}^2)\left[{\Gamma }_1^{0,0}\otimes {\Gamma }_2^{1,1}+(1-{\mu }_i)/2{\Gamma }_1^{1,1}\otimes {\Gamma }_2^{0,0}\right]$$

(7)

$${\Gamma }_1^{0,0}={\left(T_1^e\right)}^T\left(l_{ex}^i{\displaystyle {\int }_0^1{{\Phi }_1}^T{\Phi }_{1}d\xi }\right)T_1^e$$

(8)

$${\Gamma }_1^{0,1}={\left(T_1^e\right)}^T\left({\displaystyle {\int }_0^1{{\Phi }_1}^T\frac{d{\Phi }_1}{d\xi }d\xi }\right)T_1^e$$

(9)

$${\Gamma }_1^{1,0}={\left(T_1^e\right)}^T\left(l_{ex}^i{\displaystyle {\int }_0^1\frac{d{\Phi }_1}{d\xi }{\Phi }_{1}d\xi }\right)T_1^e$$

(10)

$${\Gamma }_1^{1,1}={\left(T_1^e\right)}^T\left(\frac{1}{l_{ex}^i}{\displaystyle {\int }_0^1\frac{d{{\Phi }_1}^T}{d\xi }\frac{d{\Phi }_1}{d\xi }d\xi }\right)T_1^e$$

(11)

in which:

$$\{\begin{array}{c}{T}_1^e={\left\{{\phi }_1^T\left({\xi }_1\right){\phi }_1^T\left({\xi }_2\right)\cdots {\phi }_1^T\left({\xi }_{n+1}\right)\right\}}^T\hfill \\ T_2^e={\left\{{\phi }_2^T\left({\eta }_1\right){\phi }_2^T\left({\eta }_2\right)\cdots {\phi }_2^T\left({\eta }_{n+1}\right)\right\}}^T\hfill \end{array}$$

(12)

where i denotes two sections A and B; t, E, and $\rho$ are the thickness, the Young’s moduli, and material densities of the two sections A and B, respectively, ${\Gamma }_2^{a,k}$(a, k = 0, 1) is similar to ${\Gamma }_1^{a,k}$(a, k = 0, 1) if $l_{ex}^i$, $d\xi$, $T_1^e$, and ${\phi }_1$ are replaced by $l_{ey}^i$, $d\eta$, $T_2^e$, and ${\phi }_2$, respectively.

Due to the independent interpolation of displacements u and v, we can change the location of elemental matrices for solving Equation (2) to:

$$K^{e_i,j}=\left[\begin{array}{ccccc}{K}_{1,1}^e& K_{1,2}^e& \cdots & K_{1,n^2+2n}^e& K_{1,{\left(n+1\right)}^2}^e\\ K_{2,1}^e& K_{2,2}^e& \cdots & K_{2,n^2+2n}^e& K_{2,{\left(n+1\right)}^2}^e\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ K_{n^2+2n,1}^e& K_{n^2+2n,2}^e& \cdots & K_{n^2+2n,n^2+2n}^e& K_{n^2+2n,{\left(n+1\right)}^2}^e\\ K_{{\left(n+1\right)}^2,1}^e& K_{{\left(n+1\right)}^2,2}^e& \cdots & K_{{\left(n+1\right)}^2,n^2+2n}^e& K_{{\left(n+1\right)}^2,{\left(n+1\right)}^2}^e\end{array}\right]$$

(13)

where:

$$K_{a,k}^e=\left[\begin{array}{cc}{K}_{1_{a,k}}^{e,i}& K_{2_{a,k}}^{e,i}\\ K_{3_{a,k}}^{e,i}& K_{4_{a,k}}^{e,i}\end{array}\right],\left(a,k=1,\cdots ,{\left(n+1\right)}^2\right)$$

(14)

In order to simplify the calculation, the nodes of the unit cell are divided to nine subvectors and then Equation (1) can be rewritten as:

$$\left(K-{\omega }^{2}M\right)v=Dv=\left[\begin{array}{ccc}{d}_{11}& \cdots & d_{19}\\ ⋮& \ddots & ⋮\\ {d_{19}}^T& \cdots & d_{99}\end{array}\right]\left[\begin{array}{c}{v}_1\\ ⋮\\ v_9\end{array}\right]$$

(15)

According to the periodic BCs between the boundary nodes at $x=L_x$, $y=L_y$ and at $x=0$, $y=0$, the follow relationship can be established:

$$\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\\ v_5\\ v_6\\ v_7\\ v_8\\ v_9\end{array}\right]=\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\\ v_1{e}^{i{k}_y{L}_y}\\ v_2{e}^{i{k}_x{L}_x}\\ v_3{e}^{i{k}_x{L}_x}\\ v_3{e}^{i{k}_y{L}_x}\\ v_3{e}^{i\left(k_x{L}_x+k_y{L}_y\right)}\end{array}\right]$$

(16)

where $k_x$ and $k_y$ denote the wave numbers. DOFs of boundary nodes are related to the wave numbers. The inner degrees of freedom (DOFs) in $v_4$ will be reduced using the follow dynamic consideration matrix [49],

$$D^{red}=T_1^T{DT}_1-T_1^T{DT}_2{\left(T_2^T{DT}_2\right)}^{-1}{T}_2^T{DT}_1$$

(17)

where: $T_1=\left[\begin{array}{cc}{I}_{n_1}& 0_{n_1,n_2}\\ 0_{n_i,n_1}& 0_{n_i,n_2}\\ 0_{n_2,n_1}& I_{n_2}\end{array}\right]$ and $T_2=\left[\begin{array}{c}{0}_{n_1,n_i}\\ I_{n_i}\\ 0_{n_2,n_i}\end{array}\right]$, where $n_1=2\left(10m+10n-1\right)$, $n_2=2\left(10m+10n+1\right)$ and $n_i$ is the inner DOFs of the unit cell. m and n are the numbers of elements in x, y-directions. The matrices $I$ and $0$ are identity and zero matrices with the corresponding dimensions. The final equation can be presented as the dispersion relation of the 2DPCs:

$$\overline{D}\left(\omega ,k_x,k_y\right)={\Lambda }_L^T{D}^{red}{\Lambda }_R=0$$

(18)

where:

$${\Lambda }_R=\left[\begin{array}{ccc}{I}_{m_1}& 0& 0\\ 0& I_{m_2}& 0\\ 0& 0& I_{m_3}\\ {\lambda }_y{{\rm I}}_{m_1}& 0& 0\\ 0& {\lambda }_x{I}_{m_2}& 0\\ 0& 0& {\lambda }_x{I}_{m_3}\\ 0& 0& {\lambda }_y{I}_{m_3}\\ 0& 0& {\lambda }_x{\lambda }_y{I}_{m_3}\end{array}\right] \text{and} {\Lambda }_L=\left[\begin{array}{ccc}{I}_{m_1}& 0& 0\\ 0& I_{m_2}& 0\\ 0& 0& I_{m_3}\\ {\lambda }_y^{-1}{{\rm I}}_{m_1}& 0& 0\\ 0& {\lambda }_x^{-1}{I}_{m_2}& 0\\ 0& 0& {\lambda }_x^{-1}{I}_{m_3}\\ 0& 0& {\lambda }_y^{-1}{I}_{m_3}\\ 0& 0& {\lambda }_x^{-1}{\lambda }_y^{-1}{I}_{m_3}\end{array}\right]$$

(19)

where $m_1=2\left(11m-1\right)$, $m_2=2\left(11n-1\right)$, and $m_3=2$, which represent a symmetric eigenvalue problem relating k and ω for the discretized structure, whose solutions give WFEM estimates of the dispersion relations for the continuous structure. Corresponding to each value of k, there will be a discrete set of frequencies that occur in equal pairs. Each frequency will have an associated eigenvector. This eigenvector defines the wave motion in the periodic section at that frequency.

Rectangular plate elements are used universally in engineering practice for the simplicity of the formulation. Thus, the effectiveness compute of the band structures of 2DPCs with rectangular lattice are very important. Different structures possess diverse BGs properties. A rectangular lattice with L_x unequal to L_y has different BG characteristic to a square lattice. The process of band structure calculations of these two lattices is basically the same, only a variation with different boundary conditions and the value of wave vectors.

3. Numerical Investigation

According to the formulation of two-dimensional BSWI plane elastomechanical elements with a square lattice, which was provided in Section 2, a verification example is given. As shown in Figure 1, the band structure of 2DPCs composed of epoxy (section A) and lead (section B) arranged in a square lattice is studied, with a filling fraction f = 11% and the lattice constant L_x and L_y are fixed at 3 cm.

Table 1. Material properties.

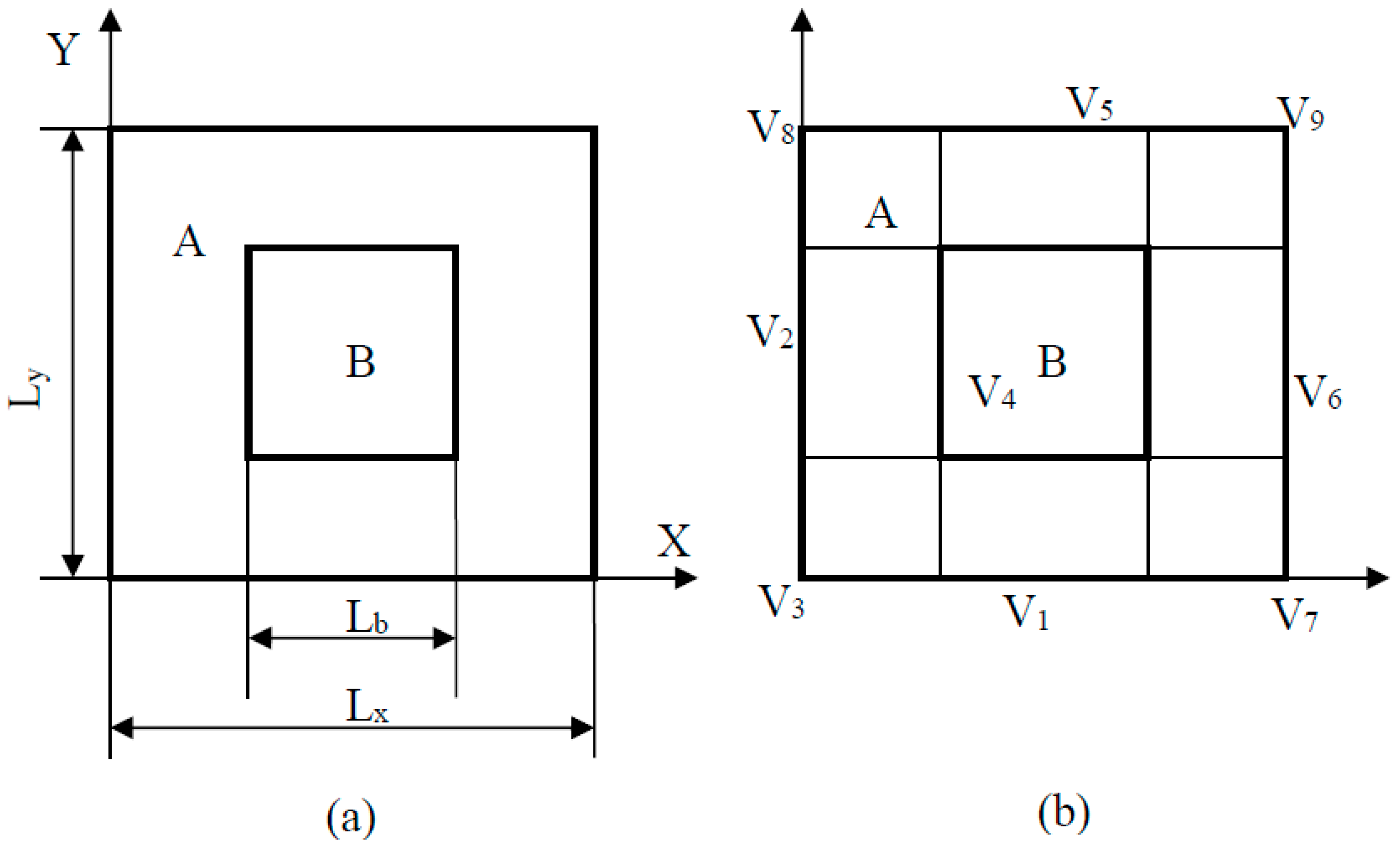
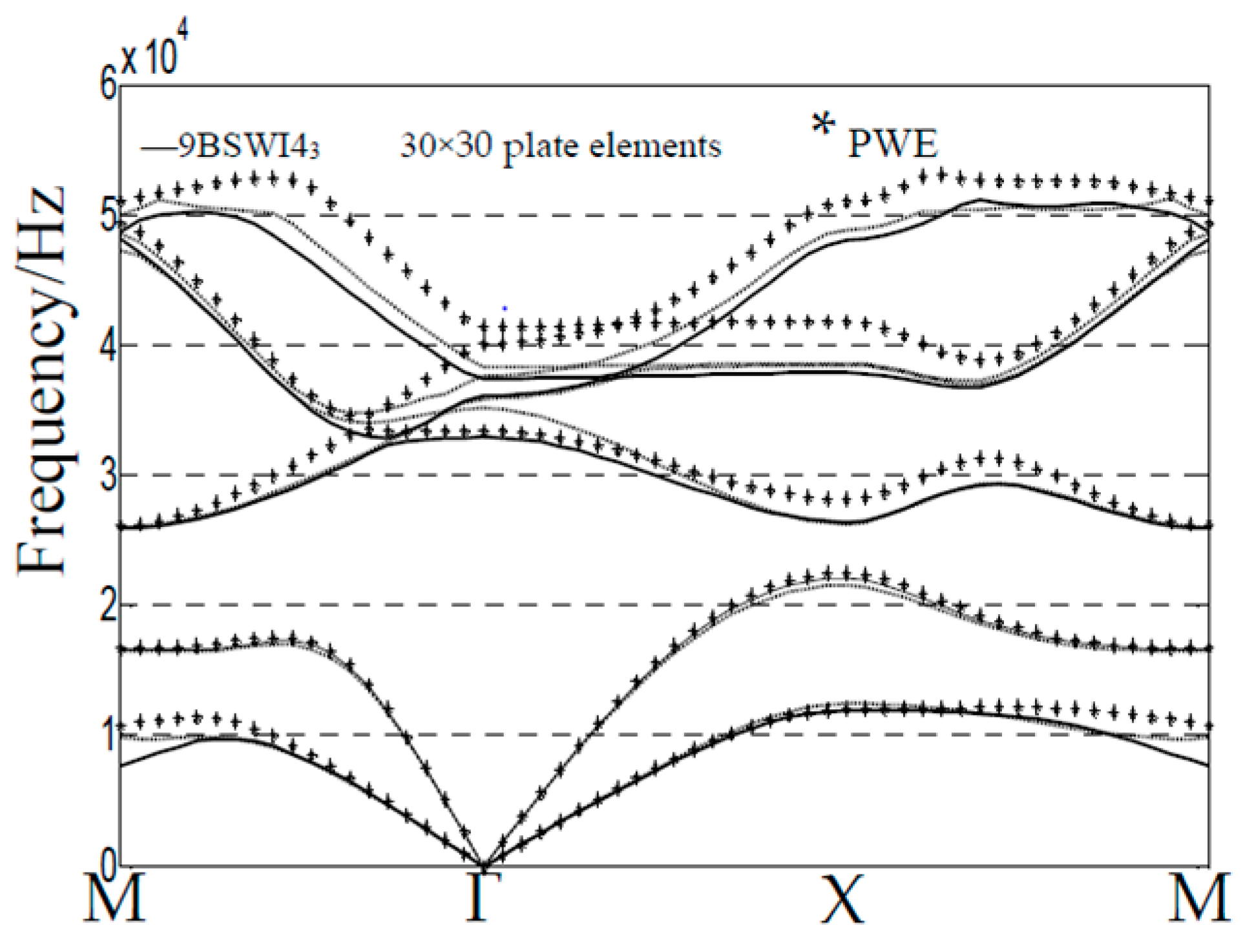
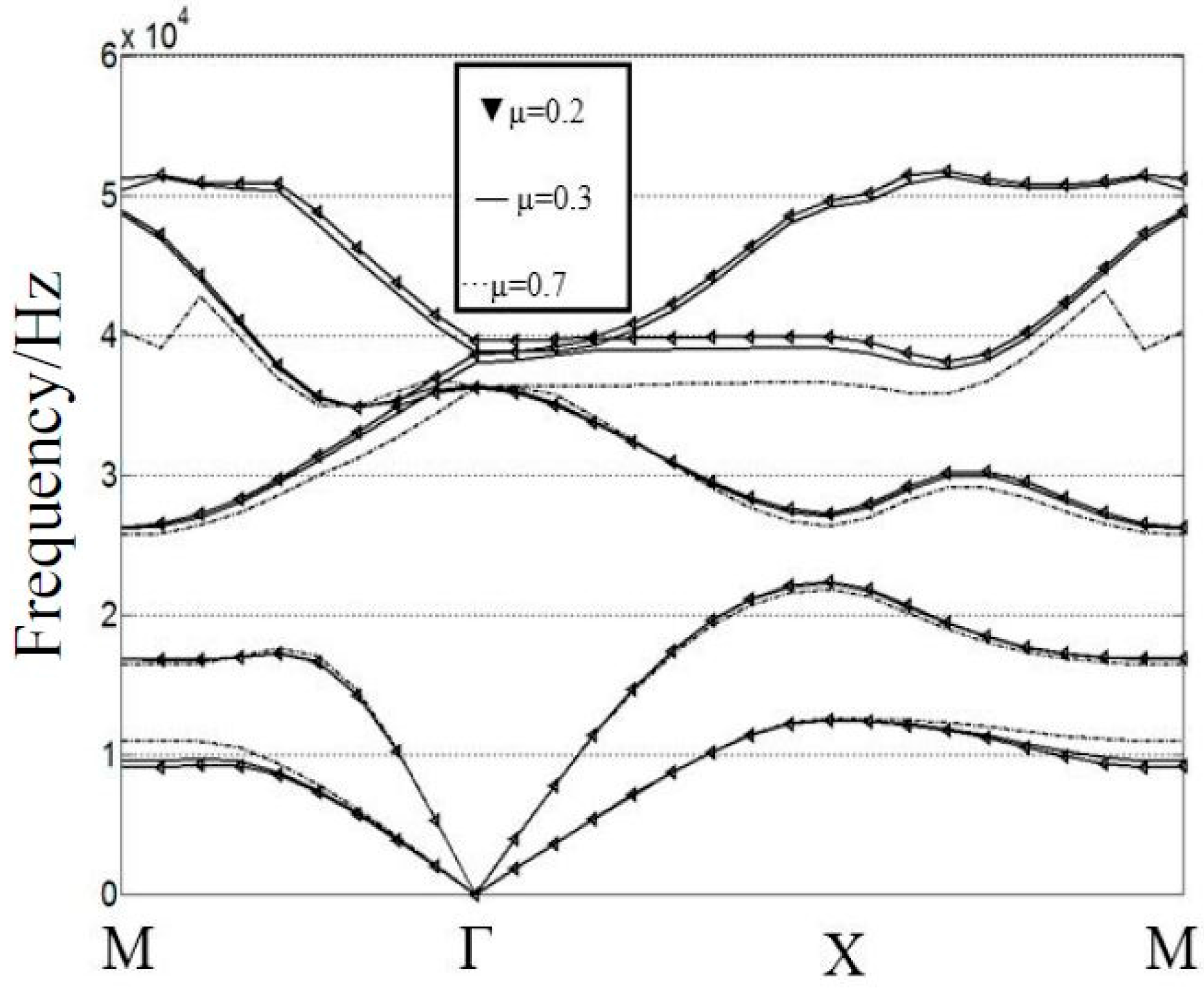
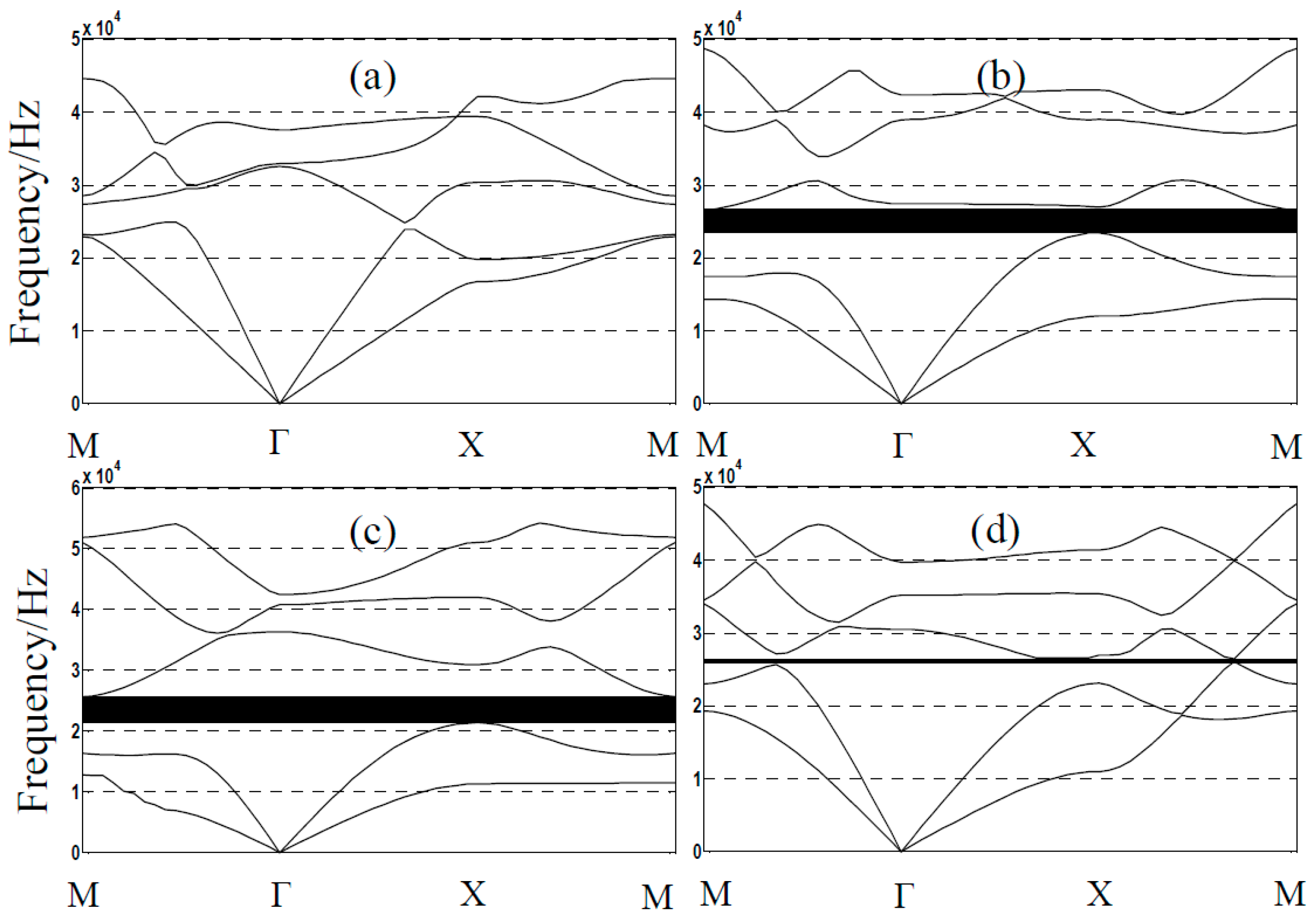
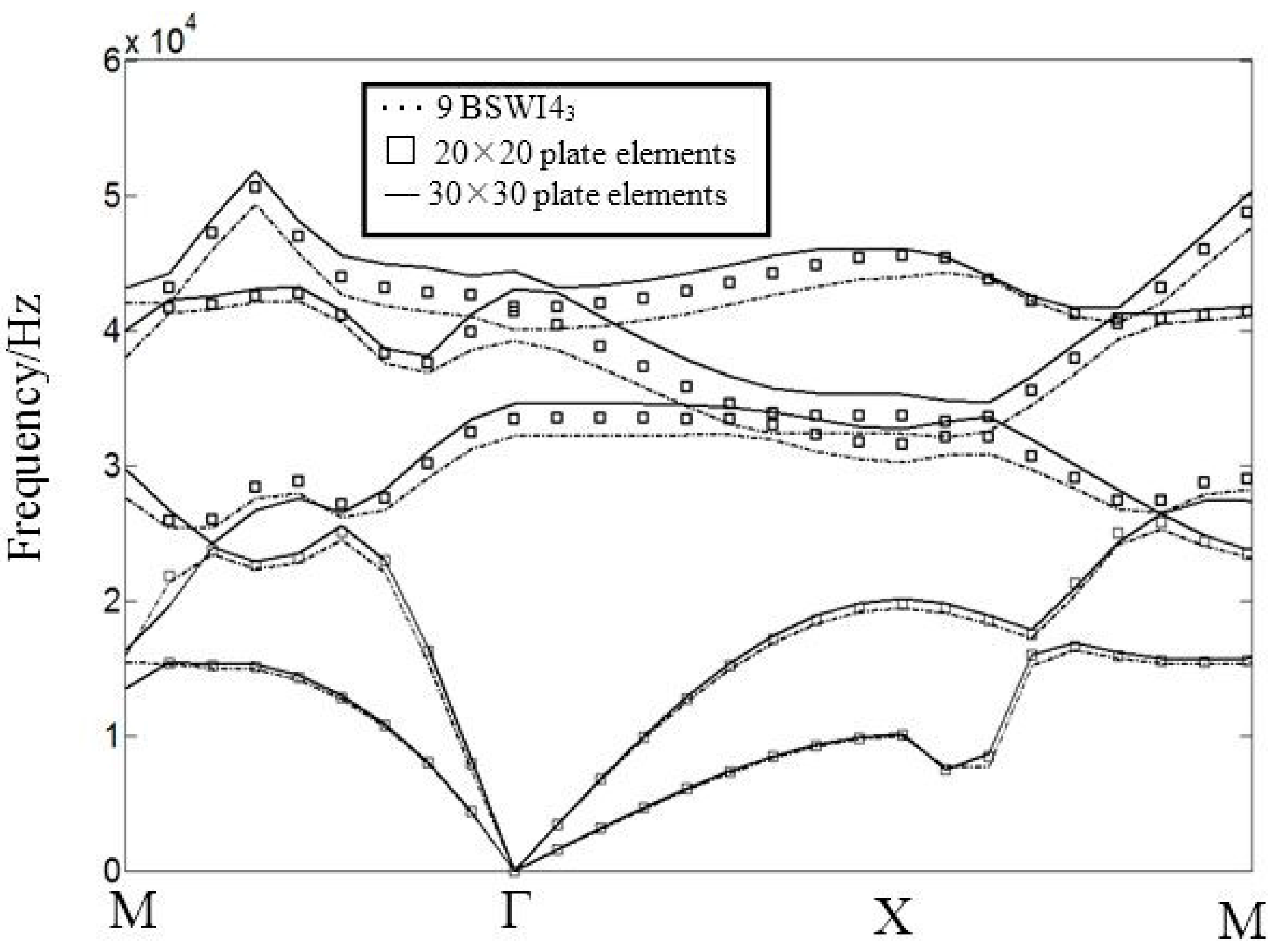
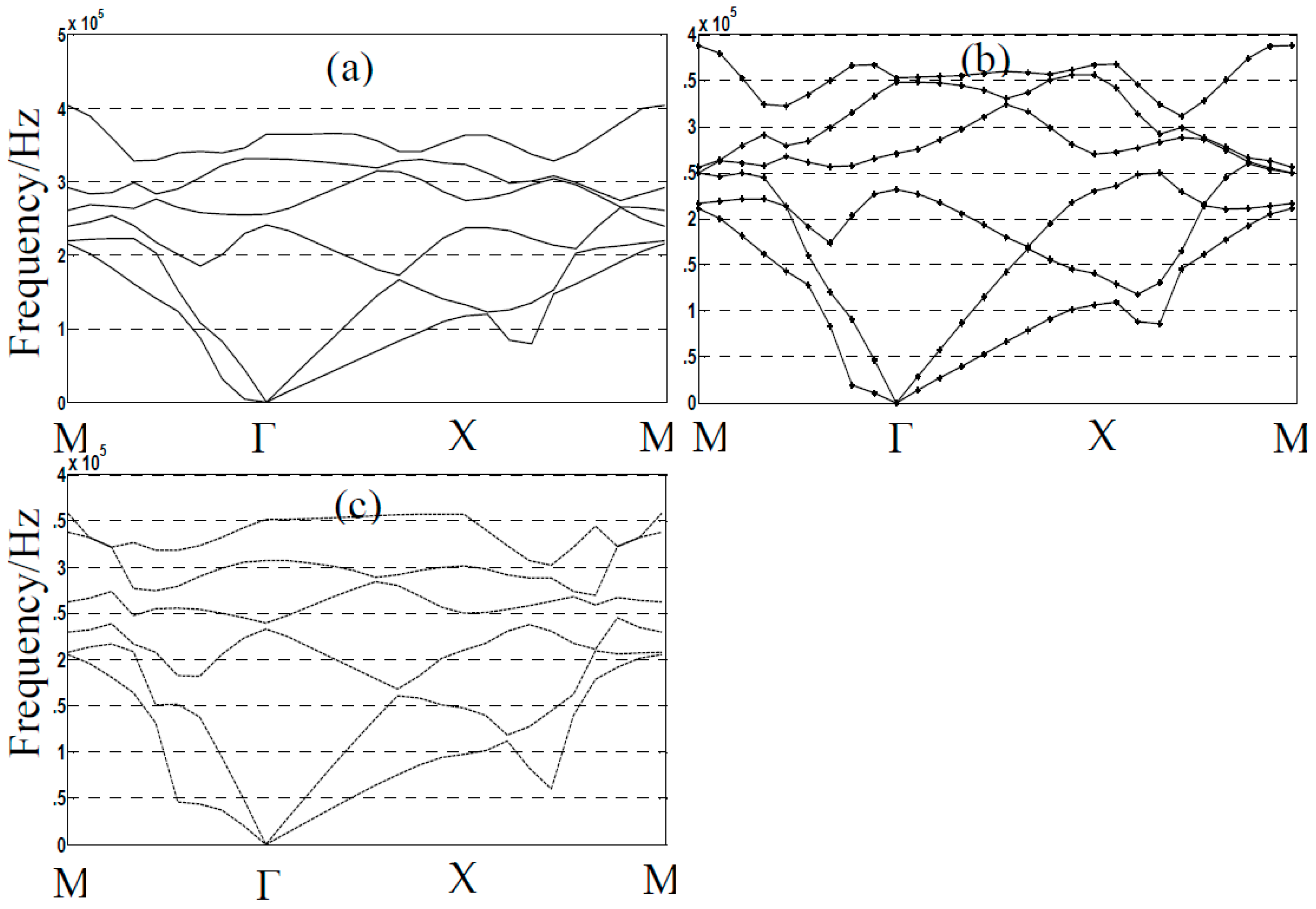
Materials	Density(ρ) (Kg/m3)	Young’s Modules(E)1010 Pa	Possion’s Ratios (ν)
Lead	11,600	4.08	0.369
Epoxy	1180	0.435	0.368

shows the material parameters of lead and epoxy.

In order to verify the reliability of the wavelet-based FEM in band structure calculations of 2DPCs, a numerical example is studied. For the same structural and material parameters, we employ nine ($m=3,n=3$) BSWI4₃ (the scaling functions of the tensor product BSWI for four orders at the scale j = 3) plane elastomechanical elements (1922 DOFs), 900 ($m=30,n=30$) (7442 DOFs) traditional plate elements and 441 plane waves (PWE) to calculate the band structures of 2DPCs, respectively. The results are shown in Figure 2 and solid, dashed, dotted and star lines denote the current formulation, 900 traditional plate elements and PWE method, respectively. As shown in Figure 2, the results from WFEM are excellent as compared with those from the traditional FEM and PWE method in the low-frequency region and nine BSWI4₃ elements can achieve the same accuracy as that of the traditional FEM with much fewer elements and DOFs. For the results in the high-frequency region, WFEM has a better convergence and higher stability than traditional FEM. The traditional FEM has been successful in studying band structures of one- and two-dimensional PCs. Thus, WFEM can be used to calculate the band structure of 2DPCs.

Furthermore, band structures of 2DPCs with different materials and structural parameters are investigated using the current formulation. Frequency band structures of 2DPCs with different Possion’s ratios are studied and the results are shown in Figure 3, triangle lines correspond to ν = 0.2, full lines to ν = 0.3, and dotted lines ν = 0.7, respectively. Frequency band structures of 2DPCs with different filling fractions are investigated with results shown in Figure 4. As shown in Figure 4, the first band-gap width is increased by increasing the filling fractions until reaching a maximum value 4.09 kHz at f = 45%, and then to shrink, which are similar to Reference [50]. The comparison of the dispersion relations with different Possion’s ratios in Figure 4 has shown that the material properties have little influence on band structures. However, the band structure of a 2DPC with different filling fractions leads to a dramatic change. Thus, the influence of filling fraction on the wave propagation in 2DPCs is much stronger than the material properties.

Rectangular plates have very important application in practical engineering. Band structures of different lattice forms are studied using the current formulation. We adopt a rectangular lattice with L_x unequal to L_y to observe changes in the band structure. The following structural parameters are used: L_x = 3 cm, L_y = 2 cm, L_a = L_b = 1.6 cm, and the filling ratio f = 43%. We also employ nine ($m=3,n=3$) BSWI4_j plane elastomechanical elements with j = 3 (1922 DOFs) and 20 × 20 (3362 DOFs) and 30 × 30 (7442 DOFs) traditional plate elements to calculate the band structures of 2DPCs, with the results shown in Figure 5. Furthermore, band structures of 2DPCs with solid-vacuum mediums composed of square holes embedded in rectangular lattices are studied using current formulation. Structural parameters: lattice constant L_x = 3 cm, L_y = 2 cm and L_a = L_b = 0.4, 0.5 and 0.6 cm. The results are shown in Figure 6 and full lines, star lines, and dotted lines correspond to L_a = L_b = 0.4, 0.5 and 0.6 cm, respectively.

Finally, band structures of a 2DPC skew plate with different angles of inclination are investigated using the current formulation with the results shown in Figure 7 and star lines, triangle lines, and full lines corresponding to 30, 45, and 60 angles of inclination, respectively. According to the construction of WFEM, the detailed expressions of stiffness and mass matrices are shown in [35,36].

4. Conclusions

A numerical method for calculating band structures of 2DPCs is developed based on BSWI plane elastomechanical plate element and corresponding model of the unit cell. The band-gap calculation problem reduces to a quadratic or quartic polynomial eigenvalue problem after the application of a dynamic condensation. This formalism corresponds to a classical ω (k) problem, where unknown frequencies are calculated for real wave numbers. Numerical examples are conducted to verify the accuracy and efficiency of the WFEM in band-gap calculation problems. It can achieve higher accuracy than traditional FEM with fewer numbers of elements and DOFs usually in high frequency domain. This study also indicates that different filling fractions and structural parameters can cause changes of wave propagation characteristics in the 2DPCs. The band-gap calculation model of 2DPCs consists of solid-vacuum mediums is also constructed using the current formulation. Two-dimensional (2D) wavelet-based element is a useful tool to compute BGs of 2DPCs for reason of BSWI interpolating bases possess character of continuity. Furthermore, the current method enriches the numerical simulation methods to study the band-gaps mechanism and wave propagation characteristics of PCs.

Our work provides a means for calculating band structures of 2DPCs. Other two-dimensional wavelet-based band-gap calculation models would be investigated in future studies by use of the similar technique. However, because of the complexity of the tensor product wavelet technique, it is difficult to extend the present method to solve PCs with three-dimensional (3D) periodicity. The usage of the wavelet-based boundary element method might be a good choice to perform the wavelet-based approximation equation.