Bloch Modes and Evanescent Modes of Photonic Crystals: Weak Form Solutions Based on Accurate Interface Triangulation
Abstract
: We propose a new approach to calculate the complex photonic band structure, both purely dispersive and evanescent Bloch modes of a finite range, of arbitrary three-dimensional photonic crystals. Our method, based on a well-established plane wave expansion and the weak form solution of Maxwell’s equations, computes the Fourier components of periodic structures composed of distinct homogeneous material domains from a triangulated mesh representation of the inter-material interfaces; this allows substantially more accurate representations of the geometry of complex photonic crystals than the conventional representation by a cubic voxel grid. Our method works for general two-phase composite materials, consisting of bi-anisotropic materials with tensor-valued dielectric and magnetic permittivities ε and μ and coupling matrices ζ. We demonstrate for the Bragg mirror and a simple cubic crystal closely related to the Kelvin foam that relatively small numbers of Fourier components are sufficient to yield good convergence of the eigenvalues, making this method viable, despite its computational complexity. As an application, we use the single gyroid crystal to demonstrate that the consideration of both conventional and evanescent Bloch modes is necessary to predict the key features of the reflectance spectrum by analysis of the band structure, in particular for light incident along the cubic [111] direction.1. Introduction
A photonic crystal (PhC) is a composite material with a periodic and symmetric spatial arrangement of at least two components with different macroscopic electromagnetic properties, such as the dielectric constant ε (or only its real part in the original definition [1,2]) and, more generally, also the magnetic permittivity μ and the coupling constant ζ [3]. The photonic band structure represents the dispersion relation between the Bloch wave vector k and frequency ω of the periodic electromagnetic field configurations, called Bloch modes, which are commensurate with the periodicity and symmetry of the PhC.
The photonic band structure (PBS) is a concept [2] that is often invoked when one is interested in the reflectance or transmission properties of a slab of photonic crystal, even though the finite nature of the slab breaks the spatial periodicity. The existence of a photonic band gap, i.e., a frequency range for which no Bloch modes exist in the infinite PhC, is commonly interpreted as a stop band, i.e., a frequency interval for which no light can penetrate through the photonic crystal and is, hence, reflected. Similarly, it is often assumed that light with a frequency that matches the frequency of a given Bloch mode may penetrate through the crystal, subject to sufficient coupling of the incident light and the Bloch mode, which acts as a transmission channel.
Simple approaches to evaluate the degree of coupling between an incoming plane wave and the Bloch modes of a PhC suffice in many situations to correlate features of the band structure to the transmission or reflectance spectra [4], e.g., for light incident onto a semi-infinite single gyroid or a four-srs PhC along the [100] or [110] lattice direction [5]. The single gyroid is a complex network-like ordered PhC with structural chirality, of relevance both as a biophotonic and as a synthetic material [6]; see Figure 1.
However, the general solution of the problem of the reflectance of a plane wave incident onto a finite or semi-infinite slab of a PhC is a scattering problem that involves not only the purely dispersive Bloch modes, but also evanescent Bloch modes, whose amplitude decreases away from the interface; see Figure 2. While the bulk modes themselves can be extracted to high accuracy from, e.g., finite element method (FEM) calculations (cf. [7,8]), the scattering problem itself is conveniently solved in Fourier space using Floquet’s theorem and the orthogonality of plane waves [9–12]. Hence, the accuracy is lost laterally as a result of the numerical Fourier cutoff. We therefore use a similar approach as in [13] and solve the bulk eigenvalue equation also in Fourier space to obtain the generalized Bloch modes, including those that are evanescent. This earlier work [13] did not mention how the Fourier transforms are performed while presumably having the same memory limitation (without mentioning this fact explicitly) due to matrix inversion (see Section 3.2), as the authors show a convergence diagram for a very small number of plane waves N < 1500 in a two-dimensional case only. If we assume that some kind of discrete Fourier transformation has been done, our algorithm provides roughly one order of magnitude increased accuracy for the same number of plane waves (cf. Section 5.1) and is further more general in terms of the material properties: We consider for examaple anisotropy as well as Condon cross-coupling, see constitutive Equations (1) and (2).
While a slow geometrical convergence is part of any numerical Fourier approach for piecewise continuous functions due to the Gibbs phenomenon (a truncated Fourier sum overshoots the original function at discontinuities) and cannot be entirely avoided [16], our approach allows one to compute the components of the material matrices with machine precision avoiding staircase effects, which are a problem in the standard approach [17] based on a regular spatial lattice that is well known to yield additional numerical errors, cf. [18–20] for the finite difference time domain (FDTD) methods. Figure 3 illustrates the representation of a complex three-dimensional PhC, the same single gyroid structure as shown in Figure 1, by voxels (Figure 3b) and by a mesh (Figure 3c) and the apparent advantage of the latter. One of the contributions of this article is the demonstration that the complex photonic band structure can be directly computed from a mesh representation, hence eliminating the error due to conventional discrete Fourier transformations that is particularly large for a small number of Fourier components, compared to error related to the Gibbs phenomenon.
2. Generalized Bloch Mode Equation
In this section, the differential eigenvalue equation that yields the Bloch modes is derived: the bases are Maxwell’s equations in the monochromatic form with a fixed frequency ω = ck0 (with the vacuum speed of light c and the vacuum wave number ) and lateral wave vector (or, equivalently, the angle of incidence). Each Bloch mode that is able to couple to an incident plane wave is thus characterized by the wave number in the surface normal direction, which plays the role of an eigenvalue.
Here, and in the following, the lattice constant of the PhC is set to a = 1, so that electromagnetic fields (or, more precisely, the complex spatial amplitudes in a monochromatic approach) are considered as functions , etc., i.e., we omit the spatial dimension. As a result, all wave numbers are also dimensionless. In practice, scaling with the lattice constant yields the physical solution from this slightly more abstract formulation.
2.1. Material Parameters and Maxwell’s Equations
The PhC is assumed to be a combination of linear bi-anisotropic materials that satisfy Lorentz-reciprocity [3]. The corresponding constitutive equations have the following general form:
These two equations relate the displacement field D and the magnetic flux B to the electric field E and the magnetic field H, respectively. The microscopic physics is described by the symmetric permittivity and permeability matrices and and the coupling matrix , all . (Note that these assumptions of the material properties of the constituent materials are rather broad, encompassing lossy and anisotropic materials with a spatially varying orientation of the permittivity and permeability matrices and bi-isotropic materials with coupling between electric and magnetic contributions to the displacement field and the magnetic flux. The scalar case goes back to Condon [29], where the coupling ζ is directly related to the chirality κ via [30]. Evidently, the standard case of a PhC made of an isotropic dielectric material is covered by this formalism as , and ζ = 0.) Note that the material parameters may also be frequency dependent without further restriction in our algorithm. For the sake of clearer nomenclature, we have restricted the notation to frequency-independent material properties.
The macroscopic Maxwell equations in the monochromatic form are given by (with k0 = ω/c the vacuum wave number and using conventional Gaussian units [31]) (The divergence equations, i.e., the Coulomb and the Gauss law, are redundant here; due to the Poincaré lemma [32] for a differential two-form in , i.e., ∇ · F = 0 ⇔ F = ∇ × A for some A.):
Equations (3) and (4) have the form of a system of six linear first-order partial differential equations that can be written as:
2.2. Geometry
We consider PhCs composed of two types of material (indexed by zero and one), whose spatial distribution is given by the indicator function χ : Ω → {0, 1} that takes the value χ(r) = α for a given point r that is occupied by material with α = 0, 1. The PhC and, hence, χ are periodic, and we denote the three basis vectors of the PhC lattice as . The unit cell of the PhC is the parallelepiped spanned by these basis vectors. It is a composition Ω = Ω0 ∪ Ω1 of two spatial domains Ωα = {r ∊ Ω | χ(r) = α} that are separated by an interfacial surface S = ∂Ω1 ∩ ∂Ω2. (Note that the interfacial surface S is not necessarily represented by a single connected component. For example, a Bragg mirror has two non-connected planar surfaces between its two domains; Section 5.1.) Each material function can be expressed by f(r) = f0 + (f1 − f0)χ(r) with constant parameters fα (f = εij, μij, ζij; i, j = 1, 2, 3).
2.3. The Wave Vector Eigenvalue Equation
We now develop the operators that allow one to express the problem of solving the partial differential Equation (5) in a weak formulation, i.e., as a solution of a corresponding integral equation with lesser differentiability requirements. This approach, which provides the general basis for finite element methods [33] and which is developed in this section for the spatially continuous situation, lends itself to a discretization by simplices, i.e., triangulations, rather than discretizing the volume into voxels, avoiding systematic errors in the numerical approximation of the original structure, such as symmetry breaks (see the Appendix of [18] as an example) and the introduction of sharp interface angles.
We solve Equation (5) for all bulk PhC modes that can couple to an incoming plane wave with wave vector . The z-direction coincides with the inclination direction of the semi-infinite or slab-like PhC structure. Due to the spatial periodicity and Floquet’s theorem, the fields that solve Equation (5) are elements of the linear solution space with basis functions:
The vector is referred to as the Bloch wave vector, although, in contrast to classical Bloch modes, is complex in general. (The wave numbers kx, ky parallel to the interface are conserved as a result of the boundary conditions, which becomes immediately evident in Fourier space. From a group theoretical perspective, one could also argue that the solution in the whole space is laterally of the Bloch form as a result of the periodicity, and the phase factor exp{ık‖ · T‖} can be interpreted as the character of a set of infinite one-dimensional irreducible representations that are all orthogonal to each other; cf. [18]).
We rearrange Equation (5) to convert it into the following form:
The rank of the matrix M in Equation (11) is four, while its dimension is six, leading to spurious modes polarized in the z-direction and with an infinite eigenvalue. Reduction to a wave equation as in [34] yields a full second order eigenvalue equation just for one of the fields E or H for ζ ≠ 0, which is of same complexity as the original linear form presented here.
Instead, we eliminate the z components of the fields, as, for example, done in [11,12], to obtain a reduced problem of dimension four. We first introduce block-matrices:
2.4. The Weak Form of the Eigenvalue Problem
We now convert Equation (10) into a weak form that is discretized in the following section. We define the Banach space V of functions that map the translational unit cell Ω onto the complex plane. (More precisely, V is a special type of Sobolev space for which we need to assume square integrability for differentiating up to second order. Furthermore, we need to assume periodicity in the sense that on the boundary of Ω, f(r) = f(r + T) and also for the derivative of f. However, with a plane wave expansion, our discretized Galerkin space naturally meets both restrictions. In fact, infinite differentiability is a too strong of a requirement that leads to the well-known Gibbs phenomenon [16].) The corresponding norm for v ∊ V is (v, v)1/2 with the sesquilinear form (v, w) = ∫Ω d3r v*w, where (·)* denotes complex conjugation and d3r = dr1dr2dr3 the volume element. More generally, the sesquilinear form for v, w ∊ Vn is (v, w) = ∫Ω d3r v · w with the n-dimensional scalar product defined by . Using those definitions, the reduced strong problem Equation (10) has the following weak form:
All solutions of Equation (11) thus form a complete set of basis functions (see Floquet’s theorem above) for the solution of Equation (5), for fixed lateral dispersion and physical boundary conditions at infinity (see the previous Section 2.3.)
3. Plane Wave Expansion
All plane waves that meet the periodicity requirement serve as a complete basis set for the Banach space V and may hence be used as test functions in each of the components of u in Equation (11):
Here, we introduce the unit vector ei, whose i-th component is one, and any other vanishes, and the reciprocal lattice vectors where B is the reciprocal basis matrix B = 2π(AT)−1, that is, the transposed inverse of the lattice matrix A = (a1, a2, a3). The field vector v is expanded by the same plane wave basis and substituted by its Fourier series:
3.1. Fourier Integrals
The Fourier–Galerkin equation is composed of integrals of the form ∫Ω d3r f(r) exp{ı(G) · r}, where f(r) is either a material function or a constant. In this section, we derive a method to calculate these Fourier integrals up to machine precision using a triangulation of the interfacial surface S. It corresponds to an analogous method that has been developed in two dimensions (Lemma 5.4, the direct method in [35]). (Sorets [35] also describes a way to substantially decrease the computational cost compared to the direct method using Gaussian quadratures and the fast Fourier transform. As the calculation of the Fourier integrals is not time critical for our purpose (it scales with n2 if n is the number of nodes of the triangulation and is done once for a given geometry), we do not use this generally very useful idea here.)
We use the expression f(r) = f0 + ∆f χ(r) (with the indicator function χ(r) and ∆f:= f1 − f0; Section 2.2) to calculate the integral integral over the unit cell:
It is convenient to introduce lattice coordinates rL, defined by ArL = r (with the lattice matrix A), for which the unit cell transforms into the unit cube ΩL:= [0, 1]3 = A−1Ω. Note that we are not constrained to a cubic (or orthorhombic) lattice system; any crystal system is valid and equally simple to treat. The Jacobi determinant for the linear transformation into lattice coordinates is simply the volume of the original unit cell VΩ = ∫Ω d3r. The scalar product in the exponent transforms according to G · r = G · ArL = ATG · rL = 2π B−1G · rL = 2π l · rL and the Fourier transformation is given by (if f(r) is constant (f0 = f1), this equation simplifies to the trivial expression and (cf. [36])):
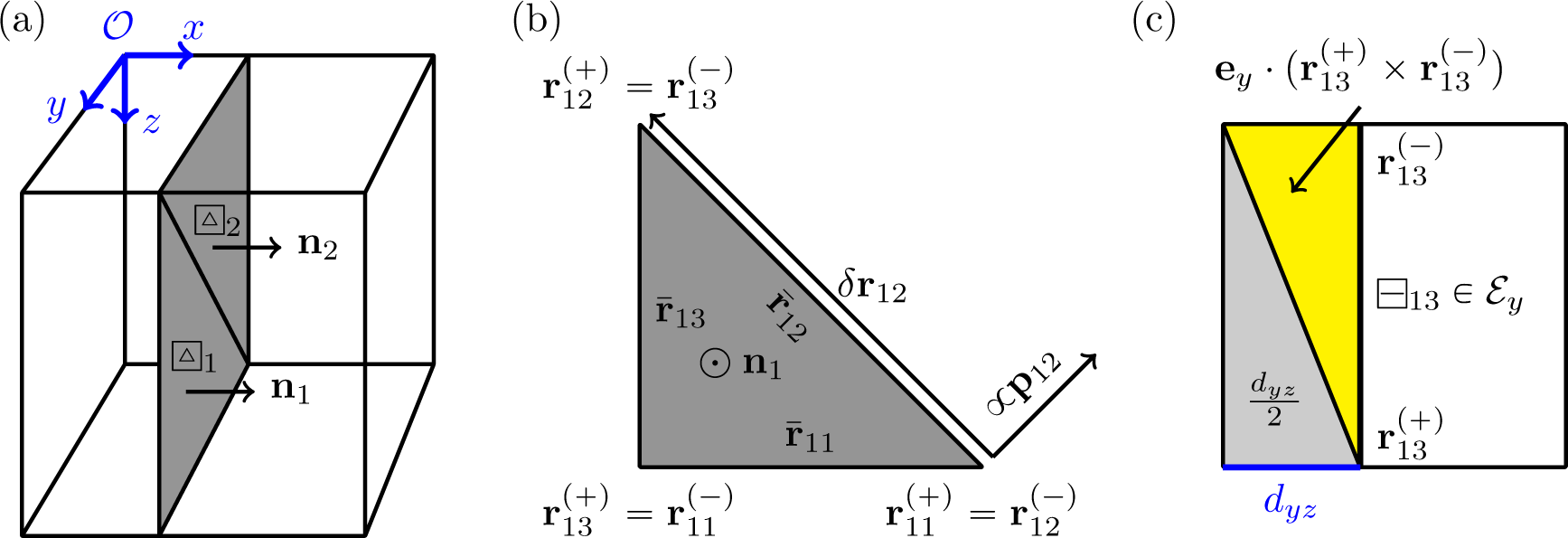
The integrals in in this equation may be solved analytically in special cases. Generally, we assume that the surface is given by a triangulation SL = {⍍τ | τ = 1, 2, …, N⍍}; see Figure 4. Recursive application of Stokes’ theorem in Euclidean and for a differential d − 1-form ω allows one to express the volume integrals as a sum over the vertices of the triangulated surface SL: In particular, we start with the divergence theorem in d = 3 that yields facet integrals and apply the divergence theorem in d = 2 onto each facet (equivalent to Green’s theorem) to obtain line integrals that are evaluated at their end points (divergence theorem in d = 1, aka the second fundamental theorem of calculus). We introduce local vectors for the triangle τ with edges ⊟τη (η = 1, 2, 3) indexed in a right rotating sense, as seen from region ; see Figure 5b:
Edge end points:
Edge centre points:
Edge end-to-end vector:
Triangle normal vector:
Triangle unit normal:
Edge normal vector:
We first calculate the volume integral for the case that l = 0 in Equation (12) as a sum over the triangles ⍍τ and the area of the planar surface that is a boundary of both the region and the j-th face of the unit cube (note that integrand vanishes for the remaining three cube faces with rj = 0). ∂Ωj corresponds to the gray surface domain in Figure 3c. The set of edges that represent part of the boundary of ∂Ωj is used in the following. Using the Stokes’ recurrence procedure described above, the volume integral over reduces to:
We now reduce Equation (12) for all other cases l ≠ 0 for which the first term vanishes trivially. The integral in the second term is in the first reduction step written as a sum over the triangles ⍍τ using the scaled lattice vector sl = l/(2πi l · l):
The vector r is split into its normal component and its tangential part for each ⍍τ; and similar for l. Following the Stokes’ reduction procedure, again distinguishing cases and , the volume integral finally reduces to:
3.2. The Discrete Problem with a Finite Number of Basis Wave Functions
The mapping from the continuous to the Bloch form is described by the action of the Bloch-Galerkin operator that produces N × N Bloch matrices according to:
Equation (11) transforms into the generalized algebraic eigenvalue equation:
We solve Equation (18) with an Arnoldi algorithm [38] for modes with the Ne largest eigenvalues and, hence, smallest |kz|. (To the best of our knowledge, Arnoldi is still one of the fastest iterative eigensolvers for non-Hermitian operators.) Note that the described formalism apparently yields duplicate modes (v‖)N, with eigenvalues kz + G⊥ (with G⊥ denoting all distinct linear combinations of ai · ez) that are all equivalent, if Ne is large enough. Duplicate modes therefore need to be identified (by their eigenvalue) and removed from the solution space basis to obtain a non-singular scattering problem; Section 4.
As the modes with the smallest eigenvalues of kz are the ones that are physically most relevant, an inversion of the Schur complement is necessary to use the Arnoldi algorithm efficiently. Therefore, at least in the straightforward implementation described here, it is necessary to store the full matrix. The computational cost (LU-factorization and matrix-vector multiplication) and the storage demand hence both scale with N2, where the latter defines a practical hard limit for any machine: e.g., 6 GB of memory are necessary for N = 5000 plane waves to store S alone (assuming complex double entries that use 16 B each); while, in practice, including the factorization is 3–4-times as much.
Any similar algorithm solving Equation (18) is therefore limited to very small discretization sizes. However, the exact spatial representation for each of the plane wave components and flexibility in the cut-off enable us to obtain reasonable convergence (below one percent for N ≈ 1000), as demonstrated in the next section.
Well-established plane wave methods (like MPB) that compute the ordinary band structure k0(k) for a real valued wave vector and a dielectric PhC do not suffer from the same intricacy, as direct matrix inversion can be avoided and the operator (in the magnetic wave equation) is Hermitian. Therefore, a fast Fourier transform in combination with the diagonal material matrices in real space and derivative matrices in reciprocal space can be used that has a smaller computational cost proportional to N log(N) and, more importantly, memory usage that only scales with N [17].
The approach described in Section 3.1 has two important advantages compared to discrete Fourier transformations for a small number of plane waves N that include:
Precise geometrical representation: The Fourier coefficients for the material constants are calculated to machine precision compared to N´−1 precision for the fast Fourier transformation [35].
Flexible cut-off: We use a spherical cut-off, including the plane waves corresponding to the N smallest G vectors. This choice is neither isotropic nor unique for most N. However, it is motivated by the trivial solution for constant material functions, where the magnitude of kz is directly correlated to the magnitude of G. Large G plane wave contributions scale in particular in first order perturbation theory with 1/|G|. In that sense, the spherical cut-off is better suited than the three-dimensional fast Fourier cut-off, which is always rectangular [39]. This helps to use a fixed small N more efficiently. In order to discretize the ball with radius RN in reciprocal space that contains N plane waves, the fast Fourier method requires the evaluation of modes inside a parallelepiped encompassing this ball. Modes that are in the parallelepiped, but not in the ball, do not enhance the precision, but slow down computations. For the simple, face-centered and body-centered cubic lattice systems 1.9, 3.8 and 7.6, as many points are thus necessary to obtain the same precision in the limit N → ∞. For finite N, the ratios are even larger. As an example, consider 1000 plane waves in the spherical cut-off. The number of plane waves that need to be taken into account for the parallelepiped cut-off to obtain the same precision is at least 2197, 4096 and 8000 for the three cubic lattice systems.
We show in Section 5 that the above advantages lead to substantially improved accuracy of the eigenvalues for small N ≲ 5000.
4. Scattering Problem
In this section, we solve the scattering problem where a semi-infinite or a finite slab of PhC material is illuminated by a plane wave, using the solutions of Equation (11). We first construct the correct solution from the countably infinite number of modes in all domains in Section 4.1 and then describe the procedure to numerically calculate the reflection and transmission rates in Section 4.2.
4.1. Exact Solution
We look for the unique solution of Equation (5) for an empty half-space (referred to as the air domain with and ζ = 0) and the other half given by the PhC structure with one plane wave source at z = −8 and no external sources elsewhere, similar to the situation illustrated in Figure 2. A general solution in the air domain is given by any superposition of all plane waves:
The complete solution in the whole space is hence laterally Bloch-periodic (cf. Section 2.3) with the wave vector fixed by the plane wave source above:
Equation (20) selects all possible states for the actual scattering problem from the general solution for the left half space provided by Equation (19):
Equation (11) for the right half space yielding solutions vλ(r) with corresponding eigenvalue forms a complete solution basis in the PhC domain that is conformal with the lateral periodicity. A general solution for the semi-infinite scattering problem is thus given by:
The Maxwell boundary conditions at the interface are:
The PhC termination at z0 yields an infinite set of non-homogeneous equations:
Maxwell’s Equation (5) is therefore solved in both half-spaces and at the boundary if the mode coefficients are such that Equation (25) is satisfied for any Bragg order.
Scattering at a finite slab is done in the same way, except that in that case, the Bloch mode sum iterates over all , and there is a second set of homogeneous equations similar to Equation (25) for the right interface that involves the transmission amplitudes , whereas the Bloch mode amplitudes play the role of transfer amplitudes τλ in both sets of equations.
4.2. Algebraic Solution with a Numerical Cut-off
Equation (25) can be solved for both σ0 numerically for the finite number of Bragg orders Nb with the smallest |G‖| and using the 2Nb linear independent Bloch modes with the smallest |kz| to obtain the 2Nb reflection amplitudes and the 2Nb transmission amplitudes tλ. (For the same reason given for the Fourier cut-off in Section 3.2, the absolute value of kz is correlated to the Bragg order and justifies the chosen cut-offs.) As the scattering part is, in terms of computational cost, negligible compared to the calculation of the PhC eigenmodes, we here calculate the full scattering matrix that handles incoming plane waves in different Bragg orders (if existing) and from both sides of a finite slab.
The interfacial scattering matrices are obtained in the following, where the input port is referred to as left and the output as right. The modes on the left of the interface are labelled by 1 and the modes on the right by 2. Further, the modes that are propagating or increase their energy towards the right or left are labelled + or −, respectively. The four types of mode coefficient vectors of length 2Nb are then given by , and the corresponding scattering matrix is:
The four matrix sub-blocks can be interpreted as left reflection S11, right reflection S22, transmission from left to right S21 and transmission from right to left S12 (cf. Figure 4 in [12]).
These coefficient vectors are multiplied from the left by the field matrices to satisfy the Maxwell boundary conditions; Equation (24). For each Bragg order i, we define the orthonormal planar basis and with the surface normal nint of the interface between air and PhC. Using this basis, the entries of the vacuum field matrices can be expressed by:
For a semi-infinite slab, the reflection and transmission amplitude vectors are obtained by multiplication of the left interface scattering matrix with the coefficient vector of the incoming plane wave, i.e., the vector with all of the 4Nb entries vanishing, except for the zero Bragg order in :
The scattering matrix for a finite slab is obtained by the Redheffer star product (Equation (22) in [12]) between both interfacial scattering matrices (no phase matrix as in the generalized Airy formulae [41] are necessary due to the global choice of origin for Sl and Sr.):
As for the semi-infinite slab, reflection and transmission amplitude vectors are given by the product of the scattering matrix with the coefficient vector of the incoming plane wave:
5. Specific PhC Geometries
The convergence characteristics of our method are demonstrated by two numerical examples: a Bragg mirror for which the analytical solution is known, and an inverse (complement) simple cubic sphere packing. The convergence rate is generally only linear, limited by the Gibbs phenomenon. However, coupling to an incident plane wave, which is of theoretical interest and naturally performed in the Fourier basis projected onto the surface, suffers from the same phenomenon, even if the eigenstates are exactly known as for a slice in the lamellar grating [10].
As an application, we also calculate the complex band structure of a non-chiral simple cubic truncated octahedron (cf. Figure 4) made of a material with intrinsic chirality and the chiral body-centered cubic gyroid structure (see, for example, [5,15]). The results are analysed in detail for both geometries.
5.1. Convergence Behaviour
The convergence behaviour is quantified by the absolute value of the relative difference between the eigenvalue for a discretization of N plane waves and the analytical solution , i.e., . The convergence rate is said to be of order o if limN→∞ δkz(N)∝N−o/d (note the factor 1/d in the exponent that stems from the spatial dimension d of the problem); it is called linear, quadratic and cubic if o = 1, 2, 3, respectively.
A one-dimensional PhC with a unit cell and the two material domains and Ω1 = Ω\Ω0 is referred to as a Bragg mirror [2]. The analytical solution can be found either by separation of variables [10] of the Bloch mode equation or by interface matching of the single domain solutions using the Bloch boundary condition [42]. There are four solutions for a given angle of incidence and frequency with the eigenvalue of the form where both A and B are functions of the frequency, the parallel wave vector and the structure parameters (di, εi, μi, ζi) [42].
We use the analytical solution for to quantify the convergence behaviour of our method for a Bragg mirror; Figure 6. The wave number kz converges with cubic order in the case of normal incidence (Figure 6A) and linearly otherwise (Figure 6B). This discrepancy can be explained by the Gibbs phenomenon [16]: all field components of the eigenmodes are continuous and continuously differentiable in the first case, while the z component of both the E and the H field are discontinuous in the second case, yielding, respectively, cubic and linear convergence behaviour for our method that is based on a global Fourier expansion of the fields.
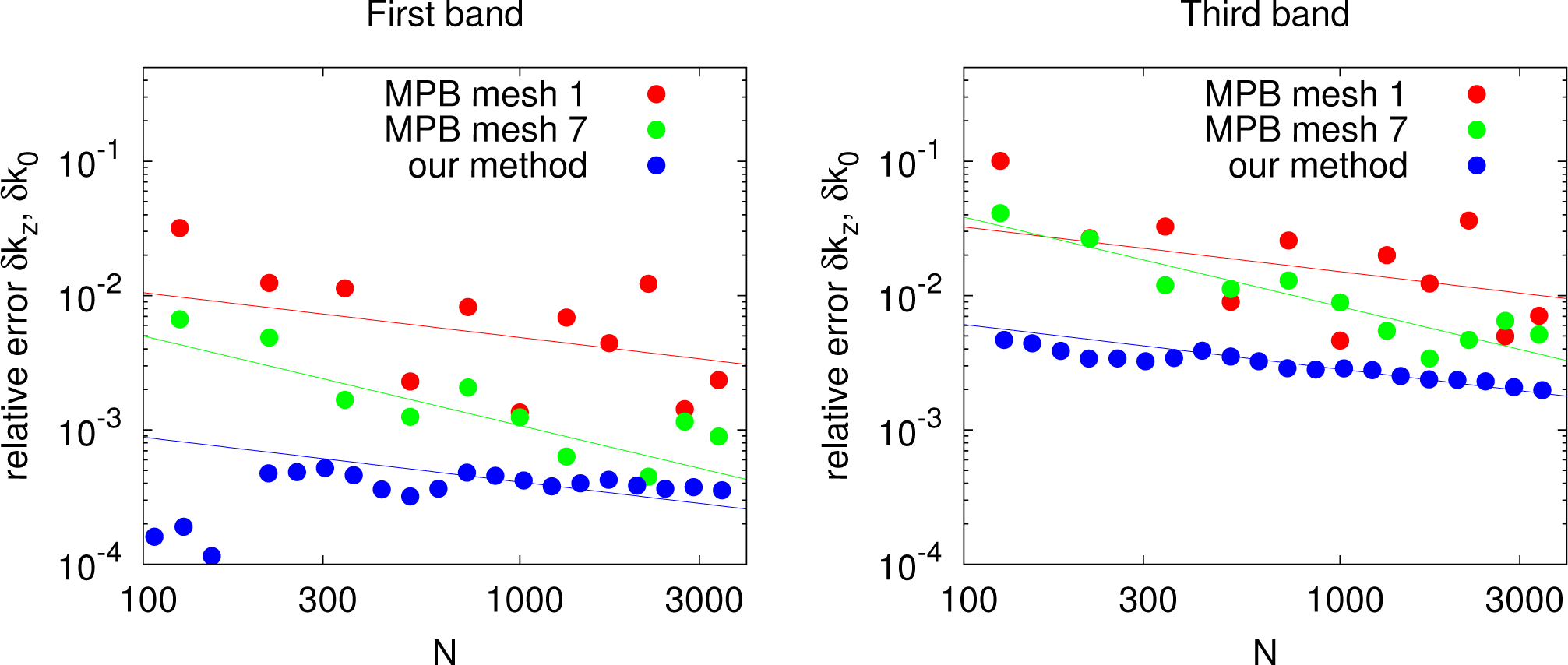
We also investigate the convergence behaviour for a more realistic three-dimensional example of air spheres of radius 0.3a in a dielectric matrix with ε = 12. In this case, we compare our results with those of MPB (Figure 7), as an analytic reference solution is not available. We first calculate the eigenfrequencies for the wave vector ka/(2π) = (0, 0, 0.2)T using MPB with a high resolution of 128 (i.e., N = 1283 ≈ 2 × 106) and a sub-pixel mesh of seven [17] for averaging the dielectric constant at the interfaces. The resulting frequencies for the first and the third band are then used to set k0 for our algorithm, and the relative error of kz is calculated with respect to . We compare the relative error of our results to MPB results for the same discretization range and a relative error calculated with respect to the N = 1283 solution.
Note that this comparison serves solely the purpose to show that the triangulated exact Fourier transformation is superior to the fast Fourier transformation if the eigenvalues kz(k0, k‖), rather than k0pkq, are needed, and hence, a full matrix representation of the material constants is necessary. If this is not the case, the standard procedure [17] without full matrix storage is much better suited and allows system sizes that are ≈ 3 orders of magnitude larger. Figure 7 shows that the numerical error of our method is below 1%, even for very small discretization sizes N ≈ 100 and below the results obtained with MPB in the range of interest. The expected convergence rates, linear in our case and for MPB without averaging, quadratic for MPB with averaging, fit the data well. The coefficient largely depends on the quality of geometrical representation that is approximated with linear (quadratic) accuracy in the case of MPB and with negligible error in our case and on the field intensities of the respective mode near the surface where the plane wave expansion produces a large deviation (linear rate without averaging) from the true solution.
5.2. Truncated Octahedron
As a three-dimensional test case with a non-chiral geometry, we use a simple cubic crystal that is generated from a dual lattice of truncated octahedra (cf. Figure 4), with the interface closely related to the Kelvin foam [44]. This geometry is of symmetry (as in a CsCl crystal) and is topologically equivalent to the triply-periodic minimal surface structure [45] in which the two spatial domains are separated by the oriented Schwarz Psurface [46].
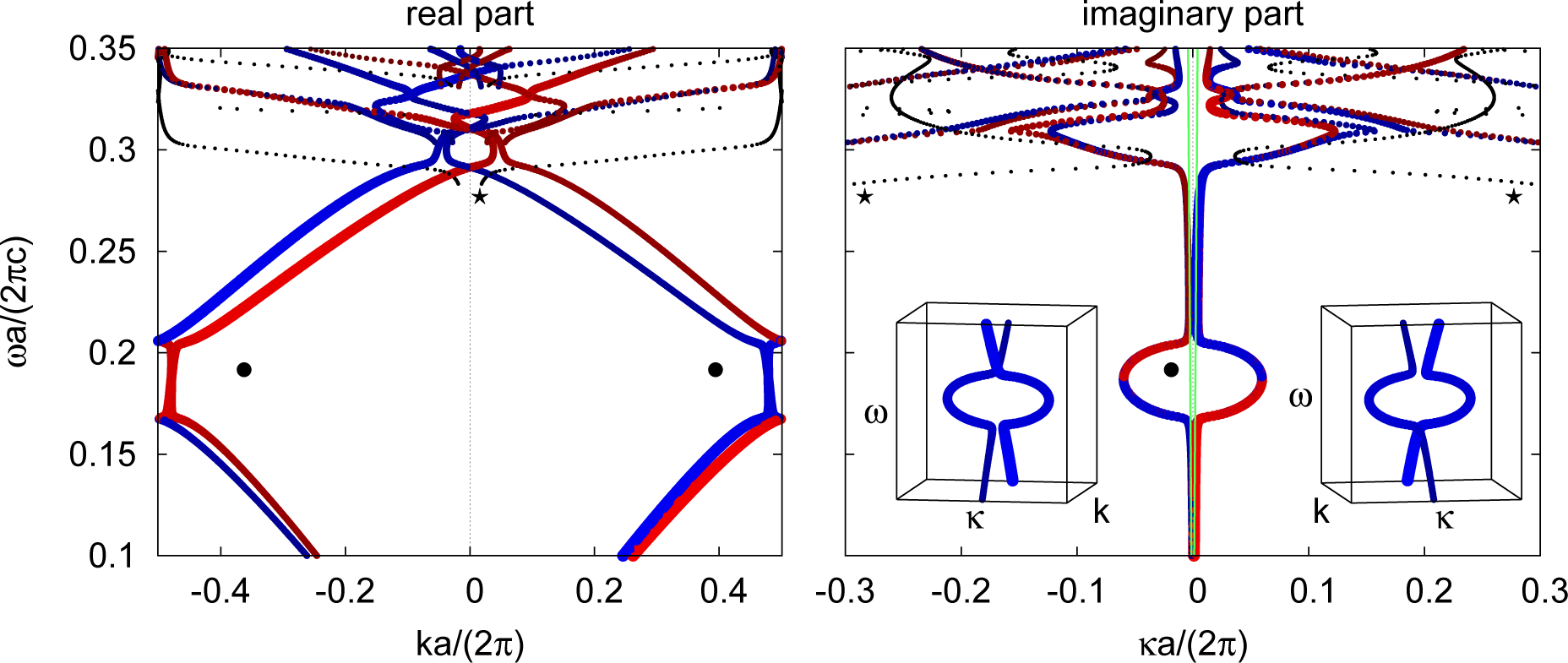
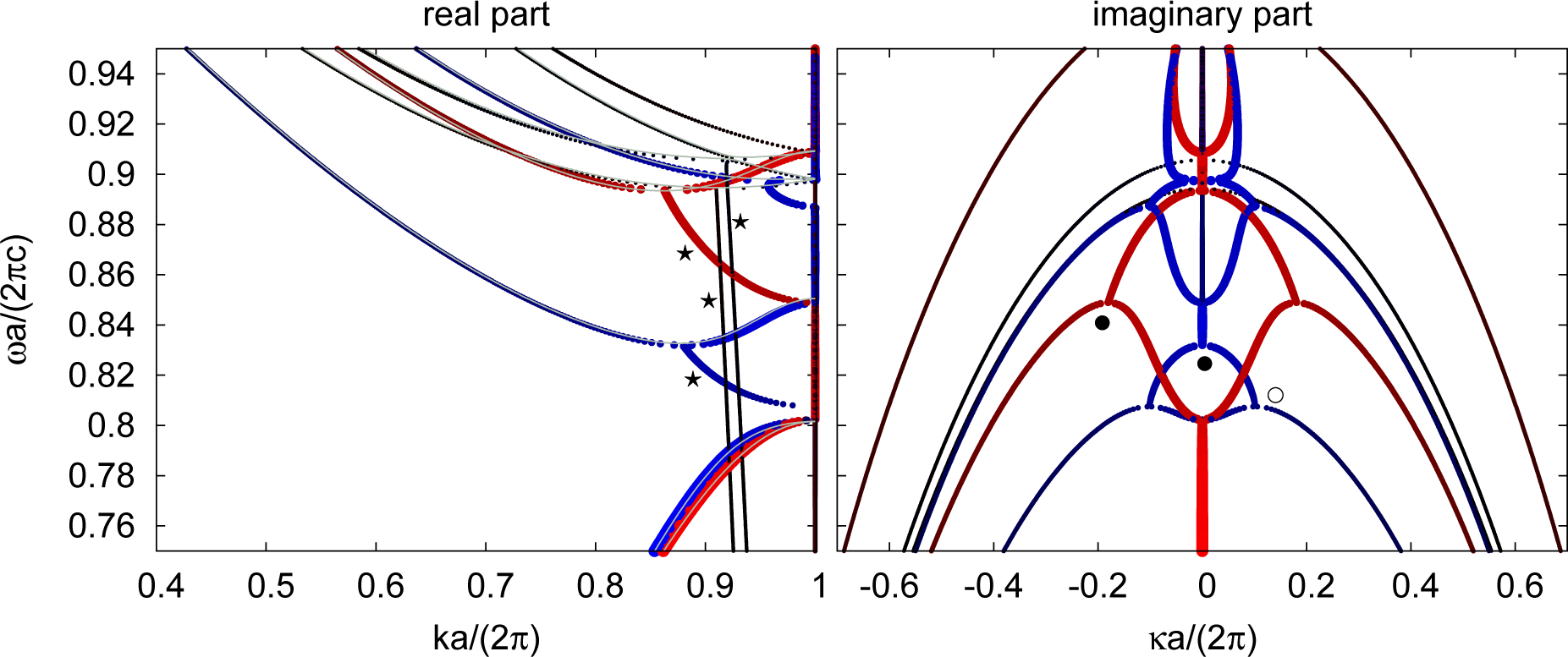
In the actual PhC under investigation, one of the two domains of this structure is left empty (air) and the other made of an artificial material that we call rotion (The name is motivated by the property that the semi-major axisof the polarization ellipse of a plane wave travelling through the bulk material is rotated due to finite coupling constant ζ. We introduce rotion with the frequency independent coupling constant only to demonstrate the validity of our algorithm. For a physical material, the rotation length is expected to be in first order relative to the wave length and, hence, ζ∝ω [29].) with permittivity ε = 12 + 0.1ı close to silicon, permeability μ = 1.5 and intrinsic chirality corresponding to ζ = 0.2ı. For this PhC, Figure 8 shows the reduced frequency plotted over the real part (the propagation constant k, left) and the imaginary part (the decay rate κ, right) of the reduced wave number in the [100] surface inclination direction. This kind of plot is referred to as a complex band structure (CBS) diagram in the following.
In the band structure plots shown here, the different colors and point sizes (referred to as the mode profile) represent, respectively, the circular polarization index and the coupling index. The color bar ranges from blue (LCP-philic, where LCP is the abbreviation of left circularly polarized) over black (no preferred polarization) to red (RCP-philic, where RCP is the abbreviation of right circularly polarized); modes with small points show weak coupling to a plane wave compared to those with a larger point size. A more formal definition is given in [5,18]; the actual color and size code is the same as is in Figure 4 in [18].
While the mode profile clearly indicates that the material corresponding to Figure 8 is indeed chiral, the color scheme mainly serves here as a guide to the eye to identify corresponding points on the left and right part of the CBS diagrams. As both diagrams can only be read simultaneously, we do not show the propagation constant of a mode whose decay rate is outside of the range of the right ordinate and vice versa; see, for example, the two bands that seem to end at ⋆ in Figure 8.
None of the Bloch modes are purely propagating with κ = 0 caused by the finite energy dissipation within the rotion material region of the PhC. The green lines in Figure 8 represent the modes in a homogeneous slab of rotion, where k0 = ±(2n±/Im{ε})κ with the refractive index is a good approximation [31]. The decay rate for all PhC modes is stronger, except for the low frequency limit, where the PhC can be approximated by a homogeneous effective medium [47] with material constants between those of rotion and air. (A Bragg mirror structure yields and with . Aspnes argues for the special case of μ = 1 and ζ = 0, that any effective constant must have a value between those two extrema that are contributions of interface parts parallel and perpendicular to a field component. Evidently, an effective constant for a three-dimensional PhC cannot be described by a tensor and must instead be described by a function of the solid angle of k.)
The insets in the right half of Figure 8 show a three-dimensional plot of the LCP-philic modes in the box of dimensions 0.3 < ka/(2π) < 0.7, −0.1 < κa/(2π) < 0.1 and 0.12 < ωa/(2πc) < 0.25 from two different angles. These insets illustrate that due to finite absorption, 2 LCP-philic single bands that are at no point degenerate exist over the whole frequency range (an explanation is given in Section 5.3). For the RCP-philic case, the situation is similar, although the actual position of the bands compared to the LCP case is perturbed on the k axis. This feature cannot be seen in the regular CBS diagram, as especially in the bandgap (•), two LCP and two RCP bands are k-degenerate, while, respectively, one LCP and one RCP band are κ-degenerate.
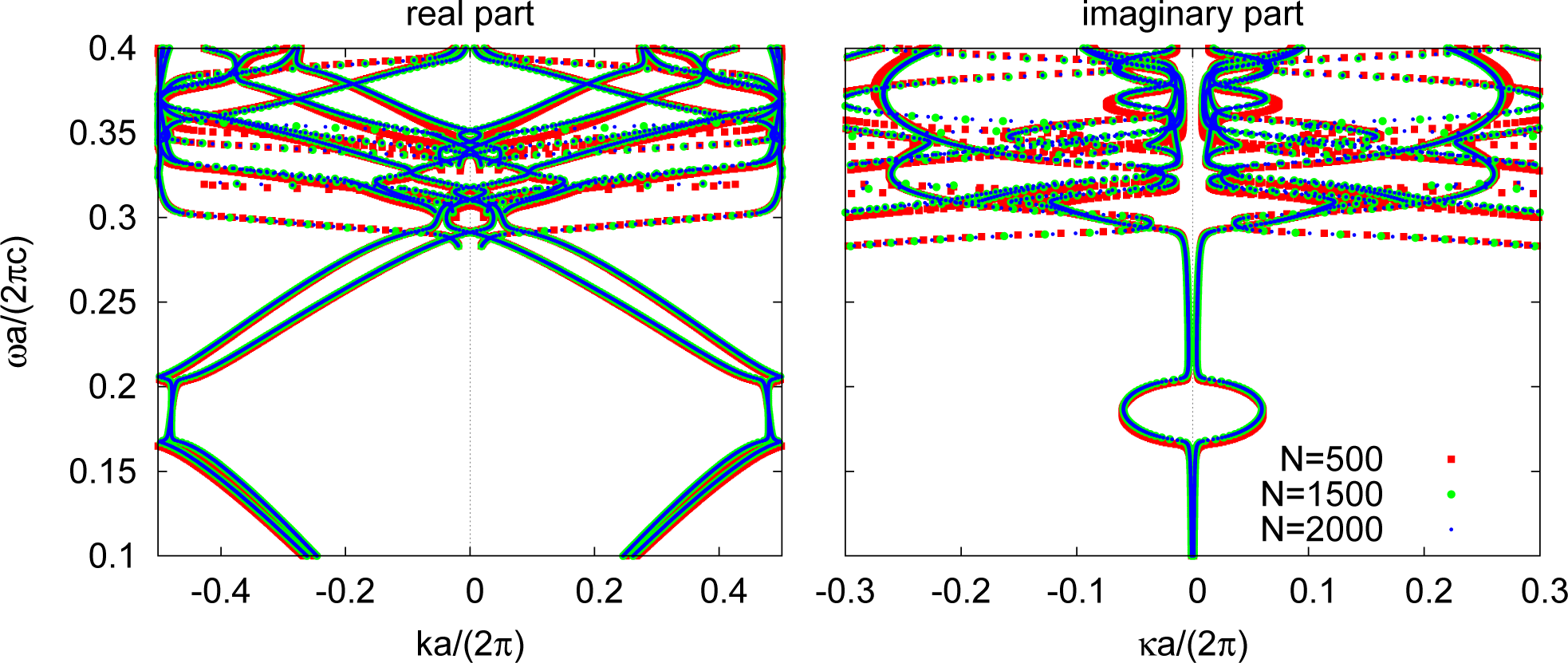
The CBS diagram without the mode profile for the same PhC is shown again in Figure 9 for three different numbers of plane waves N = 500, 1500 and 2000, to demonstrate the well-behaved convergence of the solutions of Equation (18). The k, κ values for N = 2000 lie on top of those for N = 1500, except for flat bands (∂k0/∂k ≪ 1 or ∂k0/∂κ ≪ 1), where the solution appears far from converged as a result of the frequency discretization.
5.3. Complex Band Structure of and Reflectance at the Single Gyroid PhC
The single gyroid PhC is composed of two interwoven material domains, each a single connected component with a network-like topology, that are separated by a gyroid constant mean curvature surface [22]. It is chiral, i.e., it cannot be superposed with its mirror image by rotations and translations alone, with body-centered cubic symmetry I4132. The single gyroid is found in many biological and chemical systems at several length scales [48] and, in particular, in butterfly PhCs [5,14,23,49,50].
The geometry of the PhC that is discussed in this work is defined by an interfacial surface S of a mesh of 2 × 104 triangles based on a nodal surface approximation [45] of the constant mean curvature surface given by:
This PhC serves as model for the chiral nanostructure found in the wing scales of the butterfly, Callophrys rubi [5,14,23,49,50]; see Figure 1. It exists in two enantiomeric forms, which are mirror images of each other (note that we here analyse the opposite enantiomer to the one discussed in [14], leading to identical optical behaviour when LCP and RCP are exchanged).
5.3.1. Complex Band Structure Along the Cubic [100] Direction
Figure 10 shows the CBS diagram along the cubic [100] direction. Note the four evanescent Bloch modes with finite propagation constant and decay rate at the frequency marked by the symbol ⋆. The two weak coupling modes are perturbations of the eight vacuum modes (Another two modes are found mirrored at the H point, due to time reversal symmetry. Three of the remaining four modes exhibit a fork in the decay rate diagram, the two other RCP and LCP modes marked with a ⋆ and another LCP band. The last band joins with the real band structure above ωa/(2πc) = 0.95 and is only visible in the decay rate diagram.), with G‖a/(2π) = (±1, 0, 0)T and (0, ±1, 0)T, which are equivalent to the H point at ka/(2π) = (0, 0, 1)T and for which the decay rate is determined by , forming a half-ellipse in the k = const. plane within the k, κ, ω parameter space. The elliptical a shape is closely reflected in the decay rate part of the CBS diagram in Figure 10, while the plane seems tilted around the (k, ω) = 0 axis. This evanescent band segment is continued at the minimum of the purely propagating band part above. We refer to such points where an evanescent (or mainly evanescent) band segment joins with a dispersive (or mainly dispersive) segment as a fork point.
The behaviour at fork points is, as shown below, a consequence of the holomorphic nature of the operator Θ(kz) in Equation (5) that yields holomorphic eigenvalues ωn(kz) (we call them bands) [51]. At fork points , the complex derivative ω′(kz) vanishes. As a result, the complex frequency in the vicinity of a fork point is given by its Taylor expansion:
The forking behaviour can be illustrated by the complex function cos(z) with z = x + ıy and . Consider the bands of this function that satisfy , and therefore, either sin(x) = 0 or sinh(y) = 0, describing the forked (Note that the fork points of Γ are not to be confused with the branch points in the conventional sense of complex analysis. Specifically, the function cos(z) is single-valued and, hence, does not have branch points, but shows forking. The forking results from considering a complex function , ; restricted to the subset Γ of the whole parameter space , where adopts real values, such that , path illustrated in Figure 11 in the complex plane. The resulting CBS diagram for the real part of the function cos(z) is shown in Figure 11B.
The evanescent parts of the bands labeled by ⋆ are joined to the propagating part via the forks that are described above. The same kind of forks also occur for non-vanishing decay rates (•). Note that points with ω′(kz) = 0 cease to exist with finite dissipation (the imaginary part is usually not zero any more). A fork undergoes a topological chance if dissipation is turned on, similar to the vertex disconnection operation in [52], and the situation for finite absorption is illustrated by the insets in the decay-rate part of Figure 8.
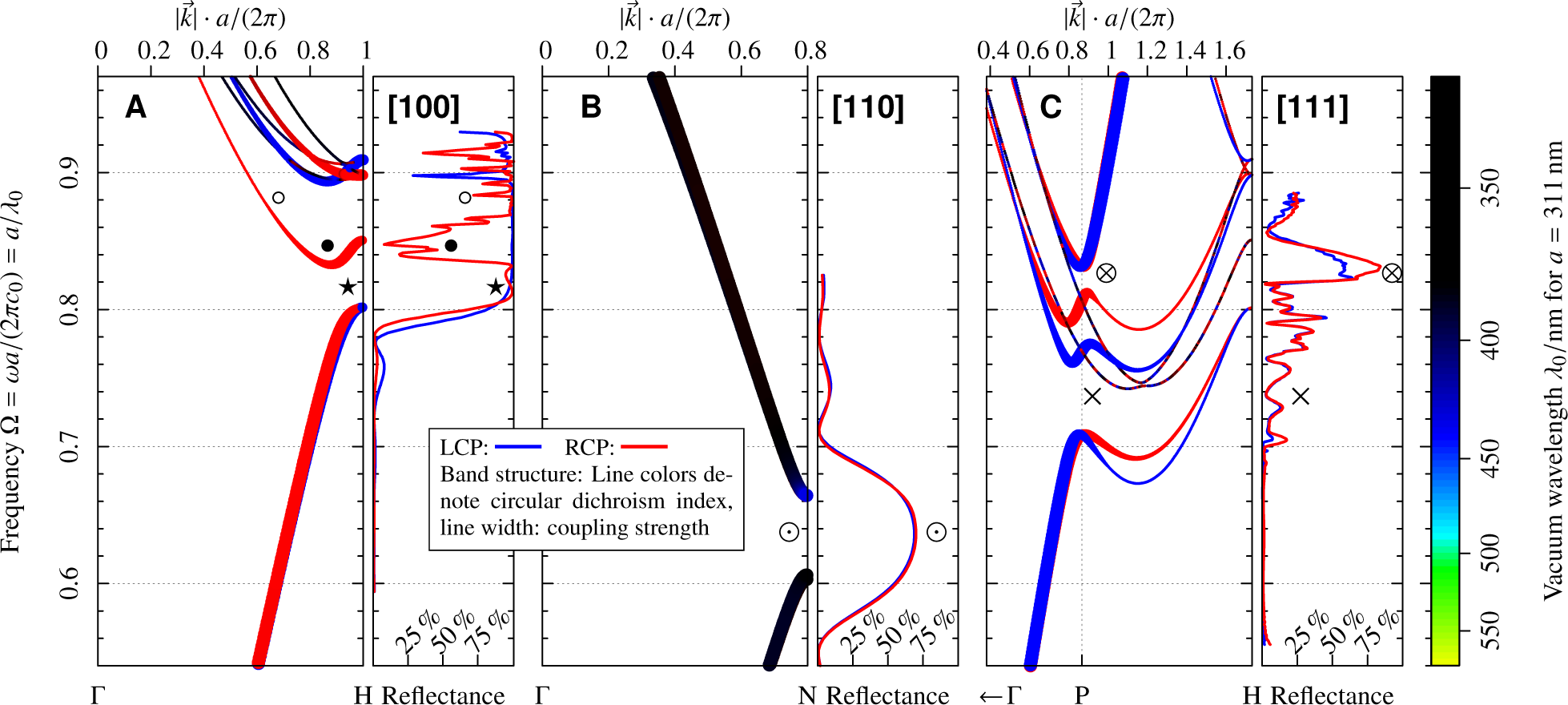
5.3.2. Scattering at a Semi-Infinite Slab with [100] Inclination
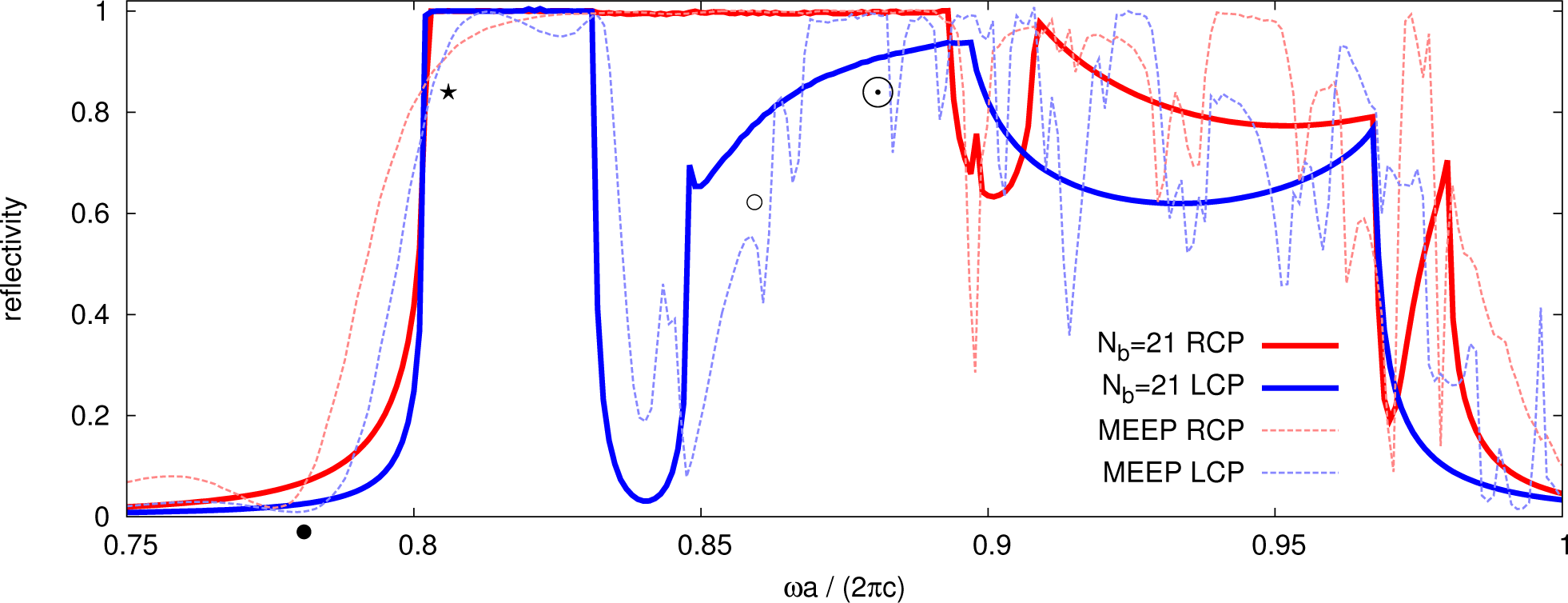
Importantly, there is a fork (○) within the indirect bandgap above the fundamental bands (0.8 < ωa/(2πc) < 0.83). The decay rate therefore increases rapidly away from the propagating band edges, compared with the ordinary oval shape of a direct bandgap in the decay rate diagram (cf. Figure 8 at •). This explains why the slope in the reflectivity at the same position is large for a moderate number of unit cells, as seen in Figure 12, at ⋆ for the weak saturated dashed curves that correspond to the result of an MEEP simulation calculating the average of the reflectance spectra of a normally incident plane wave that is scattered, respectively, at a finite slab with varying thickness around 6a inclined in [100]. The data is taken from Figure 5A in [14].
The bold solid and dashed lines in Figure 12 correspond to the reflectance spectrum at a semi-infinite slab obtained by our method for N = 1503 plane waves and Nb = 13 Bragg orders and N = 2517 plane waves and Nb = 21 Bragg orders, respectively. The number of Bragg orders corresponds to a scattering Equation (25) with 2Nb Bloch modes (including evanescent modes) and the same number of plane waves (in the air domain). All spectra are shown for RCP and LCP incident light, where we have calculated the amplitudes for s and p polarizations, as described in Section 4, and performed a basis change afterwards. The bold spectra contain reflectance in both polarization states (Polarization conversion where RCP incident light gets reflected as RCP light (and similar for LCP) is covered here. It is weaker than direct reflection within the frequency range shown here, yet not vanishing. This is generally the case for reflection at the single gyroid structure that has no pure n-fold rotation symmetry with n > 2 in the propagation direction, the presence of which would prevent conversion, as shown in [18].) in the zero Bragg order, which is equal to the full reflectance below reduced frequency ωa/(2πc) = 1, where all non-zero Bragg orders are evanescent in the air domain.
Evidently, the reflectance at the semi-infinite structure is one for frequencies where no purely propagating Bloch mode exists and no resonances of thin-film Fabry–Pérot (•) and Fano (e.g., at ○, ⊙) shape, which are found in finite slabs only, in the frequency region below the first wood anomaly (ωa/(2πc) = 1) that is shown here.
There is an instructive explanation for the sharp resonances of Fano shape given in [41] for a two-dimensional grating slab that is homogeneous in the propagation direction. The main idea can be adopted for non-homogeneous three-dimensional PhC slabs:
The Neumann series in the Redheffer star product (Equation (32)) diverges if at a complex frequency ω0 + ıγ, the product of the internal reflection matrices has an eigenvalue of one (all eigenvalues have a norm less than or equal to one, due to energy conservation, so that the series converges in any other case). A Fano resonance at frequency ω0 is close to the complex eigenfrequency ω0 + ıγ of a slab mode, aka guided mode, determined by , with a high-quality factor corresponding to γ ≪ ω0. A resonance with a symmetric (⊙) or asymmetric (○) Fano line shape results in the reflection and transmission spectra close to ω0. The same type of internal matrix singularity-induced resonance does not occur for non-diffracting structures, where no guided modes can be excited, as the internal reflections are described by scalars with magnitude smaller than one below the critical angle.
Slowly modulating thin film Fabry–Pérot resonances, on the contrary, also appear in homogeneous thin-films at all angles of incidence. In the case of a PhC, if the Fourier coefficients of all significantly involved Bloch modes only slowly modulate with frequency and if only one propagating Bloch mode acts as a transfer channel in each direction, the frequency dependence of the change of the fields due to a pass back and forth through the structure is dominated by the optical phase shift of the transfer modes . A sinusoidal modulation (compressed or stretched, depending on the slope of the bands) of the scattering parameters with frequency results.
Absorption evidently weakens the resonance effects described above (cf. Figure 7B in [14]), as it decreases the induced norm of both and and, hence, increases the speed of convergence of the corresponding Neumann series.
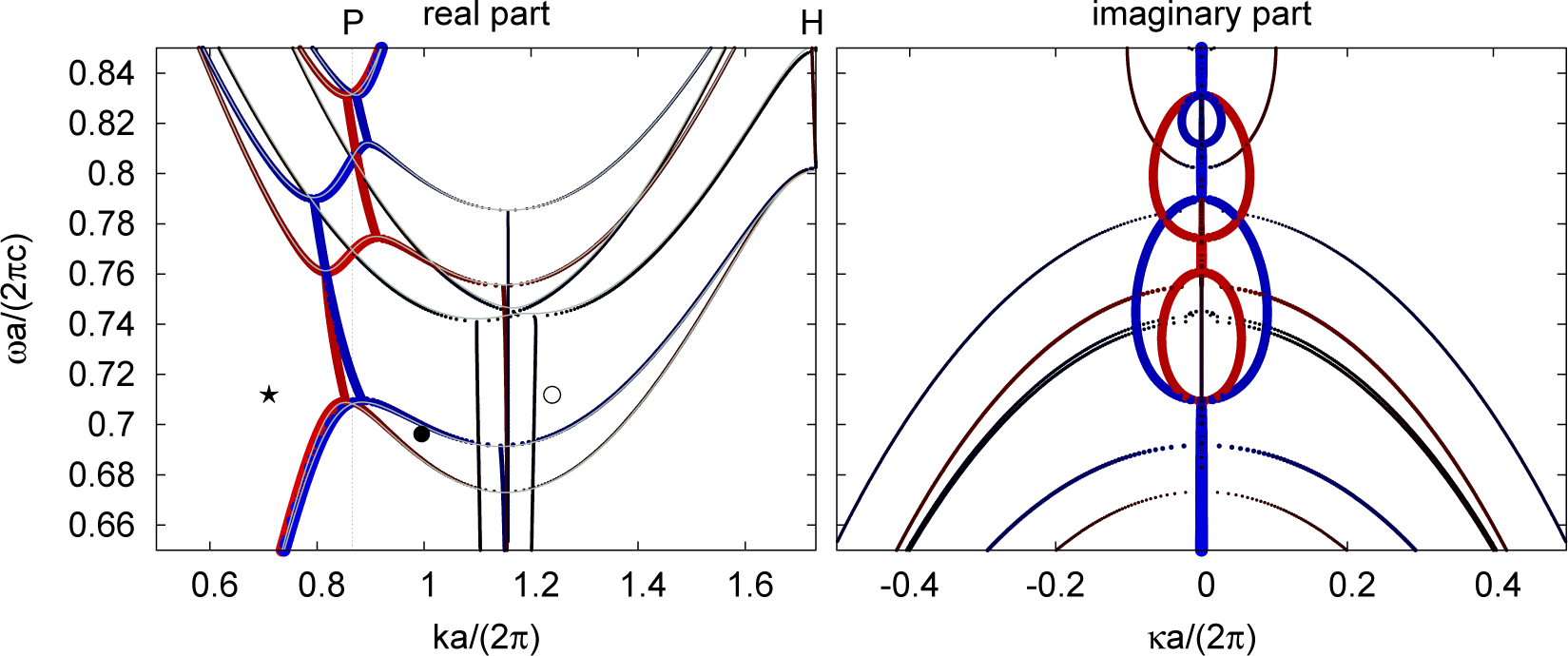
5.3.3. Complex Band Structure along the Cubic [111] Direction
Figure 13 shows the CBS diagram of the gyroid PhC along its cubic [111] direction. Note that the band structure is extended beyond the Brillouin zone edge at the P point (k = (0.5, 0.5, 0.5)T 2π/a) to the H(k = (1, 1, 1)T 2π/a ≡ (1, 0, 0)T 2π/a) point to cover all modes that are by their lateral dispersion able to couple to a wave at normal incidence.
No partial bandgap is found within the shown frequency region. The evanescent bands at ωa/(2πc) ≈ 0.73 (⋆) do not exhibit a fork within the decay rate plot and are coupling to the incident plane wave. They can henceforth act as a communication channel between the incident wave and the weakly coupling propagating bands at the same frequency (○). The presence of this communication channel explains why the reflectance rates are small in the whole frequency range despite the absence of strongly coupling and propagating bands in a broad region within this range: this region is marked with (×) in Figure 14C, which is reproduced from [14]. The absence of such a communication channel in the [100] and [110] directions explains the high reflectivity there; cf. the regions marked with (⋆) and (⊙).
6. Conclusions
The relevance of complex structures for nanofabricated or self-assembled photonic and plasmonic materials is likely to increase further. The single gyroid geometry, which epitomises a complex network-like morphology, only represents the current pinnacle of this trend, with an ever-increasing plethora of geometric candidate structures and with ever-increasing abilities to fabricate structures of almost arbitrary complexity by direct writing techniques, at smaller and smaller length scales.
While direct simulation methods, such as FDTD or FEM methods, provide the most immediately accessible data for the material properties (such as transmission, reflectance or, in the case, of chiral materials, also optical activity and circular dichroism), the photonic band structure remains an invaluable tool to gain insight into the physics behind these observations. A significant limitation in this regard is the fact that methods based on the solution of Hermitian positive-definite eigenproblems (such as the one implemented in MPB) are limited to the purely dispersive modes and cannot compute the evanescent modes. Numerical methods, such as the one developed here, to calculate the full complex band structure (including evanescent modes) are needed. Furthermore, solving the actual scattering problem requires the smallest kz(k0, k‖), rather than ω(k), yielding more numerical intricacies related to a necessary matrix inversion by an LU decomposition that requires computational time and memory.
We hope that the work of this article and of related previous work [5,14,18] will make a substantial contribution to the informed use of complex band diagrams for the interpretation of photonic properties. This contribution is three-fold:
Our method provides access to the full complex band structure, including the evanescent modes (in contrast to the method implemented in MPB). In this context, note also the previous work of [13].
Our method calculates the band structure as a function kz(k0, k‖) necessary for scattering problems. While suffering from computational cost, we have shown that reasonable convergence can be obtained by the more accurate representation of complex geometries by a mesh representation of the interfacial surface, rather than by cubic voxel representations of the solid matrix. In this context, note also the previous work on two-dimensional Fourier transforms [35].
Our method is not restricted to lossless dielectric materials, but is equally applicable to materials with arbitrary values of the complex dielectric tensor (including losses) and also those with magnetic permittivity and coupling tensor , all of which are not covered by the method implemented in MPB.
Algorithmic improvements to the method are desirable, e.g., to improve the convergence behaviour beyond a first-order method or to reduce the computational complexity of . Both points could be addressed, for example, by using a Nédélec finite element basis [54] on a three-dimensional triangulation instead of the plane wave basis used here. The method in its current implementation is, however, sufficiently fast to deal with complex photonic materials, as demonstrated in Section 5.
The example of the single gyroid geometry demonstrates both the necessity to include evanescent modes for the analysis of transmission spectra and the applicability of the methods developed here. This necessity is most evident for the [111] direction, for which the transmission spectrum cannot be rationalised by consideration of the (purely dispersive) Bloch modes alone.
Acknowledgments
Gerd E. Schröder-Turk acknowledges the hospitality and support of the Department of Applied Maths at the Australian National University in Canberra. We thank the “Engineering of Advanced Materials” cluster of excellence at the Friedrich-Alexander University Erlangen-Nuremberg for financial support. We are grateful to Johannes Hielscher for the discussion and thorough comments on the manuscript. We thank the anonymous reviewers for their very constructive criticism and for pointing us to [35].
Author Contributions
Matthias Saba developed the concept and the method described in the article, implemented its algorithmic solution, analysed and interpreted the data for the photonic crystal structures discussed here and wrote the manuscript. Gerd E. Schröder-Turk interpreted the photonic data, critically commented on the concept and method and wrote the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- John, S. Strong Localization of Photons in Certain Disordered Dielectric Superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar]
- Joannopoulos, J.; Johnson, S.; Winn, J.; Meade, R. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NY, USA, 2008. [Google Scholar]
- Karkashadze, D.; Bogdanov, F.; Zaridze, R.; Bijamov, A.; Hafner, C.; Erni, D. Simulation of Finite Photonic Crystals Made of Biisotropic or Chiral Material. In Advances in Electromagnetics of Complex Media and Metamaterials; NATO Science Series; Zouhdi, S., Sihvola, A., Arsalane, M., Eds.; Springer: Berlin, Germany, 2002; Volume 89, pp. 175–193. [Google Scholar]
- Lee, J.; Chan, C.T. Polarization gaps in spiral photonic crystals. Opt. Express 2005, 13, 8083–8088. [Google Scholar]
- Saba, M.; Thiel, M.; Turner, M.; Hyde, S.T.; Gu, M.; Große-Brauckmann, K.; Neshev, D.; Mecke, K.; Schröder-Turk, G.E. Circular Dichroism in Biomimetic Cubic Chiral Nets. Phys. Rev. Lett. 2011, 106. [Google Scholar] [CrossRef]
- Dolan, J.A.; Wilts, B.D.; Vignolini, S.; Baumberg, J.J.; Steiner, U.; Wilkinson, T.D. Optical Properties of Gyroid Structured Materials: From Photonic Crystals to Metamaterials. Adv. Opt. Mater. 2014. [Google Scholar] [CrossRef]
- Lawrence, F.J.; Botten, L.C.; Dossou, K.B.; McPhedran, R.C.; Martijn de Sterke, C. A flexible Bloch mode method for computing complex band structures and impedances of two-dimensional photonic crystals. J. Appl. Phys. 2012, 111. [Google Scholar] [CrossRef]
- Dossou, K.B.; Botten, L.C. A combined three-dimensional finite element and scattering matrix method for the analysis of plane wave diffraction by bi-periodic, multilayered structures. J. Comput. Phys. 2012, 231, 6969–6989. [Google Scholar]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1981, 71, 811–818. [Google Scholar]
- Botten, I.C.; Craig, M.S.; McPhedran, R.C.; Adams, J.L.; Andrewartha, J.R. The dielectric lamellar diffraction grating. Opt. Acta. 1981, 28, 413–428. [Google Scholar]
- Whittaker, D.M.; Culshaw, I.S. Scattering-matrix treatment of patterned multilayer photonic structures. Phys. Rev. B 1999, 60, 2610–2618. [Google Scholar]
- Rumpf, R.C. Improved formulation of scattering matrices for semi-analytical methods that is consistent with convention. Prog. Electromagn. Res. B 2011, 35, 241–261. [Google Scholar]
- Feng, C.S.; Mei, L.M.; Cai, L.Z.; Yang, X.L.; Wei, S.S.; Li, P. A plane-wave-based approach for complex photonic band structure and its applications to semi-infinite and finite system. J. Phys. D 2006, 39. [Google Scholar] [CrossRef]
- Saba, M.; Wilts, B.; Hielscher, J.; Schröder-Turk, G.E. Absence of circular polarisation in reflections of butterfly wing scales with chiral Gyroid structure. Mater. Today Proc. 2014. [Google Scholar] [CrossRef]
- Turner, M.D.; Saba, M.; Zhang, Q.; Cumming, B.P.; Schröder-Turk, G.E.; Gu, M. Miniature chiral beamsplitter based on gyroid photonic crystals. Nat. Photon. 2013, 7, 801–805. [Google Scholar]
- Hamming, R.W. Numerical Methods for Scientists and Engineers; Dover: New York, NY, USA, 1986. [Google Scholar]
- Johnson, S.G.; Joannopoulos, J.D. Block-iterative frequency-domain methods for Maxwell’s equations in a planewave basis. Opt. Express 2001, 8, 173–190. [Google Scholar]
- Saba, M.; Turner, M.D.; Mecke, K.; Gu, M.; Schröder-Turk, G.E. Group theory of circular-polarization effects in chiral photonic crystals with four-fold rotation axes applied to the eight-fold intergrowth of gyroid nets. Phys. Rev. B 2013, 88. [Google Scholar] [CrossRef]
- Cangellaris, A.; Wright, D. Analysis of the numerical error caused by the stair-stepped approximation of a conducting boundary in FDTD simulations of electromagnetic phenomena. IEEE Trans. Antennas Propag. 1991, 39, 1518–1525. [Google Scholar]
- Farjadpour, A.; Roundy, D.; Rodriguez, A.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G.; Burr, G.W. Improving accuracy by subpixel smoothing in the finite-difference time domain. Opt. Lett. 2006, 31, 2972–2974. [Google Scholar]
- Schoen, A.H. Infinite Periodic Minimal Surfaces without Self-Intersections; Technical Note TN D-5541; NASA: Washington, DC, USA, 1970. [Google Scholar]
- Große-Brauckmann, K. Gyroids of constant mean curvature. Exp. Math. 1997, 6, 33–50. [Google Scholar]
- Michielsen, K.; Stavenga, D.G. Gyroid cuticular structures in butterfly wing scales: Biological photonic crystals. J. R. Soc. Interface 2008, 5, 85–94. [Google Scholar]
- Hur, K.; Francescato, Y.; Giannini, V.; Maier, S.A.; Hennig, R.G.; Wiesner, U. Three-Dimensionally Isotropic Negative Refractive Index Materials from Block Copolymer Self-Assembled Chiral Gyroid Networks. Angew. Chem. Int. Ed. 2011, 50, 11985–11989. [Google Scholar]
- Lu, L.; Fu, L.; Joannopoulos, J.D.; Soljačić, M. Weyl points and line nodes in gyroid photonic crystals. Nat. Photon. 2013, 7, 294–299. [Google Scholar]
- Vignolini, S.; Yufa, N.A.; Cunha, P.S.; Guldin, S.; Rushkin, I.; Stefik, M.; Hur, K.; Wiesner, U.; Baumberg, J.J.; Steiner, U. A 3D Optical Metamaterial Made by Self-Assembly. Adv. Mater. 2011, 24, OP23–OP27. [Google Scholar]
- Oh, S.S.; Demetriadou, A.; Wuestner, S.; Hess, O. On the Origin of Chirality in Nanoplasmonic Gyroid Metamaterials. Adv. Mater. 2012, 25, 612–617. [Google Scholar]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar]
- Condon, E.U. Theories of Optical Rotatory Power. Rev. Mod. Phys. 1937, 9, 432–457. [Google Scholar]
- Sihvola, A.H. Electromagnetic Modeling of Bi-Isotropic Media. PIER 1994, 9, 45–86. [Google Scholar]
- Jackson, J. Classical Electrodynamics; John Wiley & Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Spivak, M. Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus; Westview Press: Boulder, CO, USA, 1971. [Google Scholar]
- Boffi, D.; Fortin, M.; Brezzi, F. Mixed Finite Element Methods and Applications; Springer: Berlin, Germany, 2013. [Google Scholar]
- Dossou, K.; Fontaine, M. A high order isoparametric finite element method for the computation of waveguide modes. Comput. Methods Appl. Mech. Eng. 2005, 194, 837–858. [Google Scholar]
- Sorets, E. Fast Fourier Transforms of Piecewise Constant Functions. J. Comput. Phys. 1995, 116, 369–379. [Google Scholar]
- Schröder-Turk, G.E.; Mickel, W.; Kapfer, S.C.; Schaller, F.M.; Breidenbach, B.; Hug, D.; Mecke, K. Minkowski tensors of anisotropic spatial structure. New J. Phys. 2013, 15. [Google Scholar] [CrossRef]
- Cromwell, P.R. Polyhedra; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Lehoucq, R.B.; Sorensen, D.C.; Yang, C. ARPACK Users Guide: Solution of Large Scale Eigenvalue Problems by Implicitly Restarted Arnoldi Methods; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Rayleigh, L. On the Dynamical Theory of Gratings. Proc. R. Soc. A 1907, 79, 399–416. [Google Scholar]
- Botten, L.C.; McPhedran, R.C.; Byrne, M.A.; Asatryan, A.A.; Nicorovici, N.A.; Norton, A.H.; de Sterke, C.M. The Modelling of Fano Resonances in Photonic Crystal Slabs. Available online: http://www.opticsinfobase.org/abstract.cfm?URI=META-2006-ThD15 accessed on 2 January 2015.
- Cao, Y.; Li, J. Complete band gaps in one-dimensional photonic crystals with negative refraction arising from strong chirality. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
- Brakke, K.A. The surface evolver. Exp. Math. 1992, 1, 141–165. [Google Scholar]
- Thomson, W. On the division of space with minimum partitional area. Philos. Mag. 1887, 24, 503–514. [Google Scholar]
- Michielsen, K.; Kole, J.S. Photonic band gaps in materials with triply periodic surfaces and related tubular structures. Phys. Rev. B 2003, 68. [Google Scholar] [CrossRef]
- Schwarz, H.A. Gesammelte Mathematische Abhandlungen; Springer: Berlin, Germany, 1933; Volume 2. [Google Scholar]
- Aspnes, D.E. Local field effects and effective medium theory: A microscopic perspective. Am. J. Phys. 1982, 50, 704–709. [Google Scholar]
- Hyde, S.T.; O’Keeffe, M.; Proserpio, D.M. A short history of an elusive yet ubiquitous structure in chemistry, materials and mathematics. Angew. Chem. Int. Ed. 2008, 47, 7996–8000. [Google Scholar]
- Saranathan, V.; Osuji, C.; Mochrie, S.; Noh, H.; Narayanan, S.; Sandy, A.; Dufresne, E.; Prum, R. Structure, function, and self-assembly of single network gyroid (I4132) photonic crystals in butterfly wing scales. Proc. Natl. Acad. Sci. USA 2010, 107, 11676–11681. [Google Scholar]
- Schröder-Turk, G.; Wickham, S.; Averdunk, H.; Large, M.; Poladian, L.; Brink, F.; Fitz Gerald, J.; Hyde, S.T. The chiral structure of porous chitin within the wing-scales of. Callophrys rubi. J. Struct. Biol. 2011, 174, 290–295. [Google Scholar]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin, Germany, 1995. [Google Scholar]
- Nachtrab, S.; Kapfer, S.C.; Rietzel, D.; Drummer, D.; Madadi, M.; Arns, C.H.; Kraynik, A.M.; Schröder-Turk, G.E.; Mecke, K. Tuning Elasticity of Open-Cell Solid Foams and Bone Scaffolds via Randomized Vertex Connectivity. Adv. Eng. Mater. 2012, 14, 120–124. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College: New York, USA, 1976. [Google Scholar]
- Nédélec, J. A new family of mixed finite elements in ℝ3. Numer. Math. 1986, 50, 57–81. [Google Scholar]






© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saba, M.; Schröder-Turk, G.E. Bloch Modes and Evanescent Modes of Photonic Crystals: Weak Form Solutions Based on Accurate Interface Triangulation. Crystals 2015, 5, 14-44. https://doi.org/10.3390/cryst5010014
Saba M, Schröder-Turk GE. Bloch Modes and Evanescent Modes of Photonic Crystals: Weak Form Solutions Based on Accurate Interface Triangulation. Crystals. 2015; 5(1):14-44. https://doi.org/10.3390/cryst5010014
Chicago/Turabian StyleSaba, Matthias, and Gerd E. Schröder-Turk. 2015. "Bloch Modes and Evanescent Modes of Photonic Crystals: Weak Form Solutions Based on Accurate Interface Triangulation" Crystals 5, no. 1: 14-44. https://doi.org/10.3390/cryst5010014
APA StyleSaba, M., & Schröder-Turk, G. E. (2015). Bloch Modes and Evanescent Modes of Photonic Crystals: Weak Form Solutions Based on Accurate Interface Triangulation. Crystals, 5(1), 14-44. https://doi.org/10.3390/cryst5010014




